Successive Interference Cancellation Based Throughput Optimization for Multi-Hop Wireless Rechargeable Sensor Networks †
Abstract
1. Introduction
- We formulate constraints on the network and the energy consumption model, and we meet the SIC constraints under a different power of the multi-hop WRSNs.
- Based on this energy consumption model, we construct an optimization model in which the optimization objective is to maximize the vacation time percentage of the mobile charger (MC).
- We reformulate the original problem into a linear problem with only one quadratic term, and we finally calculate a feasible near-optimal solution to the original problem within the level of error setting in advance.
2. Problem Description
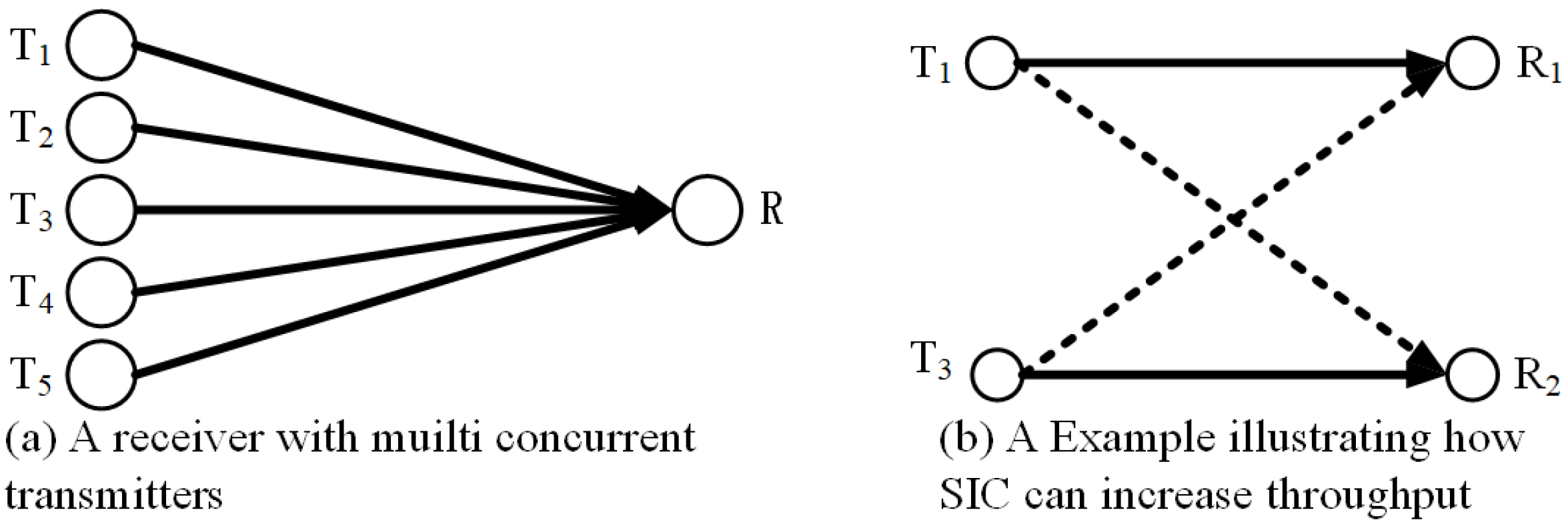
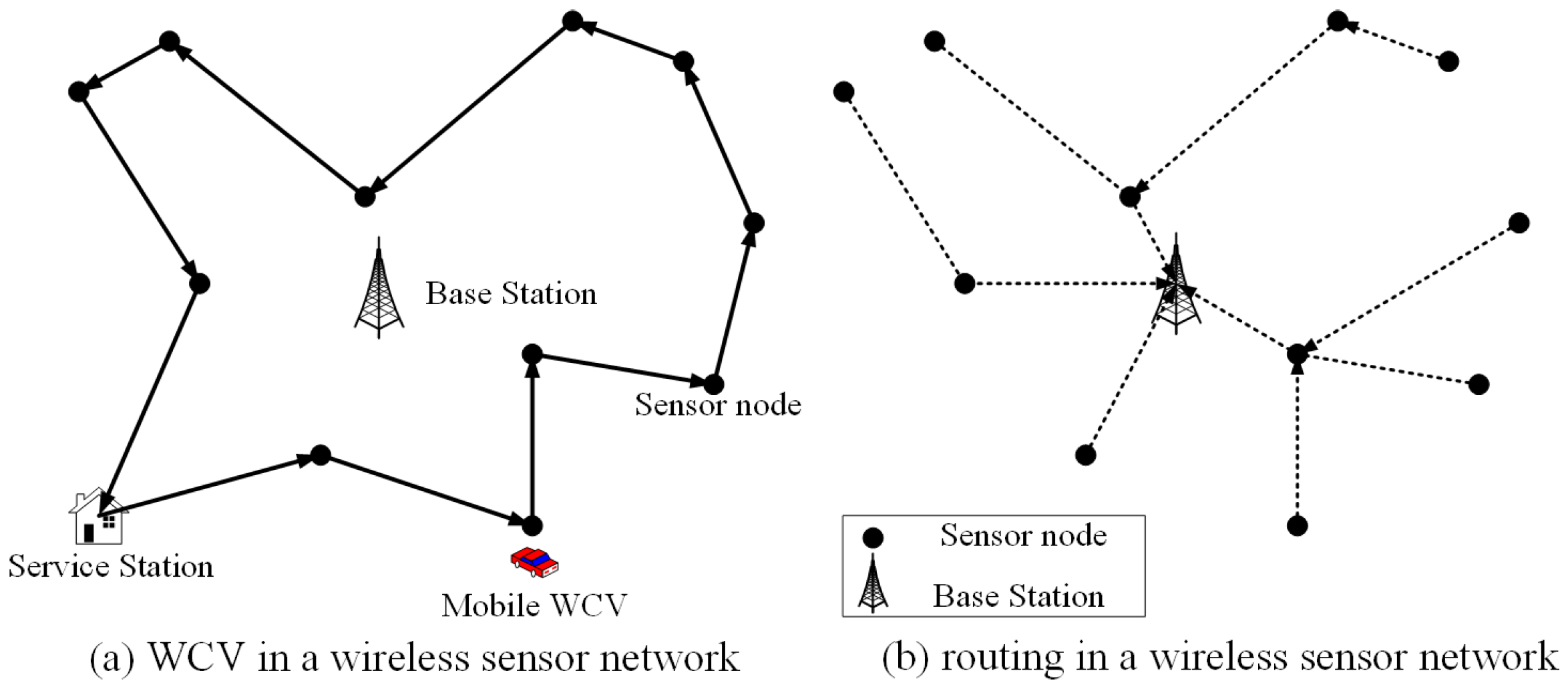
2.1. Multi-Hop Network Scenario with SIC
2.2. Sensor Power Supply Model
3. The Mathematical Model for SIC Multi-Hop Wireless Networks
3.1. The Mathematical Model for SIC Multi-Hop Wireless Networks
3.2. Optimization for SIC Multi-Hop Wireless Networks
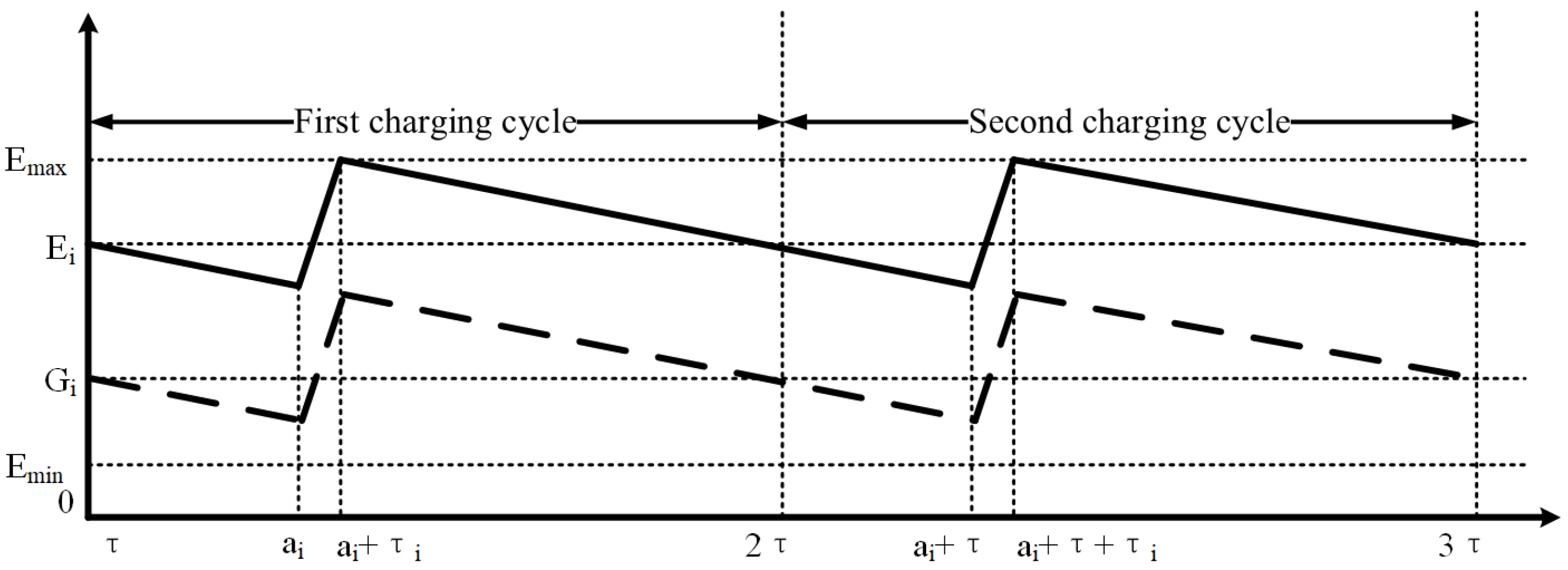
4. The Mathematical Model for Recharging Cycle
4.1. Rechargeable Energy Cycle Construction
4.2. Mathematical Formulation
| max | ||
| s.t. | ; | |
| Half duplex constraint: (1), (2); | ||
| Recharging cycle constraint: (8); | ||
| Flow balance constraints: (5); | ||
| Energy constraints: (6), (10), (11); | ||
| Variables: | ||
| Constants: |
4.3. Reformulation
| max | ||
| s.t. | Flow balance constraints: (5) | |
| Vaction constraints: (15); | ||
| Energy balance constraints: (16); | ||
| variables | ||
| constants |
4.4. A Near-Optimal Solution
| max | ||
| s.t. | (10), (28), (21)∼(27) | |
| Variables: | ||
| Constants: |
4.5. Proof of Near-Optimality
- Preset a feasible target error .
- Set .
- Calculate the relaxed linear optimization problem with m linear segment and gain its solution through the solver Gurobi.
- Construct a feasible solution for the linear fitted problem by setting and = {1 - - }
- Gain a feasible near-optimal solution () to the original optimization problem .
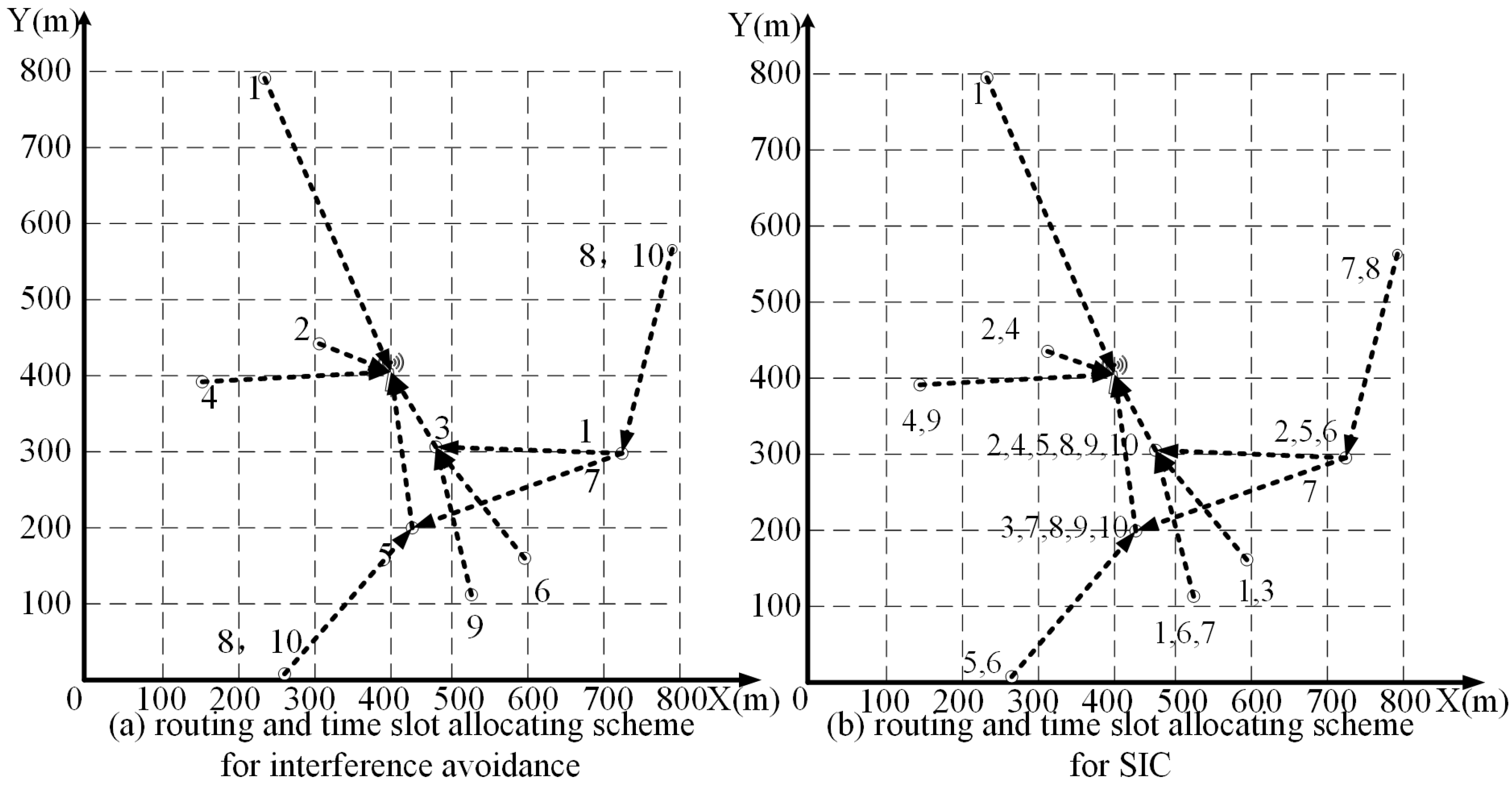
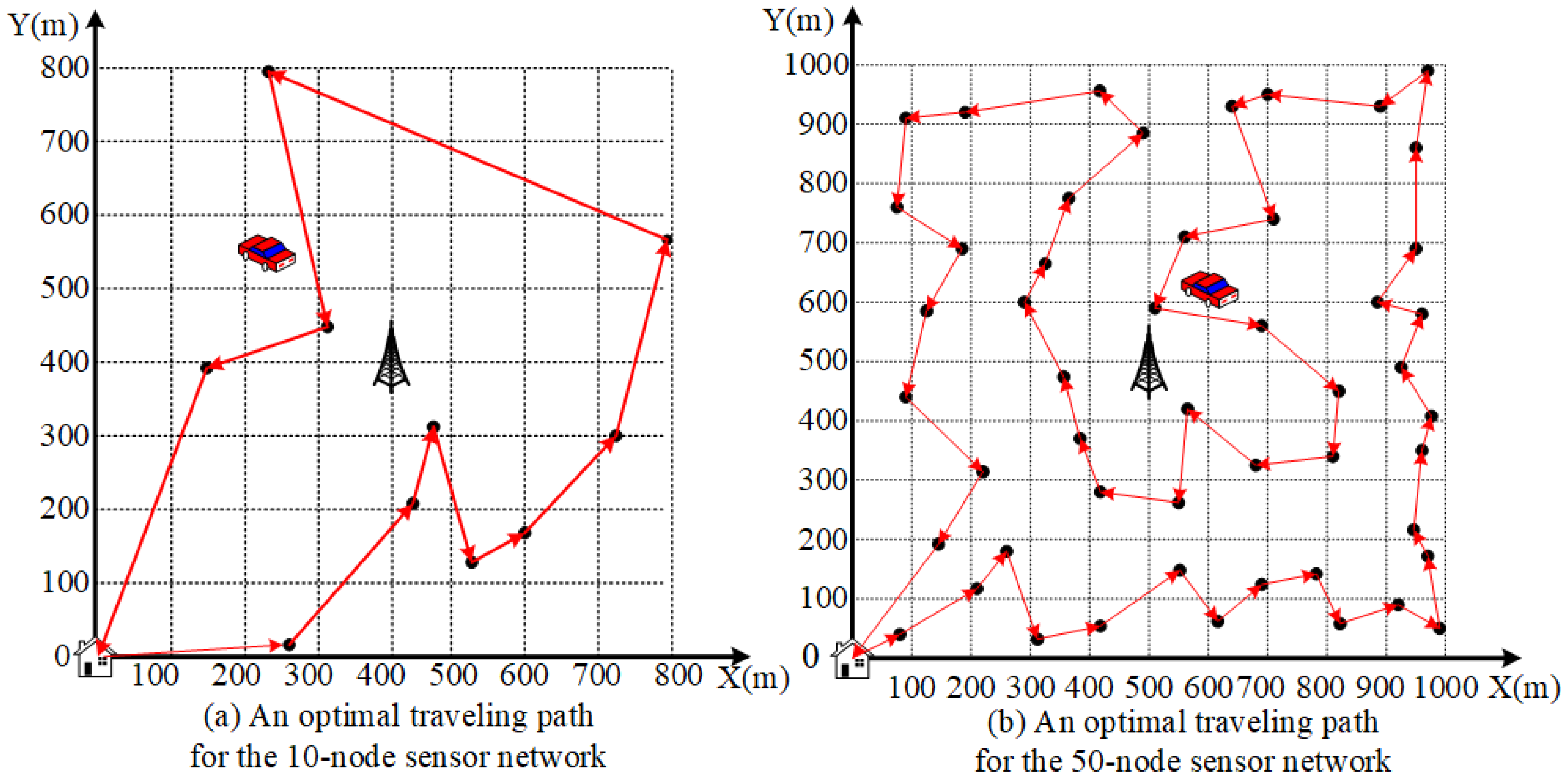
5. Simulation
5.1. Simulation Setting
5.2. Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Antonio, P.; Grimaccia, F.; Mussetta, M. Architecture and methods for innovative heterogeneous wireless sensor network applications. Remote Sens. 2012, 4, 1146–1161. [Google Scholar] [CrossRef]
- Yu, L.; Wang, N.; Meng, X. Real-Time forest fire detection withwireless sensor networks. In Proceedings of the 2005 International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 26 September 2005; pp. 1214–1217. [Google Scholar]
- Liu, M.; Gong, G.H.; Wen, Y.G.; Chen, G.H.; Cao, J.N. The last minute: Efficient data evacuation strategy for sensor networks in postdisaster applications. In Proceedings of the IEEE Conference on Computer Communications, Shanghai, China, 10–15 April 2011; pp. 1–5. [Google Scholar]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A surveyon environmental monitoring. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Kim, S.; Pakzad, S.; Culler, D.; Demmel, J.; Fenves, G.; Glaser, S.; Turon, M. Health monitoring of civil infrastructures using wireless sensor networks. Inf. Process. Sens. Netw. 2007, 365, 254–263. [Google Scholar]
- Meninger, S.; Mur-Miranda, J.O.; Amiranda, R.; Amirtharajah, R.; Chandrakasan, A. Vibration-to-electric energy conversion. IEEE Trans. Very Large Scale Integr. Syst. 2001, 9, 64–76. [Google Scholar] [CrossRef]
- Arunraja, M.; Malathi, V.; Sakthivel, E. Energy conservation in WSN through multilevel data reduction scheme. Microprocess. Microsyst. 2015, 39, 348–357. [Google Scholar] [CrossRef]
- Prak, C.; Chou, P.H. Ambimax: Autonomous energy harvesting platform for multi-supply wireless sensor nodes. IEEE Commun. Mag. 2007, 1, 168–177. [Google Scholar]
- Ren, X.; Liang, W.; Xu, W. Data collection maximization in renewable sensor networks via time-slot scheduling. IEEE Commun. Comput. 2015, 64, 168–177. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled mangentuc resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, X.; Hackworth, S.A.; Sclabassi, R.J.; Sun, M. In vitro and vivo studies on wireless powerung of medical sensors and implantable devices. In Proceedings of the IEEE/NIH Life Science Systems and Applications Workshop (LiSSA), Bethesda, MD, USA, 9–10 April 2009; pp. 84–87. [Google Scholar]
- Noura, M.; Nordin, R. A survey on interference management for device-to-deviceF(D2D) communication and its challenges in 5G networks. J. Netw. Comput. Appl. 2016, 71, 130–150. [Google Scholar] [CrossRef]
- Weber, S.P.; Andrews, J.G.; Yang, X.; Veciana, G.D. Transmission capacity of wireless ad hoc networks with successive interference cancellation. IEEE Trans. Inf. Theory 2007, 51, 2799–2814. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, S.; Li, H.; Zhao, N.; Leung, V.C.M. Interference-Alignment and Soft-space-reuse based cooperative transmission for multi-cell massive MIMO networks. IEEE Trans. Wirel. Commun. 2018, 17, 1907–1922. [Google Scholar] [CrossRef]
- Gupta, V.K.; Nambiar, A.; Kasbekar, G.S. Complexity analysis, potential game characterization and algorithms for the inter cell interference coordination with fixed transmit power problem. IEEE Trans. Veh. Technol. 2018, 4, 3054–3068. [Google Scholar] [CrossRef]
- Liu, R.; Shi, Y.; Liu, K.S.; Shen, M.; Wang, Y.; Li, Y. Bandwith-aware High-throughput routing with successive interference cancelation in multihop wireless networks. IEEE Trans. Veh. Technol. 2015, 64, 5866–5877. [Google Scholar] [CrossRef]
- Jiang, C.; Shi, Y.; Yuan, X.; Hou, Y.T.; Lou, W.; Kompella, S.; Midkiff, S.F. Cross-layer optimization for multi-hop wireless networks with successive interference cancellation. IEEE Trans. Wirel. Commun. 2016, 17, 5819–5831. [Google Scholar] [CrossRef]
- Ma, C.; Wu, W.; Cui, Y.; Wang, X. On the performance of successive interference cancellation in D2D-enabled cellular networks. In Proceedings of the 2015 IEEE Conference on Computer Communications, Hong Kong, China, 25 April–1 May 2015; pp. 37–45. [Google Scholar]
- Jalaian, C.T.; Yuan, X.; Shi, Y.; Hou, Y.T.; Lou, W.; Midkiff, S.F.; Dasari, V. On the integration of SIC and MIMO DoF for interference cancellation in wireless networks. Wirel. Netw. 2018, 24, 2357–2374. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, X.; Wang, J.; Xu, J. Multi-Hop Recharging Sensor Wireless Networks Optimization With Successive Interference Cancellation. In Proceedings of the International Conference on Wireless Algorithms, Systems, and Applications, Honolulu, HI, USA, 24–26 June 2019; pp. 482–493. [Google Scholar]
- Hou, Y.T.; Shi, Y.; Sherali, H.D. Rate alloction and network lifetime problems for wireless sensor networks. IEEE/ACM Trans. Netw. 2008, 16, 321–334. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, L.; Hou, Y.T.; Sherali, H.D. On Renewable Sensor Networks with Wireless Energy Transfer; Technical Report; The Bradley Department of Electrical and Computer Engineering, Virginia Tech: Blacksburg, VA, USA, 2010. [Google Scholar]
- The Fastest Solver Gurobi Optimization. Available online: https://www.gurobi.com/ (accessed on 2 January 2020).
- Concorde TSP Solver. Available online: http://www.tsp.gatech.edu/concorde/ (accessed on 2 January 2020).
| Symbol | Definition |
|---|---|
| B | The base station in the Wireless Rechargeable Sensor Networks (WRSNs) |
| The maximum number of signals for a SIC receive node j can decode | |
| c | The rate of energy consumption for receiving a unit of data rate |
| The rate of energy consumption for transmitting a unit of data rate | |
| Channel gain from receive node i to transmit node j | |
| The set of nodes within the interference range of node i | |
| The set of nodes in the WRSN | |
| The power of node i | |
| The transmit power of receive node i to transmit node j in time slot t | |
| The average transmission power of node i in time slot t | |
| The transmission power of node i with the data rate R | |
| The data rate generated by node i | |
| The flow rate from receive node i to transmit node j | |
| R | The fixed flow rate from receive node i to transmit node j |
| A binary variable indicating weather node i is sending data to node j in time slot t | |
| The time of one single travel cycle for mobile charger (MC) | |
| The time of recharging node i | |
| The time of one single travel through the shortest Hamiltonian cycle | |
| The vacation time of MC | |
| divide by (i.e.,) | |
| m | The number of piecewise linear segments to approximate the parabola |
| The presetting target error | |
| A substitute for in piecewise linear approximation | |
| The weight about () | |
| A binary variable indicating weather falls within the kth segment |
| i | Coordinates | i | Coordinates | i | Coordinates | i | Coordinates | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | (235,635) | 4 | 2 | (580,130) | 9 | 3 | (311,354) | 16 | 4 | (708,240) | 5 |
| 5 | (268, 6) | 14 | 6 | (432,160) | 17 | 7 | (509,93) | 19 | 8 | (775,454) | 13 |
| 9 | (149,312) | 13 | 10 | (461,247) | 16 |
| The Size of Square | B | The Increasing in Throughput | ||
|---|---|---|---|---|
| 800×800 | (400,400) | 10 | 91.06% | 450.00% |
| 800×800 | (400,400) | 30 | 89.99% | 340.01% |
| 800×800 | (400,400) | 50 | 88.01% | 334.78% |
| 800×800 | (400,400) | 80 | 87.43% | 291.43% |
| 1000×1000 | (500,500) | 30 | 67.85% | 264.78% |
| 1000×1000 | (500,500) | 50 | 69.89% | 253.34% |
| 1000×1000 | (500,500) | 80 | 74.86% | 223.26% |
| 1500×1500 | (750,750) | 80 | 49.04% | 195.62% |
| 1500×1500 | (750,750) | 100 | 34.20% | 183.37% |
| 1500×1500 | (750,750) | 150 | 28.01% | 170.83% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Ding, X.; Xu, J.; Wang, J.; Shi, L. Successive Interference Cancellation Based Throughput Optimization for Multi-Hop Wireless Rechargeable Sensor Networks. Sensors 2020, 20, 327. https://doi.org/10.3390/s20020327
Zhang P, Ding X, Xu J, Wang J, Shi L. Successive Interference Cancellation Based Throughput Optimization for Multi-Hop Wireless Rechargeable Sensor Networks. Sensors. 2020; 20(2):327. https://doi.org/10.3390/s20020327
Chicago/Turabian StyleZhang, Peng, Xu Ding, Juan Xu, Jing Wang, and Lei Shi. 2020. "Successive Interference Cancellation Based Throughput Optimization for Multi-Hop Wireless Rechargeable Sensor Networks" Sensors 20, no. 2: 327. https://doi.org/10.3390/s20020327
APA StyleZhang, P., Ding, X., Xu, J., Wang, J., & Shi, L. (2020). Successive Interference Cancellation Based Throughput Optimization for Multi-Hop Wireless Rechargeable Sensor Networks. Sensors, 20(2), 327. https://doi.org/10.3390/s20020327




