A Modified Residual-Based RAIM Algorithm for Multiple Outliers Based on a Robust MM Estimation
Abstract
1. Introduction
2. Related Works
3. Camouflage Effect of an RB RAIM Detector in Multi-Outlier Mode
3.1. Baseline of an RB RAIM Detector
3.2. Camouflage Effect of Residuals
- It is a symmetric matrix, ;
- It is an idempotent matrix, and ; and
- The diagonal elements are and .
- (1)
- The combination of outliers. The diagonal elements of are differentiated depending on the geometry.
- (2)
- The magnitude and direction of outliers. The ratio of two biases is , taking two outliers as an example.
4. An RB RAIM Based on a Robust MM Estimation
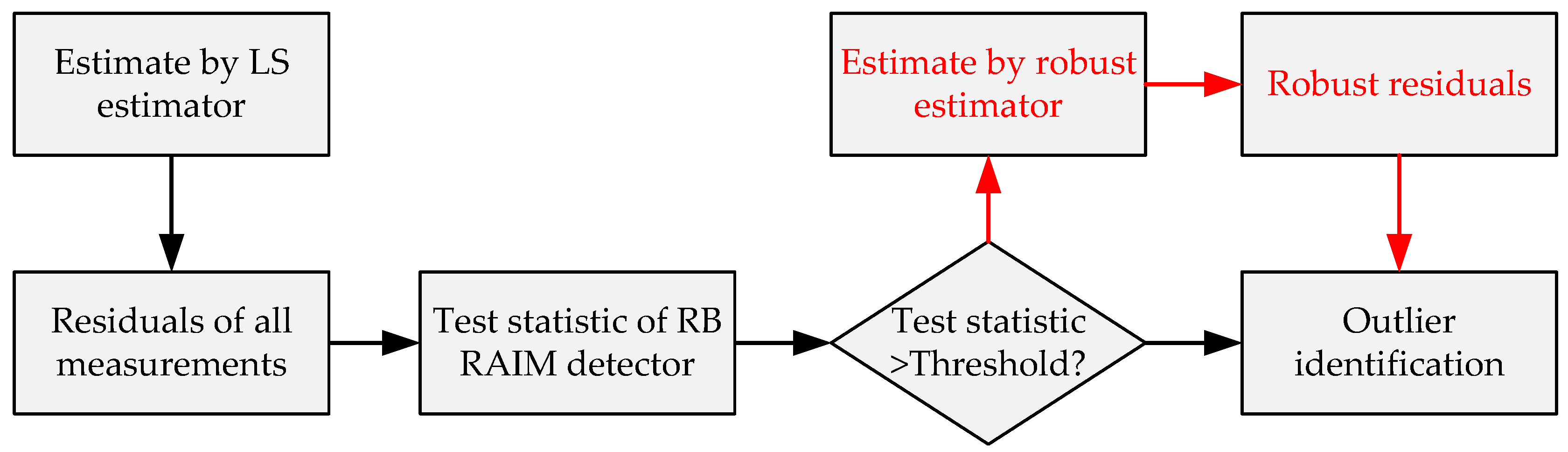
4.1. Robust Principle and an RB RAIM Detector Based on a Robust Estimation
4.2. Robust MM Estimation
4.2.1. Least Trimmed Squares Estimator
- At least satellites are required to complete the positioning solution. Defining the basic lower limit of the trimmed parameter is the maximum of and ;
- In general, the PDOP decreases as the number of visible satellites increases. The accuracy deteriorates, which affects the effectiveness of the corresponding residuals;
- The value of the trimmed parameter should be as large as possible to avoid too many subsets to be calculated; and
- All possible multiple outlier modes need to be within the effective robust range to ensure the robustness of the estimation, which defines the upper limit of the trimmed parameter according to the integrity requirements.
4.2.2. Equivalent Weight Function of the M Estimation
4.3. Fast Subsets Selection Based on the Characteristic Slope
- If , the process is terminated and the result is output;
- If , move the satellite back to and take the set as the selected subset, terminate the process and output the result;
- If the number of remaining satellites of the constellation meets the protection threshold , mark the constellation as a protected one; if , take the current set as the selected subset, terminate the process and output the result;
- If , terminate the process and take the current set as the selected subset.
5. Algorithm Verification and Simulation Results
5.1. Simulation Conditions
- Detector 1: Baseline RB RAIM detector based on the LS estimator.
- Detector 2: RB RAIM detector based on the M estimator with IGG III function with the constant values and .
- Detector 3: RB RAIM detector based on the MM estimator; the trimmed parameter was .
- Detector 4: RB RAIM detector proposed in this paper; the trimmed parameter was and the termination criteria were , and .
5.2. Comparison of Double Outlier Combinations with a Fixed Bias
5.3. Double Outlier Mode with the Largest Characteristic Slope
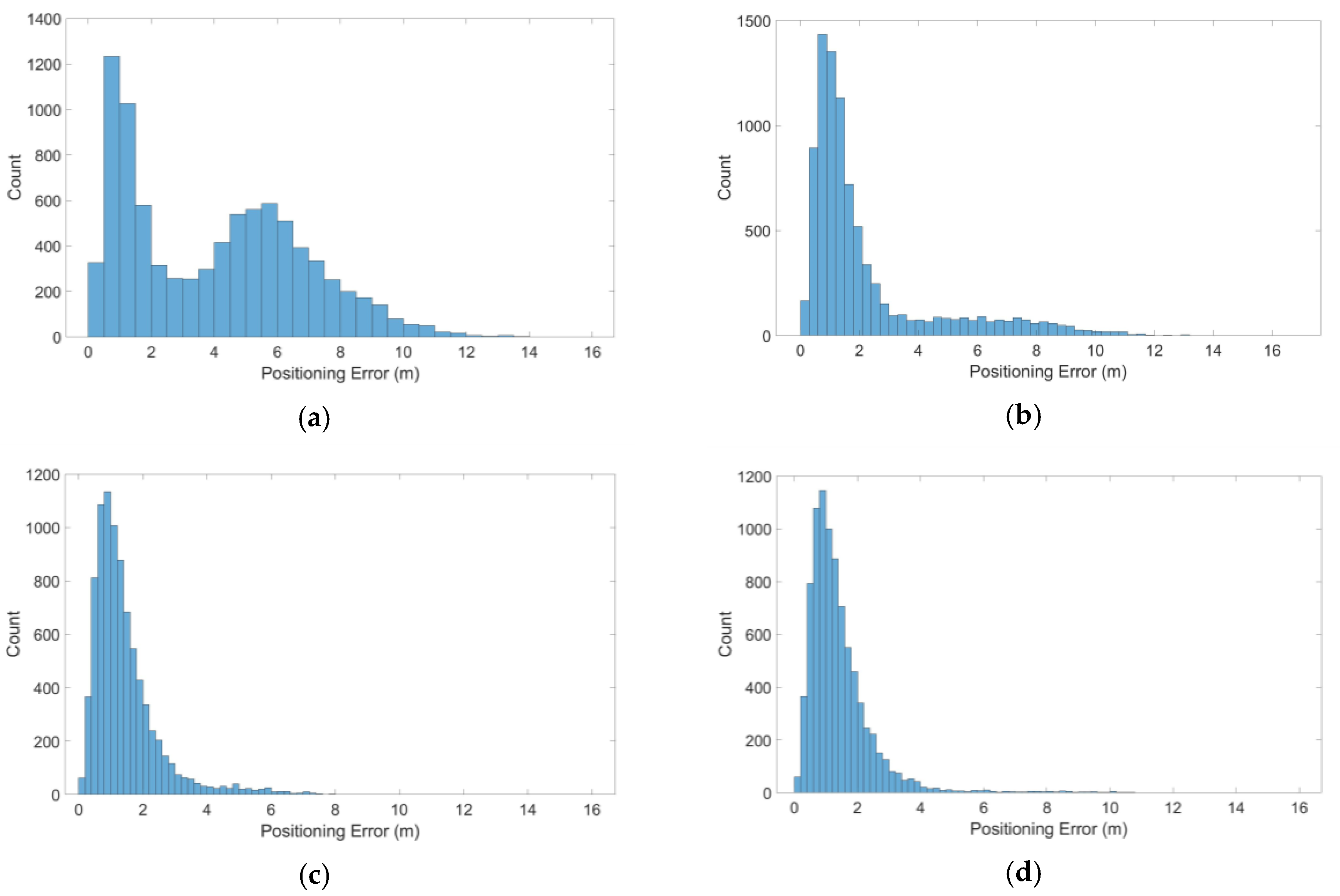
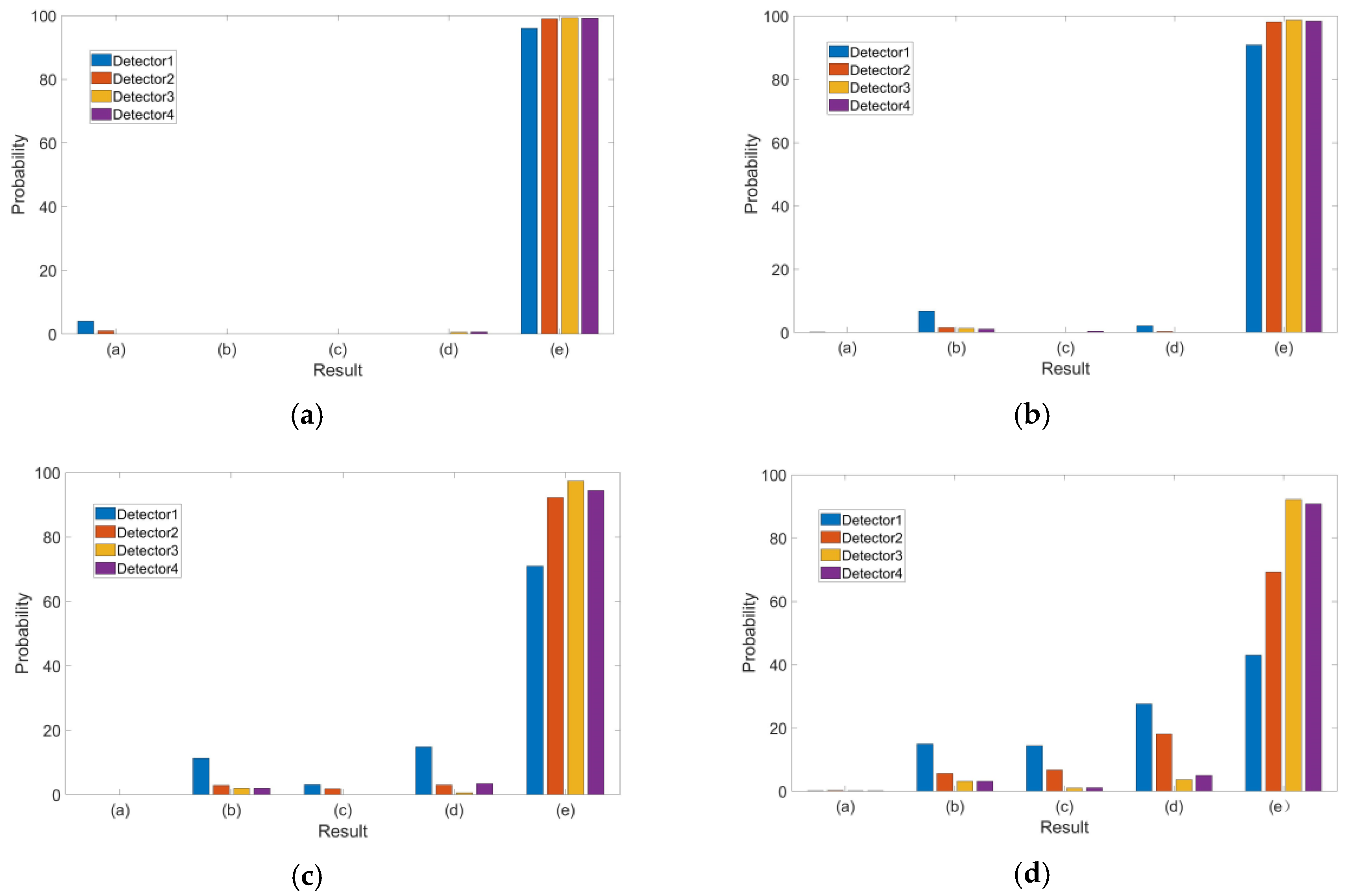
5.4. Detection and Exclusion for a Multiple Outlier Mode
- (a)
- None of the outliers were excluded and some normal pseudo-ranges were excluded;
- (b)
- Some of the outliers were excluded;
- (c)
- Some of the outliers were excluded and some normal pseudo-ranges were also excluded;
- (d)
- All of the outliers were excluded and some normal pseudo-ranges were also excluded; and
- (e)
- All of the outliers were excluded and none of the normal pseudo-ranges were excluded.
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, L.; Huan, W.; Chun, J.; Lin, Z.; Yunxi, Z. Integrity and continuity allocation for the RAIM with multiple constellations. GPS Solut. 2017, 21, 1503–1513. [Google Scholar]
- Fu, L.; Zhang, J.; Li, R.; Cao, X.; Wang, J. Vision-Aided RAIM: A New Method for GPS Integrity Monitoring in Approach and Landing Phase. Sensors 2015, 15, 22854–22873. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Imparato, D.; Rizos, C.; Wang, J. On hypothesis testing in RAIM algorithms: Generalized likelihood ratio test, solution separation test and a possible alternative. Meas. Sci. Technol. 2019, 30, 075001. [Google Scholar] [CrossRef]
- Zrinjski, M.; Barkovi, U.; Matika, K. Development and Modernization of GNSS. Geod. List 2019, 73, 45–65. [Google Scholar]
- Peter, T.; Davide, I.; Christian, T. Does RAIM with Correct Exclusion Produce Unbiased Positions? Sensors 2017, 17, 1508. [Google Scholar]
- Yawei, Z.; Joerger, M.; Pervan, B. Fault Exclusion in Multi-Constellation Global Navigation Satellite Systems. J. Navig. 2018, 71, 1281–1298. [Google Scholar]
- Joerger, M.; Chan, F.C.; Langel, S.; Pervan, A.B. Raim Detector and Estimator Design to Minimize the Integrity Risk. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 17–21 September 2012; pp. 2785–2807. [Google Scholar]
- Sun, R.; Wang, G.; Zhang, W.; Hsu, L.; Ochieng, W. A gradient boosting decision tree based GPS signal reception classification algorithm. Appl. Soft Comput. 2019, 86, 105942. [Google Scholar] [CrossRef]
- Hsu, L.T.; Gu, Y.; Kamijo, S. NLOS Correction/Exclusion for GNSS Measurement Using RAIM and City Building Models. Sensors 2015, 15, 17329–17349. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. RAIM with optimal integrity and continuity allocations under multiple failures. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1235–1247. [Google Scholar] [CrossRef]
- Hewitson, S.; Wang, J. GNSS Receiver Autonomous Integrity Monitoring (RAIM) for multiple outliers. Eur. J. Navig. 2006, 4, 47–57. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P. Exclusion for Advanced RAIM: Requirements and a Baseline Algorithm. In Proceedings of the International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 27–29 January 2014. [Google Scholar]
- Rippl, M. Real Time Advanced Receiver Autonomous Integrity Monitoring in DLR’s Multi-Antenna GNSS Receiver. In Proceedings of the International Technical Meeting of the Institue of Navigation, DLR, Newport Beach, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced Raim User Algorithm Description: Integrity Support Message Processing, Fault Detection, Exclusion, and Protection Level Calculation. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
- Rippl, M.; Schroth, G.; Belabbas, B.; Meurer, M. A Probabilistic Assessment on the Range Consensus (RANCO) RAIM Algorithm. In Proceedings of the Ion International Technical Meeting, DLR, Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Schroth, G.; Rippl, M.; Ene, A.; Blanch, J.; Belabbas, B.; Walter, T.; Enge, P.; Meurer, M. Enhancements of the Range Consensus Algorithm (RANCO). In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Juan, B.; Todd, W.; Per, E. Fixed Subset Selection to Reduce Advanced RAIM Complexity. In Proceedings of the International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 29 January–1 February 2018. [Google Scholar]
- Ge, Y.; Wang, Z.; Zhu, Y. Reduced ARAIM monitoring subset method based on satellites in different orbital planes. GPS Solut. 2017, 21, 1443–1456. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. Efficient Multiple Fault Exclusion with a Large Number of Pseudorange Measurements. In Proceedings of the 2015 International Technical Meeting of the Institute of Navigation, Dana Point, CA, USA, 26–28 January 2015. [Google Scholar]
- Walter, T.; Blanch, J.; Enge, P. Reduced Subset Analysis for Multi-Constellation Araim. In Proceedings of the 2014 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 27–29 January 2014. [Google Scholar]
- Mathieu, J.; Steven, L.; Boris, P. Integrity Risk Minimization in RAIM Part 2: Optimal Estimator Design. J. Navig. 2016, 69, 709–728. [Google Scholar]
- Hwang, Y.; Brown, R. RAIM-FDE revisited: A new breakthrough in availability performance with NIORAIM (novel integrity-optimized RAIM). Navigation 2006, 53, 41–52. [Google Scholar] [CrossRef]
- Song, D.; Shi, C.; Wang, Z.; Wang, C.; Jing, G. Correlation-weighted least squares residual algorithm for RAIM. Chin. J. Aeronaut. 2020, 33, 1505–1516. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J. GNSS receiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geod. Geodyn. 2016, 7, 117–123. [Google Scholar] [CrossRef]
- Adarsh, P.; Arun, S.; Sivaraman, B.; Pradeep, R. Robust Estimation via Robust Gradient Estimation. J. R. Statal Soc. Ser. B 2020, 82, 601–627. [Google Scholar]
- Wang, J.; Wang, J. Mitigation the Effects of Multiple Outliers on GNSS Navigation with M-Estimation Schemes. In Proceedings of the IGNSS Symposium 2007, Sydney, Australia, 4–6 December 2007; pp. 1–9. [Google Scholar]
- Liu, X.; Zuo, Y.; Wang, Q. Finite sample breakdown point of Tukey’s halfspace median. Sci. China Math. 2017, 60, 861–874. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J.L. A comparison of outlier detection procedures and robust estimation methods in GPS positioning. J. Navig. 2009, 62, 699–709. [Google Scholar] [CrossRef]
- Yai-Fung, L.; Sharipah, S.; Hazlina, A. Robust Linear Discriminant Analysis with Highest Breakdown Point Estimator. J. Telecommun. Electron. Comput. Eng. 2018, 10, 7–12. [Google Scholar]
- Akram, M.A.; Liu, P.; Wang, Y.; Qian, J. GNSS Positioning Accuracy Enhancement Based on Robust Statistical MM Estimation Theory for Ground Vehicles in Challenging Environments. Appl. Sci. 2018, 8, 876. [Google Scholar] [CrossRef]
- Mount, D.; Netanyahu, N.; Piatko, C.; Wu, A.; Silverman, R. A practical approximation algorithm for the LTS estimator. Comput. Stats Data Anal. 2016, 99, 148–170. [Google Scholar] [CrossRef]
- Zhao, J.; Song, D.; Xu, C.; Zheng, X. A modified LSR algorithm based on the critical value of characteristic slopes for RAIM. IEEE Access 2019, 7, 70102–70116. [Google Scholar] [CrossRef]
- Sun, R.; Cheng, Q.; Xie, F.; Zhang, W.; Lin, T.; Ochieng, W. Combining Machine Learning and Dynamic Time Wrapping for Vehicle Driving Event Detection Using Smartphones. IEEE Trans. Intell. Transp. Syst. 2019, 99, 1–14. [Google Scholar] [CrossRef]










| Scheme | Function | Parameter |
|---|---|---|
| Cauchy | ||
| Huber | ||
| Tukey | ||
| IGG III |
| Error | Function | Parameter |
|---|---|---|
| Tropospheric delay | is the elevation angle | |
| User error | For GPS: , For BDS: , | |
| Multiple path | ||
| Noise |
| RMSE (m) | 95% (m) | Max (m) | Time (s) | |
|---|---|---|---|---|
| Detector 1 | 3.6112 | 5.8041 | 10.5030 | 10.7667 |
| Detector 2 | 3.2587 | 5.1707 | 7.5235 | 11.5730 |
| Detector 3 | 1.8418 | 2.6215 | 3.6394 | 173.8353 |
| Detector 4 | 1.8418 | 2.6215 | 3.6394 | 33.5331 |
| RMSE (m) | 95% (m) | Max (m) | Time (s) | |
|---|---|---|---|---|
| Detector 1 | 4.8796 | 8.8160 | 13.8602 | 231.6745 |
| Detector 2 | 3.1876 | 7.7496 | 16.1177 | 298.7104 |
| Detector 3 | 1.7912 | 3.4720 | 8.5700 | 4711.9302 |
| Detector 4 | 1.8132 | 3.4850 | 11.2629 | 832.5141 |
| One Outlier | Two Outliers | |||||||
| (a) | (b) + (c) | (d) + (e) | (e) | (a) | (b) + (c) | (d) + (e) | (e) | |
| Detector 1 | 4% | 0% | 96% | 96% | 0% | 7% | 93% | 91% |
| Detector 2 | 1% | 0% | 99% | 99% | 0% | 2% | 98% | 98% |
| Detector 3 | 0% | 0% | 100% | 99% | 0% | 1% | 99% | 99% |
| Detector 4 | 0% | 0% | 100% | 99% | 0% | 1% | 99% | 98% |
| Three Outliers | Four Outliers | |||||||
| (a) | (b) + (c) | (d) + (e) | (e) | (a) | (b) + (c) | (d) + (e) | (e) | |
| Detector 1 | 0% | 14% | 86% | 71% | 0% | 29% | 71% | 43% |
| Detector 2 | 0% | 6% | 94% | 91% | 0% | 13% | 87% | 69% |
| Detector 3 | 0% | 2% | 98% | 97% | 0% | 4% | 96% | 92% |
| Detector 4 | 0% | 2% | 98% | 95% | 0% | 4% | 96% | 91% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xu, Y. A Modified Residual-Based RAIM Algorithm for Multiple Outliers Based on a Robust MM Estimation. Sensors 2020, 20, 5407. https://doi.org/10.3390/s20185407
Wang W, Xu Y. A Modified Residual-Based RAIM Algorithm for Multiple Outliers Based on a Robust MM Estimation. Sensors. 2020; 20(18):5407. https://doi.org/10.3390/s20185407
Chicago/Turabian StyleWang, Wenbo, and Ying Xu. 2020. "A Modified Residual-Based RAIM Algorithm for Multiple Outliers Based on a Robust MM Estimation" Sensors 20, no. 18: 5407. https://doi.org/10.3390/s20185407
APA StyleWang, W., & Xu, Y. (2020). A Modified Residual-Based RAIM Algorithm for Multiple Outliers Based on a Robust MM Estimation. Sensors, 20(18), 5407. https://doi.org/10.3390/s20185407





