Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN
Abstract
1. Introduction
2. Methodology
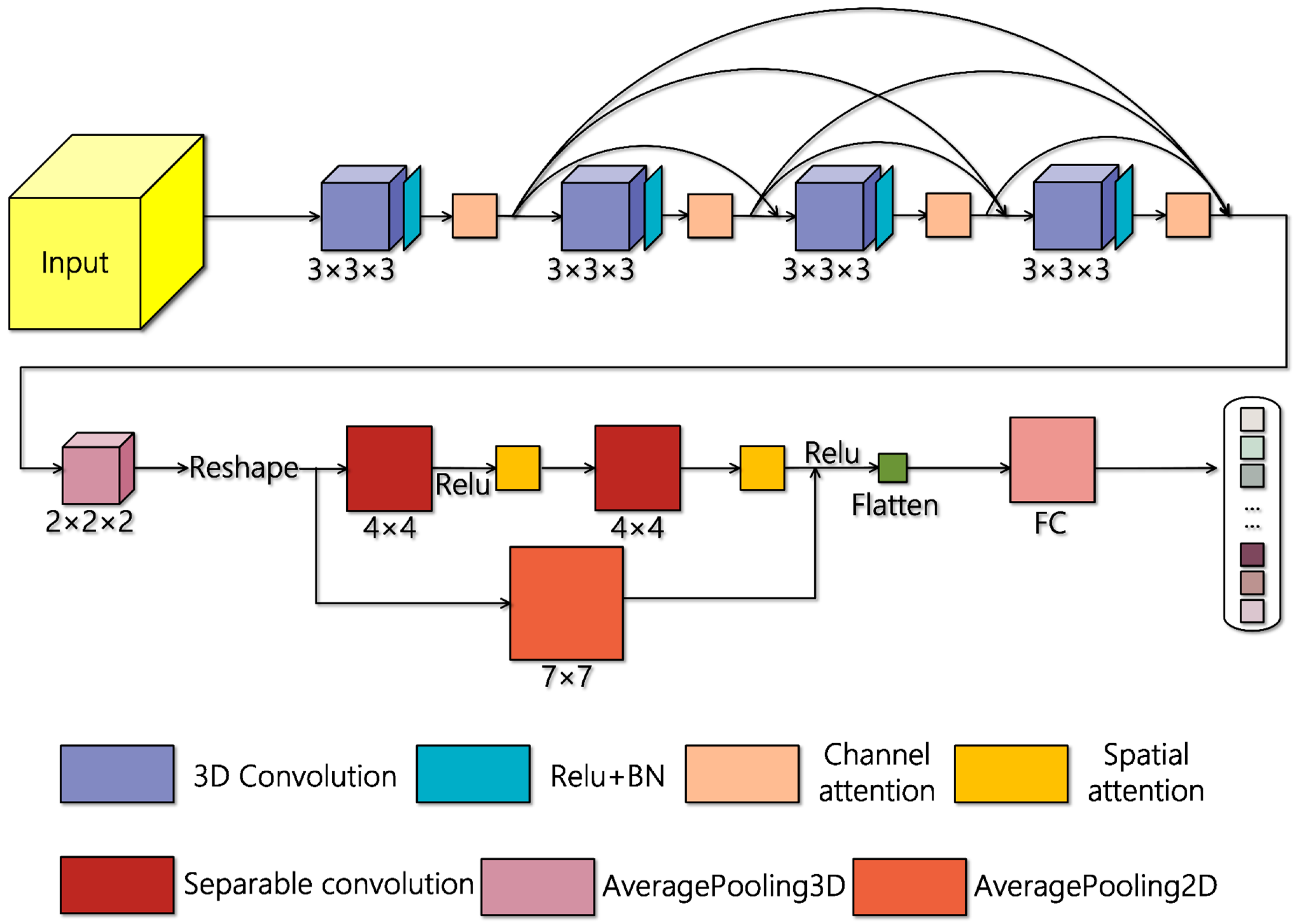
2.1. AD-HybridSN Model
2.2. Convolutional Layers Used in Our Proposed Model
2.3. Multiscale Feature Reuse Module
2.4. Attention Mechanism
2.4.1. Channel Attention Module
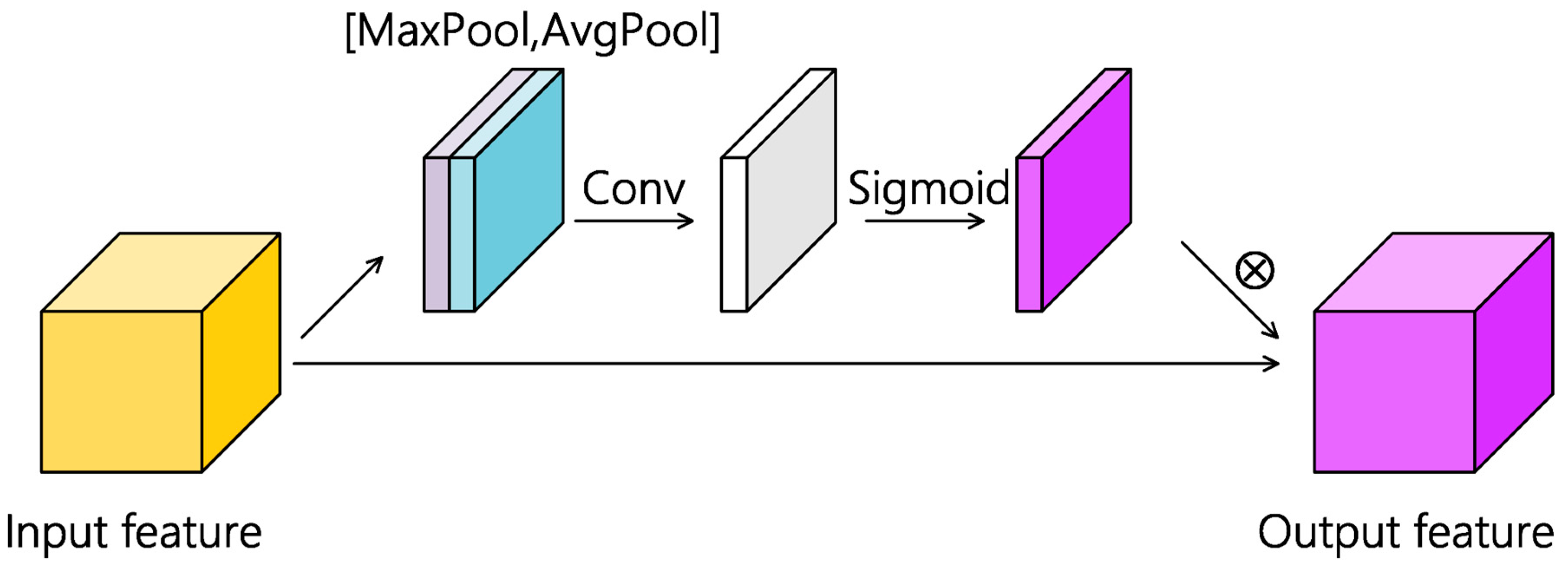
2.4.2. Spatial Attention Module
3. Datasets and Contrast Models
4. Experimental Results and Discussion
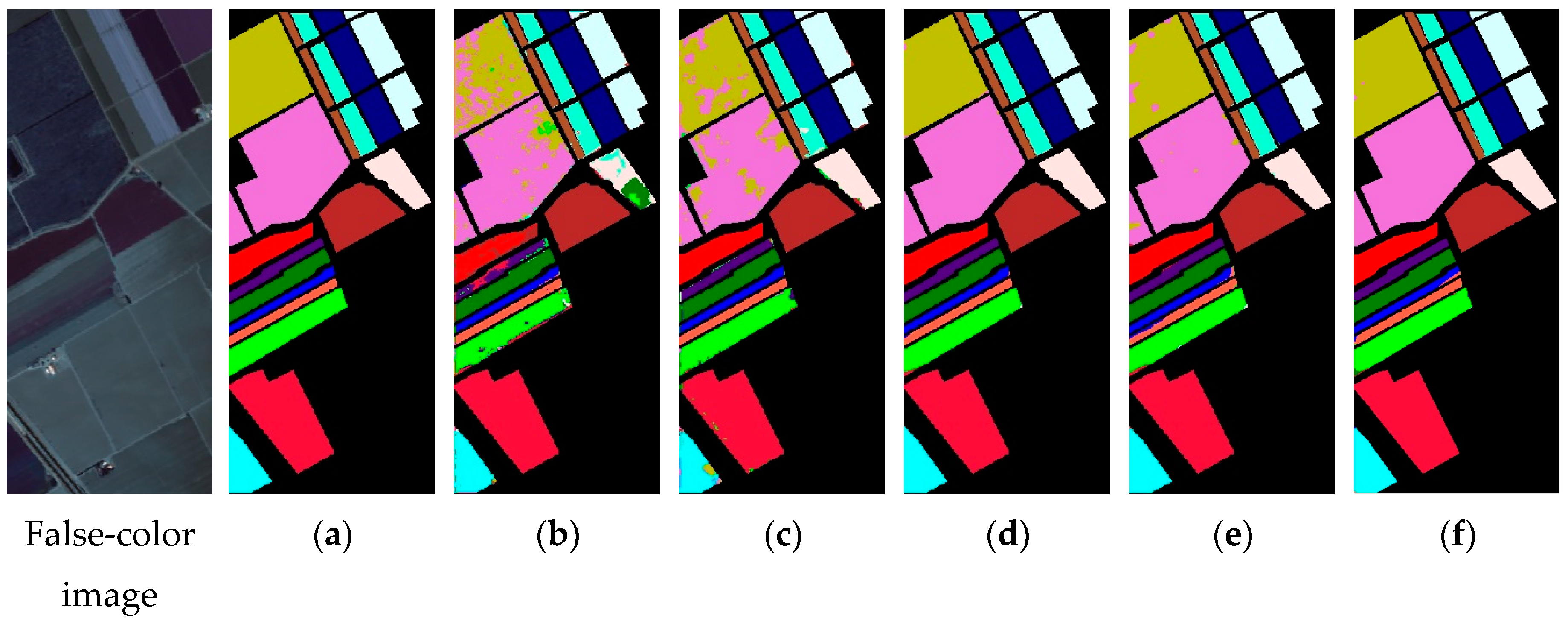
4.1. Experimental Results
4.2. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Luo, J.H.; Wu, J.X. A Survey on Fine-grained Image Categorization Using Deep Convolutional Features. Acta Autom. Sin. 2017, 43, 1306–1318. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Zhang, H.K.; Li, Y.; Jiang, Y.N. Deep Learning for Hyperspectral Imagery Classification: The State of the Art and Prospects. Acta Autom. Sin. 2018, 44, 961–977. [Google Scholar]
- Pan, B.; Shi, Z.; Xu, X. MugNet: Deep learning for hyperspectral image classification using limited samples. ISPRS J. Photogramm. Remote Sens. 2018, 145, 108–119. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Pattern Recognition and Computer Vision (CVPR), College Park, MD, USA, 25–26 July 2017; pp. 1–9. [Google Scholar]
- Wu, P.; Cui, Z.; Gan, Z.; Liu, F. Three-Dimensional ResNeXt Network Using Feature Fusion and Label Smoothing for Hyperspectral Image Classification. Sensors 2020, 20, 1652. [Google Scholar] [CrossRef]
- Tang, Z.; Jiang, W.; Zhang, Z.; Zhao, M.; Zhang, L.; Wang, M. DenseNet with Up-Sampling block for recognizing texts in images. Comput. Appl. 2020, 32, 7553–7561. [Google Scholar] [CrossRef]
- Zhu, H.; Miao, Y.; Zhang, X. Semantic Image Segmentation with Improved Position Attention and Feature Fusion. Neural Process. Lett. 2020, 52, 329–351. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, C.; Coleman, S.; Kerr, D. DENSE-INception U-net for medical image segmentation. Comput. Meth. Programs Biomed. 2020, 192, 105395. [Google Scholar] [CrossRef]
- Mu, Y.; Chen, T.-S.; Ninomiya, S.; Guo, W. Intact Detection of Highly Occluded Immature Tomatoes on Plants Using Deep Learning Techniques. Sensors 2020, 20, 2984. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Yan, Y.; Zheng, J.; Li, B. A fast face detection method via convolutional neural network. Neurocomputing 2020, 395, 128–137. [Google Scholar] [CrossRef]
- Das, N.; Hussain, E.; Mahanta, L.B. Automated classification of cells into multiple classes in epithelial tissue of oral squamous cell carcinoma using transfer learning and convolutional neural network. Neural Networks 2020, 128, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shen, X.; Zhou, Y.; Wang, X.; Li, T.-Q. Classification of breast cancer histopathological images using interleaved DenseNet with SENet (IDSNet). PLoS ONE 2020, 15, e0232127. [Google Scholar] [CrossRef]
- Chen, Y.S.; Jiang, H.L.; Li, C.Y.; Jia, X.P.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral-Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1608. [Google Scholar] [CrossRef]
- François, C. Deep Learning with Python, 1st ed.; Posts and Telecom Press: Beijing, China, 2018; p. 6. [Google Scholar]
- Liao, W.; Pizurica, A.; Scheunders, P.; Philips, W.; Pi, Y. Semisupervised Local Discriminant Analysis for Feature Extraction in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 184–198. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E.; Bruce, L.M. Locality-Preserving Dimensionality Reduction and Classification for Hyperspectral Image Analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1185–1198. [Google Scholar] [CrossRef]
- Samaniego, L.; Bardossy, A.; Schulz, K. Supervised classification of remotely sensed imagery using a modified k-NN technique. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2112–2125. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, J.; Crawford, M.M. Best-bases feature extraction algorithms for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1368–1379. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. A relative evaluation of multiclass image classification by support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1335–1343. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Z.; Yue, J.; Zhang, X.; Luo, L. On combining multiscale deep learning features for the classification of hyperspectral remote sensing imagery. Int. J. Remote Sens. 2015, 36, 3368–3379. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X. Deep 3D convolutional network combined with spatial-spectral features for hyperspectral image classification. Acta Geod. Cartogr. Sin. 2019, 48, 53–63. [Google Scholar]
- Meng, Z.; Li, L.; Jiao, L.; Feng, Z.; Tang, X.; Liang, M. Fully Dense Multiscale Fusion Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2718. [Google Scholar] [CrossRef]
- Swalpa, K.R.; Gopal, K.; Shiv, R.D.; Bidyut, B.C. HybridSN: Exploring 3-D-2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning Deep Hierarchical Spatial–Spectral Features for Hyperspectral Image Classification Based on Residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; So Kweon, I. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Wang, L.; Peng, J.; Sun, W. Spatial–Spectral Squeeze-and-Excitation Residual Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 884. [Google Scholar] [CrossRef]
- Li, G.; Zhang, C.; Lei, R.; Zhang, X.; Ye, Z.; Li, X. Hyperspectral remote sensing image classification using three-dimensional-squeeze-and-excitation-DenseNet (3D-SE-DenseNet). Remote Sens. Lett. 2020, 11, 195–203. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative Adversarial Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar]
- Zhong, Z.; Li, J.; Clausi, D.A.; Wong, A. Generative Adversarial Networks and Conditional Random Fields for Hyperspectral Image Classification. IEEE T. Cybern. 2020, 50, 3318–3329. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Yu, A.; Xue, Z. A semi-supervised convolutional neural network for hyperspectral image classification. Remote Sens. Lett. 2017, 8, 839–848. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Farah, I.R.; Solaiman, B. Hyperspectral imagery classification based on semi-supervised 3-D deep neural network and adaptive band selection. Expert Syst. Appl. 2019, 129, 246–259. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Li, Y. Hyperspectral images classification with hybrid deep residual network. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2235–2238. [Google Scholar]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.Q.; Wan, G.; Wang, R.R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 99, 1–15. [Google Scholar] [CrossRef]
- Ke, X.; Zhang, Y. Fine-grained vehicle type detection and recognition based on dense attention network. Neurocomputing 2020, 399, 247–257. [Google Scholar] [CrossRef]
- Bo, Z.H.; Zhang, H.; Yong, J.H.; Gao, H.; Xu, F. DenseAttentionSeg: Segment hands from interacted objects using depth input. Appl. Soft. Comput. 2020, 92, 9. [Google Scholar] [CrossRef]






| Number | Name | Training | Validation | Testing | Total |
|---|---|---|---|---|---|
| 1 | Alfalfa | 2 | 3 | 41 | 46 |
| 2 | Corn-notill | 71 | 72 | 1285 | 1428 |
| 3 | Corn-min | 42 | 41 | 747 | 830 |
| 4 | Corn | 12 | 12 | 213 | 237 |
| 5 | Grass/Pasture | 24 | 24 | 435 | 483 |
| 6 | Grass/Trees | 36 | 37 | 657 | 730 |
| 7 | Grass/Pasture-mowed | 2 | 1 | 25 | 28 |
| 8 | Hay-windrowed | 24 | 24 | 430 | 478 |
| 9 | Oats | 1 | 1 | 18 | 20 |
| 10 | Soybean-notill | 48 | 49 | 875 | 972 |
| 11 | Soybean-mintill | 123 | 122 | 2210 | 2455 |
| 12 | Soybean-clean | 30 | 29 | 534 | 593 |
| 13 | Wheat | 10 | 10 | 185 | 205 |
| 14 | Woods | 63 | 63 | 1139 | 1265 |
| 15 | Building-Grass-Trees-Drives | 19 | 20 | 347 | 386 |
| 16 | Stone-steel Towers | 5 | 4 | 84 | 93 |
| Total | 512 | 512 | 9225 | 10,249 | |
| Number | Name | Training | Validation | Testing | Total |
|---|---|---|---|---|---|
| 1 | Brocoli_green_weeds_1 | 20 | 20 | 1969 | 2009 |
| 2 | Brocoli_green_weeds_2 | 37 | 37 | 3652 | 3726 |
| 3 | Fallow | 20 | 20 | 1936 | 1976 |
| 4 | Fallow_rough_plow | 14 | 14 | 1366 | 1394 |
| 5 | Fallow_smooth | 27 | 27 | 2624 | 2678 |
| 6 | Stubble | 39 | 40 | 3880 | 3959 |
| 7 | Celery | 36 | 36 | 3507 | 3579 |
| 8 | Grapes_untrained | 113 | 112 | 11,046 | 11,271 |
| 9 | Soil_vinyard_develop | 62 | 62 | 6079 | 6203 |
| 10 | Corn_senesced_green_weeds | 33 | 33 | 3212 | 3278 |
| 11 | Lettuce_romaine_4wk | 11 | 10 | 1047 | 1068 |
| 12 | Lettuce_romaine_5wk | 19 | 20 | 1888 | 1927 |
| 13 | Lettuce_romaine_6wk | 9 | 9 | 898 | 916 |
| 14 | Lettuce_romaine_7wk | 11 | 10 | 1049 | 1070 |
| 15 | Vinyard_untrained | 72 | 73 | 7123 | 7268 |
| 16 | Vinyard_vertical_trellis | 18 | 18 | 1771 | 1807 |
| Total | 541 | 541 | 53,047 | 54,129 | |
| Number | Name | Training | Validation | Testing | Total |
|---|---|---|---|---|---|
| 1 | Asphalt | 66 | 66 | 6499 | 6631 |
| 2 | Meadows | 186 | 186 | 18,277 | 18,649 |
| 3 | Gravel | 21 | 21 | 2057 | 2099 |
| 4 | Trees | 30 | 31 | 3003 | 3064 |
| 5 | Metal sheets | 14 | 13 | 1318 | 1345 |
| 6 | Bare soil | 50 | 50 | 4929 | 5029 |
| 7 | Bitumen | 14 | 13 | 1303 | 1330 |
| 8 | Bricks | 37 | 37 | 3608 | 3682 |
| 9 | Shadows | 9 | 10 | 928 | 947 |
| Total | 427 | 427 | 41,922 | 42,776 | |
| No. | Training Samples | Res-2D-CNN | Res-3D-CNN | HybridSN | R-HybridSN | AD-HybridSN |
|---|---|---|---|---|---|---|
| 1 | 2 | 12.07 | 27.07 | 61.10 | 45.73 | 49.02 |
| 2 | 71 | 78.46 | 83.45 | 92.20 | 95.44 | 94.79 |
| 3 | 42 | 60.00 | 75.37 | 96.48 | 97.41 | 98.21 |
| 4 | 12 | 42.84 | 56.06 | 77.11 | 93.17 | 96.46 |
| 5 | 24 | 81.87 | 92.90 | 94.30 | 96.71 | 96.94 |
| 6 | 36 | 92.30 | 96.50 | 97.27 | 99.30 | 98.20 |
| 7 | 2 | 27.40 | 67.80 | 89.00 | 98.60 | 100.00 |
| 8 | 24 | 99.44 | 98.27 | 97.97 | 100.00 | 99.90 |
| 9 | 1 | 3.61 | 60.28 | 83.89 | 64.44 | 65.28 |
| 10 | 48 | 74.42 | 83.22 | 95.18 | 96.01 | 95.57 |
| 11 | 123 | 82.74 | 89.38 | 97.78 | 98.31 | 99.03 |
| 12 | 30 | 57.36 | 63.55 | 86.25 | 91.95 | 90.57 |
| 13 | 10 | 84.19 | 88.43 | 89.00 | 98.70 | 98.32 |
| 14 | 63 | 92.57 | 97.89 | 98.23 | 99.43 | 98.85 |
| 15 | 19 | 64.65 | 81.57 | 83.04 | 90.94 | 98.24 |
| 16 | 5 | 81.85 | 92.98 | 85.42 | 96.13 | 98.04 |
| KAPPA | 0.754 ± 0.030 | 0.840 ± 0.025 | 0.935 ± 0.008 | 0.963 ± 0.005 | 0.966 ± 0.004 | |
| OA (%) | 78.48 ± 2.58 | 86.04 ± 2.19 | 94.31 ± 0.65 | 96.76 ± 0.44 | 97.02 ± 0.30 | |
| AA (%) | 64.74 ± 3.16 | 78.42 ± 2.87 | 89.01 ± 1.23 | 91.39 ± 2.09 | 92.34 ± 1.41 | |
| No. | Training Samples | Res-2D-CNN | Res-3D-CNN | HybridSN | R-HybridSN | AD-HybridSN |
|---|---|---|---|---|---|---|
| 1 | 20 | 59.97 | 97.63 | 99.90 | 99.99 | 99.81 |
| 2 | 37 | 99.48 | 99.82 | 100.00 | 99.97 | 100.00 |
| 3 | 20 | 60.01 | 92.35 | 99.48 | 99.54 | 99.98 |
| 4 | 14 | 98.27 | 98.87 | 98.59 | 99.13 | 99.17 |
| 5 | 27 | 94.80 | 96.85 | 99.08 | 98.92 | 99.50 |
| 6 | 39 | 99.89 | 99.98 | 99.59 | 99.93 | 100.00 |
| 7 | 36 | 97.21 | 98.80 | 99.96 | 99.70 | 99.97 |
| 8 | 113 | 83.53 | 87.19 | 99.13 | 98.44 | 99.70 |
| 9 | 62 | 99.26 | 99.55 | 99.97 | 99.99 | 100.00 |
| 10 | 33 | 84.95 | 93.58 | 98.70 | 97.84 | 98.96 |
| 11 | 11 | 90.00 | 91.44 | 98.34 | 99.04 | 99.22 |
| 12 | 19 | 97.15 | 99.26 | 99.68 | 99.89 | 99.92 |
| 13 | 9 | 95.74 | 97.74 | 97.21 | 94.93 | 95.59 |
| 14 | 11 | 94.84 | 98.29 | 97.58 | 93.51 | 97.49 |
| 15 | 72 | 72.28 | 78.62 | 98.45 | 96.84 | 99.57 |
| 16 | 18 | 91.12 | 87.12 | 99.85 | 99.45 | 99.00 |
| KAPPA | 0.862 ± 0.015 | 0.918 ± 0.010 | 0.992 ± 0.003 | 0.986 ± 0.003 | 0.995 ± 0.001 | |
| OA (%) | 87.61 ± 1.38 | 92.68 ± 0.87 | 99.25 ± 0.31 | 98.74 ± 0.24 | 99.59 ± 0.10 | |
| AA (%) | 88.66 ± 2.32 | 94.82 ± 0.98 | 99.09 ± 0.49 | 98.57 ± 0.42 | 99.24 ± 0.20 | |
| No. | Training Samples | Res-2D-CNN | Res-3D-CNN | HybridSN | R-HybridSN | AD-HybridSN |
|---|---|---|---|---|---|---|
| 1 | 66 | 91.32 | 89.83 | 91.78 | 96.79 | 97.28 |
| 2 | 186 | 97.50 | 96.54 | 99.77 | 99.74 | 99.87 |
| 3 | 21 | 18.51 | 70.08 | 92.24 | 91.44 | 95.75 |
| 4 | 30 | 95.09 | 95.99 | 91.01 | 94.18 | 93.11 |
| 5 | 14 | 99.19 | 99.72 | 97.76 | 99.82 | 98.16 |
| 6 | 50 | 89.59 | 80.84 | 99.38 | 99.31 | 99.96 |
| 7 | 14 | 42.90 | 69.64 | 96.83 | 95.52 | 98.07 |
| 8 | 37 | 87.04 | 80.31 | 90.72 | 93.55 | 96.53 |
| 9 | 9 | 97.75 | 96.70 | 72.17 | 93.86 | 96.31 |
| KAPPA | 0.854 ± 0.012 | 0.870 ± 0.019 | 0.946 ± 0.013 | 0.969 ± 0.005 | 0.978 ± 0.004 | |
| OA (%) | 89.025 ± 0.89 | 90.19 ± 1.42 | 95.94 ± 0.95 | 97.64 ± 0.38 | 98.32 ± 0.28 | |
| AA (%) | 79.877 ± 2.75 | 86.63 ± 1.82 | 92.41 ± 2.14 | 96.02 ± 0.83 | 97.23 ± 0.61 | |
| R-HybridSN | D-HybridSN | AD-HybridSN | ||
|---|---|---|---|---|
| Indian Pines | KAPPA | 0.963 ± 0.005 | 0.958 ± 0.006 | 0.966 ± 0.004 |
| OA | 96.76 ± 0.44 | 96.34 ± 0.50 | 97.02 ± 0.30 | |
| AA | 91.39 ± 2.09 | 91.58 ± 1.64 | 92.34 ± 1.41 | |
| Salinas | KAPPA | 0.986 ± 0.003 | 0.993 ± 0.002 | 0.995 ± 0.001 |
| OA | 98.74 ± 0.24 | 99.40 ± 0.20 | 99.59 ± 0.10 | |
| AA | 98.57 ± 0.42 | 99.33 ± 0.24 | 99.24 ± 0.20 | |
| University of Pavia | KAPPA | 0.969 ± 0.005 | 0.972 ± 0.004 | 0.978 ± 0.004 |
| OA | 97.64 ± 0.38 | 97.91 ± 0.27 | 98.32 ± 0.28 | |
| AA | 96.02 ± 0.83 | 96.74 ± 0.62 | 97.23 ± 0.61 | |
| 1% | 0.8% | 0.6% | 0.4% | |||||
|---|---|---|---|---|---|---|---|---|
| OA (%) | AA (%) | OA (%) | AA (%) | OA (%) | AA (%) | OA (%) | AA (%) | |
| HybridSN | 95.94 | 92.41 | 94.60 | 89.69 | 93.31 | 87.50 | 90.62 | 80.96 |
| R-HybridSN | 97.64 | 96.02 | 96.60 | 93.94 | 95.76 | 92.91 | 93.46 | 86.82 |
| AD-HybridSN | 98.32 | 97.23 | 97.57 | 95.61 | 97.24 | 95.40 | 96.13 | 92.15 |
| 50 | 40 | 30 | 20 | |||||
|---|---|---|---|---|---|---|---|---|
| OA (%) | AA (%) | OA (%) | AA (%) | OA (%) | AA (%) | OA (%) | AA (%) | |
| HybridSN | 96.70 | 96.64 | 95.70 | 95.64 | 93.06 | 93.87 | 88.76 | 90.31 |
| R-HybridSN | 97.38 | 97.36 | 95.79 | 96.25 | 94.99 | 94.98 | 90.47 | 92.24 |
| AD-HybridSN | 98.32 | 98.31 | 97.14 | 97.36 | 96.33 | 96.70 | 93.98 | 94.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wei, F.; Feng, F.; Wang, C. Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN. Sensors 2020, 20, 5191. https://doi.org/10.3390/s20185191
Zhang J, Wei F, Feng F, Wang C. Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN. Sensors. 2020; 20(18):5191. https://doi.org/10.3390/s20185191
Chicago/Turabian StyleZhang, Jin, Fengyuan Wei, Fan Feng, and Chunyang Wang. 2020. "Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN" Sensors 20, no. 18: 5191. https://doi.org/10.3390/s20185191
APA StyleZhang, J., Wei, F., Feng, F., & Wang, C. (2020). Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN. Sensors, 20(18), 5191. https://doi.org/10.3390/s20185191




