Performance Analysis of Millimeter-Wave UAV Swarm Networks under Blockage Effects
Abstract
1. Introduction
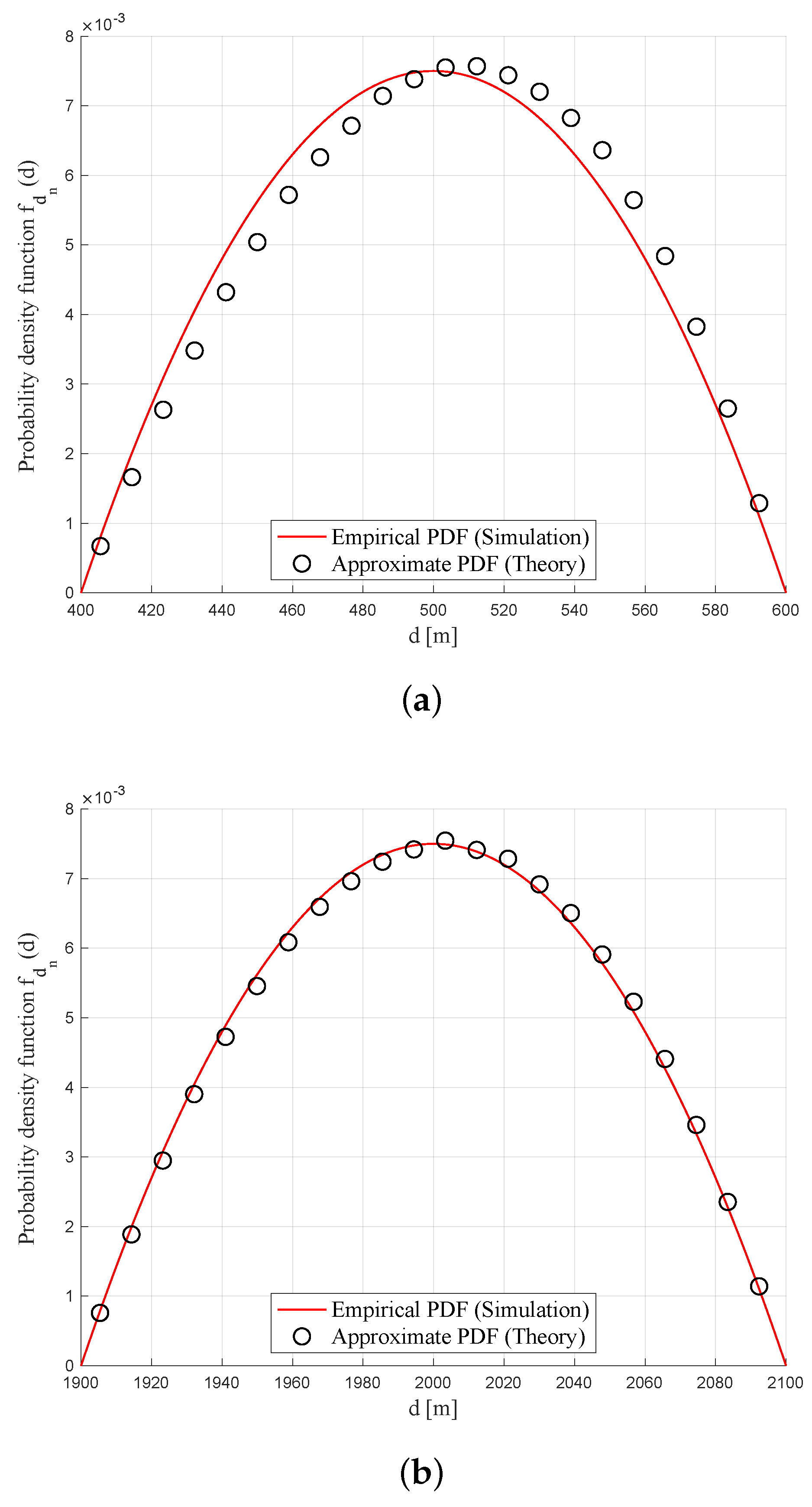
- We present the statistics of the distance between an arbitrary UAV BS in a sphere-shaped swarm to the user. To be specific, the probability density function (PDF) of the distance is derived, and its approximate version to obtain the first and second moments in closed forms is also provided.
- Assuming random blockages between the UAV swarm and the receiver, we derive a closed-form expression of the outage rate, which is defined by the likelihood to have no LoS path.
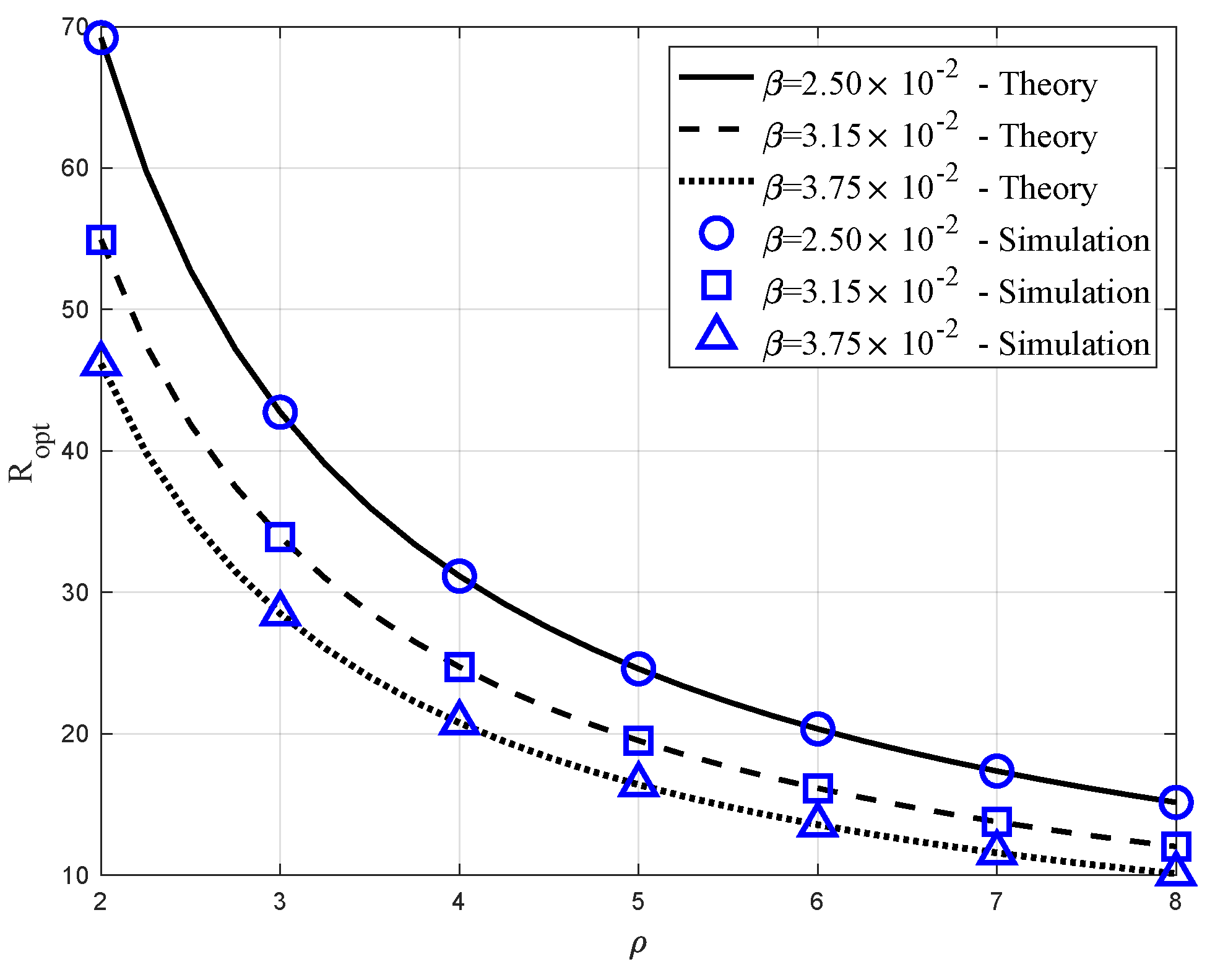
- Using the derived outage rate, we present how it changes with various system parameters. In particular, we show that there exists an optimal value of the size of the UAV swarm to minimize the outage probability. Further, the optimal size of the spherical UAV swarm is derived in a closed-form.
- We present both simulation and theoretical results to show the impact of various system parameters. In addition, by comparing the two results, we validate our analysis.
2. Related Work
3. System Model
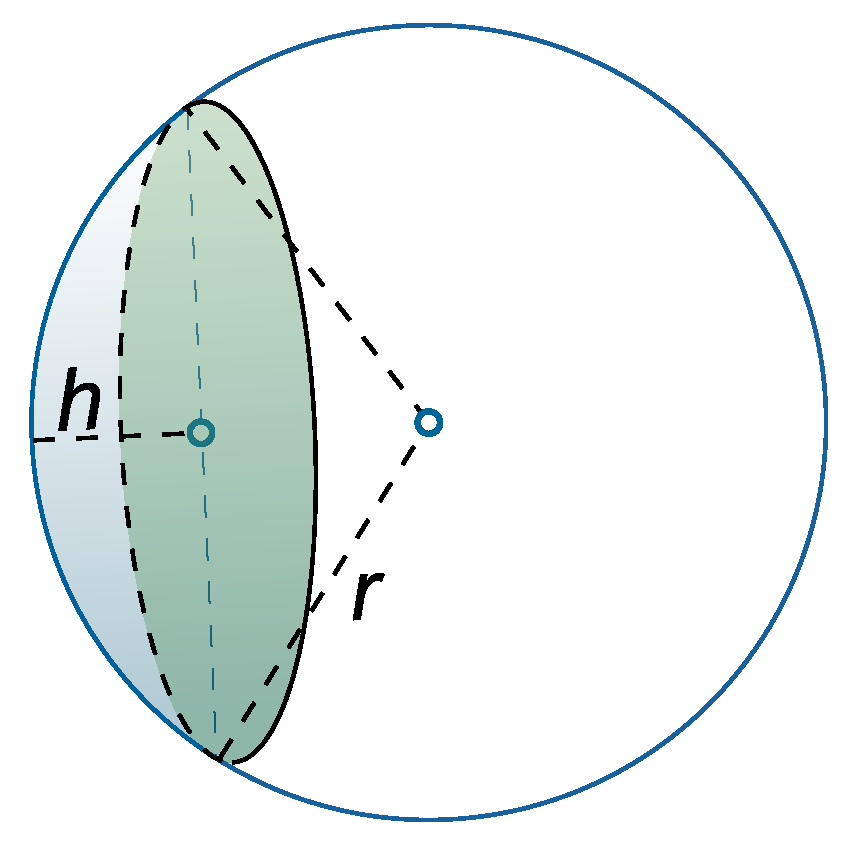
4. Distance Distribution and Path Loss Statistics
5. Outage Probability Analysis
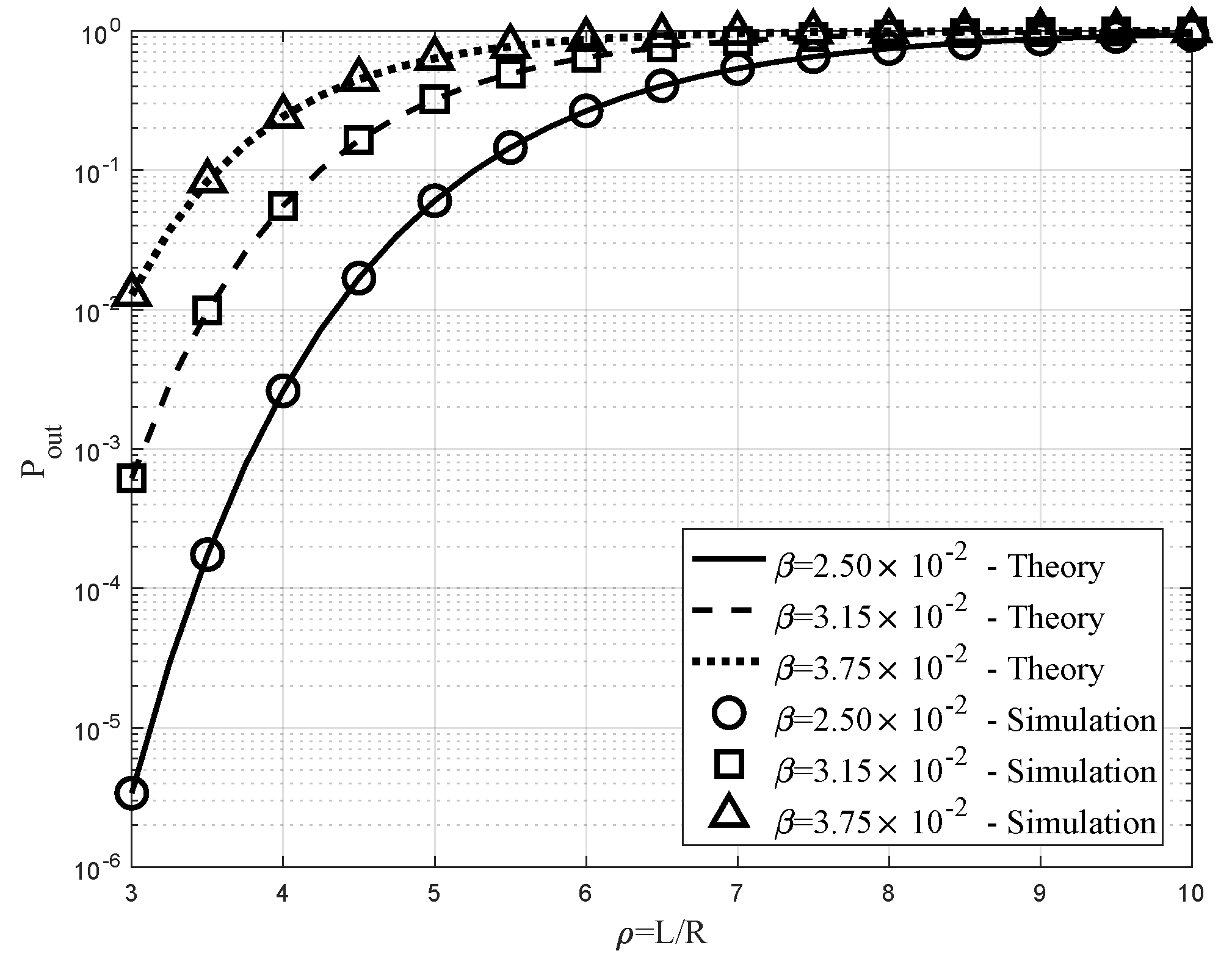
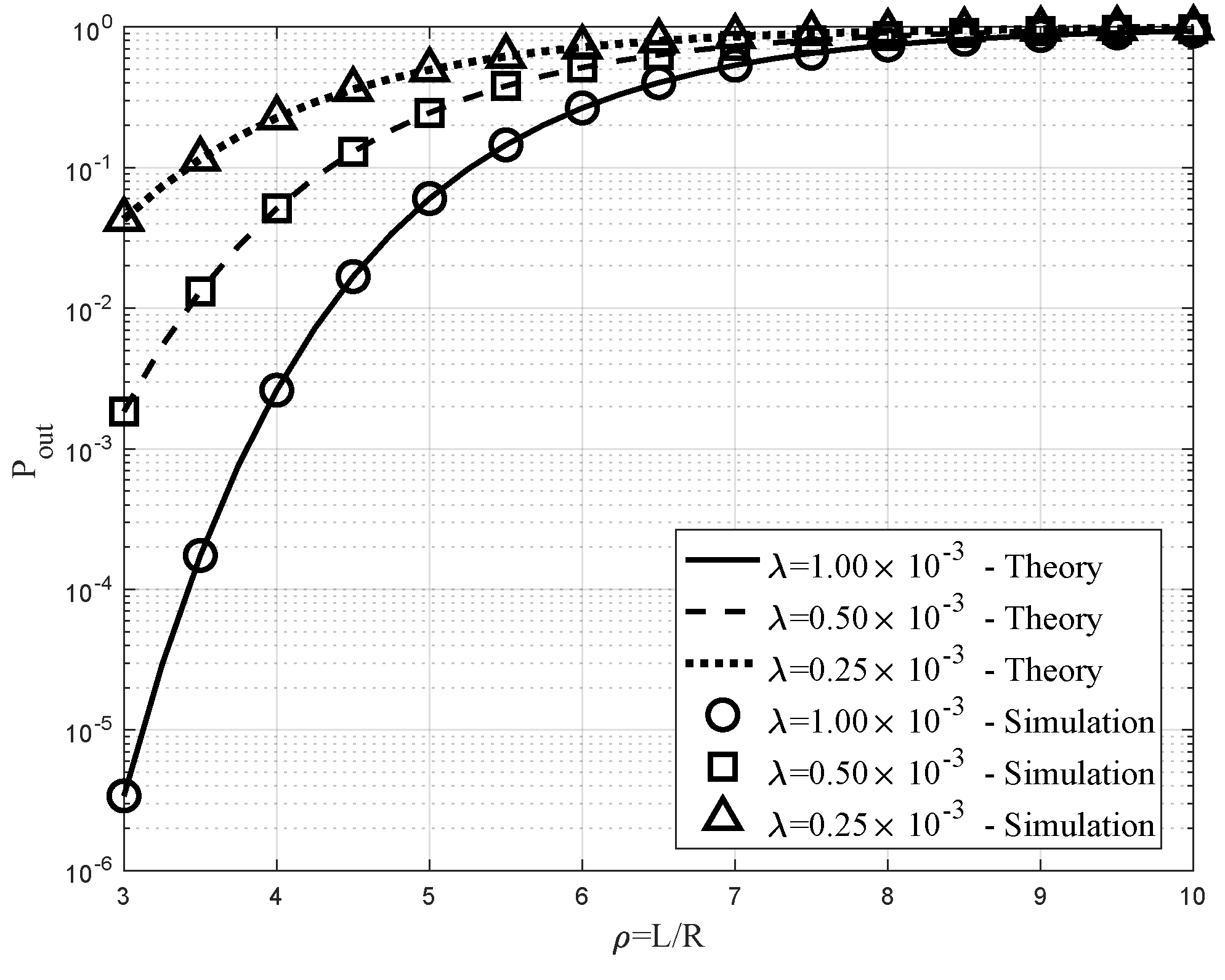
6. Numerical Results
6.1. Impact of R on
6.2. Impacts of and on
6.3. Impacts of and on
6.4. Verus
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 5G | Fifth generation |
| A2G | Air-to-ground |
| AP | Access point |
| B5G | Beyond fifth generation |
| BS | Base station |
| CDF | Cumulative distribution function |
| LoS | Line-of-sight |
| mmWave | Millimeter-wave |
| Probability distribution function | |
| PPP | Poisson point process |
| SISO | Single-input-single-output |
| UAV | Unmanned aerial vehicle |
| UDN | Ultra-dense network |
| UE | User equipment |
References
- Xiao, Z.; Xia, P.; Xia, X. Enabling uav cellular with millimeter-wave communication: Potentials and approaches. IEEE Commun. Mag. 2016, 54, 66–73. [Google Scholar] [CrossRef]
- Jan, M.A.; Hassan, S.A.; Jung, H. Chapter five-UAVs: Communication aspects and cellular service provisioning. In Drones in Smart-Cities; Al-Turjman, F., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 79–91. Available online: http://www.sciencedirect.com/science/article/pii/B9780128199725000057 (accessed on 16 August 2020).
- Akram, M.U.; Saeed, U.; Hassan, S.A.; Jung, H. UAV-based air-to-ground channel modeling for diverse environments. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea, 25–28 May 2020. [Google Scholar]
- Jan, M.A.; Hassan, S.A.; Jung, H. QoS-based performance analysis of mmWave UAV-assisted 5G hybrid heterogeneous network. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2020. [Google Scholar]
- Jung, H.; Lee, I.-H. Coverage probability and area spectral efficiency of clustered linear unmanned vehicle sensor networks. Sensors 2017, 17, 2550. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.H. Secrecy rate analysis of open-loop analog collaborative beamforming under position estimation error of virtual antenna array. IEEE Wirel. Commun. Lett. 2019, 8, 1337–1340. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.H. Secrecy performance analysis of analog cooperative beamforming in three-dimensional Gaussian distributed wireless sensor networks. IEEE Trans. Wirel. Commun. 2019, 18, 1860–1873. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.H. Analog cooperative beamforming with spherically-bound random arrays for physical-layer secure communications. IEEE Commun. Lett. 2018, 22, 546–549. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.H. Secrecy rate of analog collaborative beamforming with virtual antenna array following spatial random distributions. IEEE Wirel. Commun. Lett. 2018, 7, 626–629. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.-H. Distributed null-steering beamformer design for physical layer security enhancement in Internet-of-Things networks. IEEE Syst. J. 2020, 1–12. [Google Scholar] [CrossRef]
- Feng, Z.; Ji, L.; Zhang, Q.; Li, W. Spectrum management for mmwave enabled uav swarm networks: Challenges and opportunities. IEEE Commun. Mag. 2019, 57, 146–153. [Google Scholar] [CrossRef]
- Wang, X.; Kong, L.; Kong, F.; Qiu, F.; Xia, M.; Arnon, S.; Chen, G. Millimeter wave communication: A comprehensive survey. IEEE Commun. Surv. Tutor. 2018, 20, 1616–1653. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Bai, T.; Vaze, R.; Heath, R.W. Analysis of blockage effects on urban cellular networks. IEEE Trans. Wirel. Commun. 2014, 13, 5070–5083. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.-H. Connectivity analysis of millimeter-wave device-to-device networks with blockage. Int. J. Antennas Propag. 2016, 2016, 7939671. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.-H. Outage analysis of multihop wireless backhaul using millimeter wave under blockage effects. Int. J. Antennas Propag. 2017, 2017, 4519365. [Google Scholar] [CrossRef]
- Stoyan, D.; Kendall, W.; Mecke, J. Geometry and Its Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Choi, J. On the macro diversity with multiple BSs to mitigate blockage in millimeter-wave communications. IEEE Commun. Lett. 2014, 18, 1653–1656. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.-H. Outage analysis of millimeter-wave wireless backhaul in the presence of blockage. IEEE Commun. Lett. 2016, 20, 2268–2271. [Google Scholar] [CrossRef]
- Thornburg, A.; Bai, T.; Heath, R.W. Performance analysis of outdoor mmwave ad hoc networks. IEEE Trans. Signal Process. 2016, 64, 4065–4079. [Google Scholar] [CrossRef]
- Thornburg, A.; Bai, T.; Heath, R.W. Interference statistics in a random mmwave ad hoc network. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2904–2908. [Google Scholar]
- Naqvi, S.A.R.; Hassan, S.A.; Pervaiz, H.; Ni, Q. Drone-aided communication as a key enabler for 5G and resilient public safety network. IEEE Commun. Mag. 2018, 56, 36–42. [Google Scholar] [CrossRef]
- Solomitckii, D.; Gapeyenko, M.; Semkin, V.; Andreev, S.; Koucheryavy, Y. Technologies for efficient amateur drone detection in 5G millimeter-wave cellular infrastructure. IEEE Commun. Mag. 2018, 56, 43–50. [Google Scholar] [CrossRef]
- Khuwaja, A.A.; Chen, Y.; Zhao, N.; Alouini, M.; Dobbins, P. A survey of channel modeling for UAV communications. IEEE Commun. Surv. Tutor. 2018, 20, 2804–2821. [Google Scholar] [CrossRef]
- Heimann, K.; Tiemann, J.; Boecker, S.; Wietfeld, C. On the potential of 5G mmwave pencil beam antennas for uav communications: An experimental evaluation. In Proceedings of the 22nd International ITG Workshop on Smart Antennas (WSA 2018), Bochum, Germany, 14–16 March 2018; pp. 1–6. [Google Scholar]
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.; Schneckenburger, N. A survey of air-to-ground propagation channel modeling for unmanned aerial vehicles. IEEE Commun. Surv. Tutor. 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Orsino, A.; Ometov, A.; Fodor, G.; Moltchanov, D.; Militano, L.; Andreev, S.; Yilmaz, O.N.C.; Tirronen, T.; Torsner, J.; Araniti, G.; et al. Effects of heterogeneous mobility on D2D- and drone-assisted mission-critical MTC in 5G. IEEE Commun. Mag. 2017, 55, 79–87. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Lee, I.-H.; Jung, H. User selection and power allocation for downlink NOMA systems with quality-based feedback in rayleigh fading channels. IEEE Wirel. Commun. Lett. 2020, 1. [Google Scholar] [CrossRef]
- AlQerm, I.; Shihada, B. Energy efficient traffic offloading in multi-tier heterogeneous 5G networks using intuitive online reinforcement learning. IEEE Trans. Green Commun. Netw. 2019, 3, 691–702. [Google Scholar] [CrossRef]
- Becvar, Z.; Vondra, M.; Mach, P.; Plachy, J.; Gesbert, D. Performance of mobile networks with UAVs: Can flying base stations substitute ultra-dense small cells? In Proceedings of the European Wireless 2017; 23th European Wireless Conference, Dresden, Germany, 17–19 May 2017; pp. 1–7. [Google Scholar]
- Teng, Y.; Liu, M.; Yu, F.R.; Leung, V.C.M.; Song, M.; Zhang, Y. Resource allocation for ultra-dense networks: A survey, some research issues and challenges. IEEE Commun. Surv. Tutor. 2019, 21, 2134–2168. [Google Scholar] [CrossRef]
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-dense networks: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Chen, S.; Qin, F.; Hu, B.; Li, X.; Chen, Z. User-centric ultra-dense networks for 5G: Challenges, methodologies, and directions. IEEE Wirel. Commun. 2016, 23, 78–85. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, S.; Jiang, C.; Long, K.; Leung, V.C.M.; Poor, H.V. Energy efficient user association and power allocation in millimeter-wave-based ultra dense networks with energy harvesting base stations. IEEE J. Sel. Areas Commun. 2017, 35, 1936–1947. [Google Scholar] [CrossRef]
- Kwon, G.; Park, H. Joint user association and beamforming design for millimeter wave UDN with wireless backhaul. IEEE J. Sel. Areas Commun. 2019, 37, 2653–2668. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M.A. Multi-packet interference in opportunistic large array broadcasts over disk networks. IEEE Trans. Wirel. Commun. 2013, 12, 5631–5645. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M. Multi-packet opportunistic large array transmission on strip-shaped cooperative routes or networks. IEEE Trans. Wirel. Commun. 2014, 13, 144–158. [Google Scholar] [CrossRef]
- Wang, H.; Ding, G.; Gao, F.; Chen, J.; Wang, J.; Wang, L. Power control in UAV-supported ultra dense networks: Communications, caching, and energy transfer. IEEE Commun. Mag. 2018, 56, 28–34. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y.; Guizani, M. Secure uav communication networks over 5G. IEEE Wirel. Commun. 2019, 26, 114–120. [Google Scholar] [CrossRef]
- Wang, X.; Feng, W.; Chen, Y.; Ge, N. UAV swarm-enabled aerial CoMP: A physical layer security perspective. IEEE Access 2019, 7, 120901–120916. [Google Scholar] [CrossRef]
- Huo, Y.; Dong, X.; Lu, T.; Xu, W.; Yuen, M. Distributed and multilayer UAV networks for next-generation wireless communication and power transfer: A feasibility study. IEEE Internet Things J. 2019, 6, 7103–7115. [Google Scholar] [CrossRef]
- Wang, L.; Che, Y.L.; Long, J.; Duan, L.; Wu, K. Multiple access mmwave design for UAV-aided 5G communications. IEEE Wirel. Commun. 2019, 26, 64–71. [Google Scholar] [CrossRef]
- Cheema, M.A.; Shehzad, M.K.; Qureshi, H.K.; Hassan, S.A.; Jung, H. A Drone-Aided Blockchain-based Smart Vehicular Network. arXiv 2020, arXiv:2007.12912. [Google Scholar]
- Nawaz, F.; Hassan, S.A.; Hashmi, A.J.; Jung, H. A physical-layer scheduling approach in large-scale cooperative networks. IEEE Access 2019, 7, 134338–134347. [Google Scholar] [CrossRef]
- Jung, H.; Lee, I.-H. Performance analysis of millimeter-wave multi-hop machine-to-machine networks based on hop distance statistics. Sensors 2018, 18, 204. [Google Scholar] [CrossRef]
- Jung, H.; Weitnauer, M.A. Analysis of link asymmetry in virtual multiple-input-single-output (VMISO) systems. Ad Hoc Netw. 2017, 63, 20–29. [Google Scholar] [CrossRef]

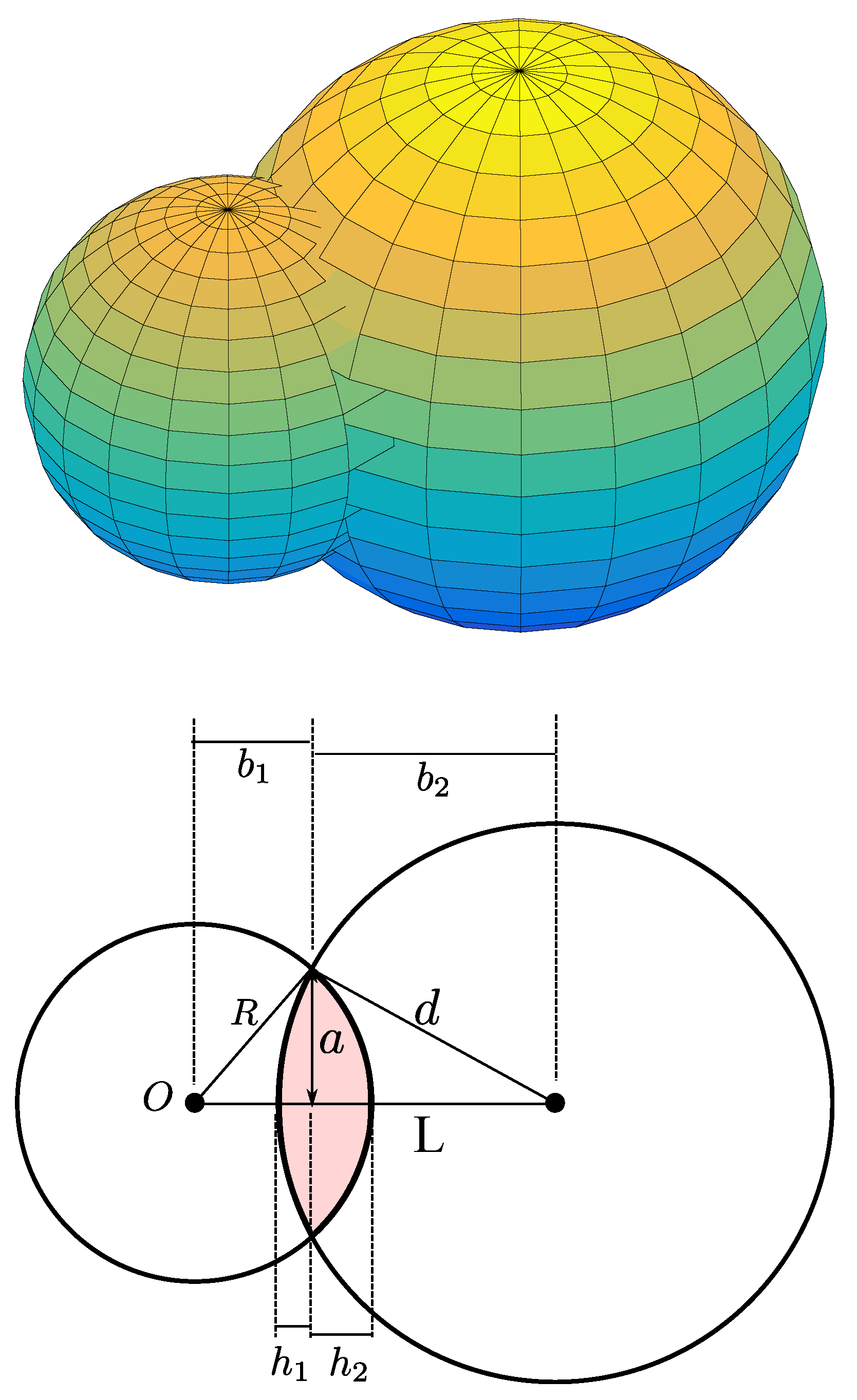

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, H.; Lee, I.-H. Performance Analysis of Millimeter-Wave UAV Swarm Networks under Blockage Effects. Sensors 2020, 20, 4593. https://doi.org/10.3390/s20164593
Jung H, Lee I-H. Performance Analysis of Millimeter-Wave UAV Swarm Networks under Blockage Effects. Sensors. 2020; 20(16):4593. https://doi.org/10.3390/s20164593
Chicago/Turabian StyleJung, Haejoon, and In-Ho Lee. 2020. "Performance Analysis of Millimeter-Wave UAV Swarm Networks under Blockage Effects" Sensors 20, no. 16: 4593. https://doi.org/10.3390/s20164593
APA StyleJung, H., & Lee, I.-H. (2020). Performance Analysis of Millimeter-Wave UAV Swarm Networks under Blockage Effects. Sensors, 20(16), 4593. https://doi.org/10.3390/s20164593





