An Automatic Unmixing Approach to Detect Tissue Chromophores from Multispectral Photoacoustic Imaging
Abstract
1. Introduction
2. Non-Negative Matrix Factorization (NNMF)
3. Experimental Methods
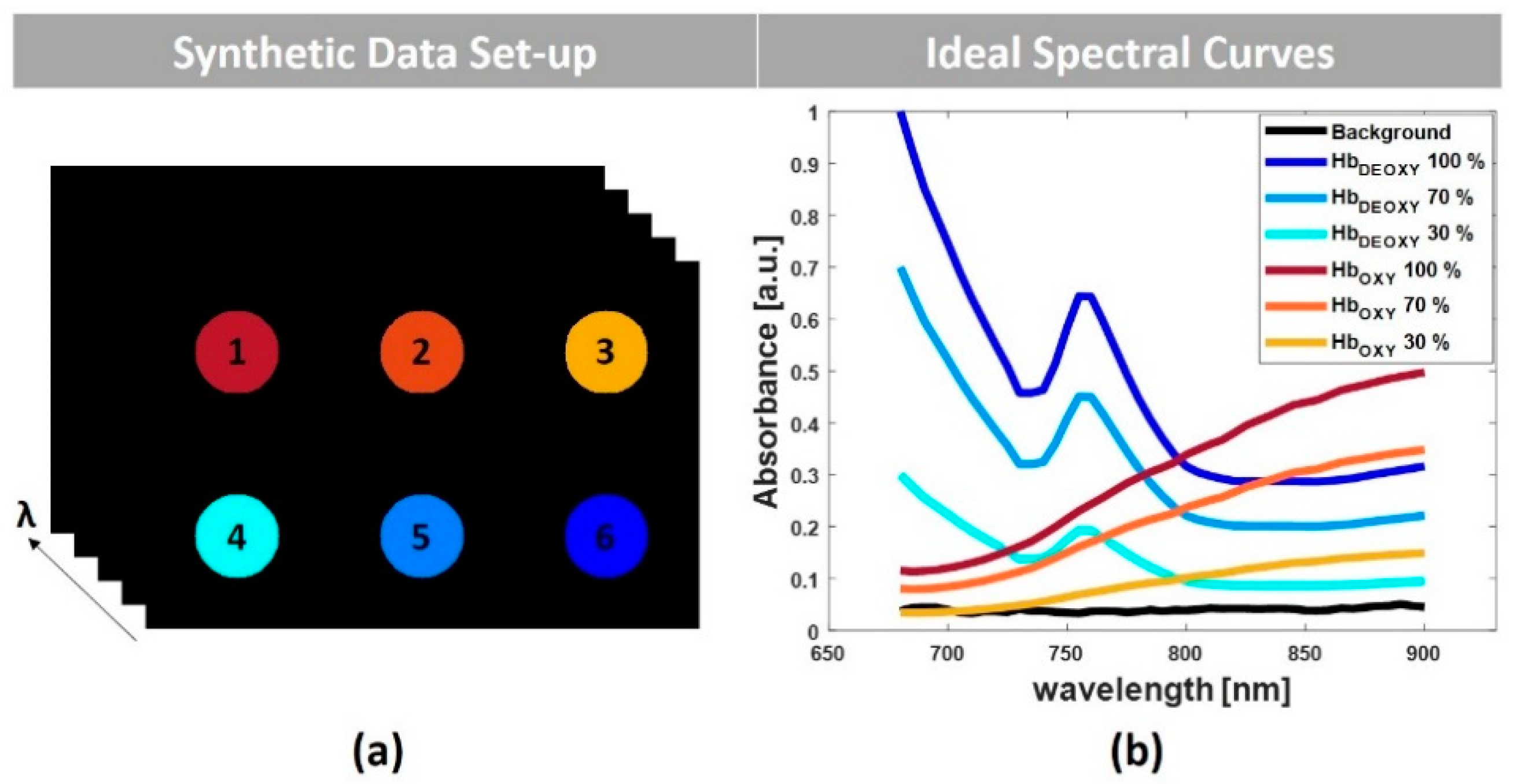
3.1. Simulated Multispectral PA Images
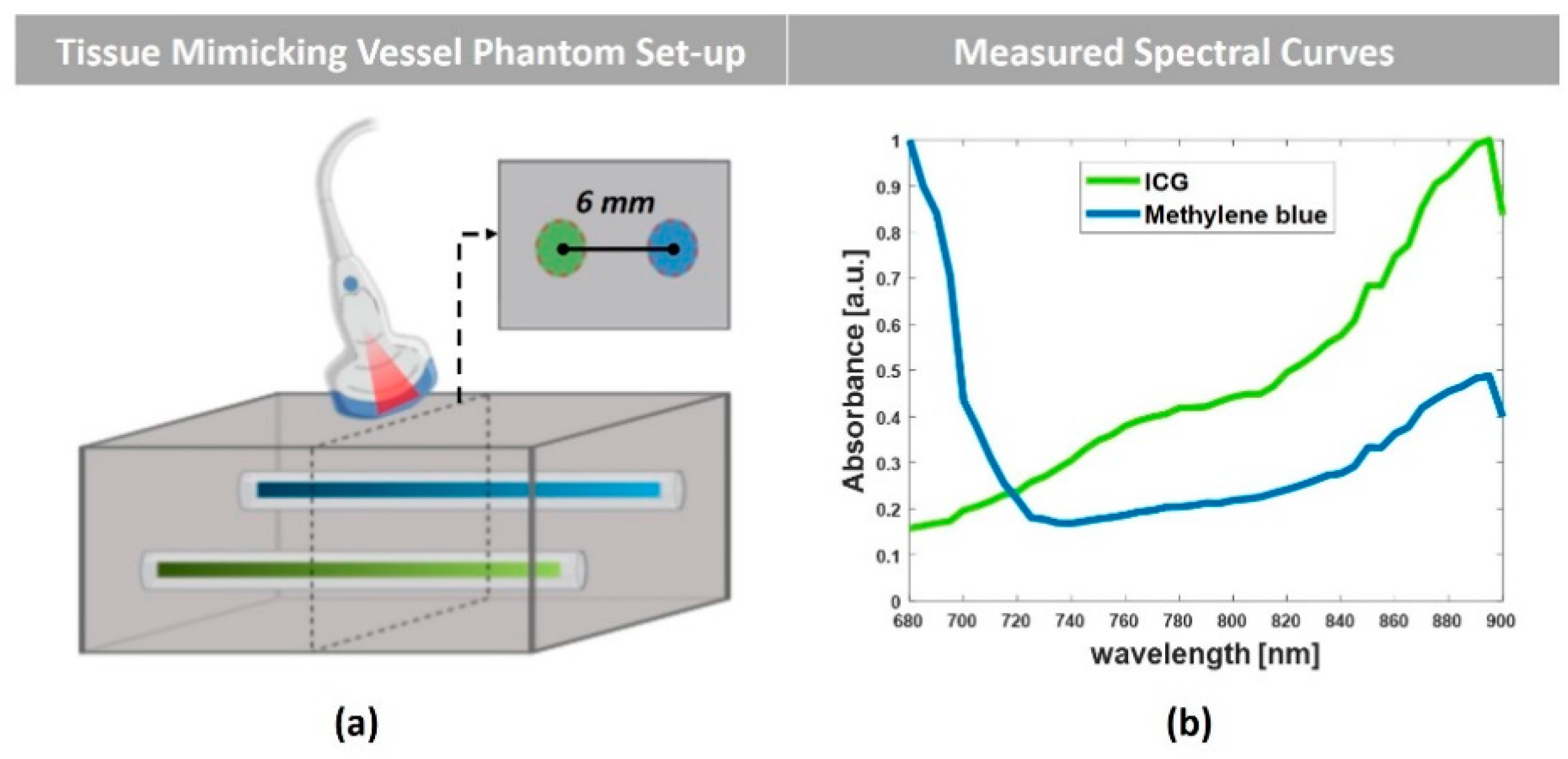
3.2. Experimental Set-Up and Tissue-Mimicking Vessel Phantom
3.3. In-Vivo Study
4. Results and Discussion
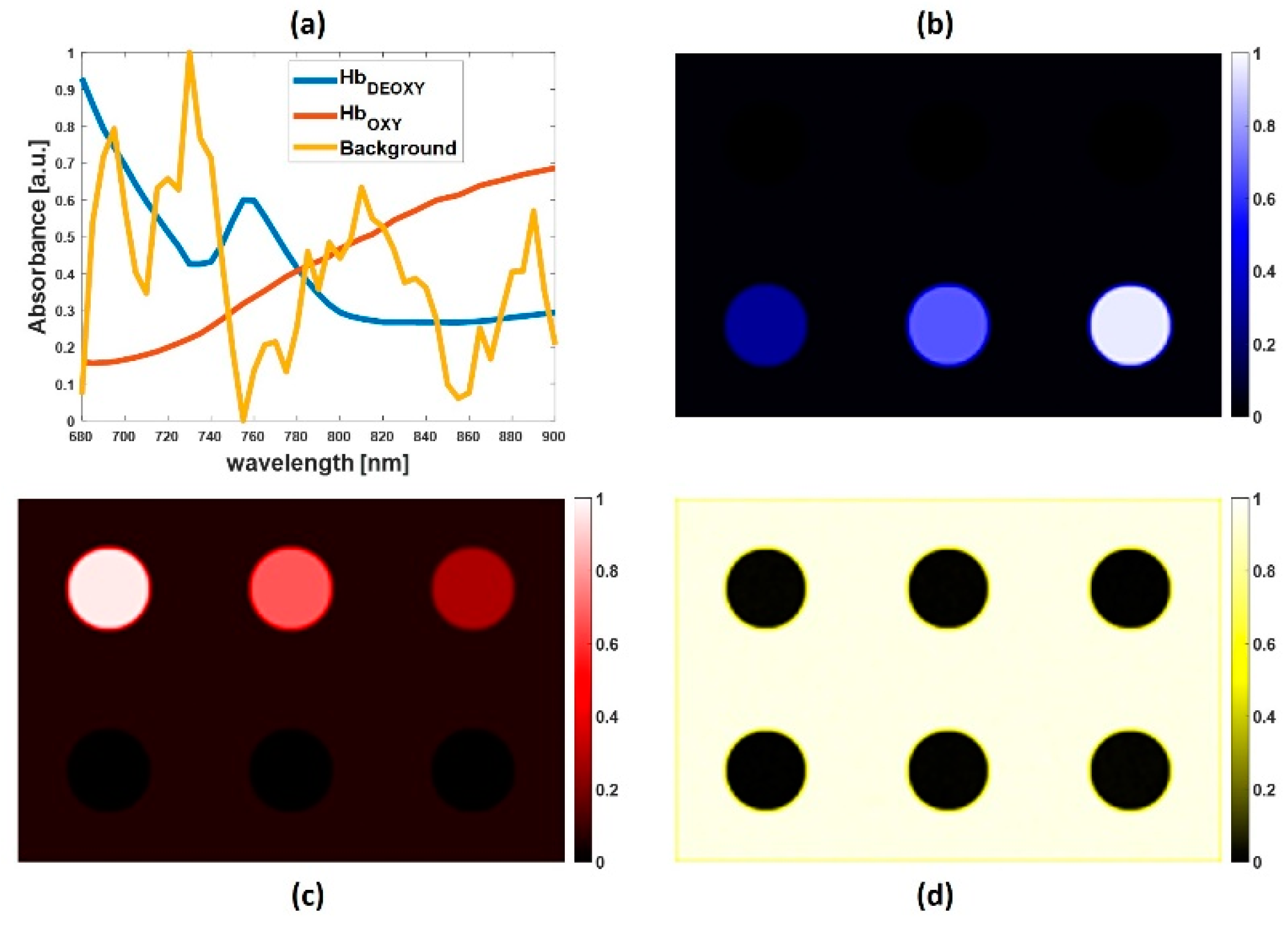
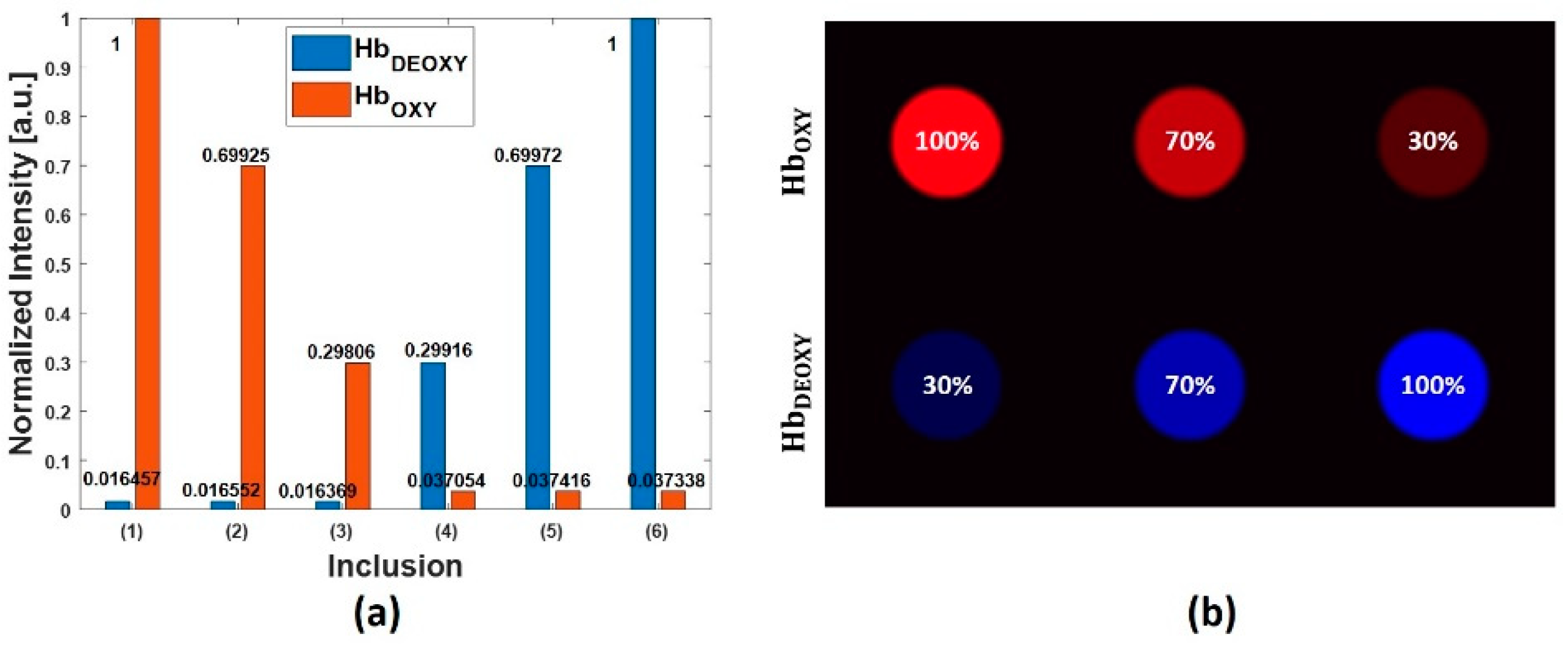
4.1. Simulated Multispectral PA Images
4.2. Tissue-Mimicking Vessel Phantom
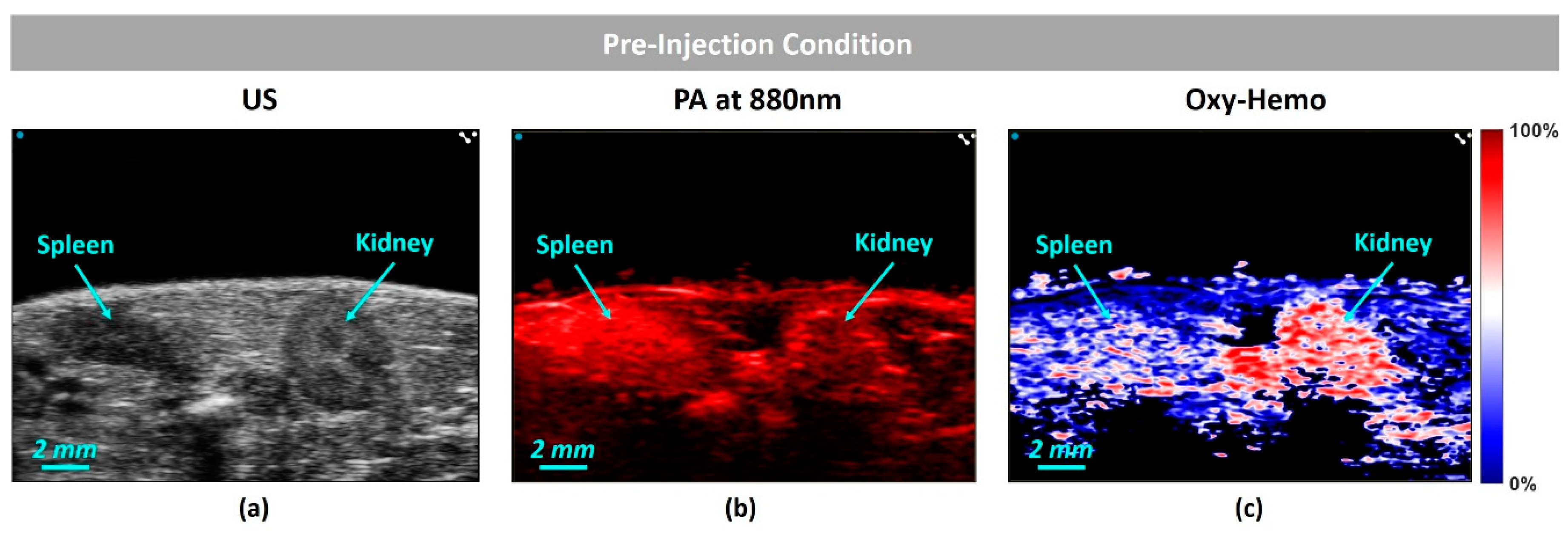
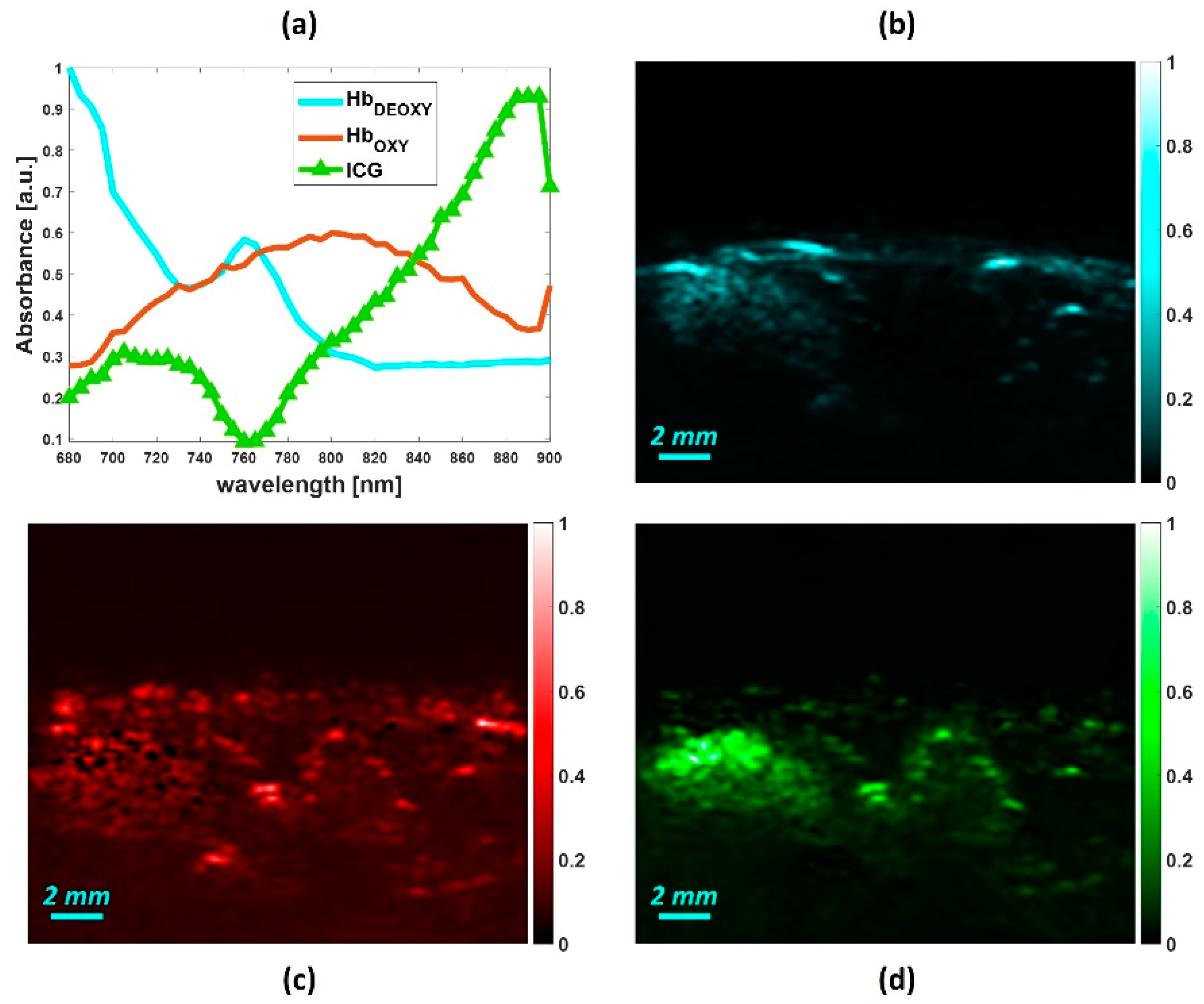
4.3. In-Vivo Study
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cox, B.; Laufer, J.G.; Arridge, S.R.; Beard, P.C. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012, 17, 061202. [Google Scholar] [CrossRef] [PubMed]
- Razansky, D.; Vinegoni, C.; Ntziachristos, V. Multispectral photoacoustic imaging of fluorochromes in small animals. Opt. Lett. 2007, 32, 2891. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, J.; Kaplan, B.; Powell, S.; Prohaska, S.; Laufer, J. Quantitative PA tomography of high resolution 3-D images: Experimental validation in a tissue phantom. Photoacoustics 2020, 17, 100157. [Google Scholar] [CrossRef] [PubMed]
- Jnawali, K.; Chinni, B.; Dogra, V.; Rao, N. Automatic cancer tissue detection using multispectral photoacoustic imaging. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 309–320. [Google Scholar] [CrossRef]
- Needles, A.; Heinmiller, A.; Sun, J.; Theodoropoulos, C.; Bates, D.; Hirson, D.; Yin, M.; Foster, F. Development and initial application of a fully integrated photoacoustic micro-ultrasound system. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 888–897. [Google Scholar] [CrossRef]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Diot, G.; Metz, S.; Noske, A.; Liapis, E.; Schroeder, B.; Ovsepian, S.V.; Meier, R.; Rummeny, E.; Ntziachristos, V. Multispectral Optoacoustic Tomography (MSOT) of human breast cancer. Clin. Cancer Res. 2017, 23, 6912–6922. [Google Scholar] [CrossRef]
- Wilson, K.E.; Wang, T.Y.; Willmann, J.K. Acoustic and photoacoustic molecular imaging of cancer. J. Nucl. Med. 2013, 54, 1851–1854. [Google Scholar] [CrossRef]
- Heijblom, M.; Piras, D.; van den Engh, F.M.; van der Schaaf, M.; Klaase, J.M.; Steenbergen, W.; Manohar, S. The state of the art in breast imaging using the Twente Photoacoustic Mammoscope: Results from 31 measurements on malignancies. Eur. Radiol. 2016, 26, 3874–3887. [Google Scholar] [CrossRef]
- Bauer, D.R.; Olafsson, R.; Montilla, L.G.; Witte, R.S. 3-D photoacoustic and pulse echo imaging of prostate tumor progression in the mouse window chamber. J. Biomed. Opt. 2011, 16, 026012. [Google Scholar] [CrossRef]
- Margolis, R.; Wessner, C.; Stanczak, M.; Liu, J.B.; Li, J.; Nam, K.; Forsberg, F.; Eisenbrey, J.R. Monitoring Progression of Ductal Carcinoma In Situ Using Photoacoustics and Contrast-Enhanced Ultrasound. Transl. Oncol. 2019, 12, 973–980. [Google Scholar] [CrossRef] [PubMed]
- Gargiulo, S.; Albanese, S.; Mancini, M. State-of-the-Art Preclinical Photoacoustic Imaging in Oncology: Recent Advances in Cancer Theranostics. Contrast Media Mol. Imaging 2019, 2019, 5080267. [Google Scholar] [CrossRef] [PubMed]
- Jose, J.; Manohar, S.; Kolkman, R.G.M.; Steenbergen, W.; Leeuwen, T.G. Van Imaging of tumor vasculature using Twente photoacoustic systems. J. Biophotonics 2009, 717, 701–717. [Google Scholar] [CrossRef] [PubMed]
- Manohar, S.; Dantuma, M. Current and future trends in photoacoustic breast imaging. Photoacoustics 2019, 16, 100134. [Google Scholar] [CrossRef] [PubMed]
- Rao, A.P.; Bokde, N.; Sinha, S. Photoacoustic imaging for management of breast cancer: A literature review and future perspectives. Appl. Sci. 2020, 10, 767. [Google Scholar] [CrossRef]
- Liu, S.; Wang, H.; Zhang, C.; Dong, J.; Liu, S.; Xu, R.; Tian, C. In Vivo Photoacoustic Sentinel Lymph Node Imaging Using Clinically-Approved Carbon Nanoparticles. IEEE Trans. Biomed. Eng. 2019. [Google Scholar] [CrossRef]
- Jose, J.; Grootendorst, D.J.; Vijn, T.W.; van Leeuwen, T.G.; Steenbergen, W.; Manohar, S.; Wouters, M.; Ruers, T.J.; van Boven, H. Initial results of imaging melanoma metastasis in resected human lymph nodes using photoacoustic computed tomography. J. Biomed. Opt. 2011, 16, 096021. [Google Scholar] [CrossRef]
- Alaeian, M.; Orlande, H.R.B.; Machado, J.C. Temperature estimation of inflamed bowel by the photoacoustic inverse approach. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3300. [Google Scholar] [CrossRef]
- Sheikh, R.; Cinthio, M.; Dahlstrand, U.; Erlov, T.; Naumovska, M.; Hammar, B.; Zackrisson, S.; Jansson, T.; Reistad, N.; Malmsjo, M. Clinical Translation of a Novel Photoacoustic Imaging System for Examining the Temporal Artery. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 472–480. [Google Scholar] [CrossRef]
- Xia, W.; Singh, M.K.A.; Maneas, E.; Sato, N.; Shigeta, Y.; Agano, T.; Ourselin, S.; West, S.J.; Desjardins, A.E. Handheld real-time LED-based photoacoustic and ultrasound imaging system for accurate visualization of clinical metal needles and superficial vasculature to guide minimally invasive procedures. Sensors 2018, 18, 1394. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, X.; Dong, X.; Yuan, J.; Fabiilli, M.L.; Wang, X. LEd-based photoacoustic imaging for monitoring angiogenesis in fibrin scaffolds. Tissue Eng. Part C Methods 2019, 25, 523–531. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.; Xu, G.; Zhu, Y.; Burton, M.; Sarazin, J.; Schiopu, E.; Gandikota, G.; Wang, X. Detecting joint inflammation by an LED-based photoacoustic imaging system: A feasibility study. J. Biomed. Opt. 2018, 23, 110501. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Xu, G.; Yuan, J.; Jo, J.; Gandikota, G.; Demirci, H.; Agano, T.; Sato, N.; Shigeta, Y.; Wang, X. Light emitting diodes based photoacoustic imaging and potential clinical applications. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Razansky, D.; Distel, M.; Vinegoni, C.; Ma, R.; Perrimon, N.; Köster, R.W.; Ntziachristos, V. Multispectral opto-acoustic tomography of deep-seated fluorescent proteins in vivo. Nat. Photonics 2009, 3, 412–417. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.R.; Beard, P.C. Estimating chromophore distributions from multiwavelength photoacoustic images. JOSA A 2009, 26, 443–455. [Google Scholar] [CrossRef]
- Glatz, J.; Deliolanis, N.C.; Buehler, A.; Razansky, D.; Ntziachristos, V. Blind source unmixing in multi-spectral optoacoustic tomography. Opt. Express 2011, 19, 3175. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Principal components analysis. Int. Encycl. Educ. 2010, 374–377. [Google Scholar]
- Hyvärinen, A. Independent component analysis: Recent advances. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110534. [Google Scholar] [CrossRef]
- Le, Q.V.; Karpenko, A.; Ngiam, J.; Ng, A.Y. ICA with reconstruction cost for efficient overcomplete feature learning. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation, Inc.: San Diego, CA, USA, 2011; pp. 1017–1025. [Google Scholar]
- Ngiam, J.; Koh, P.W.; Chen, Z.; Bhaskar, S.; Ng, A.Y. Sparse filtering. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation, Inc.: San Diego, CA, USA, 2011; pp. 1125–1133. [Google Scholar]
- Wang, P.; Wang, P.; Wang, H.-W.; Cheng, J.-X. Mapping lipid and collagen by multispectral photoacoustic imaging of chemical bond vibration. J. Biomed. Opt. 2012, 17, 0960101. [Google Scholar] [CrossRef]
- Arabul, M.U.; Rutten, M.C.M.; Bruneval, P.; van Sambeek, M.R.H.M.; van de Vosse, F.N.; Lopata, R.G.P. Unmixing multi-spectral photoacoustic sources in human carotid plaques using non-negative independent component analysis. Photoacoustics 2019, 15, 100140. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Lil, S.; Hou, X.; Zhangl, H.; Cheng, Q. Learning Spatially Localized, Parts-B ased Representation. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Buciu, I. Non-negative matrix factorization, a new tool for feature extraction: Theory and applications. Int. J. Comput. Commun. Control 2008, 3, 67–74. [Google Scholar]
- Li, L.; Yang, J.; Xu, Y.; Qin, Z.; Zhang, H. Documents clustering based on max-correntropy nonnegative matrix factorization. Proc. Int. Conf. Mach. Learn. Cybern. 2014, 2, 850–855. [Google Scholar]
- Luo, X.; Zhou, M.; Xia, Y.; Zhu, Q. An efficient non-negative matrix-factorization-based approach to collaborative filtering for recommender systems. IEEE Trans. Ind. Inform. 2014, 10, 1273–1284. [Google Scholar]
- Montcuquet, A.-S.; Herve, L.; Garcia, F.P.N.Y.; Dinten, J.-M.; Mars, J.I. Nonnegative matrix factorization: A blind spectra separation method for in vivo fluorescent optical imaging. J. Biomed. Opt. 2010, 15, 56009. [Google Scholar]
- Lipovetsky, S. PCA and SVD with nonnegative loadings. Pattern Recognit. 2009, 42, 68–76. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2001; pp. 556–562. [Google Scholar]
- Prahl, S. Tabulated Molar Extinction Coefficient for Hemoglobin in Water. Available online: https://omlc.org/index.html (accessed on 5 June 2020).
- Toumia, Y.; Cerroni, B.; Trochet, P.; Lacerenza, S.; Oddo, L.; Domenici, F.; Paradossi, G. Performances of a Pristine Graphene—Microbubble Hybrid Construct as Dual Imaging Contrast Agent and Assessment of Its Biodistribution by Photoacoustic Imaging. Part. Part. Syst. Charact. 2018, 35, 1800066. [Google Scholar] [CrossRef]
- Song, W.; Tang, Z.; Zhang, D.; Burton, N.; Driessen, W.; Chen, X. RSC Advances Comprehensive studies of pharmacokinetics and biodistribution of indocyanine green and liposomal indocyanine green by multispectral optoacoustic. RSC Adv. 2014, 5, 3807–3813. [Google Scholar] [CrossRef]
- Gröhl, J.; Kirchner, T.; Adler, T.; Maier-Hein, L. Estimation of blood oxygenation with learned spectral decoloring for quantitative photoacoustic imaging (LSD-qPAI). arXiv 2019, arXiv:1902.05839. [Google Scholar]
- Brochu, F.M.; Joseph, J.; Tomaszewski, M.; Bohndiek, S.E. Light fluence correction for quantitative determination of tissue absorption coefficient using multi-spectral optoacoustic tomography. In Proceedings of the European Conference on Biomedical Optics 2015, Munich, Germany, 21–25 June 2015; p. 95390Z. [Google Scholar]

| Data Set-Up | Chromophores | Correlation Value |
|---|---|---|
| Synthetic data | Oxyhemoglobin | 1 |
| Deoxyhemoglobin | 1 | |
| Vessel mimicking phantom | ICG | 0.9943 |
| Methylene Blue | 0.8344 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grasso, V.; Holthof, J.; Jose, J. An Automatic Unmixing Approach to Detect Tissue Chromophores from Multispectral Photoacoustic Imaging. Sensors 2020, 20, 3235. https://doi.org/10.3390/s20113235
Grasso V, Holthof J, Jose J. An Automatic Unmixing Approach to Detect Tissue Chromophores from Multispectral Photoacoustic Imaging. Sensors. 2020; 20(11):3235. https://doi.org/10.3390/s20113235
Chicago/Turabian StyleGrasso, Valeria, Joost Holthof, and Jithin Jose. 2020. "An Automatic Unmixing Approach to Detect Tissue Chromophores from Multispectral Photoacoustic Imaging" Sensors 20, no. 11: 3235. https://doi.org/10.3390/s20113235
APA StyleGrasso, V., Holthof, J., & Jose, J. (2020). An Automatic Unmixing Approach to Detect Tissue Chromophores from Multispectral Photoacoustic Imaging. Sensors, 20(11), 3235. https://doi.org/10.3390/s20113235





