Abstract
Global Navigation Satellite System (GNSS) operation can be affected by several environmental factors, of which ionospheric scintillation is one of the most significant. Scintillation is usually characterized by two indices, namely the amplitude scintillation index (S4) and phase scintillation index (σφ). However, these two indices can only be generated by specialized GNSS receivers, which are not widely available all around the world. To popularize the study of scintillation, this article proposes to use more accessible parameters, namely multipath (MP) and rate of change of total electron content index (ROTI), to characterize scintillation. Using GPS data obtained on six days in total from three stations, namely PRU2 and SAO0P located in Sao Paulo, Brazil and SNA0P located in Antarctica, respectively, both the time series plots and 2D maps were generated to investigate the relationship of scintillation indices (S4 and σφ) with MP and ROTI. To prevent the effect of the real multipath error, a 30-degree satellite elevation mask is applied to all the data. As the scintillation indices S4 and σφ have a sampling interval of 1 min, MP and ROTI are calculated with the same sampling interval for a more direct comparison. The results show that the structural similarity (SSIM) and correlation coefficient (CC) between parameters was greater than 0.7 for 70% of outputs. In addition, the variogram and cross-variogram are applied to investigate the spatial structure of the MP, ROTI, S4 and σφ in order to support the results of SSIM and CC. With outputs in three forms, promising spatial and temporal relationships between parameters was observed.
1. Introduction
Ionospheric scintillation is one of the main error sources that can reduce the quality of positioning outputs or even lead to loss of lock on satellites, and hence can cause significant errors in Global Navigation Satellite System (GNSS) receiver operation [1]. A series of methods have been implemented to mitigate scintillation effects on positioning. For instance, in Aquino et al. [2], the tracking error variances of GNSS receiver phase locked loop (PLL) and delay locked loop (DLL) is used to modify the least squares stochastic model and the positioning accuracy was shown to be improved by 17–21%. Furthermore, Bougard et al. [3] attempted to exclude scintillation affected satellites from the positioning calculation with the technique of receiver autonomous integrity monitoring (RAIM) specific for precise point positioning (PPP), which considerably improved the PPP accuracy. Loss of signal lock and cycle slips are the primary problems under scintillation, which are relatively severe when using a single satellite constellation. Therefore, it was proposed that the data of GPS and GLONASS could be integrated to obtain more reliable positioning solutions under moderate to strong scintillation [4], which improves the accuracy of the positioning output by 60% compared to using GPS alone. By using these approaches, the effects of scintillation can be mitigated to a certain extent. However, specialized receivers that can generate the scintillation indices, namely the amplitude scintillation index (S4) and phase scintillation index (σφ) [5] are not available worldwide, which limits the application of these approaches. Though the S4 index can be computed with low-cost receivers or common geodetic GNSS receivers [6,7], the σφ index cannot be generated in the same way. In order to overcome this problem, it is proposed to investigate the relationship of two parameters, namely multipath (MP) and rate of change of total electron content index (ROTI), that can be obtained from standard generic receivers to represent scintillation indices (S4 and σφ).
Studies on the relationship between scintillation and MP or ROTI were initiated respectively by Romano et al. [8] and Basu et al. [9]. According to Romano [8], a certain relationship can be observed between MP and scintillation parameters. Specifically, MP has a negative influence on the presentation of ionospheric scintillation [8]. Hancock et al. [10] also demonstrated an agreement between MP and scintillation parameters. It has been demonstrated previously that ROTI can be used to indicate the occurrence of scintillation [9]. It has been further demonstrated that the correlation between ROTI and scintillation parameters is strong with a correlation coefficient exceeding 0.6 on average, even higher than 0.8 sometimes [11]. In this paper, the relationship between MP and ROTI with S4 and σφ in both the spatial and temporal domains is investigated. Additionally, propagation patterns of all four parameters are studied to investigate the spatial similarity over time.
The purpose of this study is to investigate the relationship of S4 and σφ with MP and ROTI. Several objectives are set as follows:
- (1)
- Compare the time series plots of the four parameters to observe the temporal relationship to confirm if during periods of scintillation all parameters are similarly affected.
- (2)
- Thereafter, two types of 2D maps are constructed, mean value maps and occurrence percentage maps, where the former is to evaluate whether abnormally high value areas are in similar spatial regions and the latter is to investigate the referred areas with clearer outputs. As scintillation mainly occurs at night and in the early morning local time, the maps are first generated with a period of 6 h.
- (3)
- Furthermore, the maps with 5 min periods are generated to observe the relationship during times when the largest variations of the parameters are observed.
- (4)
- Finally, the structural similarity (SSIMs) and Pearson correlation coefficient (CC) between maps are calculated to evaluate the similarity between the parameters. Variograms and cross-variograms are also used to evaluate the spatial correlation in the maps.
2. Materials and Methods
2.1. Data and Instrumentation
Data used in this study were collected from three stations, PRU2 (51.41° W, 22.12° S), SAO0P (46.65° W, 23.55° S) located in Sao Paulo, Brazil and SNA0P (2.84° W, 71.67° S) located in Antarctica. The receivers in PRU2, SAO0P and SNA0P stations are Septentrio PolaRxS 2.1.1, Septentrio PolaRxS 2.9.6 located in Sao Paulo, Brazil and Septentrio PolaRxS 2.9.0 located in Antarctica, respectively. The Septentrio PolaRxS is a multi-frequency multi-constellation receiver specialized for monitoring ionospheric activity. As scintillation activity is mainly strong in two global areas, namely the equatorial and polar regions, where the causes leading to the generation of scintillation are completely different [12], data from three stations located in these two regions is used. All the parameters are acquired with a sampling interval of 1 min for the purpose of comparison.
2.2. Software
MATLAB version 2019a and TEQC [13,14] were the main software used in this study. MATLAB was used for calculation and visualization, whereas TEQC was utilized to generate quality control (QC) parameters. The R Language and Environment for Statistical Computing [15] (Version 3.5.1) and the R package gstat (Version 1.1–6) [15,16,17] was used for the geostatistical computations.
2.3. ROTI
ROTI is one of the two standard parameters that is calculated. The Total Electron Content (TEC) is obtained first, according to Holding [18]:
where is the geometric distance including errors; is 1 or 2, representing two frequencies; is the true geometric distance between the satellite and receiver; is the speed of the light; is the receiver clock error; is the satellite clock error; is code bias caused by receiver hardware delay; is code biases caused by satellite hardware delay; is the ionospheric delay; is the tropospheric delay; is the multipath error (i.e., multipath pseudo range error); and represents other unconsidered errors. Then raw TEC values can be calculated with Equations (2)–(4):
where is the frequency of the GNSS signal and the subscript is as mentioned above. STEC is the slant TEC representing the TEC along the satellite-receiver link. STEC can be converted into vertical TEC (VTEC) using the mapping function defined in [18] as:
where is radius of the Earth and is the height of the ionosphere layer. ROTI is defined as the standard deviation of the rate of VTEC (ROT) as in [19]:
In this study, the ROTI estimated over a 5-min interval is used, which was originally defined by Pi et al. [19]. Additionally, the moving average is applied in ROTI calculation so that the time interval is the same as other parameters.
2.4. MP
Multipath is a type of interference to GNSS receivers which is caused by reflected signals. In this paper, a 30° satellite elevation mask is applied to all the parameters, which removes most of the multipath effects. An assumption is then made that in general, MP values that are higher than average for signals above 30° during scintillation events are likely to be affected by scintillation and not multipath. MP1 and MP2 can be calculated using Equations (9) and (10) defined in [13]:
where is the pseudorange observable for frequency ; is the phase observable for frequency ; is the carrier phase multipath for frequency ; , where is the frequency of signal ; is a bias terms, which is defined as:
where is the integer wavelength phase ambiguity for frequency . In this paper, MP1 and MP2 are generated using the quality control (QC) command of the TEQC software on the receiver independent exchange format (RINEX) version 2.11 files from the three stations, which include both observation and navigation files [14].
2.5. Ionospheric Pierce Point (IPP)
As this study focuses on ionospheric effects, the results are analyzed at the ionospheric boundary, where the IPP coordinates are calculated. Prior to that, an intermediate quantity, which is the intersection angle of receiver and the IPP to the center of Earth, is calculated using Equation (13):
where is the elevation angle of the satellite from the receiver. The coordinates of the IPP can then be calculated in latitude and longitude using Equations (14) and (15):
where and are respectively the latitude and longitude of the receiver position; is the azimuth angle of the satellite from the receiver.
2.6. Methodology
Figure 1 shows the flowchart of the methodology. As shown in Figure 1, 30° cutoff is applied to all the data. The time series plots of all four parameters are generated before normalization to observe the general relationship and the scintillation intensity. Then all the data is normalized using the normalization method namely P-Norm [20] as described in Section 2.9 so that the different parameters vary in the same range. Next, two types of maps are generated, the mean value map and the occurrence percentage map, where each map is generated using data from a single station with a spatial resolution of 1°. Mean value maps are generated first to investigate the spatial relationship, where the mean values are calculated for each grid cell. To achieve this the parameter values with the IPP coordinates located in the same grid are averaged and visualized on a map. After that, in order to more clearly visualize high values, occurrence percentage maps are generated. These show the percentage of values greater than a threshold for each 1° grid cell. The method for calculating the threshold is given in Equation (17). Compared with the mean value map, this map shows only the extreme values.
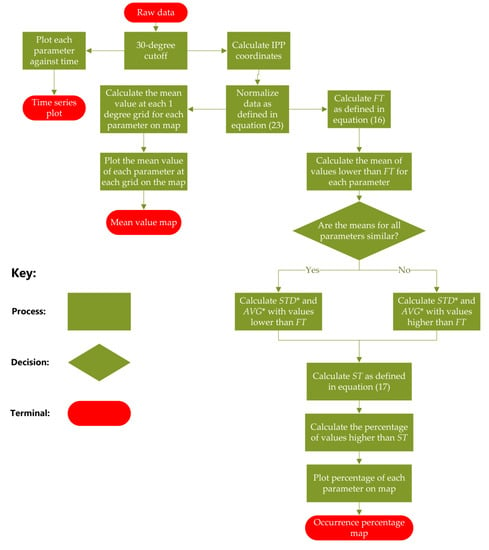
Figure 1.
Flow chart for data processing and visualization.
To generate these extreme values a threshold is applied, which is determined using the standard deviation and mean of values for each parameter. For the Antarctic data, as the station is located in the high latitudes, phase scintillation is considerably more likely than amplitude scintillation [12,21]. Therefore, S4 is not considered for the Antarctic data, where MP, ROTI and σφ fluctuate with different magnitudes from each other during the period with low scintillation and with similar magnitudes to each other during scintillation period. In order to mitigate biases, the different parameters values should be filtered first, where the values lower than a threshold as defined in Equation (17) are not used for occurrence percentage calculation.
This is realized by applying two thresholds, determined using Equations (16) and (17) below:
where and respectively represent the first threshold and the second threshold; and are the standard deviation and mean of all values for each parameter; and are the standard deviation and mean of values higher or lower than , dependent on the characteristics of the data, which is explained in more detail in Figure 1; x is a real number, which can be adjusted in order to distinctly show maps within different durations. For the Antarctic data, the size of the four parameters during the non-scintillation period are of different magnitude. Take the dataset in Antarctica on 2 April 2017 as an example, the mean of MP, ROTI, S4 and σφ during non-scintillation period (values lower than ) respectively are 0.00026, 0.0032, 0.00051, 0.00066, where ROTI is not of the same magnitude as the other three parameters. Therefore, values higher than the is used for the calculation. For the Brazilian data, the situation is different, the sizes of all four parameters during non-scintillation period vary with similar magnitude to each other. Take the dataset in Brazil on 13 September 2017 as an example, the mean of MP, ROTI, S4 and σφ during non-scintillation period (values lower than ) respectively are 0.00033, 0.00045, 0.00030 and 0.00057, which are similar to each other. Hence, the values lower than the are used for calculating for the Brazilian data. After following this process, the percentage of number of values larger than the thresholds can be drawn on each grid of maps. In this paper, thresholds are chosen to be relatively large (x is comparatively large) in order to show distinct extreme value areas on percentage occurrence maps.
In addition to generating mean value maps for 6 h, maps were also constructed for 5-min duration during scintillation period. Maps containing data for five minutes with scintillation are generated in order to compare parameters at more specific time.
2.7. Structural Similarity (SSIM) and Pearson Correlation Coefficient (CC)
The structural similarity index (SSIM) is an index for quantifying the similarity between two images. Three aspects are combined: luminance, contrast and structure [22]. These three components can show different characteristics of images. The comparison of luminance (), contrast () show the difference in the means and variances respectively whereas structure () quantifies the correlation. The similarities between images are higher with larger SSIM values. Therefore, SSIM is applied here for comparing maps of scintillation indices with those of MP and ROTI in order to describe spatial similarities. SSIM is calculated according to Equations (18)–(20) [22]:
where and are two non-negative image signals, is the mean of image m, is the mean of image , is the variance of image m, is the variance of image n, is the covariance between image and . The parameters and were introduced to prevent instability if the value of the denominator is small. Following convention = 0.01, and L is the dynamic range of the pixel values [22]. In this research, the default SSIM command in MATLAB version 2019a was used.
The correlation between and is defined as . This is estimated using the standard Pearson correlation coefficient (CC). Note from Equation (18) that this is the same as except for the inclusion of . CC and can differ substantially when CC is small. This can also lead to high values of SSIM.
2.8. Variograms
Geostatistics provides a set of tools and methods to analyze spatially referenced data. Of particular interest is a tool known as the sample variogram, which is defined as:
where is the semi-variance for two points separated by distance , is the attribute value at location and is the number of observations separated by distance . The variogram provides information about the spatial dependence and spatial structure in the data. When is small, the difference between two observations of , separated by is expected to be small. When is large, the difference is expected to be large. An example variogram for field observations of the heavy metal, Cadmium, is shown in Figure 2.
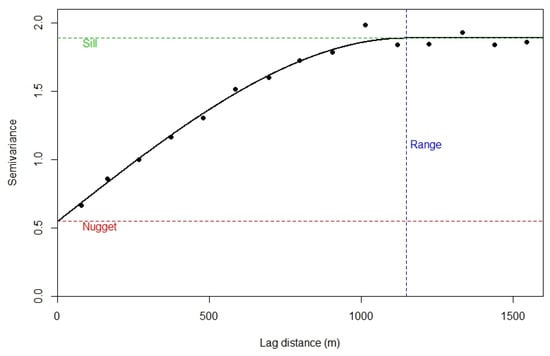
Figure 2.
Illustration of the sample variogram (black points) and modelled variogram (black line). This is for an example dataset of heavy metals from the River Meuse in the Netherlands (Pebesma, 2004).
The solid line in Figure 2 is a model that has been fitted to the sample variogram. This allows us to estimate for all values of . The model is parameterized by the sill, nugget and range. The variogram sill represents the maximum variability in the data. The nugget represents a combination of non-spatial variability and micro-scale variability (variability at lags less than ). The range is the limit of spatial correlation. We expect two observations separated by distances larger than the range to be uncorrelated. A flat variogram (commonly referred to as “pure nugget”) indicates that there is no spatial structure in the data.
The concept behind the variogram can be extended to consider the spatial cross-correlation between two variables. This allows us to investigate how correlated is with . The sample cross-variogram is given as:
The sample variogram and modelled variogram can be used as exploratory tools to investigate the spatial structure in a dataset. They can also be used in predictive mapping to interpolate datasets. The concepts are further explained in detail by Goovaerts et al. [23], Webster and Oliver [24] and Webster et al. [25]. Cressie [26] gives a more detailed theoretical treatment. Examples in remote sensing are given by Atkinson and Curran [27], Van der Meer [28] and Odongo et al. [29].
Here we use the variogram and cross-variogram to investigate the spatial structure in the four variables (MP, ROTI, S4, σφ) and to investigate the cross-correlation between the four variables. In all calculations we used degrees as the unit of distance. We acknowledge that it is preferred to work with a projected coordinate system. However, we defend this choice because we work with reasonably small distances and use the variogram for data exploration rather than for prediction.
2.9. Normalization
As various parameters vary greatly in their maximum and minimum values, normalization is applied so that parameters can be compared within a certain size range. P-Norm is applied in this research, which is defined by MATHWORKS [20] as Equations (23) and (24):
where is P-Norm; is the vector before normalization; is the serial number of ; is the total number of vectors; can be any positive real value, which is selected to be 2 here namely 2-Norm because it is the standard norm and most widely applied in P-Norm; is the normalized vector.
3. Results
3.1. Brazil Data
Figure 3a–c shows the time series of the four parameters, namely S4 (top row), σφ (second row from top), MP (third row from top) and ROTI (bottom row) respectively on 8 September 2017 and 13 September 2017 at SAO0P station and 12 March 2011 at PRU2 station.
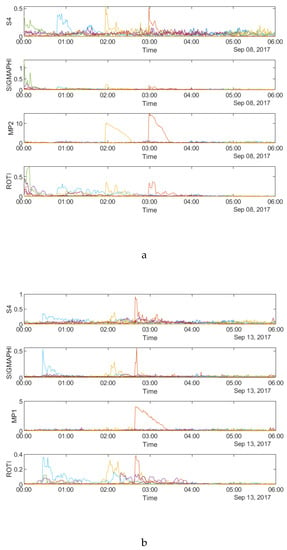
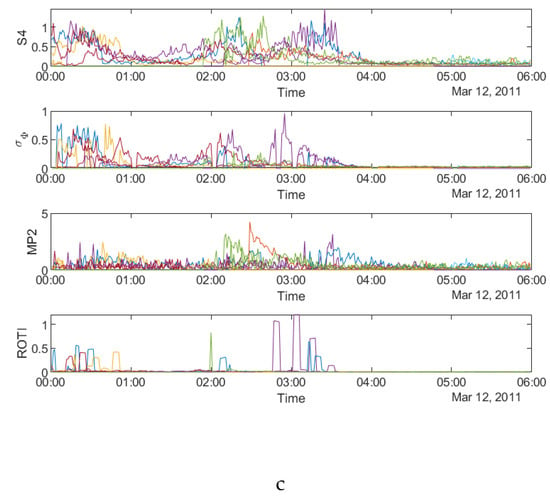
Figure 3.
Time series plots of four parameters: (a) during 00:00:00–06:00:00 UTC on 8 September, 2017 at SAO0P station; and (b) during 00:00:00-06:00:00 UTC on 13 September 2017 at SAO0P station; (c) during 00:00:00–06:00:00 UTC on 12 March 2011 at PRU2 station.
Figure 3 shows that all four parameters fluctuate during the first four hours on all the three days, which indicates a relationship between the parameters in the time domain. It can be seen from all the panels that there are fewer peaks on the MP plots which means that fewer satellites are affected by MP than scintillation. Figure 4a–c shows the time series plots of four parameters for a single satellite respectively on 8 September 2017 and 13 September 2017 at SAO0P station and 12 March 2011 at PRU2 station. As shown in Figure 4, the temporal relationship becomes clearer with the time series plots for a single satellite, where all four parameters have a similar peak period on each day.
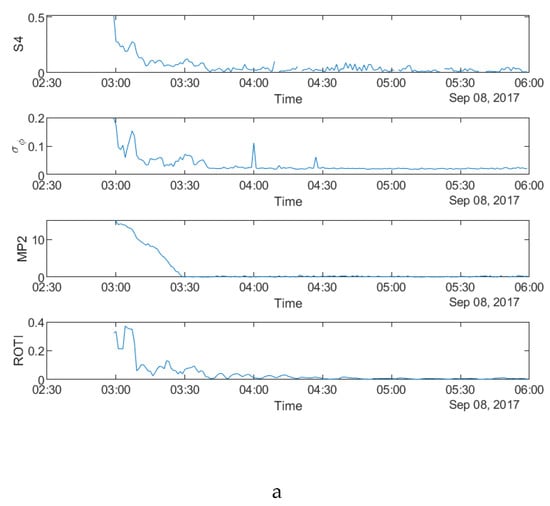
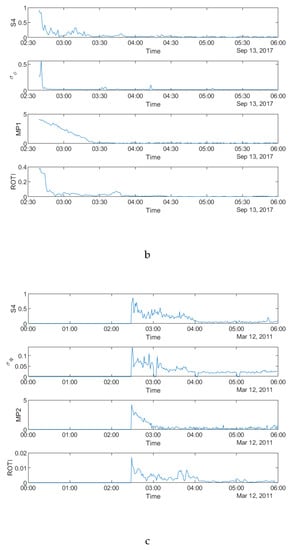
Figure 4.
Time series plots of four parameters: (a) during 00:00:00-06:00:00 UTC on 8 September 2017 for PRN10 at SAO0P station; (b) during 00:00:00–06:00:00 UTC on 13 September 2017 for PRN10 at SAO0P station; (c) during 00:00:00–06:00:00 UTC on 12 March 2011 for PRN25 at PRU2 station.
The panels a–c of Figure 5 show the spatial mean value 2D maps as a function of IPP latitude and longitude calculated in each 1° grid cell, for the four parameters respectively on 8 September and 13 September 2017 at SAO0P station and 12 March 2011 at PRU2 station.
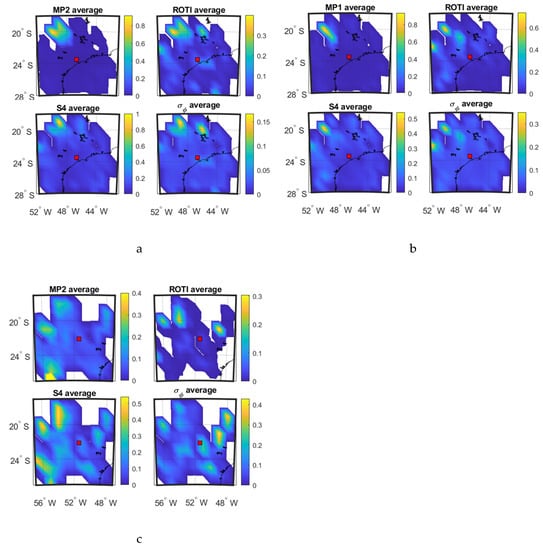
Figure 5.
Mean value maps of four parameters: (a) during 00:00:00–06:00:00 UTC on 8 September 2017 at SAO0P station; and (b) during 00:00:00–06:00:00 UTC on 13 September 2017 at SAO0P station; (c) during 00:00:00-06:00:00 UTC on 12 March 2011 at PRU2 station.
It can be observed from Figure 5a,b that the affected areas (shown in yellow) of all the parameters focus on the northwest corner on the maps, which indicates that there is a relationship between the parameters in the spatial domain. As shown in Figure 5c, high value areas of S4 and MP are both located on the left part of maps while ROTI agrees with σφ on the east part of maps, though ROTI also shows similarities in the northwest corner with S4. The same relationship pattern can also be observed from Figure 5a,b that MP mainly correlates with S4 while ROTI respectively correlates with part of S4 and σφ.
Table 1, Table 2 and Table 3 show the SSIM and CC calculated between the 4 parameters shown in Figure 5a–c respectively. From Table 1, Table 2 and Table 3, it is clear that MP is more correlated with S4 while ROTI is more highly correlated with σφ, although the CC in Table 3 shows a different pattern of ROTI. Most of the SSIM and CC values exceed 0.6 and some exceed 0.8. This indicates a high correlation between the parameters and a high level of structural similarity.

Table 1.
SSIM and CC between the maps shown in Figure 5a.

Table 2.
SSIM and CC between the maps shown in Figure 5b.

Table 3.
SSIM and CC between the maps shown in Figure 5c.
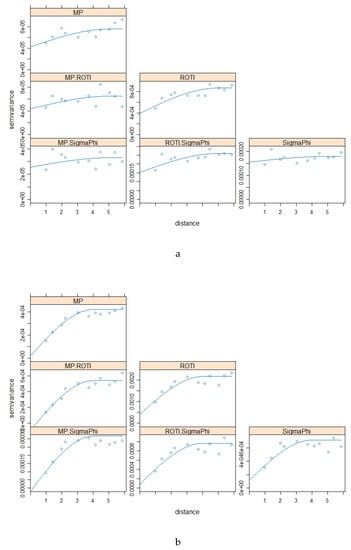
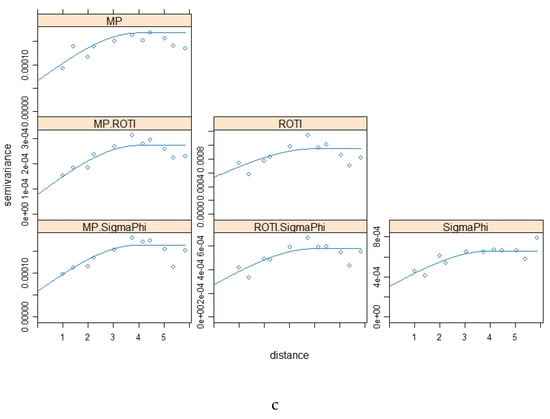
The variograms and cross variograms for Figure 5a,b,c are shown in Figure 6a,b,c respectively. The variogram and cross-variograms show clear evidence of spatial structure, with a range of approximately 5° to 6°. This shows that the four variables (parameters) co-vary, suggesting that they have similar spatial structures.
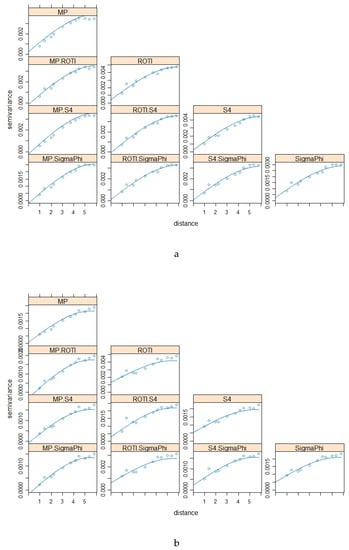
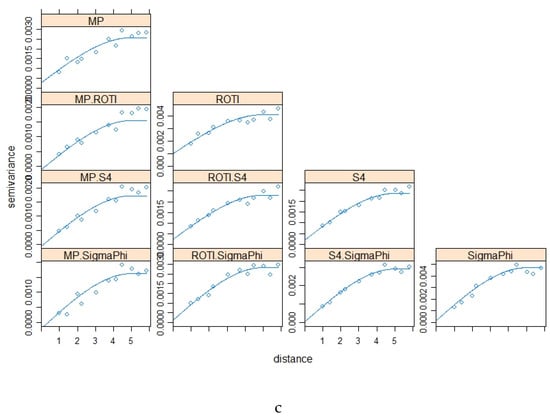
Figure 7a–c show the occurrence percentage maps as a function of IPP latitude and longitude for the four parameters on 8 September and 13 September 2017 at SAO0P station and 12 March 2011 at PRU2 station.
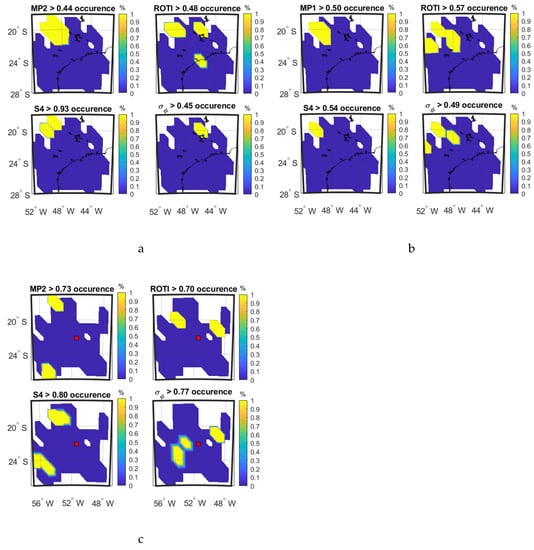
Figure 7.
Occurrence percentage maps of four parameters: (a) during 00:00:00–06:00:00 UTC on 8 September, 2017 at SAO0P station; (b) during 00:00:00–06:00:00 UTC on 13 September 2017 at SAO0P station; (c) during 00:00:00–06:00:00 UTC on 12 March 2011 at PRU2 station.
Figure 7a shows that high values of MP cover the high values of S4 while high values of ROTI cover high value of σφ. A similar result is observed in Figure 7b. For Figure 7c, high values of MP do not clearly overlap with high values of S4 and high values of ROTI do not clearly overlap with high values of σφ. These observations are reflected in the CC values shown in Table 4, Table 5 and Table 6.

Table 4.
SSIM and CC between the maps shown in Figure 7a.

Table 5.
SSIM and CC between the maps shown in Figure 7b.

Table 6.
SSIM and CC between the maps shown in Figure 7c.
Figure 8a–c shows the occurrence percentage maps as a function of IPP latitude and longitude of four parameters on 8 September and 13 September 2017 at SAO0P station and 12 March 2011 at PRU2 station during the period when the parameters show the largest variation as observed from Figure 3.
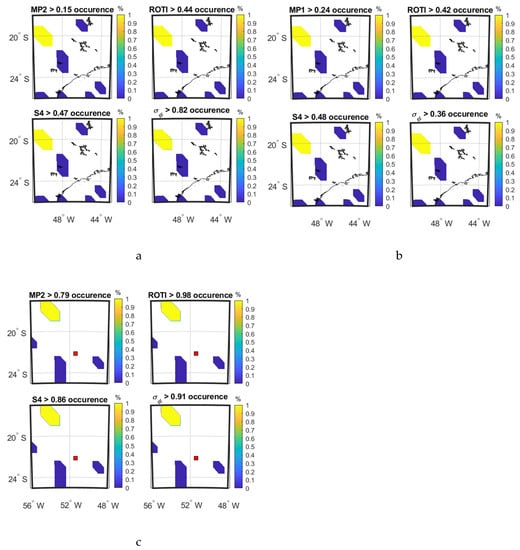
Figure 8.
Occurrence percentage maps of four parameters: (a) during 02:59:00–03:04:00 UTC on 8 September 2017 at SAO0P station; (b) during 02:39:00–02:44:00 UTC on 13 September 2017 at SAO0P statinon; (c) during 03:31:00–03:36:00 UTC on 12 March 2011 at PRU2 station.
Taking a data period of 5 min with scintillation, as shown in Figure 8, all the parameters are active at the same locations. The SSIM and CC between the parameters in the maps of Figure 8a,b,c are shown in Table 7, Table 8 and Table 9 respectively. These show that the four parameters are perfectly correlated in all four maps. The SSIMs are less than 1 in Table 7 and Table 8, indicating that the mean values of the parameters differ.

Table 7.
SSIM and CC between the maps shown in Figure 8a.

Table 8.
SSIM and CC between the maps shown in Figure 8b.

Table 9.
SSIM and CC between the maps shown in Figure 8c.
The time evolution of the four parameters at every 5 min interval on 08 September 2017 during 01:55–02:10 UT and on 13 September during 02:40–02:55 UT respectively are shown in Figure 9 and Figure 10, which are presented in the form of mean value maps. The SSIM and CC between the parameters in the maps of Figure 9 and Figure 10 are shown respectively in Table 10 and Table 11.
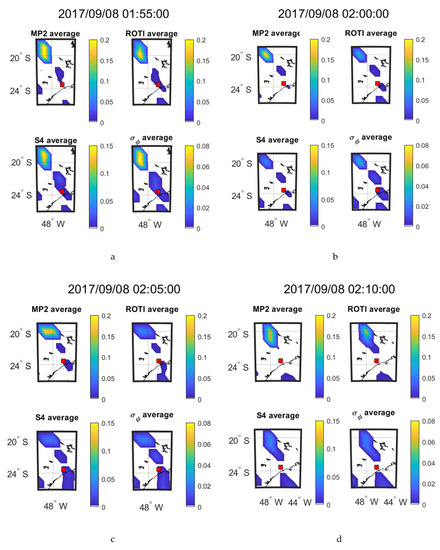
Figure 9.
Consecutive 5 min means over 20 min at SAO0P station on 8 September 2017.
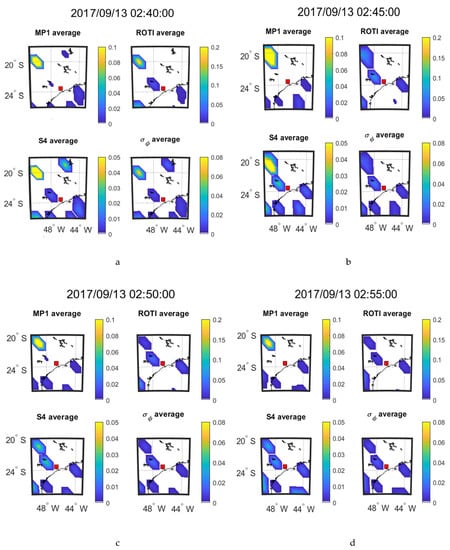
Figure 10.
Consecutive 5 min means over 20 min at SAO0P station on 13 September 2017.

Table 10.
SSIM and CC between the maps shown in Figure 9.

Table 11.
SSIM and CC between the maps shown in Figure 10.
As shown in Figure 9 and Figure 10, mean value maps with 5-min interval are constructed to observe the movements of scintillation and the corresponding change of other parameters. It can be seen from Figure 9 that large value areas (yellow areas) of all the parameters move toward southeast after 20-min propagation. Similarly, it can be observed from Figure 10 that large value areas of all the parameters move southeastward slightly over the 20 min. Therefore, MP, ROTI, S4 and σφ share the same propagation direction as observed on both the days from Figure 9 and Figure 10. Table 10 shows that the parameters in Figure 9 maintain very high correlations (CC) throughout the 20-min period. The SSIMs fluctuate due to changes in the mean values of the parameters. For Figure 10 and Table 11 shows that ROTI and S4 and ROTI and σφ maintain a high correlation across the 20-min period. The correlation between MP and S4 declines over the 20-min period. The correlation between MP and σφ is high in the first 5 min but drops sharply and these two parameters are uncorrelated for the remainder of the period.
3.2. Antarctica Data
The time series plots of the four parameters at SNA0P station on 2 April, 13 October 2016 and 9 May 2016 are shown respectively in Figure 11.
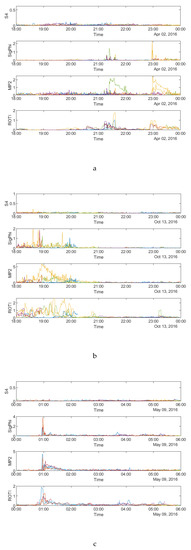
Figure 11.
Time series plots of four parameters at SNA0P station: (a) during 18:00:00–24:00:00 UTC on 2 April, 2016; (b) during 18:00:00–24:00:00 UTC on 13 October, 2016; (c) during 00:00:00–06:00:00 UTC on 9 May, 2016.
As shown in Figure 11, S4 does not have any high values on all three days whereas σφ still fluctuates in accordance with the feature of scintillation occurrence observed at high latitudes. Therefore, S4 is not considered for comparison in the following paragraphs. Furthermore, it can be seen that all the other three parameters are mainly noisy during the last three hours on 2 April 2016, between 18 and 21 UT on 13 October 2016 and first two hours on 9 May 2016. Different from the data of SAO0P station (Figure 3), the number of satellites affected by scintillation and MP is similar. Figure 12a–c shows the time series plots of the four parameters obtained from a single satellite at SNA0P station respectively on 2 April, 13 October 2016 and 9 May 2016. As shown in Figure 12, a similar high value period can be seen in plots of four parameters on 2 April 2016 and 9 May 2016 though a minor delay exists on 13 October 2016, which supports the temporal relationship between MP, ROTI and σφ.
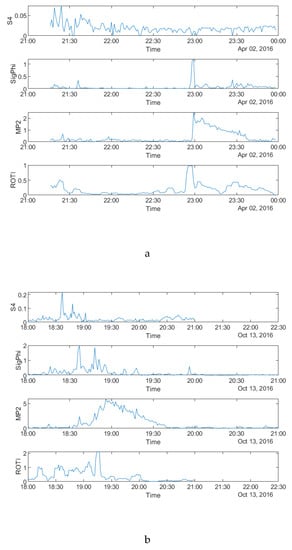
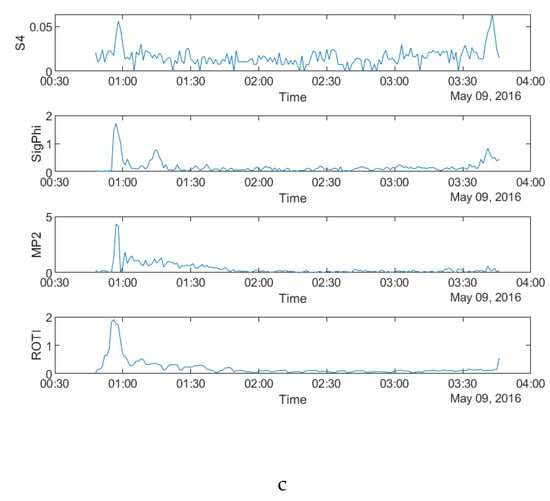
Figure 12.
Time series plots of four parameters at SNA0P station on: (a) during 18:00:00–24:00:00 UTC on 2 April 2016 for PRN03; (b) during 18:00:00–24:00:00 UTC on 13 October 2016 for PRN17; (c) during 00:00:00–06:00:00 UTC on 9 May 2016 for PRN08.
Figure 13 shows the mean value maps as a function of IPP latitude and longitude of the three parameters.
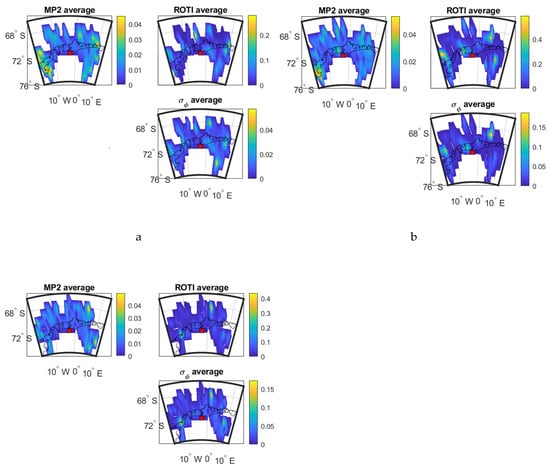
Figure 13.
Mean value maps of three parameters at SNA0P station: (a) during 18:00:00–24:00:00 UTC on 2 April 2016; (b) during 18:00:00–24:00:00 UTC on 13 October 2016; (c) during 00:00:00–06:00:00 UTC on 9 May 2016.
As shown in Figure 13, the mean value maps are not as distinct as those in Brazil which can be caused by the sparse distribution of data at the high latitude area. Therefore, the occurrence percentage maps are more useful to this dataset in order to show more details. However, it can still be seen that the high value areas of σφ maps include those of MP and ROTI maps. The SSIM and CC values between the parameters shown in Figure 13a–c are illustrated in Table 12, Table 13 and Table 14 respectively. As shown in Table 12, Table 13 and Table 14, SSIM values between MP&ROTI and σφ are all higher than 0.6, where most exceed 0.7. CC values in Table 12, Table 13 and Table 14 show low correlation between MP and σφ, the correlations between ROTI and σφ are high.

Table 12.
SSIM and CC between the maps shown in Figure 13a.

Table 13.
SSIM and CC between the maps shown in Figure 13b.

Table 14.
SSIM and CC between the maps shown in Figure 13c.
Figure 14 shows the variograms and cross variograms for the results presented in Figure 13. The variograms and cross-variograms do show evidence of a common spatial structure in the three parameters; however, this is less clear than those for the Brazil data. In particular there is no evidence of spatial correlation for the data from 2016 April 2 (Figure 13a). For 2016 October 13 the variograms and cross-variograms show a clear common spatial structure with a range of approximately 3.5°. For the dataset from 2016 May 9 there is weak evidence of spatial structure.
Figure 15 shows the occurrence percentage maps as a function of IPP latitude and longitude for the three parameters respectively on 2 April 2016, 13 October 2016 and 9 May 2016.
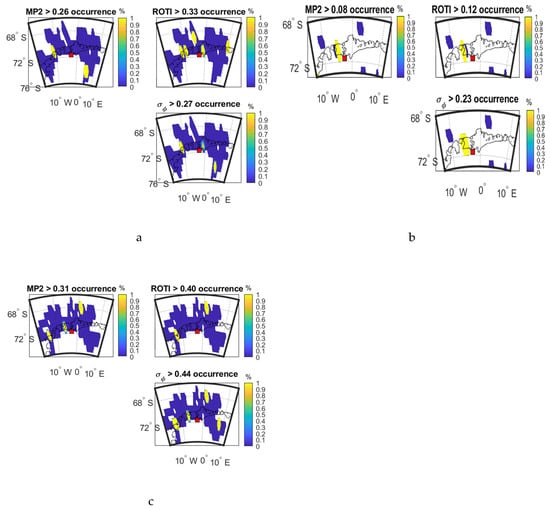
Figure 15.
Occurrence percentage maps of three parameters at SNA0P station: (a) during 18:00:00–24:00:00 UTC on 2 April 2016; (b) during 18:00:00–24:00:00 UTC on 13 October 2016; (c) during 00:00:00-06:00:00 UTC on 9 May 2016.
As shown in maps of Figure 15a, the high value areas of MP and ROTI separately correspond to different areas of σφ. For instance, some satellites signals less influenced by MP may be more affected by ROTI. Therefore, the combination of two parameters can cover more areas of σφ than a single parameter. As shown in Figure 15b, high-value areas of ROTI overlap high-value areas of σφ while MP does not. However, as shown in Figure 15c, MP includes more high-value areas that are spatially-coincident with high-value areas of σφ than ROTI on 9 May 2016.
Table 15, Table 16 and Table 17 show the SSIM and CC between the three parameters shown in Figure 15a–c.

Table 15.
SSIM and CC between the maps shown in Figure 15a.

Table 16.
SSIM and CC between the maps shown in Figure 15b.

Table 17.
SSIM and CC between the maps shown in Figure 15c.
Figure 16 shows the occurrence percentage maps as a function of IPP latitude and longitude of three parameters during the time period when largest variations were observed in Figure 11.
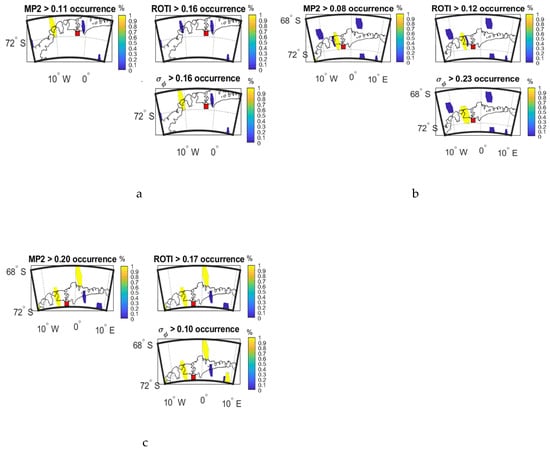
Figure 16.
Occurrence percentage maps of three parameters at SNA0P station: (a) during 22:59:00–23:04:00 UTC on 2 April 2016; (b) during 18:36:00–18:41:00 UTC on 13 October 2016; (c) during 01:01:00-01:06:00 UTC on 9 May 2016.
Figure 16a shows that, within a specific time period, MP has the same high-value area as σφ. Figure 16b shows that MP and ROTI both share the high-value areas with σφ. From Figure 16c, both MP and ROTI agree with σφ for most of the high value areas. These observations are reflected in the CC and SSIM values shown in Table 18, Table 19 and Table 20.

Table 18.
SSIM and CC between the maps shown in Figure 16a.

Table 19.
SSIM and CC between the maps shown in Figure 16b.

Table 20.
SSIM and CC between the maps shown in Figure 16c.
Figure 17 and Figure 18 show the time evolution of the three parameters during 23:10–23:25 on 2 April and during 18:50−19:05 on 13 October 2016, respectively. The SSIM and CC between the parameters in the maps of Figure 17 and Figure 18 are shown in Table 21 and Table 22.
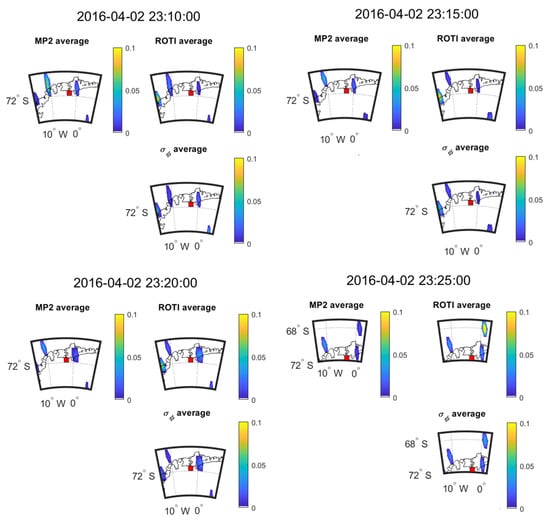
Figure 17.
Consecutive 5 min means over 20 min at SNA0P station on 2 April 2016.
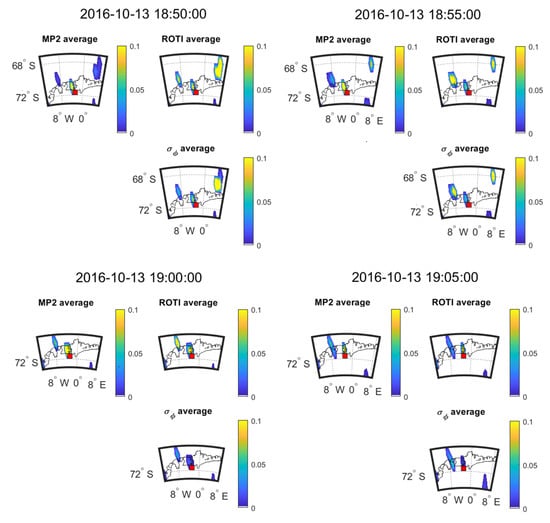
Figure 18.
Consecutive 5 min means over 20 min at SNA0P station on 13 October 2016.

Table 21.
SSIM and CC between the maps shown in Figure 17.

Table 22.
SSIM and CC between the maps shown in Figure 18.
Figure 17 and Figure 18 show the change in the 5-min mean values for 2016 April 2 and 2016 October 3 respectively. Figure 17 shows that large value areas of all the parameters move towards northeast across 20 min. However, in Figure 18, the large value areas of parameters move towards the southeast over the 20 min. Again, all the parameters have the same direction for propagation. The results shown in Table 21 and Table 22 are calculated from six and four points, respectively, leading to a high level of uncertainty in the estimation of CC and SSIM. As such we can only make qualitative observations on these plots and cannot back those observations up with reliable CC or SSIM results.
4. Discussion
Data obtained from three stations respectively located at equatorial and high-latitude areas are utilized in order to investigate the relationship between MP, ROTI, S4 and σφ. First, as shown in Figure 3, Figure 4, Figure 11 and Figure 12, the relationship in the temporal domain can be observed from all twelve time series plots, where all the parameters show the largest variations during the same time period. Figure 5 and Figure 13 illustrate the spatial relationship for 6-h mean value maps, where high value regions occur at same location on maps. ROTI and σφ have different high value areas as compared with MP and S4 in Figure 5. This is because the relationship between ROTI and σφ and between MP and S4 may differ between satellites, due to different effects of ionospheric scintillation. In addition, as shown in Figure 13, high value areas of both MP and ROTI correspond to those of σφ, but relate to different parts of the maps. Hence, it may be possible to identify areas affected by scintillation by combining MP and ROTI maps. It also suggests that MP and ROTI relate to different types of scintillation. This hypothesis can be further evaluated with the occurrence percentage maps. As shown in Figure 7, MP and ROTI separately show similar high value areas as S4 and σφ. As shown in Figure 15, MP and ROTI agree with σφ over different areas. Next, occurrence percentage maps for 5 min as shown in Figure 8 and Figure 16 suggest similar high value areas for all parameters. Finally, the propagation maps as shown in Figure 9, Figure 10, Figure 17, and Figure 18, where all the parameters move in the similar direction over time, further indicate the spatial similarity between MP&ROTI and S4&σφ.
The Pearson CC and SSIM were both used to quantify the relationship between pairs of maps. CC evaluates the linear correlation whereas SSIM provides a more complete evaluation of map similarity [30]. As discussed in Section 2.7 can be inflated at low values of CC leading to an overoptimistic assessment of the map similarity. For the Brazil data, most of the SSIMs and CCs between S4 and MP exceed those between S4 and ROTI while σφ correlates more with ROTI than MP. For the Antarctica data, both MP and ROTI sometimes have high similarities with σφ. The variograms and cross-variograms (Figure 6 and Figure 14) were used to illustrate the spatial correlation in the parameters as well the cross-correlation between parameters. The variograms show clear spatial structure, with a range of 5 to 6°, for the Brazil data. Likewise, the cross-variograms show a common spatial structure. Whereas CC quantifies the bi-variate correlation the cross-variograms quantifies whether the spatial structure is common between the different parameters. This gives evidence of strong spatial correlation between the four parameters and backs-up the results observed for the SSIM and CC. For the Antarctica case study there is clear evidence of spatial correlation for the dataset from 2016-10-13, with a common range of approximately 3.5°. There is less clear evidence for the dataset from 2016-05-09 (common range of approximately 3.5°) and no evidence of spatial correlation for the dataset from 2016-04-02
The purpose of this paper is to explore the relationship between MP, ROTI and scintillation parameters. We aim to better understand the relationships first, leaving open the possibility to use these relationships to provide supplementary information that may assist in overcoming the limitations of using specialized ionospheric scintillation monitoring receivers. The relationship between MP and scintillation has been investigated by Romano et al. [8] and shows that the presence of obstacles in the vicinity of receivers can lead to the increase of S4 that shows some agreement with areas of MP measured using code-carrier divergence (CCD) standard deviation. Romano et al. [8] also shows that a high percentage of the higher S4 values and CCD are below 30°. In this study, all data has a 30° satellite mask applied which should significantly reduce any MP effect in the vicinity of the station. Therefore, the high values of S4, σφ and MP in this study all occur for satellites at high elevations (>30°), giving support to the theory that the higher values of MP are being influenced by the scintillation events evidenced from the high scintillation indices values during the corresponding time window.
The relationship between MP values from the TEQC software and σφ was observed by Hancock et al. [10] through occurrence number plots and time series plots from data collected in Hong Kong, which provided initial evidence that the study of the relationship between MP and scintillation parameters may be interesting and of possible use in the mitigation of errors during scintillation events. Following on Romano et al. [8] and Hancock et al. [10] this study provides a much deeper statistical analysis of the relationships between MP, S4 and σφ. Furthermore, the ionospheric index ROTI is added in this study to give additional evidence that scintillation is real rather than a product of the physical environment around the receiver as claimed by Romano et al. [8].
The relationship between ROTI and scintillation has been investigated [9,11,31,32,33]. The scatter plot and the time series plot are common methods used in recent studies to demonstrate the linear relationship between ROTI, S4 and σφ [9,11,31,32]. Additionally, the relationship between ROTI and scintillation has been shown to be affected by changes in elevation angle [11]. Correlation coefficients have shown distinctly higher values when the satellite elevation angle exceeds 60° when compared to satellites with elevation angles lower than 60°. However, this investigation focuses on elevations higher than 30°, focusing on satellites with higher elevation angles thus taking advantage of the stronger relationship between scintillation and ROTI shown by Yang and Liu [11]. Analysis of the relationship between MP and the scintillation parameters with respect to the effects of elevation angle are not part of this study.
Acharya and Majumdar [33], used statistical analysis to conclude that the probability density distribution of S4 can be obtained using ROTI, thereafter, the occurrence probability of scintillation can be estimated. Therefore, Acharya and Majumdar [33] gives the conclusion about strong evidence of a relationship between ROTI and S4, which in general agrees with the analysis from this study. In addition, Carrano et al. [31] also demonstrated the theoretical relationship between ROTI and S4 and has demonstrated that this relationship is highly dependent on the sampling rate. They also provide reasons why this relationship varies between different dates and in different regions. These factors have not been investigated in this study and further work is required in this area. Therefore, the investigation on the relationship based on first principles and on the formulae between MP and scintillation is required in future work.
Investigations [9,31,32,33] focus on S4, where σφ was not investigated. Therefore, the investigation on σφ is less thorough than that on S4 based on the past research [9,31,32,33]. Though σφ was investigated by Yang and Liu [11], a comparison of how both scintillation indices are related to ROTI was not undertaken. According to the graphs given by Yang and Liu [11], S4 is more correlated with ROTI than σφ, which is caused by the relative inactivity of σφ (σφ shows a maximum value less than 0.4). In contrast, both S4 and σφ are analyzed and compared in this paper with reference to their relationships with ROTI. Furthermore, analysis from the stations in this study show evidence that ROTI is more similar to σφ than to S4 both visually and statistically, giving new valuable insights into the relationships between ROTI, S4 and σφ.
Previous research has focused principally on the linear relationship between ROTI and the scintillation parameters, this study adds to this body of research by investigating the spatial relationship. This leads to the possibility of using these data sets to generate scintillation risk maps, that may be similar in principle to tracking jitter maps generated Sreeja et al. [34], and also similar to Figure 4, Figure 5, Figure 6 and Figure 7 given by Koulour et al. in [35], which visualize the effect of scintillation and can be used to identify and possibly mitigate risk caused by scintillation events. Figure 2 from Sreeja et al. in [34] shows the S4 maps as a function of time and IPP latitude where strong scintillation activity was observed between 18° S and 26° S from 8pm to 0am local time on March 9–11, 2011. By comparison, Figure 3c, Figure 5c and Figure 7c in our paper show all the parameters are intense between 18° S and 26° S from 0 am to 4 am UTC (8 pm to 0 am in local time) on March 12 2011, which is similar to the output obtained by Sreeja et al. [34].
Additionally, ROTI is the major proxy to the scintillation parameters proposed in previous research, which has shown weaknesses in the ability of ROTI to replace S4 and σφ. In this research the relationship between ROTI and the scintillation parameters S4 and σφ has been further investigated and in addition this study shows that it may be possible to add MP as additional parameter, in support of other parameters such as ROTI, computed from a standard GNSS receiver (i.e., non-scintillation monitoring receiver) that may be indicative of scintillation. However, the increase of MP does not generally indicate the occurrence of scintillation events as the scintillation measurements can be contaminated by real multipath effects [8].
5. Conclusions
Six days of data under strong scintillation from three stations, respectively located in Brazil and Antarctica, are utilized to research on the relationship between MP and ROTI and scintillation indices. The relationship in the temporal and spatial domain is evaluated with a series of data science techniques, including 2D map comparison, Pearson CC, SSIM and variograms. The propagation patterns of all parameters are demonstrated to be similar. According to the discussion, it can be concluded that:
- (1)
- A relationship between MP, ROTI and scintillation exists in both temporal and spatial domain
- (2)
- An integration between MP and ROTI can more completely represent scintillation than a single parameter. Precisely, MP and ROTI can reflect different types of scintillation. For equatorial data, MP is more correlated with S4 while ROTI is more relevant to σφ. For high latitude data, it is possible for both MP and ROTI to be correlated with σφ.
- (3)
- The propagation patterns of MP, ROTI and S4, σφ are similar, which can contribute to the prediction of scintillation with MP and ROTI.
- (4)
- MP is correlated with scintillation only when scintillation is active while ROTI correlates with scintillation during both quiet and intense periods.
In the future, a broader network with more data should be utilized to investigate the relationship with more comprehensive characteristics of MP, ROTI, S4 and σφ. Furthermore, more detailed studies on the possibility of separating the effects of real multipath and the effects of scintillation in MP data is needed that could include detailed station characterizations.
Author Contributions
C.L. and C.M.H. provided the initial idea and conception; N.A.S.H., S.V.V. and C.Y. verified the feasibility of the method. C.L. and N.A.S.H. conceived, designed and performed the experiments; C.M.H., N.A.S.H. and S.V.V. and C.Y. helped with the analysis of the data. C.L. and C.M.H. and N.A.S.H. wrote the paper; S.V.V. and C.Y. helped with the writing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Ningbo Science and Technology Bureau under Commonwealth Research Programme with project code 2019C50017.
Acknowledgments
This work is supported by Ningbo Science and Technology Bureau under Commonwealth Research Programme with project code 2019C50017. We acknowledge the University of Nottingham Ningbo China Faculty of Science and Engineering for provision of a PhD scholarship to C.L. as well as further support through a new researchers grant to N.A.S.H. and C.M.H. The authors would like to thank Vincenzo Romano and Lucilla Alfonsi on behalf of INGV for providing the Antarctica data. Monitoring stations from the network were deployed in the context of the Projects CIGALA and CALIBRA, both funded by the European Commission (EC) in the framework of the FP7-GALILEO-2009-GSA and FP7–GALILEO–2011–GSA–1a, respectively, and FAPESP Project Number 06/04008-2.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sreeja, V.; Aquino, M.; Forte, B.; Elmas, Z.; Hancock, C.; De Franceschi, G.; Alfonsi, L.; Spogli, L.; Romano, V.; Bougard, B.; et al. Tackling ionospheric scintillation threat to GNSS in Latin America. J. Space Weather Space Clim. 2011, 1, A05. [Google Scholar] [CrossRef]
- Aquino, M.; Dodson, A.; Defranceschi, G.; Alfonsi, L.; Romano, V.; Monico, J.; Marques, H.; Mitchell, C. Towards forecasting and mitigating ionospheric scintillation effects on GNSS. In Proceedings of the ELMAR, Zadar, Croatia, 12–14 September 2007. [Google Scholar]
- Bougard, B.; Simsky, A.; Sleewaegen, J.M.; Park, J.; Aquino, M.; Spogli, L.; Romano, V.; Mendonça, M.; Monico, J.F.G. CALIBRA: Mitigating the impact of ionospheric scintillation on Precise Point Positioning in Brazil. In Proceedings of the GNSS Vulnerabilities and Solutions Conference, Baška, Krk Island, Croatia, 18–20 April 2013. [Google Scholar]
- Marques, H.; Marques, H.; Aquino, M.; Veettil, S.; Monico, J. Accuracy assessment of precise point Positioning with multi-constellation GNSS data under ionospheric scintillation effects. J. Space Weather Space Clim. 2018, 8, A15. [Google Scholar] [CrossRef]
- Dierendonck, A.J.; Klobuchar, J.; Hua, Q. Ionospheric Scintillation Monitoring Using Commercial Single Frequency C/A Code Receivers. In Proceedings of the 6th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 22–24 September 1993. [Google Scholar]
- Rodrigues, F.S.; Moraes, A.O. ScintPi: A low-cost, easy-to-build GPS ionospheric scintillation monitor for DASI studies of space weather, education, and citizen science initiatives. Earth Space Sci. 2019, 6, 1547–1560. [Google Scholar] [CrossRef]
- Luo, X.; Gu, S.; Lou, Y.; Cai, L.; Liu, Z. Amplitude scintillation index derived from C/N 0 measurements released by common geodetic GNSS receivers operating at 1 Hz. J. Geod. 2020, 94, 1–14. [Google Scholar] [CrossRef]
- Romano, V.; Spogli, L.; Aquino, M.; Dodson, A.; Hancock, C. and Forte, B. GNSS station characterisation for ionospheric scintillation applications. Adv. Space Res. 2013, 52, 1237–1246. [Google Scholar] [CrossRef]
- Basu, S.; Groves, K.; Quinn, J.; Doherty, P. A comparison of TEC fluctuations and scintillations at Ascension Island. J. Atmos. Sol.-Terr. Phys. 1999, 61, 1219–1226. [Google Scholar] [CrossRef]
- Hancock, C.M.; Ligt, H.D.; Xu, T. The possibility of using GNSS quality control parameters to assess ionospheric scintillation errors. In Proceedings of the Fig Working Week, Helsinki, Finland, 29 May–2 June 2017. [Google Scholar]
- Yang, Z.; Liu, Z. Correlation between ROTI and Ionospheric scintillation indices using Hong Kong low-latitude GPS data. GPS Solutions 2015, 20, 815–824. [Google Scholar] [CrossRef]
- Jiao, Y.; Morton, Y. Comparison of the effect of high-latitude and equatorial ionospheric scintillation on GPS signals during the maximum of solar cycle 24. Radio Sci. 2015, 50, 886–903. [Google Scholar] [CrossRef]
- Estey, L.; Meertens, C. Teqc: The multi-purpose toolkit for GPS/GLONASS data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Estey, L.; Wier, S. Teqc Tutorial: Basic of Teqc Use and Teqc Products; UNAVCO: Boulder, CO, USA, 2014. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 31 October 2019).
- Pebesma, E. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-temporal interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Holding, D. Multi-GNSS vertical total electron content estimates: Data analysis and machine learning with python to evaluate ionospheric perturbations from earthquakes. Hold. Eng. Consult. 2017, 1, 5–8. [Google Scholar]
- Pi, X.; Mannucci, A.; Lindqwister, U.; Ho, C. Monitoring of global ionospheric irregularities using the Worldwide GPS Network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Mathworks. MATLAB Function Reference, 36th ed.; Natick: Mathworks, MA, USA, 2019; p. 10418. Available online: https://www.mathworks.com/help/pdf_doc/matlab/matlab_refbook.pdf (accessed on 31 October 2019).
- Shanmugam, S.; Jones, J.; Macaulay, A.; van Dierendonck, A. Evolution to modernized GNSS ionoshperic scintillation and TEC monitoring. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 24–26 April 2012. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Webster, R.; Oliver, M. Geostatistics for Environmental Scientists; John Wiley and Sons: Chichester, UK, 2008. [Google Scholar]
- Webster, R.; Atteia, O.; Dubois, J.P. Coregionalization of trace metals in the soil in the Swiss Jura. Eur. J. Soil Sci. 1994, 45, 205–218. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Curran, P.J.; Atkinson, P.M. Geostatistics and remote sensing. Prog. Phys. Geogr. 1998, 22, 61–78. [Google Scholar] [CrossRef]
- van der Meer, F. Remote-sensing image analysis and geostatistics. Int. J. Remote Sens. 2012, 33, 5644–5676. [Google Scholar] [CrossRef]
- Odongo, V.O.; Hamm, N.A.S.; Milton, E.J. Spatio-temporal assessment of Tuz Gölü, turkey as a potential radiometric vicarious calibration site. Remote Sens. 2014, 6, 2494–2513. [Google Scholar] [CrossRef]
- Kaur, A.; Kaur, L.; Gupta, S. Image recognition using coefficient of correlation and structural similarity index in uncontrolled environment. Int. J. Comput. Appl. 2012, 59, 32–39. [Google Scholar] [CrossRef]
- Carrano, C.S.; Groves, K.M.; Rino, C.L. On the relationship between the rate of change of total electron content index (ROTI), irregularity strength (CkL), and the scintillation index (S4). J. Geophys. Res. Space Phys. 2019, 124, 2099–2112. [Google Scholar] [CrossRef]
- Olwendo, J.O.; Cilliers, P.; Weimin, Z.; Ming, O.; Yu, X. Validation of ROTI for ionospheric amplitude scintillation measurements in a low-latitude region over Africa. Radio Sci. 2018, 53, 876–887. [Google Scholar] [CrossRef]
- Acharya, R.; Majumdar, S. Statistical relation of scintillation index S4 with ionospheric irregularity index ROTI over Indian equatorial region. Adv. Space Res. 2019, 64, 1019–1033. [Google Scholar] [CrossRef]
- Sreeja, V.; Aquino, M.; Elmas, Z.G. Impact of ionospheric scintillation on GNSS receiver tracking performance over Latin America—Introducing the concept of tracking jitter variance maps. Space Weather 2011, 9, S10002. [Google Scholar] [CrossRef]
- Koulouri, A.; Smith, N.D.; Vani, B.C.; Rimpilainen, V.; Astin, I.; Forte, B. Methodology to estimate ionospheric scintillation risk maps and their contribution to position dilution of precision on the ground. arXiv preprint 2019, arXiv:1911.08229. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).