Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters
Abstract
1. Introduction
1.1. Motivation
1.2. Data-Driven Air Pollutant Modeling
2. Materials
2.1. Database
2.2. Data Handling
2.3. Environmental Conditions
3. Methods
3.1. Data Pre-Processing
3.2. Modeling
3.3. Performance Metrics
4. Results
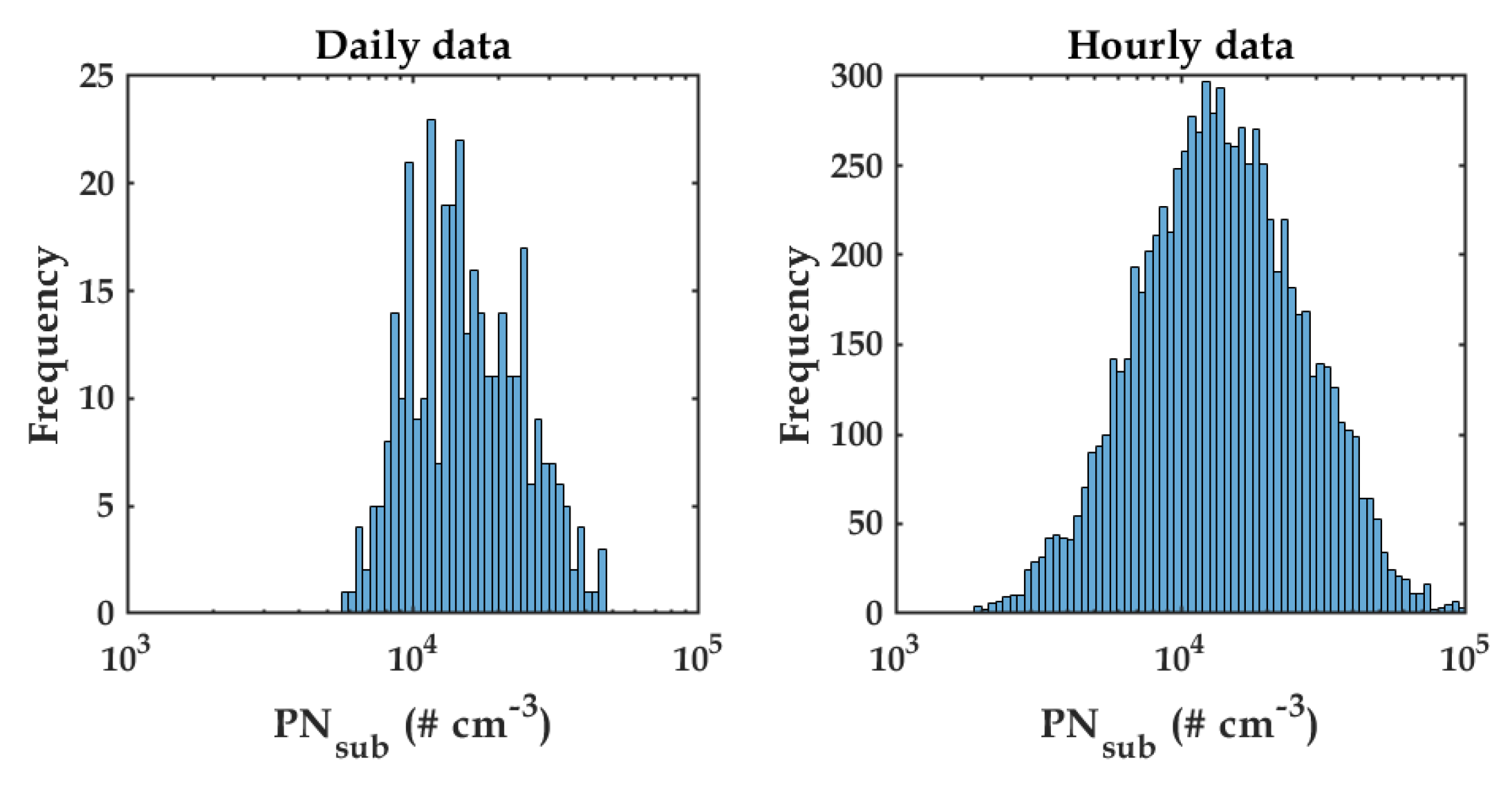
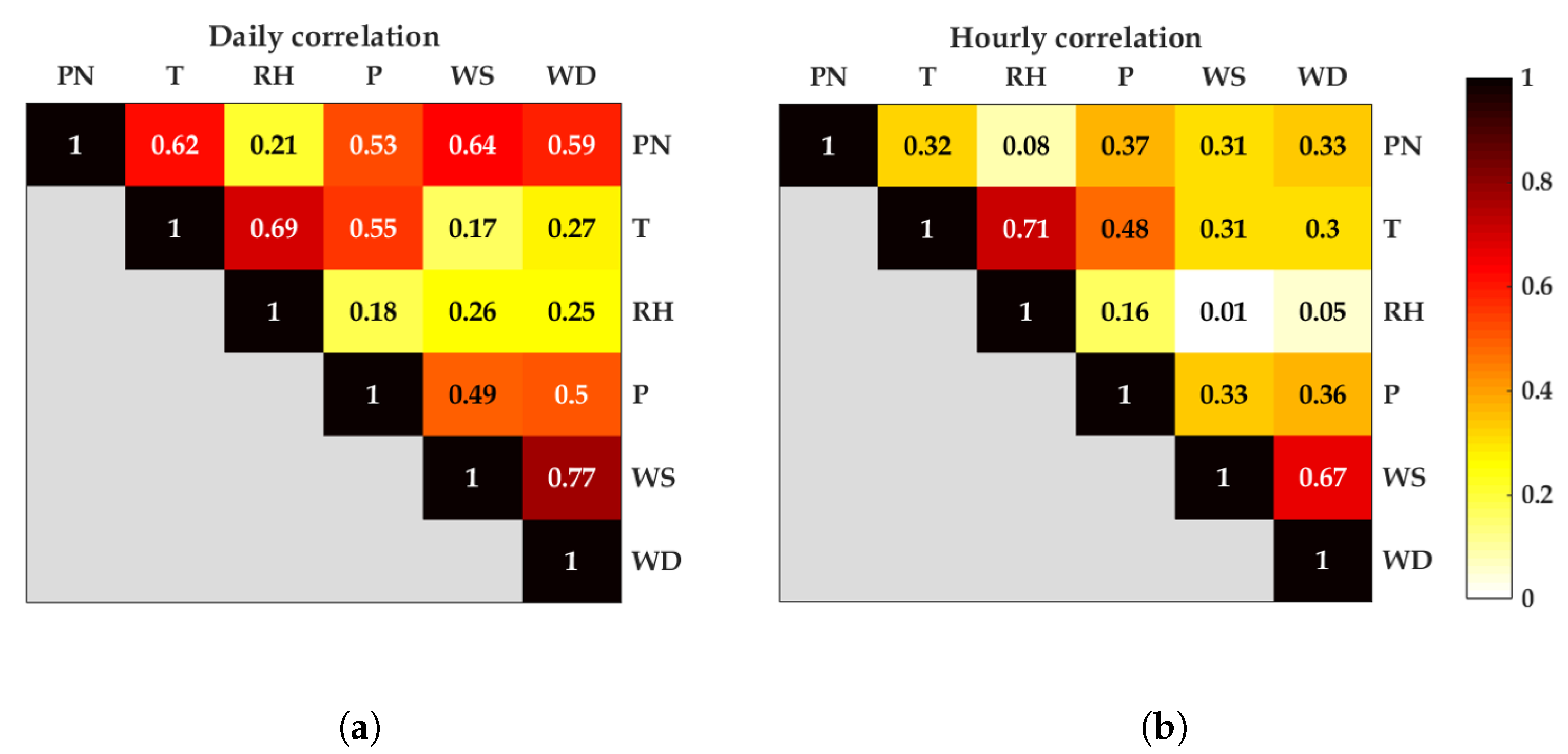
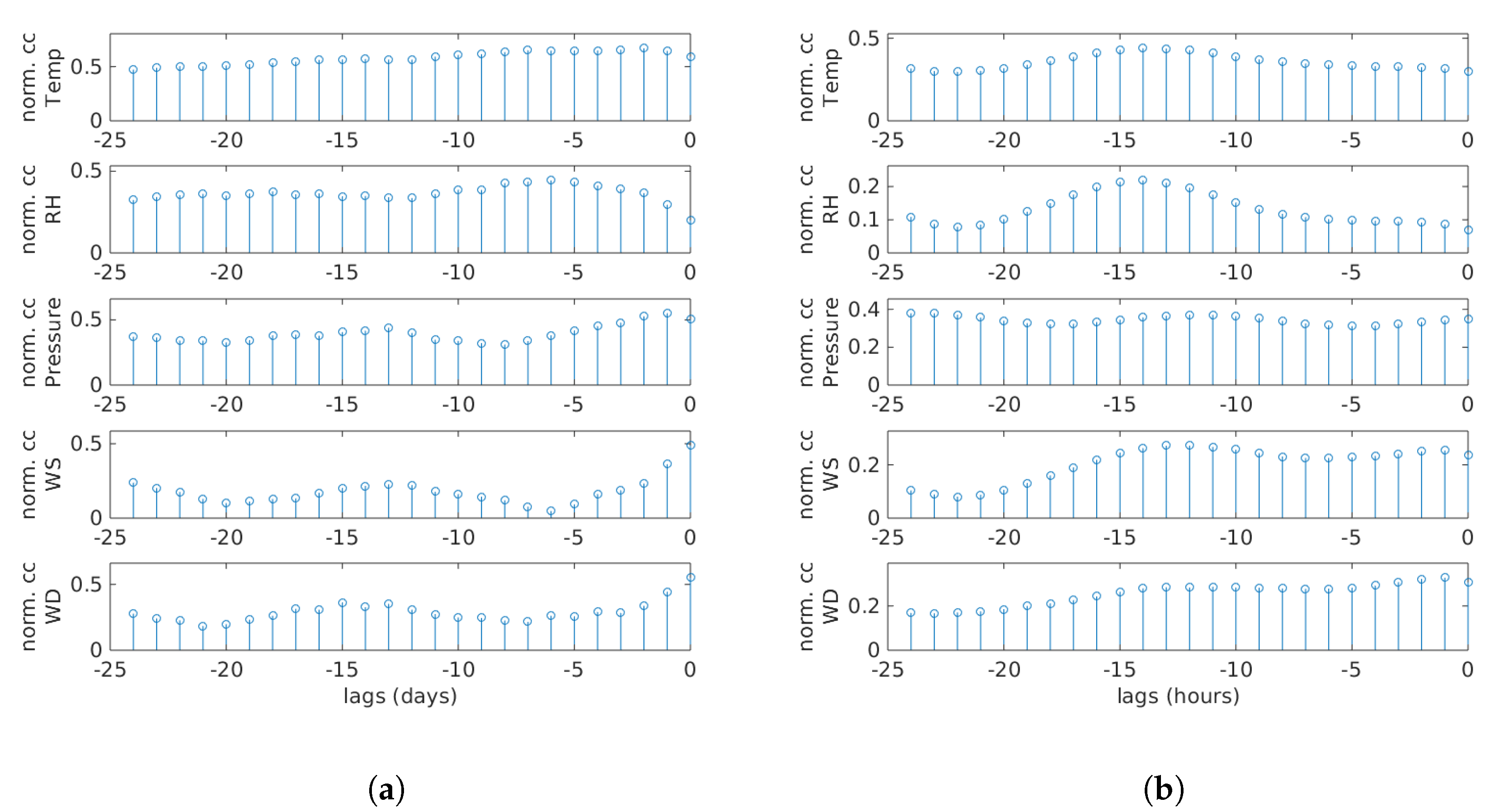
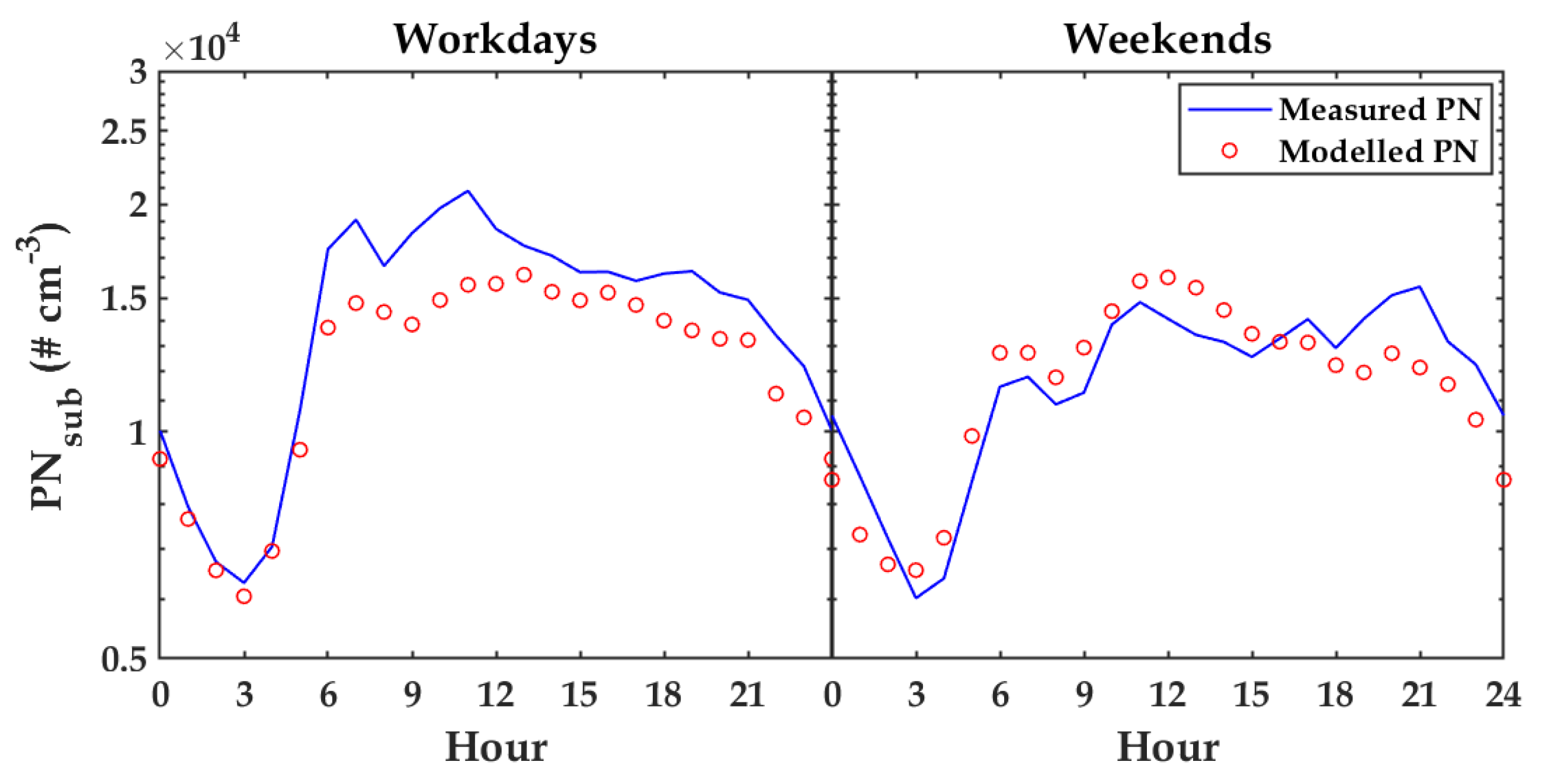
4.1. Data Analysis
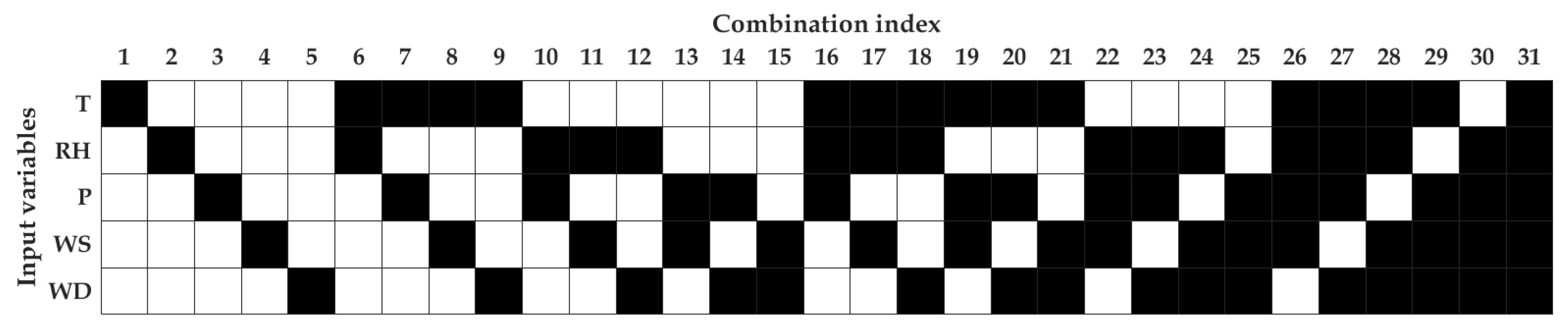
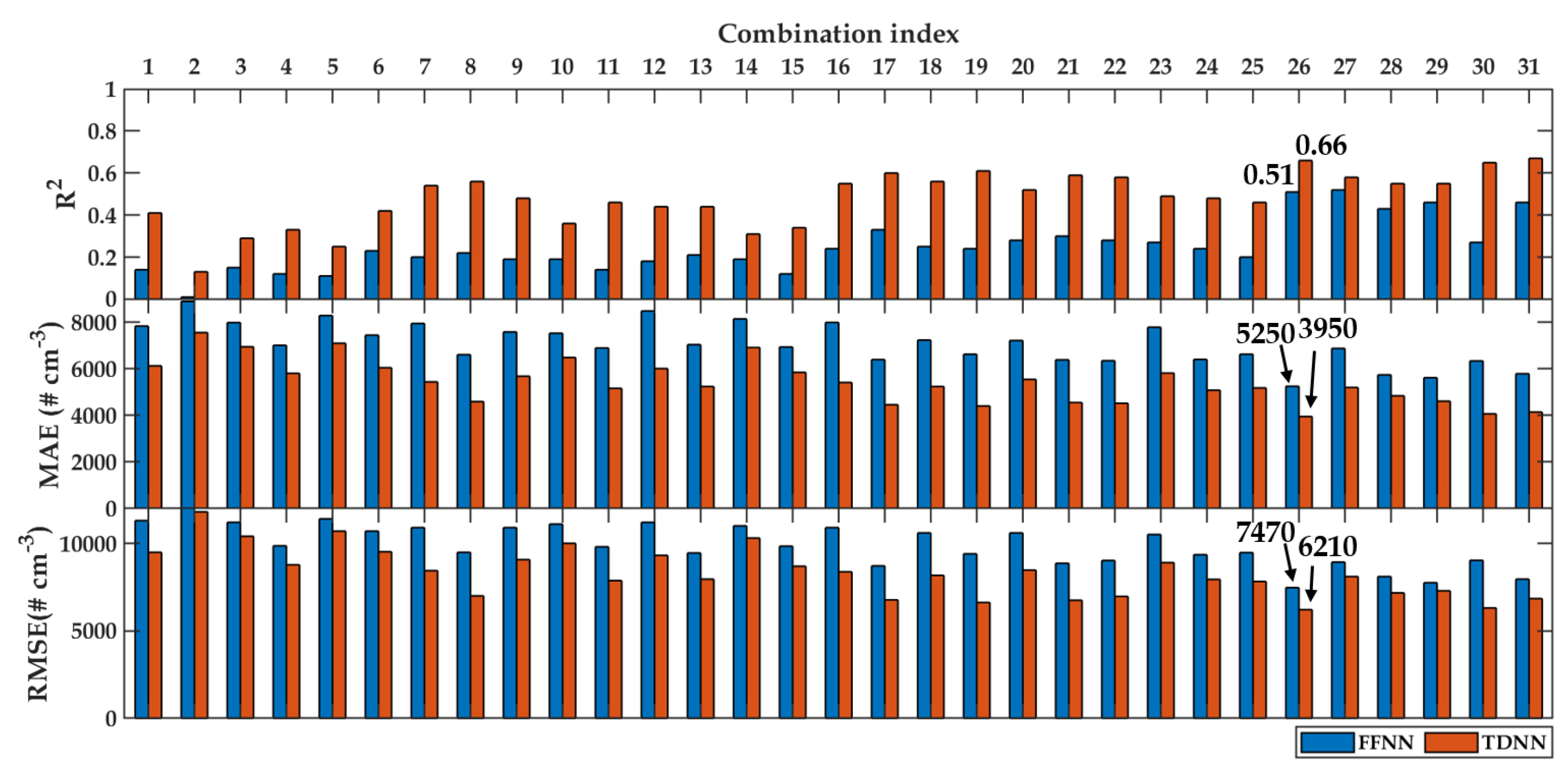
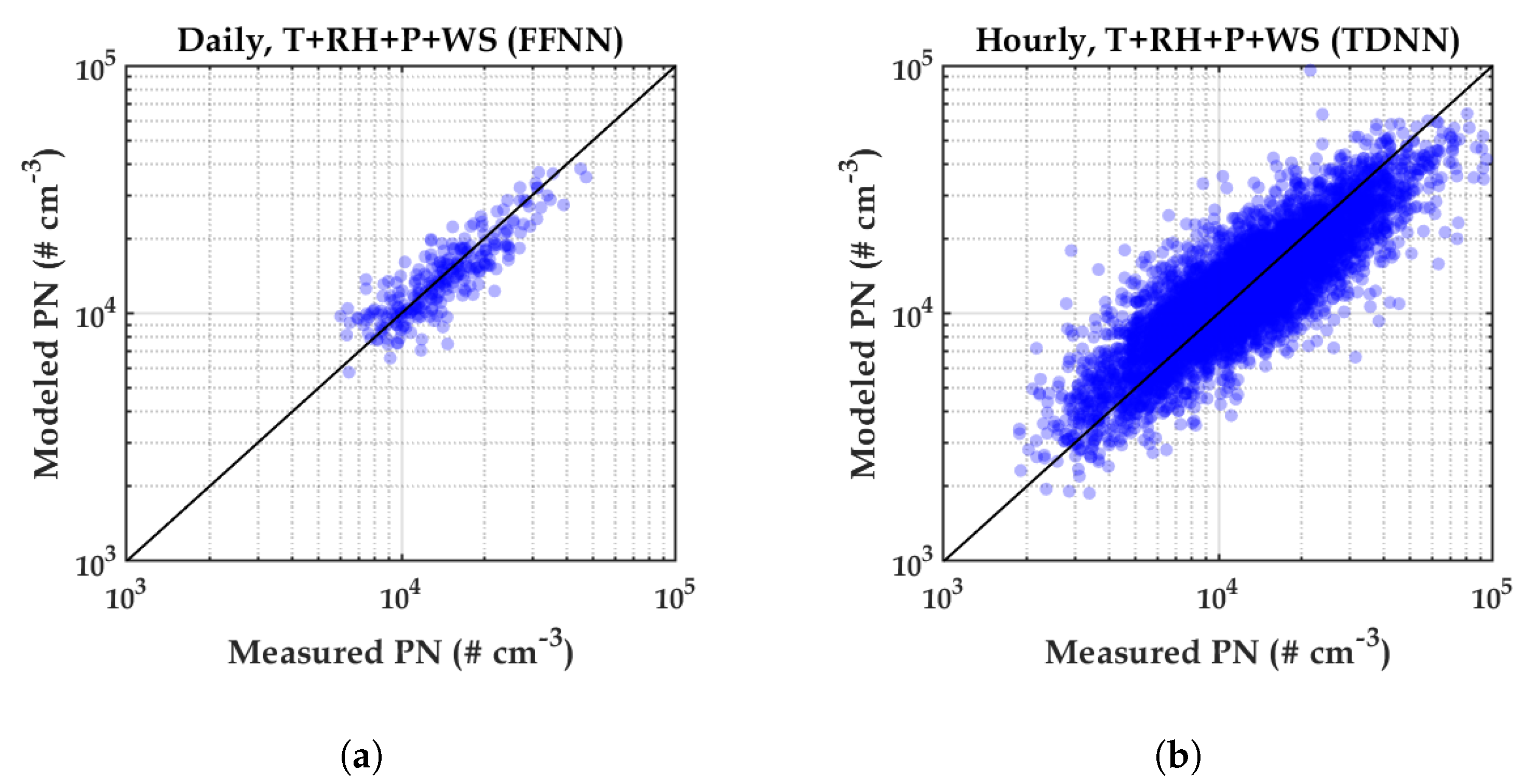
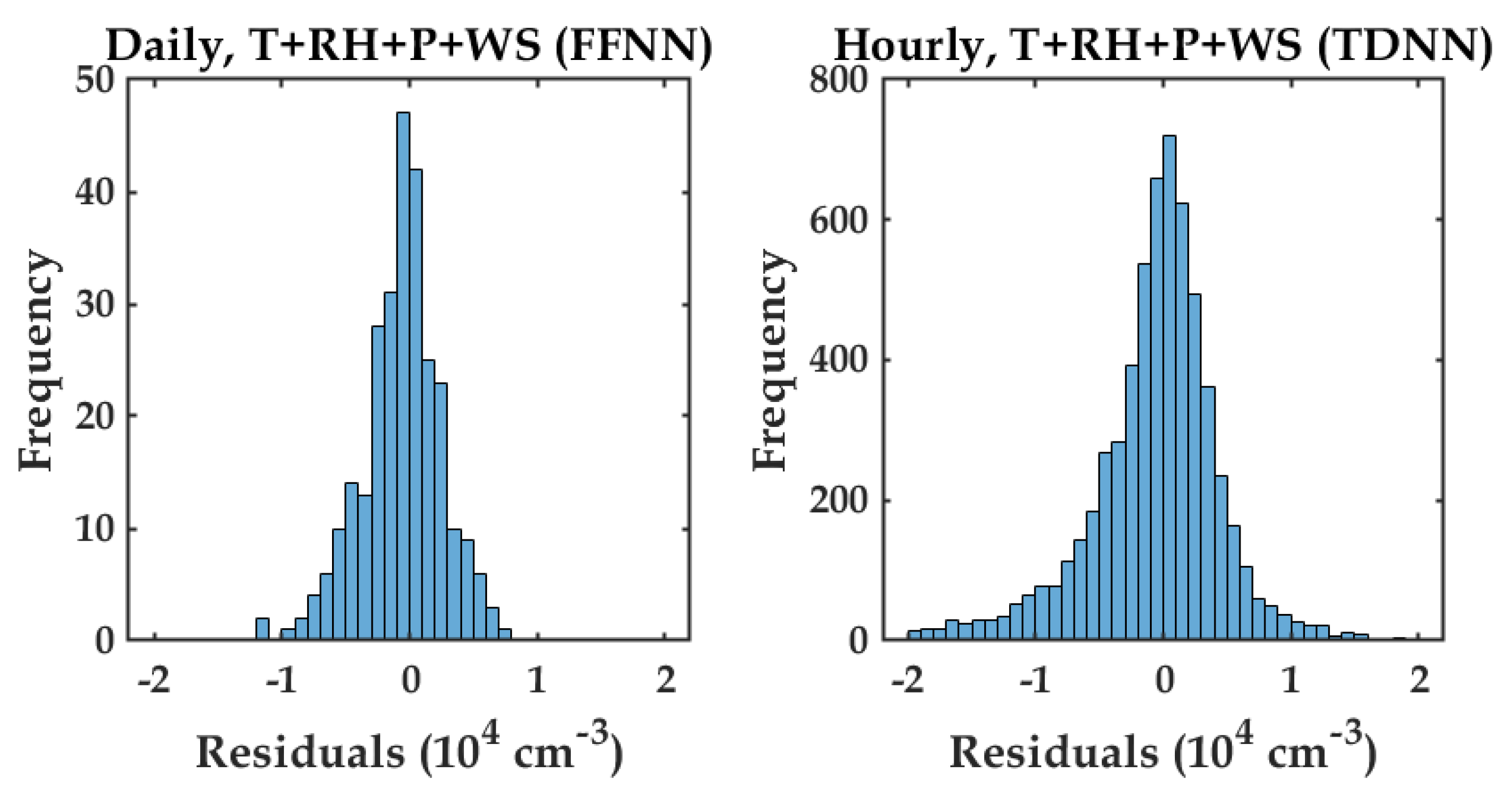
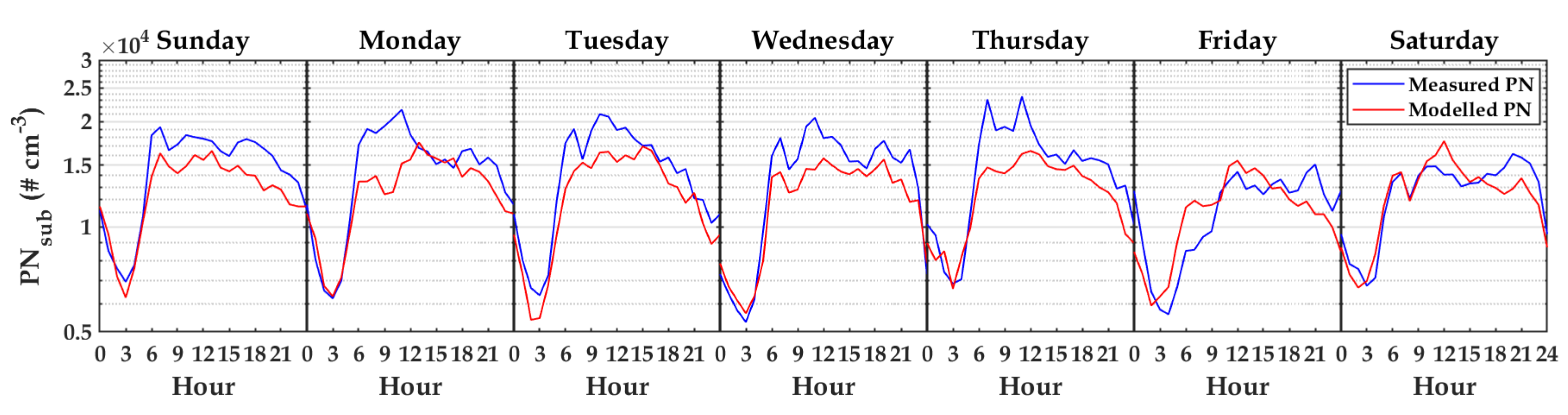
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| CMAQ | Community multiscale air quality |
| CO | Carbon monoxide |
| CPC | Condensation particle counter |
| FFNN | Feed-forward neural network |
| LASSO | Least absolute shrinkage and selection operator |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MENA | Middle East and North Africa |
| NNs | Neural networks |
| NO | Nitrogen dioxide |
| O | Ozone |
| OPS | Optical particle sizer |
| P | Absolute pressure |
| PCC | Pearson correlation coefficients |
| PM | Particulate matter |
| PM | Particulate matter smaller than 10 m |
| PM | Particulate matter smaller than 2.5 m |
| PN | Particle number |
| R | Coefficient of determination |
| ReLU | Rectified linear unit |
| RF | Precipitation |
| RH | Relative humidity |
| RMSE | Root mean squared error |
| RNN | Recurrent neural network |
| SMPS | Scanning Mobility Particle Sizer |
| SO | Sulfur dioxide |
| T | Temperature |
| TDNN | Time-delay neural network |
| UAM | Urban airshed model |
| UFPs | Ultra-fine particles |
| WD | Wind direction |
| WHO | World Health Organization |
| WS | Wind speed |
References
- WHO Global Ambient Air Quality Database. Available online: https://www.who.int/airpollution/data/en/ (accessed on 19 March 2020).
- Ayala, A.; Brauer, M.; Mauderly, J.L.; Samet, J.M. Air pollutants and sources associated with health effects. Air Qual. Atmos. Health 2012, 5, 151–167. [Google Scholar] [CrossRef]
- Mannucci, P.M.; Franchini, M. Health effects of ambient air pollution in developing countries. Int. J. Environ. Res. Public Health 2017, 14, 1048. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.F.; Xu, Y.H.; Shi, M.H.; Lian, Y.X. The impact of PM2.5 on the human respiratory system. J. Thorac. Dis. 2016, 8, E69. [Google Scholar] [PubMed]
- Fuzzi, S.; Baltensperger, U.; Carslaw, K.; Decesari, S.; Denier van der Gon, H.; Facchini, M.C.; Fowler, D.; Koren, I.; Langford, B.; Lohmann, U.; et al. Particulate matter, air quality and climate: Lessons learned and future needs. Atmos. Chem. Phys. 2015, 15, 8217–8299. [Google Scholar] [CrossRef]
- Spinazzè, A.; Fanti, G.; Borghi, F.; Del Buono, L.; Campagnolo, D.; Rovelli, S.; Cattaneo, A.; Cavallo, D.M. Field comparison of instruments for exposure assessment of airborne ultra-fine particles and particulate matter. Atmos. Environ. 2017, 154, 274–284. [Google Scholar] [CrossRef]
- Evans, K.A.; Halterman, J.S.; Hopke, P.K.; Fagnano, M.; Rich, D.Q. Increased ultra-fine particles and carbon monoxide concentrations are associated with asthma exacerbation among urban children. Environ. Res. 2014, 129, 11–19. [Google Scholar] [CrossRef]
- Reche, C.; Querol, X.; Alastuey, A.; Viana, M.; Pey, J.; Moreno, T.; Rodríguez, S.; González, Y.; Fernández-Camacho, R.; Rosa, J.; et al. New considerations for PM, Black Carbon and particle number concentration for air quality monitoring across different European cities. Atmos. Chem. Phys. 2011, 11, 6207–6227. [Google Scholar] [CrossRef]
- Frampton, M.W.; Rich, D.Q. Does particle size matter? Ultrafine particles and hospital visits in eastern Europe. Am. J. Respir. Crit. Care Med. 2016, 194, 1180–1182. [Google Scholar] [CrossRef]
- de Jesus, A.L.; Rahman, M.M.; Mazaheri, M.; Thompson, H.; Knibbs, L.D.; Jeong, C.; Evans, G.; Nei, W.; Ding, A.; Qiao, L.; et al. Ultrafine particles and PM2. 5 in the air of cities around the world: Are they representative of each other? Environ. Int. 2019, 129, 118–135. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Wraith, D.; Boor, B.E.; Hussein, T. Bayesian Proxy Modeling for Estimating Black Carbon Concentrations using White-Box and Black-Box Models. Appl. Sci. 2019, 9, 4976. [Google Scholar] [CrossRef]
- Mishra, D.; Goyal, P.; Upadhyay, A. Artificial intelligence based approach to forecast PM2.5 during haze episodes: A case study of Delhi, India. Atmos. Environ. 2015, 102, 239–248. [Google Scholar] [CrossRef]
- Jiang, P.; Dong, Q.; Li, P. A novel hybrid strategy for PM2.5 concentration analysis and prediction. J. Environ. Manag. 2017, 196, 443–457. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.E.; Cardelino, C. Application of the urban airshed model to forecasting next-day peak ozone concentrations in Atlanta, Georgia. J. Air Waste Manag. Assoc. 2000, 50, 2010–2024. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.F.; Mallard, J.W. Contributions of natural emissions to ozone and PM2.5 as simulated by the community multiscale air quality (CMAQ) model. Environ. Sci. Technol. 2011, 45, 4817–4823. [Google Scholar] [CrossRef]
- Hanna, S.R.; Lu, Z.; Frey, H.C.; Wheeler, N.; Vukovich, J.; Arunachalam, S.; Fernau, M.; Hansen, D.A. Uncertainties in predicted ozone concentrations due to input uncertainties for the UAM-V photochemical grid model applied to the July 1995 OTAG domain. Atmos. Environ. 2001, 35, 891–903. [Google Scholar] [CrossRef]
- Borrego, C.; Monteiro, A.; Ferreira, J.; Miranda, A.; Costa, A.; Carvalho, A.; Lopes, M. Procedures for estimation of modeling uncertainty in air quality assessment. Environ. Int. 2008, 34, 613–620. [Google Scholar] [CrossRef]
- Cabaneros, S.M.S.; Calautit, J.K.; Hughes, B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019, 119, 285–304. [Google Scholar] [CrossRef]
- García, M.V.; Aznarte, J.L. Shapley additive explanations for NO2 forecasting. Ecol. Inform. 2020, 56, 101039. [Google Scholar] [CrossRef]
- Nunnari, G.; Dorling, S.; Schlink, U.; Cawley, G.; Foxall, R.; Chatterton, T. Modeling SO2 concentration at a point with statistical approaches. Environ. Model. Softw. 2004, 19, 887–905. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Y.; Qin, Z.; Zhang, G. A novel hybrid forecasting model for PM10 and SO2 daily concentrations. Sci. Total. Environ. 2015, 505, 1202–1212. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Al-Hunaiti, A.; Arar, S.; Khoder, M.; Abdelmaksoud, A.S.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Shabbaj, I.I.; Almehmadi, F.M.; et al. A predictive model for steady state ozone concentration at an urban-coastal site. Int. J. Environ. Res. Public Health 2019, 16, 258. [Google Scholar] [CrossRef] [PubMed]
- Zaidan, M.A.; Dada, L.; Alghamdi, M.A.; Al-Jeelani, H.; Lihavainen, H.; Hyvärinen, A.; Hussein, T. Mutual information input selector and probabilistic machine learning utilisation for air pollution proxies. Appl. Sci. 2019, 9, 4475. [Google Scholar] [CrossRef]
- Fung, P.L.; Zaidan, M.A.; Sillanpää, S.; Kousa, A.; Niemi, J.V.; Timonen, H.; Kuula, J.; Saukko, E.; Luoma, K.; Petäjä, T.; et al. Input-Adaptive Proxy for Black Carbon as a Virtual Sensor. Sensors 2020, 20, 182. [Google Scholar] [CrossRef] [PubMed]
- Raimondo, G.; Montuori, A.; Moniaci, W.; Pasero, E.; Almkvist, E. A machine learning tool to forecast PM10 level. In Proceedings of the AMS 87th Annual Meeting, San Antonio, TX, USA, 14–18 January 2007. [Google Scholar]
- Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.A.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, S.; Chen, L.J.; Tsai, T.C. Short-term PM2. 5 forecasting using exponential smoothing method: A comparative analysis. Sensors 2018, 18, 3223. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A deep cnn-lstm model for particulate matter (PM2.5) forecasting in smart cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Mølgaard, B.; Hussein, T.; Corander, J.; Hämeri, K. Forecasting size-fractionated particle number concentrations in the urban atmosphere. Atmos. Environ. 2012, 46, 155–163. [Google Scholar] [CrossRef]
- Mølgaard, B.; Birmili, W.; Clifford, S.; Massling, A.; Eleftheriadis, K.; Norman, M.; Vratolis, S.; Wehner, B.; Corander, J.; Hämeri, K.; et al. Evaluation of a statistical forecast model for size-fractionated urban particle number concentrations using data from five European cities. J. Aerosol Sci. 2013, 66, 96–110. [Google Scholar] [CrossRef]
- Hussein, T.; Atashi, N.; Sogacheva, L.; Hakala, S.; Dada, L.; Petäjä, T.; Kulmala, M. Characterization of Urban New Particle Formation in Amman—Jordan. Atmosphere 2020, 11, 79. [Google Scholar] [CrossRef]
- Hussein, T.; Dada, L.; Hakala, S.; Petäjä, T.; Kulmala, M. Urban Aerosol Particle Size Characterization in Eastern Mediterranean Conditions. Atmosphere 2019, 10, 710. [Google Scholar] [CrossRef]
- Pearson, K. Notes on Regression and Inheritance in the Case of Two Parents; Royal Society of London: London, UK, 1895; Volume 58, pp. 240–242. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Haapasilta, V.; Relan, R.; Paasonen, P.; Kerminen, V.M.; Junninen, H.; Kulmala, M.; Foster, A.S. Exploring non-linear associations between atmospheric new-particle formation and ambient variables: A mutual information approach. Atmos. Chem. Phys. 2018, 18, 12699–12714. [Google Scholar] [CrossRef]
- Zaidan, M.A.; Canova, F.F.; Laurson, L.; Foster, A.S. Mixture of clustered Bayesian neural networks for modeling friction processes at the nanoscale. J. Chem. Theory Comput. 2017, 13, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Maren, A.J.; Harston, C.T.; Pap, R.M. Handbook of Neural Computing Applications; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Zaidan, M.; Haapasilta, V.; Relan, R.; Junninen, H.; Aalto, P.; Kulmala, M.; Laurson, L.; Foster, A. Predicting atmospheric particle formation days by Bayesian classification of the time series features. Tellus B Chem. Phys. Meteorol. 2018, 70, 1–10. [Google Scholar] [CrossRef]
- Orhan, U.; Hekim, M.; Ozer, M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model. Expert Syst. Appl. 2011, 38, 13475–13481. [Google Scholar] [CrossRef]
- Medsker, L.; Jain, L.C. Recurrent Neural Networks: Design and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Van Roode, S.; Ruiz-Aguilar, J.; González-Enrique, J.; Turias, I. An artificial neural network ensemble approach to generate air pollution maps. Environ. Monit. Assess. 2019, 191, 727. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]




| Performance Metrics | Formulation |
|---|---|
| Coefficient of Determination | |
| Mean Absolute Error | |
| Root Mean Squared Error |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaidan, M.A.; Surakhi, O.; Fung, P.L.; Hussein, T. Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters. Sensors 2020, 20, 2876. https://doi.org/10.3390/s20102876
Zaidan MA, Surakhi O, Fung PL, Hussein T. Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters. Sensors. 2020; 20(10):2876. https://doi.org/10.3390/s20102876
Chicago/Turabian StyleZaidan, Martha A., Ola Surakhi, Pak Lun Fung, and Tareq Hussein. 2020. "Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters" Sensors 20, no. 10: 2876. https://doi.org/10.3390/s20102876
APA StyleZaidan, M. A., Surakhi, O., Fung, P. L., & Hussein, T. (2020). Sensitivity Analysis for Predicting Sub-Micron Aerosol Concentrations Based on Meteorological Parameters. Sensors, 20(10), 2876. https://doi.org/10.3390/s20102876






