Gait Asymmetry Post-Stroke: Determining Valid and Reliable Methods Using a Single Accelerometer Located on the Trunk
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design and Setting
2.2. Participants
2.3. Demographic and Clinical Measures
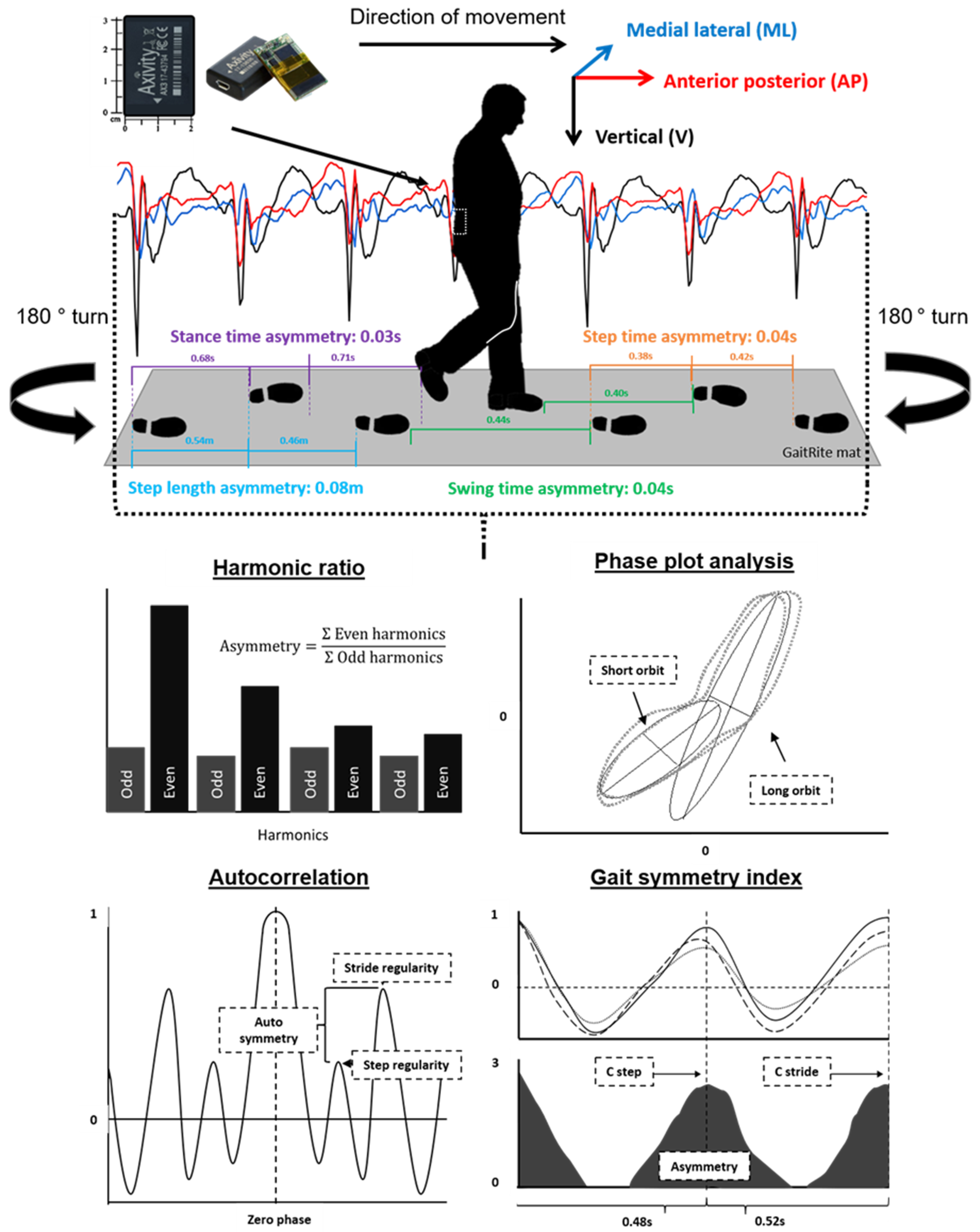
2.4. Test Protocol
2.5. Asymmetry Variables
2.6. Description of Acceleration-Derived Variables
2.6.1. Harmonic Ratio
2.6.2. Autocorrelation
2.6.3. Gait Symmetry Index
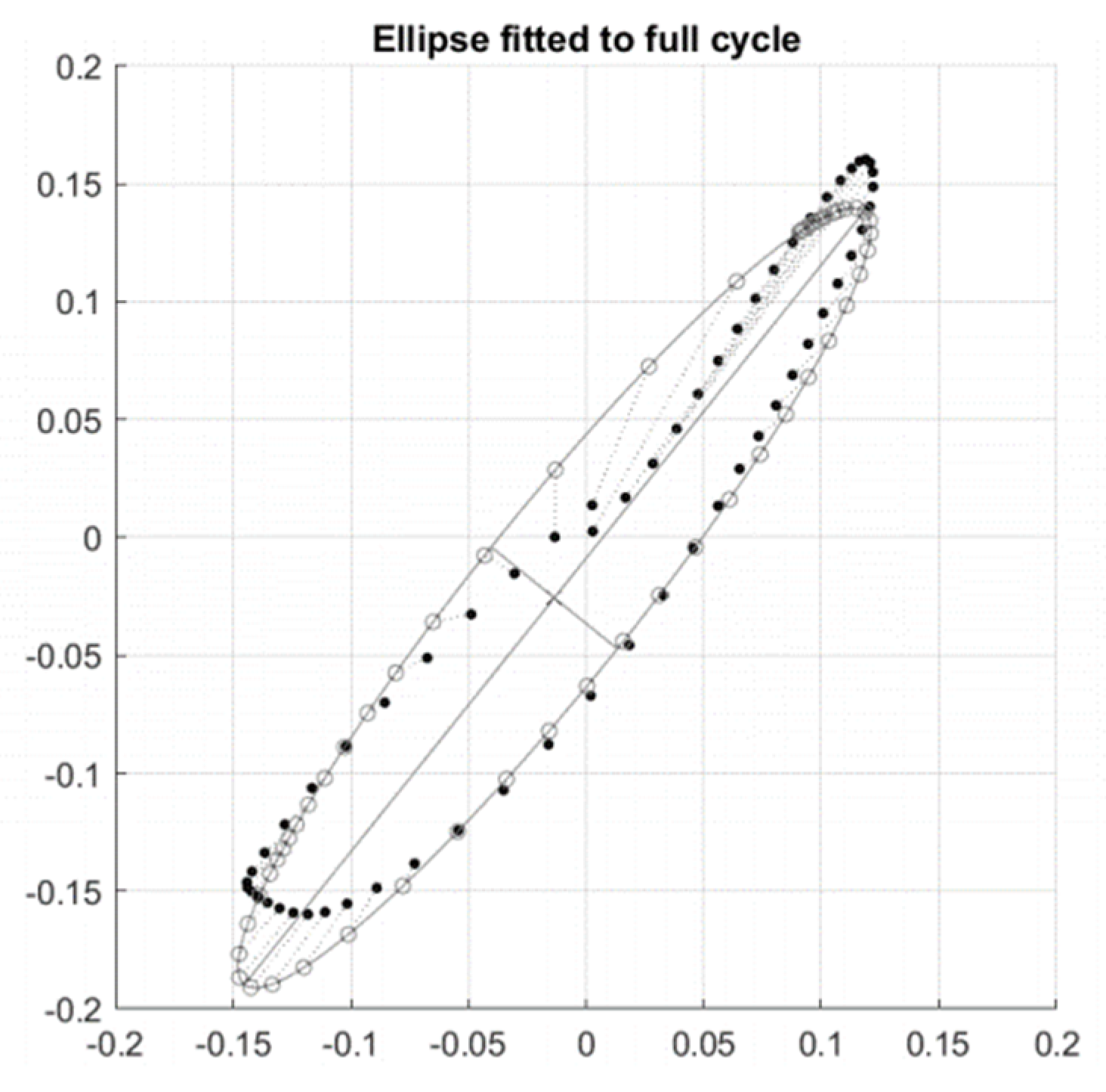
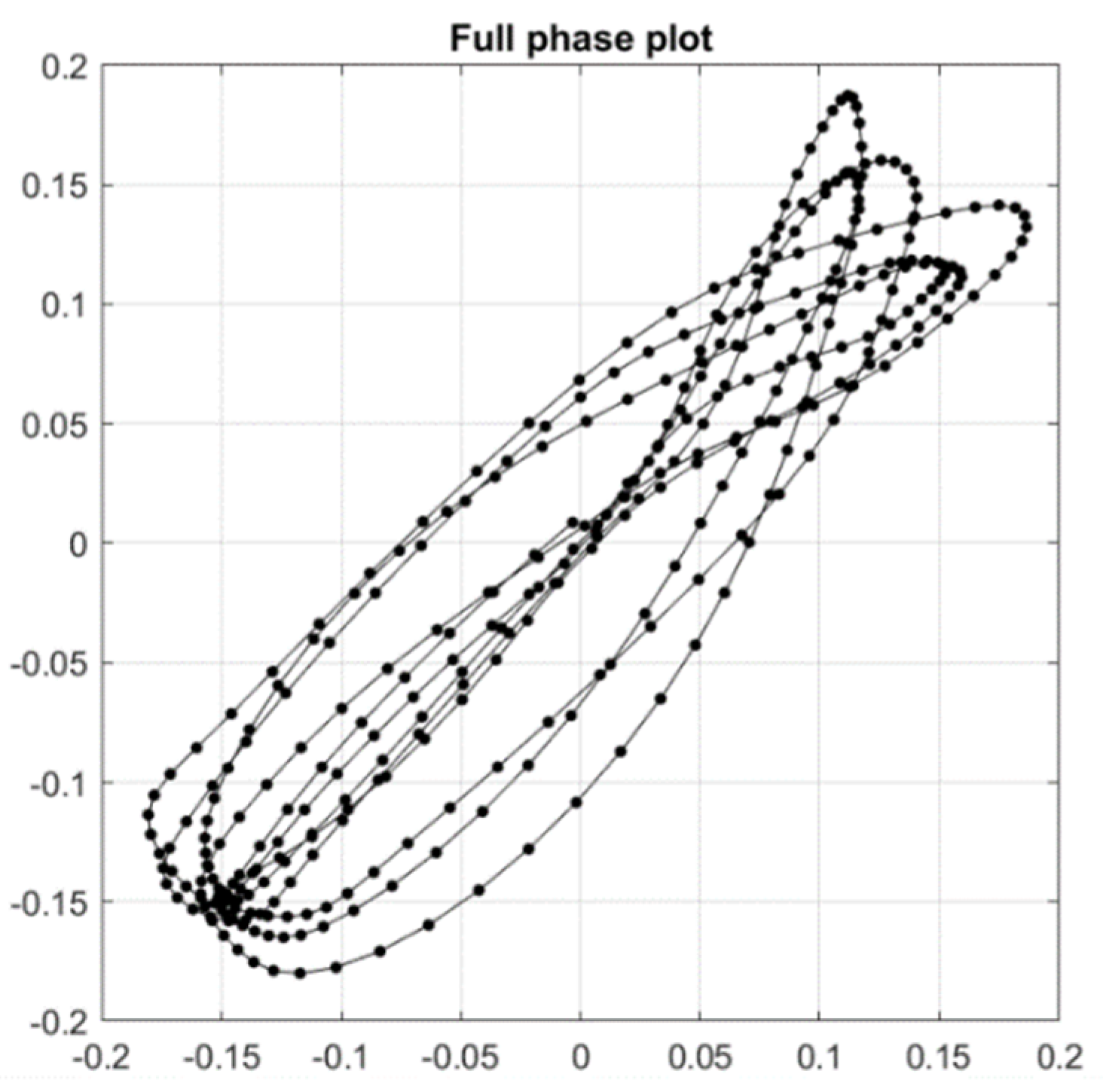
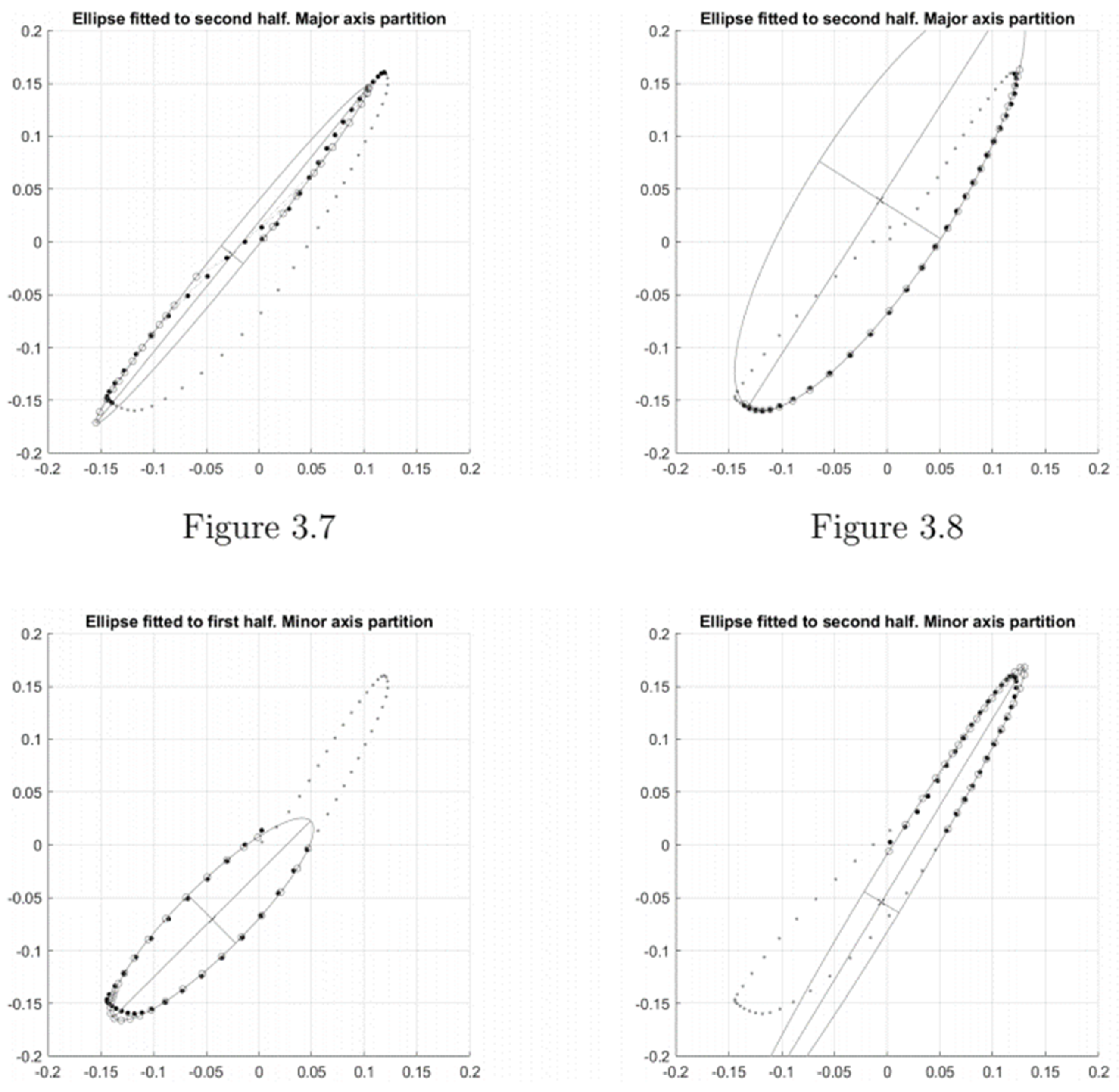
2.6.4. Phase Plot Analysis
2.6.5. Measures Indicative of Stability
2.7. Statistical Analysis
3. Results
3.1. Concurrent Validity of the Asymmetry Variables
3.2. Test–Retest Reliability of the Variables
3.3. Selection of the Most Robust Variable
4. Discussion
4.1. Limitations
4.2. Applications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Sharing
Appendix A
Appendix A.1. Acceleration-Derived Variable Definitions
| Variable | Definition |
|---|---|
| Harmonic ratio (V, ML, AP) | The step-to-step symmetry within a stride from calculating a ratio of the odd and even harmonics of a signal following fast Fourier transformation. |
| Step regularity (V, ML, AP) | Estimated as the normalized unbiased autocovariance for a lag of one step time. Thus, this feature reflects the similarity between subsequent steps of the acceleration pattern over a step. Values of this feature close to 1.0 (maximum possible value) reflect repeatable patterns between subsequent steps. |
| Stride regularity (V, ML, AP) | Estimated as the normalized unbiased autocovariance for a lag of one stride time. Thus, this feature reflects the similarity between subsequent strides of the acceleration pattern over a stride cycle. |
| Autocorrelation symmetry (V, ML, AP) | Difference between step and stride regularity designed to quantify the level of symmetry between them and indicative of symmetry during a straight walk. |
| Gait symmetry index | Calculated based upon the concept of the summation of the biased autocorrelation from all three components of movement and a subsequent calculation of step and stride timing asymmetry. |
| Orbit eccentricity (V) | Average eccentricity of all fully fitted ellipses. |
| Relative orbit inclination (V) | Average angle subtended by alternating fitted ellipses within a bout of gait. |
| Orbit width deviation (V) | Standard deviation of minor axes lengths of all fully fitted ellipses. Analogous to Principle Component Analysis (second component). |
| Short half orbit eccentricity (V) | Difference in eccentricity of two ellipses fitted to each half-cycle of a full orbit in the phase plot. Averaged over all orbits in a bout’s phase plot. |
| Short half orbit segment angle (V) | Difference in inclination of two ellipses fitted to each half-cycle of a full orbit in the phase plot. Averaged over all orbits in a bout’s phase plot. |
| Long half orbit eccentricity (V) | Difference in eccentricity of two ellipses fitted to each half-cycle of a full orbit in the phase plot. Averaged over all orbits in a bout’s phase plot. |
| Long half orbit segment angle (V) | Difference in inclination of two ellipses fitted to each half-cycle of a full orbit in the phase plot. Averaged over all orbits in a bout’s phase plot. |
| Intra step correlation (V) | Average correlation of acceleration signal corresponding to step i with that of step i-1. I.e., a lag-1 autocorrelation where a single lag is one step cycle’s duration. |
| Acceleration RMS (V, ML, AP) | The calculation of the root mean square of the acceleration signal. |
| Jerk RMS (V, ML, AP) | The calculation of the root mean square of the first time derivative of the acceleration signal (jerk). |
Appendix A.2. Explanation and Equation for Each Acceleration Derived Variable for Asymmetry
Appendix A.2.1. Harmonic Ratio
Appendix A.2.2. Autocorrelation
Appendix A.2.3. Gait Symmetry Index (GSI)
Appendix A.2.4. Phase Plot Analysis
References
- Moore, S.A.; Hickey, A.; Lord, S.; Del Din, S.; Godfrey, A.; Rochester, L. Comprehensive measurement of stroke gait characteristics with a single accelerometer in the laboratory and community: A feasibility, validity and reliability study. J. Neuroeng. Rehabil. 2017, 14, 130. [Google Scholar] [CrossRef] [PubMed]
- Gallanagh, S.; Quinn, T.J.; Alexander, J.; Walters, M.R. Physical Activity in the Prevention and Treatment of Stroke. ISRN Neurol. 2011, 2011, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Patterson, K.K.; Gage, W.H.; Brooks, D.; Black, S.E.; McIlroy, W.E. Evaluation of gait symmetry after stroke: A comparison of current methods and recommendations for standardization. Gait Posture 2010, 31, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Fini, N.A.; Holland, A.E.; Keating, J.; Simek, J.; Bernhardt, J. How physically active are people following stroke? Systematic review and quantitative synthesis. Phys. Ther. 2017, 97, 707–717. [Google Scholar] [CrossRef]
- Bull, F.; Goenka, S.; Lambert, V.; Pratt, M. Physical Activity for the Prevention of Cardiometabolic Disease; The International Bank for Reconstruction and Development/The World Bank: Washington, DC, USA, 2017; ISBN 9781464805189. [Google Scholar]
- Lee, I.M.; Shiroma, E.J.; Lobelo, F.; Puska, P.; Blair, S.N.; Katzmarzyk, P.T.; Alkandari, J.R.; Andersen, L.B.; Bauman, A.E.; Brownson, R.C.; et al. Effect of physical inactivity on major non-communicable diseases worldwide: An analysis of burden of disease and life expectancy. Lancet 2012, 380, 219–229. [Google Scholar] [CrossRef]
- Patterson, K.K.; Parafianowicz, I.; Danells, C.J.; Closson, V.; Verrier, M.C.; Staines, W.R.; Black, S.E.; McIlroy, W.E. Gait Asymmetry in Community-Ambulating Stroke Survivors. Arch. Phys. Med. Rehabil. 2008, 89, 304–310. [Google Scholar] [CrossRef]
- Balaban, B.; Tok, F. Gait Disturbances in Patients with Stroke. PM R 2014, 6, 635–642. [Google Scholar] [CrossRef]
- Wade, D.T. Measurement in neurological rehabilitation. Curr. Opin. Neurol. Neurosurg. 1992, 5, 682–686. [Google Scholar]
- Lin, J.-H.; Hsu, M.-J.; Hsu, H.-W.; Wu, H.-C.; Hsieh, C.-L. Psychometric Comparisons of 3 Functional Ambulation Measures for Patients with Stroke. Stroke 2010, 41, 2021–2025. [Google Scholar] [CrossRef]
- Wong, J.S.; Jasani, H.; Poon, V.; Inness, E.L.; McIlroy, W.E.; Mansfield, A. Inter- and intra-rater reliability of the GAITRite system among individuals with sub-acute stroke. Gait Posture 2014, 40, 259–261. [Google Scholar] [CrossRef]
- Buckley, C.; Alcock, L.; McArdle, R.; Ur Rehman, R.Z.; Del Din, S.; Mazzà, C.; Yarnall, A.J.; Rochester, L. The role of movement analysis in diagnosing and monitoring neurodegenerative conditions: Insights from gait and postural control. Brain Sci. 2019, 9, 34. [Google Scholar] [CrossRef] [PubMed]
- Iosa, M.; Fusco, A.; Giovanni, M.; Paolicci, S. Development and decline of upright gait stability. Front. Aging Neurosci. 2014, 6, 14. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wright, R.L.; Brownless, S.B.; Pratt, D.; Sackley, C.M.; Wing, A.M. stepping to the Beat: Feasibility and Potential efficacy of a home-Based auditory-cued step Training Program in chronic stroke. Front. Neurol. 2017, 8, 412. [Google Scholar] [CrossRef] [PubMed]
- Buckley, C.; Galna, B.; Rochester, L.; Mazzà, C. Upper body accelerations as a biomarker of gait impairment in the early stages of Parkinson’s disease. Gait Posture 2018, 71, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Iosa, M.; Bini, F.; Marinozzi, F.; Fusco, A.; Morone, G.; Koch, G.; Martino Cinnera, A.; Bonnì, S.; Paolucci, S. Stability and Harmony of Gait in Patients with Subacute Stroke. J. Med. Biol. Eng. 2016, 36, 635–643. [Google Scholar] [CrossRef] [PubMed]
- Viteckova, S.; Kutilek, P.; Svoboda, Z.; Krupicka, R.; Kauler, J.; Szabo, Z. Gait symmetry measures: A review of current and prospective methods. Biomed. Signal Process. Control 2018, 42, 89–100. [Google Scholar]
- Zhang, W.; Smuck, M.; Legault, C.; Ith, M.A.; Muaremi, A.; Aminian, K. Gait Symmetry Assessment with a Low Back 3D Accelerometer in Post-Stroke Patients. Sensors 2018, 18, 3322. [Google Scholar] [CrossRef]
- Huang, X.; Mahoney, J.M.; Lewis, M.M.; Guangwei, D.; Piazza, S.J.; Cusumano, J.P. Both coordination and symmetry of arm swing are reduced in Parkinson’s disease. Gait Posture 2012, 35, 373–377. [Google Scholar] [CrossRef]
- Hodt-Billington, C.; Helbostad, J.L.; Moe-Nilssen, R. Should trunk movement or footfall parameters quantify gait asymmetry in chronic stroke patients? Gait Posture 2008, 27, 552–558. [Google Scholar] [CrossRef]
- Bamford, J.; Sandercock, P.; Dennis, M.; Burn, J.; Warlow, C. Classification and natural history of clinically identifiable subtypes of cerebral infarction. Lancet 1991, 337, 1521–1526. [Google Scholar] [CrossRef]
- Brott, T.; Adams, H.P.; Olinger, C.P.; Marler, J.R.; Barsan, W.G.; Biller, J.; Spilker, J.; Holleran, R.; Eberle, R.; Hertzberg, V.; et al. Measurements of acute cerebral infarction: A clinical examination scale. Stroke 1989, 20, 864–870. [Google Scholar] [CrossRef] [PubMed]
- Esser, P.; Dawes, H.; Collett, J.; Howells, K. Insights into gait disorders: Walking variability using phase plot analysis, Parkinson’s disease. Gait Posture 2013, 38, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Dunne-Willows, M.; Watson, P.; Shi, J.; Rochester, L.; Del Din, S. A Novel Parameterisation of Phase Plots for Monitoring of Parkinson’s Disease. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Berlin, Germany, 23–27 July 2019; IEEE Explore: Berlin, Germany, 2019. [Google Scholar]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef] [PubMed]
- Lord, S.; Galna, B.; Rochester, L. Moving forward on gait measurement: Toward a more refined approach. Mov. Disord. 2013, 28, 1534–1543. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Godfrey, A.; Rochester, L. Validation of an Accelerometer to Quantify a Comprehensive Battery of Gait Characteristics in Healthy Older Adults and Parkinson’s Disease: Toward Clinical and at Home Use. IEEE J. Biomed. Health Inform. 2016, 20, 838–847. [Google Scholar] [CrossRef] [PubMed]
- McCamley, J.; Donati, M.; Grimpampi, E.; Mazzà, C. An enhanced estimate of initial contact and final contact instants of time using lower trunk inertial sensor data. Gait Posture 2012, 36, 316–318. [Google Scholar] [CrossRef]
- Buckley, C.; Galna, B.; Rochester, L.; Mazzà, C. Quantification of upper body movements during gait in older adults and in those with Parkinson’s disease: Impact of acceleration realignment methodologies. Gait Posture 2017, 52, 265–271. [Google Scholar] [CrossRef]
- Moe-Nilssen, R. A new method for evaluating motor control in gait under real-life environmental conditions. Part 1: The instrument. Clin. Biomech. 1998, 13, 328–335. [Google Scholar] [CrossRef]
- Bellanca, J.L.; Lowry, K.A.; Vanswearingen, J.M.; Brach, J.S.; Redfern, M.S. Harmonic ratios: A quantification of step to step symmetry. J. Biomech. 2013, 46, 828–831. [Google Scholar] [CrossRef]
- Moe-Nilssen, R.; Helbostad, J. Interstride trunk acceleration variability but not step width variability can differentiate between fit and frail older adults. Gait Posture 2005, 21, 164–170. [Google Scholar] [CrossRef]
- Tura, A.; Raggi, M.; Rocchi, L.; Cutti, A.G.; Chiari, L. Gait symmetry and regularity in transfemoral amputees assessed by trunk accelerations. J. Neuroeng. Rehabil. 2010, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Fleiss, J.L. The Design and Analysis of Clinical Experiments; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999; ISBN 0471820474. [Google Scholar]
- Balasubramanian, C.K.; Bowden, M.G.; Neptune, R.R.; Kautz, S.A. Relationship between step length asymmetry and walking performance in subjects with chronic hemiparesis. Arch. Phys. Med. Rehabil. 2007, 88, 43–49. [Google Scholar] [CrossRef] [PubMed]
- Boström, K.J.; Dirksen, T.; Zentgraf, K.; Wagner, H. The Contribution of Upper Body Movements to Dynamic Balance Regulation during Challenged Locomotion. Front. Hum. Neurosci. 2018, 12, 8. [Google Scholar] [CrossRef] [PubMed]
- Mahaki, M.; Bruijn, S.M.; van Dieën, J.H. The effect of external lateral stabilization on the use of foot placement to control mediolateral stability in walking and running. PeerJ 2019, 7, e7939. [Google Scholar] [CrossRef] [PubMed]
- Van de Port, I.; Punt, M.; Meijer, J.W. Walking activity and its determinants in free-living ambulatory people in a chronic phase after stroke: A cross-sectional study. Disabil. Rehabil. 2018, 16, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Godfrey, A.; Galna, B.; Lord, S.; Rochester, L.; Del-Din, S.; Godfrey, A.; Galna, B.; Lord, S.; Rochester, L. Free-living gait characteristics in ageing and Parkinson’s disease: Impact of environment and ambulatory bout length. J. Neuroeng. Rehabil. 2016, 13, 1–12. [Google Scholar] [CrossRef]
- Tamburini, A.P.; Storm, F.; Buckley, C.; Bisi, C.; Stagni, R.; Mazzà, C.; Tamburini, P.; Storm, F.; Buckley, C.; Bisi, M.C.; et al. Moving from laboratory to real life conditions: Influence on the assessment of variability and stability of gait. Gait Posture 2018, 59, 248–252. [Google Scholar] [CrossRef]
- Bernhardt, J.; Hayward, K.S.; Kwakkel, G.; Ward, N.S.; Wolf, S.L.; Borschmann, K.; Krakauer, J.W.; Boyd, L.A.; Carmichael, S.T.; Corbett, D.; et al. Agreed Definitions and a Shared Vision for New Standards in Stroke Recovery Research: The Stroke Recovery and Rehabilitation Roundtable Taskforce. Neurorehabil. Neural Repair 2017, 31, 793–799. [Google Scholar] [CrossRef]
- Espay, A.J.; Bonato, P.; Nahab, F.B.; Maetzler, W.; Dean, J.M.; Klucken, J.; Eskofier, B.M.; Merola, A.; Horak, F.; Lang, A.E.; et al. Technology in Parkinson’s disease: Challenges and opportunities. Mov. Disord. 2016, 31, 1272–1282. [Google Scholar] [CrossRef]
- Patterson, M.R.; Whelan, D.; Reginatto, B.; Caprani, N.; Walsh, L.; Smeaton, A.F.; Inomata, A.; Caulfield, B. Does external walking environment affect gait patterns? In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; Volume 2014, pp. 2981–2984. [Google Scholar]
- Yoo, G.E.; Kim, S.J. Rhythmic Auditory Cueing in Motor Rehabilitation for Stroke Patients: Systematic Review and Meta-Analysis. J. Music Ther. 2016, 53, 149–177. [Google Scholar] [CrossRef]

| Demographics (n = 23) | |
| Gender (male/female) | 19/4 |
| Age (years) | 63 ± 11 |
| Body mass index | 26 ± 4 |
| Stroke characteristics | |
| Time since stroke (months) | 66 ± 48 (range 5–201) |
| Stroke subtype (OCSP) | |
| Total anterior circulation | 11 |
| Partial anterior circulation | 6 |
| Lacunar | 3 |
| Posterior circulation | 3 |
| Stroke impairment | |
| NIHSS score (0–40) | 4 ± 3 (range 0–11) |
| NIHSS lower limb score (0–4) | 1 ± 0.7 (range 0–3) |
| Walking speed (m/s) | 0. 9 ± 0.4 |
| Marked hemiplegia (Yes/No) | 15/8 |
| Walking aid (number (%)) | 3 (13%) |
| Push Aequi ankle foot orthosis (number (%)) | 4 (17%) |
| Variables | Median (IQR) | Agreement | ||||
|---|---|---|---|---|---|---|
| T1 | T2 | Median Difference (%) | ICC21 | LOA % (95% LoA) | Rho | |
| Harmonic ratio (V) | 1.71 (1.37) | 1.70 (1.23) | −0.01 | 0.98 ** | 1.94 (2.52, 1.36) | 0.92 ** |
| Harmonic ratio (ML) | 1.38 (0.60) | 1.57 (0.72) | 0.14 | 0.71 ** | 1.56 (2.80, 0.31) | 0.71 ** |
| Harmonic ratio (AP) | 1.26 (0.97) | 1.39 (0.92) | 0.10 | 0.92 ** | 1.54 (2.34, 0.73) | 0.91 ** |
| Step regularity (V) | 0.53 (0.47) | 0.52 (0.54) | −0.02 | 0.98 ** | 0.51 (0.67, 0.34) | 0.96 ** |
| Step regularity (ML) | 0.42 (0.20) | 0.44 (0.18) | 0.04 | 0.73 ** | 0.44 (0.69, 0.19) | 0.61 ** |
| Step regularity (AP) | 0.51 (0.43) | 0.40 (0.49) | −0.20 | 0.92 ** | 0.37 (0.68, 0.07) | 0.87 ** |
| Stride regularity (V) | 0.70 (0.25) | 0.68 (0.27) | −0.03 | 0.94 ** | 0.66 (0.85, 0.46) | 0.88 ** |
| Stride regularity (ML) | 0.59 (0.14) | 0.66 (0.20) | 0.12 | 0.93 ** | 0.57 (0.78, 0.37) | 0.73 ** |
| Stride regularity (AP) | 0.74 (0.18) | 0.75 (0.13) | 0.01 | 0.87 ** | 0.70 (0.92, 0.48) | 0.74 ** |
| Autocorrelation symmetry (V) | 0.53 (0.26) | 0.52 (0.29) | 0.56 | 0.80 ** | 0.18 (0.40, −0.03) | 0.76 ** |
| Autocorrelation symmetry (ML) | 0.10 (0.19) | 0.16 (0.25) | 0.09 | 0.59 * | 0.19 (0.44, −0.05) | 0.49 * |
| Autocorrelation symmetry (AP) | 0.18 (0.15) | 0.19 (0.14) | 0.61 | 0.93 ** | 0.36 (0.62, 0.10) | 0.79 ** |
| Gait symmetry index | 0.21 (0.37) | 0.35 (0.43) | −0.02 | 0.92 ** | 0.47 (0.70, 0.23) | 0.82 ** |
| Orbit eccentricity | 7.79 (6.27) | 8.32 (15.13) | 0.00 | 0.72 ** | 0.97 (1.04, 0.91) | 0.70 ** |
| Relative orbit inclination | 0.01 (0.01) | 0.01 (0.01) | 0.07 | 0.76 ** | 11.02 (28.02, −5.99) | 0.60 ** |
| Orbit width deviation | 0.01 (0.02) | 0.00 (0.02) | −0.07 | 0.66 ** | 0.01 (0.05, −0.02) | 0.65 ** |
| Short half orbit eccentricity | 5.32 (6.35) | 4.12 (5.31) | −0.38 | 0.73 ** | 0.02 (0.07, −0.03) | 0.87 ** |
| Short half orbit segment angle | 0.02 (0.05) | 0.01 (0.04) | −0.23 | 0.95 ** | 7.74 (15.28, 0.20) | 0.57 ** |
| Long half orbit eccentricity | 5.20 (10.73) | 5.61 (6.55) | −0.16 | 0.79 ** | 0.04 (0.13, −0.05) | 0.59 ** |
| Long half orbit segment angle | 0.89 (0.41) | 0.88 (0.20) | 0.08 | 0.45 | 7.77 (26.32, −10.78) | 0.57 ** |
| Intra step correlation | 1.05 (0.04) | 1.05 (0.04) | −0.01 | 0.58 * | 0.78 (1.29, 0.28) | 0.68 ** |
| Acceleration RMS (V) | 0.18 (0.09) | 0.17 (0.06) | 0.00 | 0.03 | 1.03 (1.24, 0.83) | 0.41 |
| Acceleration RMS (ML) | 0.25 (0.15) | 0.24 (0.15) | −0.06 | 0.90 ** | 0.17 (0.24, 0.10) | 0.68 ** |
| Acceleration RMS (AP) | 8.53 (8.00) | 8.57 (7.47) | −0.04 | 0.20 | 0.26 (0.62, −0.10) | 0.21 |
| Jerk RMS (V) | 6.29 (4.18) | 6.36 (4.15) | 0.01 | 0.96 ** | 9.32 (13.49, 5.14) | 0.93 ** |
| Jerk RMS (ML) | 6.22 (4.89) | 6.42 (6.88) | 0.01 | 0.97 ** | 7.39 (10.67, 4.11) | 0.90 ** |
| Jerk RMS (AP) | 1.71 (1.37) | 1.70 (1.23) | 0.03 | 0.96 ** | 7.26 (11.23, 3.28) | 0.92 ** |
| GaitRite Variable | Acceleration Derived Variable | Spearman’s Rank Correlation Coefficient (RHO) | ICC21 (Test–Retest) | |
|---|---|---|---|---|
| Asymmetry | Step time (s) | Step regularity (V) | 0.87 | 0.98 ** |
| Swing time (s) | Harmonic ratio (V) | 0.73 | 0.98 ** | |
| Stance time (s) | Step regularity (V) | 0.72 | 0.98 ** | |
| Step length (m) | Step regularity (V) | 0.65 | 0.98 ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buckley, C.; Micó-Amigo, M.E.; Dunne-Willows, M.; Godfrey, A.; Hickey, A.; Lord, S.; Rochester, L.; Del Din, S.; Moore, S.A. Gait Asymmetry Post-Stroke: Determining Valid and Reliable Methods Using a Single Accelerometer Located on the Trunk. Sensors 2020, 20, 37. https://doi.org/10.3390/s20010037
Buckley C, Micó-Amigo ME, Dunne-Willows M, Godfrey A, Hickey A, Lord S, Rochester L, Del Din S, Moore SA. Gait Asymmetry Post-Stroke: Determining Valid and Reliable Methods Using a Single Accelerometer Located on the Trunk. Sensors. 2020; 20(1):37. https://doi.org/10.3390/s20010037
Chicago/Turabian StyleBuckley, Christopher, M. Encarna Micó-Amigo, Michael Dunne-Willows, Alan Godfrey, Aodhán Hickey, Sue Lord, Lynn Rochester, Silvia Del Din, and Sarah A. Moore. 2020. "Gait Asymmetry Post-Stroke: Determining Valid and Reliable Methods Using a Single Accelerometer Located on the Trunk" Sensors 20, no. 1: 37. https://doi.org/10.3390/s20010037
APA StyleBuckley, C., Micó-Amigo, M. E., Dunne-Willows, M., Godfrey, A., Hickey, A., Lord, S., Rochester, L., Del Din, S., & Moore, S. A. (2020). Gait Asymmetry Post-Stroke: Determining Valid and Reliable Methods Using a Single Accelerometer Located on the Trunk. Sensors, 20(1), 37. https://doi.org/10.3390/s20010037







