A Robust Noise Mitigation Method for the Mobile RFID Location in Built Environment
Abstract
1. Introduction
2. Related Works
2.1. RFID-Based Location
2.2. RFID Noise Mitigation Methods
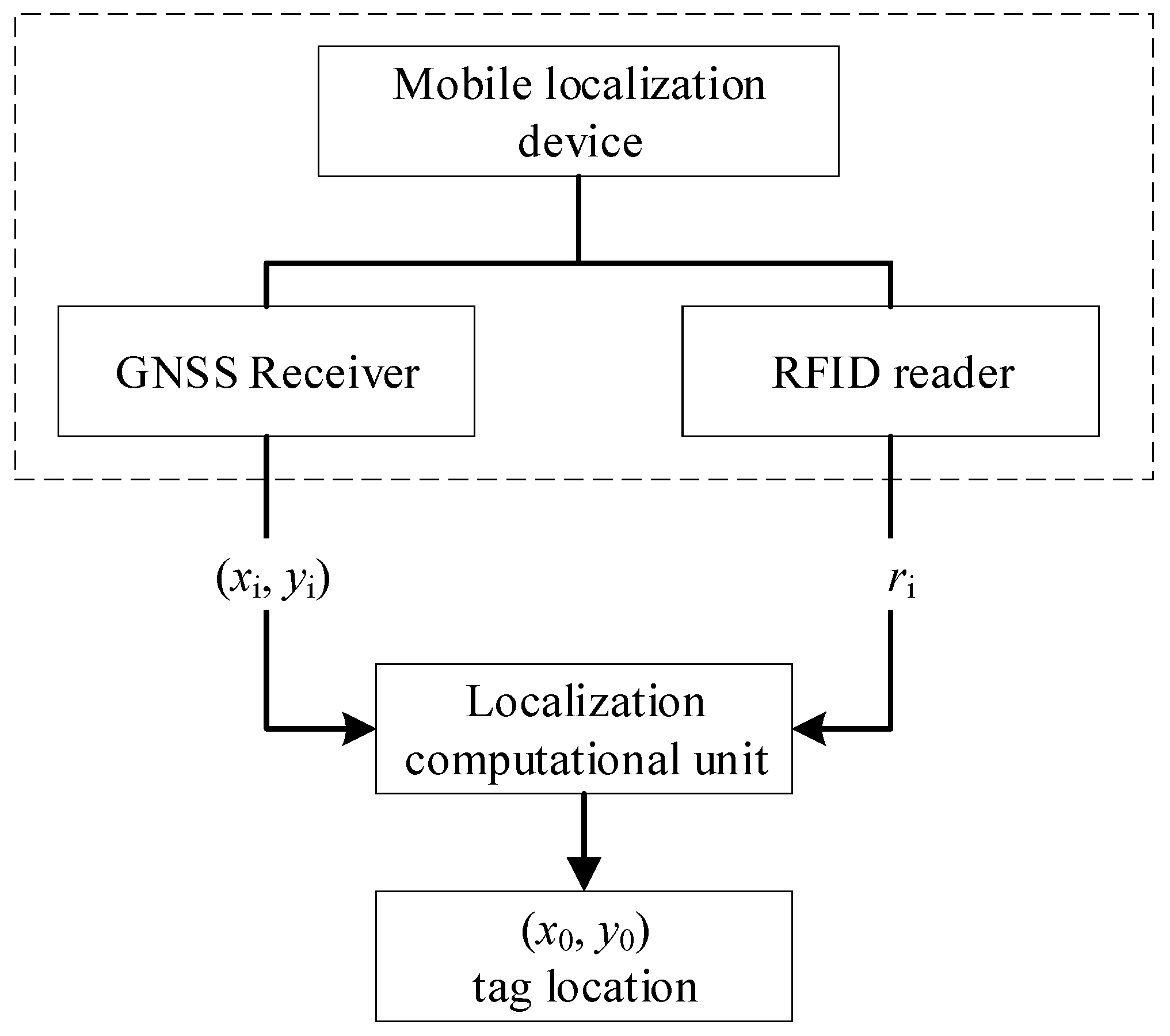
3. Mobile Localization and Problem Formulation
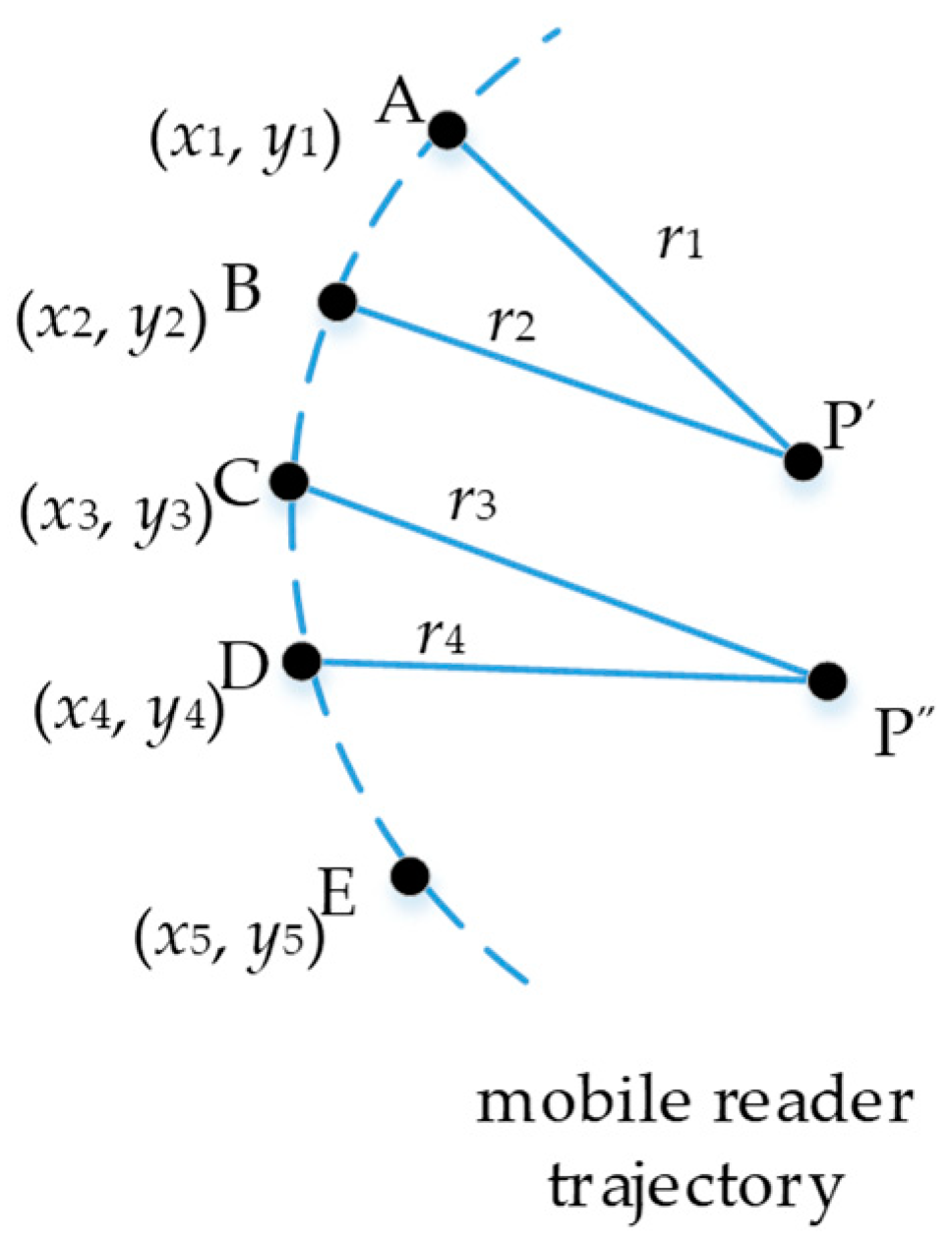
3.1. Mobile Localization Method
3.2. Noise Influence
4. A RANSAC Based Noise Mitigation Method
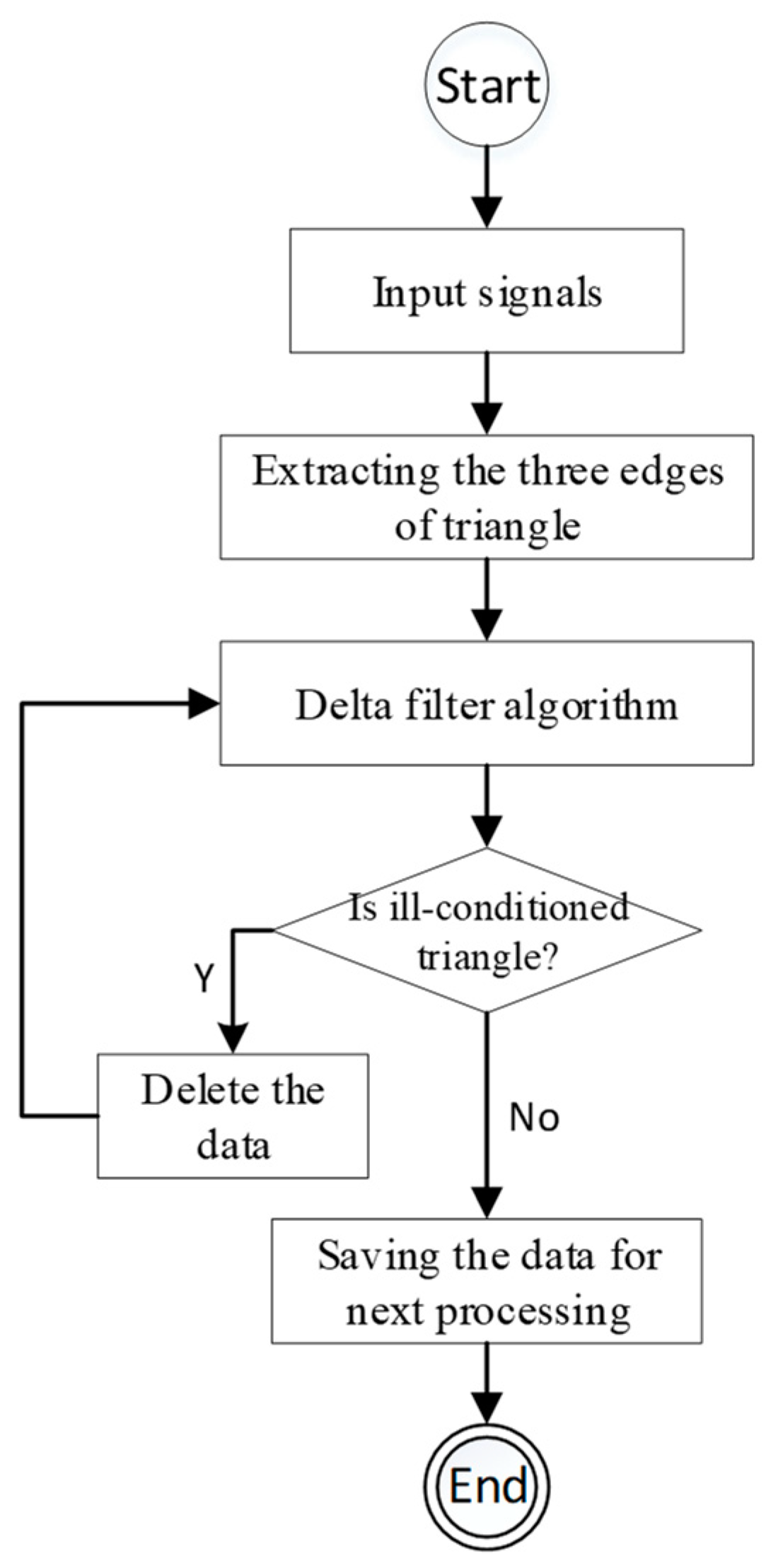
4.1. Delta Filter for RFID Measurement Data
| Algorithm 1: Delta filter algorithm | |
| Input: GNSS signal data, RFID ranging data | |
| Output: Satisfied and well-conditioned triangle data | |
| 1 | setp = point coordinate of the new point from GNSS signal data |
| 2 | setr = distance from RFID ranging signal data |
| 3 | For each point in saved reader location points set do |
| 4 | set pi = point coordinate of points set |
| 5 | set r1 = distance between pi and tag |
| 6 | set r2 = distance between p and tag |
| 7 | set r3 = distance between pi and p |
| 8 | calculate vertex angle of tag point from r1, r2, and r3 |
| 9 | if the value of the angle is within (30,120) then |
| 10 | The p, pi and tag point can build a well-conditioned triangle, |
| 11 | then add the triangle data (p, pi, target point) to a data set for the next process |
| 12 | else |
| 13 | continuous the next loop |
| 14 | end if |
| 15 | End for |
| 16 | Add (p, r) to reader location points set for next reader location processing |
4.2. A RANSAC-Based Robust Noise Detection
4.2.1. Making Hypothesis for the Mobile Localization
4.2.2. Parameters Definition for Verification
5. Experiment and Result
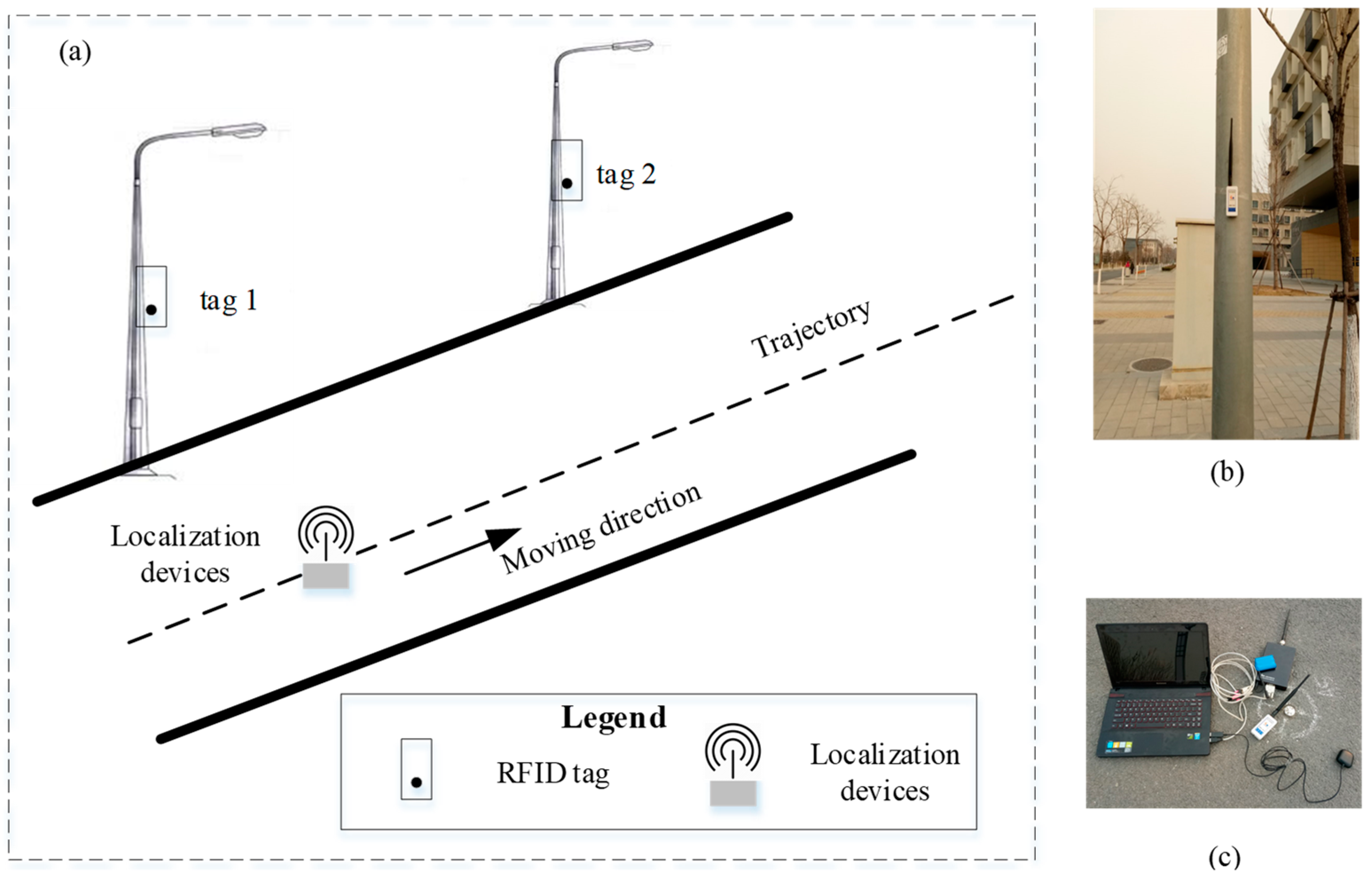
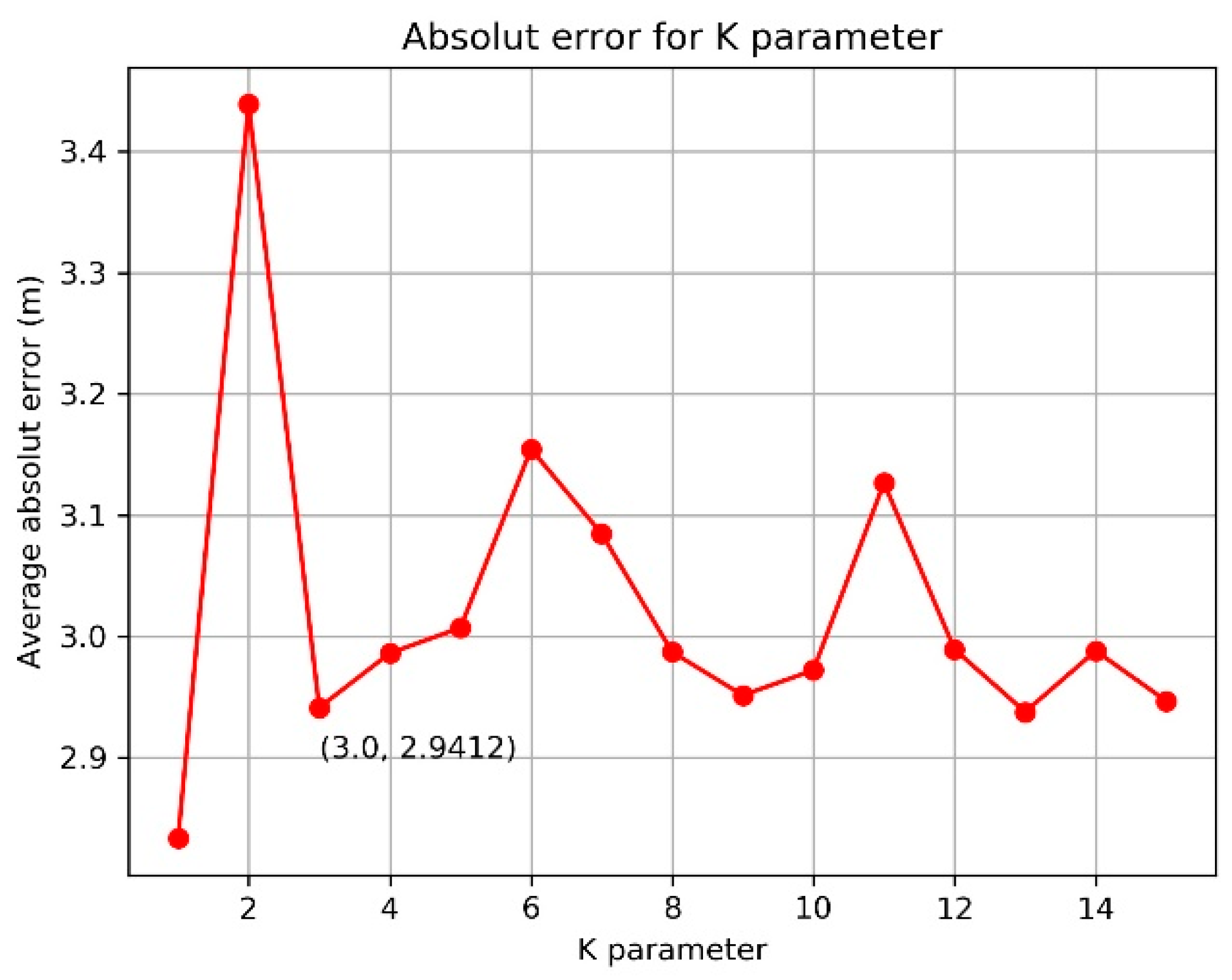
5.1. Experiment Setup
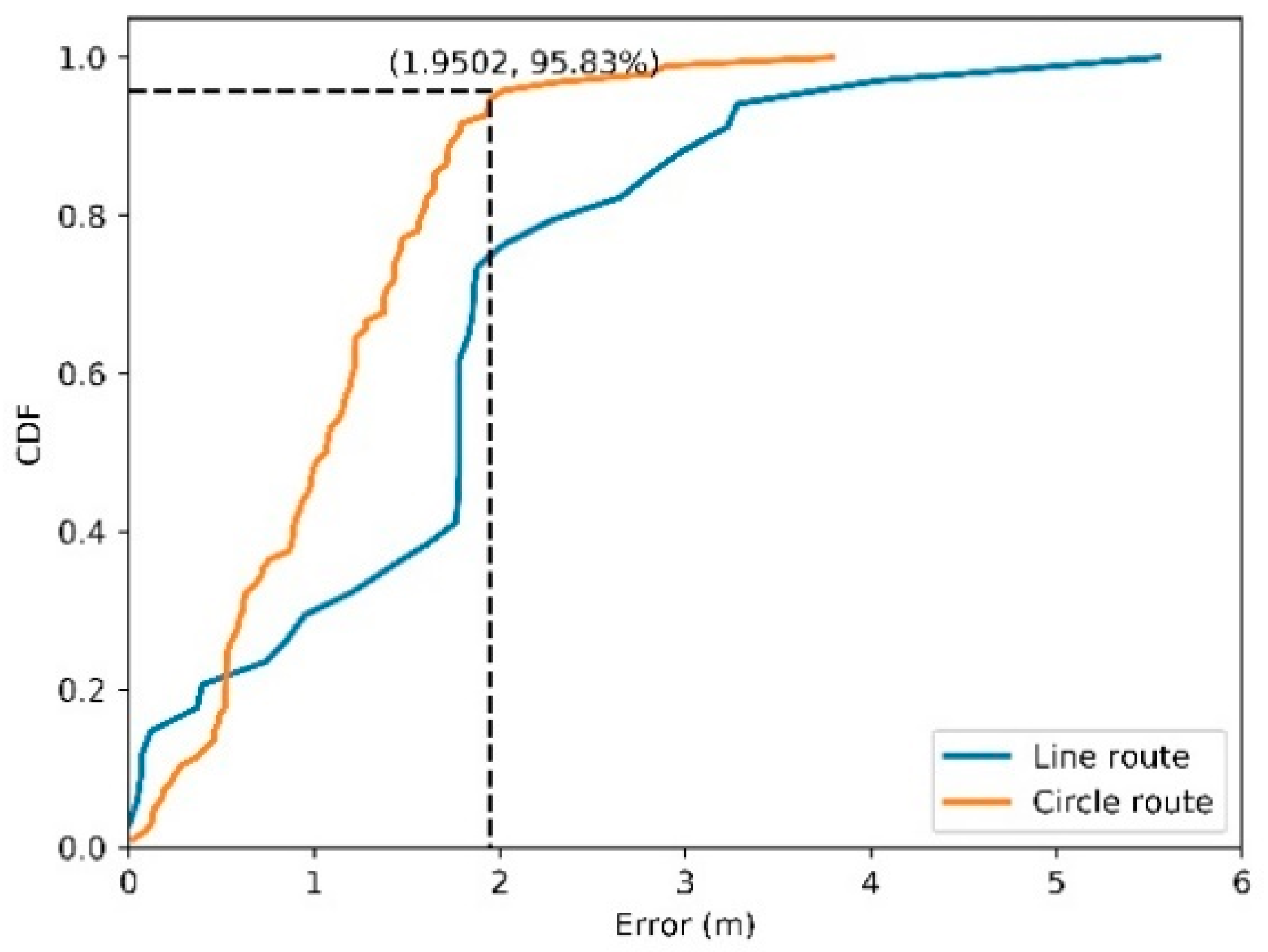
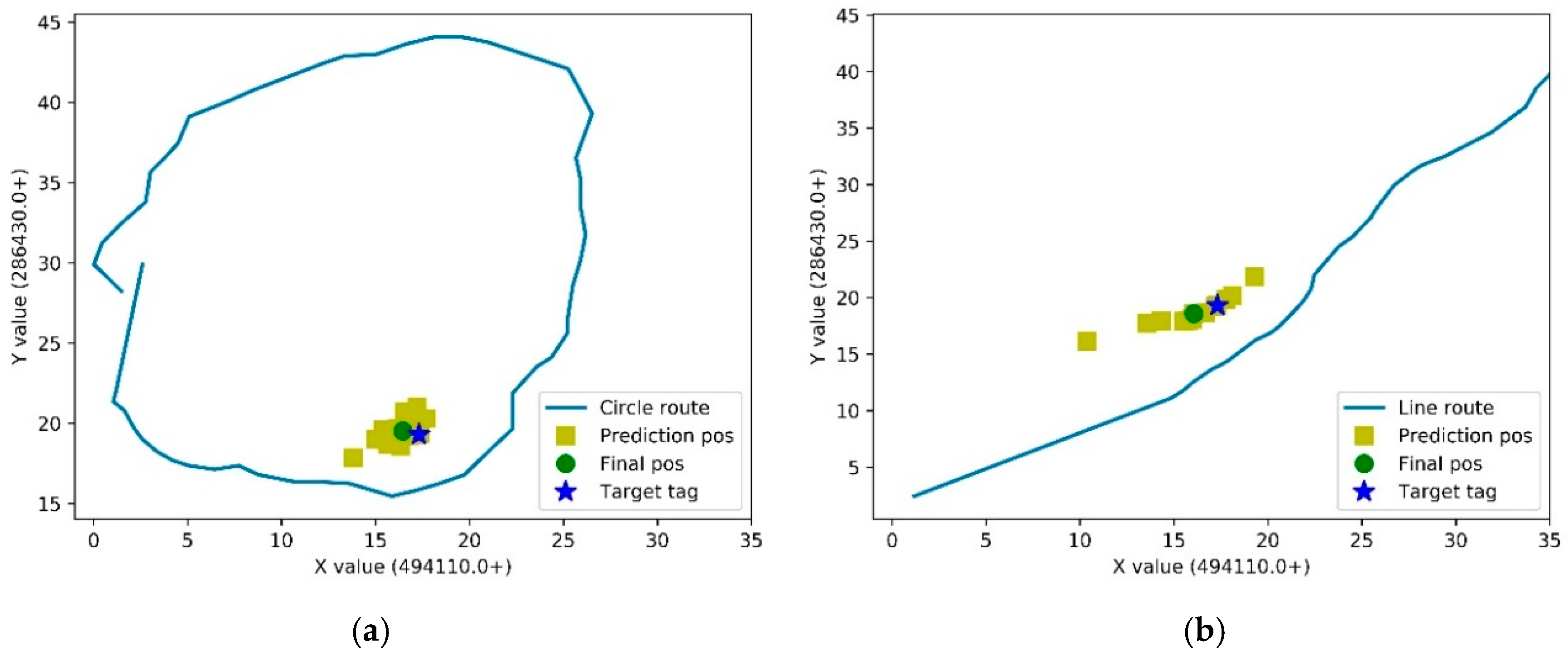
5.2. Field Test Result
6. Comparison with Existing Methods
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoang, V.-D.; Le, M.-H.; Tran, T.T.; Pham, V.-H. Improving Traffic Signs Recognition Based Region Proposal and Deep Neural Networks. In Intelligent Information and Database Systems; Springer: Cham, Switzerland, 2018; pp. 604–613. [Google Scholar]
- Tao, C.V. Mobile mapping technology for road network data acquisition. J. Geospat. Eng. 2000, 2, 1–14. [Google Scholar]
- Bean, E.Z.; Hunt, W.F.; Bidelspach, D.A. Field Survey of Permeable Pavement Surface Infiltration Rates. J. Irrig. Drain. Eng. 2007, 133, 249–255. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Wang, C.; Yu, J. Semiautomated Extraction of Street Light Poles From Mobile LiDAR Point-Clouds. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1374–1386. [Google Scholar] [CrossRef]
- Curtis, J.W.; Curtis, A.; Mapes, J.; Szell, A.B.; Cinderich, A. Using google street view for systematic observation of the built environment: Analysis of spatio-temporal instability of imagery dates. Int. J. Health Geogr. 2013, 12, 53. [Google Scholar] [CrossRef]
- Curtis, A.; Mills, J.W. Crime in Urban Post-Disaster Environments: A Methodological Framework from New Orleans. Urban Geogr. 2011, 32, 488–510. [Google Scholar] [CrossRef]
- Mills, J.W.; Curtis, A.; Kennedy, B.; Kennedy, S.W.; Edwards, J.D. Geospatial video for field data collection. Appl. Geogr. 2010, 30, 533–547. [Google Scholar] [CrossRef]
- Huang, H.; Lee, D.H.; Chang, K.; Li, W.; Acharya, T.D. Development of mobile platform for indoor positioning reference map using geomagnetic field data. Comput. Electr. Eng. 2018, 68, 557–569. [Google Scholar] [CrossRef]
- Li, N.; Becerik-Gerber, B. Performance-based evaluation of RFID-based indoor location sensing solutions for the built environment. Adv. Eng. Inform. 2011, 25, 535–546. [Google Scholar] [CrossRef]
- Motamedi, A.; Soltani, M.M.; Hammad, A. Localization of RFID-equipped assets during the operation phase of facilities. Adv. Eng. Inform. 2013, 27, 566–579. [Google Scholar] [CrossRef]
- Jing, C.; Wang, S.; Wang, M.; Du, M.; Zhou, L.; Sun, T.; Wang, J. A low-cost collaborative location scheme with GNSS and RFID for the Internet of Things. ISPRS Int. J. Geo-Inf. 2018, 7, 180. [Google Scholar] [CrossRef]
- Cai, H.; Andoh, A.R.; Su, X.; Li, S. A boundary condition based algorithm for locating construction site objects using RFID and GPS. Adv. Eng. Inform. 2014, 28, 455–468. [Google Scholar] [CrossRef]
- Li, J.; Yue, X.; Chen, J.; Deng, F. A novel robust trilateration method applied to ultra-wide bandwidth location systems. Sensors 2017, 17, 795. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Wang, Z.; Ye, N.; Wang, R.; Li, X.-Y. One More Tag Enables Fine-Grained RFID Localization and Tracking. IEEE/ACM Trans. Netw. 2018, 26, 161–174. [Google Scholar] [CrossRef]
- Bilodeau, J.-S.; Fortin-Simard, D.; Gaboury, S.; Bouchard, B.; Bouzouane, A. A practical comparison between filtering algorithms for enhanced RFID localization in smart environments. In Proceedings of the 2015 6th International Conference on Information, Intelligence, Systems and Applications (IISA), Corfu, Greece, 6–8 July 2015; pp. 1–6. [Google Scholar]
- Chai, J.; Wu, C.; Zhao, C.; Chi, H.L.; Wang, X.; Ling, B.W.K.; Teo, K.L. Reference tag supported RFID tracking using robust support vector regression and Kalman filter. Adv. Eng. Inform. 2017, 32, 1–10. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, C.; Liu, R.; Liang, G.; Zhang, H.; Ur Rehman, S. Moving object localization based on UHF RFID phase and laser clustering. Sensors 2018, 18, 825. [Google Scholar] [CrossRef]
- Zheng, V.W.; Zheng, Y.; Xie, X.; Yang, Q. Towards mobile intelligence: Learning from GPS history data for collaborative recommendation. Artif. Intell. 2012, 184, 17–37. [Google Scholar] [CrossRef]
- Casas, R.; Marco, A.; Guerrero, J.J.; Falcó, J. Robust estimator for non-line-of-sight error mitigation in indoor localization. EURASIP J. Appl. Signal Process. 2006, 2006, 156. [Google Scholar] [CrossRef]
- Janicka, J.; Rapiński, J. Filtering the results of Zigbee distance measurements with RANSAC algorithm. Acta Geodyn. Geomater. 2016, 13, 83–88. [Google Scholar] [CrossRef]
- Altaf, M.S.; Bouferguene, A.; Liu, H.; Al-Hussein, M.; Yu, H. Integrated production planning and control system for a panelized home prefabrication facility using simulation and RFID. Autom. Constr. 2018, 85, 369–383. [Google Scholar] [CrossRef]
- Ramiro Martínez-de Dios, J.; Ollero, A.; Fernández, F.; Regoli, C. On-Line RSSI-Range Model Learning for Target Localization and Tracking. J. Sens. Actuator Netw. 2017, 6, 15. [Google Scholar] [CrossRef]
- Castaldo, G.; Angrisano, A.; Gaglione, S.; Troisi, S. P-RANSAC: An integrity monitoring approach for GNSS signal degraded scenario. Int. J. Navig. Obs. 2014, 2014, 173818. [Google Scholar] [CrossRef]
- Dubbelman, G.; Duisterwinke, E.; Demi, L.; Talnishnikh, E.; Wortche, H.J.; Bergmans, J.W.M. Robust sensor cloud localization from range measurements. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3820–3827. [Google Scholar]
- Matas, J.; Chum, O. Randomized RANSAC with sequential probability ratio test. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 2, pp. 1727–1732. [Google Scholar]
- Li, R.; Sun, J.; Gong, D.; Zhu, Y.; Li, H.; Zhang, Y. ARSAC: Efficient model estimation via adaptively ranked sample consensus. Neurocomputing 2019, 328, 88–96. [Google Scholar] [CrossRef]
- Raguram, R.; Chum, O.; Pollefeys, M.; Matas, J.; Frahm, J.M. USAC: A universal framework for random sample consensus. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2022–2038. [Google Scholar] [CrossRef]
- Raguram, R.; Frahm, J.M.; Pollefeys, M. A comparative analysis of RANSAC techniques leading to adaptive real-time random sample consensus. In Proceedings of the European Conference on Computer Vision 2008, Marseille, France, 12–18 October 2008; pp. 500–513. [Google Scholar]
- Torr, P.H.S.; Murray, D.W. The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix. Int. J. Comput. Vis. 1997, 24, 271–300. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, L.T.; Chen, M.; Zhao, S.; Guo, M.; Zhang, Y. Real-Time Locating Systems Using Active RFID for Internet of Things. IEEE Syst. J. 2016, 10, 1226–1235. [Google Scholar] [CrossRef]
- Matarazzo, T.; Vazifeh, M.; Pakzad, S.; Santi, P.; Ratti, C. Smartphone data streams for bridge health monitoring. Procedia Eng. 2017, 199, 966–971. [Google Scholar] [CrossRef]
- Jayawardana, D.; Kharkovsky, S.; Liyanapathirana, R.; Zhu, X. Measurement System With Accelerometer Integrated RFID Tag for Infrastructure Health Monitoring. IEEE Trans. Instrum. Meas. 2016, 65, 1163–1171. [Google Scholar] [CrossRef]
- Maneesilp, J.; Wang, C.; Wu, H.; Tzeng, N.F. RFID Support for Accurate 3D Localization. IEEE Trans. Comput. 2013, 62, 1447–1459. [Google Scholar] [CrossRef]
- Bekkali, A.; Sanson, H.; Matsumoto, M. RFID indoor positioning based on probabilistic RFID map and Kalman Filtering. In Proceedings of the 3rd IEEE International Conference on Wireless and Mobile Computing, Networking and Communications, White Plains, NY, USA, 8–10 October 2007. [Google Scholar]
- Song, J.; Haas, C.T.; Caldas, C.H. A proximity-based method for locating RFID tagged objects. Adv. Eng. Inform. 2007, 21, 367–376. [Google Scholar] [CrossRef]
- Melendez-Pastor, C.; Ruiz-Gonzalez, R.; Gomez-Gil, J. A data fusion system of GNSS data and on-vehicle sensors data for improving car positioning precision in urban environments. Expert Syst. Appl. 2017, 80, 28–38. [Google Scholar] [CrossRef]
- Deng, Z.; Yu, Y.; Yuan, X.; Wan, N.; Yang, L. Situation and development tendency of indoor positioning. China Commun. 2013, 10, 42–55. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Tzeng, N.-F. RFID-Based 3-D Positioning Schemes. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 1235–1243. [Google Scholar]
- Ni, L.M.; Liu, Y.; Lau, Y.C.; Patil, A.P. LANDMARC: Indoor Location Sensing Using Active RFID. Wirel. Netw. 2004, 10, 701–710. [Google Scholar] [CrossRef]
- Son, Y.; Joung, M.H.; Lee, Y.W.; Kwon, O.H.; Song, H.J. Tag localization in a two-dimensional RFID tag matrix. Future Gener. Comput. Syst. 2017, 76, 384–390. [Google Scholar] [CrossRef]
- Yaacob, S.S.; Mahdin, H. An Overview on Various RFID Data Filtering Techniques Based on Bloom Filter Approach. ARPN J. Eng. Appl. Sci. 2016, 11, 1–5. [Google Scholar]
- Abreu, P.H.; Xavier, J.; Castro Silva, D.; Reis, L.P.; Petry, M. Using Kalman filters to reduce noise from RFID location system. Sci. World J. 2014, 2014, 796279. [Google Scholar]
- Xu, H.; Ding, Y.; Li, P.; Wang, R.; Li, Y. An RFID Indoor Positioning Algorithm Based on Bayesian Probability and K-Nearest Neighbor. Sensors 2017, 17, 1806. [Google Scholar] [CrossRef]
- Yang, L.; Cao, J.; Zhu, W.; Tang, S. Accurate and Efficient Object Tracking based on Passive RFID. IEEE Trans. Mob. Comput. 2015, 14, 2188–2200. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, H.; Sheng, Q.Z. A Cloud-Friendly RFID Trajectory Clustering Algorithm in Uncertain Environments. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2075–2088. [Google Scholar] [CrossRef]
- Patterson, D.J.; Fox, D.; Kautz, H.; Philipose, M. Fine-grained activity recognition by aggregating abstract object usage. In Proceedings of the Ninth IEEE International Symposium on Wearable Computers, Osaka, Japan, 18–21 October 2005; pp. 44–51. [Google Scholar]
- Wang, C.; Shi, Z.; Wu, F.; Zhang, J. An RFID indoor positioning system by using Particle Swarm Optimization-based Artificial Neural Network. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; pp. 738–742. [Google Scholar]
- Dwiyasa, F.; Lim, M.-H. Extreme Learning Machine for Active RFID Location Classification. In Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems; Springer: Cham, Switzerland, 2015; pp. 657–670. [Google Scholar]
- Liu, X.; Shannon, J.; Voun, H.; Truijens, M.; Chi, H.-L.; Wang, X. Spatial and Temporal Analysis on the Distribution of Active Radio-Frequency Identification (RFID) Tracking Accuracy with the Kriging Method. Sensors 2014, 14, 20451–20467. [Google Scholar] [CrossRef]
- Eom, K.H.; Lee, S.J.; Kyung, Y.S.; Lee, C.W.; Kim, M.C.; Jung, K.K. Improved kalman filter method for measurement noise reduction in multi sensor RFID systems. Sensors 2011, 11, 10266–10282. [Google Scholar] [CrossRef]
- Basak, N.N. Surveying and Levelling; McGraw Hill Education: New York, NY, USA, 2014; ISBN 9332901538. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Kang, M.; Gao, J.; Tang, L. Nonlinear RANSAC optimization for parameter estimation with applications to phagocyte transmigration. In Proceedings of the 2011 10th International Conference on Machine Learning and Applications and Workshops, Honolulu, HI, USA, 18–21 December 2011; pp. 501–504. [Google Scholar]
- Akbar, M.B.; Taylor, D.G.; Durgin, G.D. Amplitude and phase difference estimation bounds for multisensor based tracking of RFID Tags. In Proceedings of the 2015 IEEE International Conference on RFID (RFID), San Diego, CA, USA, 15–17 April 2015; pp. 105–112. [Google Scholar]
- Scikitlearning. RANSAC (RANdom SAmple Consensus) Algorithm. Available online: http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RANSACRegressor.html (accessed on 20 August 2002).
- Zhao, J.; Zhao, Q.; Li, Z.; Liu, Y. An improved Weighted Centroid Localization algorithm based on difference of estimated distances for Wireless Sensor Networks. Telecommun. Syst. 2013, 53, 25–31. [Google Scholar] [CrossRef]
- Laurendeau, C.; Barbeau, M. Centroid Localization of Uncooperative Nodes in Wireless Networks Using a Relative Span Weighting Method. EURASIP J. Wirel. Commun. Netw. 2009, 2010, 567040. [Google Scholar] [CrossRef]
- Berz, E.L.; Tesch, D.A.; Hessel, F.P. RFID indoor localization based on support vector regression and k-means. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; pp. 1418–1423. [Google Scholar]

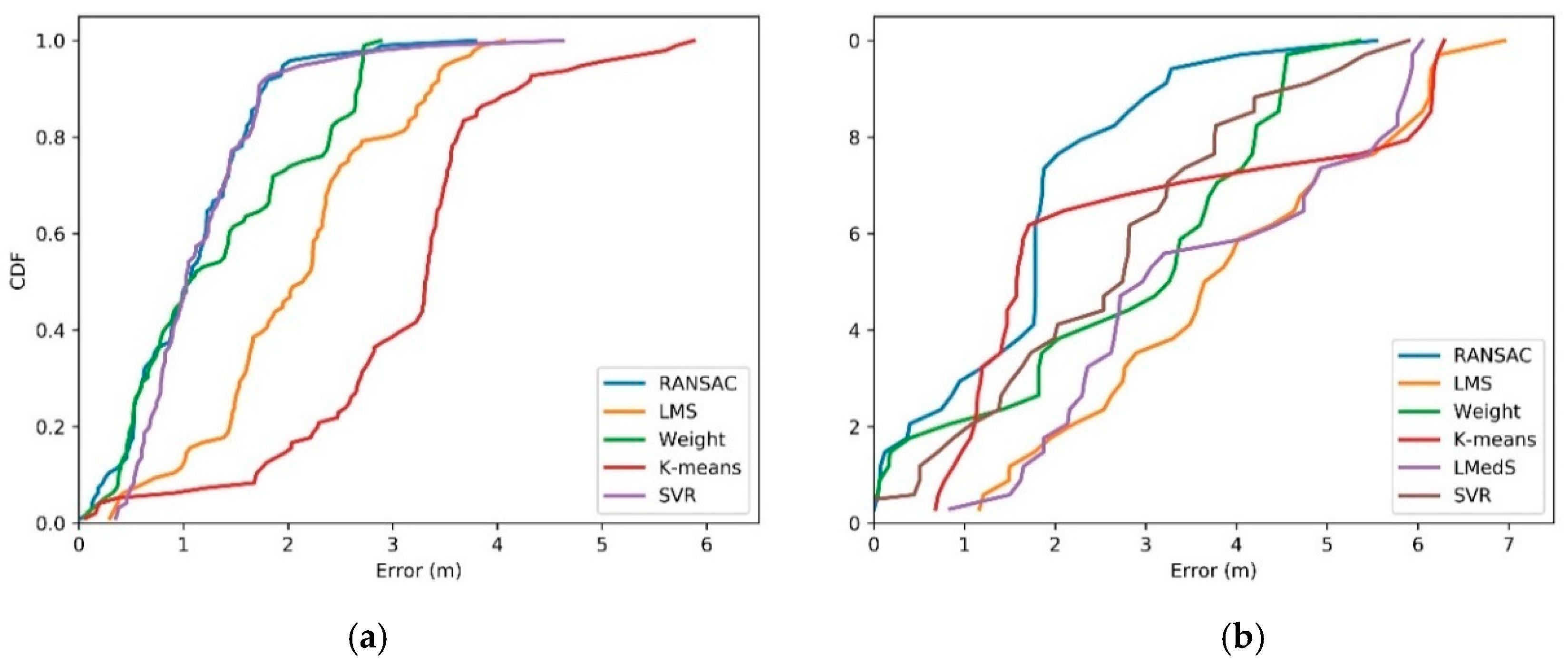
| WCL | k-Means | LMS | LMedS | SVR | RANSAC | |
|---|---|---|---|---|---|---|
| Line Route | 3.6293 | 3.6957 | 4.5916 | 4.3050 | 3.2740 | 2.6529 |
| Circle Route | 1.6345 | 3.2779 | 2.2975 | - 1 | 1.3573 | 1.2605 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, C.; Sun, T.; Chen, Q.; Du, M.; Wang, M.; Wang, S.; Wang, J. A Robust Noise Mitigation Method for the Mobile RFID Location in Built Environment. Sensors 2019, 19, 2143. https://doi.org/10.3390/s19092143
Jing C, Sun T, Chen Q, Du M, Wang M, Wang S, Wang J. A Robust Noise Mitigation Method for the Mobile RFID Location in Built Environment. Sensors. 2019; 19(9):2143. https://doi.org/10.3390/s19092143
Chicago/Turabian StyleJing, Changfeng, Tiancheng Sun, Qiang Chen, Mingyi Du, Mingshu Wang, Shouqing Wang, and Jian Wang. 2019. "A Robust Noise Mitigation Method for the Mobile RFID Location in Built Environment" Sensors 19, no. 9: 2143. https://doi.org/10.3390/s19092143
APA StyleJing, C., Sun, T., Chen, Q., Du, M., Wang, M., Wang, S., & Wang, J. (2019). A Robust Noise Mitigation Method for the Mobile RFID Location in Built Environment. Sensors, 19(9), 2143. https://doi.org/10.3390/s19092143








