Incoherent Optical Frequency-Domain Reflectometry Based on Homodyne Electro-Optic Downconversion for Fiber-Optic Sensor Interrogation
Abstract
:1. Introduction
2. Theoretical Background
2.1. Amplitude-Modulated Incoherent Frequency-Domain Reflectometry
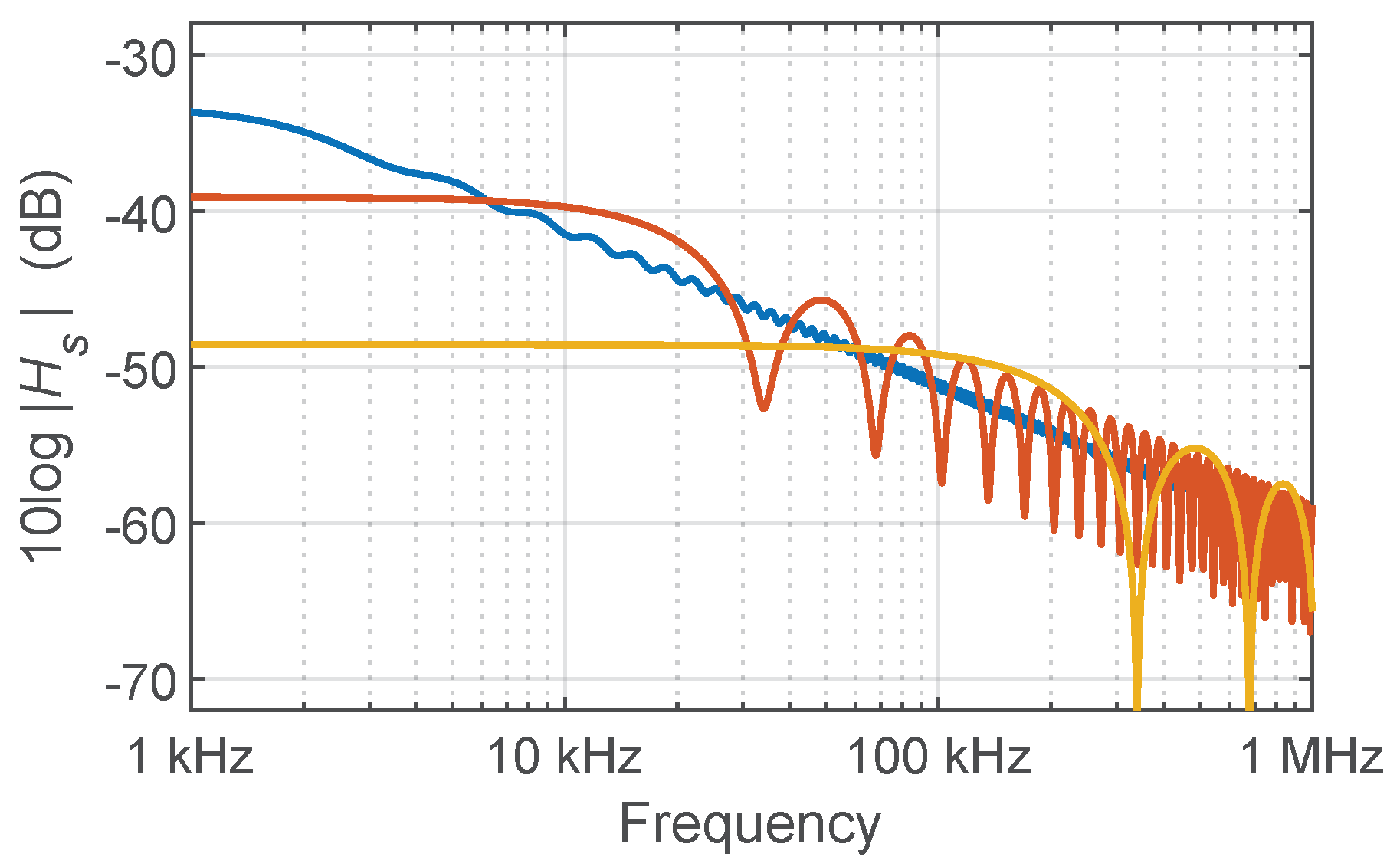
2.2. I-OFDR Using Homodyne Electro-Optic Downconversion
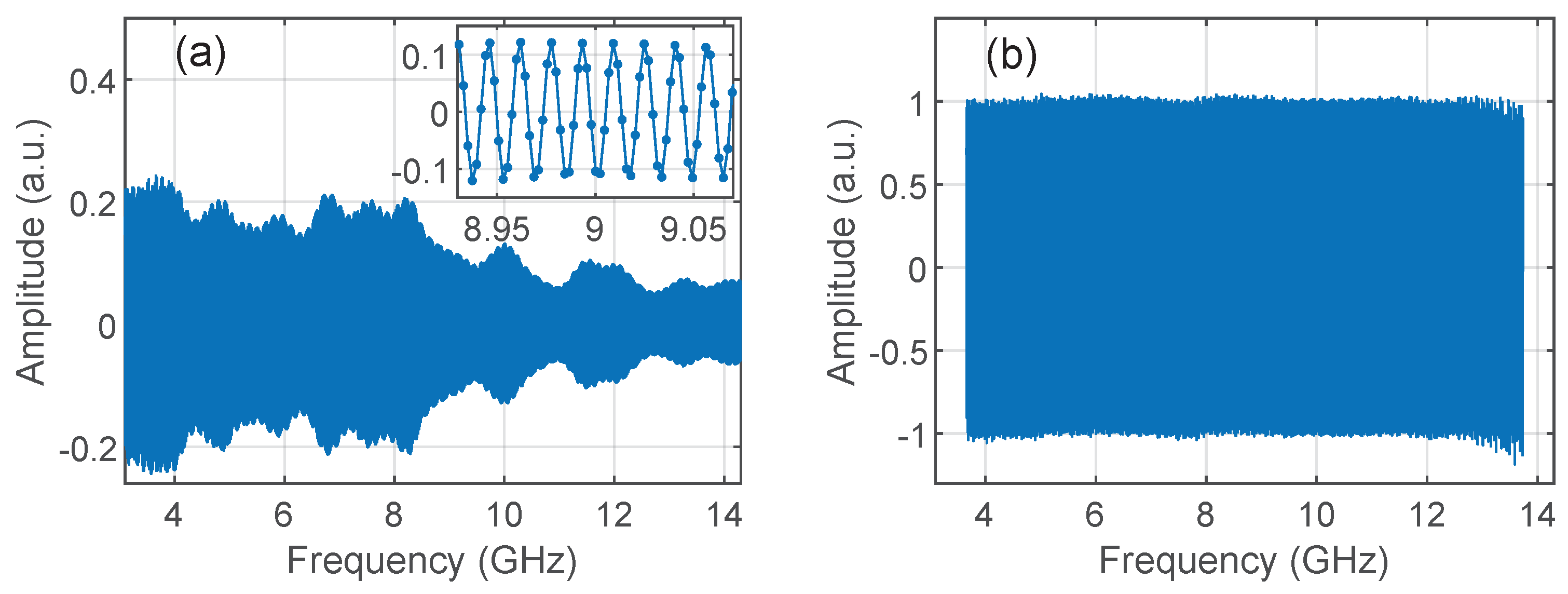
3. Experimental System and Signal Processing
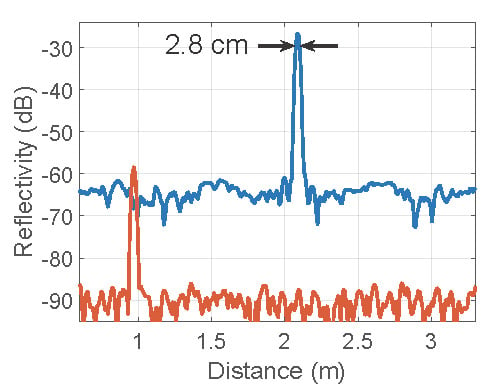
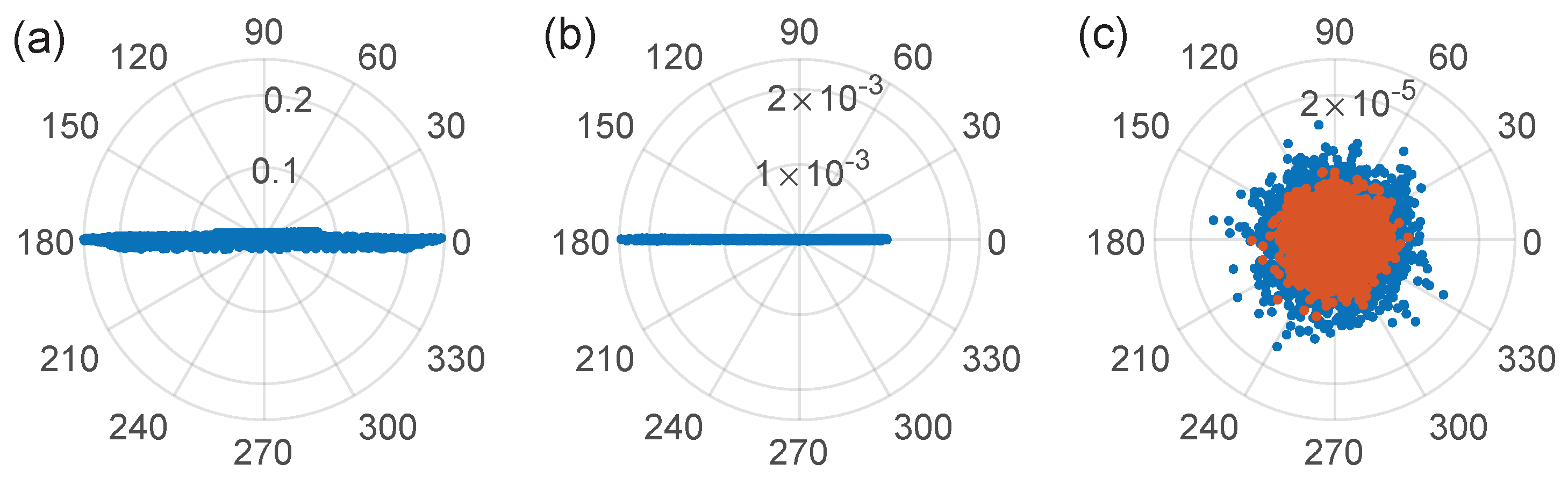
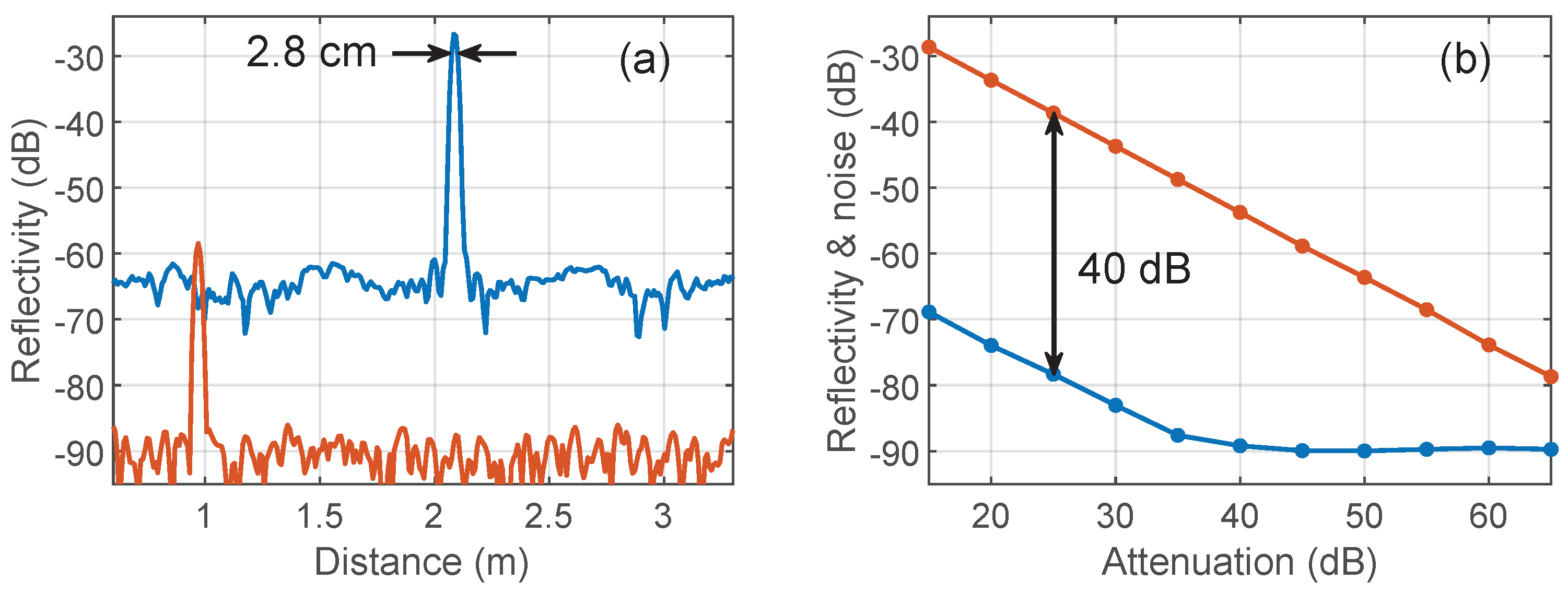
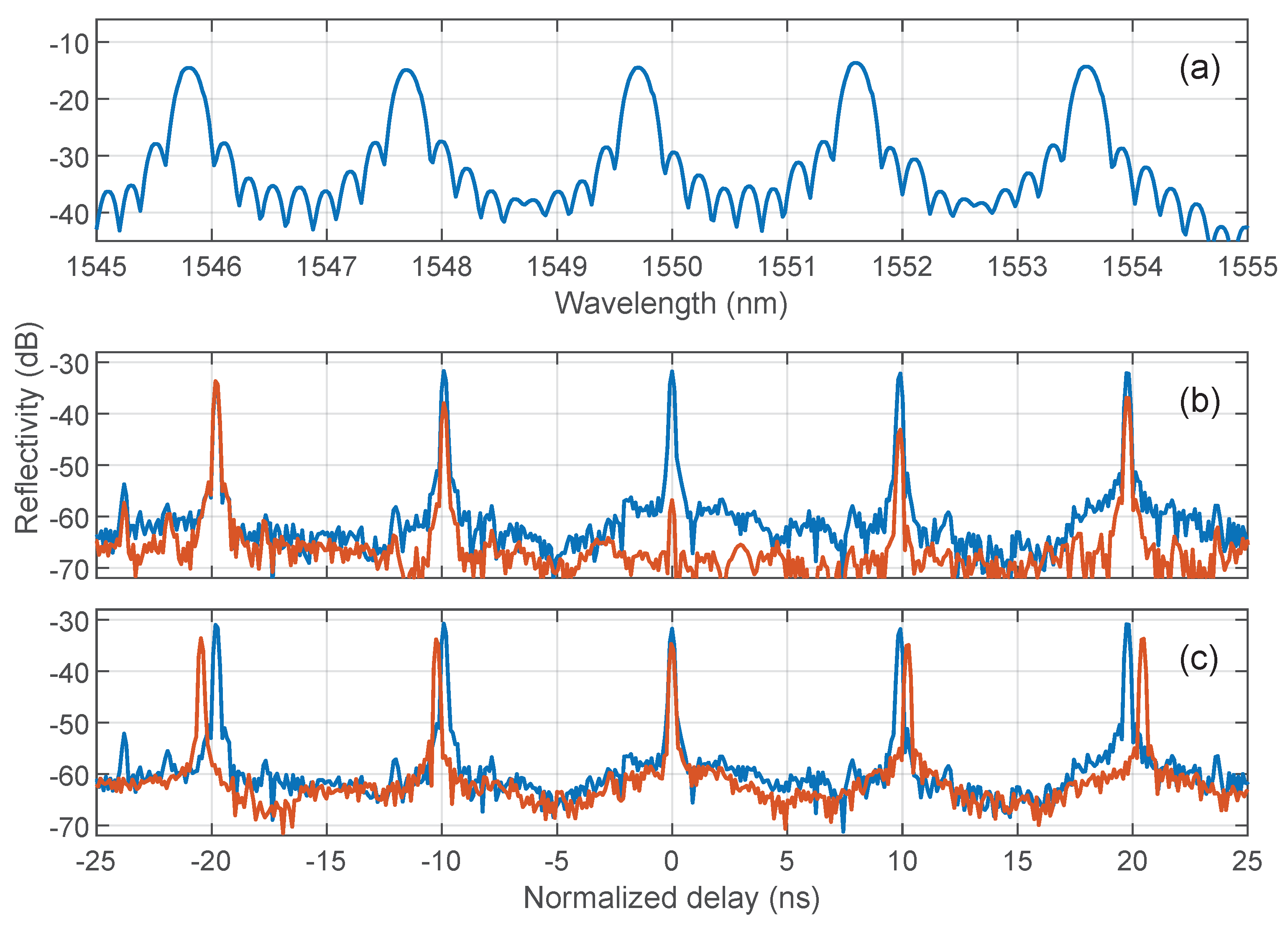
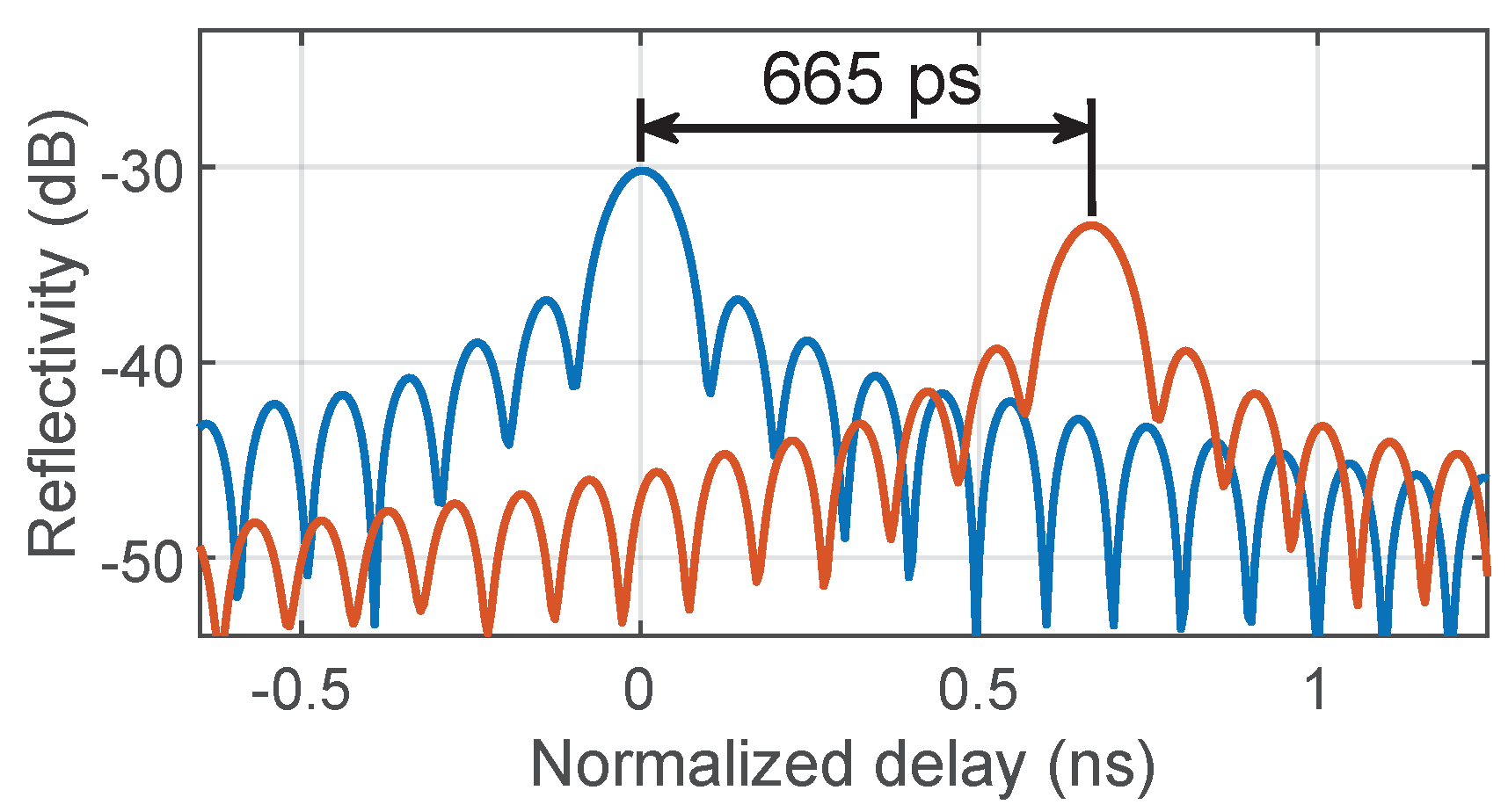
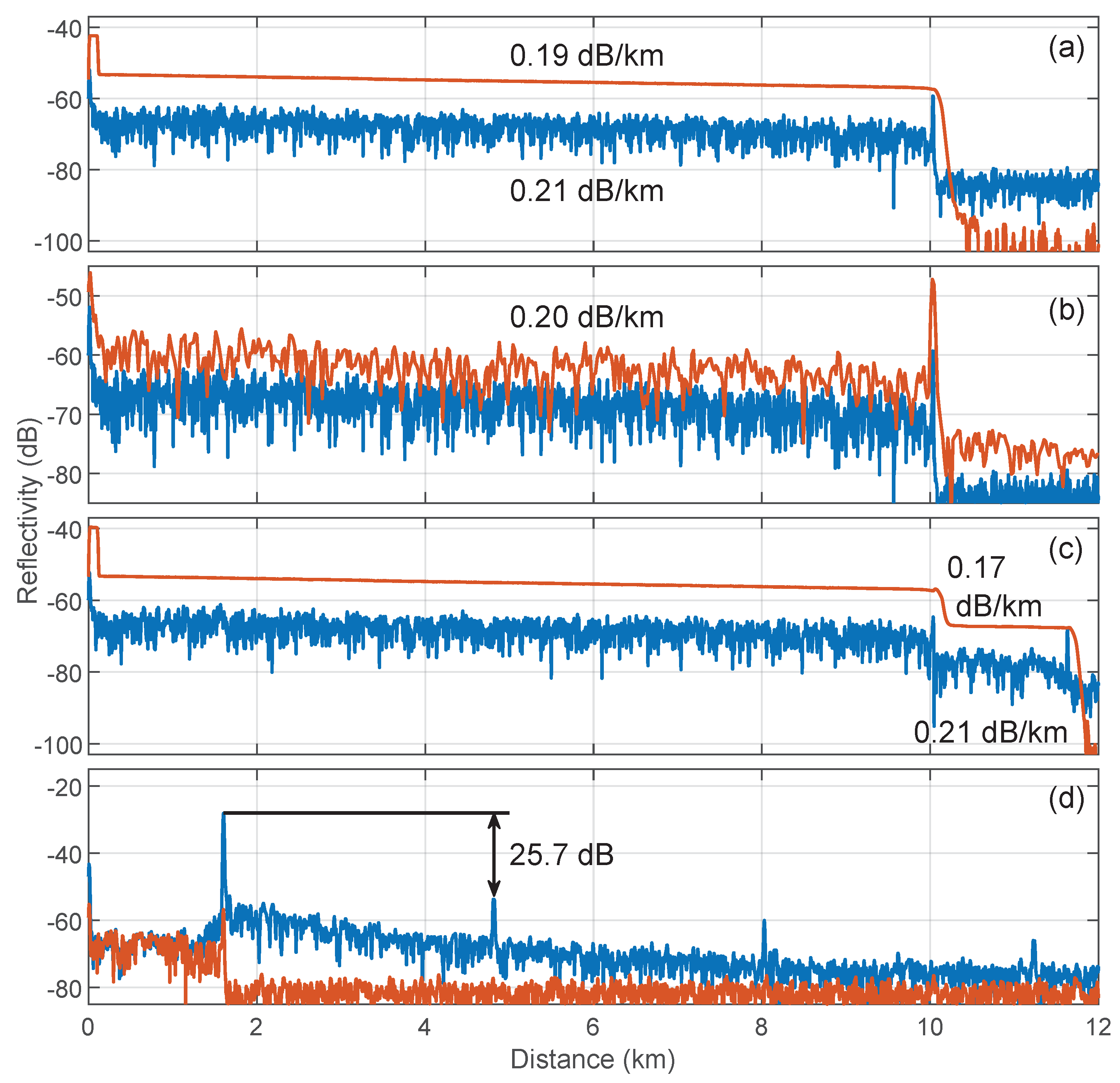
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kapron, F.P.; Kneller, D.G.; Garel-Jones, P.M. Aspects of optical frequency-domain reflectometry. In Technical Digest of the International Conference on Integrated Optics and Optical Fiber Communication; Optical Society of America: San Francisco, CA, USA, 1981. [Google Scholar]
- Ghafoori-Shiraz, H.; Okoshi, T. Fault location in optical fibers using optical frequency domain reflectometry. J. Light. Technol. 1986, 4, 316–322. [Google Scholar] [CrossRef]
- Nakayama, J.; Iizuka, K.; Nielsen, J. Optical fiber fault locator by the step frequency method. Appl. Opt. 1987, 1987 26, 440–443. [Google Scholar] [CrossRef]
- Schlemmer, B. A simple and very effective method with improved sensitivity for fault location in optical fibers. IEEE Photonics Technol. Lett. 1991, 3, 1037–1039. [Google Scholar] [CrossRef]
- Dolfi, D.W.; Nazarathy, M.; Newton, S.A. 5-mm-resolution optical-frequency-domain reflectometry using a coded phase-reversal modulator. Opt. Lett. 1988, 13, 678. [Google Scholar] [CrossRef]
- Nazarathy, M.; Dolfi, D.W. Optical frequency domain reflectometry with high sensitivity and resolution using synchronous detection with coded modulators. Electron. Lett. 1989, 25, 160–162. [Google Scholar]
- Derickson, D. Fiber Optics Test and Measurement; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Keysight Technologies. Time-Domain Analysis Using A Network Analyzer. Available online: Http://literature.cdn.keysight.com/litweb/pdf/5989-5723EN.pdf (accessed on 4 May 2019).
- Hiebel, M. Fundamentals of Vector Network Analysis; Rohde & Schwarz: Munich, Germany, 2005. [Google Scholar]
- Ricchiuti, A.L.; Barrera, D.; Sales, S.; Thévenaz, L.; Capmany, J. Long fiber Bragg grating sensor interrogation using discrete-time microwave photonic filtering techniques. Opt. Express 2013, 21, 28175–28181. [Google Scholar] [CrossRef] [PubMed]
- Werzinger, S.; Bergdolt, S.; Engelbrecht, R.; Thiel, T.; Schmauss, B. Quasi-distributed fiber Bragg grating sensing using steeped incoherent optical frequency domain reflectometry. J. Light. Technol. 2016, 34, 5270–5277. [Google Scholar] [CrossRef]
- Wei, T.; Huang, J.; Han, Q.; Xiao, H. Optical fiber sensor based on a radio frequency Mach-Zehnder interferometer. Opt. Lett. 2012, 37, 647–649. [Google Scholar] [CrossRef]
- Huang, J.; Lan, X.; Luo, M.; Xiao, H. Spatially continuous distributed fiber optic sensing using carrier based microwave interferometry. Opt. Express. 2014, 22, 18758–18767. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Lan, X.; Song, Y.; Li, Y.; Hua, L.; Xiao, H. Microwave interrogated sapphire fiber Michelson interferometer for high temperature sensing. IEEE Photonics Technol. Lett. 2015, 27, 1398–1401. [Google Scholar] [CrossRef]
- Xu, Z.; Shu, X.; Fu, H. Sensitivity enhanced fiber sensor based on a fiber ring microwave photonic filter with the Vernier effect. Opt. Express 2017, 25, 21560–21566. [Google Scholar] [CrossRef]
- Cheng, B.; Hua, L.; Zhang, Q.; Lei, J.; Xiao, H. Microwave-assisted frequency domain measurement of fiber-loop ring-down system. Opt. Lett. 2017, 42, 1209–1212. [Google Scholar] [CrossRef]
- Liehr, S.; Nöther, N.; Krebber, K. Incoherent optical frequency domain reflectometry and distributed strain detection in polymer optical fibers. Meas. Sci. Technol. 2009, 21, 017001. [Google Scholar] [CrossRef]
- Garus, D.; Gogolla, T.; Krebber, K.; Schliep, F. Brillouin optical-fiber frequency-domain analysis for distributed temperature and strain sensing. J. Light. Technol. 1997, 15, 654–662. [Google Scholar] [CrossRef]
- Karamehmedović, E.; Glombitza, U. Fiber-optic distributed temperature sensor using incoherent optical frequency domain reflectometry. Proc. SPIE 2004, 5363, 107–115. [Google Scholar]
- Köppel, M.; Werzinger, S.; Ringel, T.; Bechtold, P.; Thiel, T.; Engelbrecht, R.; Bosselmann, T.; Schmauss, B. Combined distributed Raman and Bragg fiber temperature sensing using incoherent optical frequency domain reflectometry. J. Sens. Sens. Syst. 2018, 7, 91–100. [Google Scholar] [CrossRef]
- Hervás, J.; Ricchiuti, A.L.; Li, W.; Zhu, N.H.; Fernández-Pousa, C.R.; Sales, S.; Li, M.; Capmany, J. Microwave Photonics for optical sensors. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 327–339. [Google Scholar] [CrossRef]
- Xi, L.; Cheng, R.; Li, W.; Liu, D. Identical FBG-based quasi-distributed sensing by monitoring the microwave responses. IEEE Photonics Technol. Lett. 2015, 27, 323–325. [Google Scholar] [CrossRef]
- Werzinger, S.; Härteis, L.-S.; Koeppel, M.; Schmauss, B. Time and wavelength division multiplexing of fiber Bragg gratings with bidirectional electro-optical frequency conversion. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Optical Society of America, Lausanne, Switzerland, 24–28 of September 2018. paper ThE19. [Google Scholar]
- Mao, W.; Kim, H.H.; Pan, J.K. A novel fiber Bragg grating sensing interrogation method using bidirectional modulation of a Mach-Zehnder electro-optical modulator. In Proceedings of the OECC 2010 Technical Digest, Sapporo, Japan, 5–9 July 2010; pp. 314–315. [Google Scholar]
- Hervás, J.; Fernández-Pousa, C.R.; Barrera, D.; Pastor, D.; Sales, S.; Capmany, J. An interrogation technique of FBG cascade sensors using wavelength to radio-frequency delay mapping. J. Light. Technol. 2015, 33, 2222–2227. [Google Scholar] [CrossRef]
- Clement, J.; Torregrosa, G.; Hervás, J.; Barrera, D.; Sales, S.; Fernández-Pousa, C.R. Interrogation of a sensor array of identical weak FBGs using dispersive incoherent OFDR. IEEE Photonics Technol. Lett. 2016, 28, 1154–1156. [Google Scholar] [CrossRef]
- Clement, J.; Torregrosa, G.; Maestre, H.; Fernández-Pousa, C.R. Remote picometer fiber Bragg grating demodulation using a dual-wavelength source. Appl. Opt. 2016, 55, 6523–6529. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xia, L.; Ran, Y.; Rohollahnejad, J.; Zhou, J.; Wen, J. Interrogation of ultrashort Bragg grating sensors using shifted gaussian filters. IEEE Photonics Technol. Lett. 2015, 27, 1833–1836. [Google Scholar] [CrossRef]
- Werzinger, S.; Gottinger, M.; Gussner, S.; Bergdolt, S.; Engelbrecht, R.; Schmauss, B. Model-based compressed sensing of fiber Bragg grating arrays in the frequency domain. Proc. SPIE 2017, 10323, 103236H. [Google Scholar]
- Clement, J.; Hervás, J.; Madrigal, J.; Maestre, H.; Torregrosa, G.; Fernández-Pousa, C.R.; Sales, S. Fast incoherent OFDR interrogation of FBG arrays using sparse radio frequency responses. J. Light. Technol. 2018, 36, 4393–4400. [Google Scholar] [CrossRef]
- Urban, P.J.; Amaral, G.C.; von der Weid, J.P. Fiber monitoring using a sub-carrier band in a sub-carrier multiplexed radio-over-fiber transmission system for applications in analog mobile fronthaul. J. Light. Technol. 2016, 34, 3118–3125. [Google Scholar] [CrossRef]
- Amaral, G.C.; Baldivieso, A.; Dias Garcia, J.; Villafani, D.C.; Leibel, R.C.; Herrera, L.E.Y.; Urban, P.J.; von der Weid, J.P. A low-frequency tone sweep method for in-service fault location in sub-carrier multiplexed optical fiber networks. J. Light. Technol. 2017, 35, 2017–2025. [Google Scholar] [CrossRef]
- Ye, F.; Zhang, Y.; Qian, L. Frequency-shifted interferometry – a versatile fiber-optic sensing technique. Sensors 2014, 14, 10977–11000. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhou, C.; Guo, H.; Fan, D.; Ou, Y.; Liu, Y.; Sun, C.; Qian, L. High spatial resolution multiplexing of fiber Bragg gratings using single-arm frequency-shifted interferometry. Proc. SPIE 2017, 10323, 103233S. [Google Scholar]
- Clement, J.; Maestre, H.; Torregrosa, G.; Fernández-Pousa, C.R. Incoherent optical frequency domain reflectometry using balanced frequency-shifter interferometry in a downconverted phase-modulated link. In Proceedings of the 2018 International Topical Meeting on Microwave Photonics (MWP), Toulouse, France, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Porte, H.; Mottet, A. Band pass & low-voltage symmetrical electro-optic modulator for absolute distance metrology. In Proceedings of the 2018 International Topical Meeting on Microwave Photonics (MWP), Toulouse, France, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Qi, B.; Qian, L.; Tausz, A.; Lo, H.-K. Frequency-shifted Mach-Zehnder interferometer for locating multiple weak reflections along a fiber link. IEEE Photonics Technol. Lett. 2006, 18, 295–297. [Google Scholar]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing; Pearson: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Anderson, D.R.; Johnson, L.; Bell, F.G. Troubleshooting Optical-Fiber Networks; Elsevier: San Diego, CA, USA, 2004. [Google Scholar]
- Kaiser, J.F.; Schafer, R.W. On the use of the I0-sinh window for spectrum analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 105–107. [Google Scholar] [CrossRef]
- Shadaram, M.; Kuriger, W.L. Using the optical frequency domain technique for the analysis of discrete and distributed reflections in an optical fiber. Appl. Opt. 1984, 23, 1092–1096. [Google Scholar] [CrossRef] [PubMed]
- Liehr, S. Fiber Optic Sensing Techniques Based On Incoherent Optical Frequency Domain Reflectometry. Ph.D. Thesis, BAM, Berlin, Germany, 2015. [Google Scholar]
- Ibrahim, S.K.; Van Roosbroeck, J.; O’Dowd, J.A.; Van Hoe, B.; Lindner, E.; Vlekken, J.; Farnan, M.; Karabacak, D.M.; Singer, J.M. Interrogation and mitigation of polarization effects for standard and birefringent FBGS. Proc. SPIE 2016, 9852, 98520H. [Google Scholar]
- Ibrahim, S.K.; O’Dowd, J.A.; Bessler, V.; Karabacak, D.M.; Singer, J.M. Optimization of fiber Bragg grating parameters for sensing applications. Proc. SPIE 2017, 10208, 102080P. [Google Scholar]
- Francisangelis, C.; Floridia, C.; Simões, G.C.C.P.; Schmmidt, F.; Fruett, F. On-field distributed first-order PMD measurement based on pOTDR and optical pulse width sweep. Opt. Express 2015, 23, 12582–12594. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clement, J.; Maestre, H.; Torregrosa, G.; Fernández-Pousa, C.R. Incoherent Optical Frequency-Domain Reflectometry Based on Homodyne Electro-Optic Downconversion for Fiber-Optic Sensor Interrogation. Sensors 2019, 19, 2075. https://doi.org/10.3390/s19092075
Clement J, Maestre H, Torregrosa G, Fernández-Pousa CR. Incoherent Optical Frequency-Domain Reflectometry Based on Homodyne Electro-Optic Downconversion for Fiber-Optic Sensor Interrogation. Sensors. 2019; 19(9):2075. https://doi.org/10.3390/s19092075
Chicago/Turabian StyleClement, Juan, Haroldo Maestre, Germán Torregrosa, and Carlos R. Fernández-Pousa. 2019. "Incoherent Optical Frequency-Domain Reflectometry Based on Homodyne Electro-Optic Downconversion for Fiber-Optic Sensor Interrogation" Sensors 19, no. 9: 2075. https://doi.org/10.3390/s19092075
APA StyleClement, J., Maestre, H., Torregrosa, G., & Fernández-Pousa, C. R. (2019). Incoherent Optical Frequency-Domain Reflectometry Based on Homodyne Electro-Optic Downconversion for Fiber-Optic Sensor Interrogation. Sensors, 19(9), 2075. https://doi.org/10.3390/s19092075