Characterizing Complex Mineral Structures in Thin Sections of Geological Samples with a Scanning Hall Effect Microscope
Abstract
1. Introduction
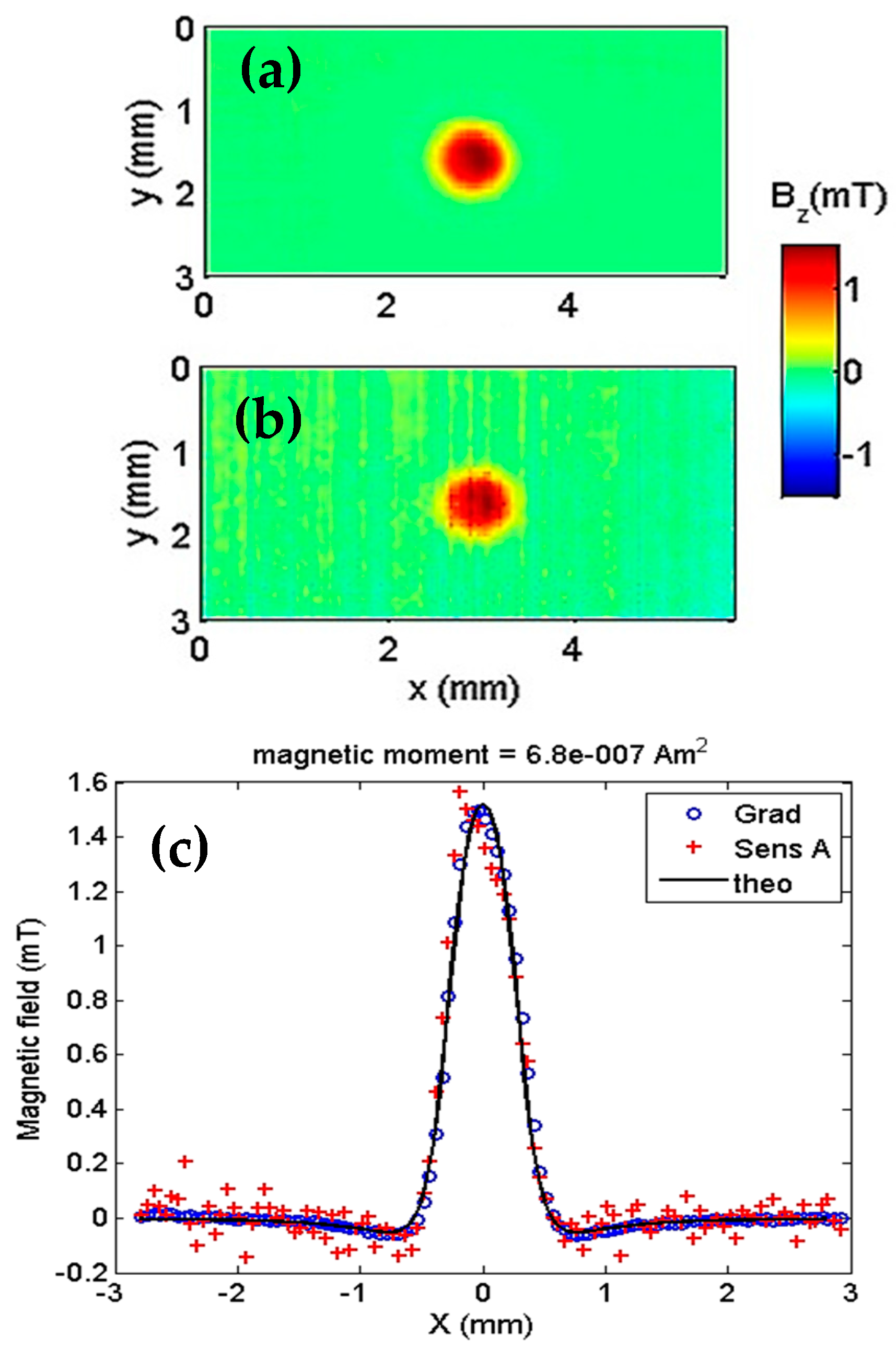
2. Scanning Magnetic Microscope
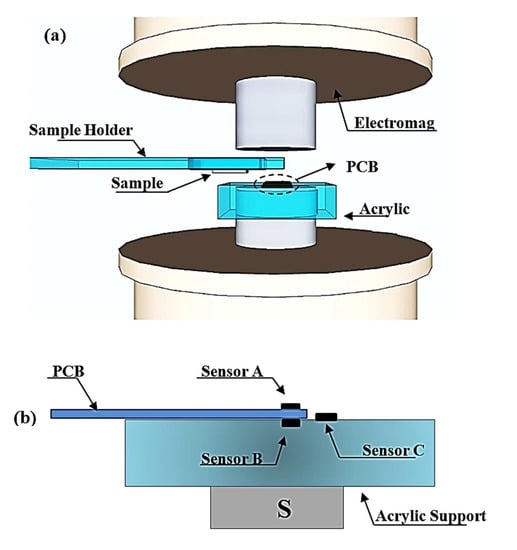
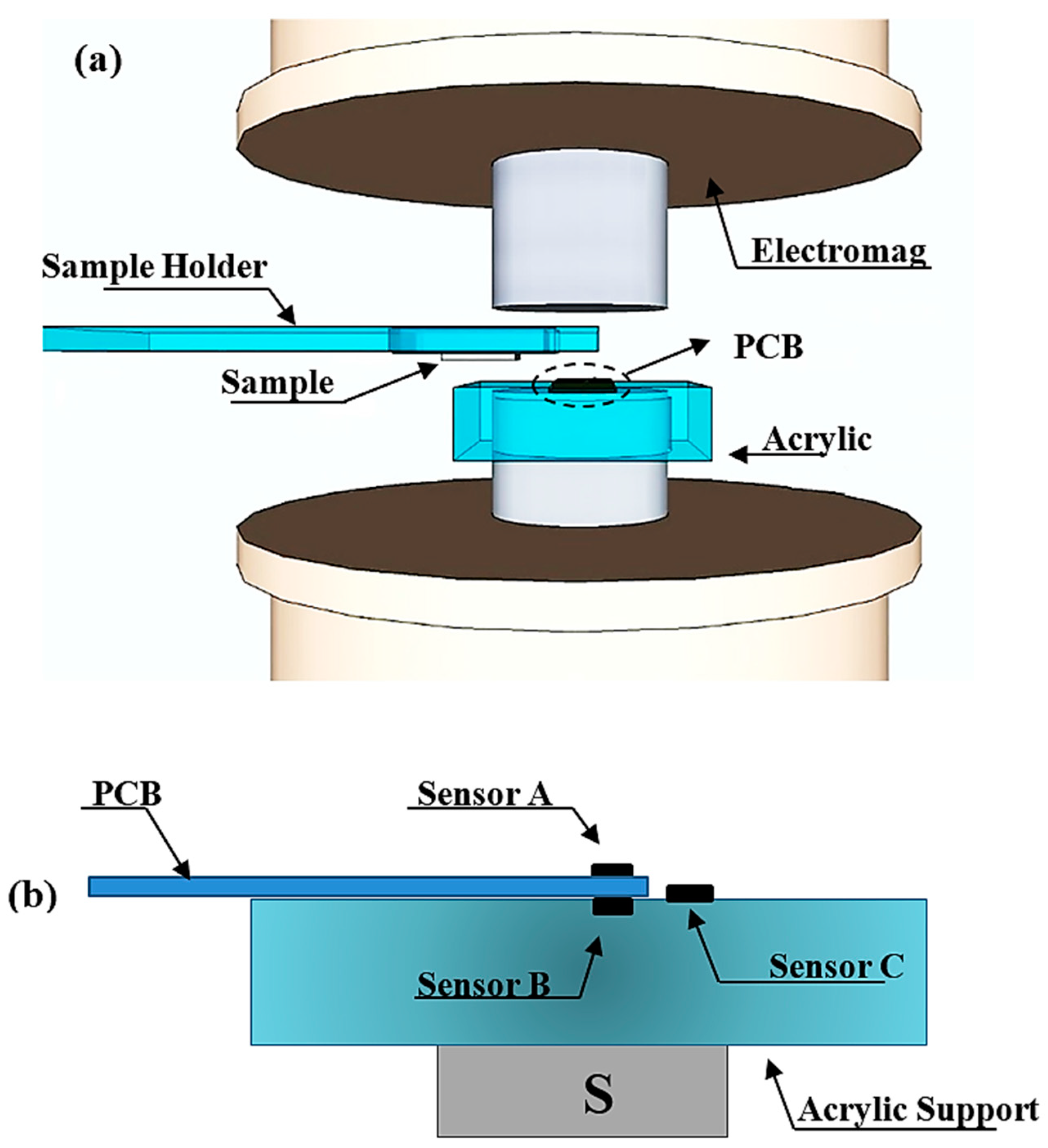
2.1. Mechanical Design
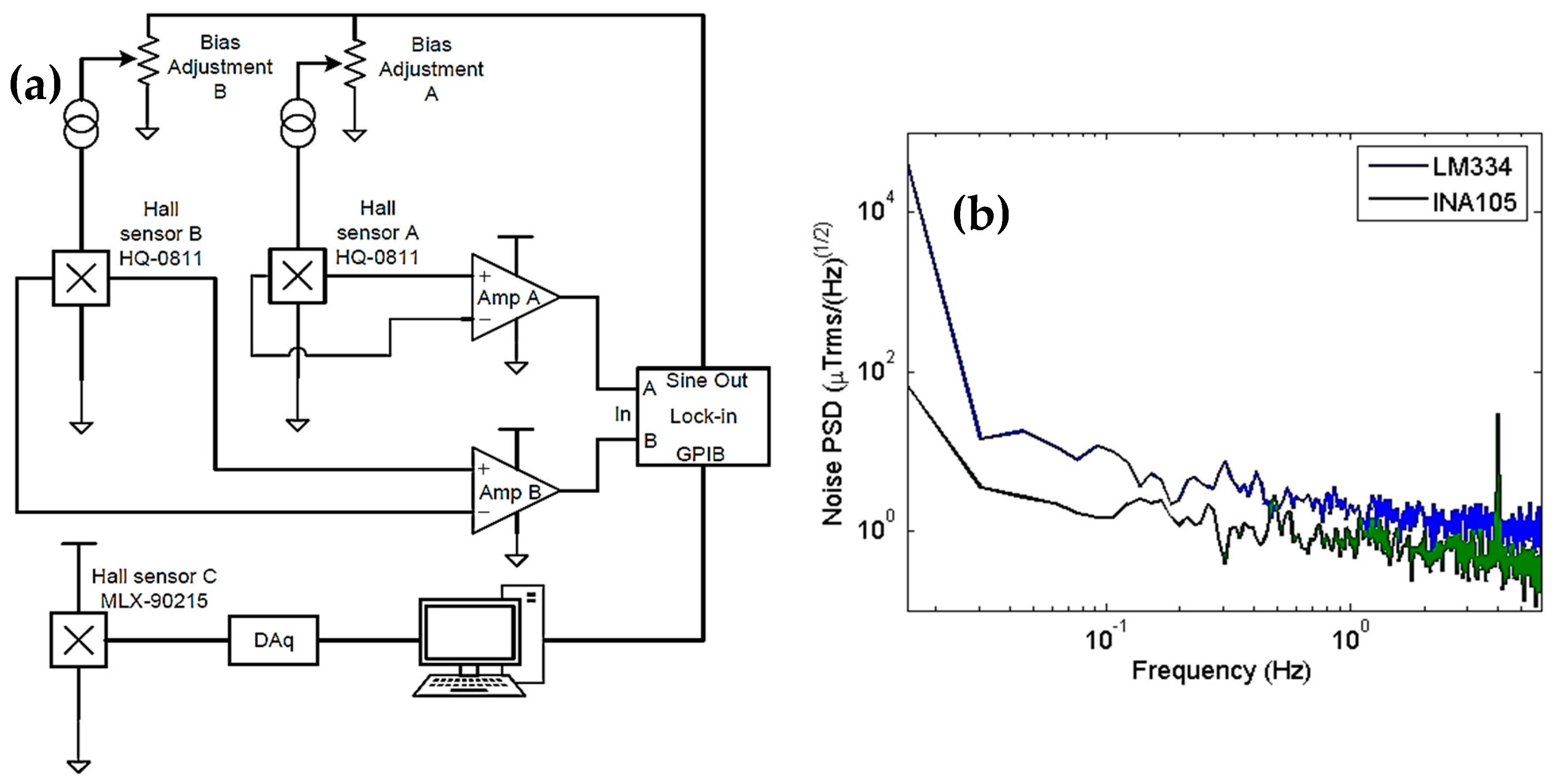
2.2. Custom Electronics
3. Measurement of Geological Samples
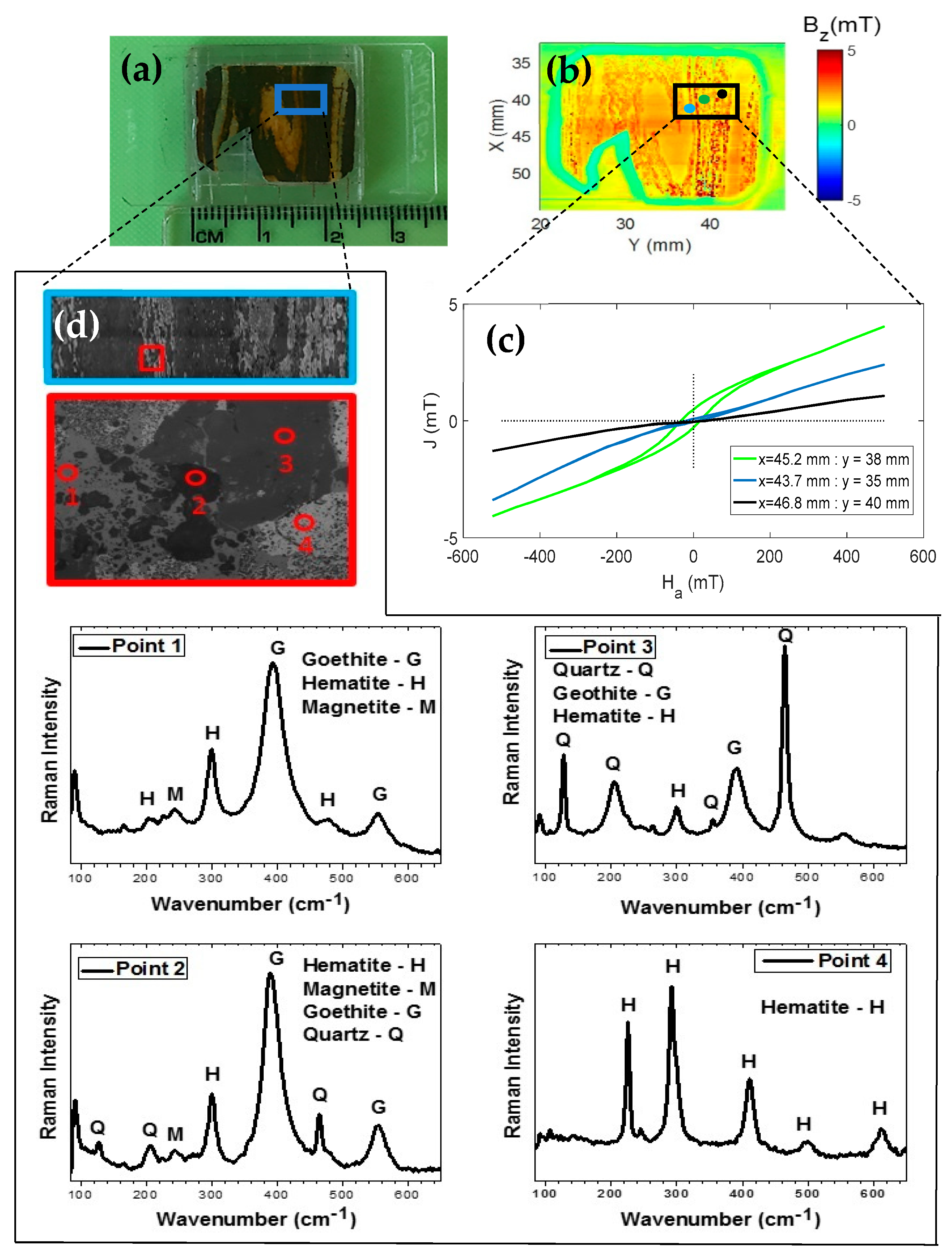
3.1. Microscopy of Geological Samples
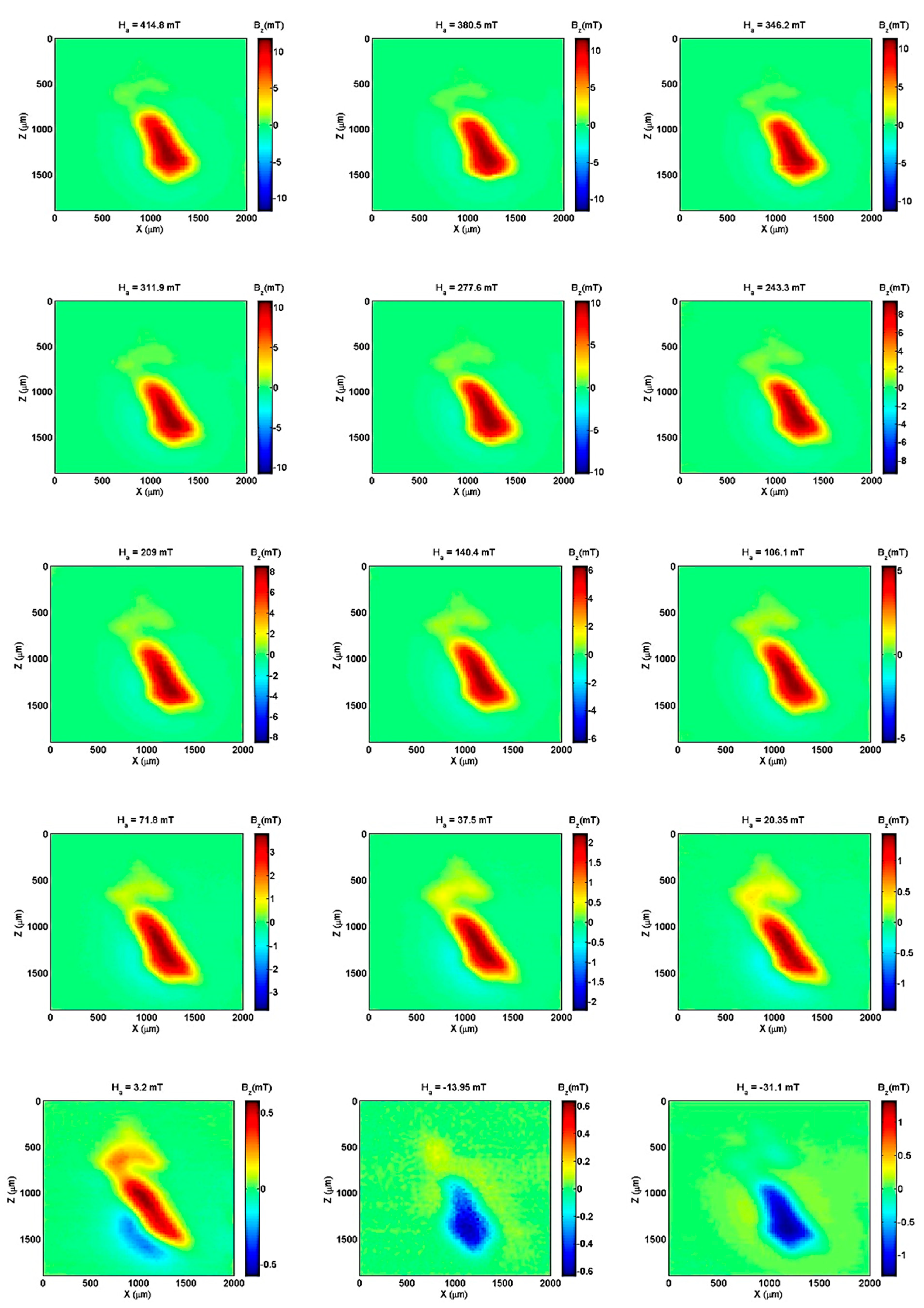
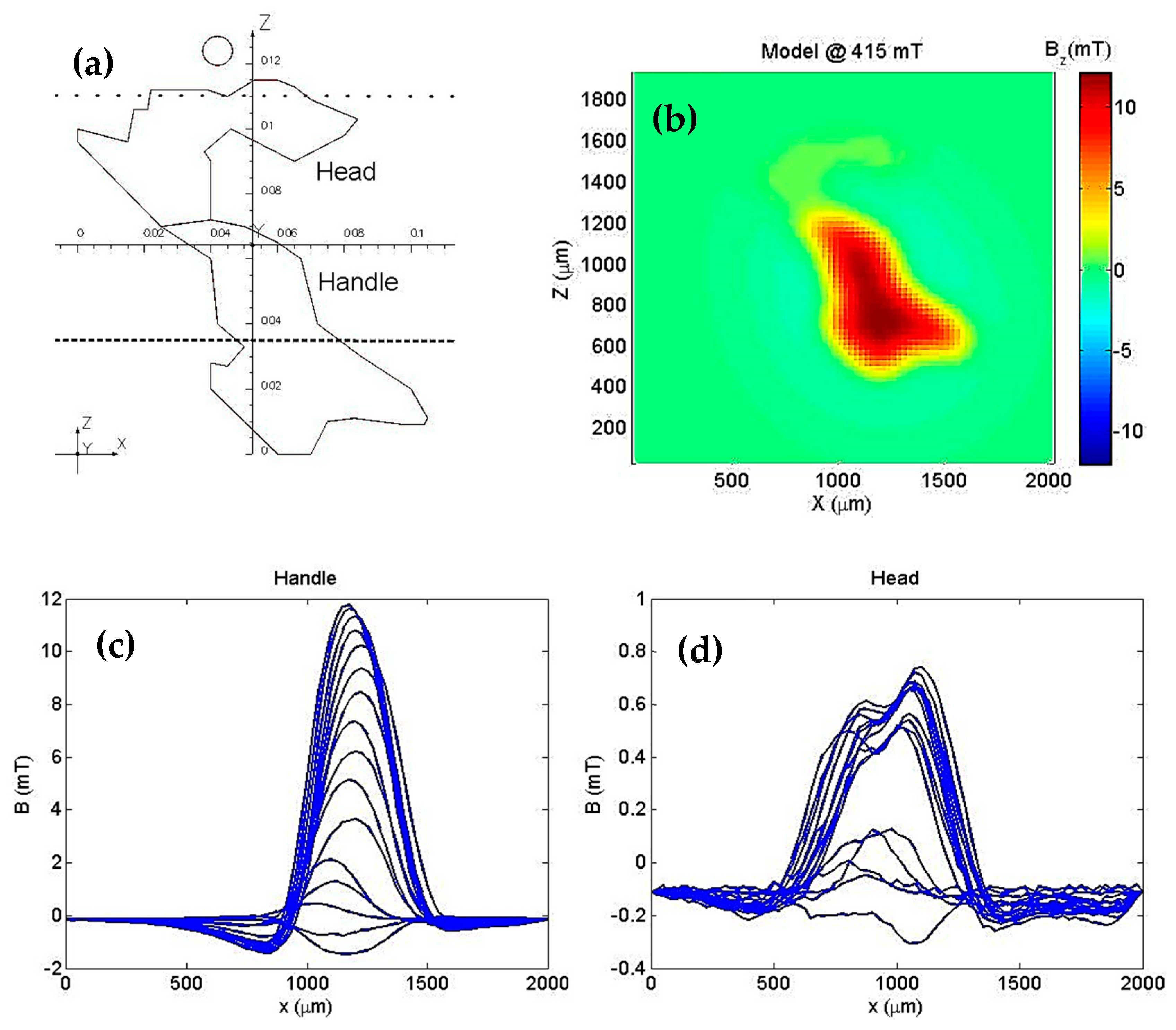
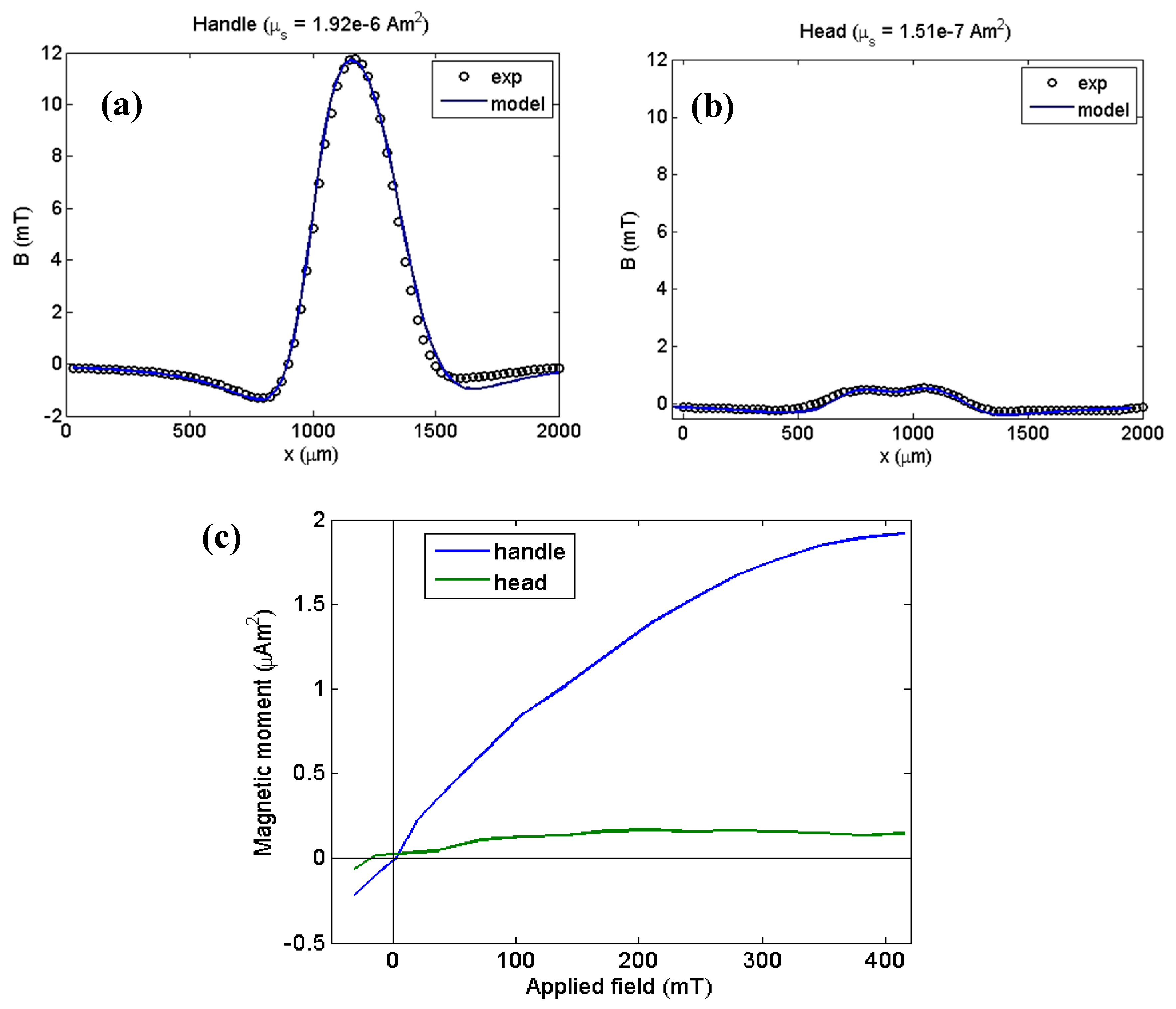
3.2. Modeling Using Current Circuit
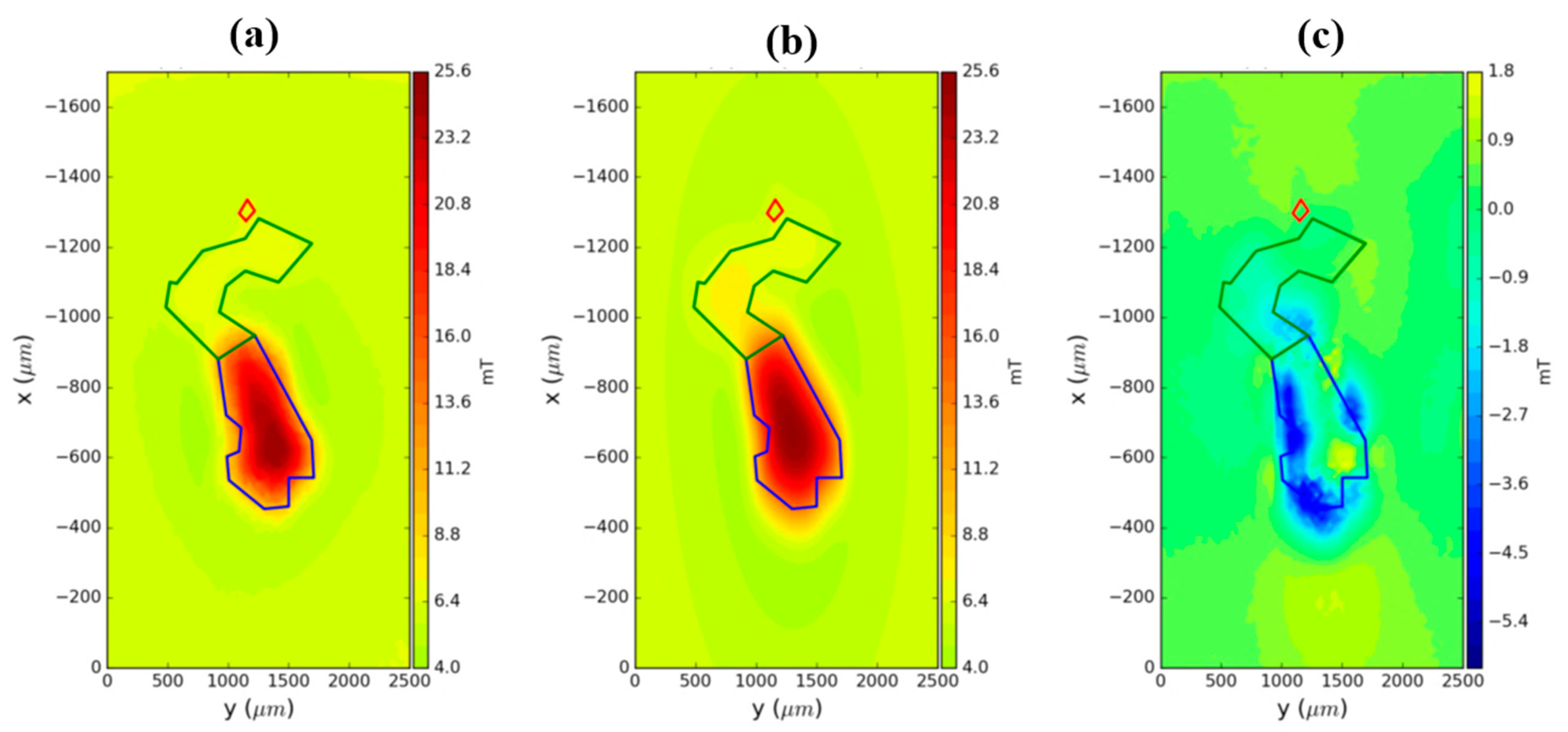
3.3. Modeling Using Polygonal Prisms
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, D.; Shiwa, M. A magnetic sensor with amorphous wire. Sensors 2014, 14, 10644–10649. [Google Scholar] [CrossRef] [PubMed]
- Rudge, J.; Xu, H.; Kolthammer, J.; Hong, Y.K.; Choi, B.C. Sub-nanosecond time-resolved near-field scanning magneto-optical microscope. Rev. Sci. Instrum. 2015, 86, 23703–23705. [Google Scholar] [CrossRef] [PubMed]
- Shaw, G.; Kramer, R.B.G.; Dempsey, N.M.; Hasselbach, K. A scanning Hall probe microscope for high resolution, large area, variable height magnetic field imaging. Rev. Sci. Instrum. 2016, 87, 113702–113710. [Google Scholar] [CrossRef] [PubMed]
- Kirtley, J.R.; Paulius, L.; Rosenberg, A.J.; Palmstrom, J.C.; Holland, C.M.; Spanton, E.M.; Schiessl, D.; Jermain, C.L.; Gibbons, J.; Fung, Y.K.K.; et al. Scanning SQUID susceptometers with sub-micron spatial resolution. Rev. Sci. Instrum. 2016, 87. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, S.Y.; Schultz, S. Scanning magnetoresistance microscopy. Appl. Phys. Lett. 1996, 69, 3263–3265. [Google Scholar] [CrossRef]
- Gregory, J.K.; Bending, S.J.; Sandhu, A. A scanning Hall probe microscope for large area magnetic imaging down to cryogenic temperatures. Rev. Sci. Instrum. 2002, 73, 733515–733519. [Google Scholar] [CrossRef]
- Schrag, B.D.; Xiao, G. Submicron electrical current density imaging of embedded microstructures. Appl. Phys. Lett. 2003, 82, 3272–3274. [Google Scholar] [CrossRef]
- Schrag, B.D.; Liu, X.Y.; Shen, W.F.; Xiao, G. Current density mapping and pinhole imaging in magnetic tunnel junctions via scanning magnetic microscopy. Appl. Phys. Lett. 2004, 84, 2937–2939. [Google Scholar] [CrossRef]
- Reis, A.L.A.; Oliveira, V.C., Jr.; Yokoyama, E.; Bruno, A.C.; Pereira, J.M.B. Estimating the magnetization distribution within rectangular rock samples. Geochem. Geophys. Geosyst. 2016, 17, 3350–3374. [Google Scholar] [CrossRef]
- Kletetschka, G.; Schnabl, P.; Šifnerová, K.; Tasáryová, Z.; Manda, S.; Pruner, P. Magnetic scanning and interpretation of paleomagnetic data from Prague Synform’s volcanics. Stud. Geophys. Geod. 2013, 57, 103–117. [Google Scholar] [CrossRef]
- Chieh, J.; Wei, W.; Liao, S.; Chen, H.; Lee, Y.; Lin, F.; Chiang, M.; Chiu, M.; Horng, H.; Yang, S. Eight-Channel AC magnetosusceptometer of magnetic nanoparticles for high-throughput and ultra-high-sensitivity immunoassay. Sensors 2018, 18, 1043. [Google Scholar] [CrossRef]
- Parra, A.C.; Casper, F.; Paul, J.; Lehndorff, R.; Haupt, C.; Jakob, G.; Kläui, M.; Hillebrands, B. Microstructure design for fast lifetime measurements of magnetic tunneling junctions. Sensors 2019, 19, 583. [Google Scholar] [CrossRef] [PubMed]
- Chemla, Y.R.; Grossman, H.L.; Poon, Y.; McDermott, R.; Stevens, R.; Alper, M.D.; Clarke, J. Ultrasensitive magnetic biosensor for homogeneous immunoassay. Proc. Natl. Acad. Sci. USA 2000, 97, 14268–14272. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, Y.; Yuan, Z.; Bai, L.; Schneider, S.; Zhao, G.; Stillman, B.; Speck, C.; Li, H. Cryo-EM structure of Mcm2-7 double hexamer on DNA suggests a lagging-strand DNA extrusion model. Proc. Natl. Acad. Sci. USA 2017, 26, E9529–E9538. [Google Scholar] [CrossRef] [PubMed]
- Rowan, C.J.; Roberts, A.P. Magnetite dissolution, diachronous greigite formation and secondary magnetizations from pyrite oxidation: Unravelling complex cmagnetizations in Neogene marine sediments from New Zealand. Earth Planet. Sci. Lett. 2006, 241, 119–137. [Google Scholar] [CrossRef]
- Weiss, B.P.; Fu, R.R.; Kehayias, P.; Bell, E.A.; Gelb, J.; Araujo, J.F.D.F.; Lima, E.A.; Borlina, C.S.; Boehnke, P.; Harrison, T.M.; et al. Secondary magnetic inclusions in detrital zircons from the Jack Hills, Western Australia and implications for the origin of the geodynamo. Geol. Soc. Am. 2018, 46, 427–433. [Google Scholar] [CrossRef]
- Fu, R.; Weiss, B.P.; Lima, E.A.; Araujo, J.F.D.F.; Gelb, J.; Glenn, D.; Kehayias, P.; Einsle, J.F.; Harrision, R.J.; Ali, G.A.; et al. Can zircons be suitable paleomagnetic recorders?—A correlative study of bishop tuff zircon grains using high resolution lab X-ray microscopes and a quantum diamond. Microsc. Microanal. 2016, 22, 1794–1795. [Google Scholar] [CrossRef]
- Fu, R.; Weiss, B.P.; Shuster, D.L.; Gattacceca, J.; Grove, T.L.; Suavet, C.; Lima, E.A.; Li, L.; Kuan, A.T. An Ancient Core Dynamo in Asteroid Vesta. Science 2012, 338, 238–242. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.M.B.; Pacheco, C.J.; Arenas, M.P.; Araujo, J.F.D.F.; Pereira, G.R.; Bruno, A.C. Novel scanning dc-susceptometer for characterization of heat-resistant steels with different states of aging. J. Magn. Magn. Mater. 2017, 442, 311–318. [Google Scholar] [CrossRef]
- Araujo, J.F.D.F.; Costa, M.C.; Louro, S.R.W.; Bruno, A.C. A portable Hall magnetometer probe for characterization of magnetic iron oxide nanoparticles. J. Magn. Magn. Mater. 2017, 426, 159–162. [Google Scholar] [CrossRef]
- Camacho, J.M.; Sosa, V. Alternative method to calculate the magnetic field of permanent magnets with azimuthal symmetry. Revista Mexicana de Física E 2013, 59, 8–17. [Google Scholar]
- Araujo, J.F.D.F.; Bruno, A.C.; Carvalho, H.R. Characterization of magnetic nanoparticles by a modular Hall magnetometer. J. Magn. Magn. Mater. 2010, 322, 2806–2809. [Google Scholar] [CrossRef]
- Araujo, J.F.D.F.; Pereira, J.M.B. A practical and automated Hall magnetometer for characterization of magnetic materials. Mod. Inst. 2010, 4, 43–53. [Google Scholar] [CrossRef]
- Araujo, J.F.D.F.; Bruno, A.C.; Louro, S.R.W. Versatile magnetometer assembly for characterizing magnetic properties of nanoparticles. Rev. Sci. Instrum. 2015, 85, 105103. [Google Scholar] [CrossRef] [PubMed]
- Spaggiari, C.V.; Wartho, J.; Wilde, S.A. Proterozoic deformation in the northwest of the Archean Yilgarn Craton, Western Australia. Precambrian Res. 2008, 162, 354–384. [Google Scholar] [CrossRef]
- Spaggiari, C.V.; Pidgeon, R.T.; Wilde, S.A. The Jack Hills greenstone belt, Western AustraliaPart 2: Lithological relationships and implications for the deposition of ≥4.0Ga detrital zircons. Precambrian Res. 2007, 155, 261–286. [Google Scholar] [CrossRef]
- Lana, C.; Gibson, R.L.; Reimold, W.U.; Minnitt, R.C.A. Geology and geochemistry of a granite-greenstone association in the southeastern Vredefort dome, South Africa. S. Afr. J. Geol. 2003, 106, 291–314. [Google Scholar] [CrossRef]
- Lima, E.A.; Bruno, A.C.; Carvalho, H.R.; Weiss, B.P. Scanning magnetic tunnel junction microscope for high-resolution imaging of remanent magnetization fields. Meas. Sci. Technol. 2014, 25. [Google Scholar] [CrossRef]
- Plouff, D. Gravity and magnetic fields of polygonal prism and application to magnetic terrain corrections. Geophysics 1976, 41, 727–741. [Google Scholar] [CrossRef]
- Uieda, L.; Oliveira, V.C., Jr.; Barbosa, V.C.F. Modeling the earth with fatiando a terra. In Proceedings of the 12th Python in Science Conference, Austin, TX, USA, 24–29 June 2013; van der Walt, S., Millman, J., Huff, K., Eds.; 2013; pp. 96–103. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araujo, J.F.D.F.; Reis, A.L.A.; Oliveira, V.C., Jr.; Santos, A.F.; Luz-Lima, C.; Yokoyama, E.; Mendoza, L.A.F.; Pereira, J.M.B.; Bruno, A.C. Characterizing Complex Mineral Structures in Thin Sections of Geological Samples with a Scanning Hall Effect Microscope. Sensors 2019, 19, 1636. https://doi.org/10.3390/s19071636
Araujo JFDF, Reis ALA, Oliveira VC Jr., Santos AF, Luz-Lima C, Yokoyama E, Mendoza LAF, Pereira JMB, Bruno AC. Characterizing Complex Mineral Structures in Thin Sections of Geological Samples with a Scanning Hall Effect Microscope. Sensors. 2019; 19(7):1636. https://doi.org/10.3390/s19071636
Chicago/Turabian StyleAraujo, Jefferson F. D. F., Andre L. A. Reis, Vanderlei C. Oliveira, Jr., Amanda F. Santos, Cleanio Luz-Lima, Elder Yokoyama, Leonardo A. F. Mendoza, João M. B. Pereira, and Antonio C. Bruno. 2019. "Characterizing Complex Mineral Structures in Thin Sections of Geological Samples with a Scanning Hall Effect Microscope" Sensors 19, no. 7: 1636. https://doi.org/10.3390/s19071636
APA StyleAraujo, J. F. D. F., Reis, A. L. A., Oliveira, V. C., Jr., Santos, A. F., Luz-Lima, C., Yokoyama, E., Mendoza, L. A. F., Pereira, J. M. B., & Bruno, A. C. (2019). Characterizing Complex Mineral Structures in Thin Sections of Geological Samples with a Scanning Hall Effect Microscope. Sensors, 19(7), 1636. https://doi.org/10.3390/s19071636