Driver Drowsiness Detection Based on Steering Wheel Data Applying Adaptive Neuro-Fuzzy Feature Selection
Abstract
:1. Introduction
1.1. Driver Drowsiness Detection
1.2. Feature Selection
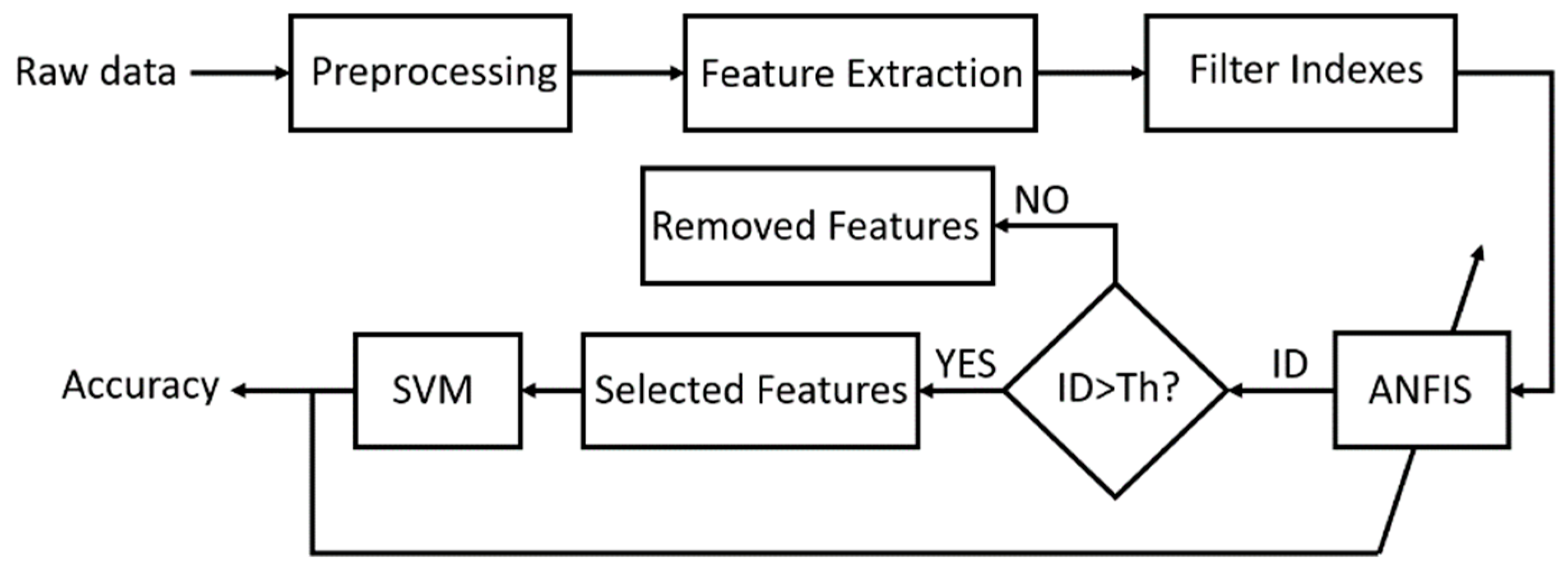
2. Materials and Methods
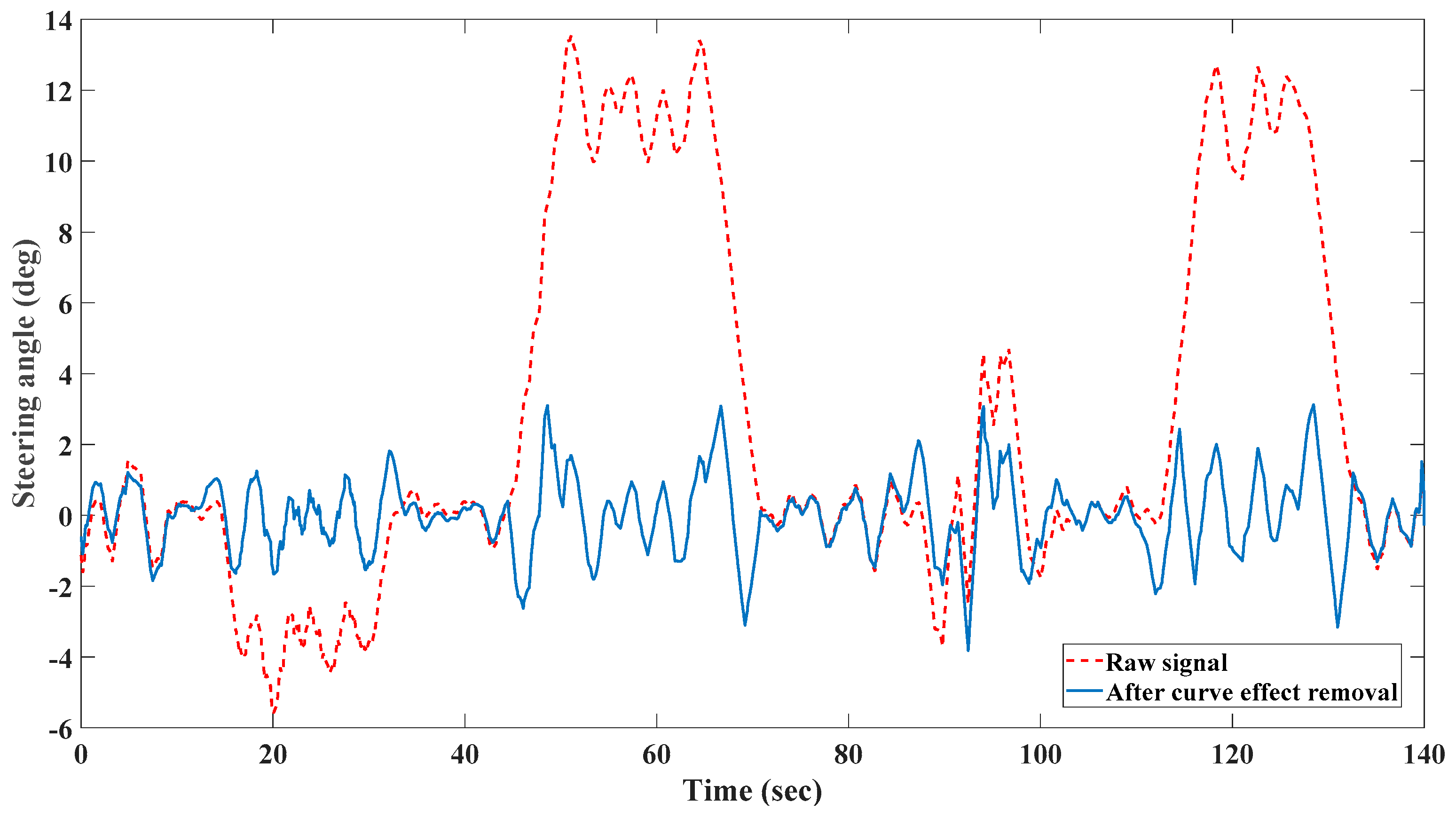
2.1. Preprocessing
2.2. Feature Extraction
2.3. Filter Method Indexes
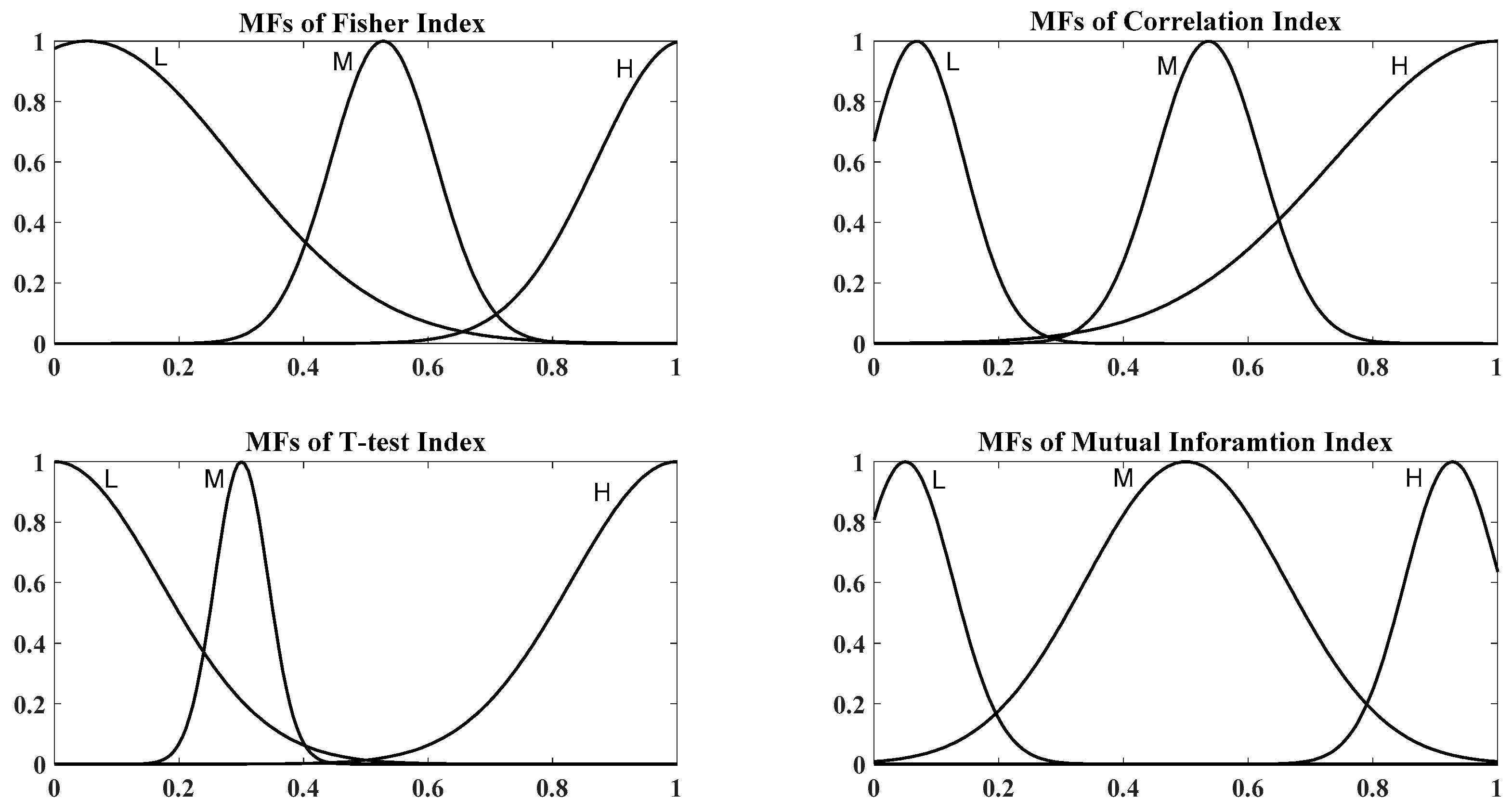
2.3.1. Fisher Index
2.3.2. Correlation Index
2.3.3. T-test Index
2.3.4. Mutual Information Index
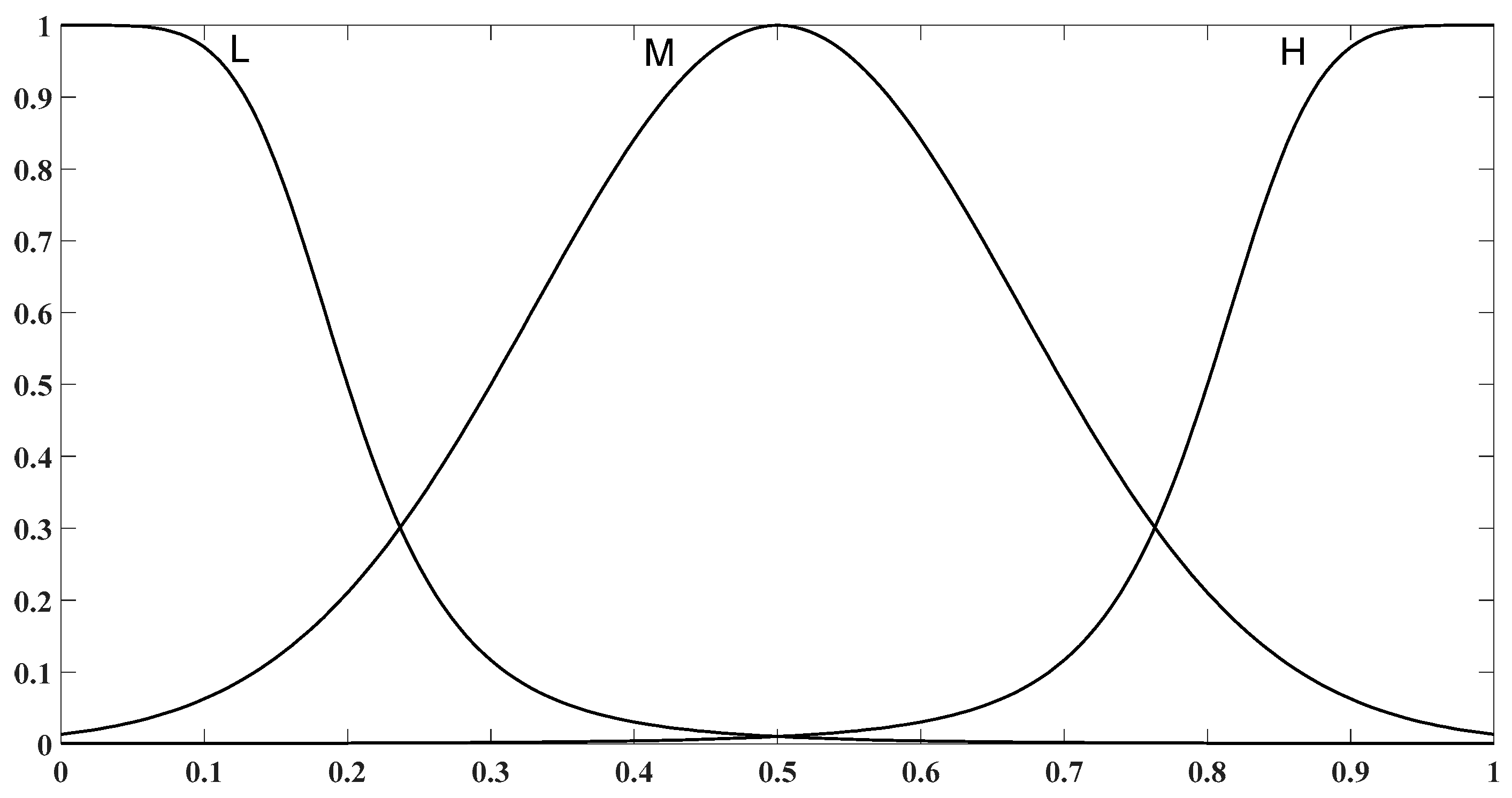
2.4. Fuzzy Inference System
2.5. ANFIS Training by PSO Algorithm
2.6. Support Vector Machine Classifier
3. Dataset and Experimental Setup
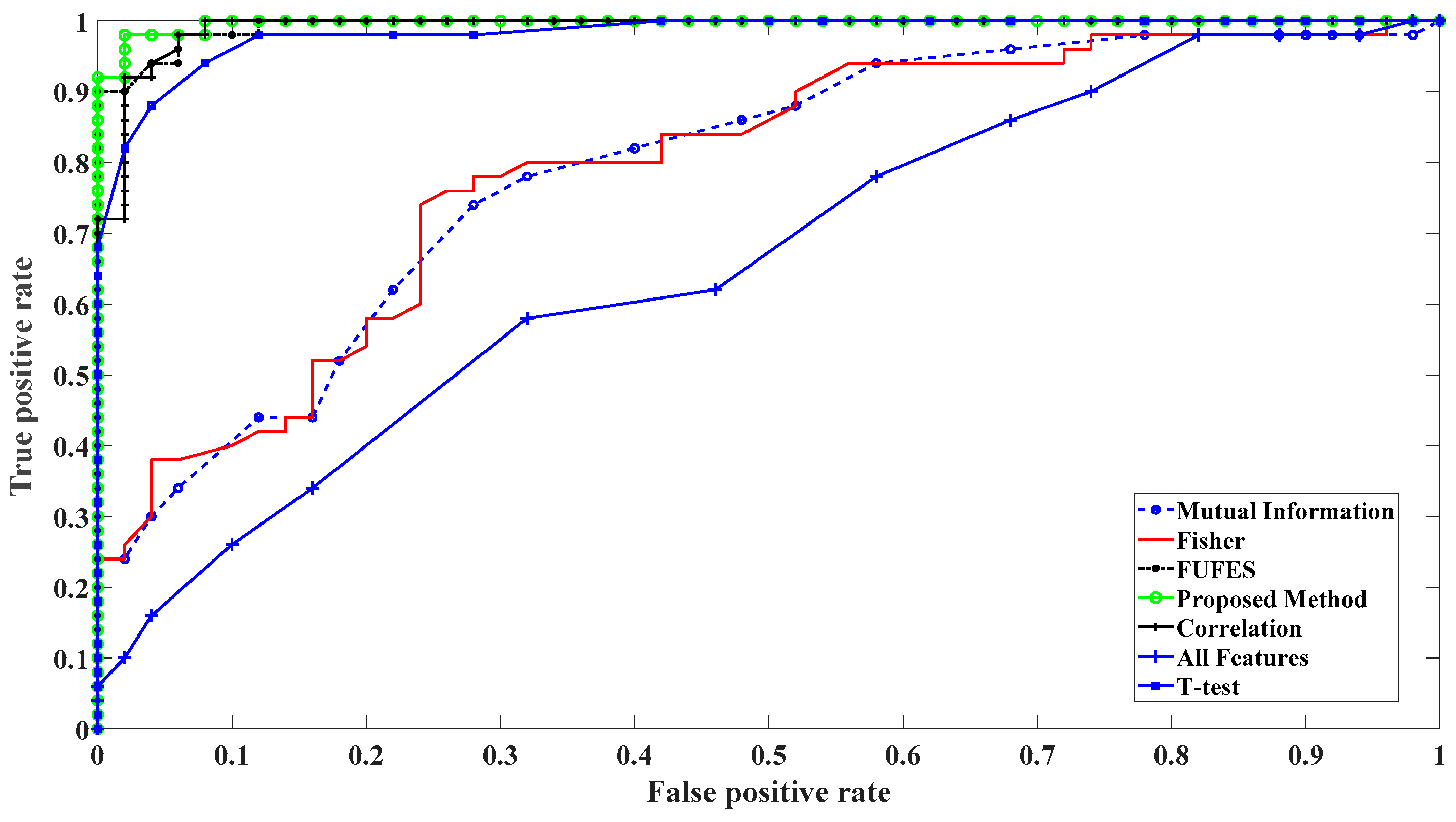
4. Results and Discussion
- (1)
- True Positive (TP): number of drowsy states that correctly classified as drowsy;
- (2)
- True Negative (TN): number of awake states that correctly identified as awake;
- (3)
- False Negative (FN): number of drowsy states that incorrectly identified as awake;
- (4)
- False Positive (FP): number of awake states that incorrectly identified as drowsy;
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- Initialization. For each of the particles:
- (a)
- Initialize the position,
- (b)
- Initialize the particles best position to its initial position,
- (c)
- Calculate the performance of each particle and if initialize the global best as g = xj(0)
- Optimization loop:
- (a)
- Update the particle velocity according to (A1)
- (b)
- Update the particle position according to (A2)
- (c)
- Evaluate the performance of the particle:
- (d)
- If , update personal best:
- (e)
- If , update global best:
- At the end of the iterative process, the best solution is the final .
References
- Australian Transport Council: National Road Safety Strategy 2011–2020. Available online: https://roadsafety.gov.au/nrss/files/NRSS_2011_2020.pdf (accessed on 13 January 2019).
- Awais, M.; Badruddin, N.; Drieberg, M. A hybrid approach to detect driver drowsiness utilizing physiological signals to improve system performance and wearability. Sensors 2017, 17, 1991. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chung, W.Y. A context-aware EEG headset system for early detection of driver drowsiness. Sensors 2015, 15, 20873–20893. [Google Scholar] [CrossRef] [PubMed]
- Manu, B.N. Facial features monitoring for real time drowsiness detection. In Proceedings of the International Conference of Innovations in Information Technology (IIT), Al-Ain, UAE, 28–30 November 2016. [Google Scholar] [CrossRef]
- Selvakumar, K.; Jerome, J.; Rajamani, K.; Shankar, N. Real-time vision based driver drowsiness detection using partial least squares analysis. J. Signal Process. Syst. 2016, 85, 263–274. [Google Scholar] [CrossRef]
- Naurois, C.J.D.; Bourdin, C.; Stratulat, A.; Diaz, E.; Vercher, J. Detection and prediction of driver drowsiness using artificial neural network models. Accid. Anal. Prev. 2017. [Google Scholar] [CrossRef]
- Daza, I.G.; Bergasa, L.M.; Bronte, S.; Yebes, J.J.; Almazan, J.; Arroyo, R. Fusion of optimized indicators from advanced driver assistance systems (ADAS) for driver drowsiness detection. Sensors 2014, 14, 1106–1113. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Shi-wu, L.; Wen-cai, S.; Meng-zhu, G.; Meng-yuan, H. Drowsiness monitoring based on steering wheel status. Transp. Res. Part D Transp. Environ. 2018. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.E.; Li, R.; Cheng, B.; Shi, J. Online detection of driver fatigue using steering wheel angles for real driving conditions. Sensors 2017, 17, 495. [Google Scholar] [CrossRef] [PubMed]
- Haupt, D.; Honzik, P.; Raso, P.; Hyncica, O. Steering wheel motion analysis for detection of the driver’s drowsiness. In Proceedings of the International Conference on Mathematical models and Methods in Modern Science, Puerto De La Cruz, Spain, 10–12 December 2011. [Google Scholar]
- Panthong, R.; Srivihok, A. Wrapper feature subset selection for dimension reduction based on ensemble learning algorithm. Procedia Comput. Sci. 2015, 15, 162–169. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection method. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Chang, Q. Feature selection methods for big data bioinformatics: A survey from the search perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Lai, Y.; Rosin, P.L. Example-based image colorization via automatic feature selection and fusion. Neurocomputing 2017, 266, 687–698. [Google Scholar] [CrossRef]
- Labani, M.; Moradi, P.; Ahmadizar, F.; Jalili, M. A novel multivariate filter method for feature selection in text classification problems. Eng. Appl. Artif. Intell. 2018, 70, 25–37. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, Y.; He, S.; Bao, J. A novel intelligent method for bearing fault diagnosis based on affinity propagation clustering and adaptive feature selection. Knowl. Based Syst. 2017, 116, 1–12. [Google Scholar] [CrossRef]
- Pacheco, F.; De Oliveira, J.V.; Sanchez, R.; Cerrada, M.; Caberra, D.; Li, C.; Zurita, G.; Artes, M. A statistical comparison of neuro-classifiers and feature selection methods for gearbox fault diagnosis under realistic conditions. Neurocomputing 2016, 194, 192–206. [Google Scholar] [CrossRef]
- Kumar, V.; Minz, S. Feature selection: A literature review. Smart Comput. Rev. 2014, 4, 211–229. [Google Scholar] [CrossRef]
- Sánchez-Maroño, N.; Alonso-Betanzos, A.; Tombilla-Sanromán, M. Filter Methods for Feature Selection—A Comparative Study. In Intelligent Data Engineering and Automated Learning; Yin, H., Tino, P., Corchado, E., Byrne, W., Yao, X., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4881, pp. 178–187. [Google Scholar] [CrossRef]
- Maldonado, S.; Lopez, J. Dealing with high-dimensional class-imbalanced datasets: Embedded feature selection for SVM classification. Appl. Soft Comput. 2018, 67, 94–105. [Google Scholar] [CrossRef]
- Mansoori, E.G.; Shafiee, K.S. On fuzzy feature selection in designing fuzzy classifiers for high-dimensional data. Evol. Syst. 2016, 7, 255–265. [Google Scholar] [CrossRef]
- Vieira, S.M.; Sousa, J.M.C.; Kaymak, U. Fuzzy criteria for feature selection. Fuzzy Sets Syst. 2012, 189, 1–18. [Google Scholar] [CrossRef]
- Cateni, S.; Colla, V.; Vannucci, M. A fuzzy system for combining filter features selection methods. Int. J. Fuzzy Syst. 2017, 19, 1168–1180. [Google Scholar] [CrossRef]
- Yin, S.; Jiang, Y.; Tian, Y.; Kaynak, O. A data-driven fuzzy information granulation approach for freight volume forecasting. IEEE Trans. Ind. Electron. 2017, 64, 1447–1456. [Google Scholar] [CrossRef]
- Ma, R.; Yu, N.; Hu, J. Application of particle swarm optimization algorithm in the heating system planning problem. Sci. World J. 2013, 2013, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, A.; Eskandarian, A.; Sayed, R.A. Effect of drowsiness on driving performance variables of commercial vehicle drivers. Int. J. Automot. Technol. 2009, 10, 391–404. [Google Scholar] [CrossRef]
- Samiee, S.; Azadi, S.; Kazemi, R.; Nahvi, A.; Eichberger, A. Data fusion to develop a driver drowsiness detection system with robustness to signal loss. Sensors 2014, 14, 17832–17847. [Google Scholar] [CrossRef] [PubMed]
- Friedrichs, F.; Yang, B. Drowsiness monitoring by steering and lane data based features under real driving conditions. In Proceedings of the European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010. [Google Scholar]
- Sheikhpour, R.; Sarram, M.A.; Gharaghani, S.; Chahooki, M.A.Z. A Survey on semi-supervised feature selection methods. Pattern Recognit. 2017, 64, 141–158. [Google Scholar] [CrossRef]
- Chormunge, S.; Jena, S. Correlation based feature selection with clustering for high dimensional data. J. Electr. Syst. Inf. Technol. 2018, 5, 542–549. [Google Scholar] [CrossRef]
- Hoffman, J.I.E. t-Test Variants: Crossover Tests, Equivalence Tests. In Biostatistics for Medical and Biomedical Practitioners; Academic Press: Cambridge, MA, USA, 2015; pp. 363–371. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estevez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Ghomsheh, V.S.; Shoorehdeli, M.A.; Teshnehlab, M. Training ANFIS structure with modified PSO algorithm. In Proceedings of the Mediterranean Conference of Control and Automation, Athens, Greece, 27–29 June 2007. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO), a tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Burbridge, R.; Buxton, B. An Introduction to Support Vector Machines for Data Mining. In Proceedings of the YOR12 Conference, Nottingham, UK, 27–29 March 2001. [Google Scholar]
- Naseri, H.; Nahvi, A.; Karan, F.S.N. A real-time lane changing and line changing algorithm for driving simulators based on virtual driver behavior. J. Simul. 2017, 11, 357–368. [Google Scholar] [CrossRef]
- Wang, M.S.; Jeong, N.T.; Kim, K.S.; Choi, S.B.; Yang, S.M.; You, S.H.; Lee, J.H.; Suh, M.W. Drowsy behavior detection based on driving information. Int. J. Automot. Technol. 2016, 17, 165–173. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C. Driver drowsiness detection based on non-intrusive metrics considering individual specifics. Accid. Anal. Prev. 2016, 95, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Krajewski, J.; Sommer, D.; Trutschel, U.; Edwards, D.; Golz, M. Steering wheel behavior based estimation of fatigue. In Proceedings of the Fifth International Driving Symposium on Human Factors in Driver Assessment, Training and Vehicle Design, Big Sky, MT, USA, 22–25 June 2009. [Google Scholar] [CrossRef]
- McDonald, A.D.; Schwarz, C.; Lee, J.D.; Brown, T.L. Real-time detection of drowsiness related lane departures using steering wheel angle. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2012, 56, 2201–2205. [Google Scholar] [CrossRef]

| Index | Time Domain Features | Descriptions |
|---|---|---|
| Range | Difference between minimum and maximum of signal | |
| Standard Deviation | Dispersion of the data around mean value | |
| Energy | Sum of the square of signal magnitude | |
| Zero Crossing Rate (ZCR) | Number of steering or steering velocity direction changes per second | |
| First Quartile | Middle number between the smallest number and the median of the signal in sliding window | |
| Second Quartile | Median of the signal in the sliding window | |
| Third Quartile | Middle value between the median and the highest value of the signal in sliding window | |
| Katz Fractal Dimension (KFD) | An index for characterizing fractal patterns or sets by quantifying their complexity as a ratio of the change in detail to the change in scale. | |
| Skewness | A measure for signal similarity | |
| Kurtosis | Measure of tailedness of the probability distribution of a random variable | |
| Sample Entropy (SamEn) | Complexity of signal in time domain based on distance in embedding dimension | |
| Shannon Entropy (ShEn) | Complexity of signal in time domain based on probability function |
| Index | Frequency Domain Features | Descriptions |
|---|---|---|
| Frequency Variability | Variance of the frequency in the defined frequency band | |
| Spectral Entropy (SpEn) | Complexity of signal in frequency domain | |
| Spectral Flux | Difference in the spectrum between two adjacent frames | |
| Center of Gravity of Frequency (CGF) | Spectral centroid of the signal | |
| Dominant Frequency | The frequency that has maximum value of the Power Spectral Density (PSD) | |
| Average Value of PSD | Mean value of PSD of a sliding window in frequency domain |
| Parameter | Notation | Value |
|---|---|---|
| Cognitive coefficient | 2 | |
| Social coefficient | 2 | |
| Number of population | 50 | |
| Inertia weight | 0.95 | |
| Random matrices 1 | , | Not constant |
| True classes | |||
|---|---|---|---|
| Awake | Drowsy | ||
| Estimated classes | Awake | TN = 24212 | FN = 538 |
| Drowsy | FP = 814 | TP = 9515 | |
| Samples | 25026 | 10053 | |
| Method | AUC | Accuracy | No. Selected Features | Selected Features |
|---|---|---|---|---|
| All features | 0.71 | 88.39 | 36 | All |
| Fisher | 0.79 | 89.73 | 6 | , , , , , |
| T-test | 0.85 | 90.21 | 5 | , , , , |
| Correlation | 0.95 | 96.47 | 25 | , , , , , , , , , , , , , , , , , , , , , , , , |
| Mutual information | 0.78 | 88.12 | 6 | , , , , , |
| FUzzy FEature Selection (FUFES) | 0.95 | 96.41 | 10 | , , , , , , , , , |
| Adaptive neuro-fuzzy feature selection | 0.97 | 98.12 | 5 | , , , , |
| Study | Method | Used variables | Accuracy |
|---|---|---|---|
| Krajewski et al., 2009 [39] | Ensemble classification using time domain, frequency domain and state space features | Steering wheel angle, lane deviation and pedal movement | 86.1 |
| McDonald et al., 2012 [40] | Random forest algorithm | Steering wheel angle | 79 |
| Samiee et al., 2014 [27] | Weighted output of three trained neural networks by used variables | Steering wheel angle, lateral displacement and eye blinking | 94.63 |
| Wang and Xu, 2016 [38] | Multilevel ordered logit (MOL) modeling using driver behavior and eye features metrics | Steering wheel angle, lateral displacement, speed, eye blinking and pupil diameter | 68.40 |
| Li et al., 2017 [9] | Warping distance between linearized approximate entropy in sliding windows | Steering wheel angle | 78.01 |
| Proposed study | Adaptive neuro-fuzzy feature selection with SVM classifier | Steering wheel angle and steering wheel velocity | 98.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arefnezhad, S.; Samiee, S.; Eichberger, A.; Nahvi, A. Driver Drowsiness Detection Based on Steering Wheel Data Applying Adaptive Neuro-Fuzzy Feature Selection. Sensors 2019, 19, 943. https://doi.org/10.3390/s19040943
Arefnezhad S, Samiee S, Eichberger A, Nahvi A. Driver Drowsiness Detection Based on Steering Wheel Data Applying Adaptive Neuro-Fuzzy Feature Selection. Sensors. 2019; 19(4):943. https://doi.org/10.3390/s19040943
Chicago/Turabian StyleArefnezhad, Sadegh, Sajjad Samiee, Arno Eichberger, and Ali Nahvi. 2019. "Driver Drowsiness Detection Based on Steering Wheel Data Applying Adaptive Neuro-Fuzzy Feature Selection" Sensors 19, no. 4: 943. https://doi.org/10.3390/s19040943
APA StyleArefnezhad, S., Samiee, S., Eichberger, A., & Nahvi, A. (2019). Driver Drowsiness Detection Based on Steering Wheel Data Applying Adaptive Neuro-Fuzzy Feature Selection. Sensors, 19(4), 943. https://doi.org/10.3390/s19040943







