Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load
Abstract
:1. Introduction
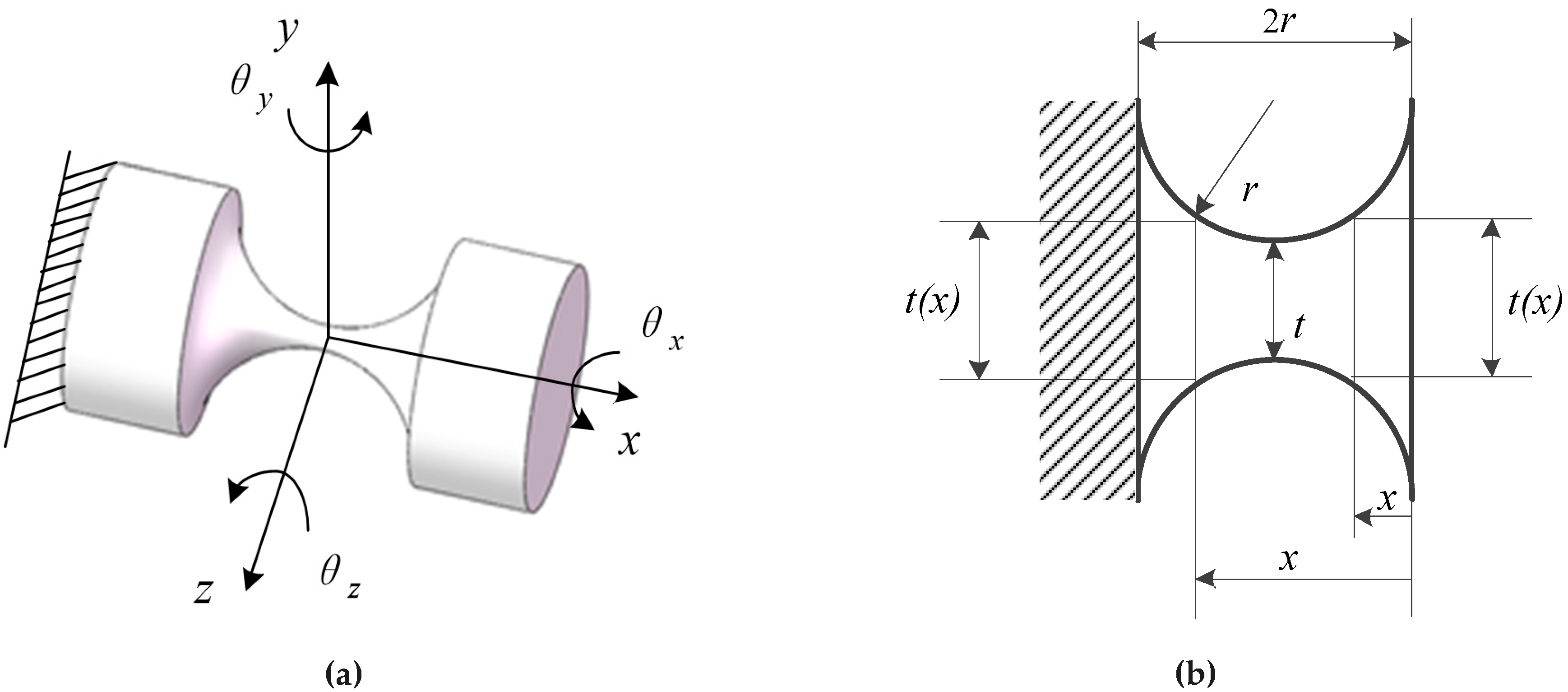
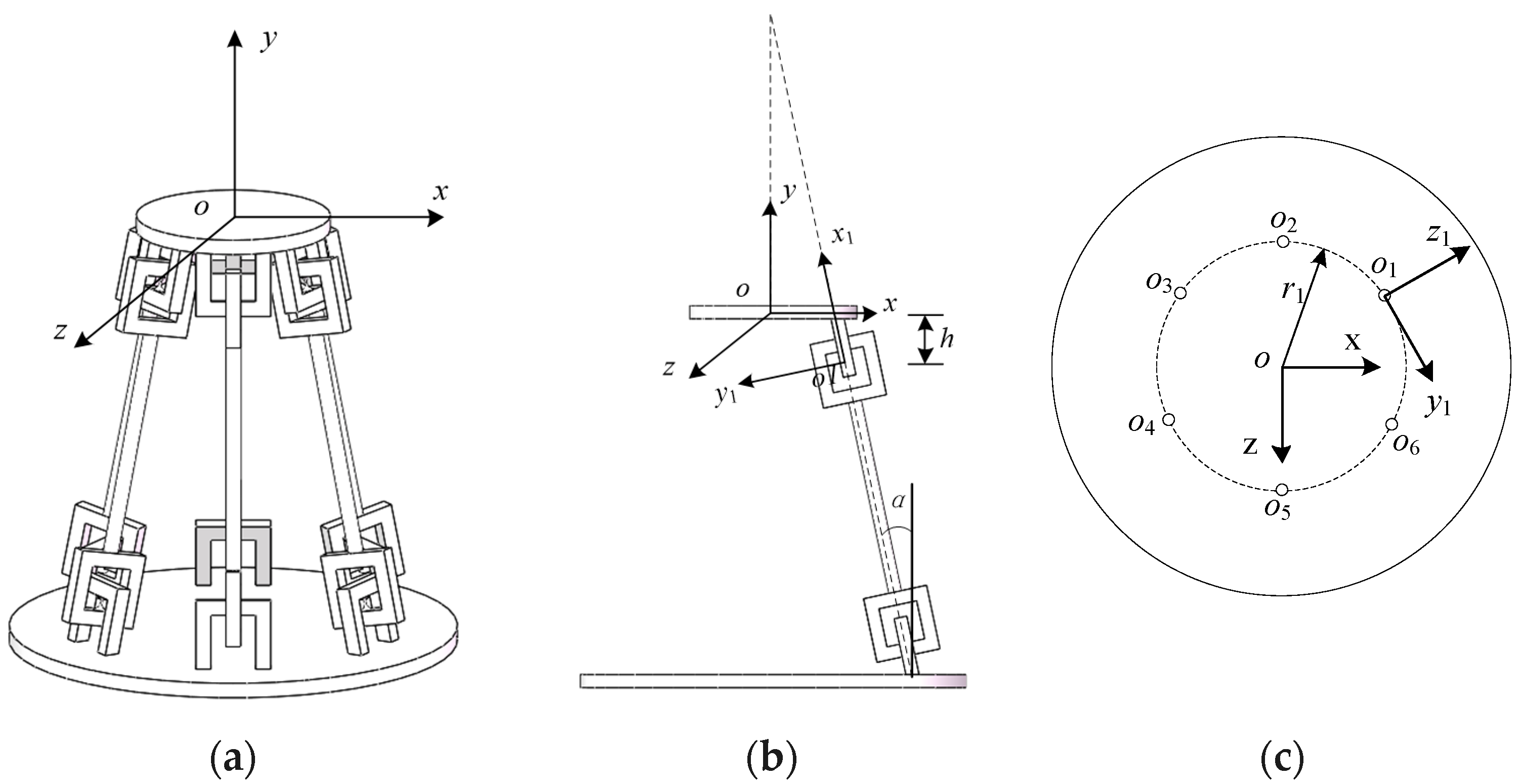
2. Analysis of the Compliant Spherical Joint Based on Screw Theory
2.1. Compliance Matrix of an RCCS (Right Circular Cross-Section) Flexural Joint
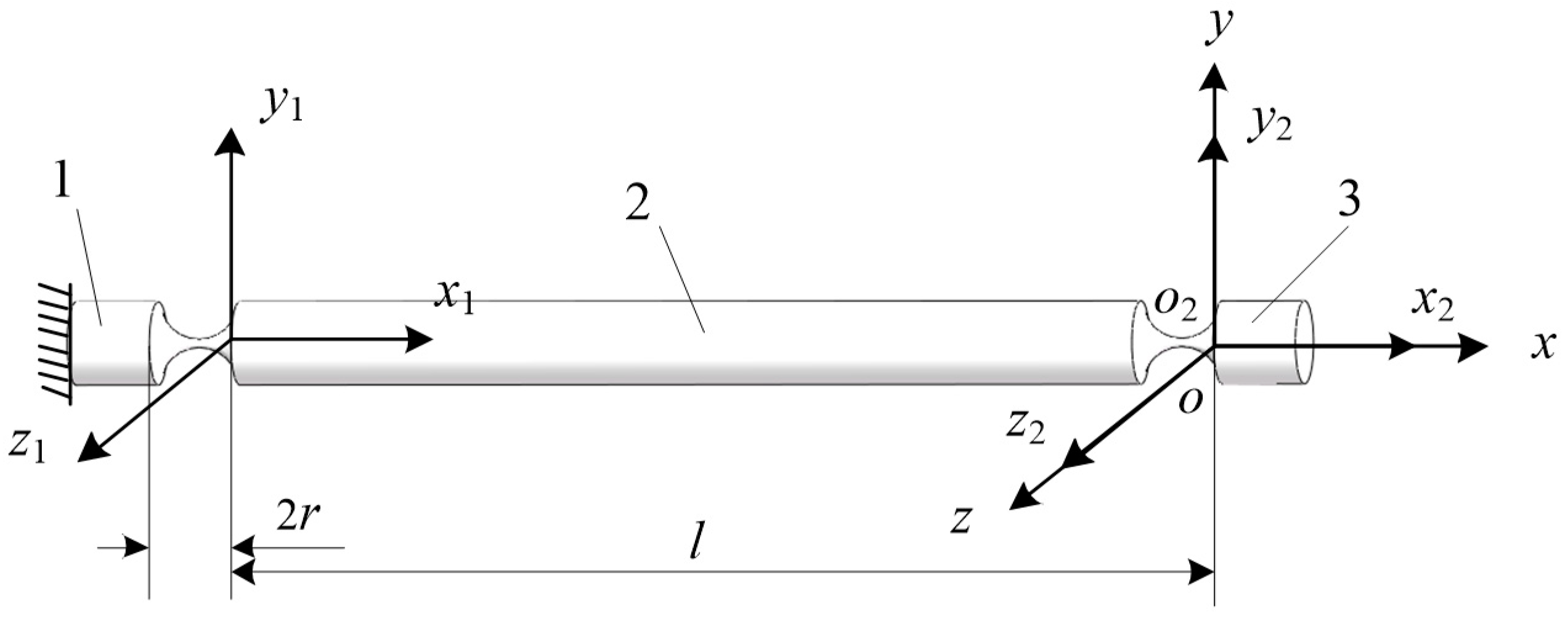
2.2. The Compliance Matrix of RCCS Serial Chain
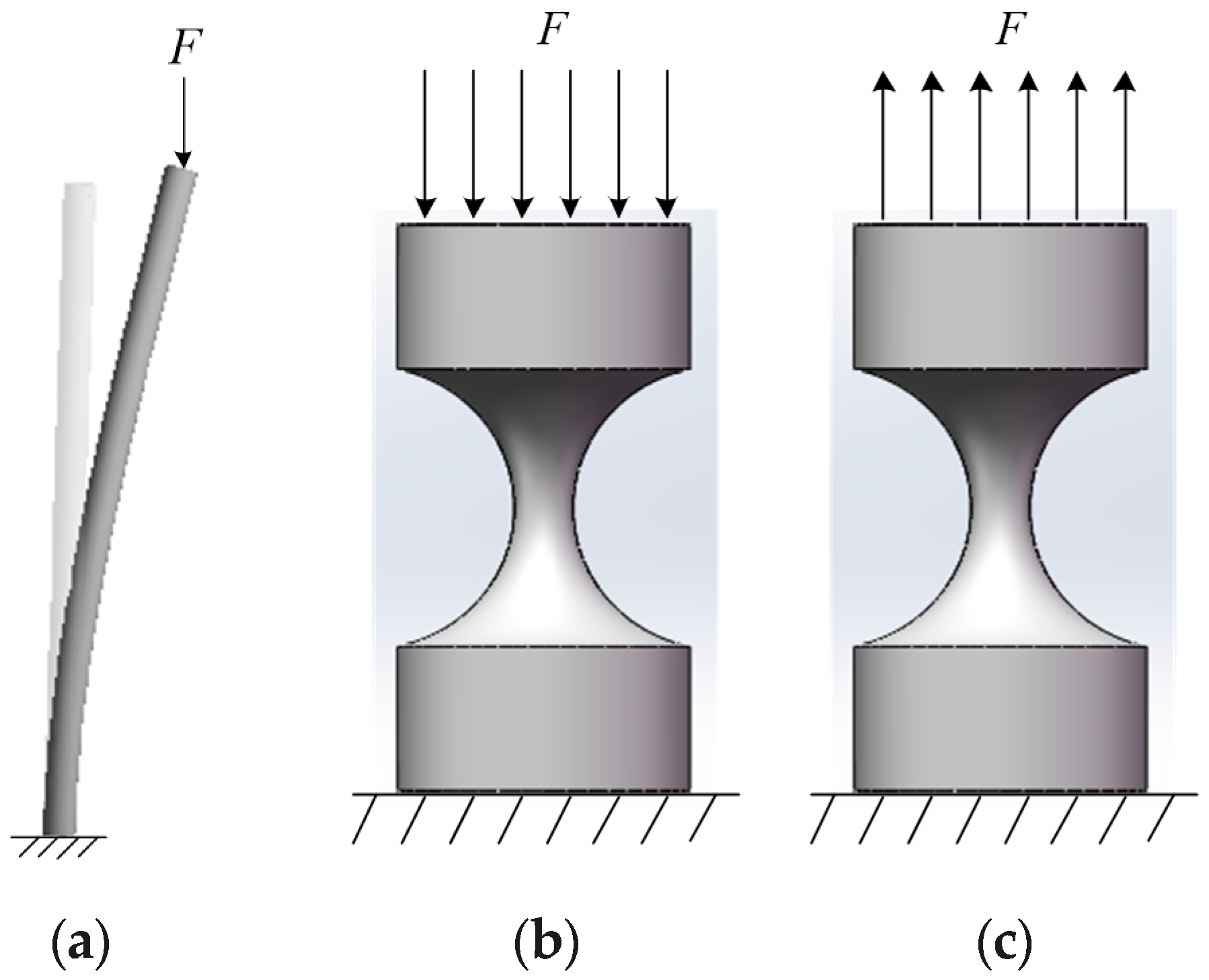
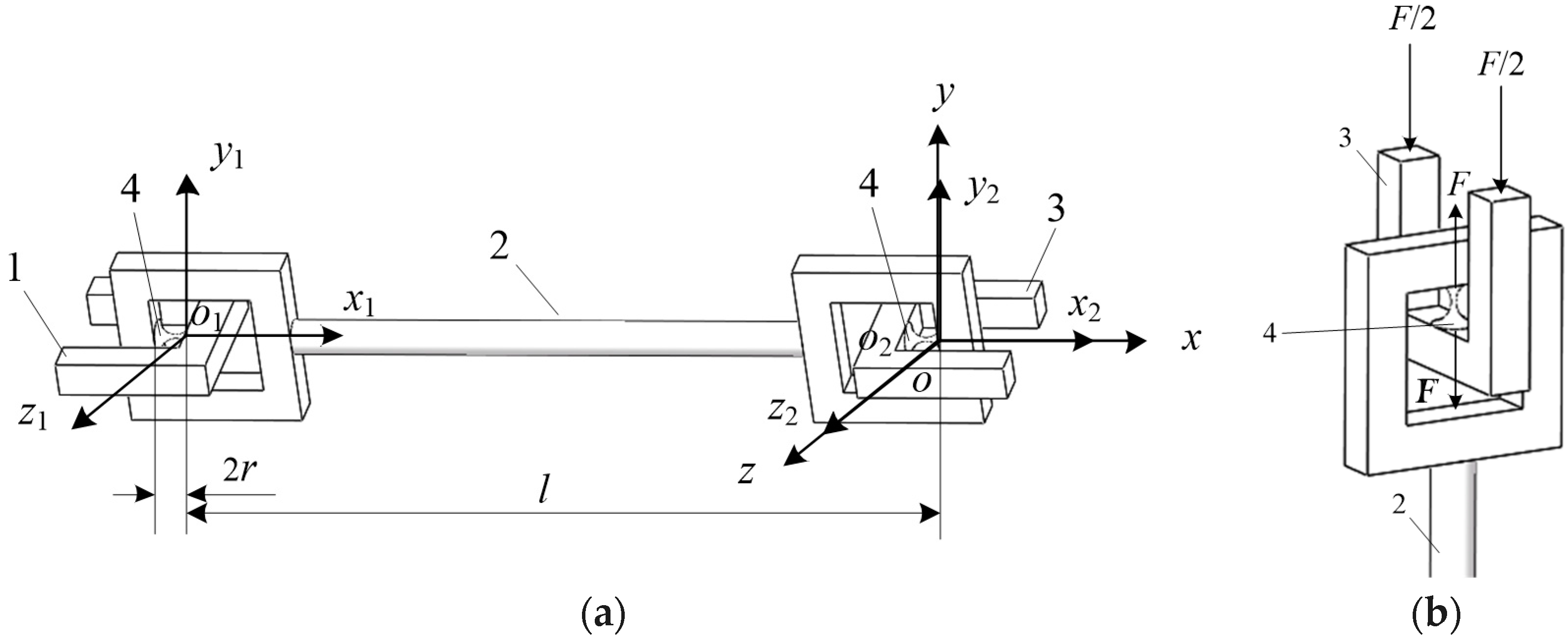
2.3. A combined Design of Serial Compliant Joints with a Function of Interchanging Press and Pull
2.4. Compliance Matrix of CPM Based on the New Serial RCCS Flexural Joint Branch Chain
3. The DOF Analysis of CPM Based on Compliant Branch
3.1. Generalized Eigenvalue Decomposition of Compliance Matrix
3.2. Judging the DOF of the CPM by the Symbolic Formulation
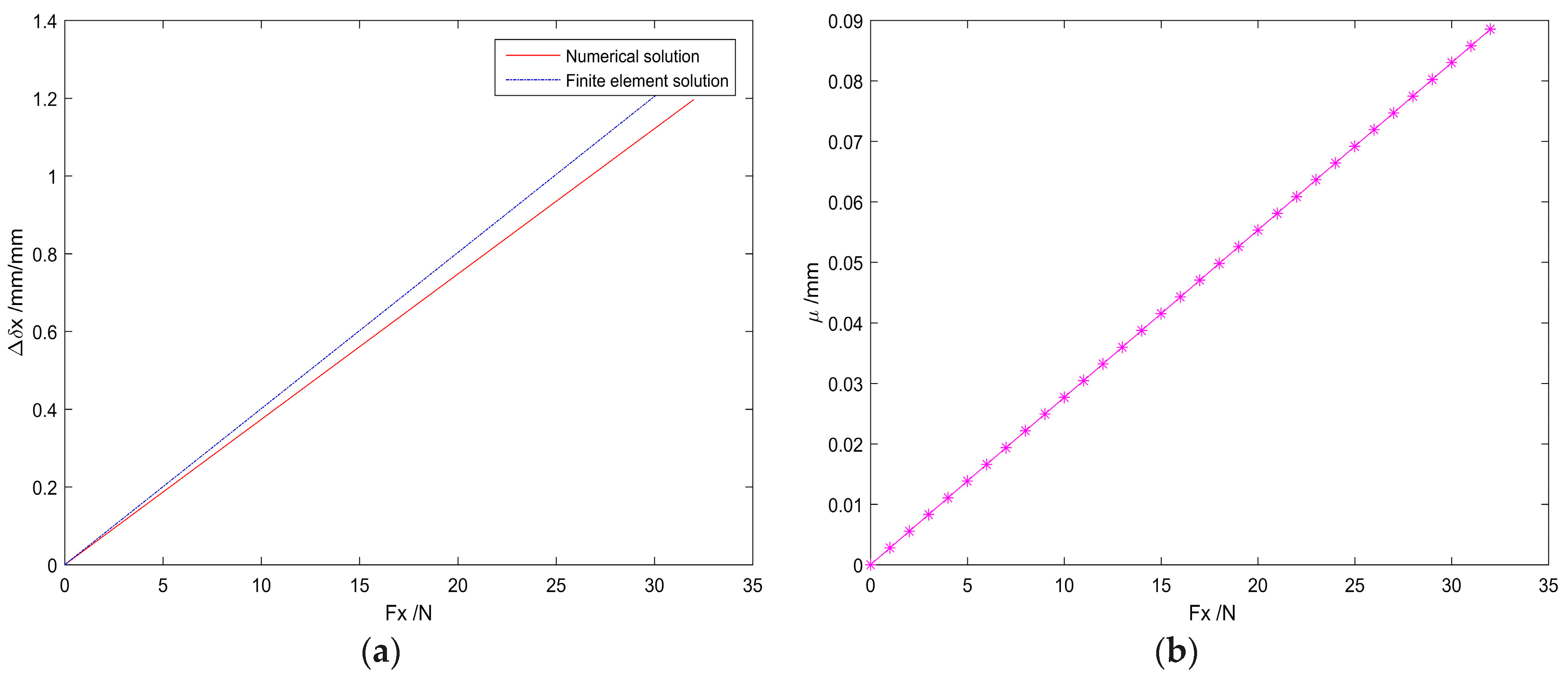
4. Numerical and Finite Element Method Normal Variable Analysis of CPM
5. Conclusions
- (1)
- The existing six DOFs CPM mobile platforms fail to bear a considerable load because of the bucking of the flexural joints. However, the proposed novel mechanism will be able to bear large loads, as much as a 32.59 N force along the x and z-axes.
- (2)
- The DOF of the mechanism was numerically analyzed by the generalized eigenvalue and eigenvector decomposition of the compliance matrix for the compliance matrix symbolic formulation of the whole mechanism, and the number of the DOF is verified by the numerical and finite element method. Under the same load, the deformation error obtained by the two methods is less than 6.89% compared with the finite element method; in addition, the load and deformation increases linearly within the yield strength range of the material.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; Gordon and Breach Science Publishers: New York, NY, USA, 2000. [Google Scholar]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Patil, C.B. Robust Design of Selectively Compliant Flexure-Based Precision Mechanisms. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Li, S.Z.; Yu, J.J.; Pei, X.; Su, H.-J.; Hopkins, J.B.; Culpepper, M.L. Type Synthesis Principle and Practice of Flexure Systems in the Framework of Screw Theory: Part III–Numerations and Synthesis of Flexure Mechanisms. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; pp. 619–628. [Google Scholar]
- Smith, S.T. Foundations of Ultra-Precision Mechanism Design; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 2003. [Google Scholar]
- Culpepper, M.L.; Anderson, G. Design of a Low-Cost Nano-Manipulator Which Utilizes a Monolithic, Spatial Compliant Mechanism. Precis. Eng. 2004, 28, 469–482. [Google Scholar] [CrossRef]
- Dagalakis, N.G.; Amatucci, E. Kinematic Modeling of a 6 Degree of Freedom Tri-Stage Micro-Positioner. In Proceedings of the American Society for Precision Engineering 16th Annual Meeting, Crystal City, VA, USA, 10–15 November 2001; pp. 200–203. [Google Scholar]
- Aguirre, A.D.; Hertz, P.R.; Chen, Y.; Fujimoto, J.G.; Piyawattanametha, W.; Fan, L.; Wu, M.C. Two-Axis MEMS Scanning Catheter for Ultrahigh Resolution Three-Dimensional and En Face Imaging. Opt. Express. 2007, 15, 2445–2453. [Google Scholar] [CrossRef] [PubMed]
- Henein, S.; Frommherz, U.; Betemps, R.; Kalt, H.; Ellenberger, U.; Flechsig, U.; Raabe, J. Mechanical Design of a Spherical Grating Monochromator for the Microspectroscopy Beamline Pollux at the Swiss Light Source. In Proceedings of the AIP Conference, Daegu, Korea, 28 May–2 June 2006; pp. 643–646. [Google Scholar]
- Wang, Z.; Chen, L.; Sun, L. An Integrated Parallel Micromanipulator with Flexure Hinges for Optical Fiber Alignment. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 2530–2534. [Google Scholar]
- Shi, H.L.; Duan, X.; Su, H.-J. Optimization of the workspace of a MEMS hexapod nanopositioner using an adaptive genetic algorithm. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4043–4048. [Google Scholar]
- Shi, H.; Su, H.-J.; Dagalakis, N.; Kramar, J.A. Kinematic modeling and calibration of a flexure based hexapod nanopositioner. Precis. Eng. 2013, 37, 117–128. [Google Scholar] [CrossRef]
- Brouwer, D.M.; Soemers, H. 6-DoFs MEMS-based precision manipulators. Mikroniek 2008, 48, 5–13. [Google Scholar]
- Brouwer, D.M.; Jong, B.R.D.; Soemers, H.M.J.R. Design and modeling of a six DOFs MEMS-based precision manipulator. Precis. Eng. 2010, 34, 307–319. [Google Scholar] [CrossRef]
- Howell, L.L.; Midha, A. Determination of the degrees of freedom of compliant mechanisms using the pseudo-rigid-body model concept. In Proceedings of the Ninth World Congress on the Theory of Machines and Mechanisms, Milan, Italy, 1–3 September 1995; pp. 1537–1541. [Google Scholar]
- Deshmukh, B.; Pardeshi, S.; Mistry, R. Development of a Four Bar Compliant Mechanism using Pseudo Rigid Body Model (PRBM). Procedia Mater. Sci. 2014, 6, 1034–1039. [Google Scholar] [CrossRef]
- Su, H.J. Mobility Analysis of Flexure Mechanisms via Screw Algebra. J. Mech. Rob. 2011, 3, 041010. [Google Scholar] [CrossRef]
- Su, H.J.; Yue, C. Type synthesis of freedom and constraint elements for design of flexure mechanisms. Mech. Sci. 2013, 4, 263–277. [Google Scholar] [CrossRef]
- Su, H.J.; Tari, H. On Line Screw Systems and Their Application to Flexure Synthesis. J. Mech. Rob. 2011, 3, 011009. [Google Scholar] [CrossRef]
- Li, T.; Deng, H.; Zhang, L. Mobility Analysis of Generalized Mechanisms via Screw Algebra. Mech. Mach. Sci. 2017, 408, 581–596. [Google Scholar]
- Yu, J.; Li, S.; Su, H.J.; Culpepper, M.L. Screw theory based methodology for the deterministic type synthesis of flexure mechanisms. J. Mech. Rob. 2011, 3, 03100814. [Google Scholar] [CrossRef]
- Su, H.J.; Dorozhkin, D.V.; Vance, J.M. A Screw Theory Approach for the Conceptual Design of Flexible Joints for Compliant Mechanisms. J. Mech. Rob. 2009, 1, 0410098. [Google Scholar] [CrossRef]
- Wei, D.; Sun, L.N.; Du, Z.J. Design of a precision compliant parallel positioner driven by dual piezoelectric actuators. Sens. Actuators A Phys. 2007, 135, 250–256. [Google Scholar]
- Su, H.J.; Tari, H. Realizing Orthogonal Motions with Wire Flexures Connected in Parallel. J. Mech. Des. 2010, 132, 121002. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, D.; Wang, Y.; Ge, Y. Design and Analysis of a Novel Six-Component F/T Sensor based on CPM for Passive Compliant Assembly. Meas. Sci. Rev. 2013, 13, 253–264. [Google Scholar] [CrossRef]
- Panda, B.; Dutta, A. Design of a partially compliant crank rocker mechanism using Ionic Polymer Metal Composite for path generation. Mater. Des. 2010, 31, 2471–2477. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, J.F.; Zeng, D.X. A general method for analyzing the degree of freedom based on screw theory. Sci. China 2009, 39, 84–93. (In Chinese) [Google Scholar]
- Selig, J.M.; Ding, X. A screw theory of static beams. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; pp. 312–317. [Google Scholar]
- Su, H.-J.; Shi, H.; Yu, J.J. Analytical Compliance Analysis and Synthesis of Flexure Mechanisms. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, ASME, Washington, DC, USA, 29–31 August 2011; pp. 169–180. [Google Scholar]
- Shi, H.L.; She, Y.; Duan, X.C. A Structural Model for Loading Analysis of a Hexapod Platform. In Proceedings of the 2015 world congress on Aeronautics, Nano, Bio, Robotics, and Energy (ANBRE15), Incheon, Korea, 25–28 August 2015. [Google Scholar]
- Jia, M.; Jia, R.P.; Yu, J.J. A Compliance-Based Parameterization Approach for Type Synthesis of Flexure Mechanisms. J. Mech. Rob. 2015, 7, 031014. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.N.; Garcia, E.; Goldfarb, M. Corner-Filleted Flexure Hinges. J. Mech. Des. 2000, 123, 346–352. [Google Scholar] [CrossRef]
- Furqan, M.; Alam, M.N. Finite Element Analysis of a Stewart Platform using Flexible Joints. In Proceedings of the 1st International and 16th National Conference on Machines and Mechanisms (iNaCoMM2013), IIT Roorkee, India, 18–20 December 2013. [Google Scholar]
- Chen, G.M.; Jia, J.Y.; Li, Z.W. Right-circular corner-filleted flexure hinges. In Proceedings of the 2005 IEEE International Conference on Automation Science and Engineering, Edmonton, AL, Canada, 1–2 August 2005; pp. 249–253. [Google Scholar]
- Lobontiu, N.; Garcia, E.; Hardau, M.; Bal, N. Stiffness characterization of corner-filleted flexure hinges. Rev. Sci. Instrum. 2004, 75, 4896–4905. [Google Scholar] [CrossRef]
- Dong, W.; Du, Z.; Sun, L. Conceptional design and kinematics modeling of a wide-range flexure hinge -based parallel manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Lobontiu, N.; Paine, J.S.N. Design of circular cross-section corner-filleted flexure hinges for three-dimensional compliant mechanisms. J. Mech. Des. 2002, 124, 479–484. [Google Scholar] [CrossRef]
- Shi, H. Modeling and Analysis of Compliant Mechanisms for Designing Nano-positioners. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2013. [Google Scholar]
- Zhang, Y. Kinematics analysis and synthesis of space agencies and compliant mechanisms. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2015. [Google Scholar]
- Miller, J.T.; Su, T.; Pabon, J.; Wicks, N.; Bertoldi, K.; Reis, P.M. Buckling of a thin elastic rod inside a horizontal cylindrical constraint. Extreme Mech. Lett. 2015, 3, 36–44. [Google Scholar] [CrossRef]
- Su, T.X.; Wicks, N.; Pabon, J.; Bertoldi, K. Mechanism by which a frictionally confined rod loses stability under initial velocity and position perturbations. Int. J. Solids Struct. 2013, 50, 2468–2476. [Google Scholar] [CrossRef]
- Shams, A.; Aureli, M.; Porfiri, M. Nonlinear buckling of a spherical shell embedded in an elastic medium with imperfect interface. Int. J. Solids Struct. 2013, 50, 2310–2327. [Google Scholar] [CrossRef]
- Su, H.-J.; Shi, H.; Yu, J.J. A Symbolic Formulation for Analytical Compliance Analysis and Synthesis of Flexure Mechanisms. J. Mech. Des. 2012, 134, 51009. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Su, H.-J.; Liao, Q. Mobility criteria of compliant mechanisms based on decomposition of compliance matrices. Mech. Mach. Theory 2014, 79, 80–93. [Google Scholar] [CrossRef]


| Variable | Value | Unit |
|---|---|---|
| E | 200 | GPa |
| ν | 0.3 | mm |
| t | 2 | mm |
| r | 5 | mm |
| l | 240 | mm |
| r1 | 72.55 | mm |
| α1 | 0 | ° |
| α2 | 0 | ° |
| α3 | 0 | ° |
| α4 | 0 | ° |
| α5 | 0 | ° |
| α6 | 0 | ° |
| β1 | 30 | ° |
| β2 | 90 | ° |
| β3 | 150 | ° |
| β4 | 210 | ° |
| β5 | 270 | ° |
| β6 | 330 | ° |
| γ1 | 102 | ° |
| γ2 | 102 | ° |
| γ3 | 102 | ° |
| γ4 | 102 | ° |
| γ5 | 102 | ° |
| γ6 | 102 | ° |
| ρ1 | 30 | ° |
| ρ2 | 90 | ° |
| ρ3 | 150 | ° |
| ρ4 | 210 | ° |
| ρ5 | 270 | ° |
| ρ6 | 330 | ° |
| ζ1 | 150 | ° |
| ζ2 | 180 | ° |
| ζ3 | 210 | ° |
| ζ4 | 240 | ° |
| ζ5 | 270 | ° |
| ζ6 | 300 | ° |
| h | 35.78 | mm |
| Fz (N) | Δδz (mm) | Mx (Nmm) | Δθx (°) | My (Nmm) | Δθy (°) | Mz (Nmm) | Δθz (°) |
|---|---|---|---|---|---|---|---|
| 5.54 | 0.22 | 5536.68 | 0.17 | 1474.42 | 0.44 | 4281.42 | 0.13 |
| 9.91 | 0.40 | 6619.62 | 0.20 | 1539.20 | 0.46 | 4958.33 | 0.15 |
| 14.09 | 0.57 | 6876.59 | 0.21 | 1675.83 | 0.50 | 5547.47 | 0.17 |
| 14.45 | 0.57 | 7302.79 | 0.22 | 1915.12 | 0.57 | 5839.59 | 0.18 |
| 17.79 | 0.71 | 7394.97 | 0.23 | 1945.70 | 0.58 | 6254.18 | 0.19 |
| 22.21 | 0.89 | 8110.67 | 0.25 | 2396.66 | 0.72 | 7216.39 | 0.22 |
| 24.09 | 0.97 | 8962.77 | 0.27 | 2435.86 | 0.73 | 7534.12 | 0.23 |
| 25.71 | 1.03 | 9247.49 | 0.28 | 2667.90 | 0.80 | 7888.29 | 0.24 |
| 26.44 | 1.06 | 9405.11 | 0.29 | 2966.74 | 0.90 | 8155.98 | 0.25 |
| 29.62 | 1.03 | 9751.75 | 0.30 | 3047.80 | 0.91 | 8976.38 | 0.27 |
| 31.03 | 1.25 | 10,003.81 | 0.31 | 3070.20 | 0.92 | 9150.62 | 0.28 |
| 32.34 | 1.30 | 10,125.49 | 0.31 | 3593.10 | 1.08 | 9909.63 | 0.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Lu, Y.; Duan, X.; Zhang, D.; Deng, W. Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load. Sensors 2019, 19, 828. https://doi.org/10.3390/s19040828
Wu X, Lu Y, Duan X, Zhang D, Deng W. Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load. Sensors. 2019; 19(4):828. https://doi.org/10.3390/s19040828
Chicago/Turabian StyleWu, Xiaochuan, Yi Lu, Xuechao Duan, Dan Zhang, and Wenyao Deng. 2019. "Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load" Sensors 19, no. 4: 828. https://doi.org/10.3390/s19040828
APA StyleWu, X., Lu, Y., Duan, X., Zhang, D., & Deng, W. (2019). Design and DOF Analysis of a Novel Compliant Parallel Mechanism for Large Load. Sensors, 19(4), 828. https://doi.org/10.3390/s19040828





