1. Introduction
Robots are expected to perform highly dynamical motions. Being able to perform these motions repeatably and reliably is an active research topic. A crucial part of these motions is the interaction of the robot with other objects or the environment. Whenever an interaction happens there exist an exchange of forces. Therefore, knowledge of the forces exchanged at contacts is a fundamental part of endowing robots with the ability to perform dynamical motions. The six-axis force-torque (FT) sensors convey a complete information of a contact force by providing measurements of the three axes of forces and three axes of torques. Robots with their base fixed to the ground have been using FT sensors to measure contact forces since a long time [
1,
2,
3]. Despite being common sensors in many floating base platforms [
4,
5,
6,
7,
8,
9], their potential use in floating base robots has not been full documented. One of the reasons is that the reliability of this sensors may decrease after mounting them [
10,
11,
12,
13]. The Model-Based In Situ Calibration Method has shown promising results in the improvement of the reliability of force torque sensors [
14]. By extending its benefits and showcasing the improvement of floating base robots performance with this method, we aim to encourage the use of this sensor in these types of platforms in more effective ways.
The most common phenomena used in FT sensors to measure forces is the change in resistance of silicon due to strain [
15]. In more technical words, the piezoresistive response to strain of semiconductor material. This material also changes resistance with temperature. Because of this, depending on the calibration procedure, the sensor might suffer from temperature drift [
14,
16,
17]. This is the undesired change of measurement due to changes in temperature. Methods to deal with temperature compensation such as an array of strain gauges in a Wheatstone Bridge configuration are ineffective in these sensors due to the inner structure of FT sensors.
Typically, the offset in FT sensors is removed before use. Commonly floating base robots use this sensor to detect and measure contacts. Thus, the time of collision is unknown a priori. Removing the offset after the sensor has established contact would make the value measured by the FT sensor incorrectly. Therefore, minimizing the effect of drift in the FT sensors can improve the reliability of the sensor in floating base robots.
The typical calibration procedure considers, first, identifying the offset when no load is applied on the sensor. Then, carefully placing some weights in specific positions to have well known forces and torques in order to span the space of the sensor. To resolve the coupling effects, it is necessary to have calibration points with as many orientations of the force vector as possible based on the sensor’s coordinate system. The calibration data should ideally be a representative dataset of what the sensor will be subjected to.
Due to the nature of the technology used, solving with least squares remains the most popular [
18]. Calibrations of these sensors are known to loose effectiveness over time. Leading companies for FT sensors [
19,
20] recommend to calibrate the sensors at least once a year. This normally implies that the sensor must be unmounted, sent back to them and then mounted again.
The most common calibration procedure is a quasi-static calibration of the sensor. Calibration procedures can be classified into ex situ when the sensor is calibrated in a place different where is used, and in situ if it is calibrated on the place it will be used.
Ex situ calibration is usually performed using specialized structures [
1,
21,
22,
23] or relying on previously calibrated sensors [
24,
25,
26,
27]. The latter has the disadvantage of trusting on the calibration of another sensor which might not be perfect. The in situ methods allow to perform the calibration in the sensor’s final destination, avoiding the decreases in performance that arise from mounting and removing the sensors from its working structure. Some in situ calibration methods have relied on other FT sensors [
27,
28]. Others exploit known relationships between some quantities such as joint torques [
29] or acceleration measurements [
10] to obtain the reference forces. Some calibrate the sensor mounted in their final position by designing a calibration bench that accommodates the sensor and the mounted structure [
30]. This requires the design of a particular structure and the mounting and dismounting of the whole part to calibrate one sensor. Six-dimensional force/torque sensors can be calibrated based on the shape from motion method with complex algorithm. This requires the use of thre different sets of weights and a minimal setup with a fixed pulley. It requires a calibration of the sensor three times per load, so in total, nine datasets [
31]. In all of these methods, the effect of temperature is either not considered or carefully controlled when calibrating without accounting for changes in the working conditions. Other methods exploit the encoders and the model of the robot to provide the reference forces and torques [
11]. This method was successfully improved to account for temperature by considering temperature effects on the sensor as linear [
14].
There are two main contributions of this paper. The first is to provide useful tips to better exploit the Model-Based in situ calibration method with temperature compensation in a simple way. The other is to showcase the impact of the improved measurements obtained with this calibration in the dynamic performance of floating base robots.
The paper is structured as follows: in
Section 2, the in situ calibration method is detailed. It also contains a description of the robotic platform and the ways the sensor information is used in such a platform.
Section 3 contains the useful tips to better exploit the Model Based in situ calibration method with temperature compensation in a simple way and shows a way to exploit the generic formulation to simultaneously estimate offset and calibration matrix. We also describe two new types of datasets with the aim to discuss how to understand sensor excitation easily. A simple non-intrusive method to exploit the resulting calibration is described. A description of the constant offset hypothesis can be found as well.
Section 4 details how the experiments were setup, the datasets used and how the results were validated. In
Section 5, the results are used to verify the usefulness of the tips, the constant offset hypothesis and improvements in floating-based robot performance when using the Model-based in situ calibration method with temperature compensation. Conclusions can be found in
Section 6.
2. Background
In this section, the developed in situ calibration method is described in detail. Starting from the general mathematical model of the FT sensor to the problem statement that is solved through the Model-Based in situ calibration method.
2.1. Mathematical Model of FT Sensors
There are two physical laws at play in strain gauge force sensors. One is common to all kinds. It is the relationship between the deformation of a spring and forces, it is the Hooke’s law of elasticity.
where
f is the force value in
,
k is a constant of the material
and
is the displacement (or strain) in
. It is valid as long as the material does not reach plastic deformation. Another definition of Hooke’s Law is the relationship between engineering stress and engineering strain for elastic deformation [
32]. Stress
(
) is expressed in terms of force applied to a certain cross-sectional area
A (
) of an object,
For FT sensors
A is the cross-section of an internal beam of the FT sensor. Strain
is the deformation of a physical body under the action of applied forces. It has no units. Strain is calculated as
Using the other definition of Hooke’s Law the relationship between stress and strain is:
where
is the modulus of elasticity of the material and depends on the kind of stress and strain applied to it. The other principle depends on the type of sensing technology. For semiconductor strain gauges it is the piesoresistive effect. The model is the linear function [
15]:
where
R is the resistance value in
,
is the strain,
is the gauge factor of the conductor,
is the resistance with no stress applied in
.
Combining both physical effects gives the following transfer function:
Therefore the most used model for predicting the force-torque from the raw strain gauges measurements of the sensor is a linear model. The inverse function is:
where
Considering possible errors during the calibration procedure, linear regression is the most suitable approximation function. Multi-axis force-torque sensors usually contain multiple strain gauges, each of them can be seen as a separate sensor. Because of this, multiple regression is a valid option for this kind of sensor. Therefore, each force axis will be calibrated using the information from all strain gauges,
where
is the force in the i-th axis in
or
depending on the axis,
is the digital response of the m-th strain gauge in bit counts,
is the slope of the linear model of the m-th strain gauge in
and
is the bias of the m-th strain gauge. The orientation of
with regards to the m-th strain gauge will change the value of
k required. It depends on the strain being normal, shear or a combination of both. As a result, the array of
coefficients
and
will be different for each
i-th axis. Taking this in consideration, the approximation function for these sensors for all axes has the following form:
where
are the 6D forces,
is the calibration matrix in
,
are the raw measurements (sensor’s response in bit counts) and
is the offset which is also a 6D force vector. Both the calibration matrix
C and the offset
o are unknown and need to be estimated. This formulation allows to calibrate all axes at the same time although they can be considered independent problems.
2.2. The Model-Based In Situ Calibration Method
Calibrating an FT in situ requires a dataset of samples
obtained from the sensor mounted on the robot. When no contact force is acting on the limb on which the FT sensor is mounted, the expected force-torque applied on the sensor can be computed using the robot model and the instantaneous joints position, velocity and acceleration [
33,
34,
35]. Since reference forces
are obtained this way, the method is named
Model Based In Situ Calibration. The robot parameters are assumed to be known. There are three main components to this method. The first is to formulate the calibration problem decoupling the offset estimation problem from the calibration matrix estimation problem. The second one is to cast the calibration matrix estimation problem as a
regularized least square problem, in which the regularization considers the known information of a previous calibration matrix. Lastly, having a way to consider other phenomena that might be creating some drift, the assumption considered is that other phenomena are also linear.
2.2.1. Least Squares Solution
The multiple linear regression problem in Equation (
9) can be solved using the least squares technique. The problem is stated as follows:
where
N is the number of data samples in the dataset. The offset is usually estimated separately from the calibration matrix. Because the offset can vary across different experiments due to temperature drift. The offset is removed from the raw measurements separately, and the calibration problem is reduced to:
where
and
are the reference 6D forces and raw measurements respectively with the offset removed.
2.2.2. Regularization
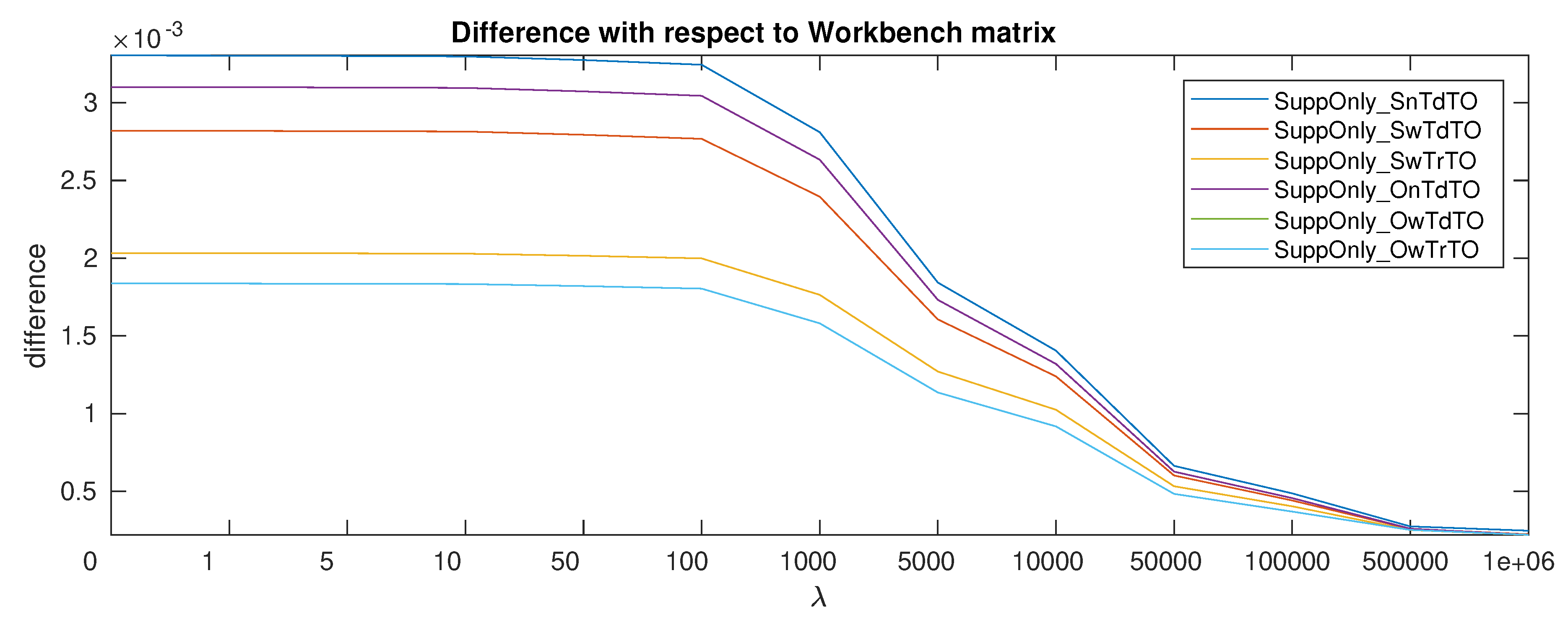
In ex situ calibration matrix estimation methods, the input data
are obtained by applying a set of known masses in known locations with the sensor mounted on a workbench. Thus, this kind of ex situ calibration matrix will be referred as
Workbench matrix. Assuming the calibration performed on the sensor was correct, the new calibration matrix must be similar to the
Workbench matrix. To enforce this assumption, a regularization term to penalize the difference with respect to the
Workbench matrix is introduced. The new calibration matrix is obtained through the following optimization problem:
where
is the
Workbench matrix given by the sensor producer,
is used to penalize the regularization term and
N is the number of data points in the dataset. The regularization is added in order to try to keep the calibration matrix as close to the
Workbench matrix, but keeping an improved performance after the sensor is mounted on the robot.
The form of the solution is obtain following these steps:
Consider the Matrix form of the least squares
where
is the matrix with the reference 6D forces where each columns is
,
where each column is
.
Given
,
indicates the column vector attained by stacking the columns of the matrix
X. Due to the definition of
, it follows that
where ⊗ is the Kronecker product.
If we consider that
, where
is a 6 by 6 identity matrix, then, using the Kronecker property mentioned in Equation (
14), we can put Equation (
13) in the column vectorized form:
The minimum of a quadratic form take place when the derivative is equal to 0. Using vector differentiation properties, the solution to Equation (
15) can be written as
where
. It is important to notice that the size of
I multiplying
should match the length of
which is
, where
a is the number of axis (six-axis for these type of sensors) and
is the number of raw signals.
2.2.3. Adding Linear Variables
When considering other phenomena as linear variables the final form of the problem can be expressed as:
where
are the added linear variables calibration coefficients and
are the added linear variable values. In this case, the problem is not only to estimate the calibration matrix
C and the offset
o, but also
which accounts for the temperature changes in the sensor.
Given that adding a linear variable can be seen as adding an extra raw signal to the previous described solution. What needs to be done is:
Augment the raw measurements matrix R with the added linear value , in R each column has all the raw measurements of a given raw signal.
Augment the Workbench matrix by adding the coefficients regarding the added linear variable , where is the added linear variable value at the time of calibration. If is not available, is recommended to set it as a vector of zeros .
Since this should be reflected in , if the Workbench coefficients of the added linear variable are not provided, it is suitable to set the last a values in the diagonal() to 0. This avoids influencing the coefficients of the added variable with any previous information.
The final form of the solution is
This formulation allows to easily expand the solution to m number of extra linear variables. The extra linear variable can have its offset removed or not. Assumptions can be made by taking the first value and consider it as the offset of that variable.
2.2.4. Offset Estimation
Two methods are proposed to remove the offset from the estimation problem.
In both cases, we end up with a modified version of the raw data in which the effect of the offset is removed. With a little abuse of notation we have:
where
and
are the data used to solve the model-based in situ calibration problem (
12).
Each offset estimation type is based on a different assumption:
physical assumption: mass generates a sphere in the force space when making spherical movements.
mathematical assumption: taking out the mean from the dataset implies no offset in the calibration data.
2.3. Calibration Data Set
Two types of datasets that were used previously to calibrate a sensor.
Grid: moving the legs creating a grid pattern while being on a fixed pole. The contact happens at the waist of the robot. The leg is not bent to avoid changes in the center of mass of the leg during the experiment.
Balancing Support leg: doing an extended one foot balancing demo with widespread leg movements. The contact is on the support leg foot. Either right (BSR) or left (BSL) depending on the support leg.
A calibration dataset could be formed by one of these kinds of dataset or a combination of them.
2.4. Previous Results
Previous results showed that the sphere estimation type using the Grid dataset gave the best results when no temperature was taken into account [
11]. Adding the temperature required considering more than one dataset to incorporate multiple temperatures. It was proven that adding the temperature led to a further increase in performance. Mixing types of datasets gave better results [
14]. The in situ offset estimation type with temperature was shown to be better, followed closely by the
centralized offset removal with or without temperature, using the same
value.
In those tests, no temperature offset was considered. The validation datasets were collected the same day in between the calibration datasets. The results shown were about the external force estimation, but how this affects robot performance was not presented.
2.5. Experimental Platform
The experimental platform is the floating base robot iCub. It is a child-sized humanoid robot originally developed during the RobotCub European Project for research in embodied cognition [
36] by the
iCub Facility at the
Italian Institute of Technology.
It has 53 degrees of freedom (DoF), weighs around 33 kg and is 104 cm tall. The DoFs are distributed as in the following way: six for each leg, three for the torso, six for the head and eyes, seven for each arm and nine for each hand. One additional servo motor is used to open and close the eyelids. For the calibration, only a subset of 32 DOFs (legs, torso, arms, and neck) are used. The version of iCub used is known as 2.5. It has Brushless Direct Current electric motor (BLDC) with an Harmonic Drive transmission, making them suitable for joint torque control.
More details on the actuation and mechanics of the iCub 2.5 can be found in [
4]. An image of the robot is presented in
Figure 1.
The iCub has various sensors including inertial measurement units (IMU), force-torque (FT) sensors, cameras, microphones, joint encoders and tactile sensor arrays, that cover the surface of the robot. Six custom-made six-axis FT sensors [
37]) are placed as shown in
Figure 1. Only the force-torque sensors mounted on the legs and feet have temperature sensors. These sensors use silicon strain gauge technology.
The interface to interact with the iCub is through Yet Another Robot Platform (YARP). More specifically, YARP supports building a robot control system as a collection of programs communicating in a peer-to-peer way, with an extensible family of connection types (tcp, udp, multicast, local, MPI, mjpg-over-http, XML/RPC, tcpros, ...) that can be swapped in and out.
2.6. Force-Torque Sensing in the ICub
The force-torque sensing has five main uses in the iCub:
To estimate the FT sensors offset before experiments.
As a threshold to know if a stable contact has been established between the robot and the ground.
To give the feedback to the low-level joint torque controller.
To estimate dynamical quantities used by high-level controllers, such as the center of pressure (CoP) and the zero moment point (ZMP).
To give feedback to high-level controllers.
To Estimate the FT Sensors Offset before Experiments
A typical sequence before using the robot, involves removing the offset when only one contact with the environment exists. This offset estimation requires the information from the mass vector. This can be imposed in a known robot configuration or measured using an IMU. This offset is then subtracted from the measurements. There are three possibilities to estimate the offset:
The robot is hanging from the torso and mass is measured with IMU.
The robot is standing on one leg and the mass is measured using IMU.
The robot is standing on one leg and the mass is imposed to be acting in the axis normal to the ground.
As a Threshold
The simplest use is as a threshold. When the load on the sensors reaches a chosen value, the controllers change state assuming a stable contact has been achieved. The chosen value can be a percentage of the total body weight of the robot. Example of applications are balancing [
38] and standing up [
39].
To Calculate Dynamic Quantities
The forces acting on a moving robot can be separated into two categories: forces exerted by contact and forces transmitted without contact (mass and, by extension, inertia forces). The CoP is linked to the former, and the ZMP to the latter. Nonetheless, it has been shown that both points coincide [
40]. Therefore, is possible to use the contact force information to calculate dynamic quantities such as the ZMP and by extension affect the estimation of the center of mass (CoM).
The CoP is defined as the point where the resultant force can be exerted with a zero resultant moment. When the contact is with a flat ground the CoP and ZMP, can be calculated as:
where
is the CoP (ZMP),
is the torque measurement of the FT sensor at the ankle and
is the vertical force measurement of the FT sensor at the ankle.
Using the linear inverted pendulum model constraining the height of the CoM to be constant (
), the CoM dynamics can be estimated from the ZMP with the following equation:
The FT sensor measurements have a direct impact on the estimation of the ZMP and as a consequence in estimation of the CoM. This information is used in a walking controller [
41].
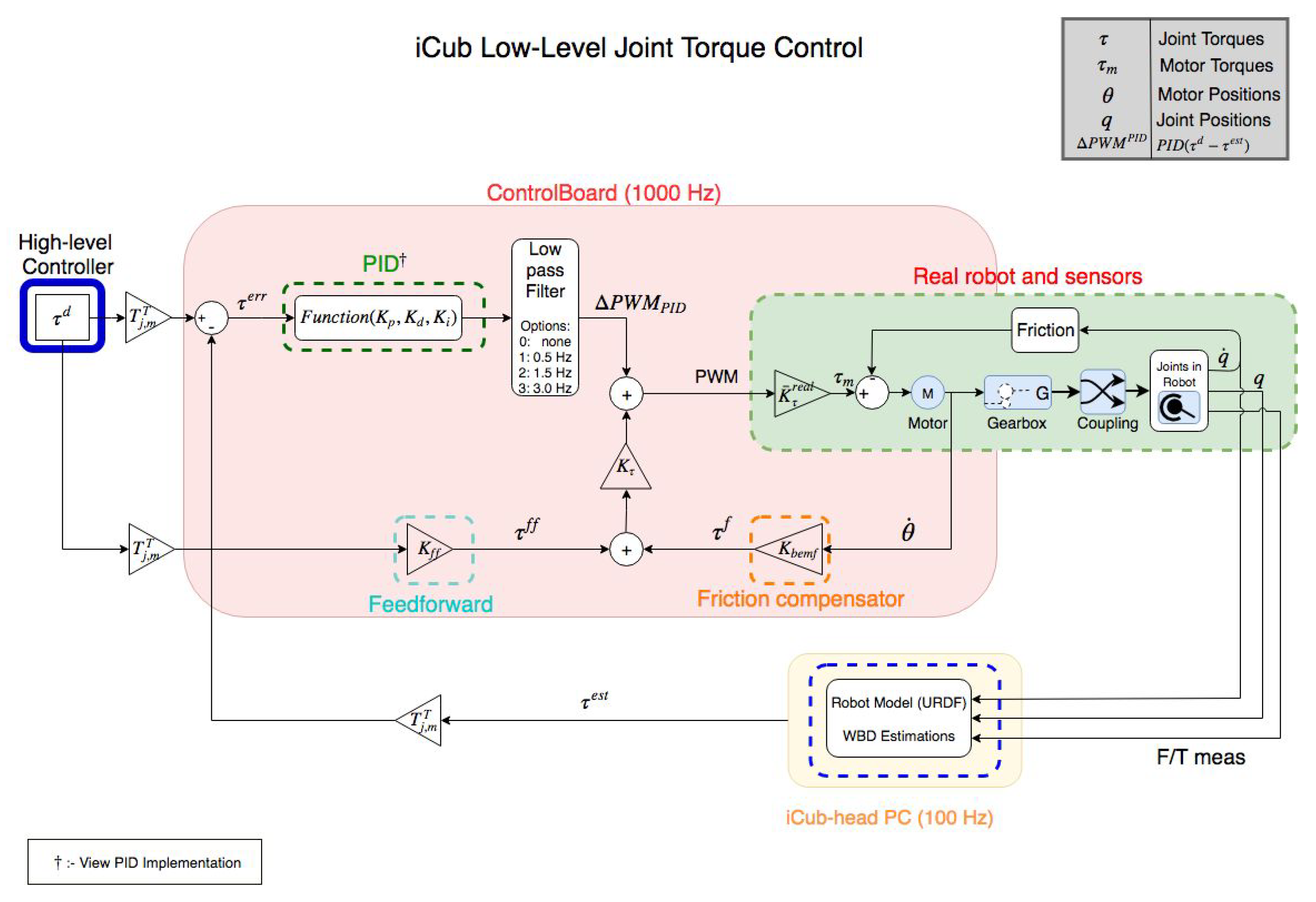
As Feedback for Joint Torque Controller
The scheme of this controller can be seen in
Figure 2. Description of the variables in the scheme can be found in
Table 1. It is a PID controller with friction compensation. The feedback values are the estimated joint torques using the measurements from the FT sensor [
35].
As Feedback for Jerk Controller
A recent method for exploiting force-torque sensing is to use the estimated contact force as feedback to a high-level jerk controller of floating base systems with contact-stable parametrised force feedback [
42].
The momentum rate-of-change equals the summation of all the external wrenches acting on the robot. In a multi-contact scenario, the external wrenches reduce to the contact forces plus the mass force:
where
is the robot’s momentum,
is the matrix mapping the
k-th contact wrench to the momentum dynamics,
is the origin of the frame associated with the
k-th contact, and
is the CoM position.
By considering the invertible parametrization
, it is possible to ensure the friction cone constraints while avoiding to use inequality constraints. The mentioned controller uses the following optimisation problem:
where
are symmetric and positive definite matrices,
is the reference momentum,
X is the adjoint transformation matrix from the contact to the base of the robot [
43] and
u is the control input.
The contact forces are calculated using the FT measurement. In this controller, the FT sensor measurements are directly used as feedback since they affect directly the computation of the momentum rate-of-change.
4. Methodology
The improvement in the measurements among the different estimation types is compared among the different kinds of possible calibration datasets to select the best way to improve the FT sensor performance. For comparison, results using the Workbench matrix are included as an estimation type in its own. At a first stage, the different dataset types were compared on their own. To further test the robustness of the in situ estimation, a different set of calibration and validation datasets were collected.
4.1. Data Sets Used
The validation datasets were taken on two different days, both different from the day the calibration datasets were collected. This was done to test the robustness to possible different ambient conditions. The datasets and their temperatures are showen in
Table 2.
The calibration datasets were grouped into:
noTz, as indicated by name none of the Z-torque datasets were included.
onlySupportLegs, from the balancing datasets, only the support leg was included. All other dataset types were included.
AllGeneral, all dataset types were included.
The reasoning behind this arrangement of datasets is to see what combination of datasets provides the best results. Since it was proven before that Grid and Balancing together improve the calibration, the variables to test are the inclusion of Z-torque and non-support leg datasets.
4.2. Defining Estimation Types
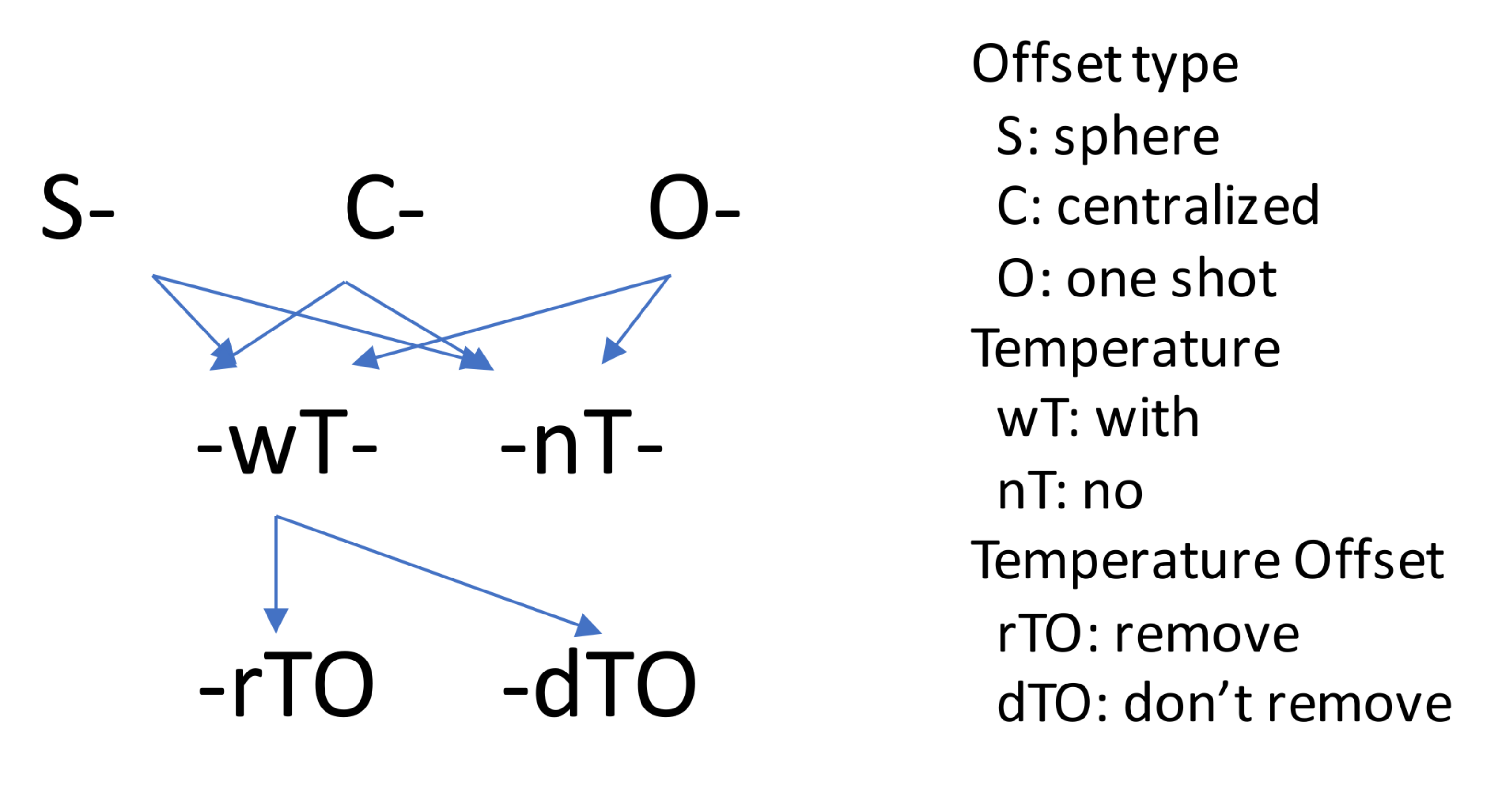
Each strategy of offset estimation is considered an estimation type. Including temperature as a linear variable (wT) or not (nT) in the estimation are also considered different estimation types. If the temperature is considered, it is possible to take the first value as an offset (rTO) or not (dTO). Considering the three offset removal possibilities, adding the temperature as a linear variable to each of them and the temperature offset option results in the following nine estimation types:
Sphere with no temperature (SnTdTO): Refers to the fact that the in situ offset removal is obtained by expecting a sphere in the force space when generating circular motions. No temperature considered.
Centralized with no temperature (CnTdTO): Refers to the centralized offset removal method without considering temperature.
One Shot with no temperature (OnTdTO): Refers to estimate the offset and the calibration matrix at the same time without considering temperature.
Sphere with temperature (SwTdTO): Refers to including temperature into the sphere type. But no temperature offset is considered.
Centralized with temperature (CwTdTO): Refers to including the temperature into the centralized type. But no temperature offset is considered.
One Shot with no temperature (OwTdTO): Refers to estimate the offset and the calibration matrix at the same time considering temperature. But no temperature offset is considered.
Sphere with temperature (SwTrTO): Refers to including temperature into the sphere type. Removing temperature offset.
Centralized with temperature (CwTrTO): Refers to including the temperature into the centralized type. Removing temperature offset.
One Shot with no temperature (OwTrTO): Refers to estimate the offset and the calibration matrix at the same time considering temperature. Removing temperature offset.
The logic behind the estimation type names can be seen in
Figure 4.
4.3. Evaluation Description
The evaluation could be roughly divided in three parts: one to observe the results of each estimation type, another to check the expected improvement on the robot of the generated calibration matrices and a third to verify the impact of using the contributions in a real robot. The sensor to calibrate is located near the hip of the left leg of an iCub robot.
4.3.1. Estimation Type Validation
To understand better the behavior of the estimation types three comparisons are done. The first uses the mean square error (MSE) calculated between the force-torque data using the new calibration matrix and the model-based estimated data. A lower value would indicate a better fitting of the data. Mean Square Error (MSE) of each axis is calculated as follows:
where
is the 6D force reference vector and
is the 6D force vector obtained using the estimated calibration matrix of each estimation type. A second way is to compute the mean of the absolute value of the difference between matrices. This is to get a general idea of how much the calibration matrices differ one from the other. The third way is looking at the offset values. This is to see how the different estimation types affect the estimation of the offset. Although there is no ground truth for the offset to serve as a comparison, similarity in the offset values might indicate a general idea of what the true offset might be.
4.3.2. External/Contact Force Estimation Validation
The selection of the best calibration matrix is done using the contact force validation described in a previous work [
11]. It emulates the contact force estimation algorithm in an offline environment. This form of evaluation permits to check the performance of the mean value of magnitude of the force or the value of each axis over a set of validation experiments. This is relevant since there is no guarantee that a
value or the same type of estimation gives the best results in all axes. The reason is that each axis can be seen as a separate problem.
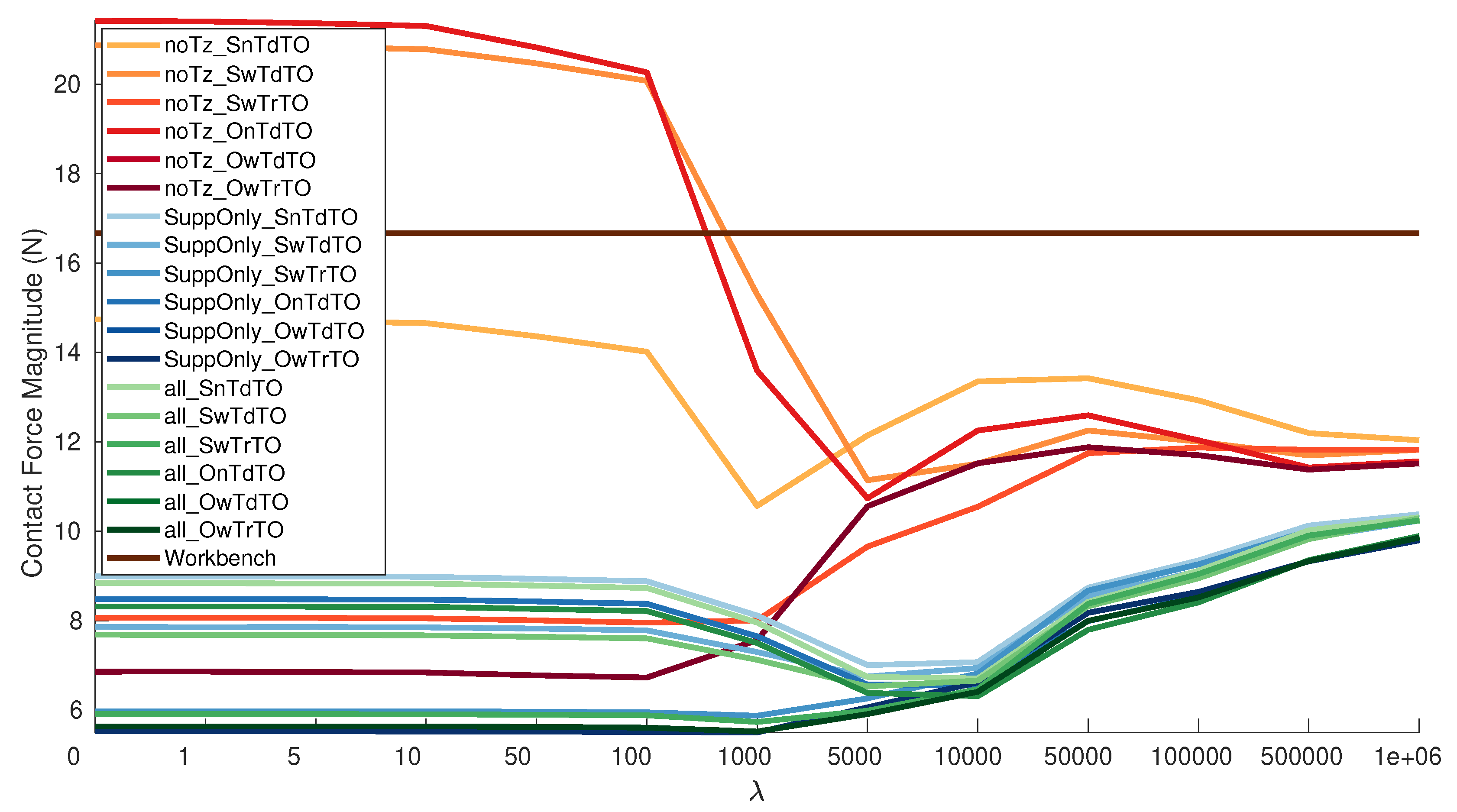
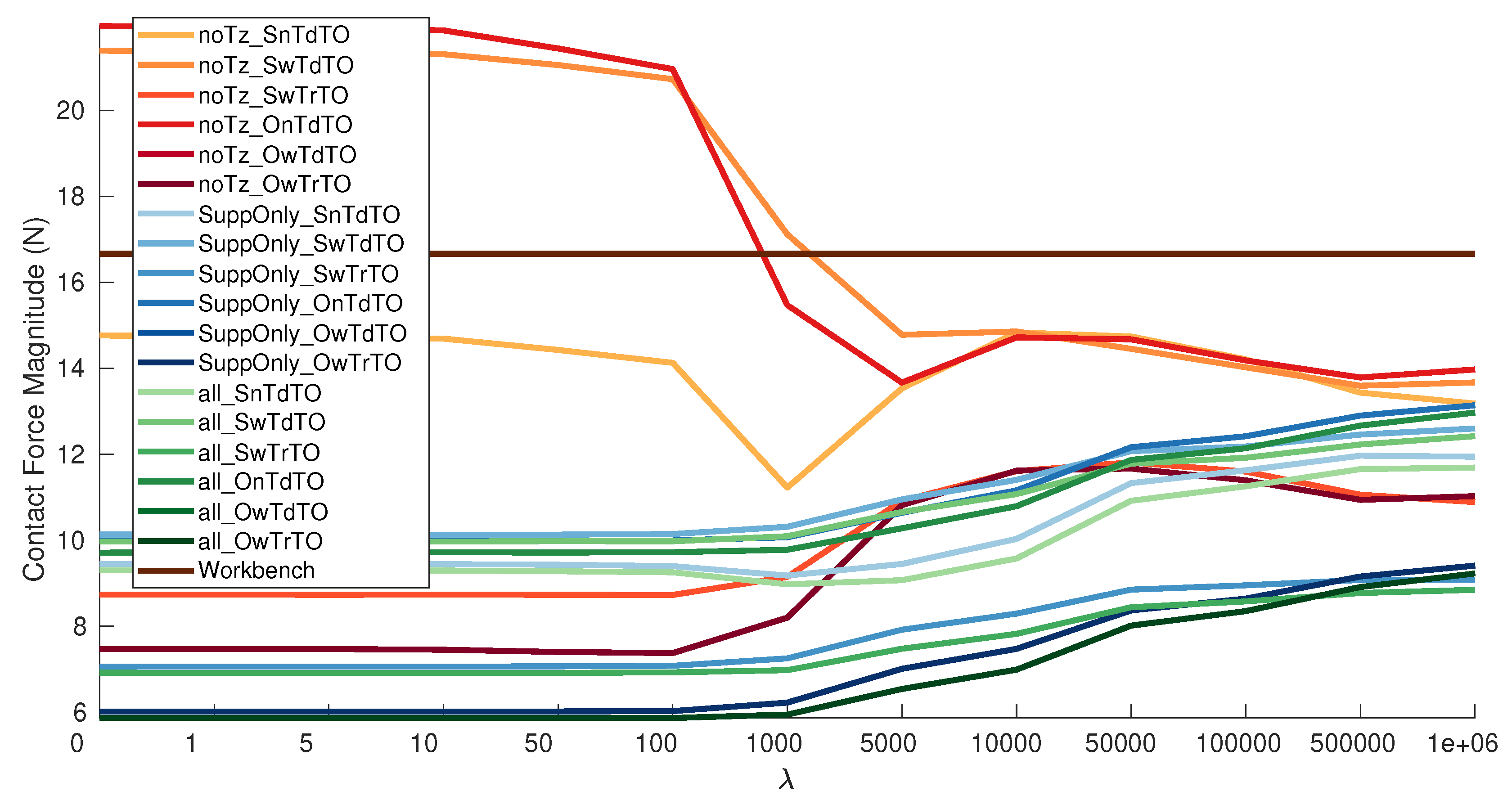
The values used are: [0, 1, 5, 10, 50, 100, 1000, 5000, 10,000, 50,000, 100,000, 500,000, 1,000,000]. The values where selected to span a reasonable range based on the tests to make C converge to , which happened when . The validation is performed on each combination of calibration dataset (3), estimation type (9), and value (13). In total 352 calibration matrices are evaluated counting the Workbench matrix.
4.3.3. Impact on Robot Behavior Evaluation
In most cases the dynamic behaviors of iCub are obtained through high-level controllers. They contain many tuning parameters that affect the behavior of the robot. The measurements of the sensor are used mainly in an indirect way by the high-level controllers. Therefore, finding quantitative measures of the improvement in the dynamic motions of the iCub caused by the in situ calibrated sensor is a challenging. Nonetheless, from the uses of the FT sensor on iCub, three quantitative methods were used:
Contact force values when switching contact.
Accepted gains values used in the low-level controller.
Simultaneous online comparison of force torque measurements performance using different offsets.
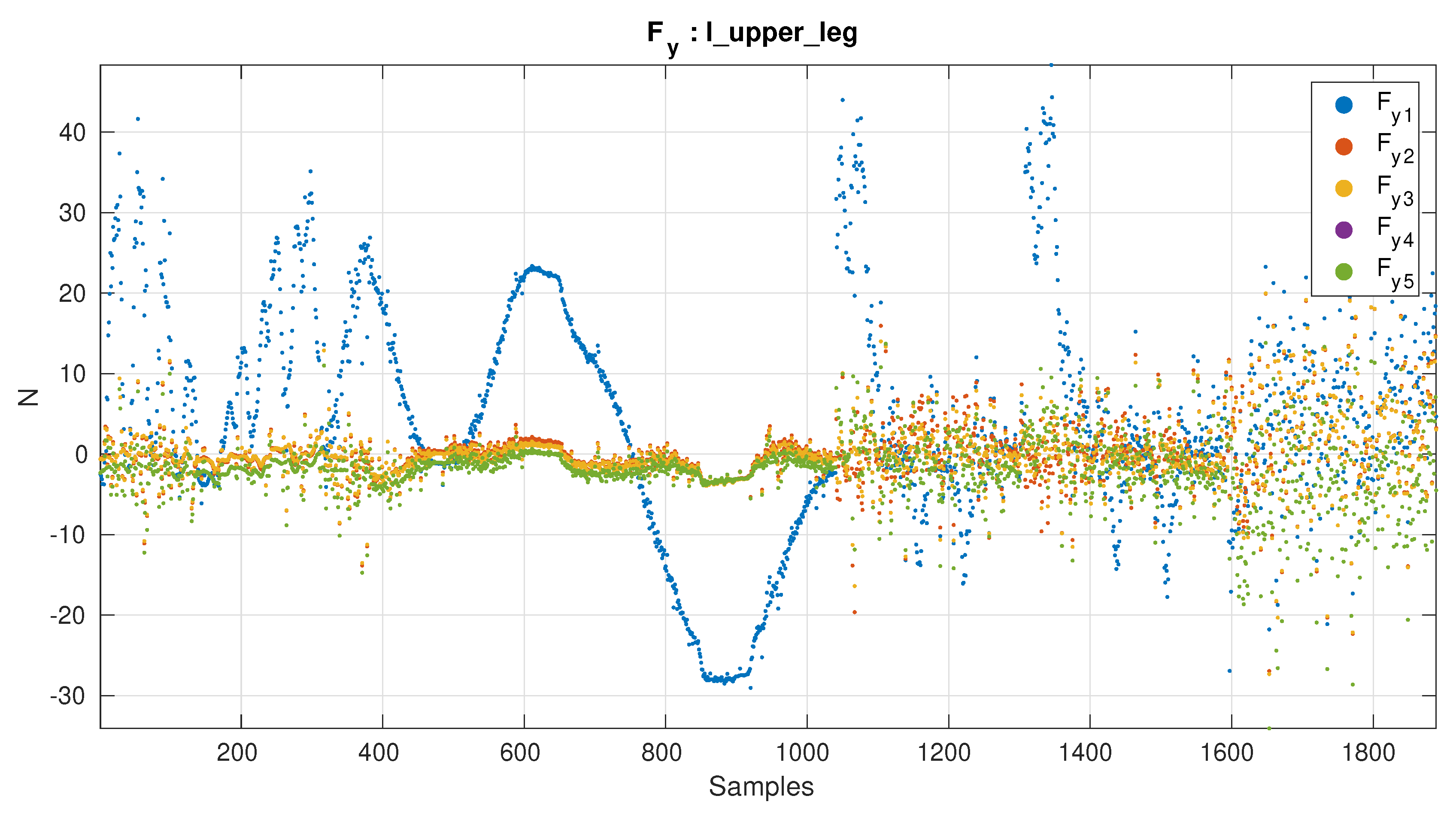
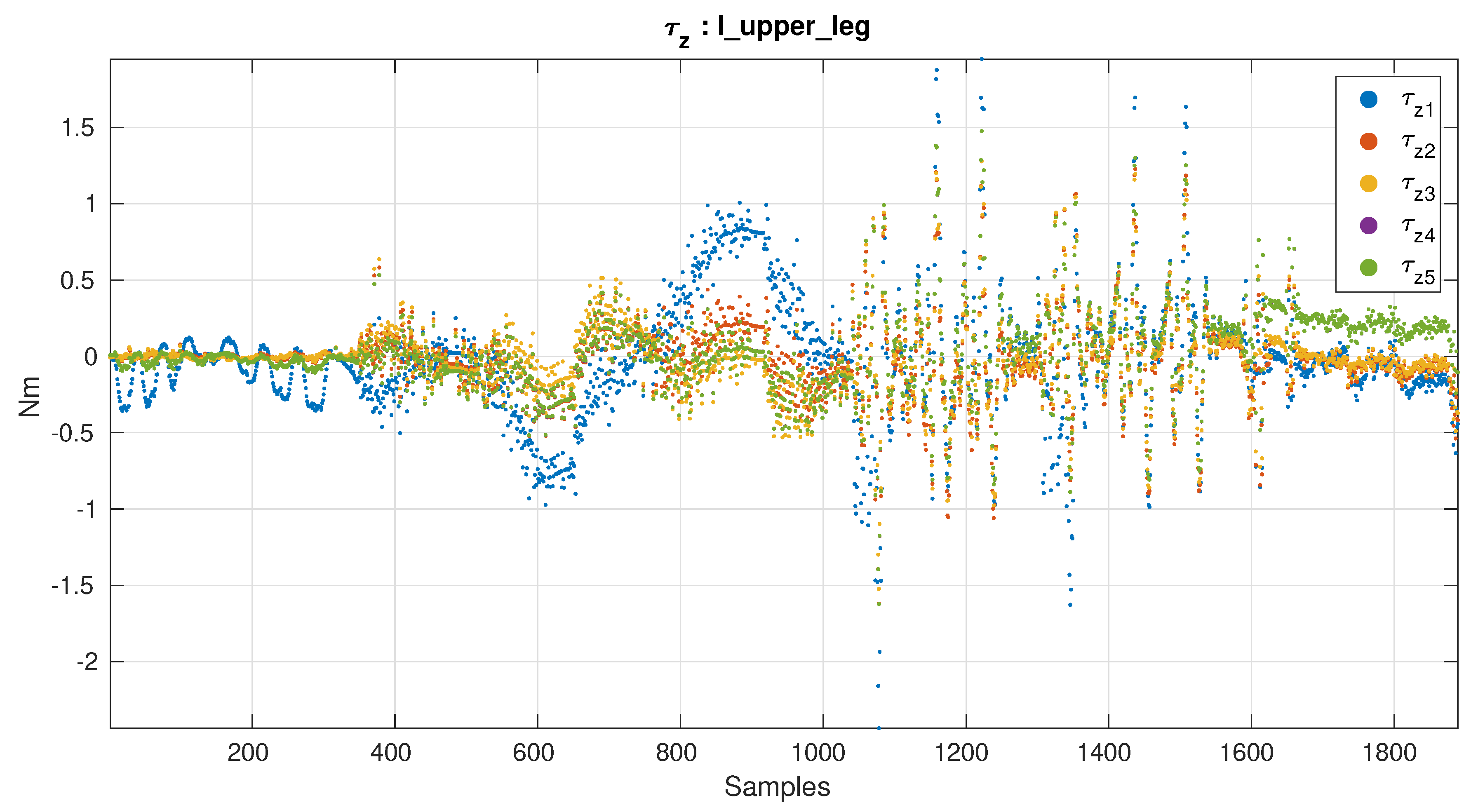
Contact force values when switching contact
The test performed consist in switching from single support to double support.
If the offset is calculated with the robot standing on one foot the sequence is:
Instead if the offset is calculated with the robot in the air the sequence is:
Since the robot is standing on flat ground it is expected that the only force acting on the robot feet is mass on the z axis. With no other force acting on the robot the forces in x and y should cancel each other in double support or be 0 when on single support. With this as a ground truth, is possible to evaluate the estimated contact forces at the feet when switching.
Accepted gains values used in the low-level controller
The robot was tuned to the maximum gain value in which the robot is able to perform the balancing demo in a satisfactory way. Beyond a certain value, the robot is observed to vibrate and fall. For this test, the high level gains of the controller are kept the same and only the low-level controller gains are changed. A higher gain value indicates that the robot is able to rely more on the measurements of the sensor as feedback. Thus, being able to use higher gains is better if it does not introduce unstable behaviors.
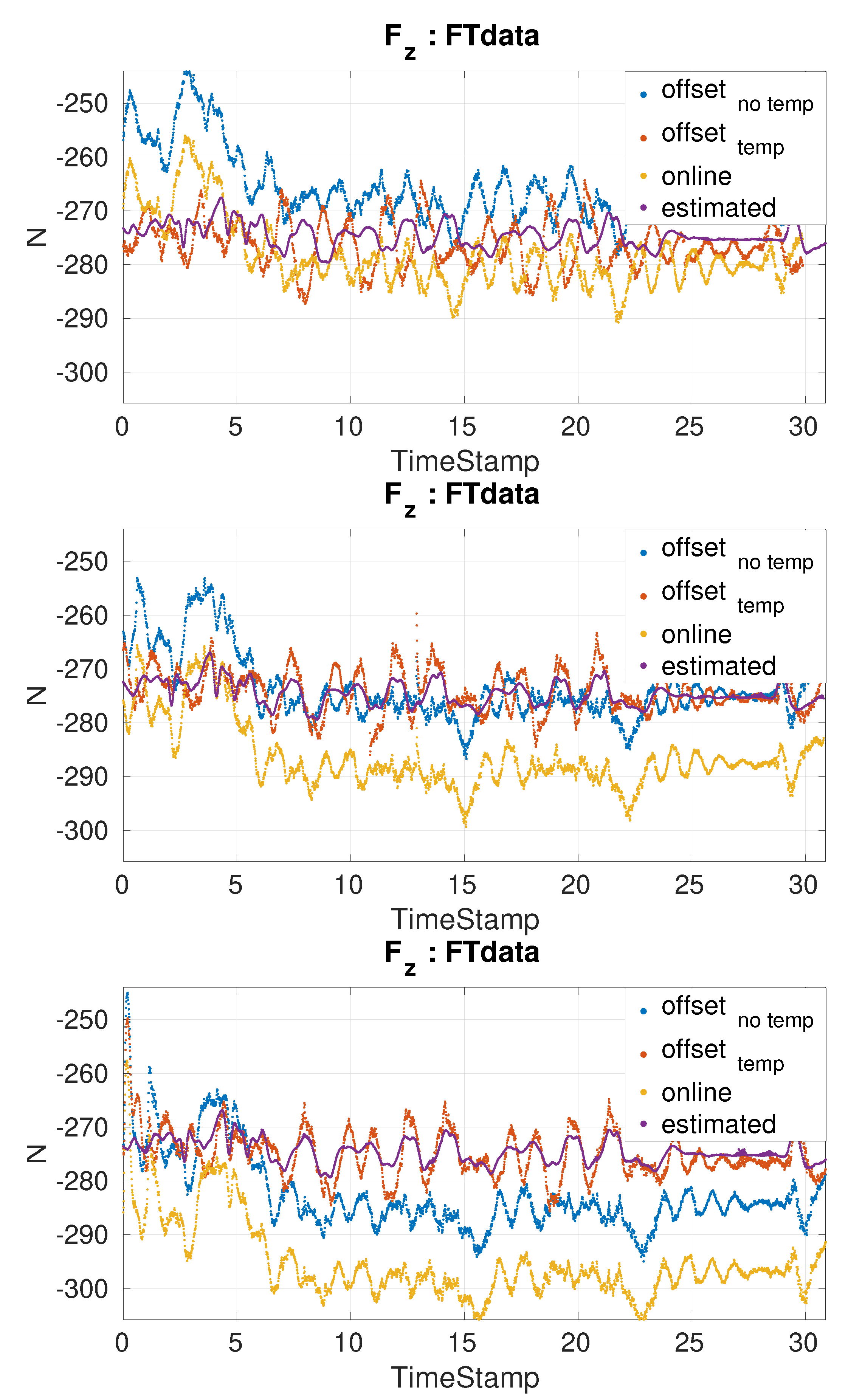
Simultaneous online comparison of force torque measurements performance using different offsets
For this experiment the offsets used were estimated with a month difference with respect to the experiment date. The comparison between the expected FT value and the actual value obtained after applying both the offset and the secondary calibration matrix correction. Three different offsets where used:
offset: is the estimated offset from the best calibration matrix without temperature one month before experiments.
offset: is the estimated offset from the best calibration matrix using temperature one month before experiments.
online: is the offset calculated on the online on the robot the day of the experiment when the robot was just turned on. The temperature was 26 . It uses the same secondary calibration matrix as the one from offset.
Three simultaneous estimation applications are launched. One for each type of offset used. The ground truth is calculated offline in the sections of the experiments in which there was only one contact with the environment. Multiple experiments were performed on the robot in the span of three hours to allow the FT sensors to heat up.
6. Conclusions
The developed algorithm has been proven to improve the measurements of the sensor and the dynamic behavior of a floating base robot. It successfully accounts for temperature drift and can be extended to account for other lineal phenomena, allowing controllers to reliably use the sensor measurements as feedback, be it directly or indirectly.
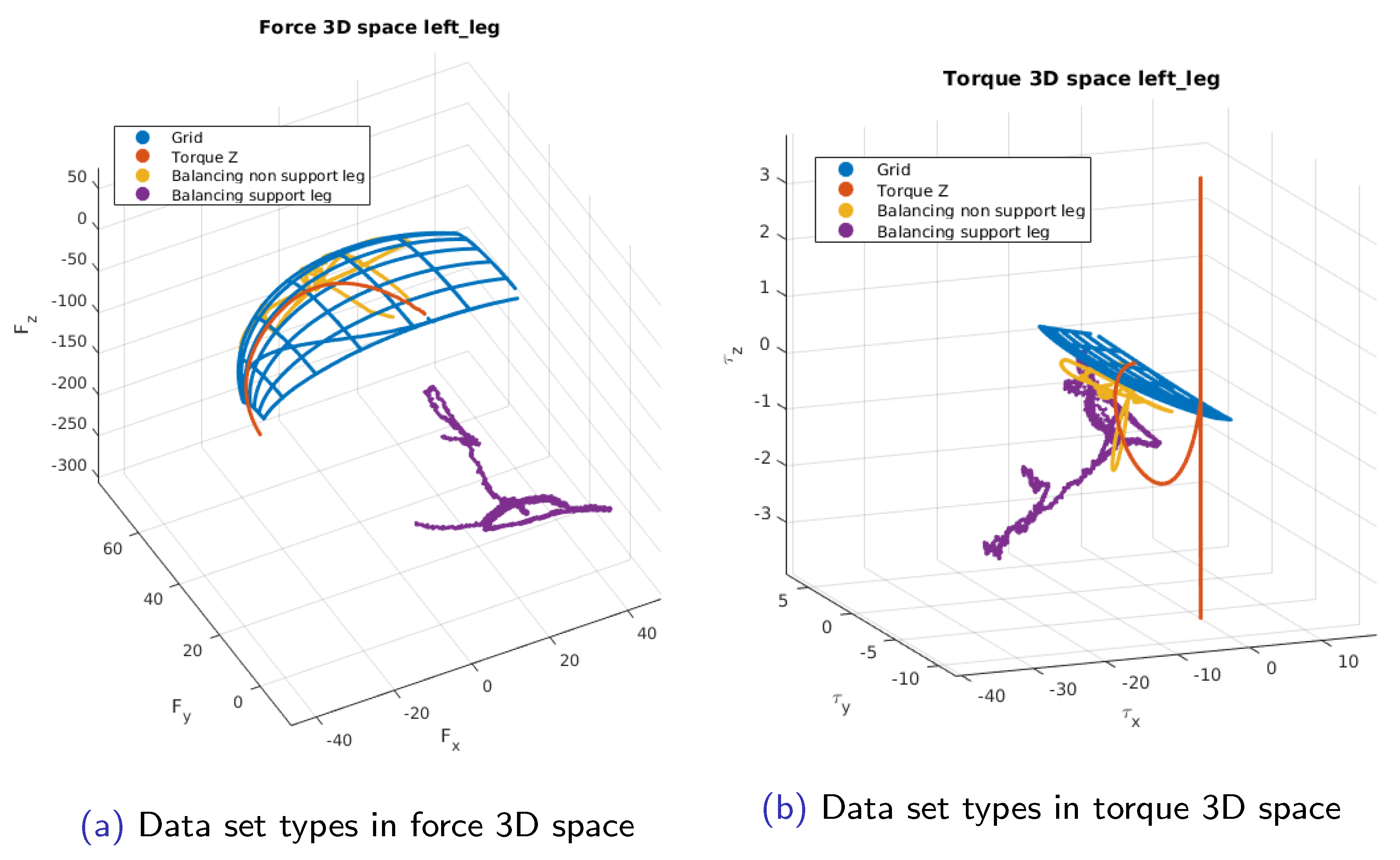
The new offset formulation is shown to give identical results as the centralized offset with the added benefit that the offset and calibration matrix are estimated simultaneously. The graphic representation of the sensor excitation in the 3D force and torque space has proven useful to provide intuitive insight into the comprehensive excitation of the sensor. In the
Figure 3, it is evident to see that Z-Torque type of dataset provides new information. It is also visible that the Balancing Non-Support Leg gives redundant information. This was confirmed when looking at the results grouping by a calibration dataset. Considering it is possible to generate random movements of the robot and then evaluate if the dataset provides new useful data, this avoids the need to carefully design the joint trajectories for the calibration data. Since the approach is model-based, robot simulations can easily provide this graphic sensor excitation representation. The use of the secondary matrix allows a simple non-intrusive way to provide the improved measurements to the robot. It was shown that by adding the temperature we are able to use the offset of the sensors as a constant. This proves that the drift is mainly generated by the temperature. Furthermore, using offsets that were estimated a month in advance proves the robustness of the estimation of both calibration matrix and offset. It also demonstrates a higher reliability of the sensor measurements. The possibility to use a constant offset eliminates the need to estimate the offset before every experiment. This is especially useful for floating base robots that have a harder time anticipating the exact time of contact. It minimizes the preparation steps for using the robot and allows to do longer experiments without the need to stop. The improvement in robot performance is clear from the contact force coherence when switching or the fact that low and high-level controllers are able to perform better when using the FT measurements after in situ calibration.
The relationship between the regularization parameter and performance is clearly shown. This may allow to further refine and guide the selection of regularization parameters. The comparison with previous results suggests that the relevance and impact of each offset estimation strategy may be linked to the amount of data available. For small amounts of data, the physical assumption gives the highest improvements. With bigger amounts of data having no assumptions to estimate more accurately the calibration. The loss of effectiveness when using the physical assumption could be related to the fact that it does not consider temperature at all for offset estimation.
As future work, ways to account for nonlinearities will be explored. Studying the dynamical response of the sensor is also interesting and might provide further improvements in the performance of the sensor.