A Bioinspired Twin Inverted Multiscale Matched Filtering Method for Detecting an Underwater Moving Target in a Reverberant Environment
Abstract
1. Introduction
2. Bioinspired Waveform Design
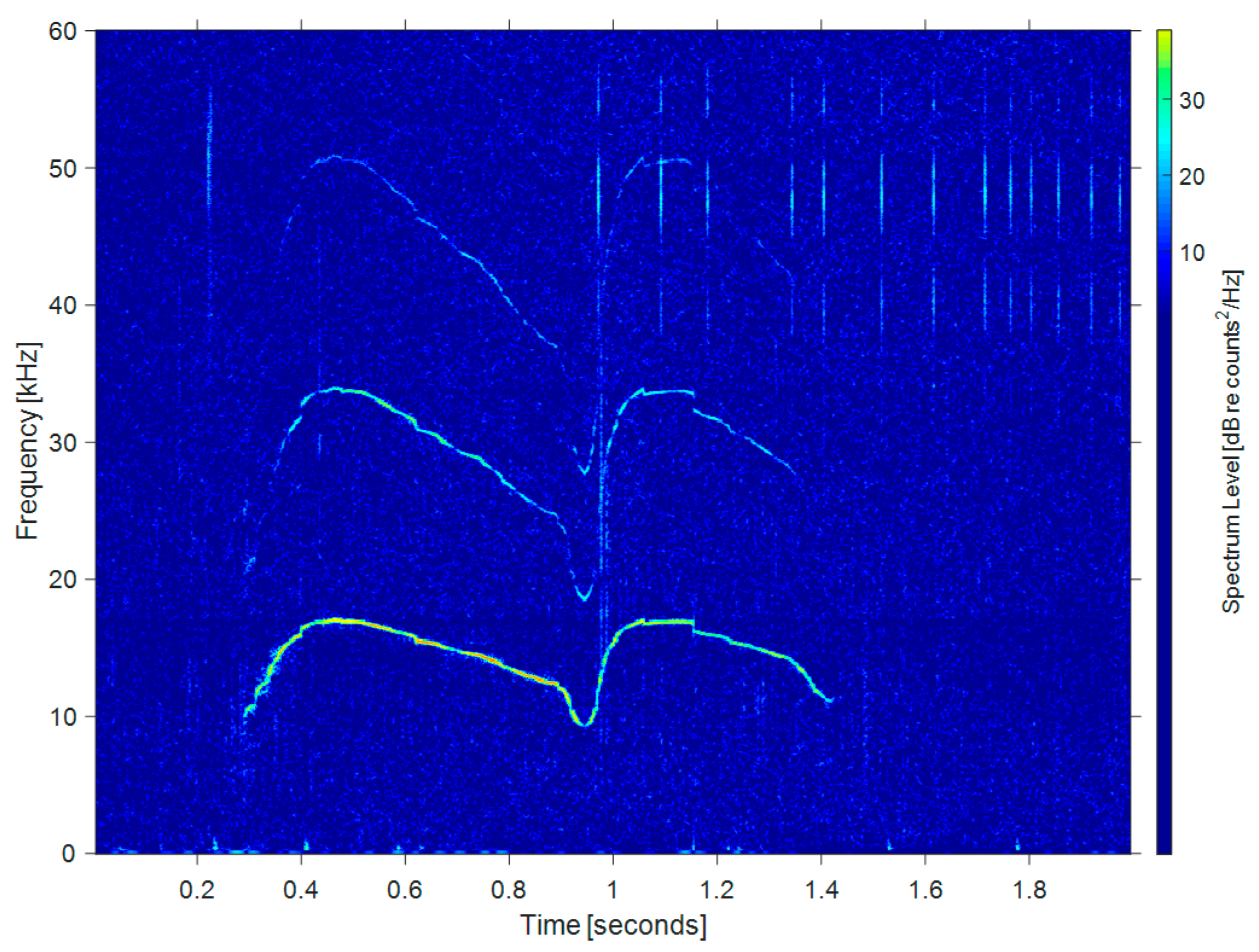
2.1. Mammal Sonar Signal Analysis
2.1.1. Waveform
2.1.2. Harmonics
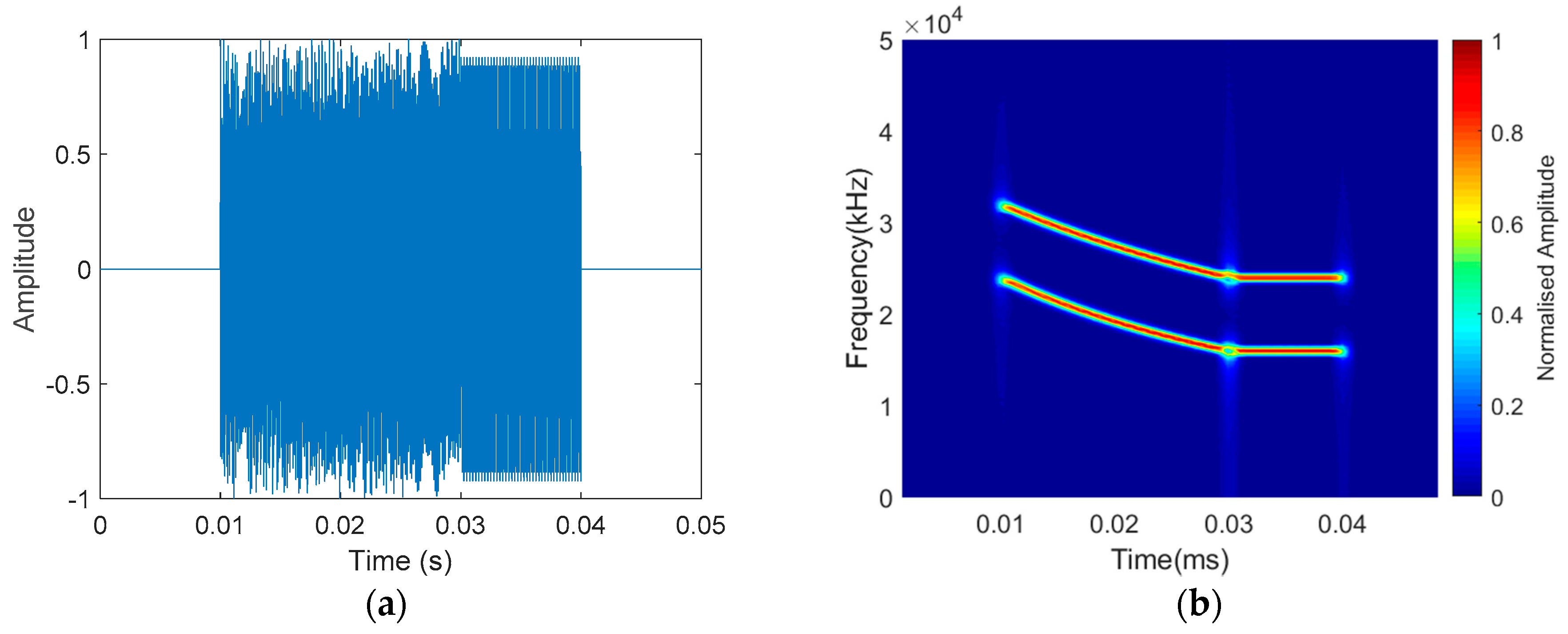
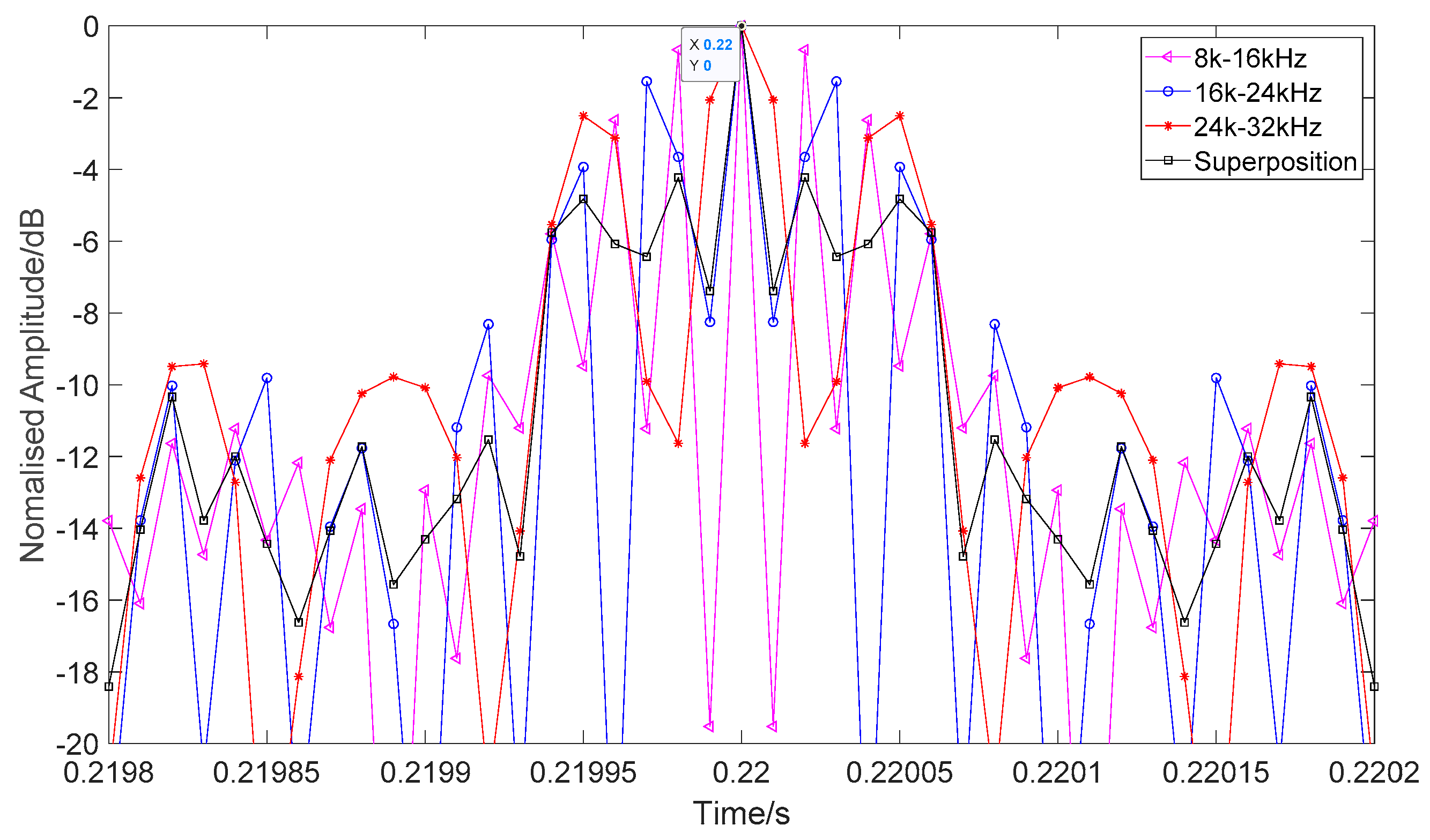
2.2. HFM-CW Multiharmonic Waveform Design
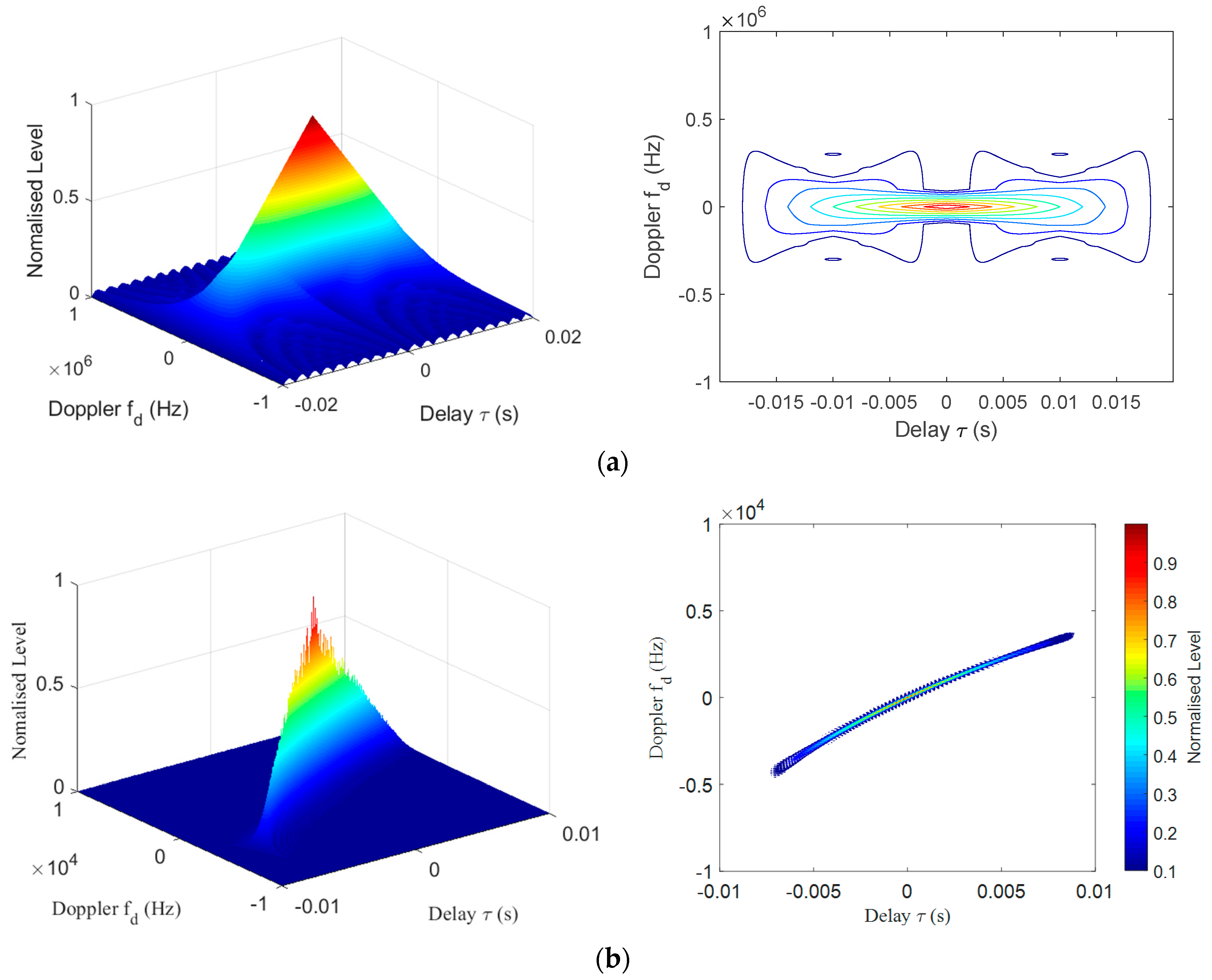
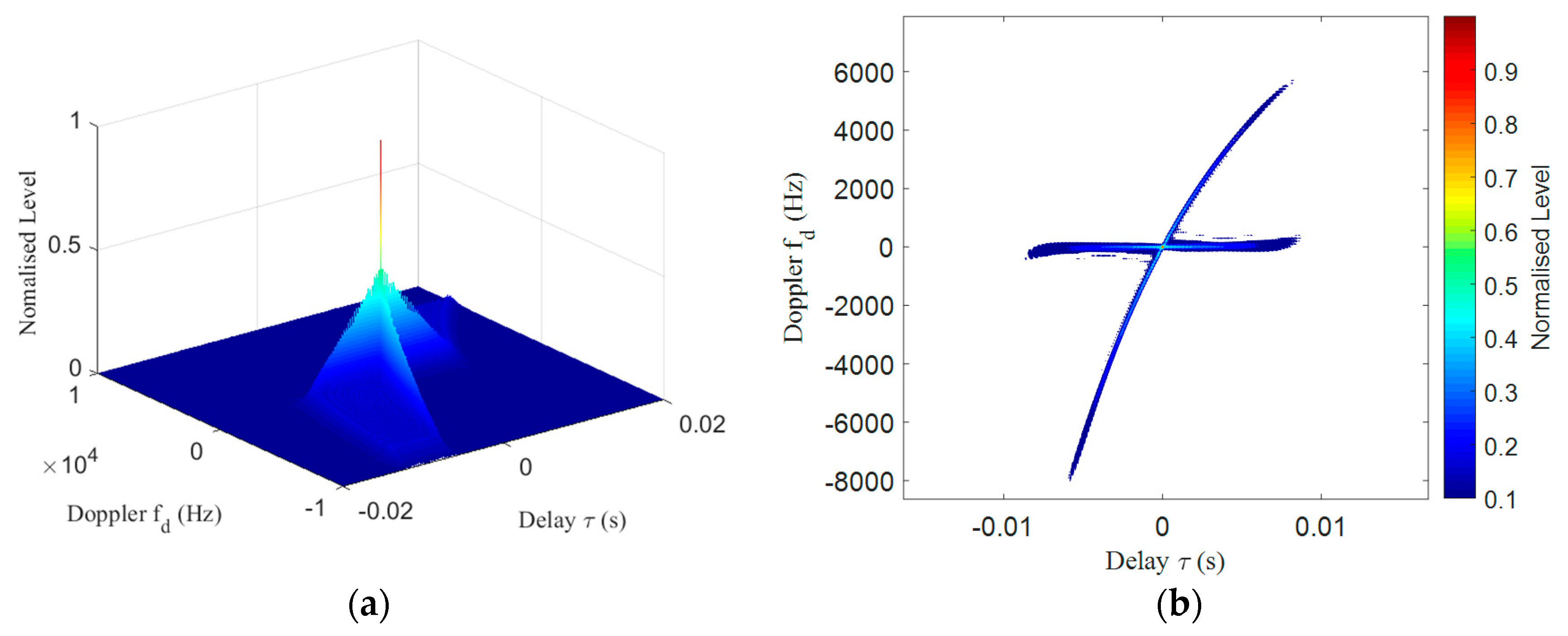
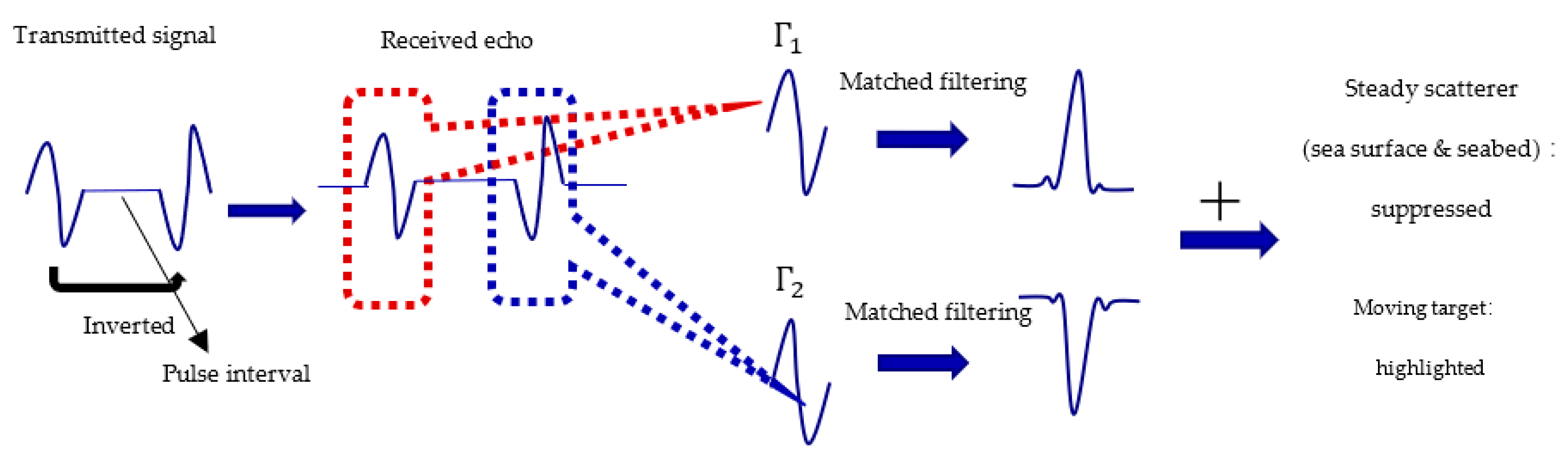
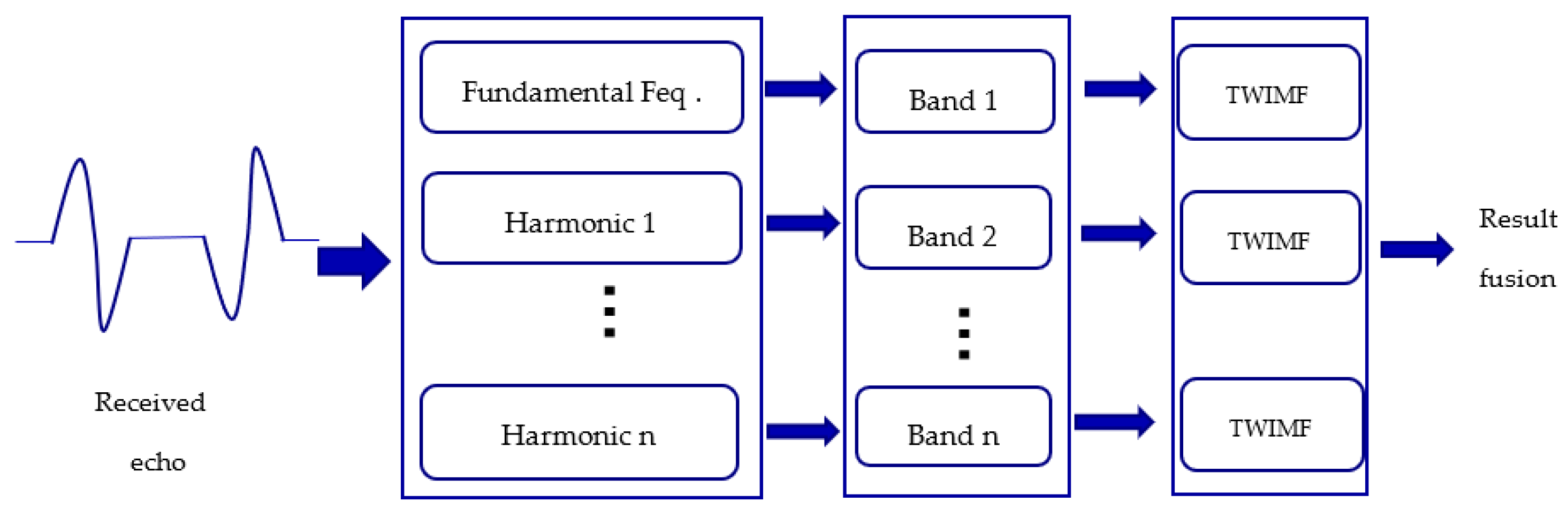
3. Twin Inverted Multiscale Matched Filtering
3.1. Twin Inverted Matched Filtering
3.2. Multiscale Matched Filtering
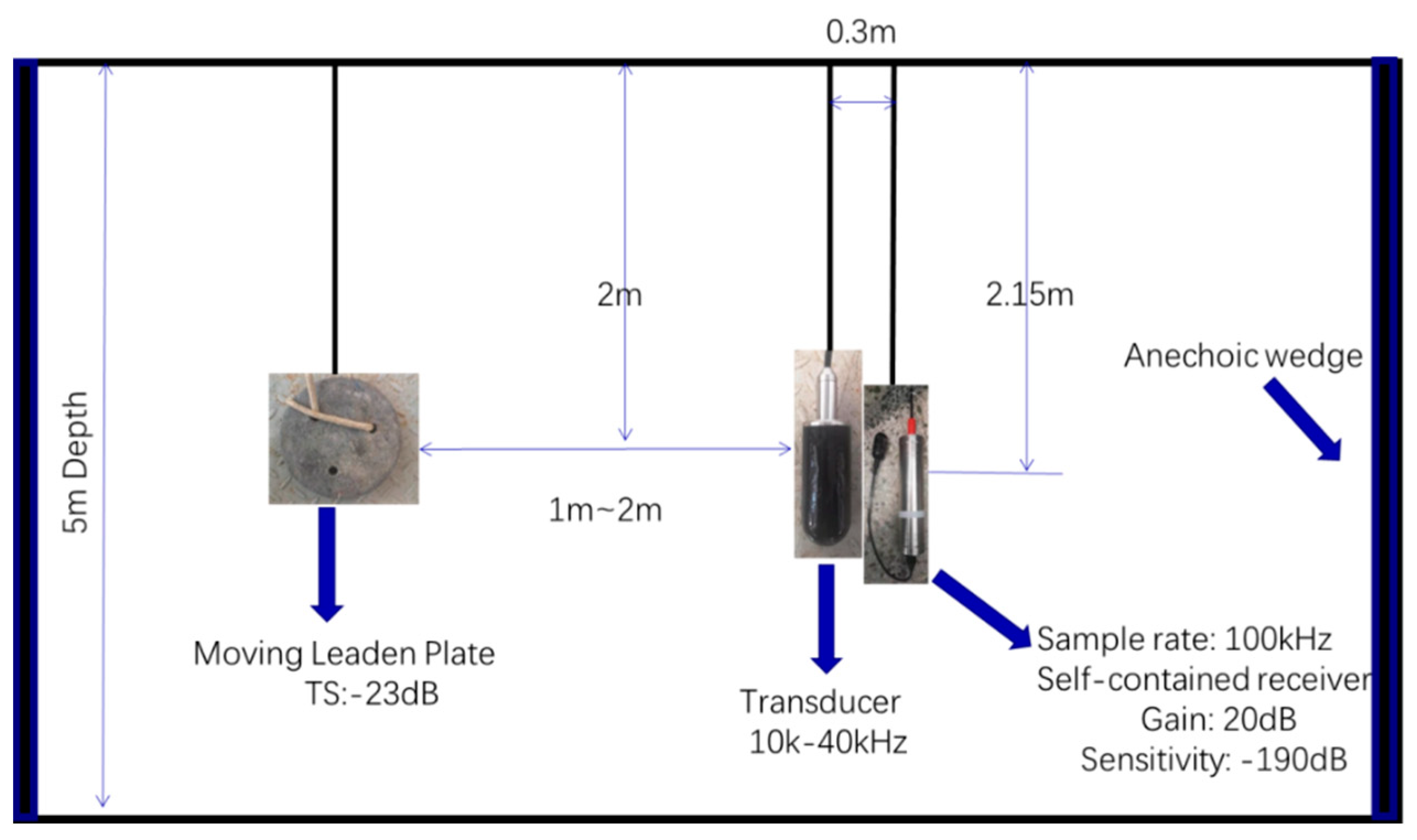
4. Experiment Results and Discussion
4.1. Experiment Arrangement and Pre-Experiment Test
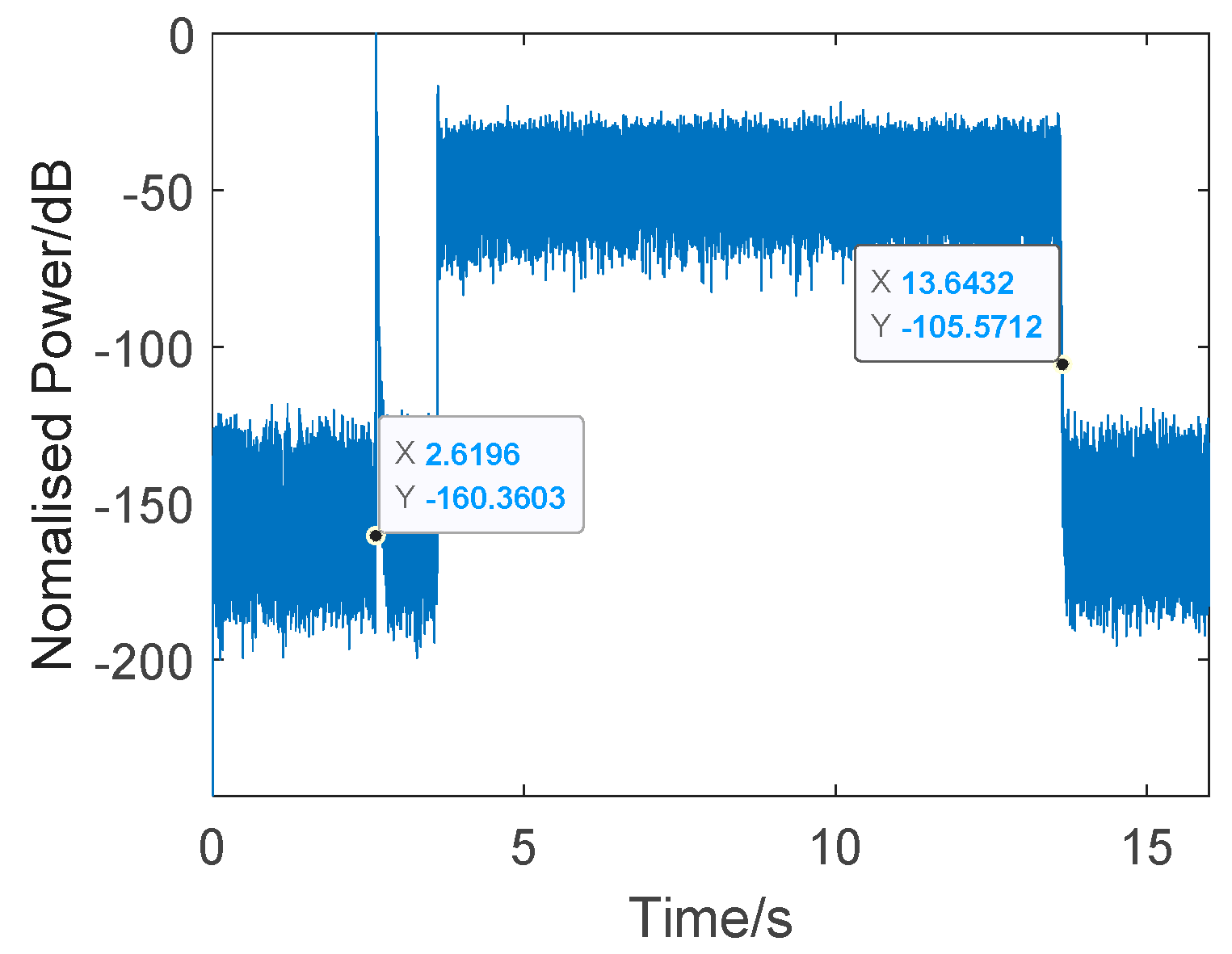
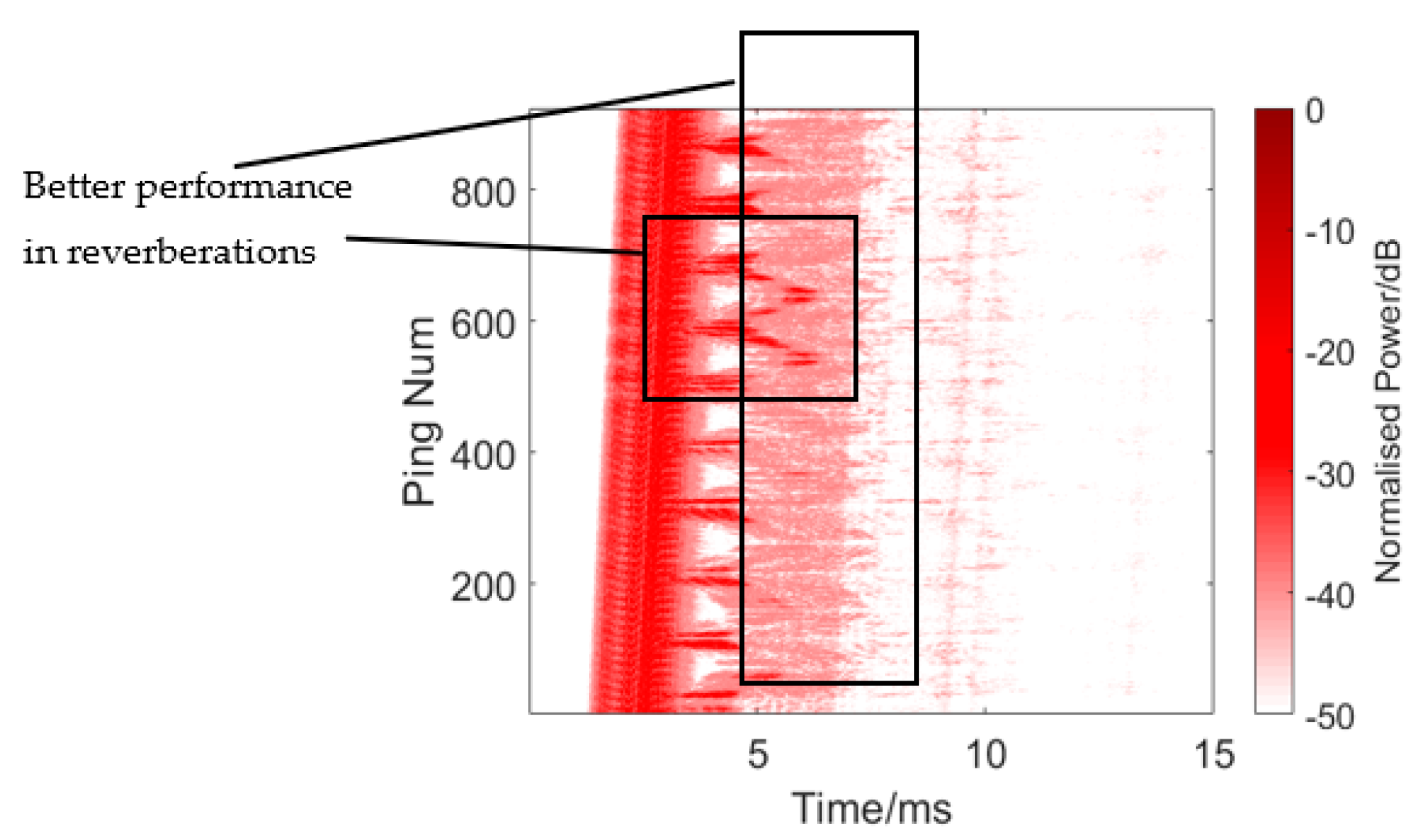
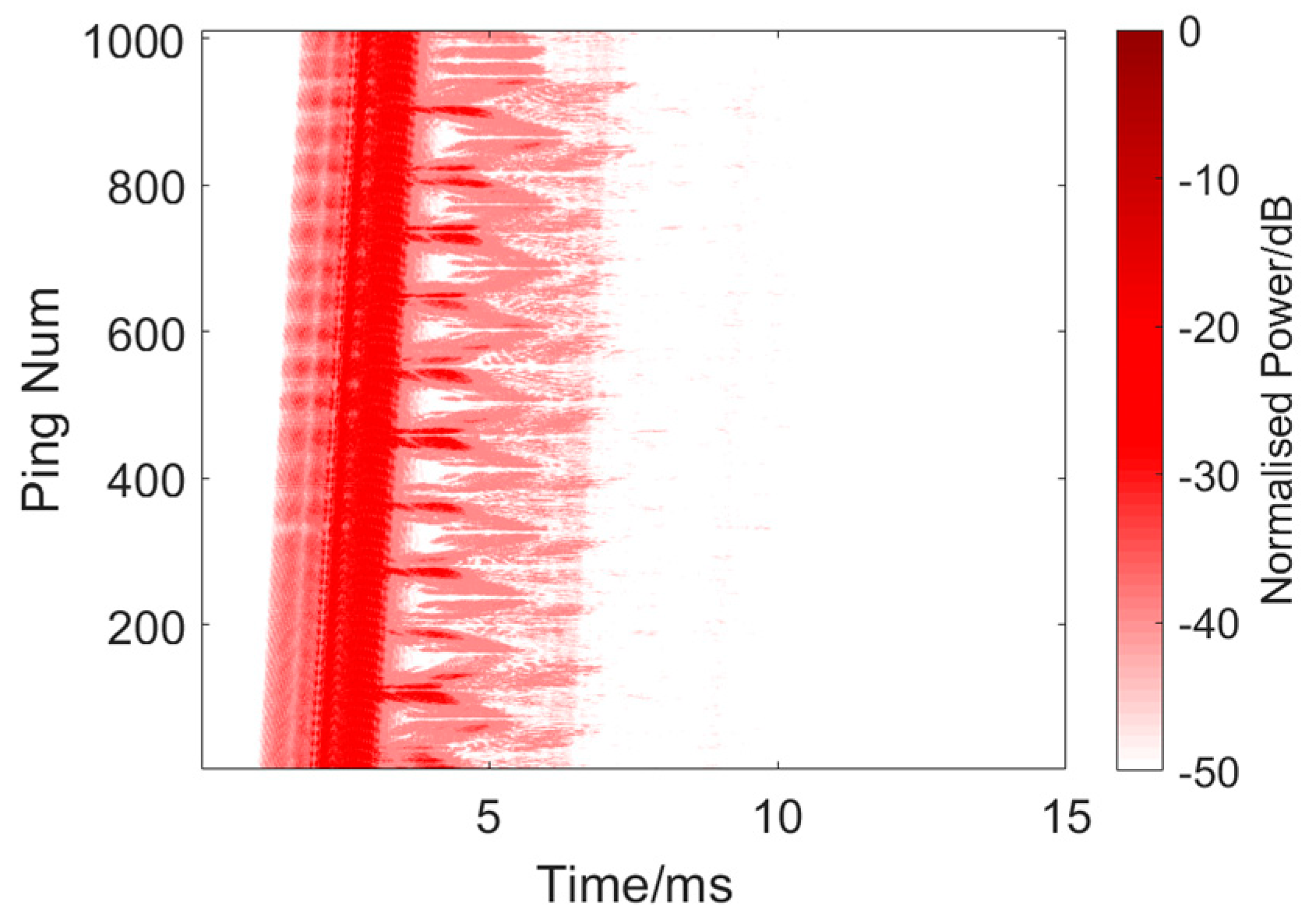
4.2. Detection Experiment Result
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; Peninsula Publishing: Newport Beach, CA, USA, 2013; ISBN 978-0932146625. [Google Scholar]
- Parker, J.; Tsagkogeorga, G.; Cotton, J.; Liu, Y.; Provero, P.; Stupka, E.; Rossiter, J. Genome-wide signatures of convergent evolution in echolocating mammals. Nature 2013, 502, 228–231. [Google Scholar] [CrossRef] [PubMed]
- Jones, G. Molecular evolution: Gene convergence in echolocating mammals. Curr. Biol. 2010, 20, R62–R64. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, Y.; Liu, Z.; Shi, P.; Zhang, J. The hearing gene Prestin unites echolocating bats and whales. Curr. Biol. 2010, 20, R55–R56. [Google Scholar] [CrossRef] [PubMed]
- Surlykke, A.; Nachtigall, P.; Fay, R.; Popper, A. Biosonar; Springer: Berlin, Germany, 2014; ISBN 978-1-4614-9145-3. [Google Scholar]
- Jiang, J.; Wang, X.; Duan, F.; Li, C.; Fu, X.; Huang, T.; Bu, L.; Ma, L.; Sun, Z. Bio-Inspired Covert Active Sonar Strategy. Sensors 2018, 18, 2436. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, L.; Zou, L. Whale-inspired sonar in covert detection. In Proceedings of the 2016 IEEE/OES China Ocean Acoustics (COA), Harbin, China, 9–11 January 2016. [Google Scholar]
- Capus, C.; Pailhas, Y.; Brown, K.; David, L. Bio-inspired wideband sonar signals based on observations of the bottlenose dolphin (Tursiops truncatus). J. Acoust. Soc. Am. 2007, 121, 594–604. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.; Phillips, M.; Bauer, E.; Moore, P.; Houser, S. Application of the Biosonar Measurement Tool (BMT) and Instrumented Mine Simulators (IMS) to exploration of dolphin echolocation during free-swimming, bottom-object searches. In Proceedings of the 2003 IEEE OCEANS, San Diego, CA, USA, 22–26 September 2003. [Google Scholar]
- Paihas, Y.; Capus, C.; Brown, K.; David, L. Benefits of dolphin inspired sonar for underwater object identification. In Proceedings of the Conference on Biomimetic and Biohybrid Systems, London, UK, 29 July–2 August 2013. [Google Scholar]
- Houser, D.; Martin, S.; Phillips, M.; Bauer, E.; Herrin, T.; Moore, P. Signal processing applied to the dolphin-based sonar system. In Proceedings of the 2003 IEEE OCEANS, San Diego, CA, USA, 22–26 September 2003. [Google Scholar]
- Friedlaender, A.; Bocconcelli, A.; Wiley, D.; Cholewiak, D.; Ware, C.; Weinrich, M.; Thompson, M. Underwater components of humpback whale bubble-net feeding behavior. Behaviour 2011, 148, 575–602. [Google Scholar] [CrossRef]
- Leighton, T.; Finfer, D.; Grover, E.; White, P. An acoustical hypothesis for the spiral bubble nets of humpback whales and the implications for whale feeding. Acoust. Bull. 2007, 22, 17–21. [Google Scholar]
- Leighton, T.G.; Finfer, D.C.; White, P.R.; Chua, G.H.; Dix, J.K. Clutter suppression and classification using twin inverted pulse sonar (TWIPS). Proc. R. Soc. A 2010, 466, 3453–3478. [Google Scholar] [CrossRef]
- Leighton, T.G.; Finfer, D.C.; Chua, G.H.; White, P.R. Clutter suppression and classification using twin inverted pulse sonar in ship wakes. J. Acoust. Soc. Am. 2011, 130, 3431–3437. [Google Scholar] [CrossRef] [PubMed]
- Metzner, W. Echolocation Behavior in Bats; Science Progress: Edinburg, TX, USA, 1991; Volume 75, pp. 453–465. [Google Scholar]
- Heffner, R.S.; Koay, G.; Heffner, H.E. Sound localization in common vampire bats: Acuity and use of the binaural time cue by a small mammal. J. Acoust. Soc. Am. 2015, 137, 42–52. [Google Scholar] [CrossRef] [PubMed]
- Bat Ecology and Bioacoustics Lab, University of Bristol. Available online: http://www.bristol.ac.uk/biology/research/behavior/batlab/ (accessed on 20 September 2019).
- Fenton, M.B.; Skowronski, M.D.; McGuire, L.P.; Faure, P.A. Variation in the use of Harmonics in the Calls of Laryngeally Echolocating Bats. Acta Chiropterologica 2011, 13, 169–178. [Google Scholar] [CrossRef]
- Lawrence, B.D.; Simmons, J.A. Measurements of atmospheric attenuation at ultrasonic frequencies and the signifi cance for echolocation by bats. J. Acoust. Soc. Am. 1982, 71, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Holderied, M.W.; Korin, C.; Fenton, M.B.; Parsons, S.; Robinson, S.; Jones, G. Echolocation call intensity in the aerial hawking bat Eptesicus bottae (Vespertilionidae) studied using stereo videogrammetry. J. Exp. Biol. 2005, 208, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Buck, J.R.; Morgenbesser, H.B.; Tyack, P.L. Synthesis and modification of the whistles of the bottlenose dolphin, Tursiops truncates. J. Acoust. Soc. Am. 2000, 108, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Levanon, N.; Mozeson, E. Radar Signals; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 0-471-47378-2. [Google Scholar]
- Sibul, L.H.; Titlebaum, E.L. Volume Properties for the Wideband Ambiguity Function. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 83–87. [Google Scholar] [CrossRef]
- Catipovic, J.; Baggeroer, A.; Von Der Heydt, K.; Koelsch, D. Design and performance analysis of a Digital Acoustic Telemetry System for the short range underwater channel. IEEE J. Ocean. Eng. 1984, 9, 242–252. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical Characterization and Computationally Efficient Modeling of a Class of Underwater Acoustic Communication Channels. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
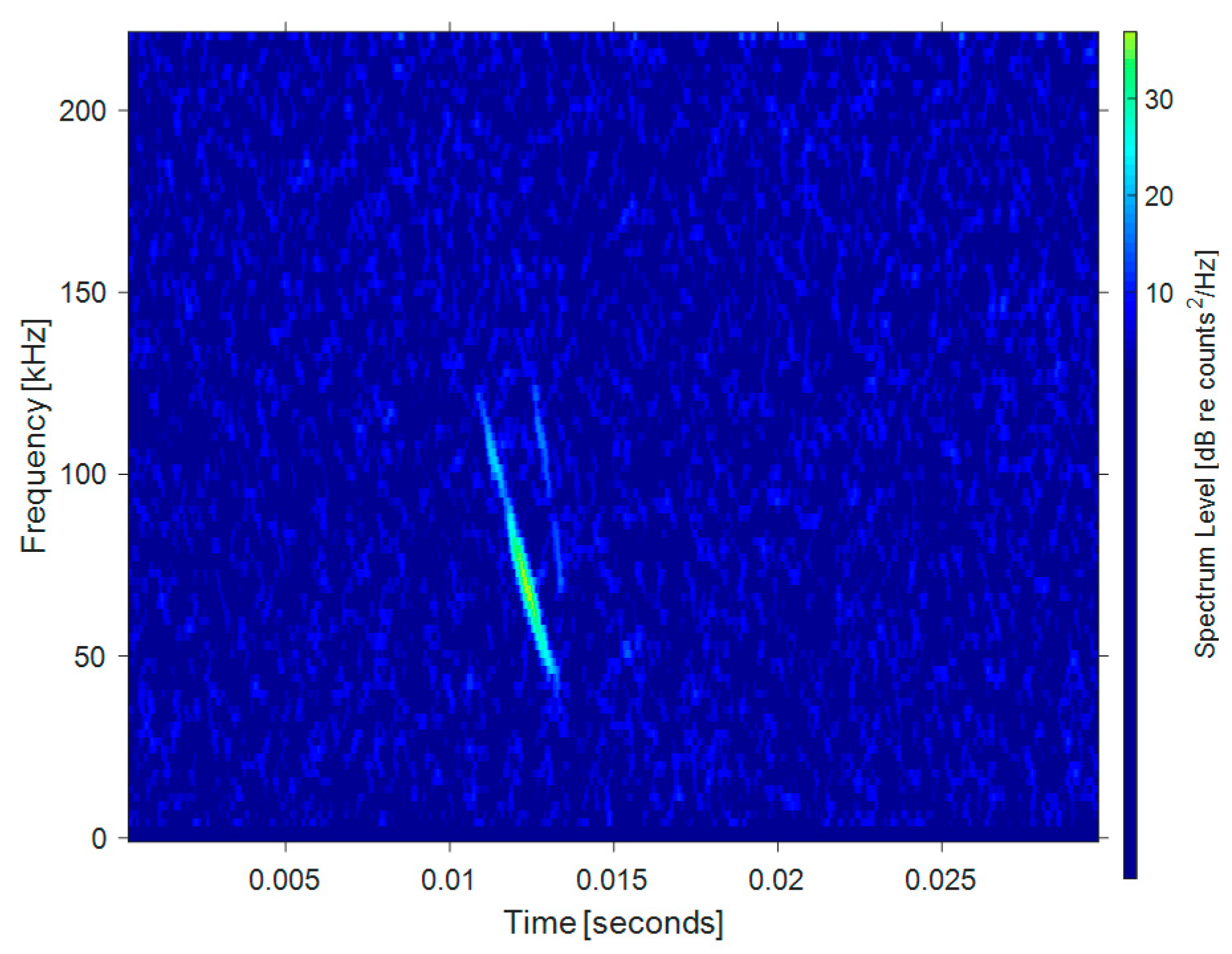
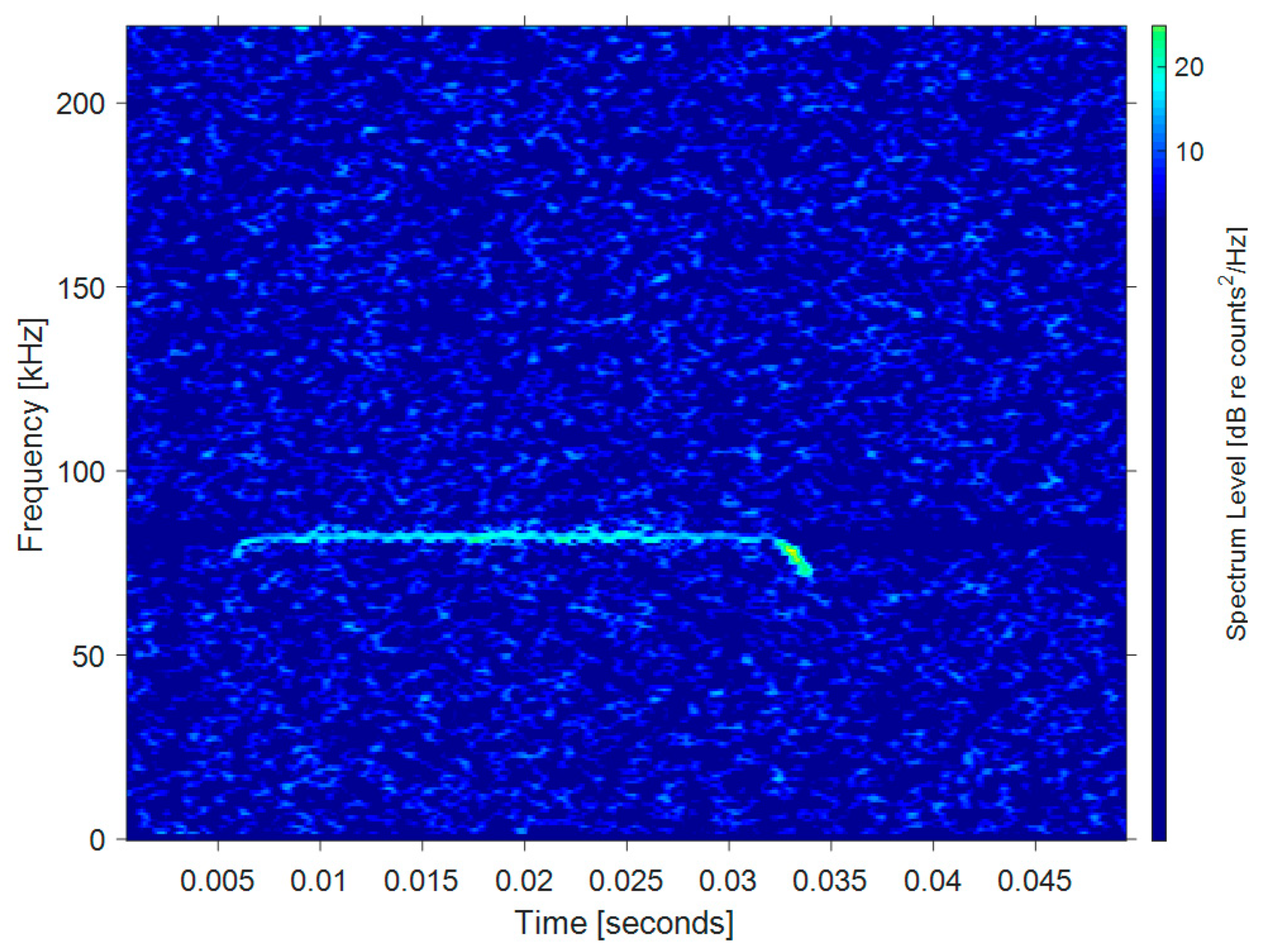
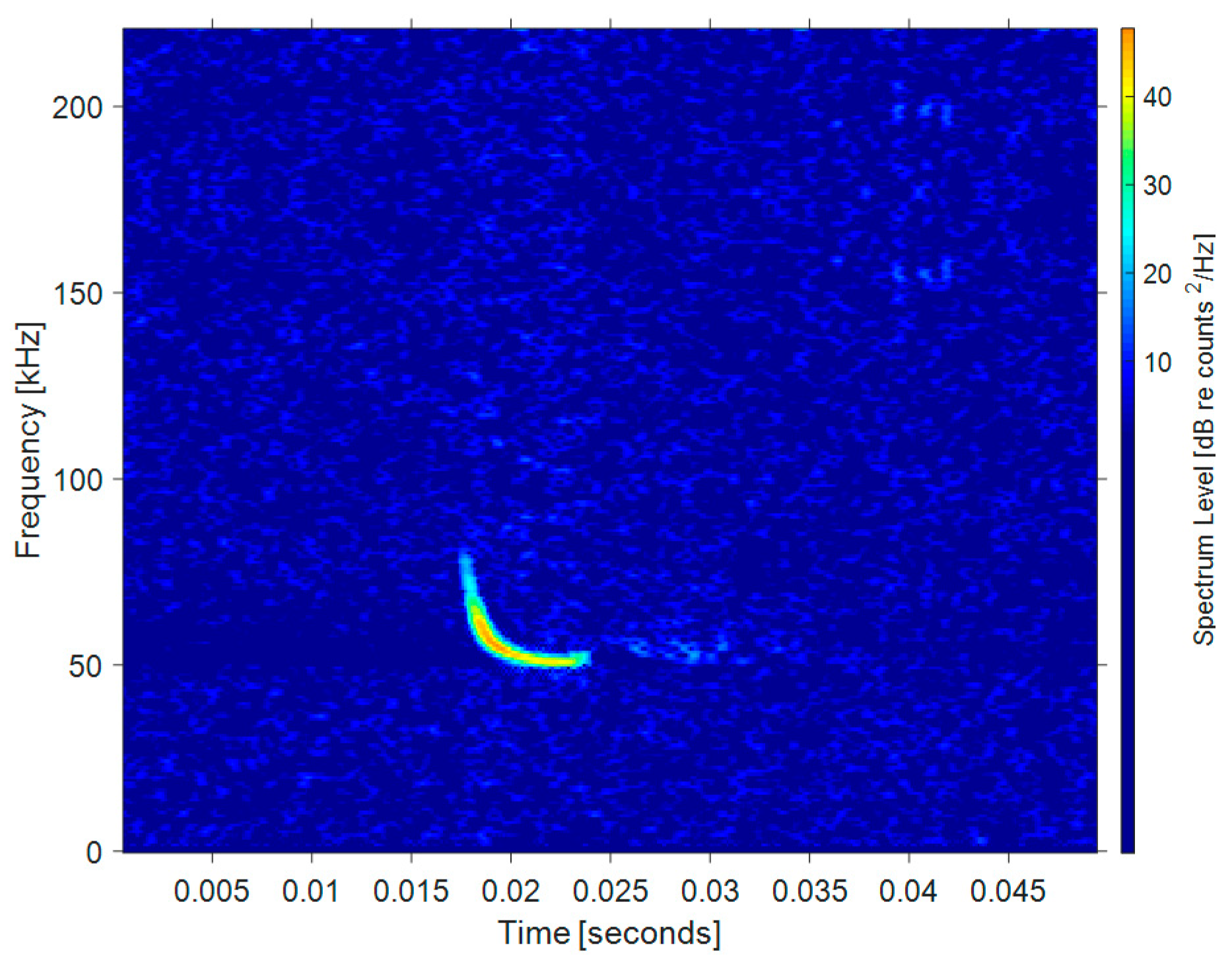
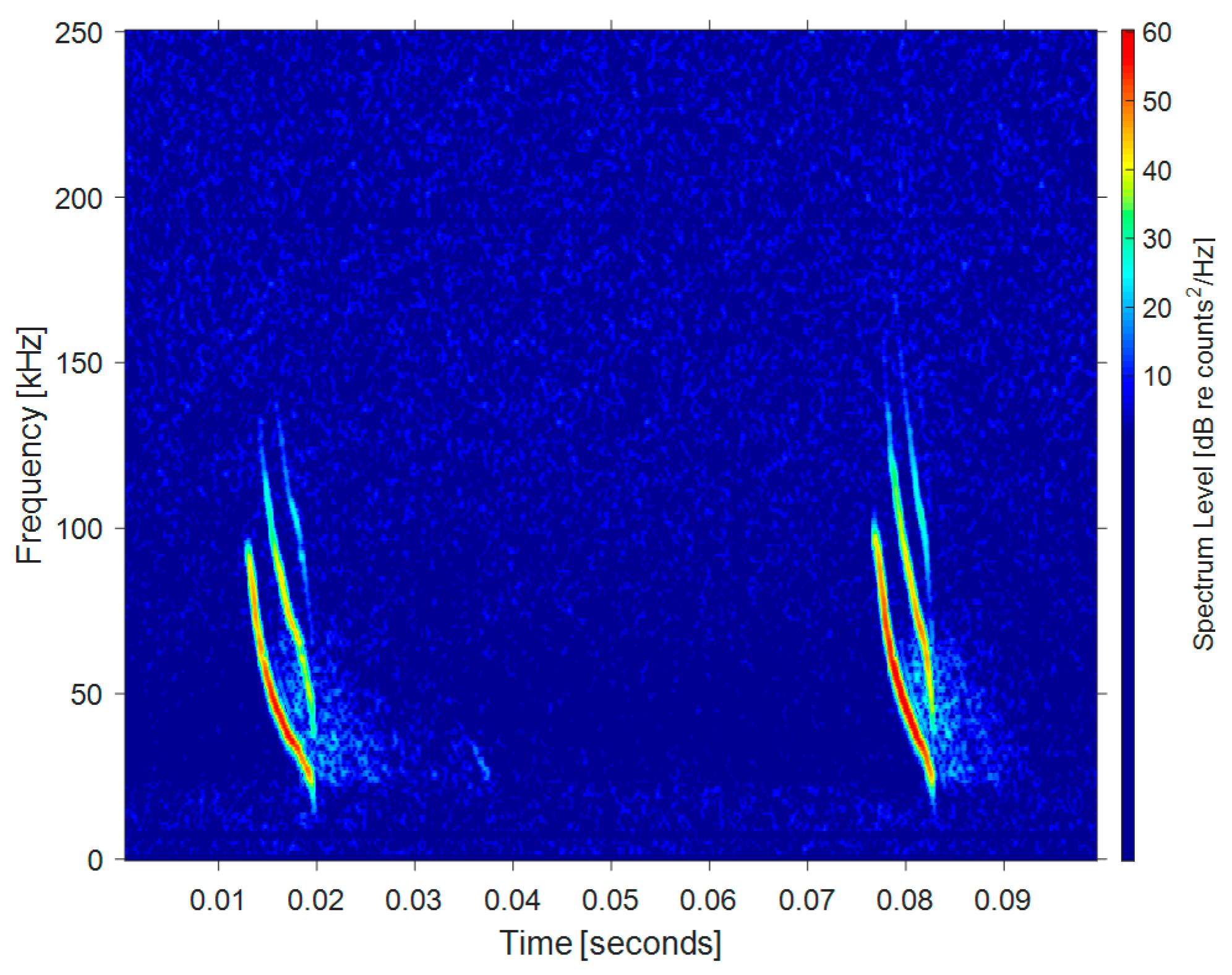
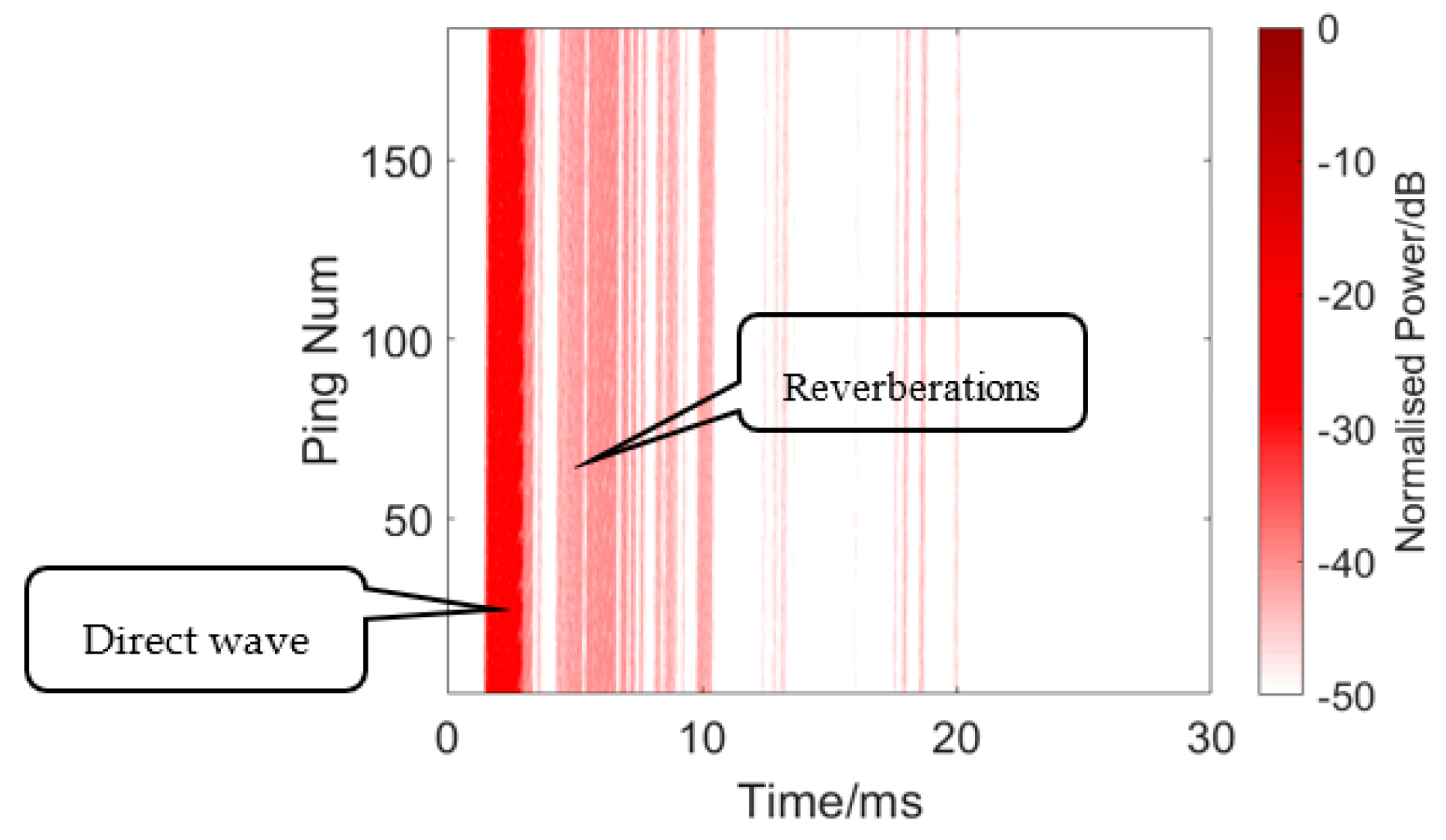
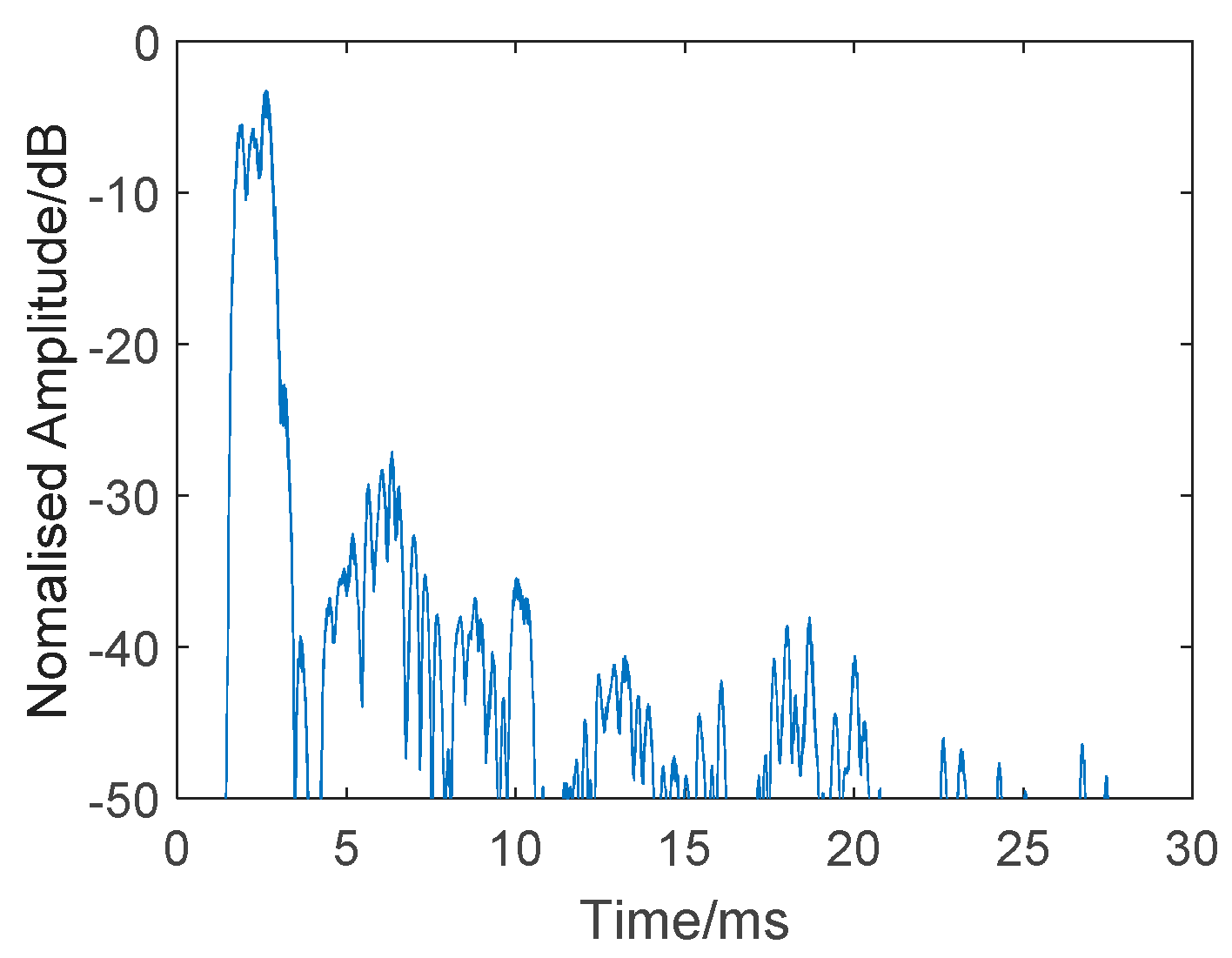
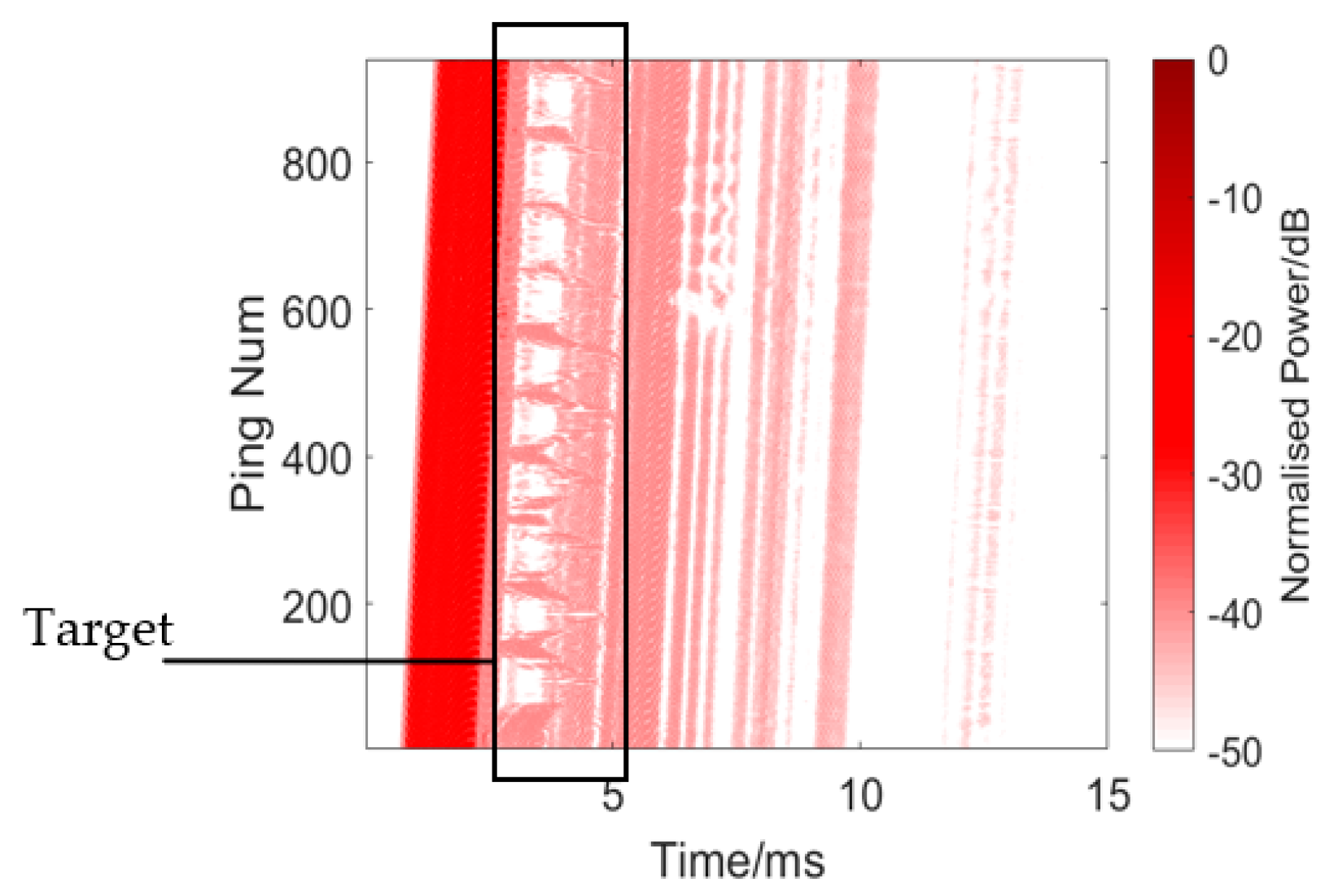
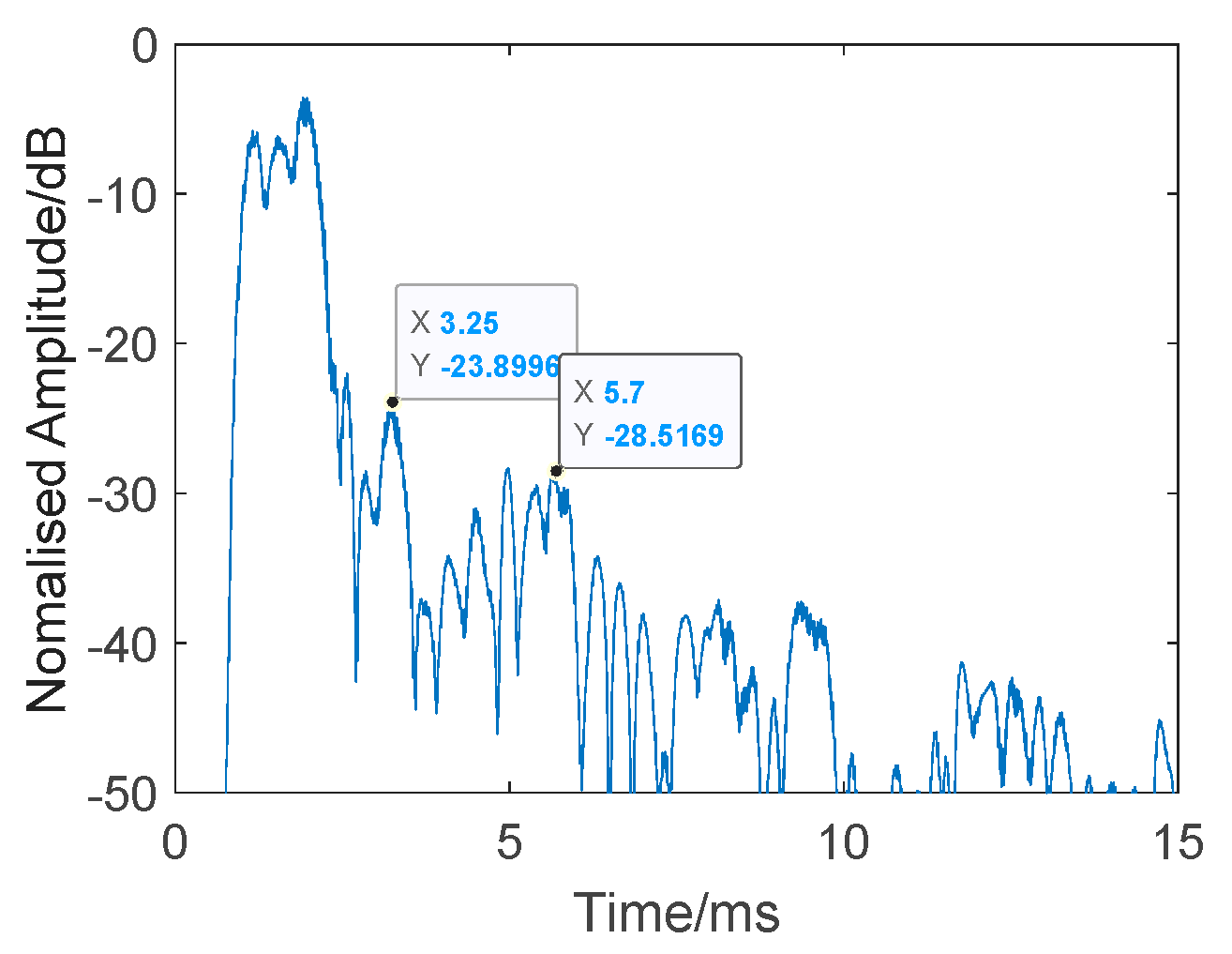
| Ping Number | Target Amplitude (dB) | Reverberation Amplitude (dB) |
|---|---|---|
| 40 | −25.3703 | −27.5527 |
| 140 | −23.8996 | −28.5169 |
| 230 | −25.9000 | −28.7457 |
| 320 | −23.8896 | −28.1379 |
| 405 | −21.1968 | −27.7738 |
| 480 | −25.8207 | −28.7363 |
| 570 | −24.1978 | −28.3268 |
| 655 | −27.9686 | −28.4560 |
| 740 | −28.2686 | −28.6865 |
| 840 | −27.3996 | −28.1339 |
| Average | −25.3911 | −28.3067 |
| Average Difference: 2.9156 dB | ||
| Ping Number | Target Amplitude (dB) | Reverberation Amplitude (dB) |
|---|---|---|
| 32 | −10.0834 | −24.2135 |
| 110 | −8.0012 | −26.7511 |
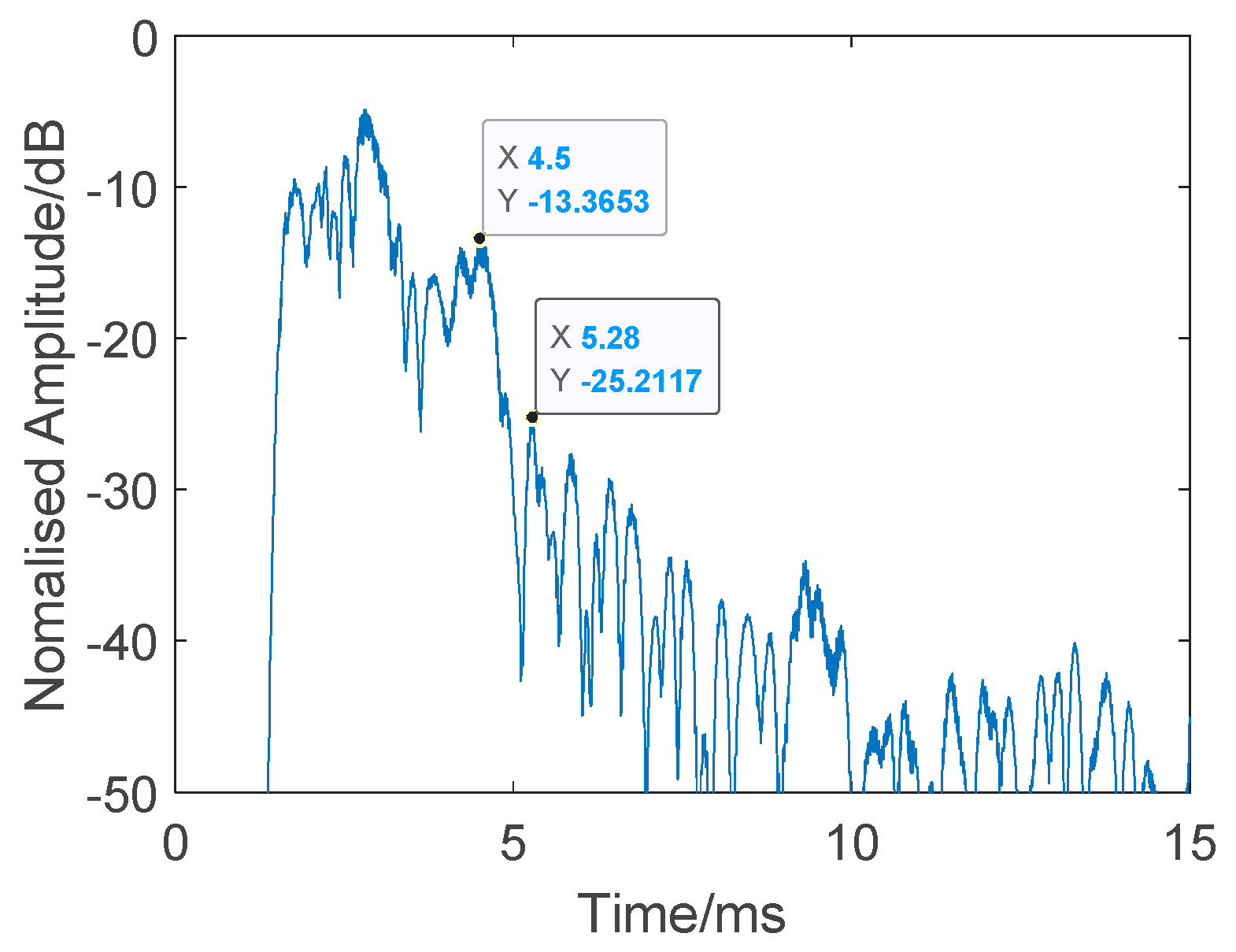
| 200 | −13.3653 | −25.2117 |
| 307 | −13.7349 | −23.3996 |
| 415 | −6.9769 | −25.3489 |
| 500 | −18.4009 | −23.6974 |
| 590 | −8.1706 | −27.5688 |
| 693 | −15.0068 | −20.496 |
| 772 | −5.8254 | −25.7930 |
| 862 | −4.7159 | −24.6019 |
| Average | −10.4281 | −24.7082 |
| Mean Difference: 14.2802 dB | ||
| Ping Number | Target Amplitude (dB) | Reverberation Amplitude (dB) |
|---|---|---|
| 20 | −19.1512 | −38.5618 |
| 100 | −10.5650 | −34.9523 |
| 187 | −15.8462 | −34.0641 |
| 275 | −14.8269 | −35.9625 |
| 452 | −12.7934 | −36.6704 |
| 544 | −13.1177 | −35.1534 |
| 652 | −18.4892 | −30.5824 |
| 730 | −12.8362 | −34.0829 |
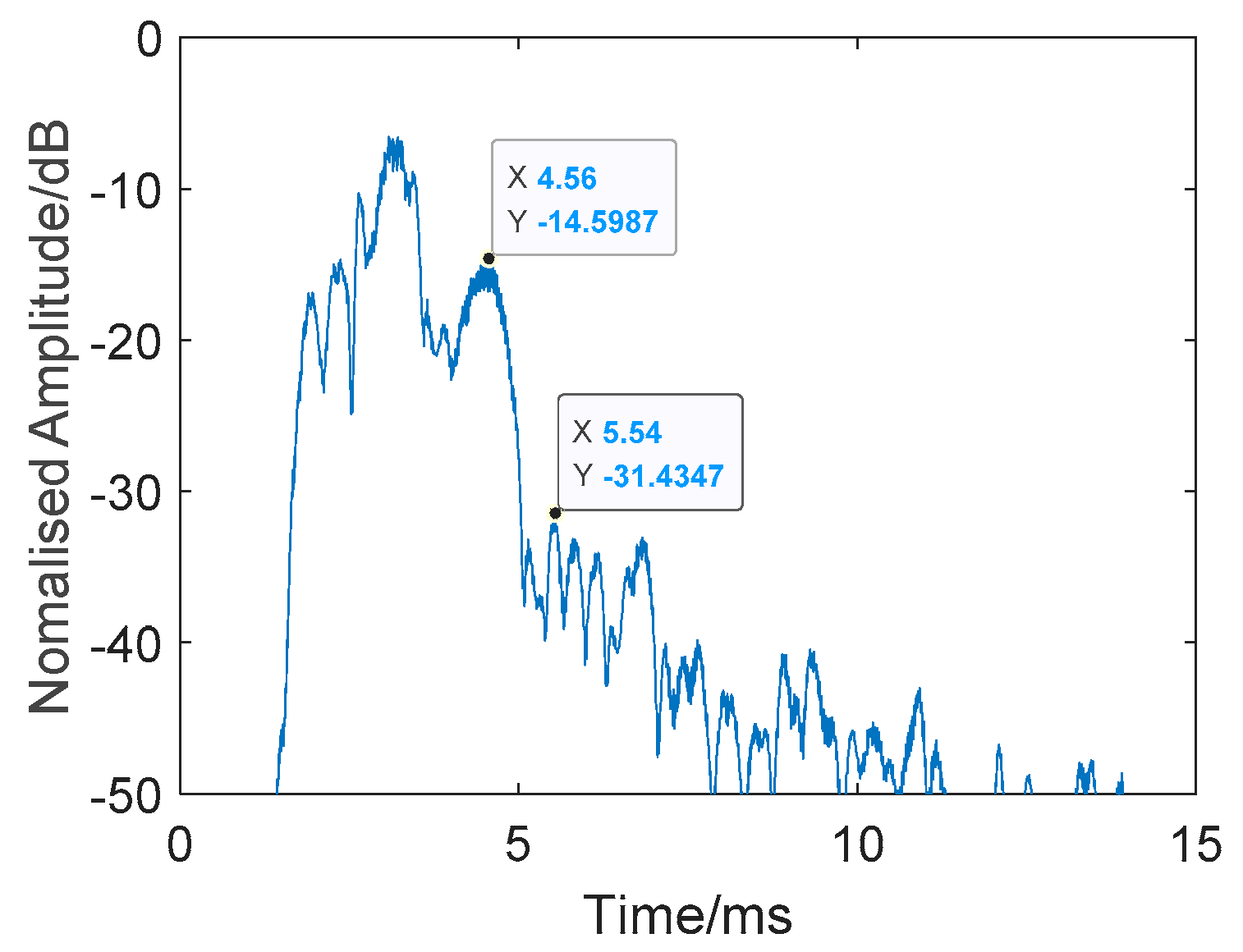
| 805 | −14.5987 | −31.4347 |
| 905 | −13.4853 | −32.8446 |
| Average: | −14.5710 | −34.4309 |
| Mean Difference: 19.8599 dB | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Dong, C.; Guo, L.; Li, L. A Bioinspired Twin Inverted Multiscale Matched Filtering Method for Detecting an Underwater Moving Target in a Reverberant Environment. Sensors 2019, 19, 5305. https://doi.org/10.3390/s19235305
Sheng X, Dong C, Guo L, Li L. A Bioinspired Twin Inverted Multiscale Matched Filtering Method for Detecting an Underwater Moving Target in a Reverberant Environment. Sensors. 2019; 19(23):5305. https://doi.org/10.3390/s19235305
Chicago/Turabian StyleSheng, Xueli, Chaoping Dong, Longxiang Guo, and Li Li. 2019. "A Bioinspired Twin Inverted Multiscale Matched Filtering Method for Detecting an Underwater Moving Target in a Reverberant Environment" Sensors 19, no. 23: 5305. https://doi.org/10.3390/s19235305
APA StyleSheng, X., Dong, C., Guo, L., & Li, L. (2019). A Bioinspired Twin Inverted Multiscale Matched Filtering Method for Detecting an Underwater Moving Target in a Reverberant Environment. Sensors, 19(23), 5305. https://doi.org/10.3390/s19235305





