Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Nano-Hyperspec Sensor
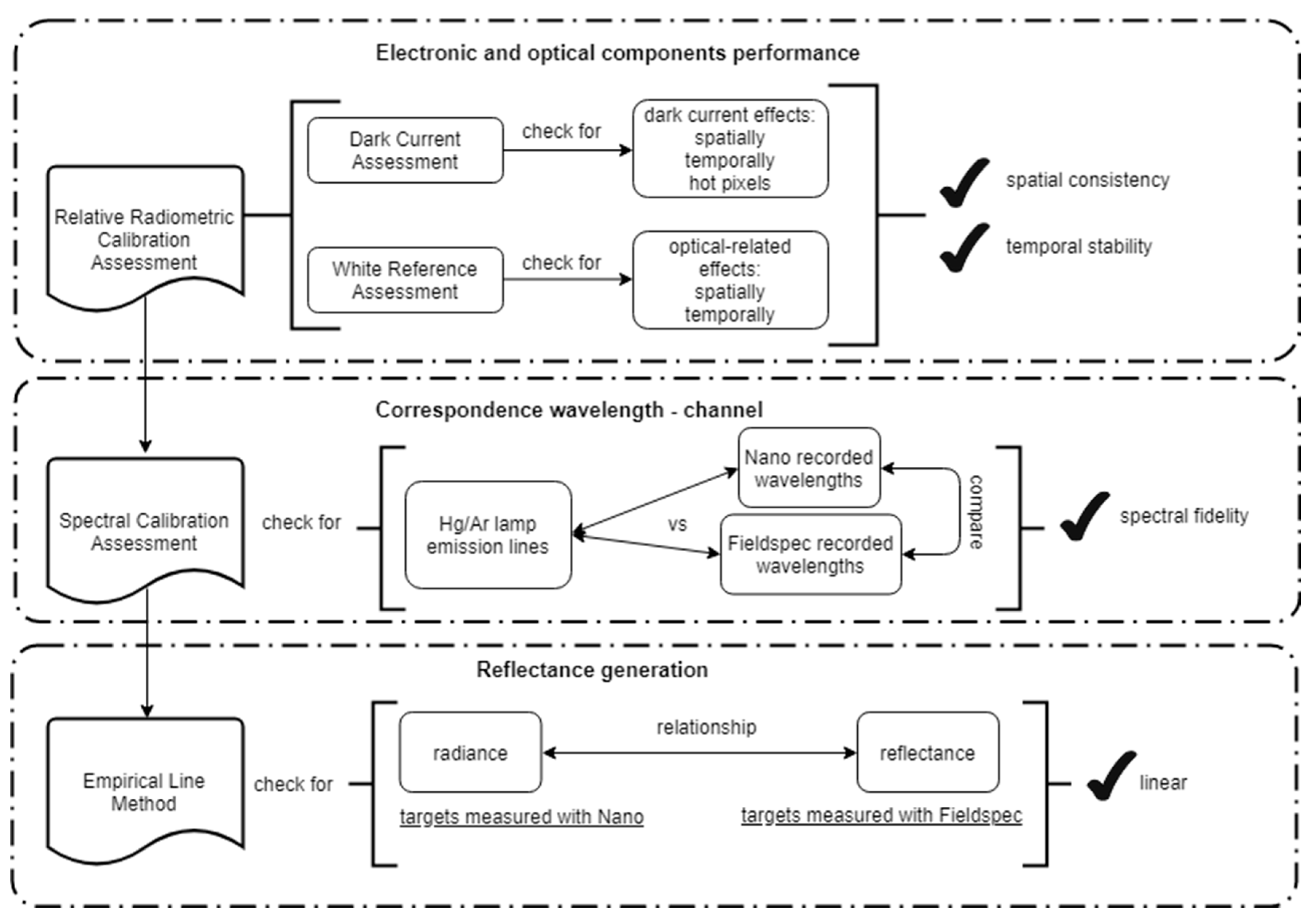
2.2. Performance Assessment Protocol
2.3. Relative Radiometric Calibration Assessment
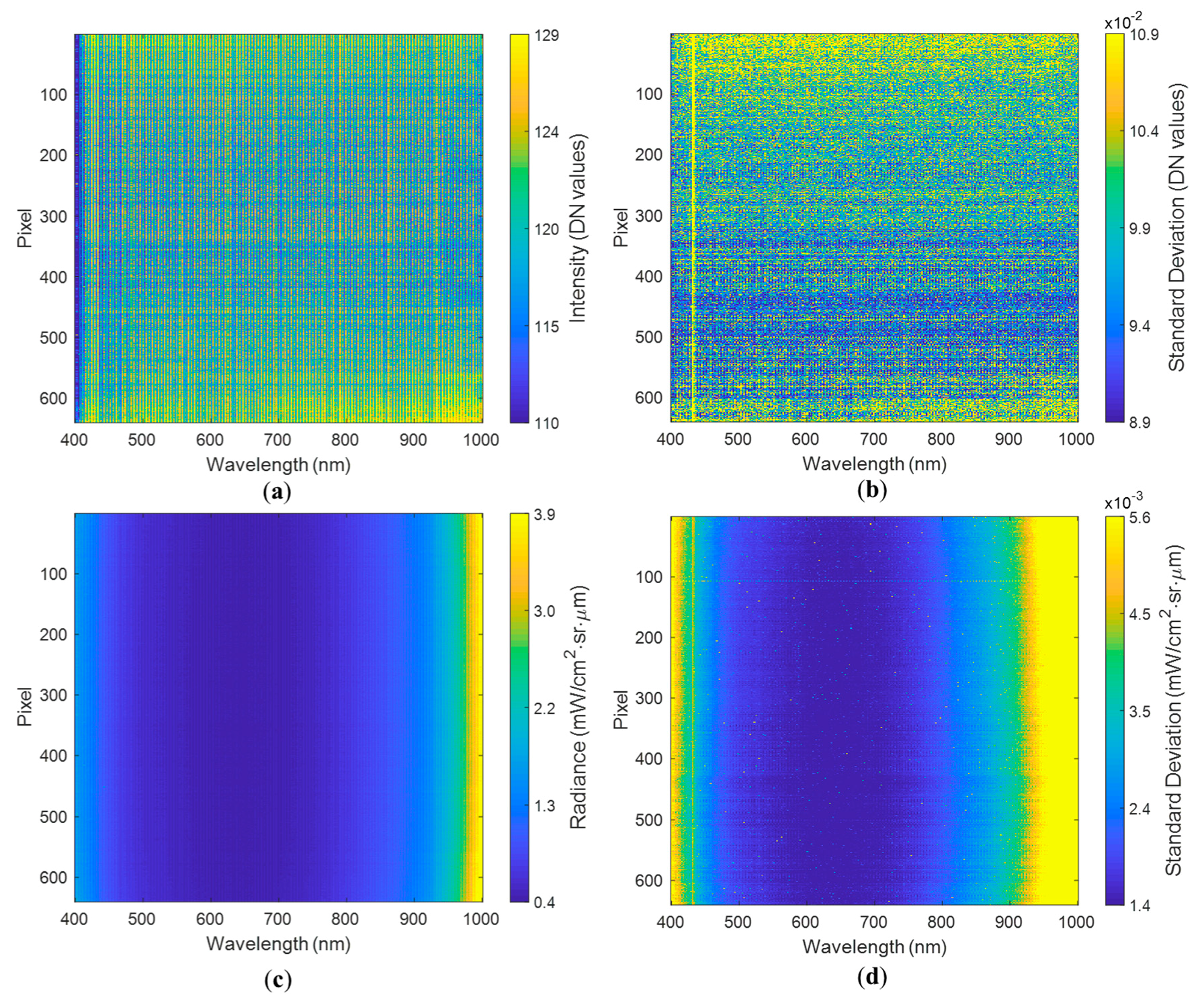
2.3.1. Dark Current Assessment
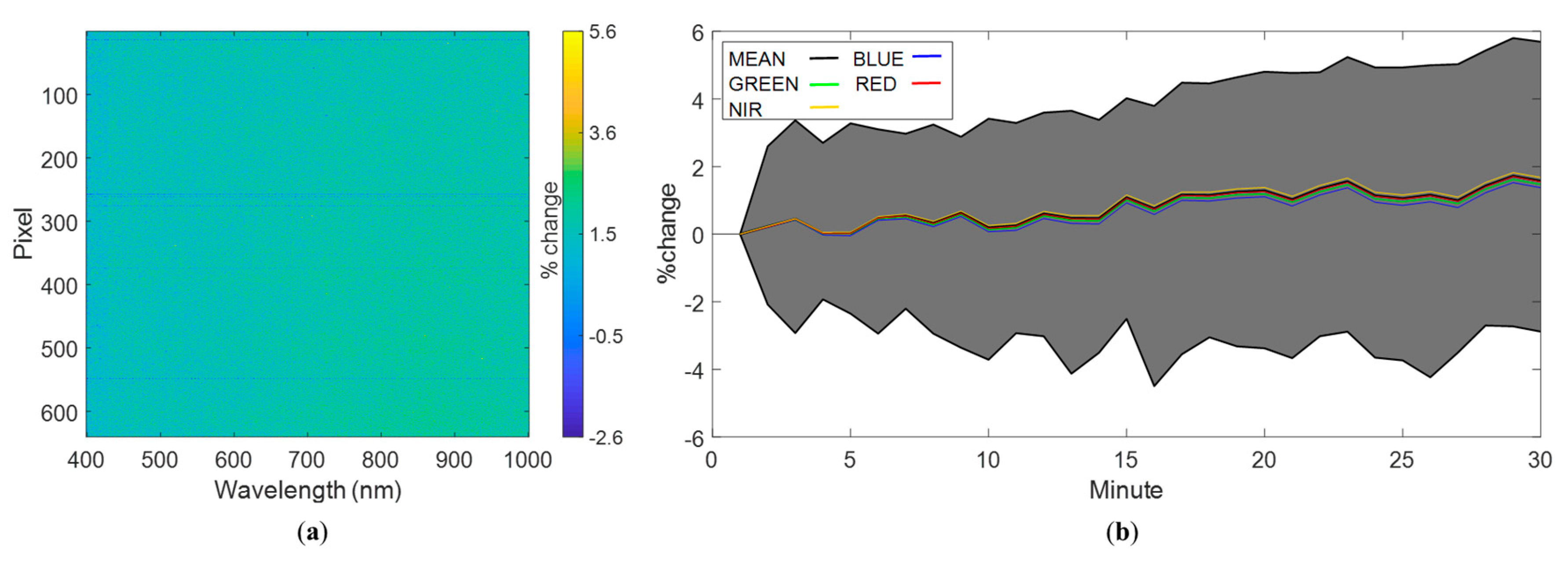
2.3.2. White Reference Assessment
2.4. Spectral Calibration Assessment
2.5. Conversion from Radiance to Reflectance
3. Results
3.1. Relative Radiometric Calibration Assessment
3.1.1. Dark Current Assessment
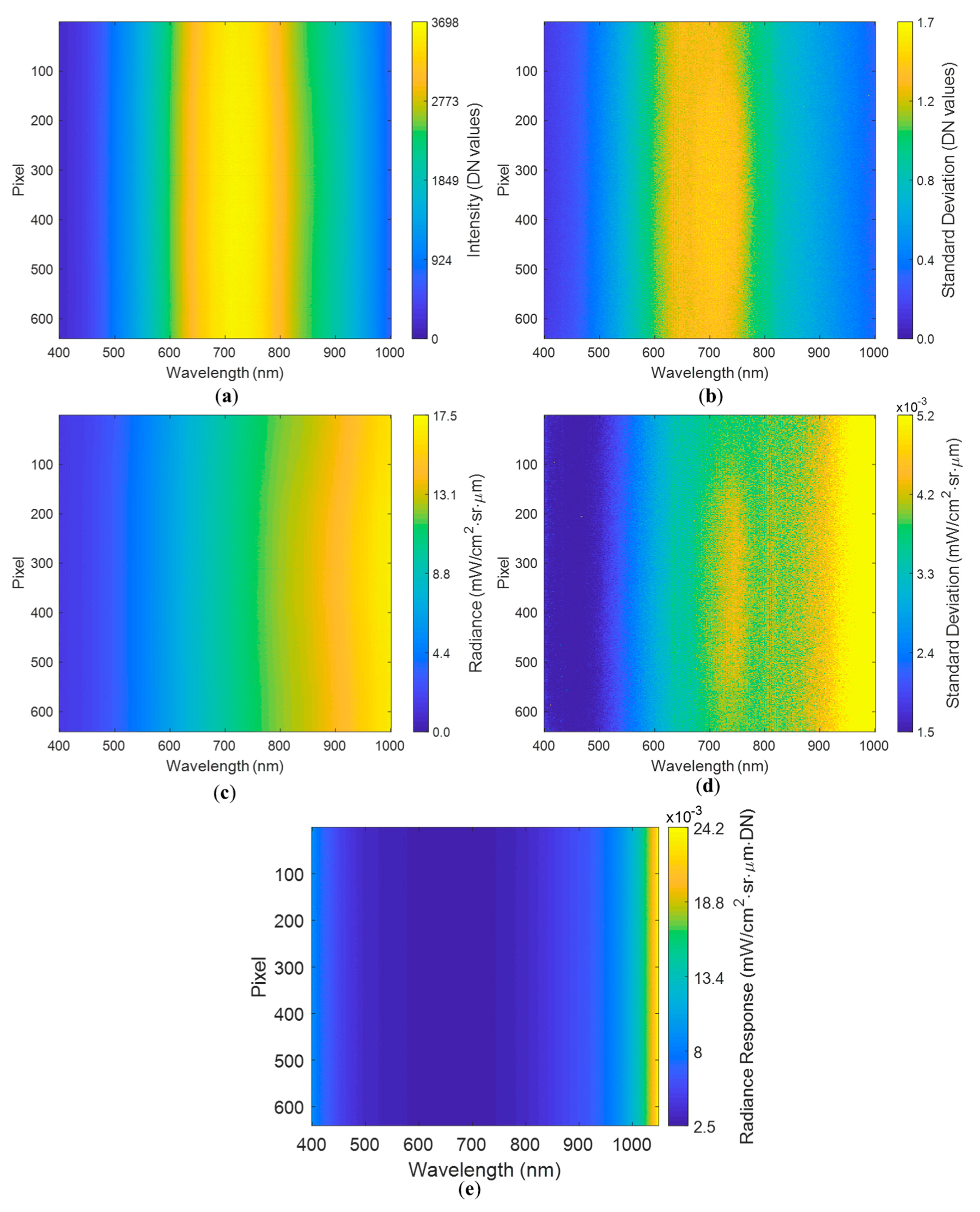
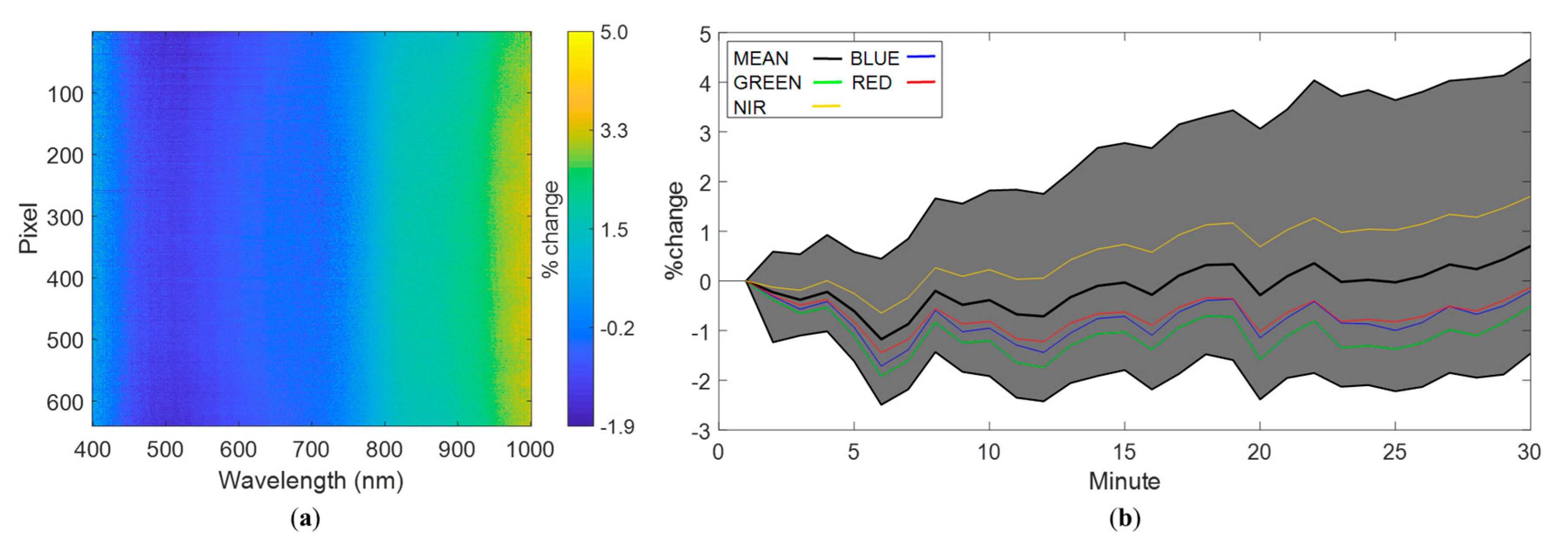
3.1.2. White Reference Assessment
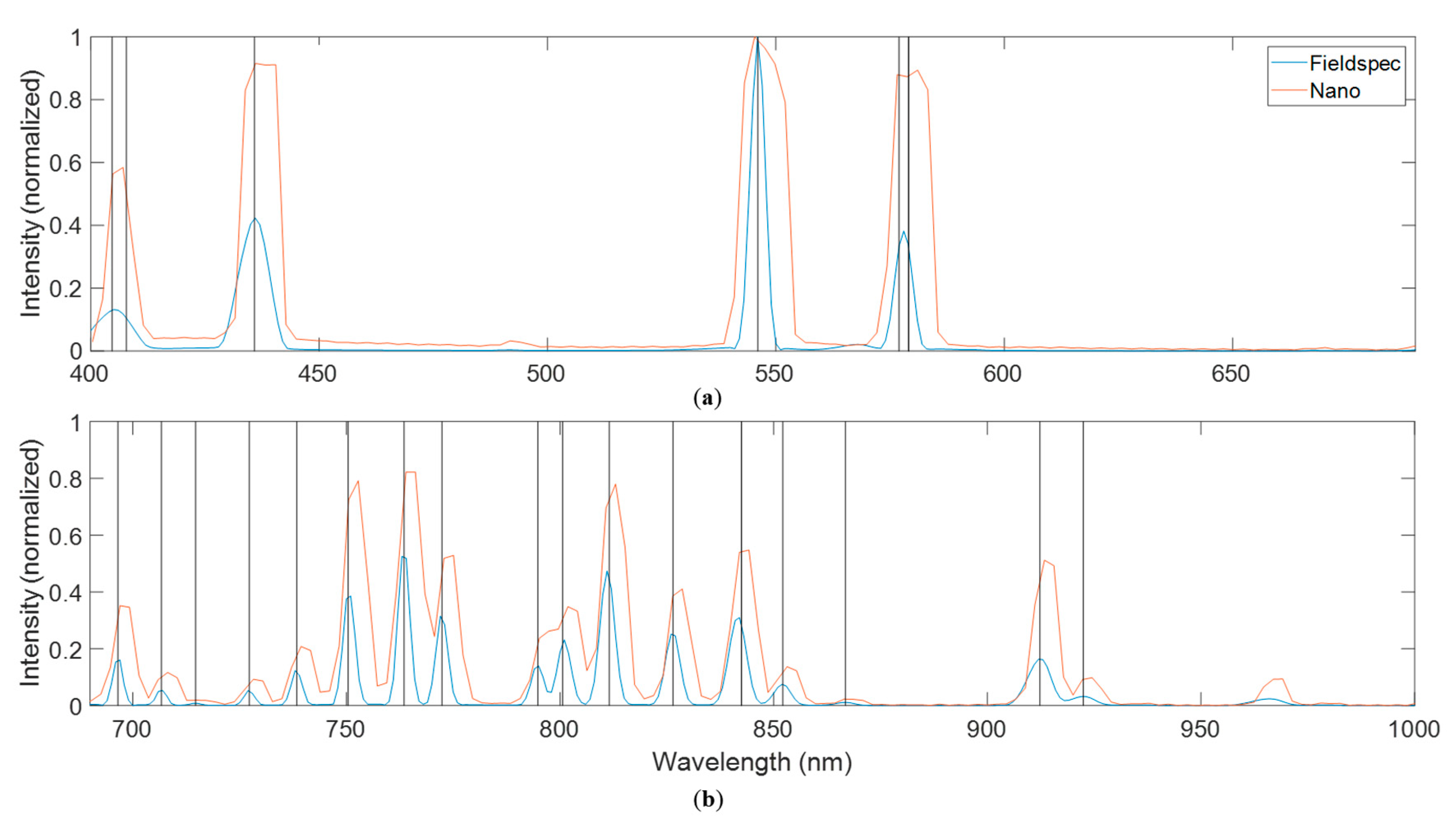
3.2. Spectral Calibration Assessment
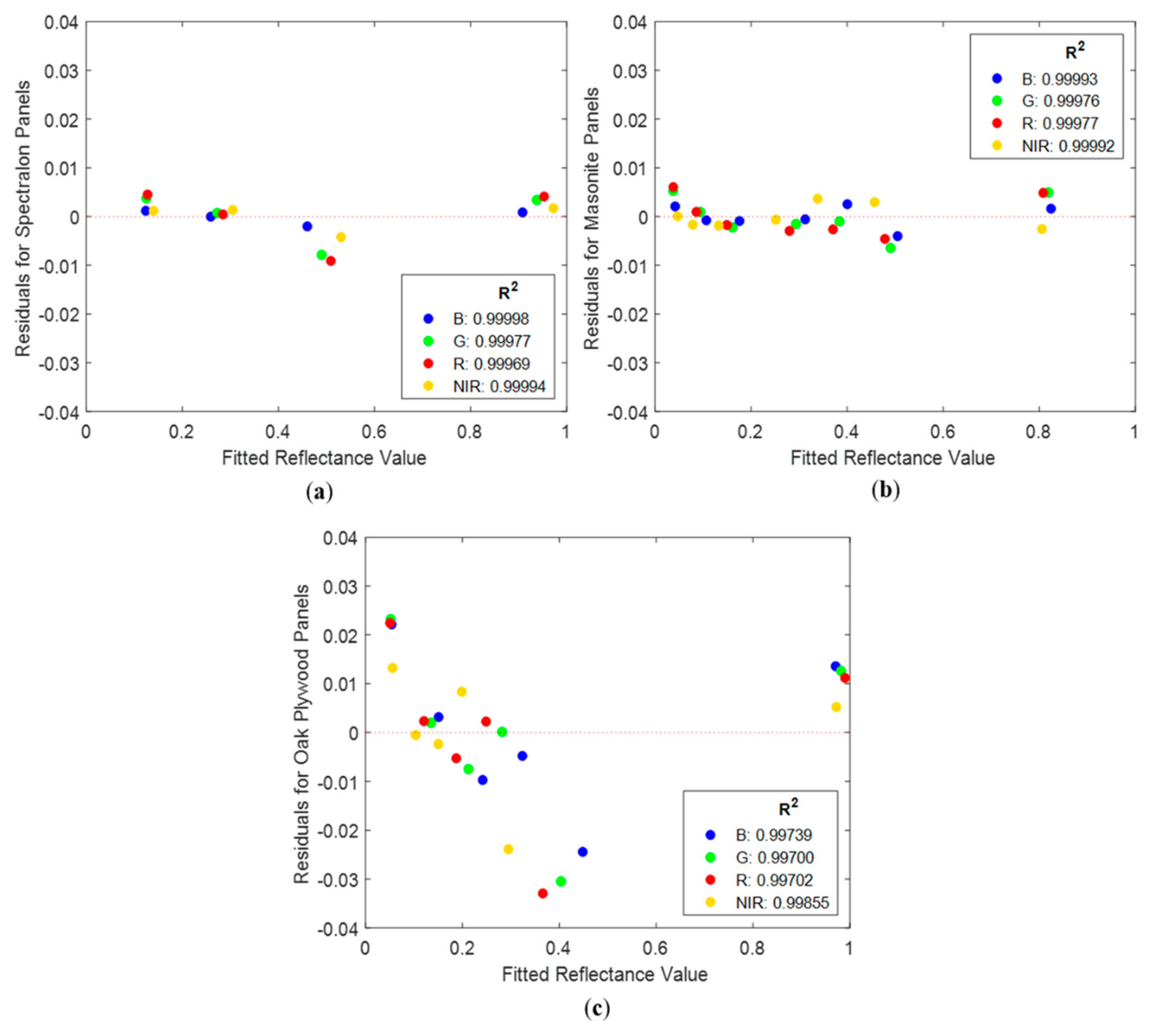
3.3. Conversion from Radiance to Reflectance
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Geladi, P.; Burger, J.; Lestander, T. Hyperspectral imaging: Calibration problems and solutions. Chemom. Intell. Lab. Syst. 2004, 72, 209–217. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive species detection in Hawaiian rainforests using airborne imaging spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- Blackburn, G.A. Hyperspectral remote sensing of plant pigments. J. Exp. Bot. 2006, 58, 855–867. [Google Scholar] [CrossRef]
- Feilhauer, H.; Asner, G.P.; Martin, R.E. Multi-method ensemble selection of spectral bands related to leaf biochemistry. Remote Sens. Environ. 2015, 164, 57–65. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Cloutis, E.A. Review Article Hyperspectral geological remote sensing: Evaluation of analytical techniques. Int. J. Remote Sens. 1996, 17, 2215–2242. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote sensing for mineral exploration. Ore Geol. Rev. 1999, 14, 157–183. [Google Scholar] [CrossRef]
- Brando, V.; Dekker, A. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Karpouzli, E.; Malthus, T.J.; Place, C.J. Hyperspectral discrimination of coral reef benthic communities in the western Caribbean. Coral Reefs 2004, 23, 141–151. [Google Scholar] [CrossRef]
- Lesser, M.P.; Mobley, C.D. Bathymetry, water optical properties, and benthic classification of coral reefs using hyperspectral remote sensing imagery. Coral Reefs 2007, 26, 819–829. [Google Scholar] [CrossRef]
- Shukla, A.; Kot, R. An Overview of Hyperspectral Remote Sensing and its applications in various Disciplines. IRA Int. J. Appl. Sci. 2016, 5, 85. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Kutser, T.; Martin, G.; Kotta, J. Feasibility of hyperspectral remote sensing for mapping benthic macroalgal cover in turbid coastal waters—A Baltic Sea case study. Remote Sens. Environ. 2006, 101, 342–351. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Honkavaara, E.; Rosnell, T.; Oliveira, R.; Tommaselli, A. Band registration of tuneable frame format hyperspectral UAV imagers in complex scenes. ISPRS J. Photogramm. Remote Sens. 2017, 134, 96–109. [Google Scholar] [CrossRef]
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and Assessment of Spectrometric, Stereoscopic Imagery Collected Using a Lightweight UAV Spectral Camera for Precision Agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The need for accurate geometric and radiometric corrections of drone-borne hyperspectral data for mineral exploration: Mephysto—A toolbox for pre-processing drone-borne hyperspectral data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Aasen, H.; Bendig, J.; Bolten, A.; Bennertz, S.; Willkomm, M.; Bareth, G. Introduction and preliminary results of a calibration for full-frame hyperspectral cameras to monitor agricultural crops with UAVs. In Proceedings of the ISPRS Technical Commission VII Symposium, Vienna, Austria, 5–7 July 2010; pp. 1–8. [Google Scholar]
- Whitehead, K.; Hugenholtz, C.H. Remote sensing of the environment with small unmanned aircraft systems (UASs), part 1: A review of progress and challenges. J. Unmanned Veh. Syst. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Heaphy, M.; Watt, M.S.; Dash, J.P.; Pearse, G.D. UAVs for data collection-plugging the gap. N. Z. J. For. 2017, 62, 23–30. [Google Scholar]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa 2007, 33. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Elmasry, G.; Sun, D.-W. Principles of Hyperspectral Imaging Technology. Hyperspectral Imaging Food Qual. Anal. Control 2010, 3–43. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Green, R.O. Spectral calibration requirement for Earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt. 1998, 37, 683–690. [Google Scholar] [CrossRef]
- Tian, H. Noise Analysis in CMOS Image Sensors. Ph.D. Thesis, Stanford University, Stanford, CA, USA, August 2000. [Google Scholar]
- Wang, C.; Myint, S.W. A simplified empirical line method of radiometric calibration for small unmanned aircraft systems-based remote sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1876–1885. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Hakala, T.; Markelin, L.; Honkavaara, E.; Scott, B.; Theocharous, T.; Nevalainen, O.; Näsi, R.; Suomalainen, J.; Viljanen, N.; Greenwell, C.; et al. Direct Reflectance Measurements from Drones: Sensor Absolute Radiometric Calibration and System Tests for Forest Reflectance Characterization. Sensors 2018, 18, 1417. [Google Scholar] [CrossRef]
- Yang, G.; Li, C.; Wang, Y.; Yuan, H.; Feng, H.; Xu, B.; Yang, X. The DOM Generation and Precise Radiometric Calibration of a UAV-Mounted Miniature Snapshot Hyperspectral Imager. Remote Sens. 2017, 9, 642. [Google Scholar] [CrossRef]
- Arngren, M. Hyperspectral NIR Camera. Available online: http://www2.imm.dtu.dk/pubdb/public/allpublications.php?year=2011&pubtype=6 (accessed on 8 October 2019).
- Liu, Y.; Wang, T.; Ma, L.; Wang, N. Spectral Calibration of Hyperspectral Data Observed From a Hyperspectrometer Loaded on an Unmanned Aerial Vehicle Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2630–2638. [Google Scholar]
- Lynch, K.; Hill, S. Miniaturized Hyperspectral Sensor for UAV Applications; Headwall Photonics, Inc. Available online: https://www.ugpti.org/smartse/research/citations/downloads/Lynch-Headwall_Small_UAVs_with_Hyperspectral_Imaging-2014.pdf (accessed on 16 October 2019).
- Gómez-Chova, L.; Alonso, L.; Guanter, L.; Camps-Valls, G.; Calpe, J.; Moreno, J. Correction of systematic spatial noise in push-broom hyperspectral sensors: Application to CHRIS/PROBA images. Appl. Opt. 2008, 47, F46–F60. [Google Scholar] [CrossRef]
- Sarkar, M.; Buttgen, B.; Theuwissen, A.J.P. Feedforward Effect in Standard CMOS Pinned Photodiodes. IEEE Trans. Electron Devices 2013, 60, 1154–1161. [Google Scholar] [CrossRef]
- Carrère, J.; Place, S.; Oddou, J.; Benoit, D.; Roy, F. CMOS image sensor: Process impact on dark current. In Proceedings of the 2014 IEEE International Reliability Physics Symposium, Waikoloa, HI, USA, 1–5 June 2014; pp. 3C.1.1–3C.1.6. [Google Scholar]
- Rozenstein, O.; Devir, A.; Karnieli, A. In-Field Absolute Calibration of Ground and Airborne VIS-NIR-SWIR Hyperspectral Point Spectrometers. Remote Sens. 2014, 6, 1158–1170. [Google Scholar] [CrossRef]
- Davis, C.O.; Bowles, J.; Leathers, R.A.; Korwan, D.; Downes, T.V.; Snyder, W.A.; Rhea, W.J.; Chen, W.; Fisher, J.; Bissett, P.; et al. Ocean PHILLS hyperspectral imager: Design, characterization, and calibration. Opt. Express 2002, 10, 210–221. [Google Scholar] [CrossRef]
- Wu, D.; Sun, D.-W. Advanced applications of hyperspectral imaging technology for food quality and safety analysis and assessment: A review — Part I: Fundamentals. Innov. Food Sci. Emerg. Technol. 2013, 19, 1–14. [Google Scholar] [CrossRef]
- Hg-1 Mercury Argon Calibration Light Source. Available online: https://oceanoptics.com/wp-content/uploads/hg1.pdf (accessed on 27 June 2019).
- Johansen, K.; Phinn, S.; Lowry, J.; Douglas, M. Quantifying indicators of riparian condition in Australian tropical savannas: Integrating high spatial resolution imagery and field survey data. Int. J. Remote Sens. 2008, 29, 7003–7028. [Google Scholar] [CrossRef]
- Mattley, Y. Plasma Monitoring with Miniature High-Resolution Spectroscopy. Florida, US, 10 April 2014. Available online: www.intins.co.kr/App-Note-Plasma-Monitoring-with-Miniature-High-Resolution-Spectroscopy1.pdf (accessed on 9 October 2019).
- Johansen, K.; Raharjo, T.; McCabe, M.F. Using Multi-Spectral UAV Imagery to Extract Tree Crop Structural Properties and Assess Pruning Effects. Remote Sens. 2018, 10, 854. [Google Scholar] [CrossRef]
- Wahab, I.; Hall, O.; Jirström, M. Remote Sensing of Yields: Application of UAV Imagery-Derived NDVI for Estimating Maize Vigor and Yields in Complex Farming Systems in Sub-Saharan Africa. Drones 2018, 2, 28. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F.; Angel, Y.; Middleton, E.M. Detection of chlorophyll and leaf area index dynamics from sub-weekly hyperspectral imagery. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII, Edinburgh, UK, 26–29 September 2016; p. 999812. [Google Scholar]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Johansen, K.; Bartolo, R.; Phinn, S. SPECIAL FEATURE—Geographic Object-Based Image Analysis. J. Spat. Sci. 2010, 55, 3–7. [Google Scholar] [CrossRef]
- Johansen, K.; Morton, M.J.; Malbeteau, Y.M.; Aragon, B.; Al-Mashharawi, S.K.; Ziliani, M.G.; Angel, Y.; Fiene, G.M.; Negrão, S.S.; Mousa, M.A. Unmanned Aerial Vehicle-Based Phenotyping Using Morphometric and Spectral Analysis Can Quantify Responses of Wild Tomato Plants to Salinity Stress. Front. Plant Sci. 2019, 10, 370. [Google Scholar] [CrossRef] [PubMed]
- Lucieer, A.; Malenovský, Z.; Veness, T.; Wallace, L. HyperUAS-Imaging Spectroscopy from a Multirotor Unmanned Aircraft System. J. Field Robot. 2014, 31, 571–590. [Google Scholar] [CrossRef]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring From an Unmanned Aerial Vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Karpouzli, E.; Malthus, T. The empirical line method for the atmospheric correction of IKONOS imagery. Int. J. Remote Sens. 2003, 24, 1143–1150. [Google Scholar] [CrossRef]
| Type of Experiment | No. of Experiments | Exposure (ms) | Files per Experiment | Data Size (GB) per Experiment |
|---|---|---|---|---|
| Dark current | 2 | 6 | 301 | 100 |
| Dark current | 2 | 12.5 | 140 | 46.9 |
| White reference | 2 | 12.5 | 137 | 46.3 |
| Spectral calibration | 1 | 1000 | 1 | 217 |
| Empirical line | 1 | 3 | 372 | 71.1 |
| Hg Emission Lines (nm) | Ar Emission Lines (nm) |
|---|---|
| 253.652 | 696.543 |
| 296.728 | 706.722 |
| 302.15 | 714.704 |
| 313.155 | 727.294 |
| 334.148 | 738.398 |
| 365.015 | 750.387 |
| 404.656 | 763.511 |
| 407.783 * | 772.376 |
| 435.833 | 794.818 |
| 546.074 ** | 800.616 *** |
| 576.96 | 811.531 |
| 579.066 | 826.452 |
| 842.465 | |
| 852.144 | |
| 866.794 | |
| 912.297 | |
| 922.45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barreto, M.A.P.; Johansen, K.; Angel, Y.; McCabe, M.F. Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera. Sensors 2019, 19, 4699. https://doi.org/10.3390/s19214699
Barreto MAP, Johansen K, Angel Y, McCabe MF. Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera. Sensors. 2019; 19(21):4699. https://doi.org/10.3390/s19214699
Chicago/Turabian StyleBarreto, M. Alejandra P., Kasper Johansen, Yoseline Angel, and Matthew F. McCabe. 2019. "Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera" Sensors 19, no. 21: 4699. https://doi.org/10.3390/s19214699
APA StyleBarreto, M. A. P., Johansen, K., Angel, Y., & McCabe, M. F. (2019). Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera. Sensors, 19(21), 4699. https://doi.org/10.3390/s19214699






