Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement
Abstract
1. Introduction
2. Principle of Fringe Projection Profilometry
3. Adaptive Binocular Fringe Dynamic Projection Method
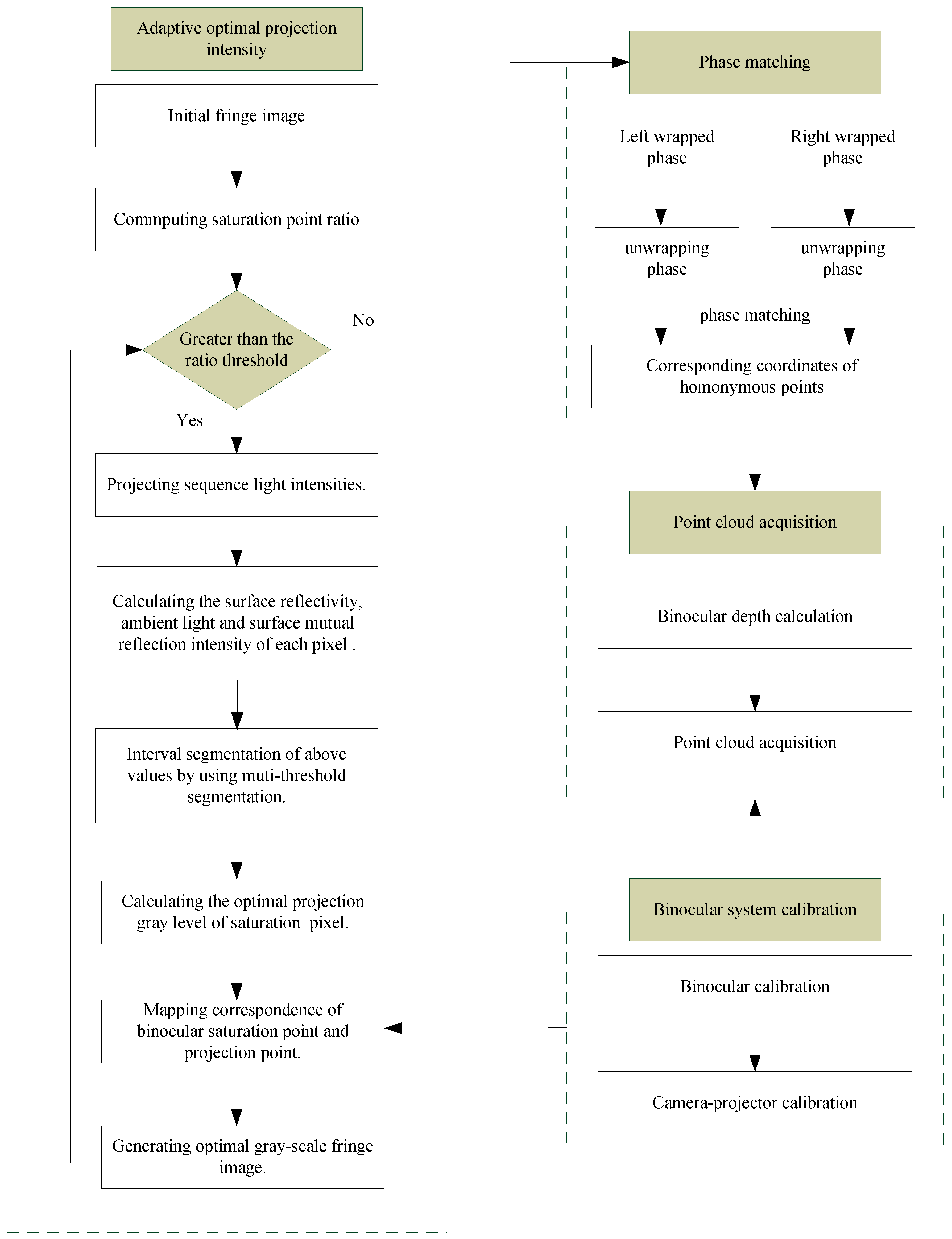
3.1. Flowchart of ABFDP Method
- Step 1. Adaptive optimal projection intensity. In this step, the intensity response function and multi-threshold segmentation are used to generate the modified fringe images. Its basic principle is that the fringe images are modified iteratively by the feedback of the deformed fringe images captured by the binocular cameras.
- Step 2. Binocular system calibration. Through binocular system calibration, the mapping correspondences of binocular images and projector image are obtained.
- Step 3. Phase matching. After calculating the absolute phase, according to the principle of equal phase of homonymy point in binocular system, binocular matching points are obtained.
- Step 4. Point cloud acquisition. In this step, point cloud information of object is obtained with the principle of triangulation.
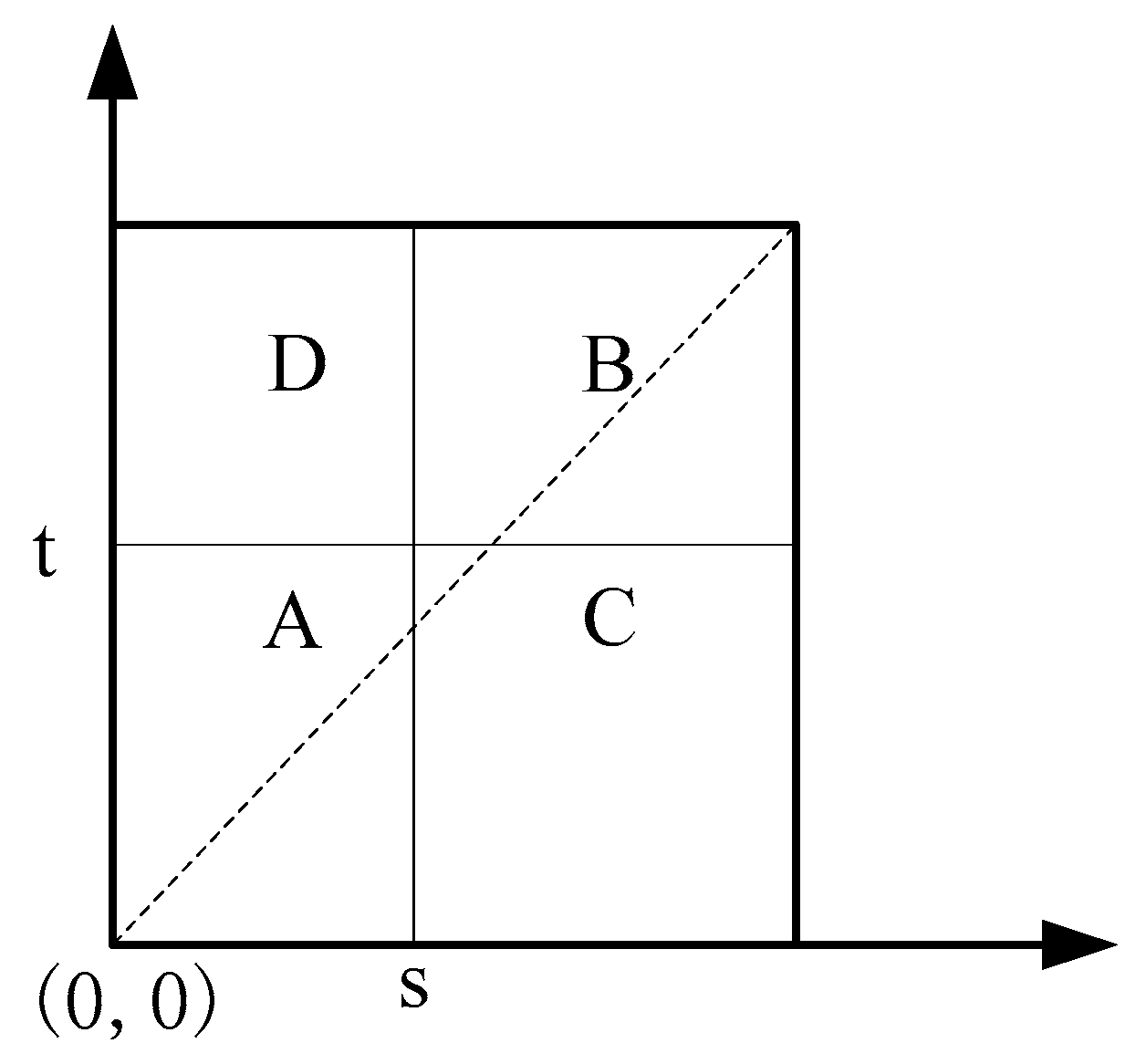
3.2. Adaptive Optimal Projection Intensity Method
3.3. Mapping Correspondence of Binocular Saturation Point and Projection Point
- Step 1. Binocular camera and left camera–projector calibration. This step is mainly used to obtain the internal and external parameters of the cameras and projector, as well as the conversion relationship of the cameras and projector.
- Step 2. Projecting a set of light intensity onto the surface of object, we can get the surface reflection characteristics and the optimal projection grays.
- Step 3. Four-step phase-shifting images are collected simultaneously by left and right cameras. The saturation points in binocular cameras are identified, and then the corresponding points in the projection image are obtained according to step 1.
- Step 4. The corrected fringe images are projected onto the surface of the object to calculate the absolute phase. Therefore, the diameter results of objects can be obtained by point cloud fitting.
4. Experiments and Results
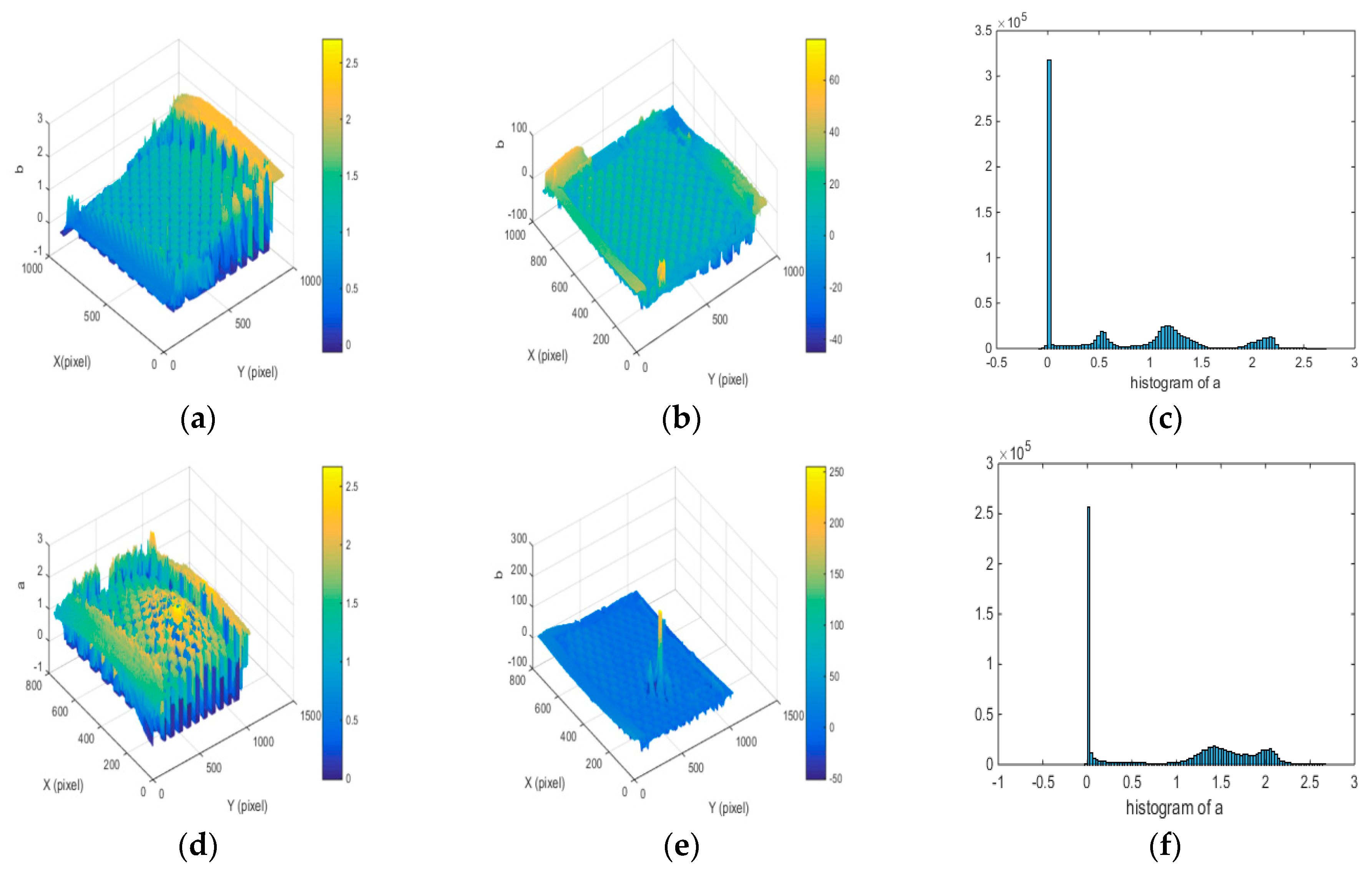
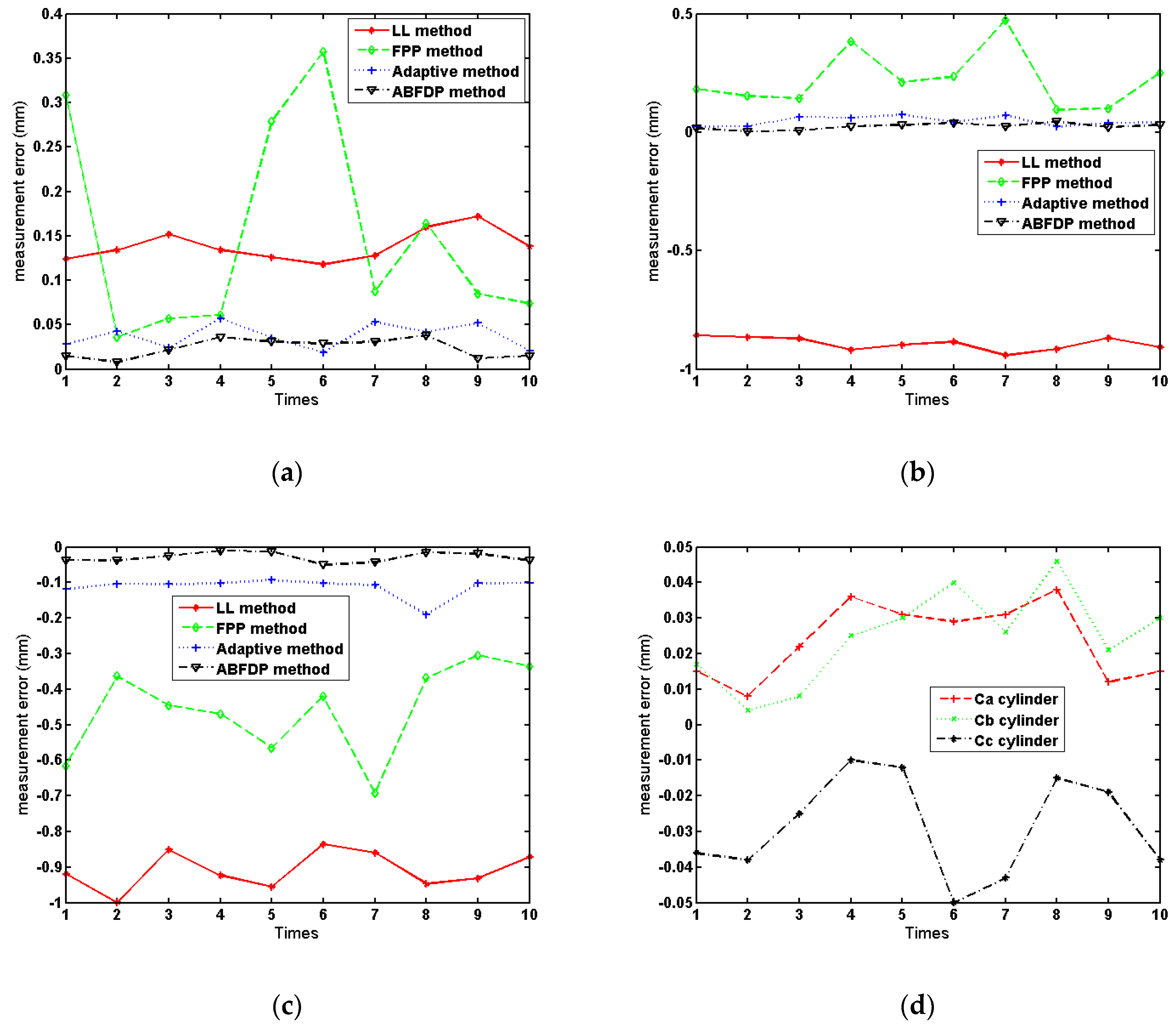
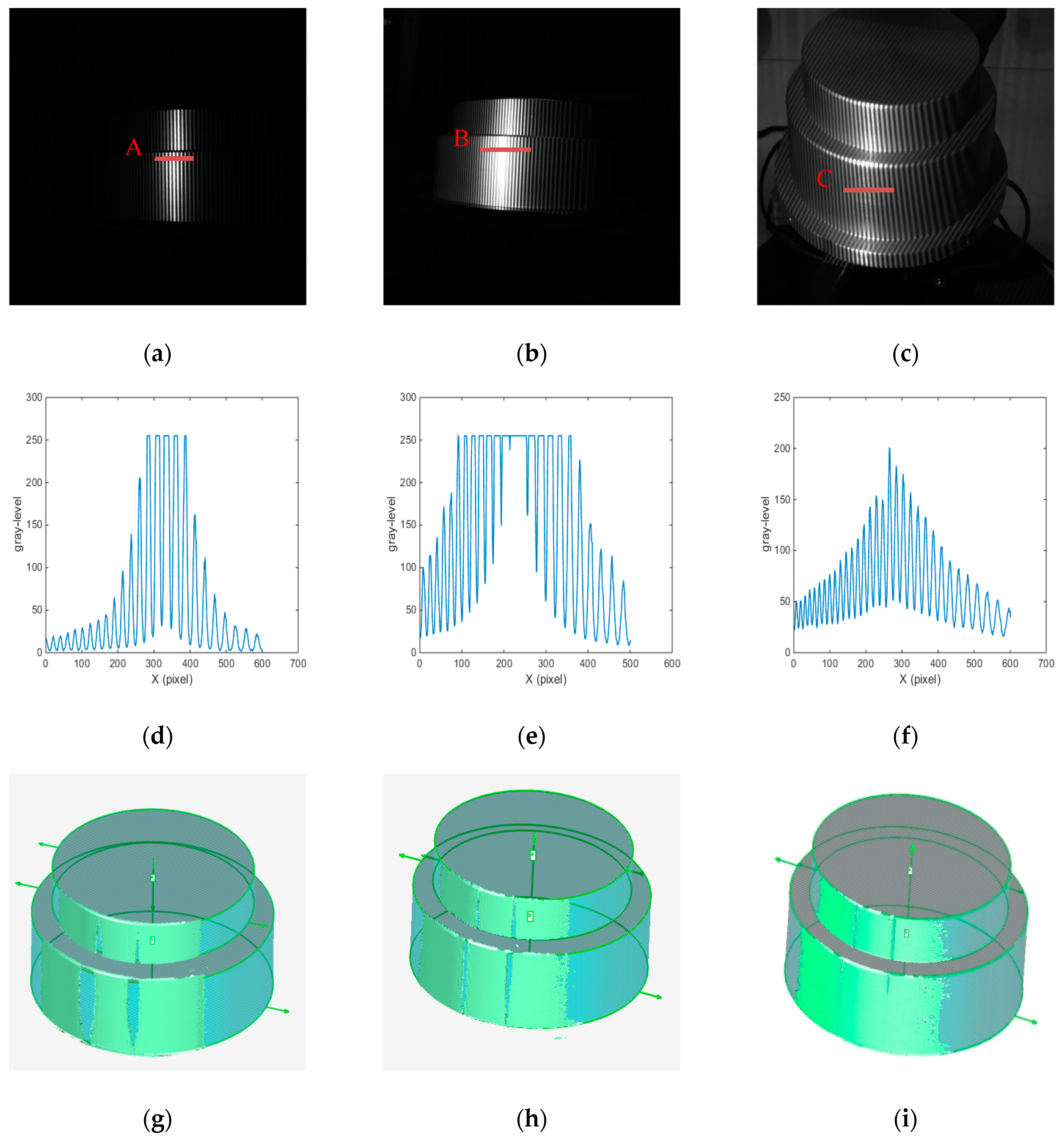
4.1. Mixed Reflectivity Materials Experiment
4.2. Shiny Metal Objects Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van der Jeught, S.; Dirckx, J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Zhang, S. Absolute phase retrieval methods for digital fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 107, 28–37. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, X.; Li, Z.; Zhong, K.; Han, L.; He, W.; Gan, W.; Xi, G.; Wang, C.; Shi, Y. High-accuracy globally consistent surface reconstruction using fringe projection profilometry. Sensors 2019, 19, 668. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Wang, X.; Ni, Y. Flexible three-dimensional reconstruction via structured-light-based visual positioning and global optimization. Sensors 2019, 19, 1583. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3D measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]
- Hyun, J.S.; Li, B.; Zhang, S. High-speed high-accuracy three-dimensional shape measurement using digital binary defocusing method versus sinusoidal method. Opt. Eng. 2017, 56, 074102. [Google Scholar] [CrossRef]
- Bell, T.; Vlahov, B.; Allebach, J.P.; Zhang, S. Three-dimensional range geometry compression via phase encoding. Appl. Opt. 2017, 56, 9285–9292. [Google Scholar] [CrossRef]
- Makhsous, S.; Mohammad, H.M.; Schenk, J.M.; Mamishev, A.V.; Kristal, A.R. A novel mobile structured light system in food 3D reconstruction and volume estimation. Sensors 2019, 19, 564. [Google Scholar] [CrossRef]
- Liberadzki, P.; Adamczyk, M.; Witkowski, M.; Sitnik, R. Structured-light-based system for shape measurement of the human body in motion. Sensors 2018, 18, 2827. [Google Scholar] [CrossRef]
- Xue, J.; Zhang, Q.; Li, C.; Lang, W. 3D face profilometry based on galvanometer scanner with infrared fringe projection in high speed. Appl. Sci. 2019, 9, 1458. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High dynamic range scanning technique. Opt. Eng. 2009, 48, 033604. [Google Scholar] [CrossRef]
- Song, Z.; Jiang, H.; Lin, H.; Tang, S. A high dynamic range structured light means for the 3D measurement of specular surface. Opt. Lasers Eng. 2017, 95, 8–16. [Google Scholar] [CrossRef]
- Jiang, C.; Bell, T.; Zhang, S. High dynamic range real-time 3D shape measurement. Opt. Express 2016, 24, 7337–7346. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.; Kofman, J. Camera-independent saturation avoidance in measuring high-reflectivity-variation surfaces using pixel-wise composed images from projected patterns of different maximum gray level. Opt. Commun. 2014, 333, 32–37. [Google Scholar] [CrossRef]
- Babaie, G.; Abolbashari, M.; Farahi, F. Dynamics range enhancement in digital fringe projection technique. Precis. Eng. 2015, 39, 243–251. [Google Scholar] [CrossRef]
- Benveniste, R.; Ünsalan, C. Nary coded structured light-based range scanners using color invariants. J. Real-time Image Process. 2014, 9, 359–377. [Google Scholar] [CrossRef]
- Chen, C.; Gao, N.; Wang, X.; Zhang, Z. Adaptive pixel-to-pixel projection intensity adjustment for measuring a shiny surface using orthogonal color fringe pattern projection. Meas. Sci. Technol. 2018, 29, 055203. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, J.; Xi, N.; Zhao, J.; Shi, Q. A robust surface coding method for optically challenging objects using structured light. IEEE Trans. Autom. Sci. Eng. 2014, 11, 775–788. [Google Scholar] [CrossRef]
- Salahieh, B.; Chen, Z.; Rodriguez, J.J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, Y.; Jiang, H.; Li, X. 3D shape measurement in the presence of strong interreflections by epipolar imaging and regional fringe projection. Opt. Express 2018, 26, 7117–7131. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Ainouz, S.; Petitjean, C.; Bensrhair, A. Specularity removal: A global energy minimization approach based on polarization imaging. Comput. Vis. Image Underst. 2017, 158, 31–39. [Google Scholar] [CrossRef][Green Version]
- Xu, Y.; Aliaga, D.G. An adaptive correspondence algorithm for modeling scenes with strong interreflections. IEEE Trans. Vis. Comput. Graph. 2009, 15, 465–480. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Kofman, J. Adaptive fringe-pattern projection for image saturation avoidance in 3D surface-shape measurement. Opt. Express 2014, 22, 9887–9901. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Gao, J.; Mei, Q.; Zhang, G.; He, Y.; Chen, X. Three-dimensional shape measurement technique for shiny surfaces by adaptive pixel-wise projection intensity adjustment. Opt. Lasers Eng. 2017, 91, 206–215. [Google Scholar] [CrossRef]
- Farahi, N.; Abolbashari, M.; Babaie, J.; Ziegert, J.; Porras-Aguilar, R.; Davies, A.; Farahi, F. Inverse projected-fringe technique for measurement of dimensions and surface profile of axisymmetric objects. Meas. Sci. Technol. 2018, 30, 015009. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q.; Zuo, C.; Feng, S. High dynamic range 3D shape measurement based on the intensity response function of a camera. Appl. Opt. 2018, 57, 1378–1386. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Liu, Y.; Yu, X.; Wu, H.; Zhang, N. Three-dimensional measurement for specular reflection surface based on reflection component separation and priority region filling theory. Sensors 2017, 17, 215. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, J.; Luo, B. High dynamic range 3D measurement based on spectral modulation and hyperspectral imaging. Opt. Express 2018, 26, 34442–34450. [Google Scholar] [CrossRef]
- Vargas, R.; Marrugo, A.G.; Pineda, J.; Meneses, J.; Romero, L.A. Camera–projector calibration methods with compensation of geometric distortions in fringe projection profilometry: a comparative study. Optica Pura Y Aplicada. 2018, 51, 1–10. [Google Scholar] [CrossRef]
- Huang, L.; Da, F.; Gai, S. Research on multi-camera calibration and point cloud correction method based on three-dimensional calibration object. Opt. Lasers Eng. 2019, 115, 32–41. [Google Scholar] [CrossRef]
- Tao, W.; Zhong, H.; Chen, X.; Selami, Y.; Zhao, H. A new fitting method for measurement of the curvature radius of a short arc with high precision. Meas. Sci. Technol. 2018, 29, 075014. [Google Scholar] [CrossRef]
- Yu, C.; Ji, F.; Jing, X.; Liu, M. Dynamic granularity matrix space based adaptive edge detection method for structured light stripes. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Q.; Zuo, C.; Tao, T.; Hu, Y.; Asundi, A. Motion-oriented high speed 3-D measurements by binocular fringe projection using binary aperiodic patterns. Opt. Express 2017, 25, 540–559. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, Z.; Duan, G.; Cheng, J.; Jiang, X.; Tan, J. Precise and robust binocular camera calibration based on multiple constraints. Appl. Opt. 2018, 57, 5130–5140. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Fang, L. An advanced analysis method of initial orbit determination with too short arc data. In Proceedings of the Tenth International Symposium on Multispectral Image Processing and Pattern Recognition (MIPPR 2017), Xiangyang, China, 28–29 October 2017; p. 1060807. [Google Scholar] [CrossRef]






| Calibration Balls | CMM/mm | Mean Value by ABFDP/mm | Mean Error by ABFDP/mm |
|---|---|---|---|
| A | 50.7991 | 50.8046 | 0.0055 |
| B | 50.7970 | 50.8021 | 0.0051 |
| C | 253988 | 25.4039 | 0.0041 |
| Cylinder Measured | CMM/mm | Line Laser Method/mm | FPP Method/mm | Adaptive Method/mm | ABFDP Method/mm |
|---|---|---|---|---|---|
| Ca | 199.750 | 199.874 | 200.059 | 199.778 | 199.765 |
| 199.884 | 199.786 | 199.793 | 199.758 | ||
| 199.902 | 199.807 | 199.774 | 199.772 | ||
| 199.884 | 199.811 | 199.807 | 199.786 | ||
| 199.876 | 200.029 | 199.785 | 199.781 | ||
| 199.868 | 200.107 | 199.769 | 199.779 | ||
| 199.878 | 199.838 | 199.803 | 199.781 | ||
| 199.910 | 199.914 | 199.792 | 199.788 | ||
| 199.922 | 199.835 | 199.802 | 199.762 | ||
| 199.888 | 199.824 | 199.771 | 199.765 | ||
| MV/mm | 199.889 | 199.901 | 199.787 | 199.774 | |
| STD/mm | 0.017 | 0.119 | 0.014 | 0.011 | |
| RMSE/mm | 0.140 | 0.189 | 0.040 | 0.026 | |
| MAE/mm | 0.139 | 0.151 | 0.037 | 0.023 | |
| Cylinder Measured | CMM/mm | Line Laser Method/mm | FPP Method/mm | Adaptive Method/mm | ABFDP Method/mm |
|---|---|---|---|---|---|
| Cb | 239.741 | 238.884 | 239.924 | 239.764 | 239.758 |
| 238.877 | 239.893 | 239.766 | 239.745 | ||
| 238.871 | 239.885 | 239.805 | 239.749 | ||
| 238.823 | 240.126 | 239.803 | 239.766 | ||
| 238.844 | 239.953 | 239.814 | 239.771 | ||
| 238.856 | 239.977 | 239.785 | 239.781 | ||
| 238.800 | 240.215 | 239.811 | 239.767 | ||
| 238.826 | 239.836 | 239.765 | 239.787 | ||
| 238.872 | 239.841 | 239.781 | 239.762 | ||
| 238.834 | 239.993 | 239.782 | 239.771 | ||
| MV/mm | 238.849 | 239.964 | 239.788 | 239.766 | |
| STD/mm | 0.027 | 0.122 | 0.019 | 0.013 | |
| RMSE/mm | 0.893 | 0.252 | 0.050 | 0.028 | |
| MAE/mm | −0.892 | 0.223 | 0.047 | 0.025 | |
| Cylinder Measured | CMM/mm | Line Laser Method/mm | FPP Method/mm | Adaptive Method/mm | ABFDP Method/mm |
|---|---|---|---|---|---|
| Cc | 276.299 | 275.380 | 275.684 | 276.180 | 276.263 |
| 275.300 | 275.936 | 276.195 | 276.261 | ||
| 275.448 | 275.853 | 276.194 | 276.274 | ||
| 275.376 | 275.830 | 276.197 | 276.289 | ||
| 275.344 | 275.734 | 276.206 | 276.287 | ||
| 275.464 | 275.879 | 276.197 | 276.249 | ||
| 275.440 | 275.607 | 276.192 | 276.256 | ||
| 275.352 | 275.931 | 276.108 | 276.284 | ||
| 275.368 | 275.994 | 276.197 | 276.280 | ||
| 275.428 | 275.963 | 276.198 | 276.261 | ||
| MV/mm | 275.390 | 275.841 | 276.186 | 276.270 | |
| STD/mm | 0.053 | 0.128 | 0.028 | 0.014 | |
| RMSE/mm | 0.910 | 0.474 | 0.116 | 0.032 | |
| RMSE/mm | −0.909 | −0.458 | −0.113 | −0.029 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Ji, F.; Xue, J.; Wang, Y. Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement. Sensors 2019, 19, 4023. https://doi.org/10.3390/s19184023
Yu C, Ji F, Xue J, Wang Y. Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement. Sensors. 2019; 19(18):4023. https://doi.org/10.3390/s19184023
Chicago/Turabian StyleYu, Changzhi, Fang Ji, Junpeng Xue, and Yajun Wang. 2019. "Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement" Sensors 19, no. 18: 4023. https://doi.org/10.3390/s19184023
APA StyleYu, C., Ji, F., Xue, J., & Wang, Y. (2019). Adaptive Binocular Fringe Dynamic Projection Method for High Dynamic Range Measurement. Sensors, 19(18), 4023. https://doi.org/10.3390/s19184023





