On the Use of Focused Incident Near-Field Beams in Microwave Imaging
Abstract
:1. Introduction
2. Motivation
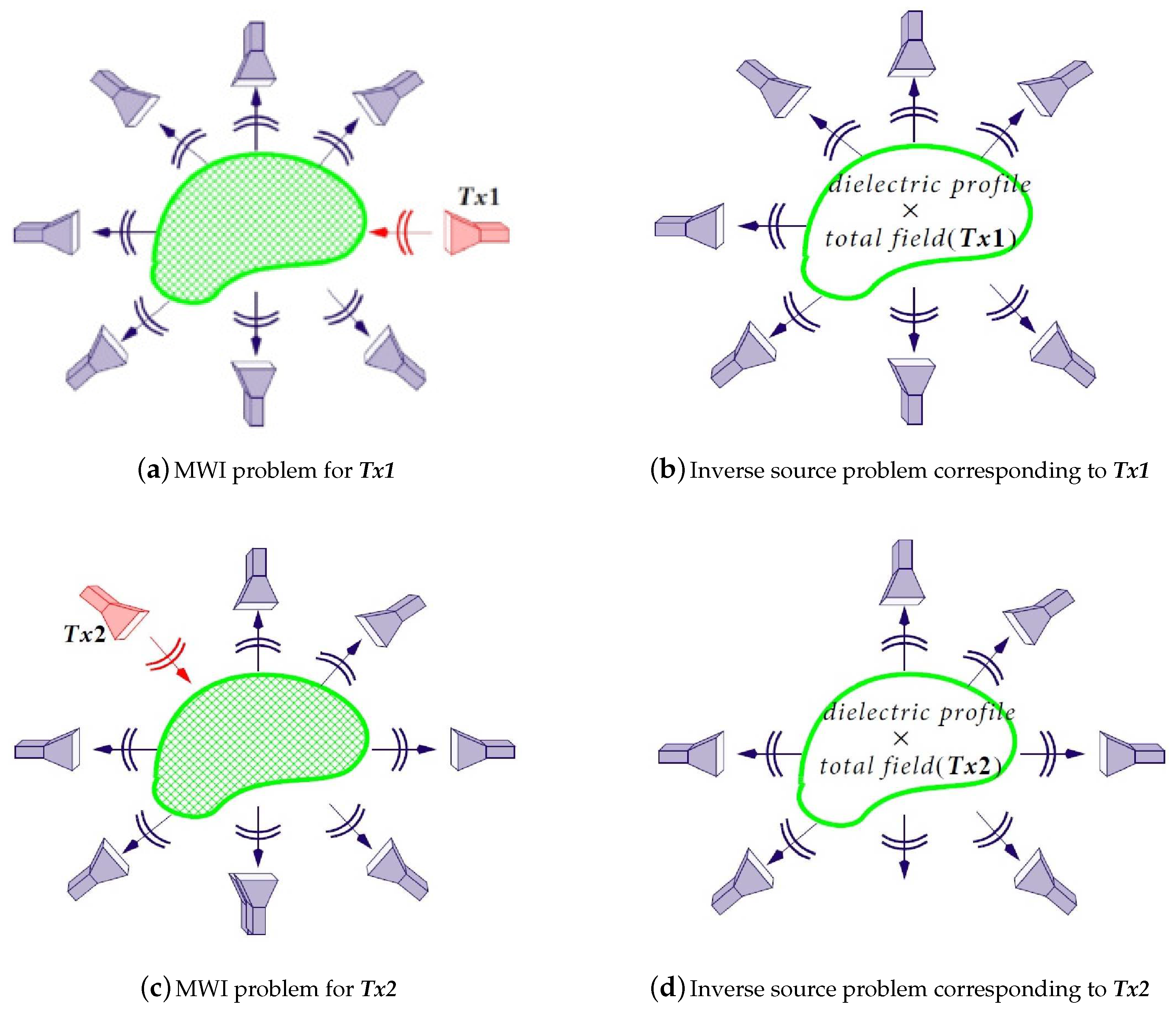
2.1. The Relation between the MWI and Inverse Source Problems
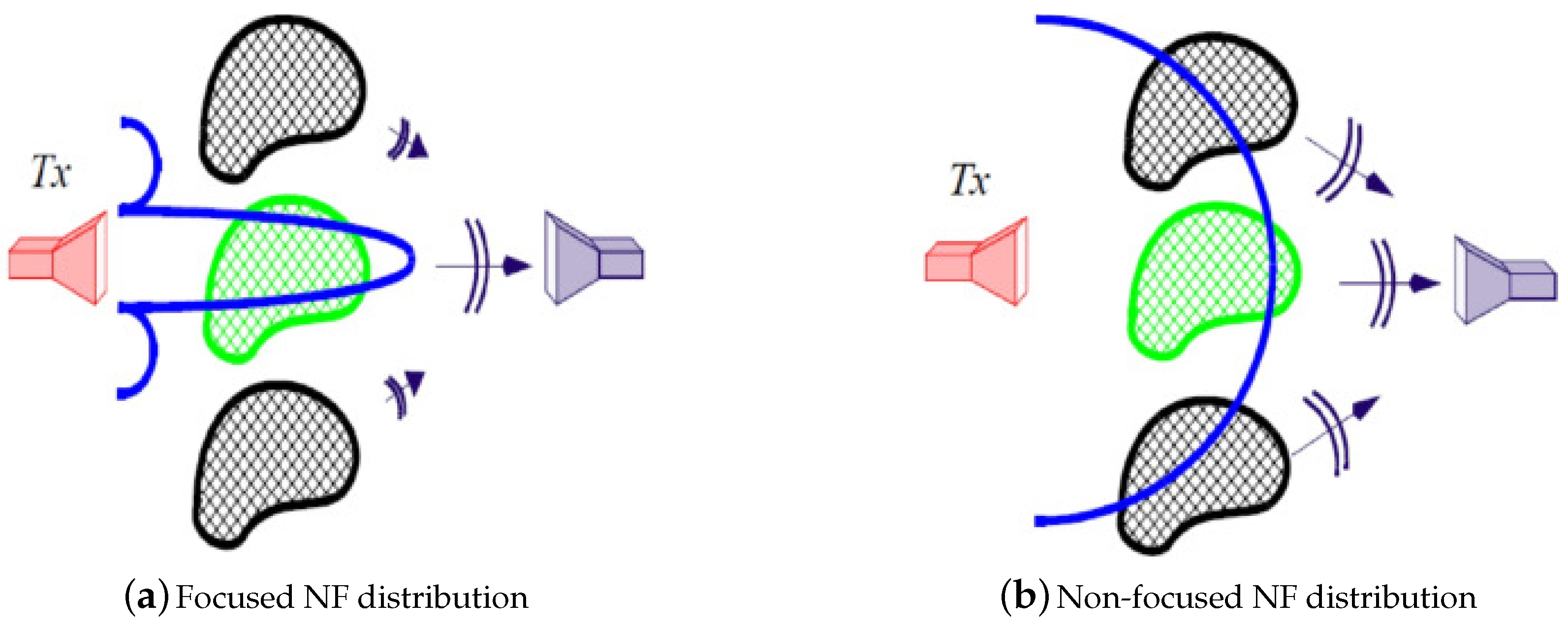
2.2. Suppressing Undesired Scattering Effects
2.3. Sufficient Measured Data
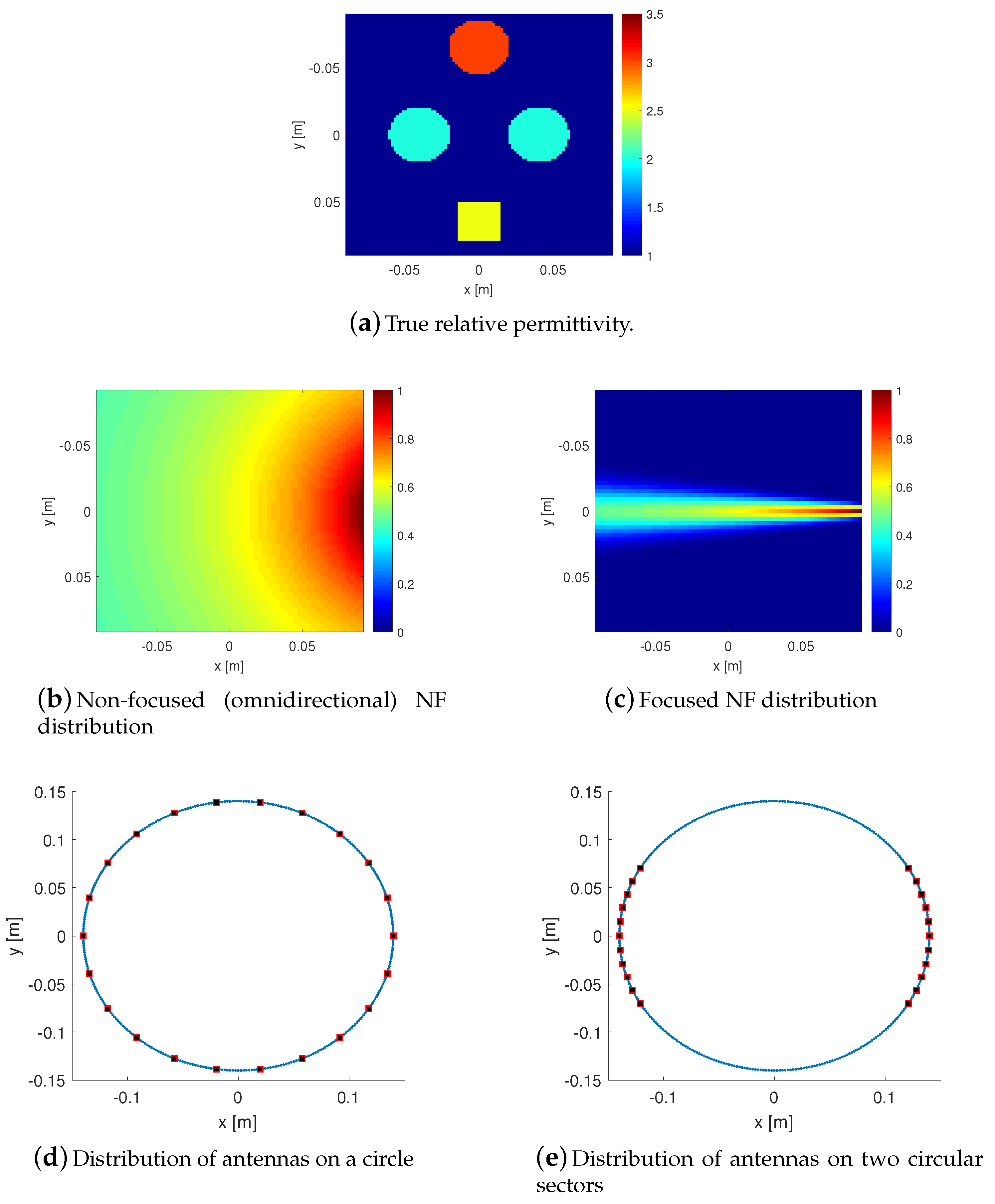
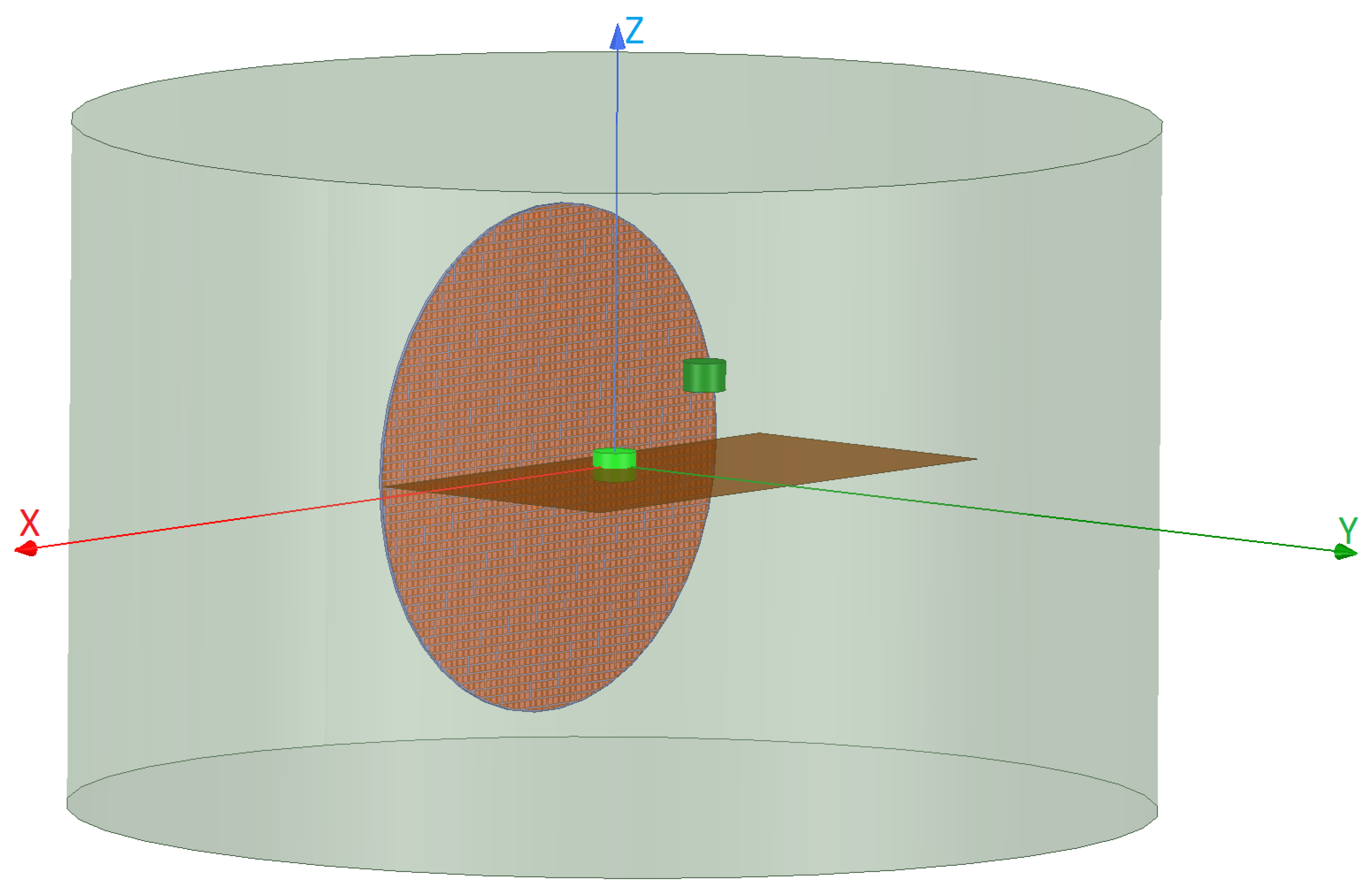
2.4. A Synthetic Test Case
3. NF Beams and Results
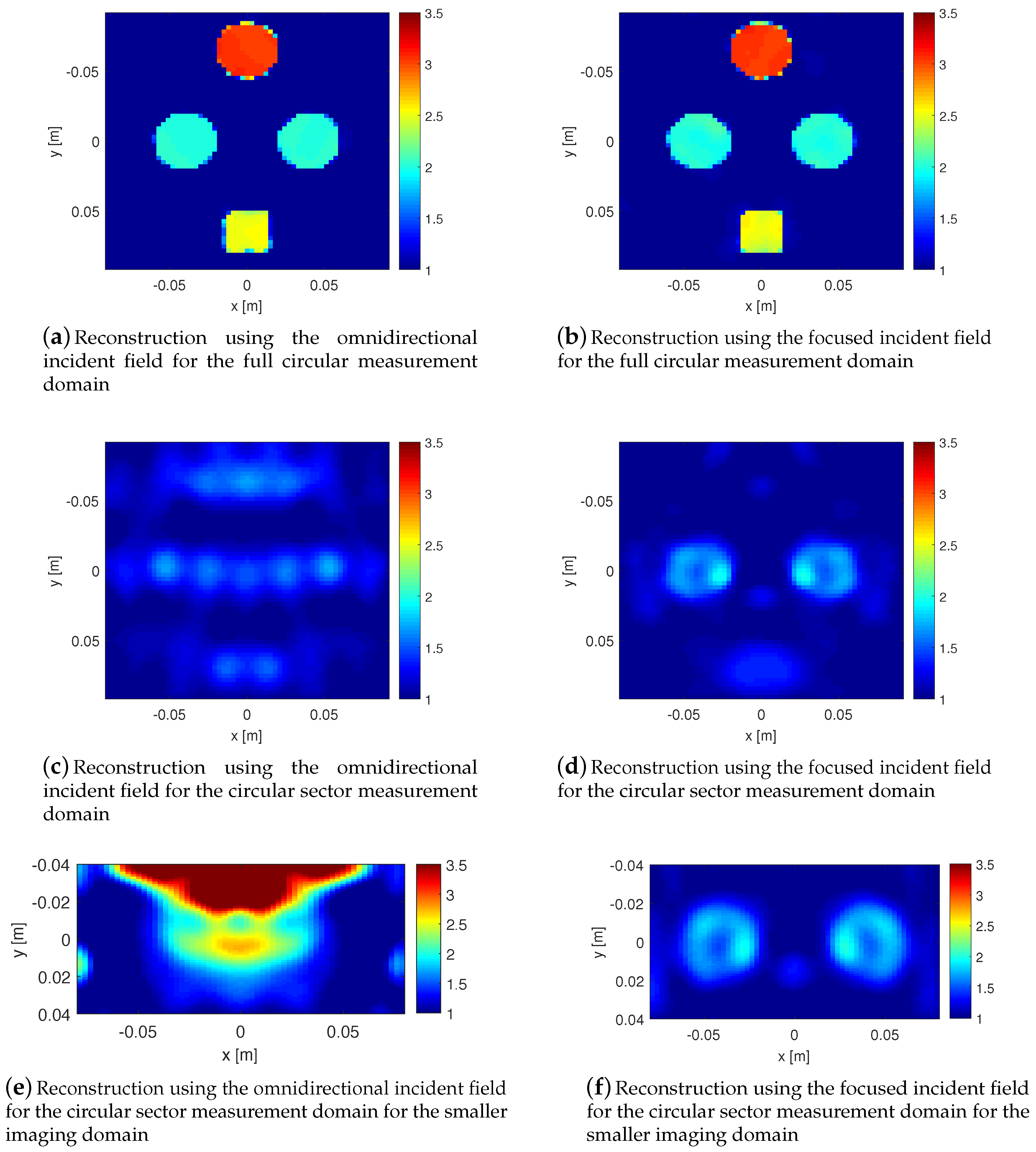
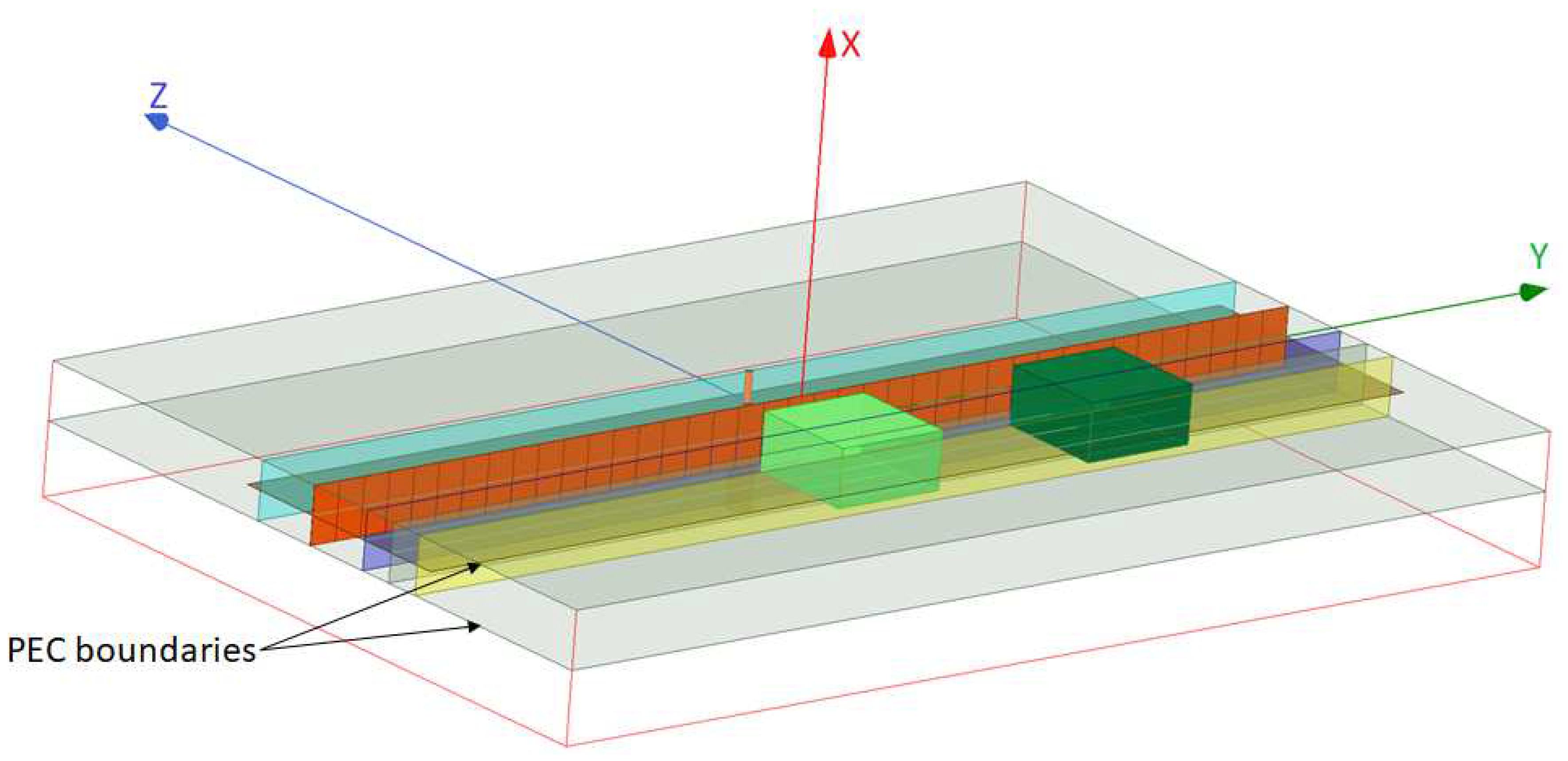
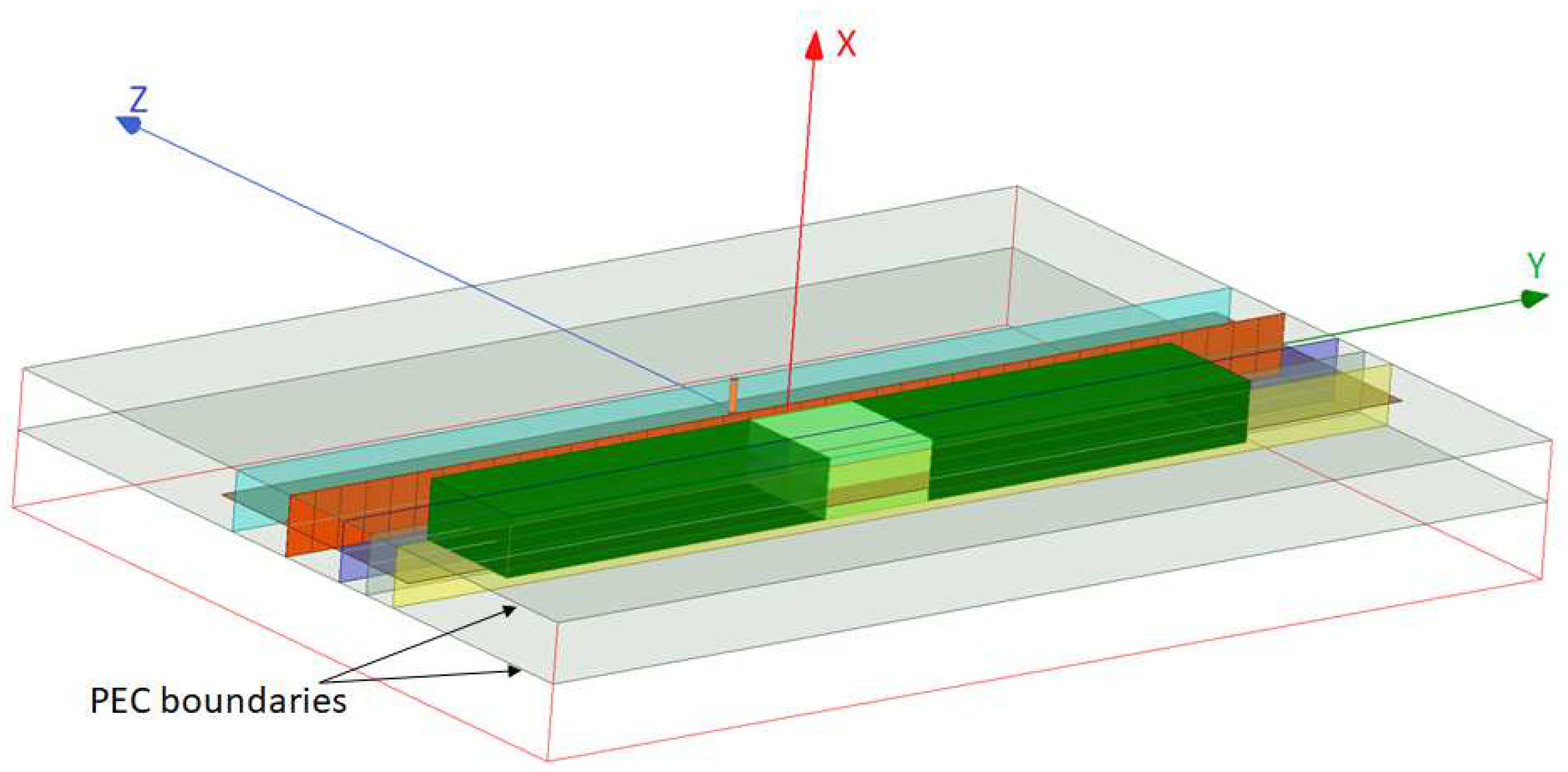
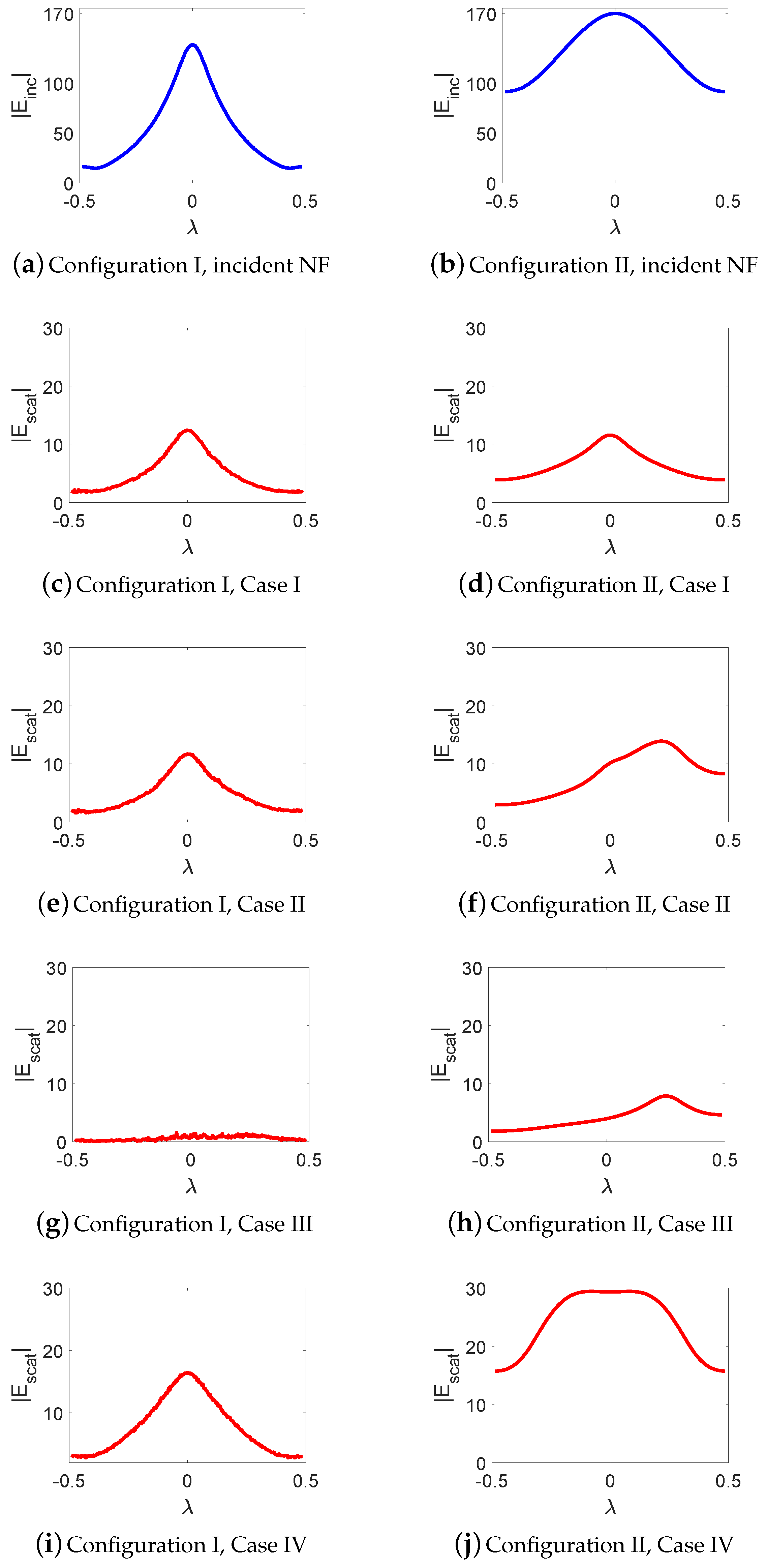
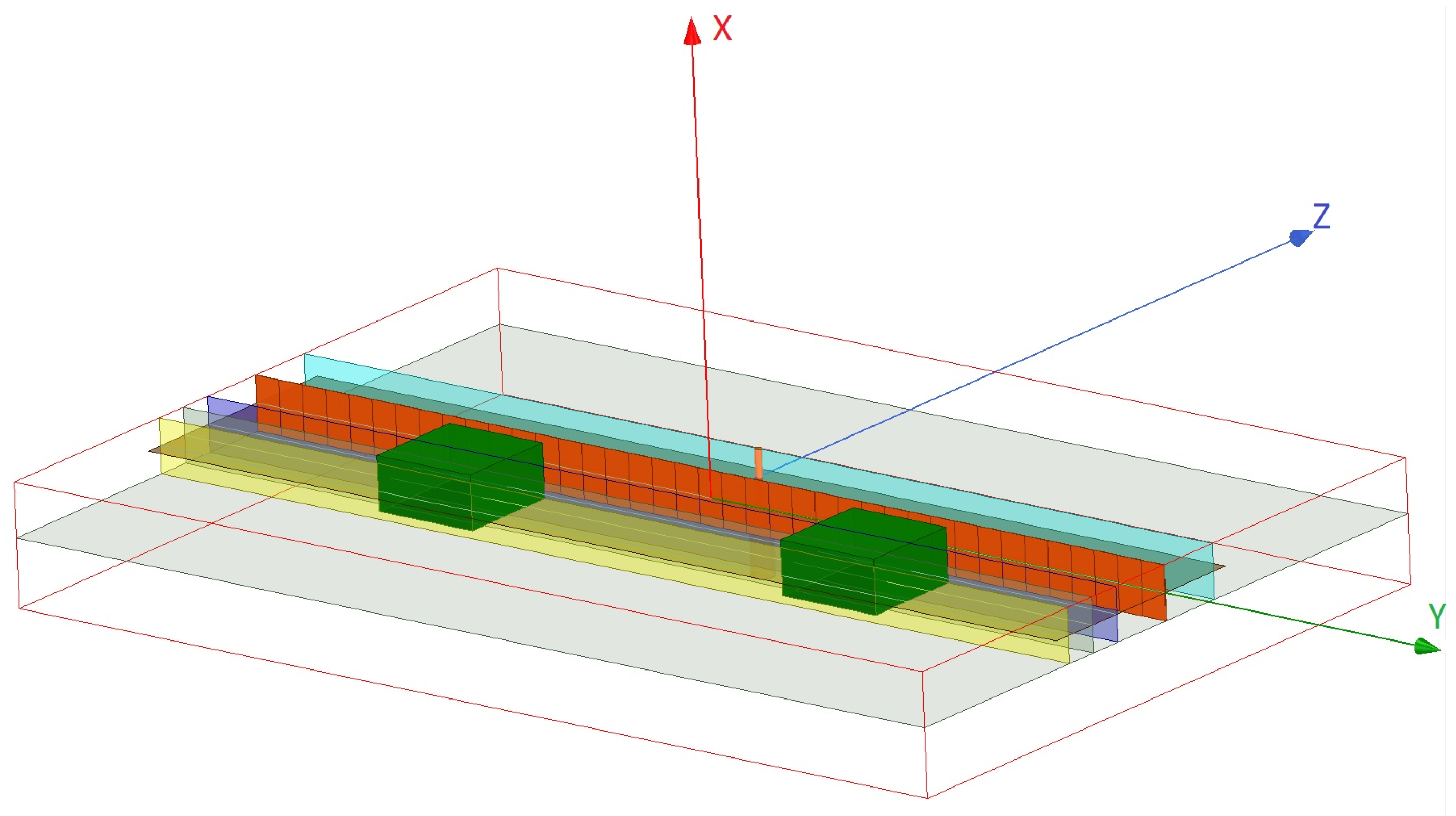
3.1. Interrogation of Objects by the NF Plate
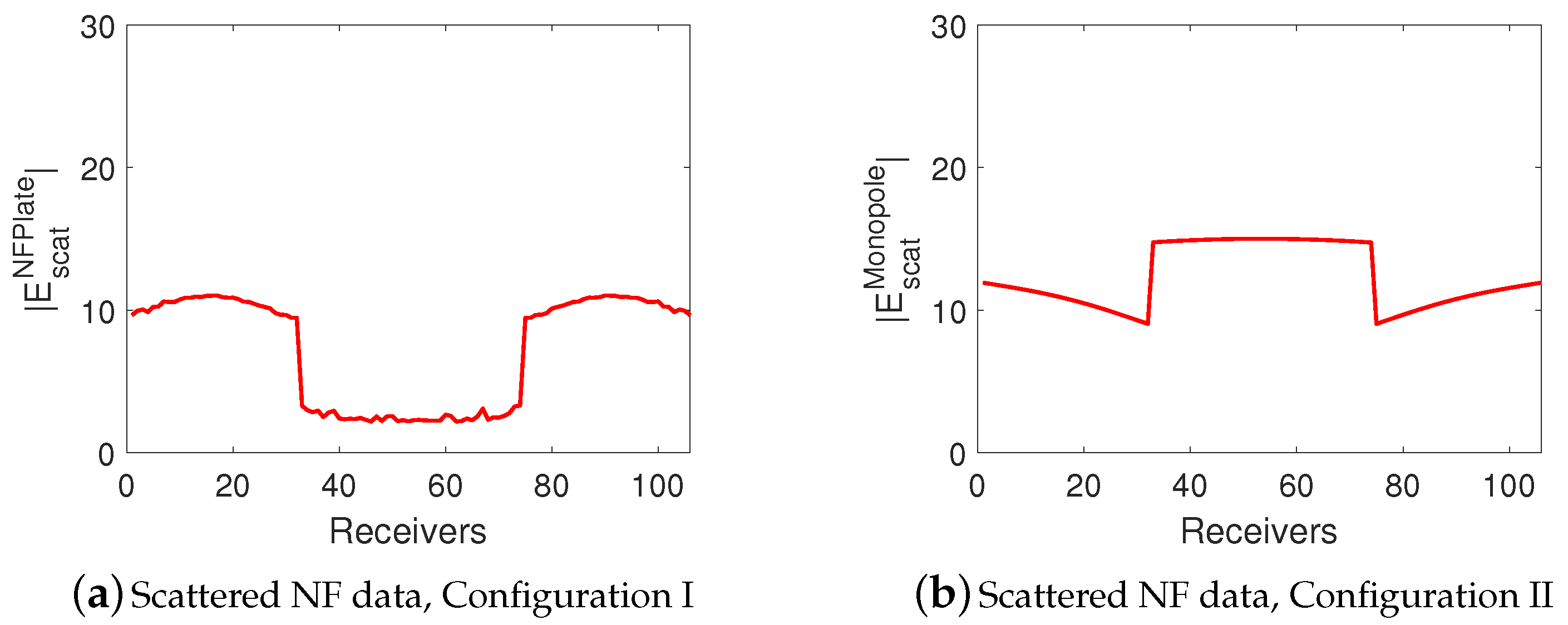
3.1.1. Analysis of the Scattered NF Data
3.1.2. Inversion Results
3.1.3. Separation Resolution Study
3.2. Interrogation of Objects by the Bessel Beam Launcher
3.2.1. Analysis of the Scattered NF Data
3.2.2. Inversion Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Visual Summary of the Different Test Cases



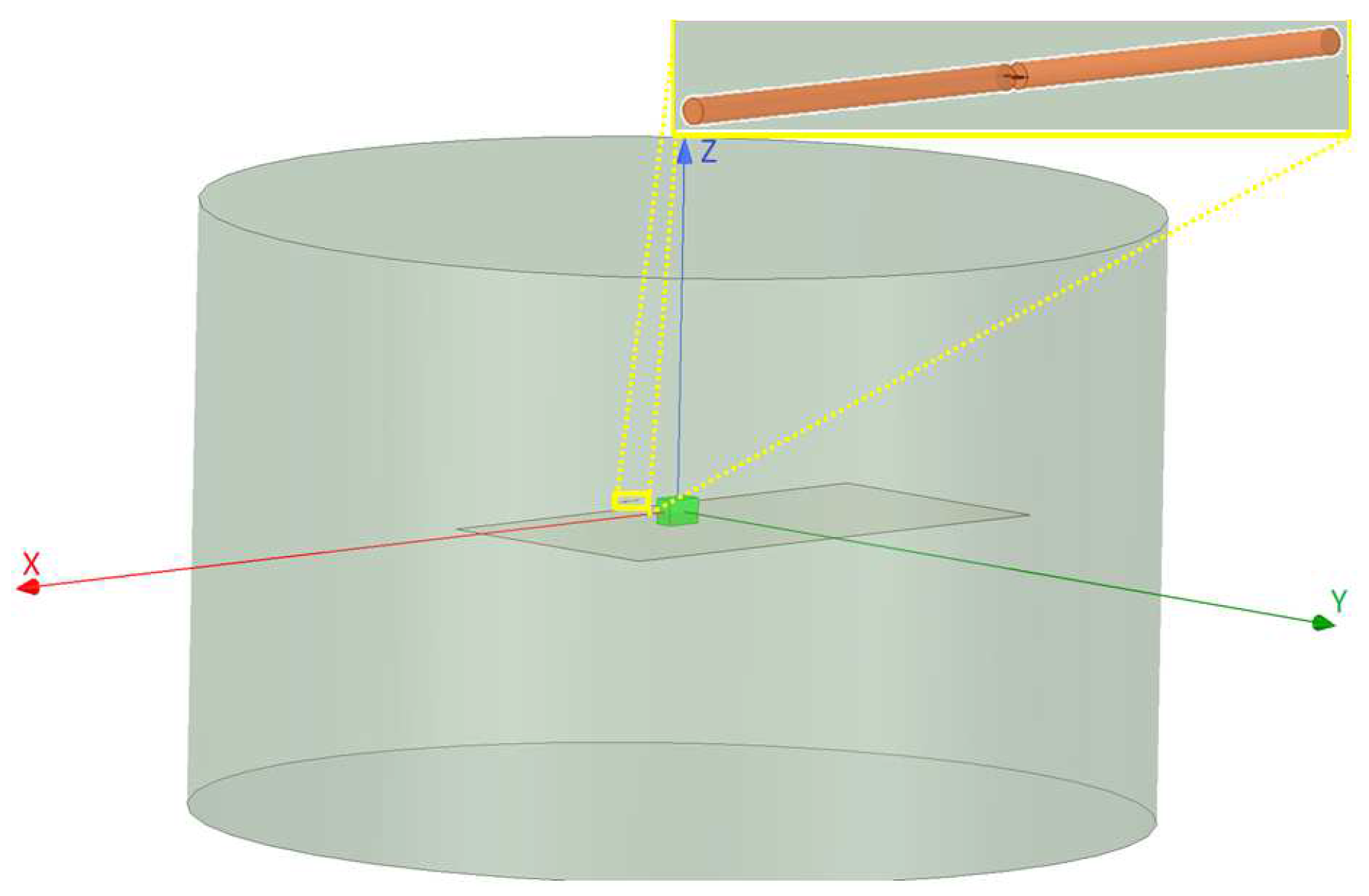
Appendix B. Simulation Details of the Separation Resolution Study
References
- Pastorino, M. Microwave Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bucci, O.M.; Bellizzi, G.; Borgia, A.; Costanzo, S.; Crocco, L.; Massa, G.D.; Scapaticci, R. Experimental Framework for Magnetic Nanoparticles Enhanced Breast Cancer Microwave Imaging. IEEE Access 2017, 5, 16332–16340. [Google Scholar] [CrossRef]
- Fear, E.C.; Hagness, S.C.; Meaney, P.M.; Okoniewski, M.; Stuchly, M.A. Enhancing breast tumor detection with near-field imaging. IEEE Microw. Mag. 2002, 3, 48–56. [Google Scholar] [CrossRef]
- Oliveri, G.; Salucci, M.; Anselmi, N.; Massa, A. Compressive Sensing as Applied to Inverse Problems for Imaging: Theory, Applications, Current Trends, and Open Challenges. IEEE Antennas Propag. Mag. 2017, 59, 34–46. [Google Scholar] [CrossRef]
- Persson, M.; Fhager, A.; Trefna, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.E.; Elam, M. Microwave-Based Stroke Diagnosis Making Global Prehospital Thrombolytic Treatment Possible. IEEE Trans. Biomed. Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mobashsher, A.T.; Abbosh, A.M.; Wang, Y. Microwave System to Detect Traumatic Brain Injuries Using Compact Unidirectional Antenna and Wideband Transceiver with Verification on Realistic Head Phantom. IEEE Trans. Microw. Theory Tech. 2014, 62, 1826–1836. [Google Scholar] [CrossRef]
- Nikolova, N.K. Introduction to Microwave Imaging; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Wu, Z.; Wang, H. Microwave Tomography for Industrial Process Imaging: Example Applications and Experimental Results. IEEE Antennas Propag. Mag. 2017, 59, 61–71. [Google Scholar] [CrossRef]
- Gibbins, D.; Byrne, D.; Henriksson, T.; Monsalve, B.; Craddock, I.J. Less Becomes More for Microwave Imaging: Design and Validation of an Ultrawide-Band Measurement Array. IEEE Antennas Propag. Mag. 2017, 59, 72–85. [Google Scholar] [CrossRef]
- Hopfer, M.; Planas, R.; Hamidipour, A.; Henriksson, T.; Semenov, S. Electromagnetic Tomography for Detection, Differentiation, and Monitoring of Brain Stroke: A Virtual Data and Human Head Phantom Study. IEEE Antennas Propag. Mag. 2017, 59, 86–97. [Google Scholar] [CrossRef]
- Boverman, G.; Davis, C.; Geimer, S.; Meaney, P.M. Image Registration for Microwave Tomography of the Breast Using Priors from Non-Simultaneous Previous Magnetic Resonance Images. IEEE J. Electromagn. RF Microw. Med. Biol. 2017, 2, 2–9. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J. Composite Tissue-Type and Probability Image for Ultrasound and Microwave Tomography. IEEE J. Multiscale Multiphys. Comput. Tech. 2016, 1, 26–35. [Google Scholar] [CrossRef]
- Jiang, H.; Li, C.; Pearlstone, D.; Fajardo, L. Ultrasound-guided microwave imaging of breast cancer: Tissue phantom and pilot clinical experiments. Med. Phys. 2005, 32, 2528–2535. [Google Scholar] [CrossRef] [PubMed]
- Scapaticci, R.; Bellizzi, G.; Catapano, I.; Crocco, L.; Bucci, O.M. An Effective Procedure for MNP-Enhanced Breast Cancer Microwave Imaging. IEEE Trans. Biomed. Eng. 2014, 61, 1071–1079. [Google Scholar] [CrossRef] [PubMed]
- Firoozy, N.; Komarov, A.S.; Landy, J.; Barber, D.G.; Mojabi, P.; Scharien, R.K. Inversion-Based Sensitivity Analysis of Snow-Covered Sea Ice Electromagnetic Profiles. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3643–3655. [Google Scholar] [CrossRef]
- Ostadrahimi, M.; Mojabi, P.; Zakaria, A.; LoVetri, J.; Shafai, L. Enhancement of Gauss–Newton Inversion Method for Biological Tissue Imaging. IEEE Trans. Microw. Theory Tech. 2013, 61, 3424–3434. [Google Scholar] [CrossRef]
- Grzegorczyk, T.M.; Meaney, P.M.; Kaufman, P.A.; diFlorio Alexander, R.M.; Paulsen, K.D. Fast 3D Tomographic Microwave Imaging for Breast Cancer Detection. IEEE Trans. Med. Imaging 2012, 31, 1584–1592. [Google Scholar] [CrossRef] [PubMed]
- De Zaeytijd, J.; Franchois, A.; Eyraud, C.; Geffrin, J.M. Full-Wave Three-Dimensional Microwave Imaging with a Regularized Gauss Newton Method; Theory and Experiment. Antennas Propag. IEEE Trans. 2007, 55, 3279–3292. [Google Scholar] [CrossRef]
- Abubakar, A.; Habashy, T.M.; Pan, G.; Li, M.K. Application of the Multiplicative Regularized Gauss Newton Algorithm for Three-Dimensional Microwave Imaging. IEEE Trans. Antennas Propag. 2012, 60, 2431–2441. [Google Scholar] [CrossRef]
- Palmeri, R.; Bevacqua, M.T.; Crocco, L.; Isernia, T.; Donato, L.D. Microwave Imaging via Distorted Iterated Virtual Experiments. IEEE Trans. Antennas Propag. 2017, 65, 829–838. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J. Overview and Classification of Some Regularization Techniques for the Gauss-Newton Inversion Method Applied to Inverse Scattering Problems. IEEE Trans. Antennas Propag. 2009, 57, 2658–2665. [Google Scholar] [CrossRef]
- Golnabi, A.H.; Meaney, P.M.; Paulsen, K.D. Tomographic Microwave Imaging with Incorporated Prior Spatial Information. IEEE Trans. Microw. Theory Tech. 2013, 61, 2129–2136. [Google Scholar] [CrossRef]
- Neira, L.M.; Veen, B.D.V.; Hagness, S.C. High-Resolution Microwave Breast Imaging using a 3-D Inverse Scattering Algorithm with a Variable-Strength Spatial Prior Constraint. IEEE Trans. Antennas Propag. 2017, 65, 6002–6014. [Google Scholar] [CrossRef]
- Baran, A.; Kurrant, D.; Zakaria, A.; Fear, E.; LoVetri, J. Breast cancer imaging using microwave tomography with radar-derived prior information. In Proceedings of the 2014 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Memphis, TN, USA, 6–11 July 2014; p. 259. [Google Scholar]
- Mojabi, P.; LoVetri, J.; Shafai, L. A Multiplicative Regularized Gauss-Newton Inversion for Shape and Location Reconstruction. IEEE Trans. Antennas Propag. 2011, 59, 4790–4802. [Google Scholar] [CrossRef]
- Meaney, P.M.; Navin, K.; Yagnamurthy, K.D.P. Pre-scaled two-parameter Gauss-Newton image reconstruction to reduce property recovery imbalance. Phys. Med. Biol. 2002, 47, 1101–1119. [Google Scholar] [CrossRef] [PubMed]
- Bayat, N.; Mojabi, P. A Mathematical Framework to Analyze the Achievable Resolution from Microwave Tomography. IEEE Trans. Antennas Propag. 2016, 64, 1484–1489. [Google Scholar] [CrossRef]
- Li, D.; Meaney, P.M.; Raynolds, T.; Pendergrass, S.A.; Fanning, M.W.; Paulsen, K.D. Parallel-detection microwave spectroscopy system for breast imaging. Rev. Sci. Instrum. 2004, 75, 2305–2313. [Google Scholar] [CrossRef]
- Ostadrahimi, M.; Mojabi, P.; Gilmore, C.; Zakaria, A.; Noghanian, S.; Pistorius, S.; LoVetri, J. Analysis of Incident Field Modeling and Incident/Scattered Field Calibration Techniques in Microwave Tomography. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 900–903. [Google Scholar] [CrossRef]
- Meaney, P.; Paulsen, K.; Chang, J.; Fanning, M.; Hartov, A. Nonactive antenna compensation for fixed-array microwave imaging. II. Imaging results. IEEE Trans. Med. Imaging 1999, 18, 508–518. [Google Scholar] [CrossRef] [PubMed]
- Bourqui, J.; Okoniewski, M.; Fear, E.C. Balanced Antipodal Vivaldi Antenna with Dielectric Director for Near-Field Microwave Imaging. IEEE Trans. Antennas Propag. 2010, 58, 2318–2326. [Google Scholar] [CrossRef]
- Bayat, N.; Mojabi, P. On an Antenna Design for 2D Scalar Near-Field Microwave Tomography. Appl. Comput. Electromagn. Soc. J. 2015, 30, 589–598. [Google Scholar]
- Bayat, N.; Mojabi, P. The Effect of Antenna Incident Field Distribution on Microwave Tomography Reconstruction. Prog. Electromagn. Res. 2014, 145, 153–161. [Google Scholar] [CrossRef]
- Bayat, N.; Mojabi, P. Near-field microwave imaging using focused near-field beams: An approach to mitigate undesired scattering effects. In Proceedings of the 2nd URSI Atlantic Radio Science Meeting (URSI AT-RASC), Las Palmas, Spain, 28 May–1 June 2018. [Google Scholar]
- Bellizzi, G.G.; Iero, D.A.M.; Crocco, L.; Isernia, T. Three-Dimensional Field Intensity Shaping: The Scalar Case. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 360–363. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Bevacqua, M.T.; Battaglia, G.M.; Crocco, L.; Isernia, T. Advances in Target Conformal SAR Deposition For Hyperthermia Treatment Planning. In Proceedings of the 2nd URSI Atlantic Radio Science Meeting (URSI AT-RASC), Las Palmas, Spain, 28 May–1 June 2018. [Google Scholar]
- Crocco, L.; Donato, L.D.; Iero, D.A.M.; Isernia, T. A New Strategy to Constrained Focusing in Unknown Scenarios. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1450–1453. [Google Scholar] [CrossRef]
- Van den Berg, P.M.; Kleinman, R.E. A contrast source inversion method. Inverse Probl. 1997, 13, 1607–1620. [Google Scholar] [CrossRef]
- Oristaglio, M.; Blok, H. Wavefield Imaging and Inversion in Electromagnetics and Acoustics; Lecture Notes; Delft University: Delft, The Netherlands, 1995. [Google Scholar]
- Chew, W.C.; Wang, Y.M.; Otto, G.; Lesselier, D.; Bolomey, J.C. On the inverse source method of solving inverse scattering problems. Inverse Probl. 1994, 10, 547. [Google Scholar] [CrossRef]
- Abubakar, A.; van den Berg, P.M.; Mallorqui, J.J. Imaging of biomedical data using a multiplicative regularized contrast source inversion method. IEEE Trans. Microw. Theory Tech. 2002, 50, 1761–1777. [Google Scholar] [CrossRef]
- Parini, C.; Gregson, S.; McCormick, J.; van Rensburg, D.J. Theory and Practice of Modern Antenna Range Measurements; The Institution of Engineering and Technology: Stevenage, UK, 2014. [Google Scholar]
- Balanis, C. Antenna Theory: Analysis and Design; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bucci, O.M.; Isernia, T. Electromagnetic inverse scattering: Retrievable information and measurement strategies. Radio Sci. 1997, 32, 2123–2137. [Google Scholar] [CrossRef] [Green Version]
- Abubakar, A.; van den Berg, P.M.; Semenov, S.Y. A Robust iterative method for Born inversion. IEEE Trans. Geosci. Remote Sens. 2004, 42, 342–354. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J. Microwave Biomedical Imaging Using the Multiplicative Regularized Gauss-Newton Inversion. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 645–648. [Google Scholar] [CrossRef]
- Grbic, A.; Jiang, L.; Merlin, R. Near-field Plates: Subdiffraction focusing with patterned surfaces. Science 2008, 320, 511–513. [Google Scholar] [CrossRef] [PubMed]
- Ettorre, M.; Grbic, A. Generation of Propagating Bessel Beams Using Leaky-Wave Modes. IEEE Trans. Antennas Propag. 2012, 60, 3605–3613. [Google Scholar] [CrossRef]
- Ettorre, M.; Rudolph, S.M.; Grbic, A. Generation of Propagating Bessel Beams Using Leaky-Wave Modes: Experimental Validation. IEEE Trans. Antennas Propag. 2012, 60, 2645–2653. [Google Scholar] [CrossRef]
- Bouchal, Z.; Wagner, J.; Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Commun. 1998, 151, 207–211. [Google Scholar] [CrossRef]
- Ahmed, N.; Lavery, M.P.J.; Huang, H.; Xie, G.; Ren, Y.; Yan, Y.; Willner, A.E. Experimental demonstration of obstruction-tolerant free-space transmission of two 50-Gbaud QPSK data channels using Bessel beams carrying orbital angular momentum. In Proceedings of the 2014 European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3. [Google Scholar]
- Zvolensky, T.; Gollub, J.N.; Marks, D.L.; Smith, D.R. Design and Analysis of a W-Band Metasurface-Based Computational Imaging System. IEEE Access 2017, 5, 9911–9918. [Google Scholar] [CrossRef]
- Epstein, A.; Eleftheriades, G.V. Huygens’ metasurfaces via the equivalence principle: Design and applications. J. Opt. Soc. Am. B 2016, 33, A31–A50. [Google Scholar] [CrossRef]





| Cases | Calibration Object’s Permittivity | Configuration I (Focused) | Configuration II (Non-Focused) |
|---|---|---|---|
| Case I | |||
| Case II | |||
| Case I | |||
| Case II |
| Cases | Calibration Object’s Permittivity | Configuration I (Focused) | Configuration II (Non-Focused) |
|---|---|---|---|
| Case I | |||
| Case II | |||
| Case III | |||
| Case IV |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayat, N.; Mojabi, P. On the Use of Focused Incident Near-Field Beams in Microwave Imaging. Sensors 2018, 18, 3127. https://doi.org/10.3390/s18093127
Bayat N, Mojabi P. On the Use of Focused Incident Near-Field Beams in Microwave Imaging. Sensors. 2018; 18(9):3127. https://doi.org/10.3390/s18093127
Chicago/Turabian StyleBayat, Nozhan, and Puyan Mojabi. 2018. "On the Use of Focused Incident Near-Field Beams in Microwave Imaging" Sensors 18, no. 9: 3127. https://doi.org/10.3390/s18093127
APA StyleBayat, N., & Mojabi, P. (2018). On the Use of Focused Incident Near-Field Beams in Microwave Imaging. Sensors, 18(9), 3127. https://doi.org/10.3390/s18093127




