Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins
Abstract
1. Introduction
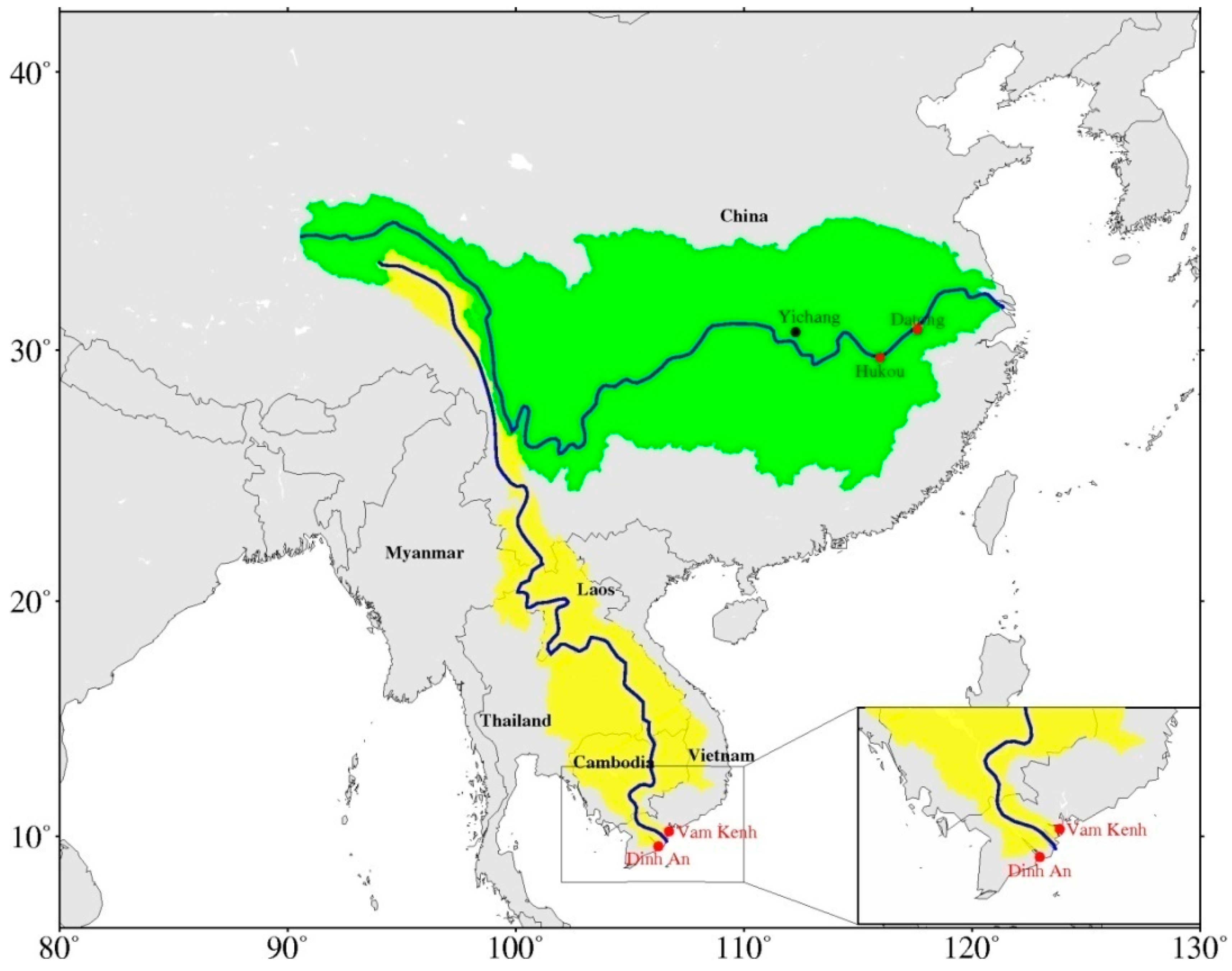
2. Geographical Setting of the Mekong River Basin (MRB) and the Yangtze River Basin (YRB)
3. Data Description
3.1. Ground-Based Observation Data
3.2. Spaceborne Data and Their Corresponding Derived Drought Indices
3.2.1. TRMM Precipitation and Its Corresponding Drought Index (TRMM-SPI)
3.2.2. GRACE Terrestrial Water Storage (TWS) and Its Corresponding Drought Index (GRACE-DSI)
4. Methodology and Assessment Scheme
4.1. Methodology
4.2. Assessment Schemes
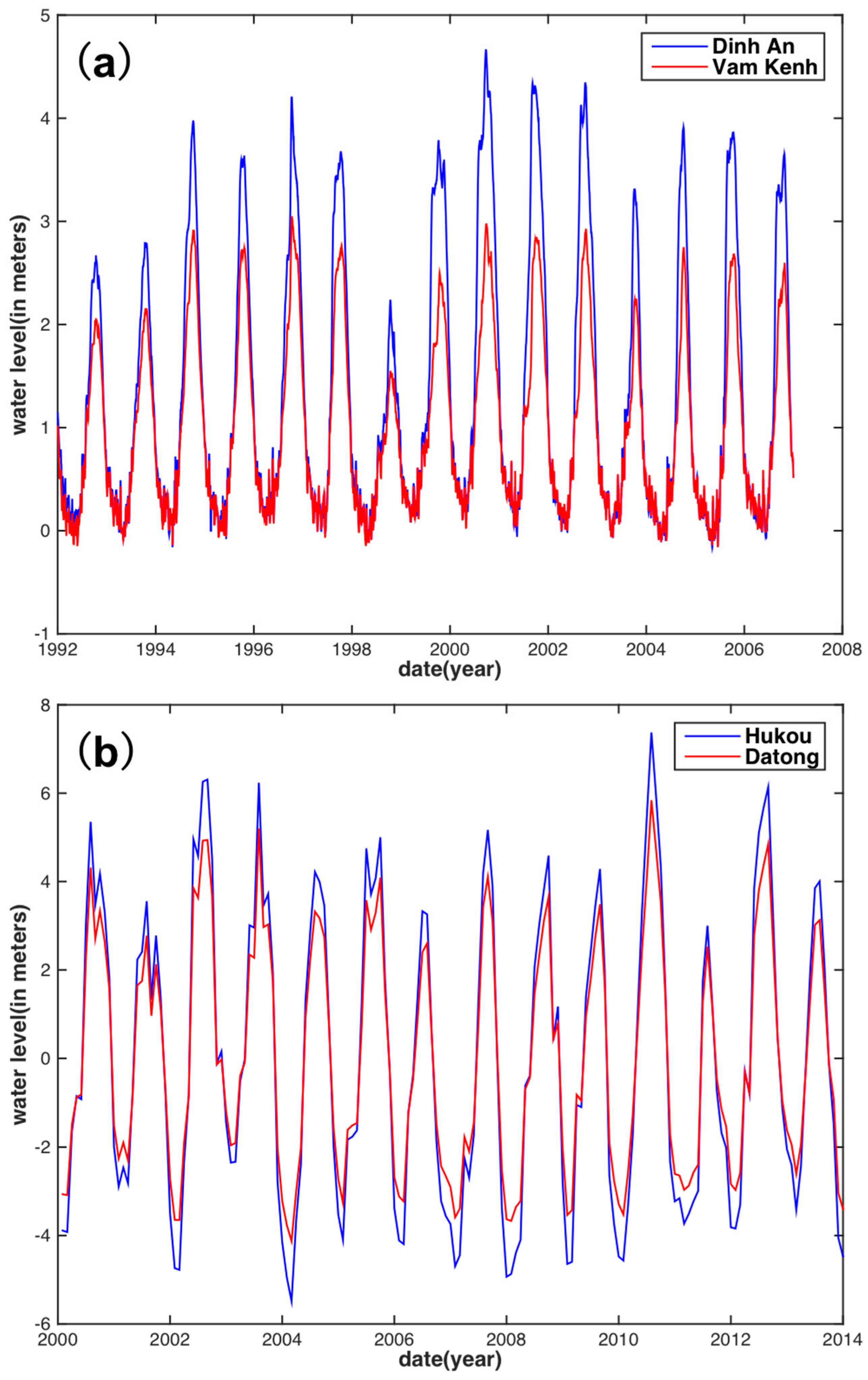
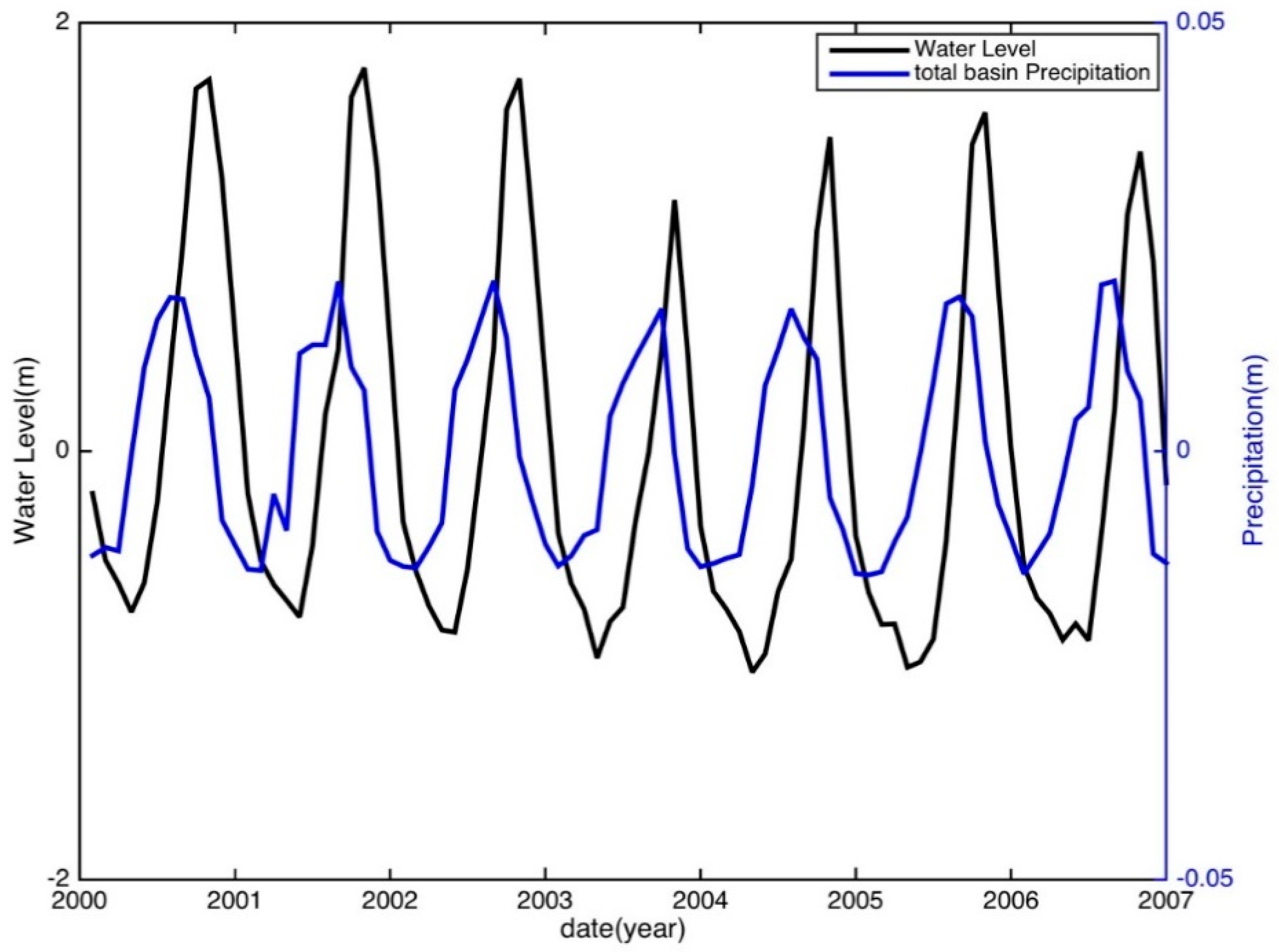
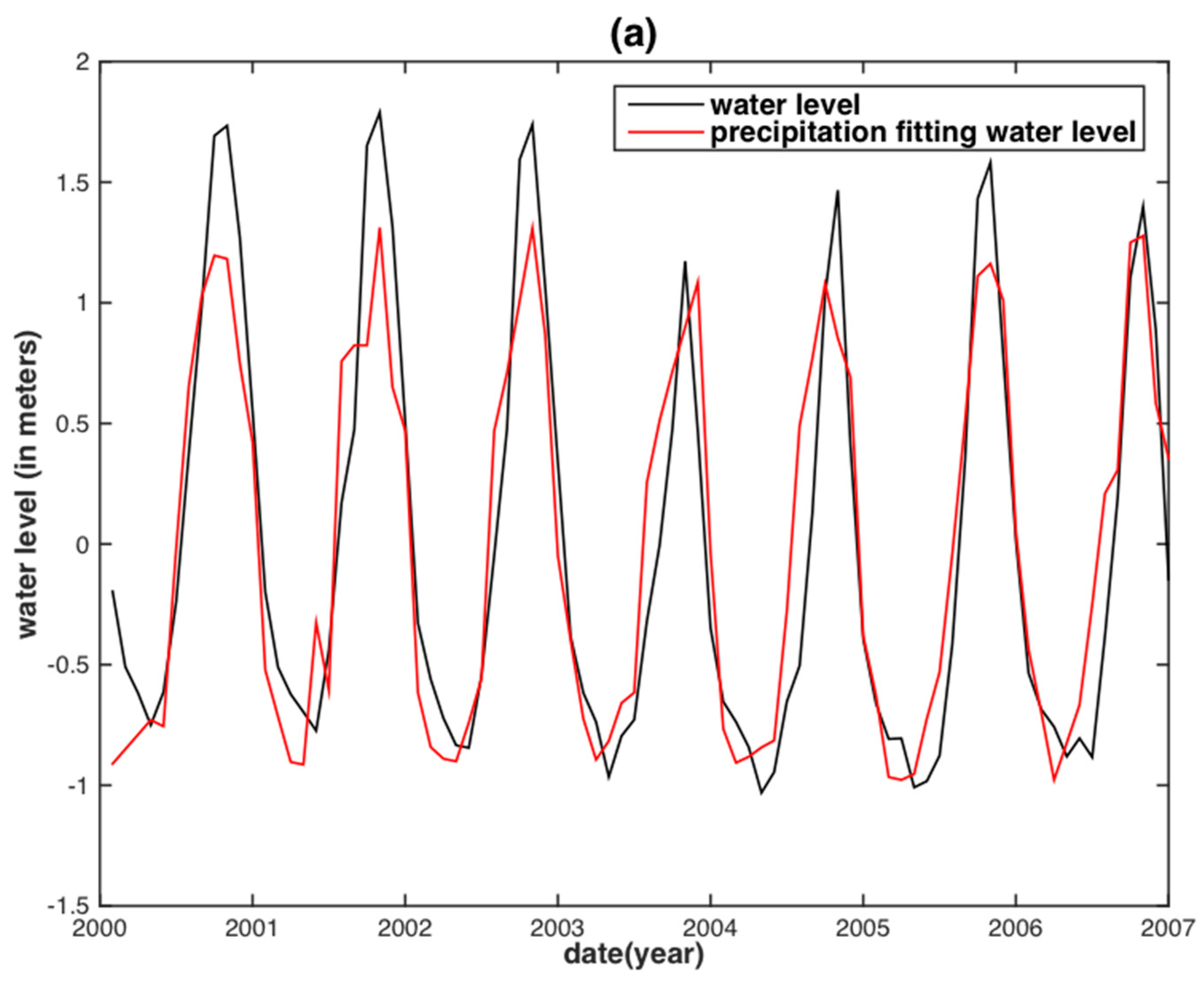
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coe, M.T.; Charon, M.B. Calculation of river discharge and prediction of lake height from satellite radar altimetry: Example for the Lake Chad basin. Water Resour. Res. 2004, 40, 1–11. [Google Scholar] [CrossRef]
- Jung, H.C.; Alsdorf, D.; Moritz, M.; Lee, H.; Vassolo, S. Analysis of the relationship between flooding area and water height in the Logone floodplain. Phys. Chem. Earth Parts A/B/C 2011, 36, 232–240. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River Discharge Estimation by Using Altimetry Data and Simplified Flood Routing Modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef]
- Grimaldi, S.; Li, Y.; Pauwels, V.R.; Walker, J.P. Remote sensing-derived water extent and level to constrain hydraulic flood forecasting models: Opportunities and challenges. Surv. Geophys. 2016, 37, 977–1034. [Google Scholar] [CrossRef]
- Jarihani, A.A.; Callow, J.N.; Johansen, K.; Gouweleeuw, B. Evaluation of multiple satellite altimetry data for studying inland water bodies and river floods. J. Hydrol. 2013, 505, 78–90. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Lettenmaier, D.P. Tracking fresh water from space. Science 2003, 301, 1491–1494. [Google Scholar] [CrossRef] [PubMed]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of river level variations with satellite altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- De Oliveira Campos, I.; Mercier, F.; Maheu, C.; Cochonneau, G.; Kosuth, P.; Blitzkow, D.; Cazenave, A. Temporal variations of river basin waters from Topex/Poseidon satellite altimetry. Application to the Amazon basin. C.R. de l’Académie des Sci.-Ser. IIA-Earth Planet. Sci. 2001, 333, 633–643. [Google Scholar] [CrossRef]
- Maheu, C.; Cazenave, A.; Mechoso, C.R. Water level fluctuations in the Plata basin (South America) from Topex/Poseidon satellite altimetry. Geophys. Res. Lett. 2003, 30, 1143. [Google Scholar] [CrossRef]
- Ovakoglou, G.; Alexandridis, T.K.; Crisman, T.L.; Skoulikaris, C.; Vergos, G.S. Use of MODIS satellite images for detailed lake morphometry: Application to basins with large water level fluctuations. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 37–46. [Google Scholar] [CrossRef]
- Guo, J.; Chang, X.; Gao, Y.; Sun, J.; Hwang, C. Lake level variations monitored with satellite altimetry waveform retracking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 80–86. [Google Scholar] [CrossRef]
- Kruus, J.; Duetsch, P.L.; Ferguson, H.L. Flood applications of satellite imagery. In Proceedings of the Fifth Annual William, Satellite Hydrology, T. Pecora Memorial Symposium on Remote Sensing, Bethesda, MD, USA, 10–15 June 1979. [Google Scholar]
- Usachev, V.F. Evaluation of flood plain inundations by remote sensing methods. In Hydrological Applications of Remote Sensing and Remote Data Transmission, Proceedings of the XVIIIth General Assembly of the International Union of Geodesy and Geophysics, Hamburg, Germany, 15–27 August 1983; International Association of Hydrological Sciences: London, UK, 1983. [Google Scholar]
- Ferreira, V.G.; Zibrila, A.; Jia, X.; Zheng, G.; Samuel, A.A. Land Water-Storage Variability over West Africa: Inferences from Space-Borne Sensors. Water 2018, 10, 380. [Google Scholar] [CrossRef]
- Westerberg, I.; Guerrero, J.L.; Seibert, J.; Beven, K.J.; Halldin, S. Stage-discharge uncertainty derived with a non-stationary rating curve in the Choluteca River, Honduras. Hydrol. Process. 2011, 25, 603–613. [Google Scholar] [CrossRef]
- Alexandridis, T.K.; Monachou, S.; Skoulikaris, C.; Kalopesa, E.; Zalidis, G.C. Investigation of the temporal relation of remotely sensed coastal water quality with GIS modelled upstream soil erosion. Hydrol. Process. 2014, 29, 2373–2384. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, 1–24. [Google Scholar] [CrossRef]
- Omute, P.; Corner, R.; Awange, J.L. The use of NDVI and its derivatives for monitoring Lake Victoria’s water level and drought conditions. Water Resour. Manag. 2012, 26, 1591–1613. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM Multisatellite Precipitation Analysis (TMPA) and its utility in hydrologic prediction in the La Plata Basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Wagner, S.; Kunstmann, H.; Bárdossy, A.; Conrad, C.; Colditz, R.R. Water balance estimation of a poorly gauged catchment in West Africa using dynamically downscaled meteorological fields and remote sensing information. Phys. Chem. Earth Parts A/B/C 2009, 34, 225–235. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Ye, X. Dry/wet conditions monitoring based on TRMM rainfall data and its reliability validation over Poyang Lake Basin, China. Water 2013, 5, 1848–1864. [Google Scholar] [CrossRef]
- Naumann, G.; Barbosa, P.; Carrao, H.; Singleton, A.; Vogt, J. Monitoring drought conditions and their uncertainties in Africa using TRMM data. J. Appl. Meteorol. Climatol. 2012, 51, 1867–1874. [Google Scholar] [CrossRef]
- Mutuga, K.J.; Nyadawa, M.O.; Home, P.G. Use of downscaled tropical rainfall measuring mission data for meteorological drought monitoring: Case study of Narumoru catchment. Int. J. Adv. Eng. Technol. 2014, 7, 1375–1385. [Google Scholar]
- Yan, N.; Wu, B.; Chang, S.; Bao, X. Evaluation of TRMM Precipitation Product for Meteorological Drought Monitoring in Hai Basin. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 012093. [Google Scholar] [CrossRef]
- Tao, H.; Fischer, T.; Zeng, Y.; Fraedrich, K. Evaluation of TRMM 3B43 precipitation data for drought monitoring in Jiangsu Province, China. Water 2016, 8, 221. [Google Scholar] [CrossRef]
- Tan, M.L.; Tan, K.C.; Chua, V.P.; Chan, N.W. Evaluation of TRMM product for monitoring drought in the Kelantan River Basin, Malaysia. Water 2017, 9, 57. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Crowley, J.W.; Mitrovica, J.X.; Bailey, R.C.; Tamisiea, M.E.; Davis, J.L. Land water storage within the Congo Basin inferred from GRACE satellite gravity data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE terrestrial water storage data into a land surface model: Results for the Mississippi River basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Forman, B.A.; Reichle, R.H.; Rodell, M. Assimilation of terrestrial water storage from GRACE in a snow-dominated basin. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
- Lee, L.J.E.; Lawrence, D.S.L.; Price, M. Analysis of water-level response to rainfall and implications for recharge pathways in the Chalk aquifer, SE England. J. Hydrol. 2006, 330, 604–620. [Google Scholar] [CrossRef]
- Jiang, T.; Su, B.; Hartmann, H. Temporal and spatial trends of precipitation and river flow in the Yangtze River Basin, 1961–2000. Geomorphology 2007, 85, 143–154. [Google Scholar] [CrossRef]
- Awange, J.L.; Sharifi, M.A.; Ogonda, G.; Wickert, J.; Grafarend, E.W.; Omulo, M.A. The falling Lake Victoria water level: GRACE, TRIMM and CHAMP satellite analysis of the lake basin. Water Resour. Manag. 2008, 22, 775–796. [Google Scholar] [CrossRef]
- Singh, A.; Seitz, F.; Schwatke, C. Inter-annual water storage changes in the Aral Sea from multi-mission satellite altimetry, optical remote sensing, and GRACE satellite gravimetry. Remote Sens. Environ. 2012, 123, 187–195. [Google Scholar] [CrossRef]
- Frappart, F.; Seyler, F.; Martinez, J.M.; Leon, J.G.; Cazenave, A. Floodplain water storage in the Negro River basin estimated from microwave remote sensing of inundation area and water levels. Remote Sens. Environ. 2005, 99, 387–399. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, K.; Yang, Y.; Qi, L.; Hayashi, S.; Watanabe, M. Measuring water storage fluctuations in Lake Dongting, China, by Topex/Poseidon satellite altimetry. Environ. Monit. Assess. 2006, 115, 23–37. [Google Scholar] [CrossRef] [PubMed]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993. [Google Scholar]
- Zhao, M.; Velicogna, I.; Kimball, J.S. Satellite observations of regional drought severity in the continental United States using GRACE-based terrestrial water storage changes. J. Clim. 2017, 30, 6297–6308. [Google Scholar] [CrossRef]
- Liu, S.; Lu, P.; Liu, D.; Jin, P.; Wang, W. Pinpointing the sources and measuring the lengths of the principal rivers of the world. Int. J. Dig. Earth 2009, 2, 80–87. [Google Scholar] [CrossRef]
- MRC (Mekong River Commission). Overview of the Hydrology of the Mekong Basin; Mekong River Commission: Vientiane, Laos, 2005; Volume 82. [Google Scholar]
- Xue, Z.; Liu, J.P.; Ge, Q. Changes in hydrology and sediment delivery of the Mekong River in the last 50 years: Connection to damming, monsoon, and ENSO. Earth Surf. Process. Landf. 2011, 36, 296–308. [Google Scholar] [CrossRef]
- Wang, B.; Lin, H. Rainy Season of the Asian–Pacific Summer Monsoon. J. Clim. 2002, 15, 386–398. [Google Scholar] [CrossRef]
- Gupta, A.; Liew, S.C. The Mekong from satellite imagery: A quick look at a large river. Geomorphology 2007, 85, 259–274. [Google Scholar] [CrossRef]
- Jacobs, J.W. The Mekong River Commission: Transboundary water resources planning and regional security. Geogr. J. 2002, 168, 354–364. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Jiang, T.; Gemmer, M.; Becker, S. Precipitation, temperature and runoff analysis from 1950 to 2002 in the Yangtze basin, China. Hydrol. Sci. J. Sci. Hydrol. 2005, 50, 65–80. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.; Jiang, T.; Wu, Y. Possible influence of ENSO on annual maximum streamflow of the Yangtze River, China. J. Hydrol. 2007, 333, 265–274. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, Z.; Liu, C. Spatial and temporal variability of daily temperature during 1961–2010 in the Yangtze River Basin, China. Quat. Int. 2013, 304, 33–42. [Google Scholar] [CrossRef]
- Tong, Z.J.; Han, Q.W. River Channel Morphology and Evolution Below Danjiangkou Dam, Hangjiang River (Interior Report in Chinese); Hydrological Bureau of Changjiang River Planning Office: Wuhan, China, 1982; pp. 23–26. [Google Scholar]
- Chen, Z.; Li, J.; Shen, H.; Wang, Z. Yangtze River of China: Historical analysis of discharge variability and sediment flux. Geomorphology 2001, 41, 77–91. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Y. Impact on the Yangtze (Changjiang) estuary from its drainage basin: Sediment load and discharge. Chin. Sci. Bull. 2001, 46, 73–80. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, Y.; Shi, Y. Climate change effect on hydrological processes over the Yangtze River basin. Quat. Int. 2011, 244, 202–210. [Google Scholar] [CrossRef]
- Ding, Y.; Chan, J.C.L. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Yu, F.; Chen, Z.; Ren, X.; Yang, G. Analysis of historical floods on the Yangtze River, China: Characteristics and explanations. Geomorphology 2009, 113, 210–216. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Lau, K.M. Interannual variability of the Asian summer monsoon: Contrasts between the Indian and the western North Pacific–East Asian monsoons. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Wu, R.; Wang, B. A contrast of the East Asian summer monsoon–ENSO relationship between 1962–77 and 1978–93. J. Clim. 2002, 15, 3266–3279. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Du, J.; Fang, J.; Xu, W.; Shi, P. Analysis of dry/wet conditions using the standardized precipitation index and its potential usefulness for drought/flood monitoring in Hunan Province, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 377–387. [Google Scholar] [CrossRef]
- Yuan, W.; Zhou, G. Comparison between standardized precipitation index and Z-index in China (in Chinese). Acta Phytoecol. Sin. 2004, 28, 523–529. [Google Scholar]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Szalai, S.; Szinell, C. Comparison of Two Drought Indices for Drought Monitoring in Hungary—A Case Study. In Drought and Drought Mitigation in Europe; Vogt, J.V., Somma, F., Eds.; Springer: Dordrecht, The Netherlands, 2000; Volume 14, pp. 161–166. ISBN 978-94-015-9472-1. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Asiah, Z. An investigation on the closure of the water budget methods over Volta Basin using multi-satellite data. In International Association of Geodesy Symposia; Jin, S., Barzaghi, R., Eds.; Springer: Cham, Switzerland, 2015; Volume 144, pp. 171–178. ISBN 978-3-319-39820-4. [Google Scholar]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the earth’s oblateness during the past 28 years. J. Geophys. Res. 2004, 109, 1–9. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth Planet. Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef]
- Chambers, D.P. Observing seasonal steric sea level variationswith GRACE and satellite altimetry. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, 1–34. [Google Scholar] [CrossRef]
- Sproles, E.A.; Leibowitz, S.G.; Reager, J.T.; Wigington, P.J., Jr.; Famiglietti, J.S.; Patil, S.D. GRACE storage-runoff hystereses reveal the dynamics of regional watersheds. Hydrol. Earth Syst. Sci. 2015, 19, 3253–3272. [Google Scholar] [CrossRef]
- Jefferson, A.; Nolin, A.; Lewis, S.; Tague, C. Hydrogeologic controls on streamflow sensitivity to climate variation. Hydrol. Process. 2008, 22, 4371–4385. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q.; Chun, K.P.; Zhou, Z.; Chu, T. Application of ENSO and drought indices for water level reconstruction and prediction: A case study in the lower Mekong River estuary. Water 2018, 10, 58. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Q.; Singh, V. Influences of ENSO, NAO, IOD and PDO on seasonal precipitation regimes in the Yangtze River basin, China. Int. J. Climatol. 2015, 35, 3556–3567. [Google Scholar] [CrossRef]
- Zhang, Z.; Chao, B.F.; Chen, J.; Wilson, C.R. Terrestrial water storage anomalies of Yangtze River Basin droughts observed by GRACE and connections with ENSO. Glob. Planet. Chang. 2015, 126, 35–45. [Google Scholar] [CrossRef]
- Lauri, H.; de Moel, H.; Ward, P.J.; Räsänen, T.A.; Keskinen, M.; Kummu, M.S. Future changes in Mekong River hydrology: Impact of climate change and reservoir operation on discharge. Hydrol. Earth Syst. Sci. 2012, 16, 4603–4619. [Google Scholar] [CrossRef]
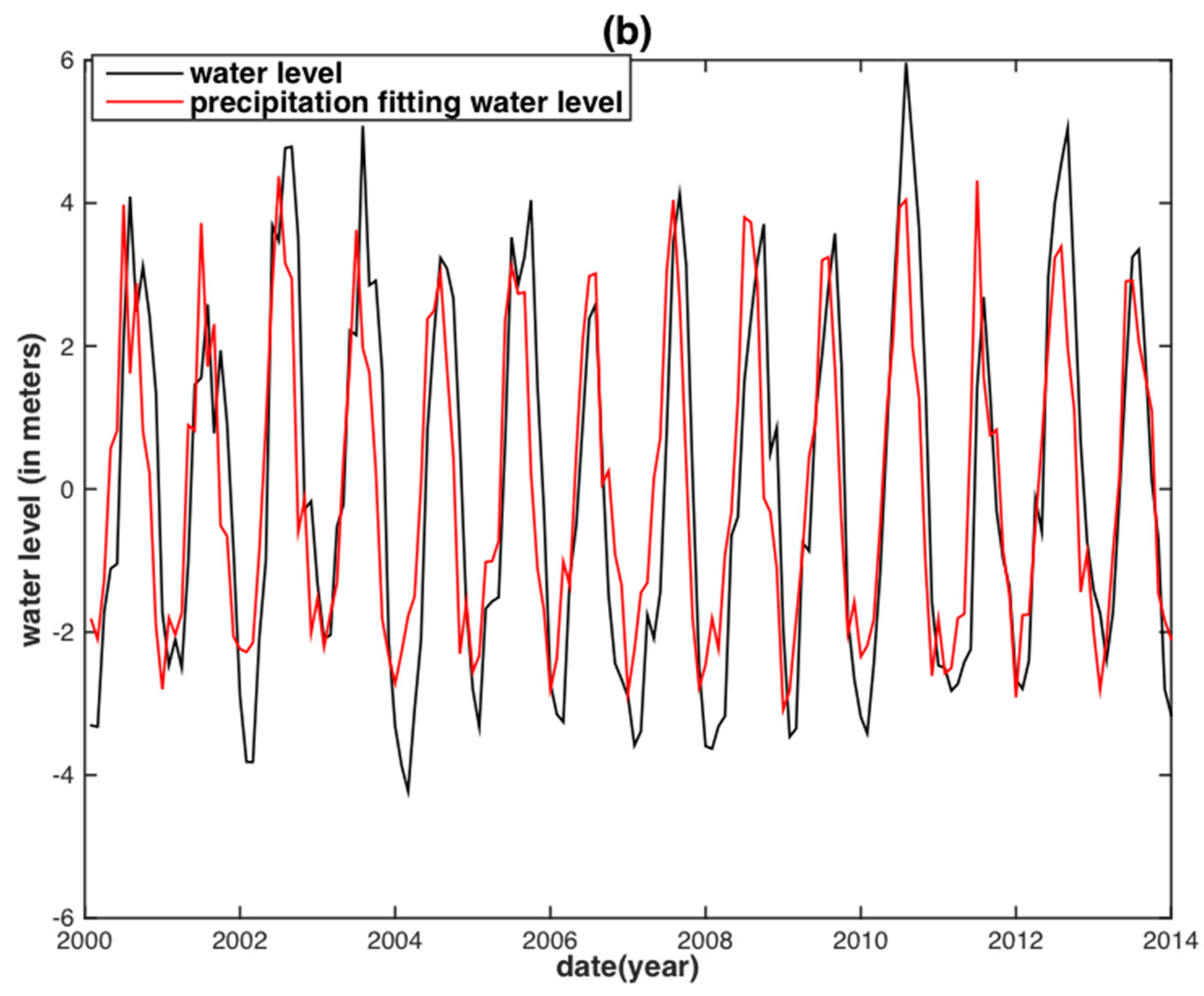
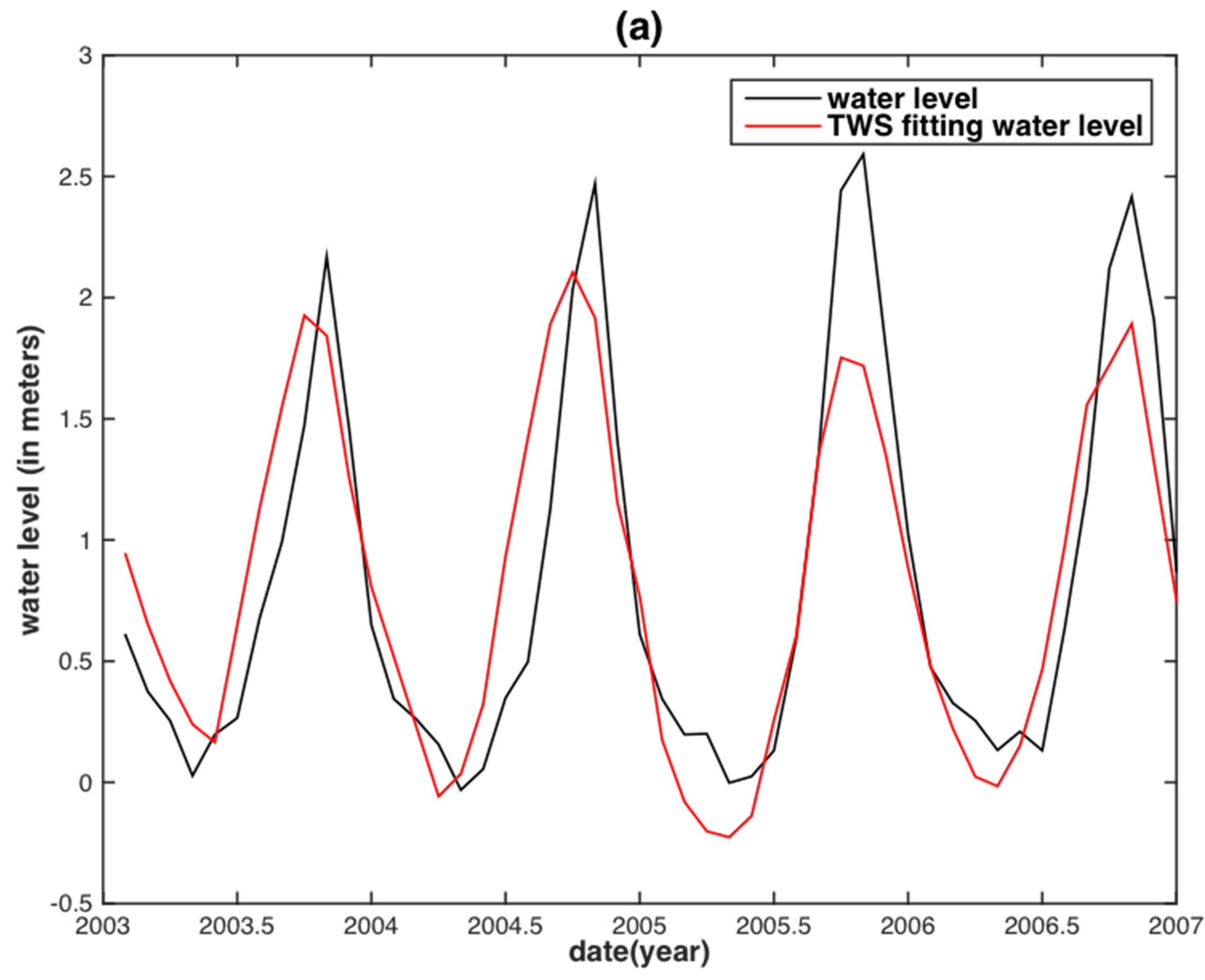
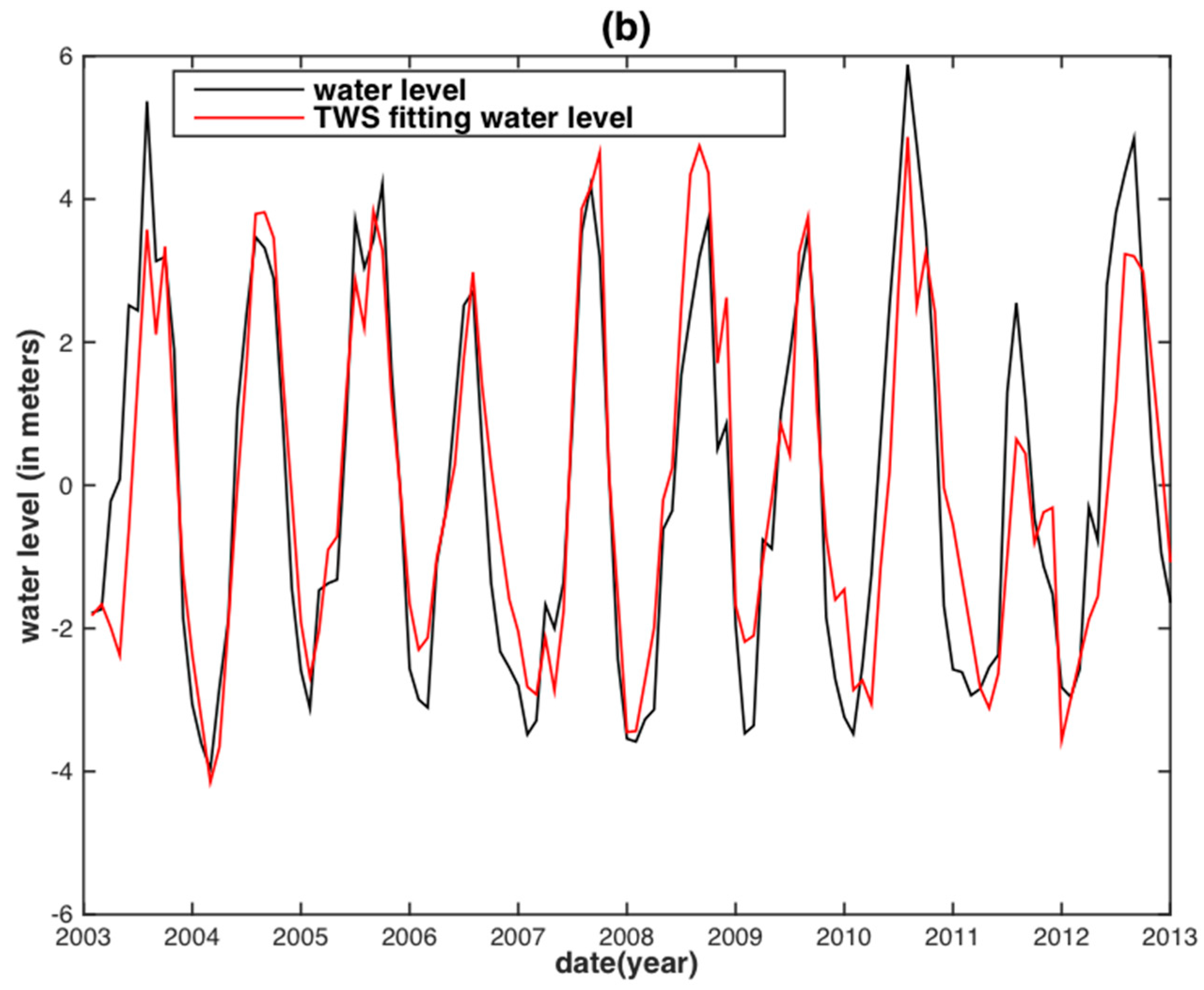
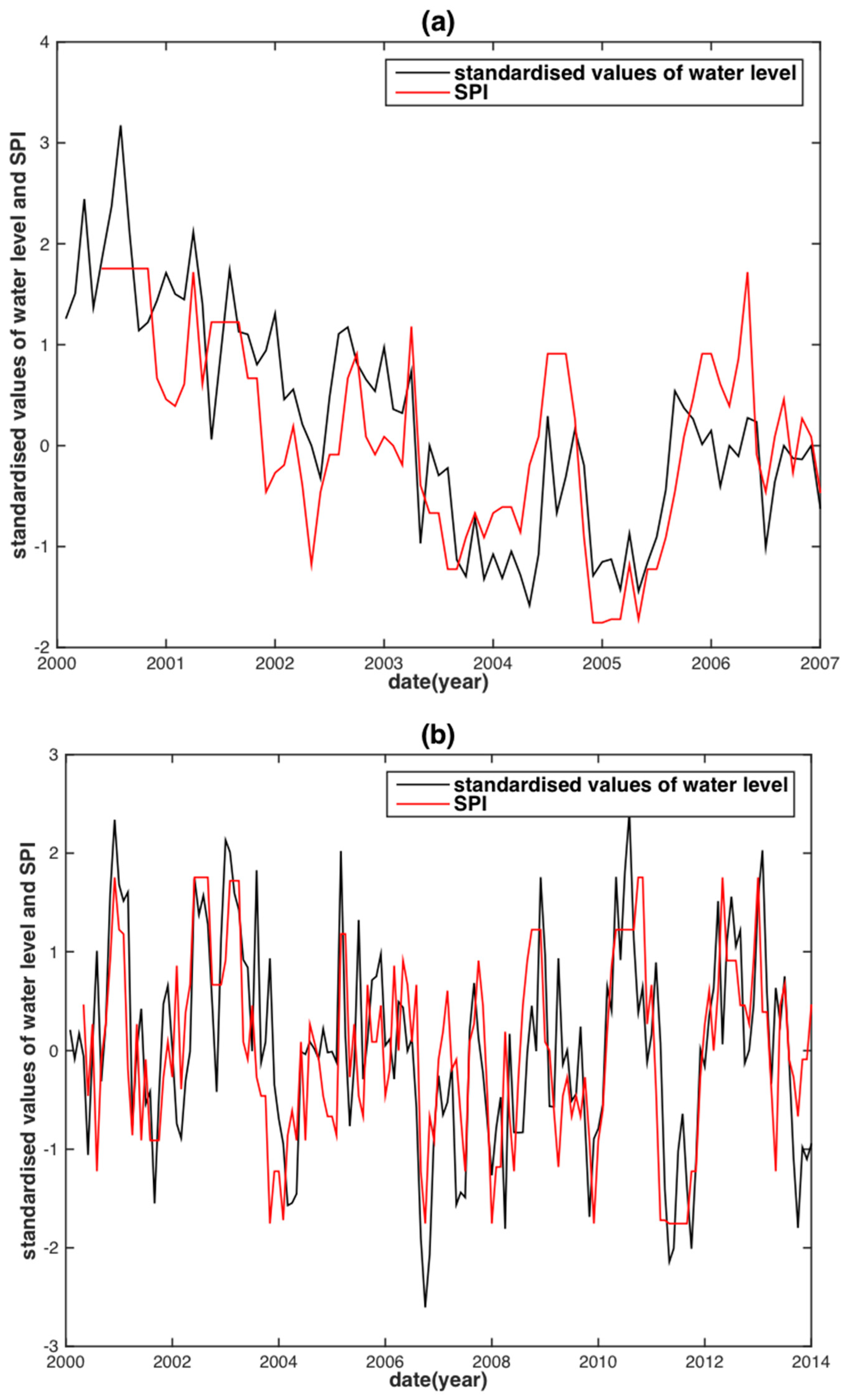
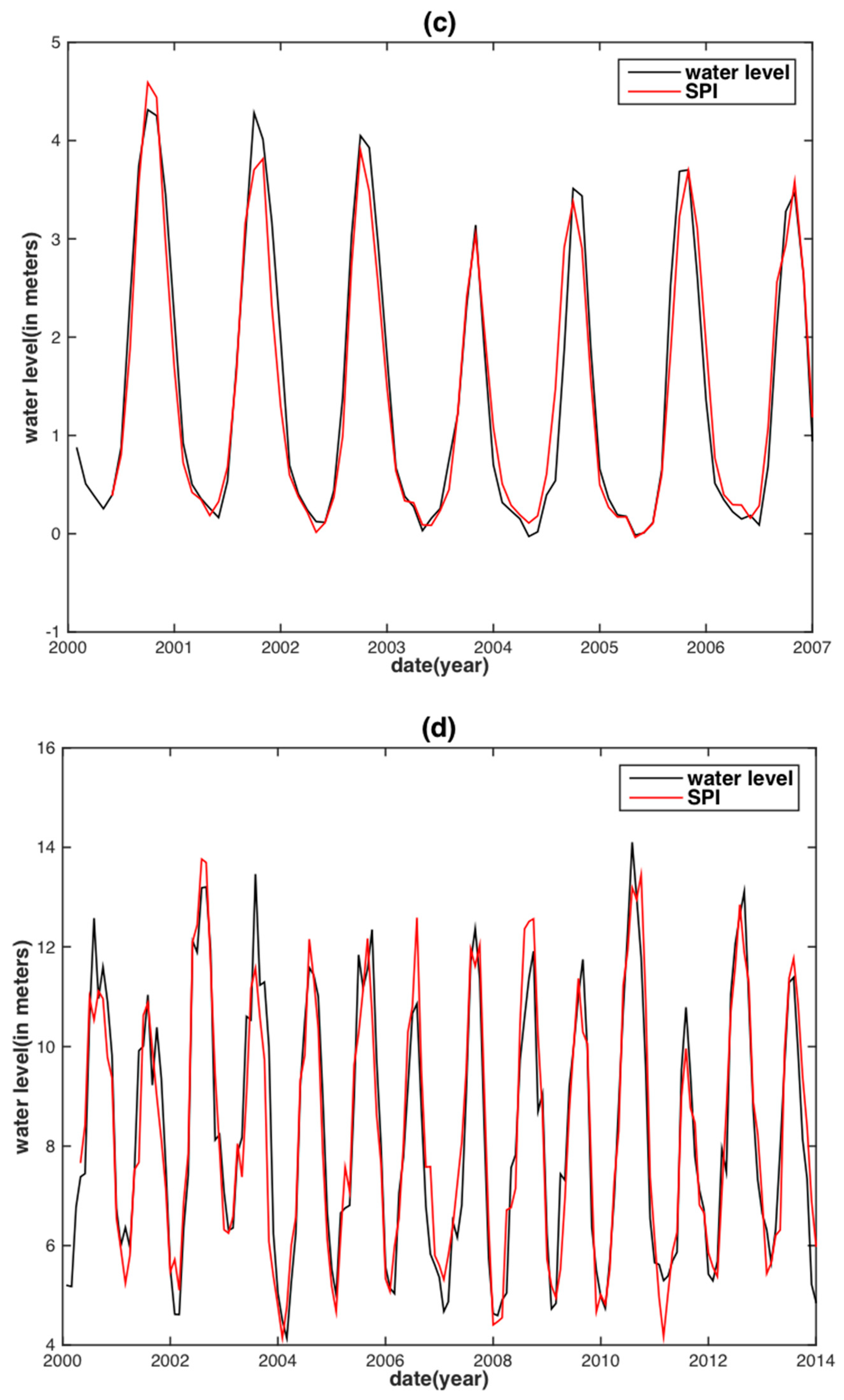
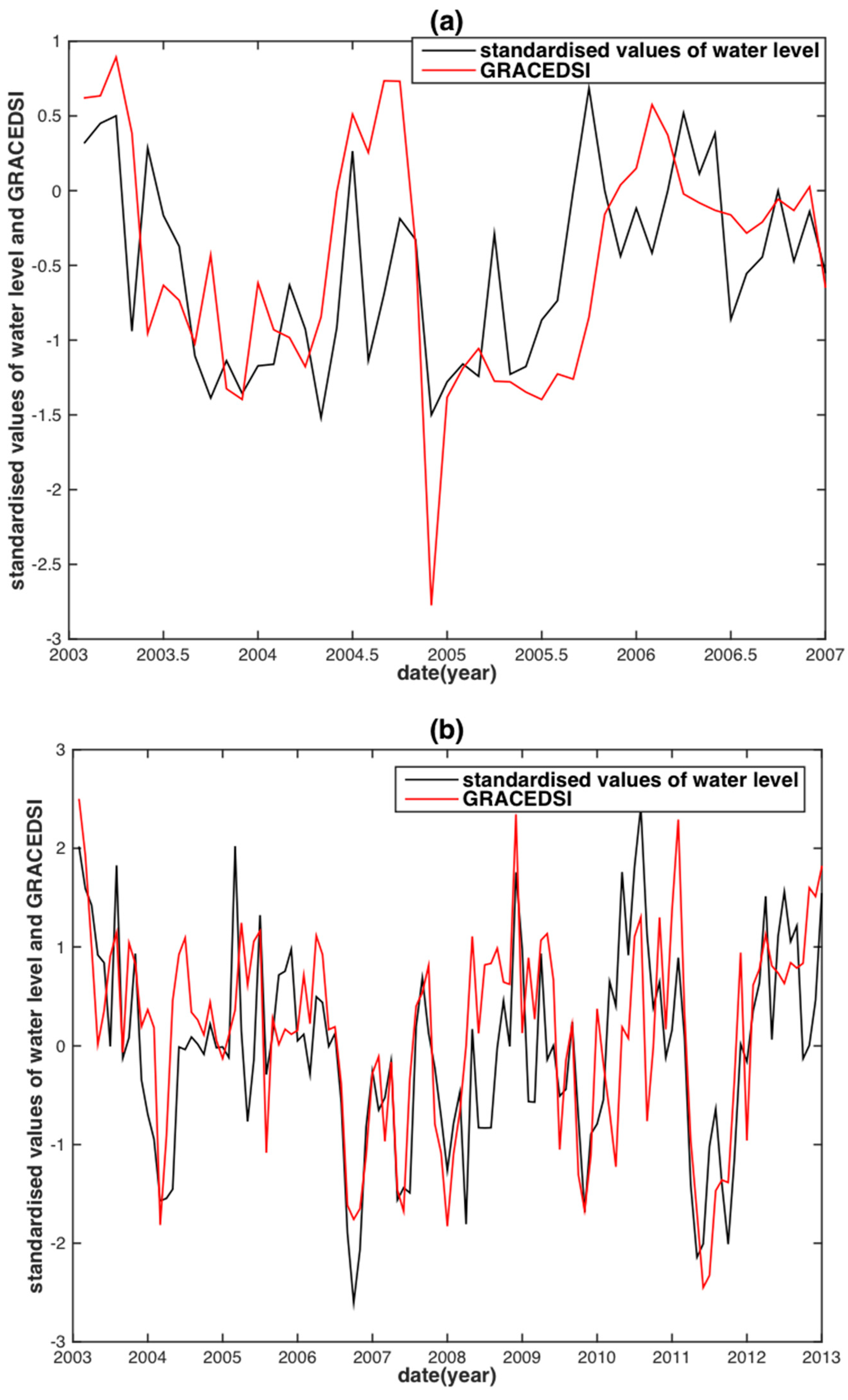
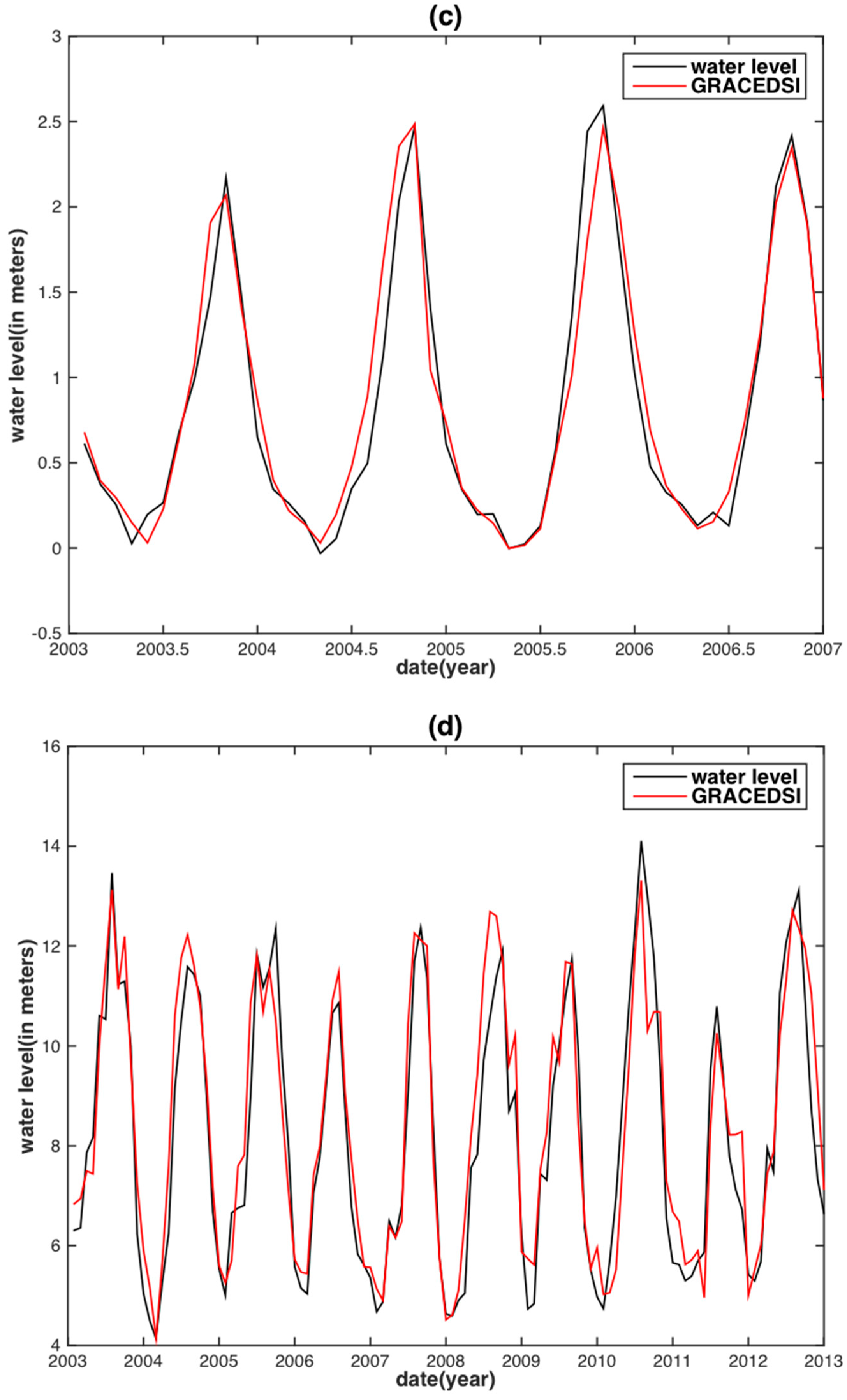
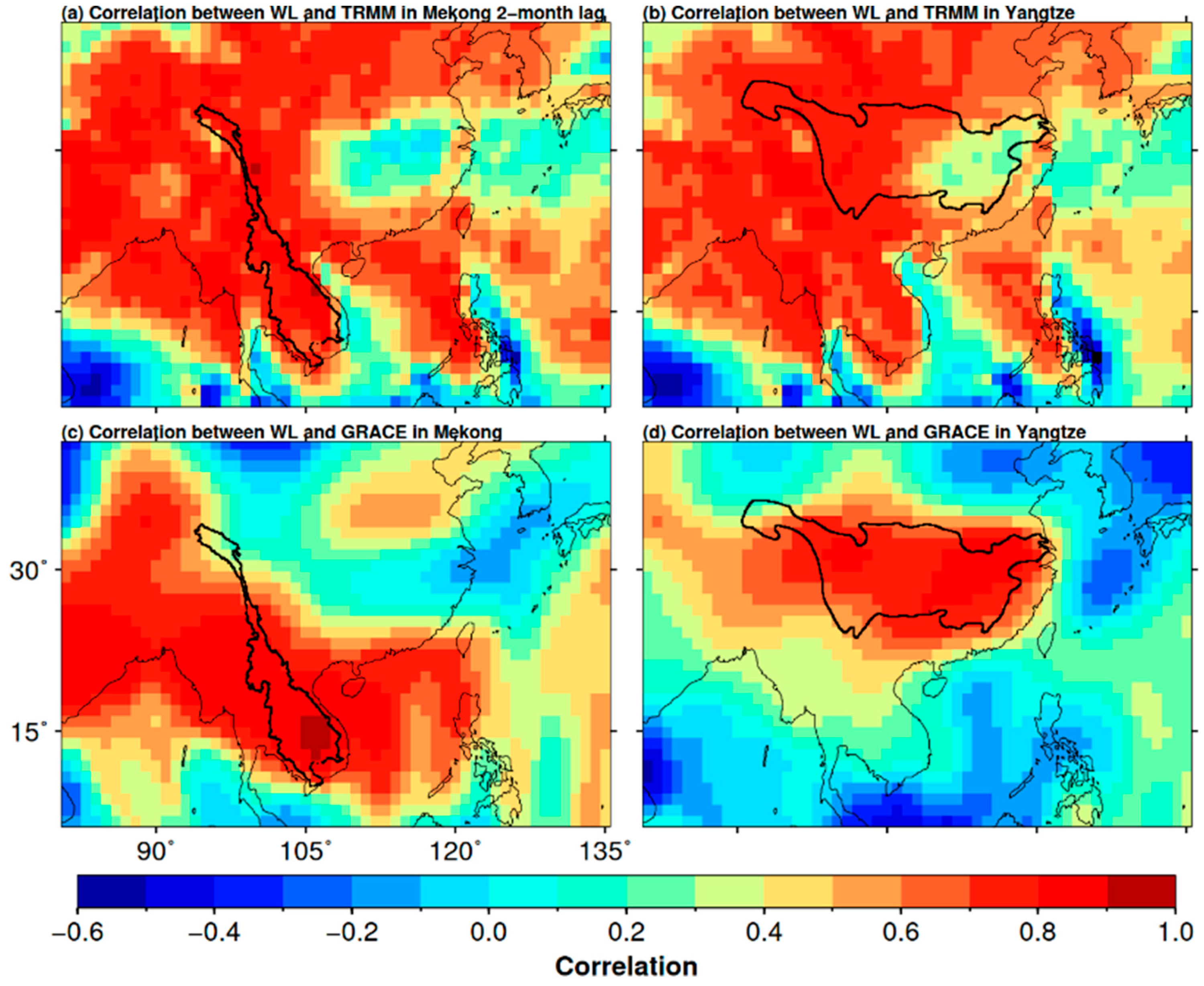

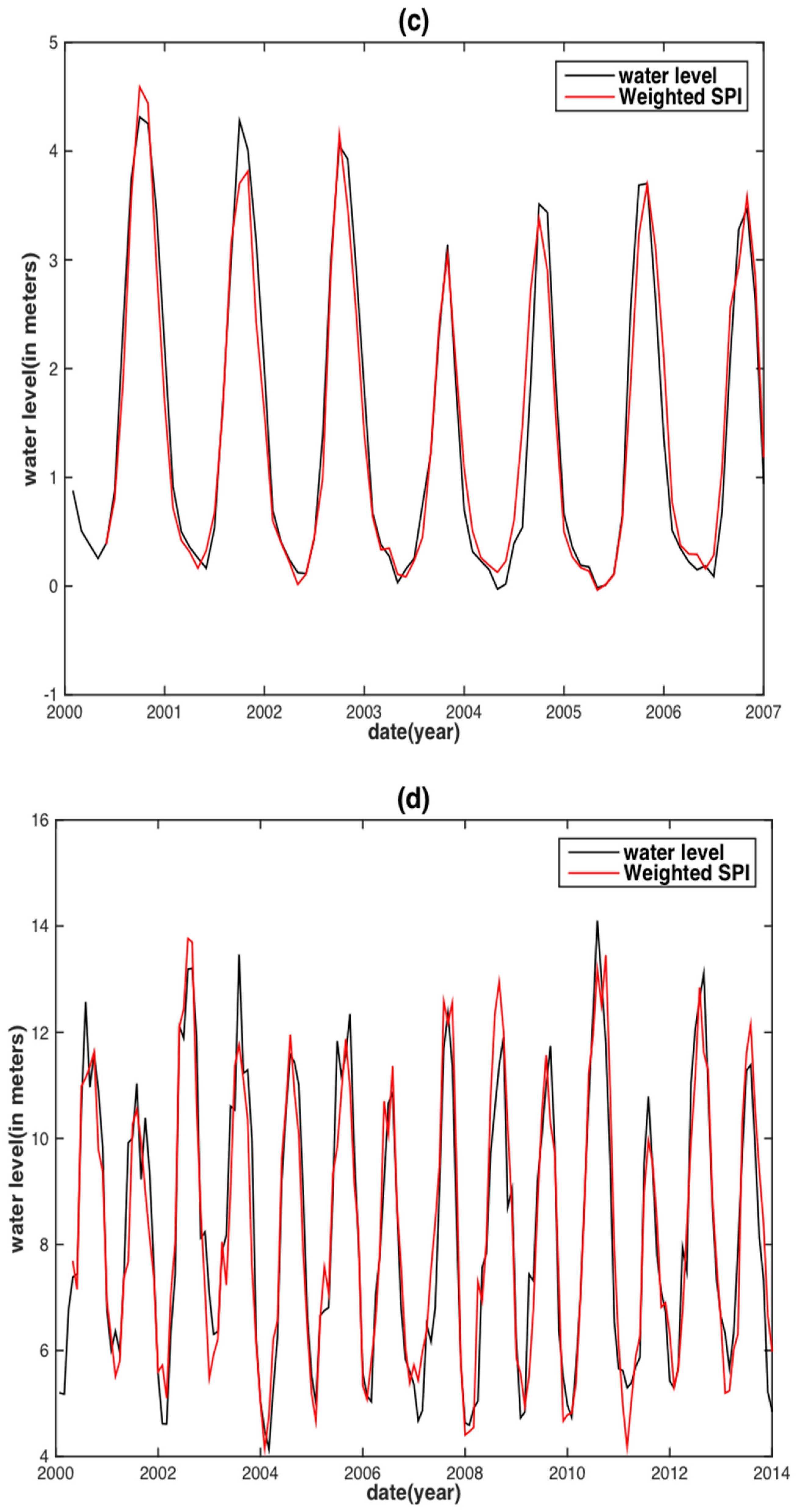
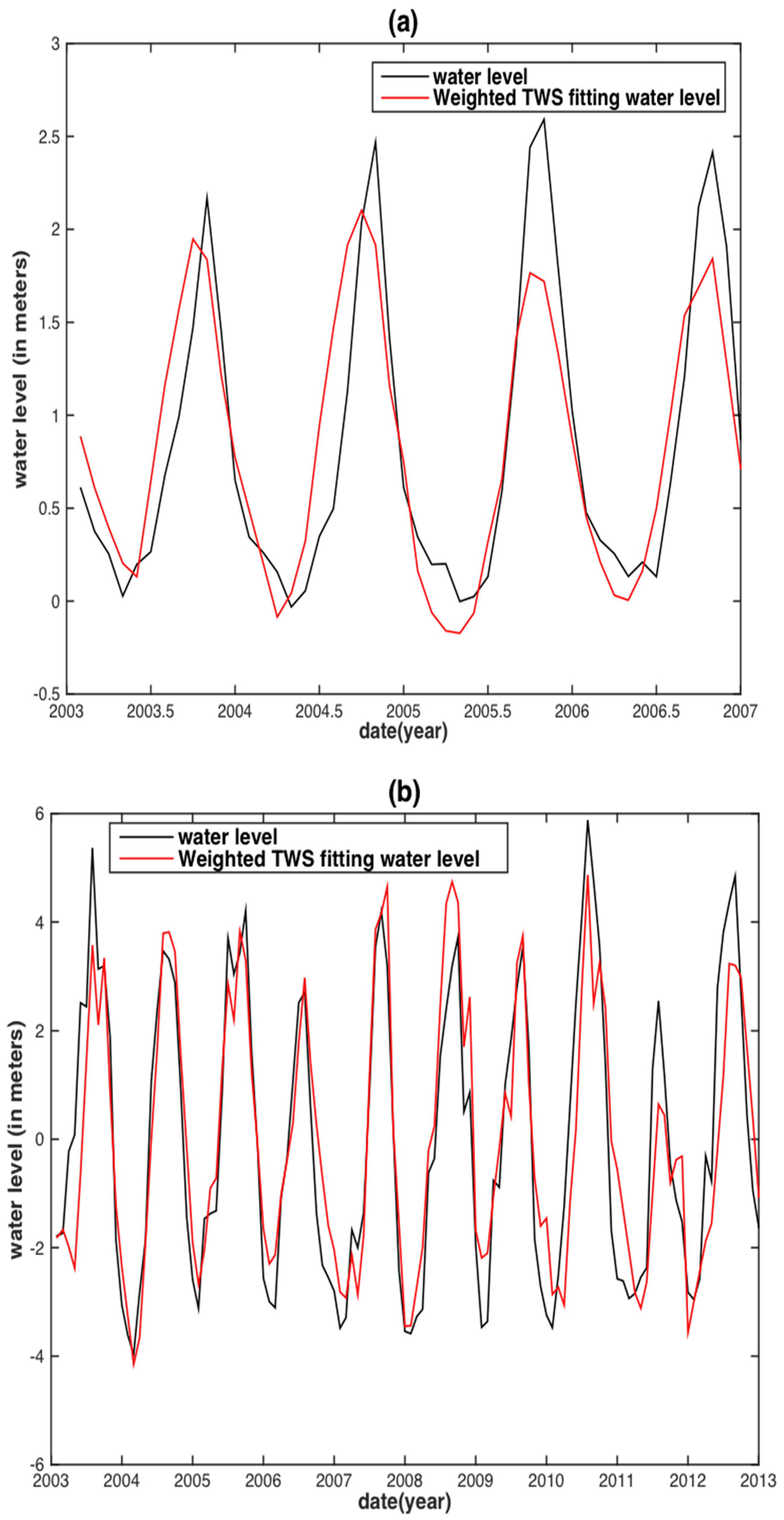
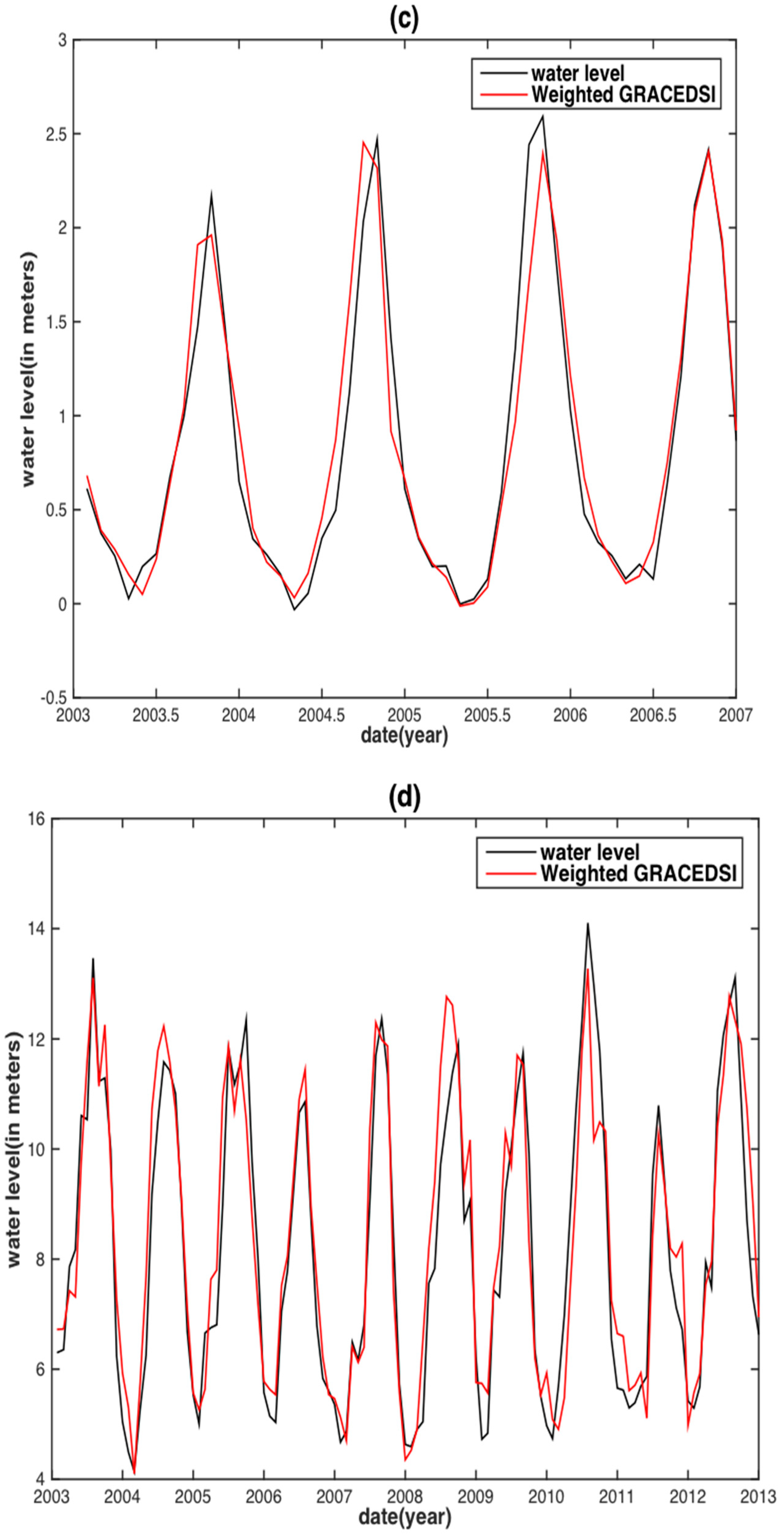
| Basin | Data | PCC | RMSE (m) | NSE |
|---|---|---|---|---|
| Mekong (Vam Kenh) | NDVI | 0.838 | 0.467 | 0.703 |
| LST | 0.881 | 0.405 | 0.776 | |
| P | 0.909 | 0.355 | 0.827 | |
| Weighted P | 0.909 | 0.356 | 0.826 | |
| TRMM-SPI | 0.975 | 0.195 | 0.949 | |
| Weighted TRMM-SPI | 0.976 | 0.193 | 0.950 | |
| TWS | 0.874 | 0.381 | 0.764 | |
| Weighted TWS | 0.879 | 0.374 | 0.772 | |
| GRACE-DSI | 0.961 | 0.341 | 0.922 | |
| Weighted GRACE-DSI | 0.964 | 0.210 | 0.928 | |
| Yangtze (Datong) | NDVI | 0.837 | 1.411 | 0.700 |
| LST | 0.819 | 1.479 | 0.671 | |
| P | 0.805 | 1.528 | 0.648 | |
| Weighted P | 0.843 | 1.385 | 0.711 | |
| TRMM-SPI | 0.941 | 0.878 | 0.884 | |
| Weighted TRMM-SPI | 0.945 | 0.850 | 0.891 | |
| TWS | 0.905 | 1.110 | 0.819 | |
| Weighted TWS | 0.914 | 1.057 | 0.836 | |
| GRACE-DSI | 0.945 | 0.881 | 0.886 | |
| Weighted GRACE-DSI | 0.946 | 0.875 | 0.887 | |
| Mekong (Dinh An prediction) | NDVI | 0.835 | 0.787 | 0.677 |
| LST | 0.900 | 0.645 | 0.783 | |
| P | 0.907 | 0.582 | 0.823 | |
| Weighted P | 0.909 | 0.576 | 0.826 | |
| TRMM-SPI | 0.974 | 0.319 | 0.948 | |
| Weighted TRMM-SPI | 0.976 | 0.307 | 0.952 | |
| TWS | 0.880 | 0.578 | 0.774 | |
| Weighted TWS | 0.882 | 0.572 | 0.779 | |
| GRACE-DSI | 0.953 | 0.370 | 0.907 | |
| Weighted GRACE-DSI | 0.959 | 0.347 | 0.919 | |
| Yangtze (Hukou prediction) | NDVI | 0.832 | 1.827 | 0.693 |
| LST | 0.821 | 1.882 | 0.674 | |
| P | 0.816 | 1.903 | 0.667 | |
| Weighted P | 0.850 | 1.737 | 0.722 | |
| TRMM-SPI | 0.942 | 1.122 | 0.884 | |
| Weighted TRMM-SPI | 0.944 | 1.099 | 0.889 | |
| TWS | 0.900 | 1.455 | 0.810 | |
| Weighted TWS | 0.911 | 1.379 | 0.829 | |
| GRACE-DSI | 0.946 | 1.122 | 0.887 | |
| Weighted GRACE-DSI | 0.947 | 1.117 | 0.888 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Fok, H.S.; Chen, Q.; Chun, K.P. Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins. Sensors 2018, 18, 3076. https://doi.org/10.3390/s18093076
He Q, Fok HS, Chen Q, Chun KP. Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins. Sensors. 2018; 18(9):3076. https://doi.org/10.3390/s18093076
Chicago/Turabian StyleHe, Qing, Hok Sum Fok, Qiang Chen, and Kwok Pan Chun. 2018. "Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins" Sensors 18, no. 9: 3076. https://doi.org/10.3390/s18093076
APA StyleHe, Q., Fok, H. S., Chen, Q., & Chun, K. P. (2018). Water Level Reconstruction and Prediction Based on Space-Borne Sensors: A Case Study in the Mekong and Yangtze River Basins. Sensors, 18(9), 3076. https://doi.org/10.3390/s18093076






