Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm †
Abstract
1. Introduction
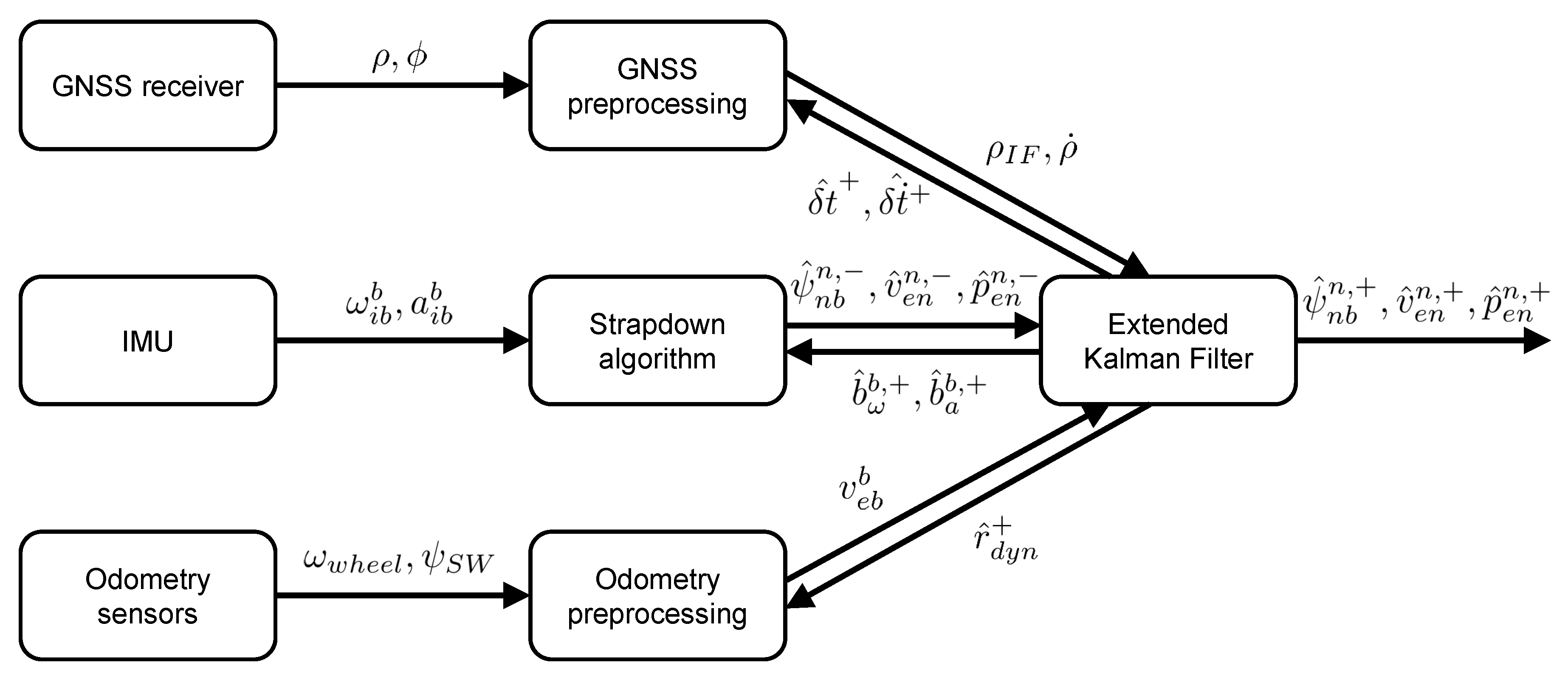
2. Utilization of GNSS
2.1. Basic GPS L1 Algorithm
- Roll and pitch angle are estimated from IMU-measured accelerations. Based on offset and noise characteristics of the IMU in use, the standard deviation is set to .
- The yaw angle is estimated from the GPS-derived velocity under the assumption that the vehicle is traveling in a straight line without side slip. Based on velocity estimation quality of the GPS-receiver used here, a standard deviation of is employed.
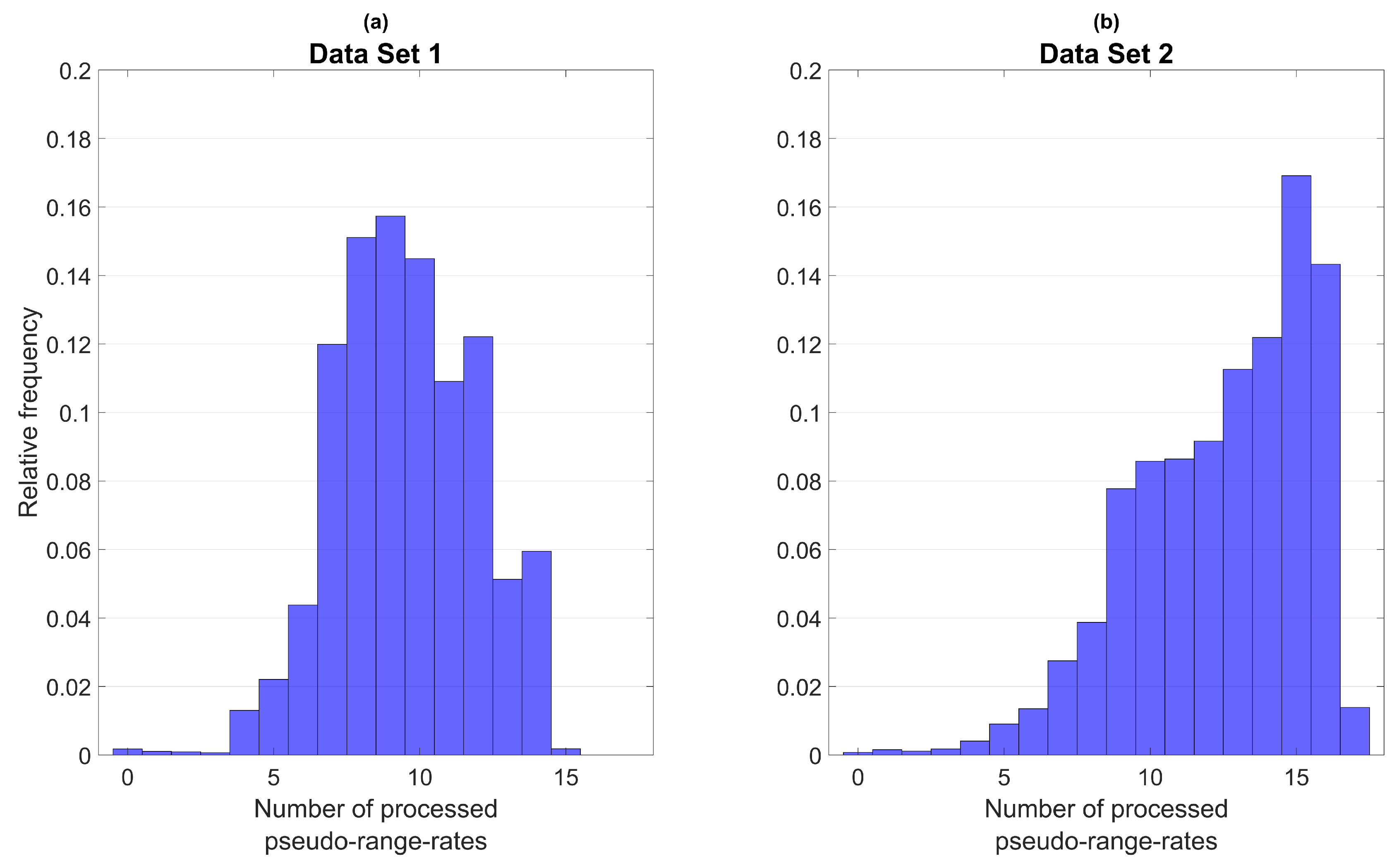
- Velocity and receiver clock drift are estimated based on pseudo-range-rate observations . The pseudo-range-rates’ variance is set to .
- Position and receiver clock bias are estimated from pseudo-ranges via a single-epoch navigation solution. The pseudo-ranges’ variance is modeled as the sum of two parts: , depending on the satellite’s elevation , and , depending on the signal’s carrier to noise ratio .
- Gyroscope and accelerometer offset are initialized as 0. Their initial variance is based on the nominal values for the bias repeatability given by the IMU’s manufacturer.
- Preprocessing: Based on the a-posteriori values of receiver clock bias and drift from the last time step, the a-priori values of these quantities are propagated. Corrections for satellite and receiver clock errors as well as ionospheric and tropospheric refraction are applied to pseudo-ranges and pseudo-range-rates. The measurement noise covariance for pseudo-range and pseudo-range-rate measurements is calculated. All measurements are assumed to be uncorrelated with each other; the variances for pseudo-ranges and pseudo-range-rates are the same as in initialization mode. Lastly, positions and velocities of the received satellites are computed.
- Measurement update: The innovation is formed as difference between the corrected pseudo-range and pseudo-range-rate measurements and their predicted counterparts. These predictions are based on the a-priori estimates of attitude, velocity and position. Plausibility checks for pseudo-ranges and pseudo-range-rates are employed to detect outliers. Finally, and the associated measurement noise covariance are used to determine corrections for the state vector’s a-priori estimates. Simultaneously, the state vector’s covariance matrix is updated to reflect the newly incorporated information.
2.2. Multi-Frequency GPS Algorithm
- Treat the new measurements exactly as the old ones, i.e. retain the assumption that all measurements are uncorrelated and assign similar variances to the new pseudo-range measurements as to the old ones.
- Treat measurements stemming from the same satellite as a batch, i.e. assign similar variances to the new pseudo-range measurements as to the old ones but assume that pseudo-range measurements on different frequencies, but from the same satellite, are highly correlated. Pseudo-ranges from different satellites are still considered to be uncorrelated.
- Introduce additional variables into the EKF’s state vector to estimate the ionospheric refraction. The simplest version of this alternative adds a single additional state representing the zenith ionospheric delay on a reference carrier frequency. The ionospheric refraction’s dependency on carrier frequency and elevation is represented in the pseudo-range measurement model. More complex versions add one state for each satellite in view, resulting in a variable-length state vector.
- Work with ionosphere-free linear combinations of pseudo-ranges.
2.3. Multi-GNSS Algorithm (GPS and Galileo)
3. Odometry Model
- Preprocessing: Employing polynomials obtained through calibration for each wheel, the wheel steering angle of each front wheel is computed from the measured steering wheel angle . Longitudinal and lateral wheel slip are estimated based on the accelerometer outputs of the IMU (corrected for the estimated IMU biases). The horizontal velocity of each wheel is computed from and as well as longitudinal and lateral slip. For the front wheels, the resulting values have to be rotated into the body coordinate frame via the wheel steering angles. Output values of the odometry preprocessing are the x- and y-components of the vehicle velocity in the body coordinate frame at each wheel as well as the corresponding covariance matrices.
- Measurement update: The innovation is formed as difference between the measured 2-D velocity at each wheel and its predicted counterpart. These predictions are based on the a-priori estimates of attitude, velocity and dynamical tire radii as well as the vehicle’s geometry, namely the leverarms from the IMU to the four wheels. Finally, and the associated measurement noise covariance are used to determine corrections for the state vector’s a-priori estimates. Simultaneously, the state vector’s covariance matrix is updated to reflect the newly incorporated information.
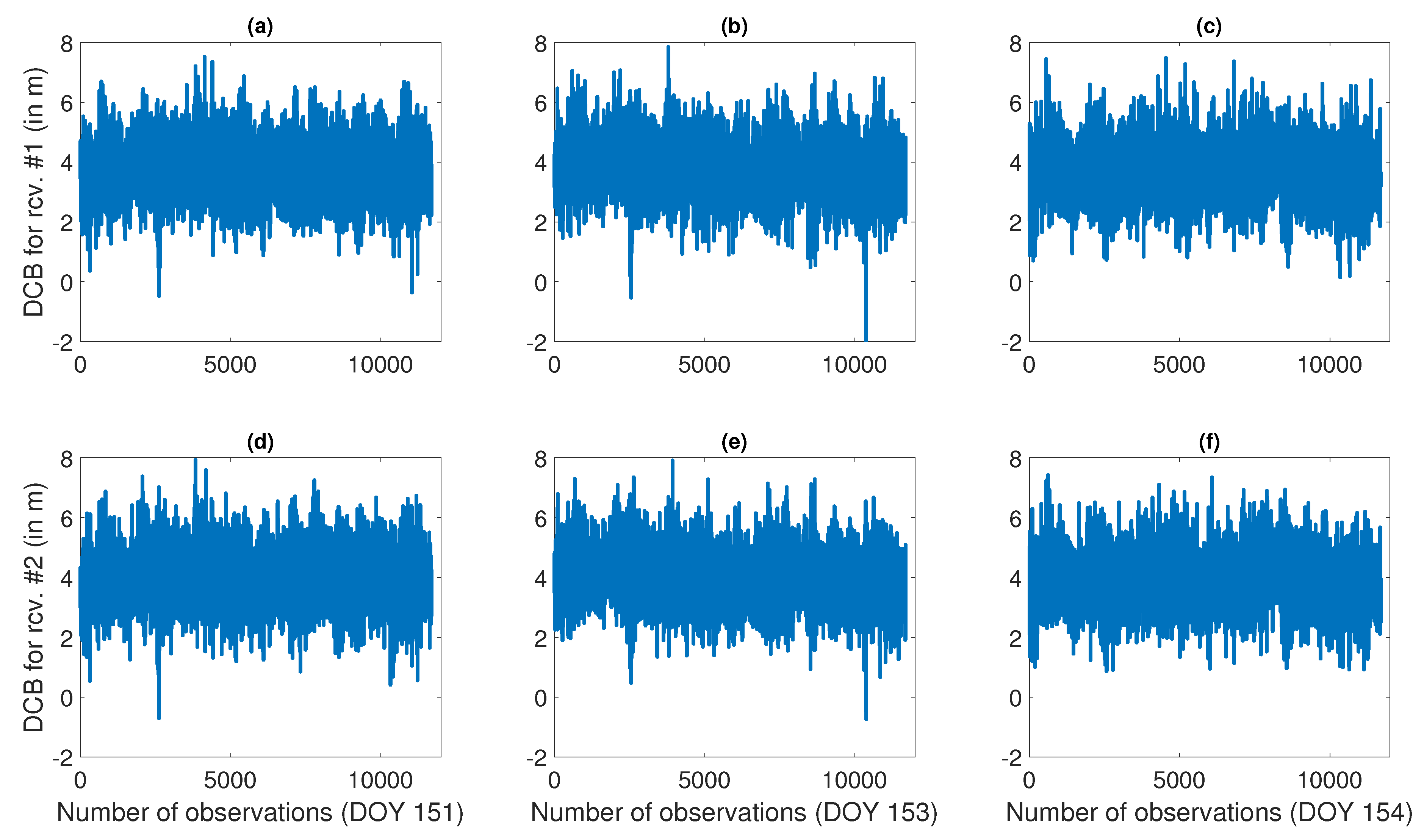
4. Calibration of Differential Code Biases
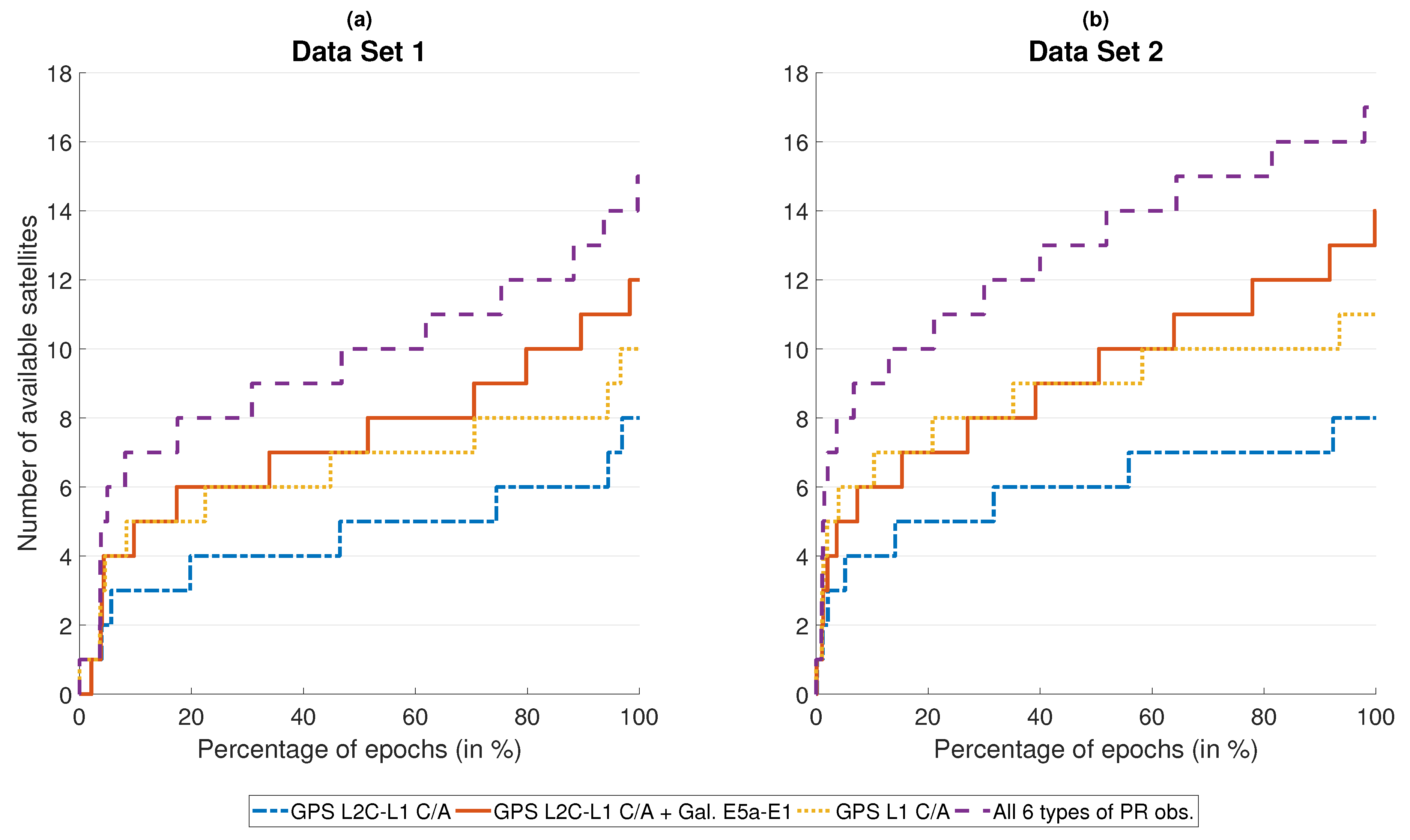
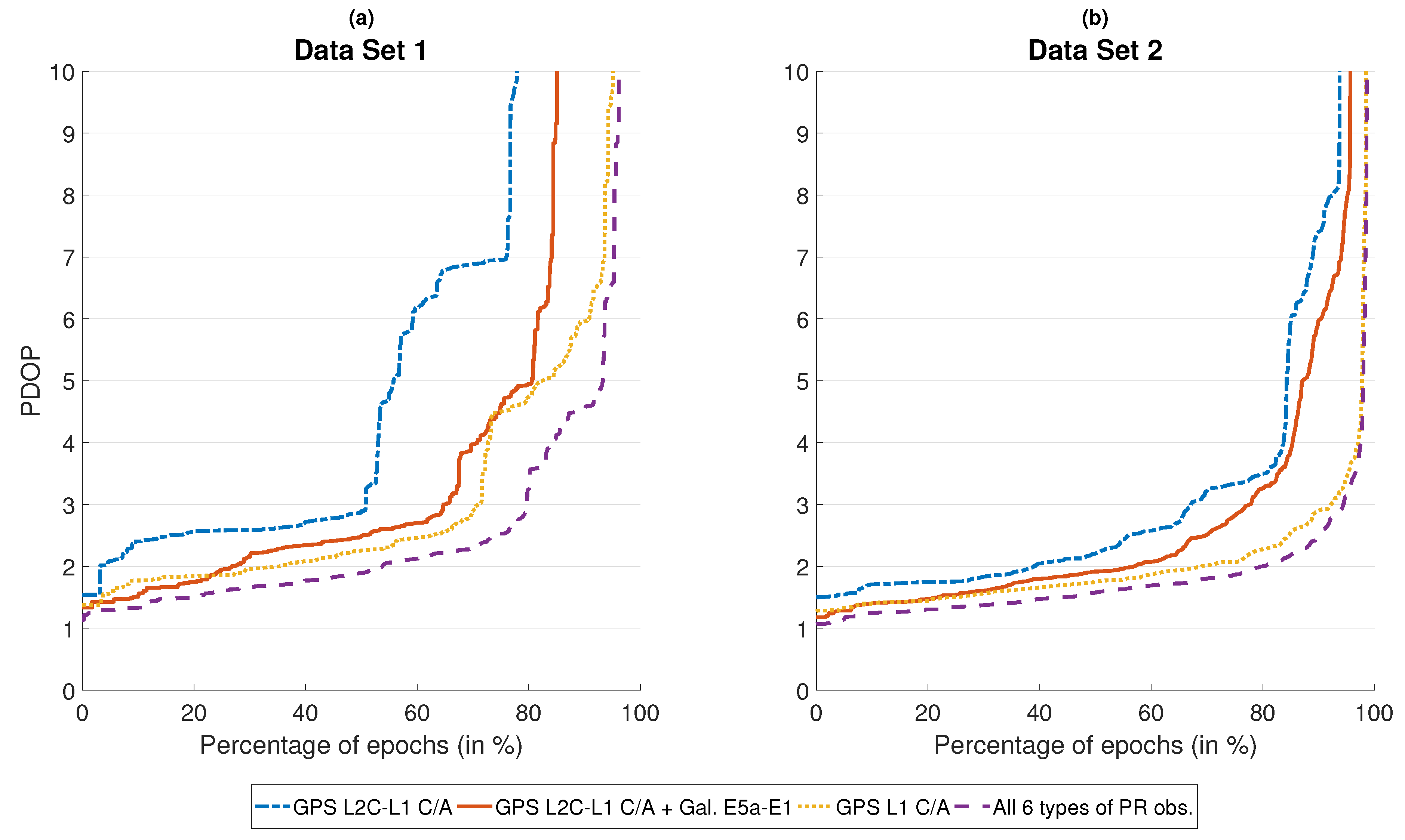
5. Localization Algorithm Performance
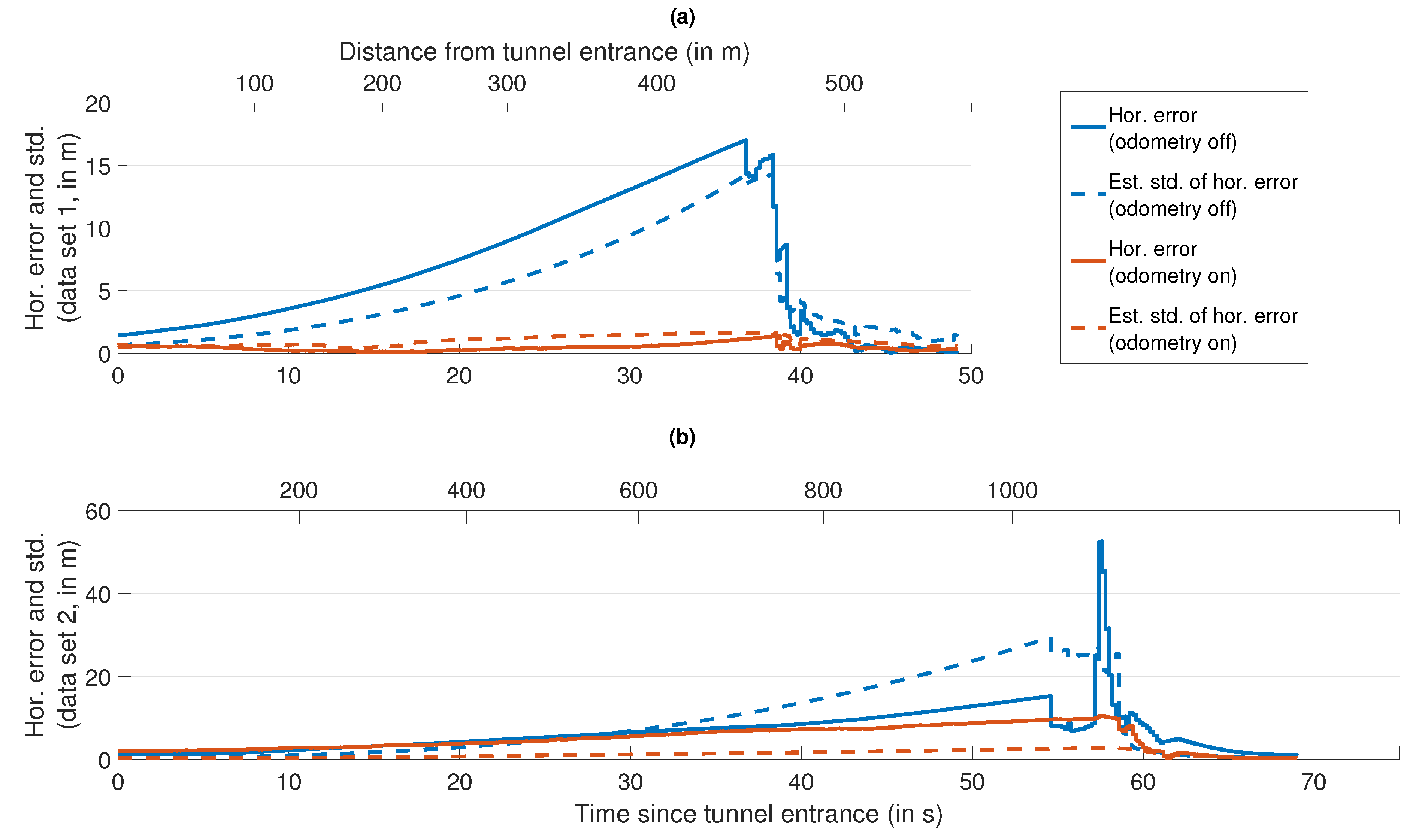
- Roughly 40 long drive over a distance of approximately 13 on the 14th of March 2018 through the inner city of Darmstadt, including a passage through a tunnel lasting roughly 40 /450 .
- Roughly 100 long drive over a distance of approximately 90 on the 14th of March 2018, including towns with multi-story buildings on both sides of the road, villages with smaller houses, country roads (with and without forest), freeways and a passage through a tunnel lasting roughly 55 /1000 .
5.1. Attitude and Velocity Accuracy
5.2. Position Accuracy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BCU | brake control unit |
| BGD | Broadcast Group Delay |
| CAN | Controller Area Network |
| CCDIS | Crustal Dynamics Data Information System |
| CDF | cumulative distribution function |
| CDMA | code division multiple access |
| CNAV | civil navigation message |
| DCB | differential code bias |
| DOY | day of year |
| EKF | Extended Kalman Filter |
| ENU | east-north-up |
| ESC | electronic stability control |
| FLU | front-left-up |
| F/NAV | freely-accessible navigation message |
| GGTO | GPS to Galileo Time Offset |
| GNSS | global navigation satellite system |
| GPGA | GPS to Galileo time system correction |
| GPS | Global Positioning System |
| IF | ionosphere-free combination |
| IGS | International GNSS Service |
| IMU | inertial measurement unit |
| IONEX | Ionosphere Map Exchange Format |
| ISB | inter-system bias |
| ISC | inter-signal correction term |
| I/NAV | integrity navigation message |
| LNAV | legacy navigation message |
| MEMS | microelectromechanical systems |
| PDOP | position dilution of precision |
| PR | pseudo-range |
| rcv. | receiver |
| RINEX | Receiver Independent Exchange Format |
| RMS | root mean square |
| RTK | real-time kinematic positioning |
| SISRE | signal in space ranging error |
| std. | standard deviation |
| SV | space vehicle |
| TEC | total electron content |
| UEE | user equipment error |
| UERE | user equivalent range error |
References
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems; Artech House: Boston, MA, USA; London, UK, 2013. [Google Scholar]
- Torre, A.D.; Caporali, A. An analysis of intersystem biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Accounting for Galileo–GPS inter-system biases in precise satellite positioning. J. Geod. 2015, 89, 81–93. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Gao, J.; Petovello, M.G.; Cannon, M.E. Development of Precise GPS/INS/Wheel Speed Sensor/Yaw Rate Sensor Integrated Vehicular Positioning System. In Proceedings of the Free and Open Source Software for Geospatial Conference (FOSS4G) 2009, Sydney, Australia, 20–23 October 2009. [Google Scholar]
- Li, T.; Petovello, M.G.; Lachapelle, G.; Basnayake, C. Ultra-tightly Coupled GPS/Vehicle Sensor Integration for Land Vehicle Navigation. J. Inst. Navig. 2010, 57, 263–274. [Google Scholar] [CrossRef]
- Klein, I.; Filin, S.; Toledo, T. Vehicle Constraints Enhancement for Supporting INS Navigation in Urban Environments. J. Inst. Navig. 2011, 58, 7–15. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Wu, Y.; Rizos, C. An enhanced MEMS-INS/GNSS integrated system with fault detection and exclusion capability for land vehicle navigation in urban areas. GPS Solut. 2014, 18, 593–603. [Google Scholar] [CrossRef]
- Betz, J.W. Engineering Satellite-Based Navigation and Timing: Global Navigation Satellite Systems, Signals, and Receivers; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Navigation Center. GPS Constellation Status; United States Coast Guard. Available online: https://www.navcen.uscg.gov/?Do=constellationStatus (accessed on 10 September 2018).
- IS-GPS-200. Interface Specification IS-GPS-200: NAVSTAR GPS Space Segment/Navigation User Segment Interfaces: Revision H, including IRNs 001 through 005; Global Positioning Systems Directorate: Los Angeles, CA, USA, 2017. [Google Scholar]
- IS-GPS-705. Interface Specification IS-GPS-705: NAVSTAR GPS Space Segment/Navigation User Segment L5 Interfaces: Revision D, including IRNs 001 through 004; Global Positioning Systems Directorate: Los Angeles, CA, USA, 2017. [Google Scholar]
- IGS. RINEX: The Receiver Independent Exchange Format: Version 3.03, Update 1; International GNSS Service (IGS), RINEX Working Group and Radio Technical Commission for Maritime Services Special Committee 104 (RTCM-SC104): Pasadena, CA, USA, 2017. [Google Scholar]
- Montenbruck, O.; Langley, R. CNAV Test Data Set; National Aeronautics and Space Administration. Available online: ftp://ftp.cddis.eosdis.nasa.gov/gnss/data/campaign/cnav/2013/06/aaaReadme.txt (accessed on 10 September 2018).
- Crustal Dynamics Data Information System. Daily RINEX-Style Files for CNAV Data; National Aeronautics and Space Administration. Available online: ftp://cddis.gsfc.nasa.gov/gnss/data/campaign/mgex/daily/rinex3/2018/cnav (accessed on 10 September 2018).
- Galileo OS-SIS-ICD. Galileo Open Service Signal-in-Space Interface Control Document: Issue 1, Revision 3; European Global Navigation Satellite Systems Agency: Prague, Czech, 2016. [Google Scholar]
- Takasu, T. RTKLIB: Open Source Program Package for RTK-GPS. In Proceedings of the Free and Open Source Software for Geospatial Conference (FOSS4G) 2009, Sydney, Australia, 20–23 October 2009. [Google Scholar]
- European GNSS Service Center. Galileo Constellation Status; European Global Navigation Satellite Systems Agency. Available online: https://www.gsc-europa.eu/system-status/Constellation-Information (accessed on 10 September 2018).
- Peyret, F. Standardization of performances of GNSS-based positioning terminals for ITS applications at CEN/CENELEC/TC5. In Proceedings of the Intelligent Transportation Systems World Congress 2013, Tokyo, Japan, 15–18 October 2013. [Google Scholar]
- Reuper, B.; Becker, M.; Leinen, S. Performance Evaluation of a Tightly Coupled GNSS/IMU Integration Algorithm with Multi-Constellation/Multi-Frequency GNSS. In Proceedings of the European Navigation Conference 2018. European Group of Institutes of Navigation (EUGIN), Gothenburg, Sweden, 14–17 May 2018. [Google Scholar]
- Waypoint. Inertial Explorer Manual; NovAtel Inc.: Calgary, AB, Canada, 2016. [Google Scholar]
| State | Description | Symbol |
|---|---|---|
| 1–3 | Attitude error | |
| 4–6 | Velocity error | |
| 7–9 | Position error | |
| 10–12 | Gyroscope offset error | |
| 13–15 | Accelerometer offset error | |
| 16 | Error of GPS receiver clock bias | |
| 17 | Error of GPS receiver clock drift |
| Processed Code Observations | Mean and Std. of Difference (in m) | Positioning Performance (Ranked) |
|---|---|---|
| L1 C/A | 0/0/0 | 2/2/4 |
| 0/0/0 | ||
| L2C(M + L)-L1 C/A | −6.5/−7.5/−6.9 | 3/3/2 |
| 1.5/ 1.8/ 2.4 | ||
| L2C(M + L)-L1 C/A | −1.5/ 0.7/−4.3 | 4/5/1 |
| > L1 C/A | 1.7/ 1.7/ 2.1 | |
| L5(I + Q)-L1 C/A | 1.6/N/A/N/A | 7/N/A/N/A |
| 11.9/N/A/N/A | ||
| L5(I + Q)-L1 C/A | −0.7/−0.5/−0.6 | 1/1/2 |
| > L1 C/A | 0.7/ 0.5/ 0.6 | |
| L5(I + Q)-L1 C/A | 3.0/−8.4/−7.4 | 6/6/6 |
| > L2C(M + L)-L1 C/A | 8.1/ 7.2/ 2.8 | |
| L5(I + Q)-L1 C/A | 0.3/−0.6/−5.3 2.0/ 1.5/ 2.1 | |
| > L2C(M + L)-L1 C/A | 5/4/5 | |
| > L1 C/A |
| State | Description | Symbol |
|---|---|---|
| 16 | Error of GPS receiver clock bias | |
| 17 | Error of GNSS receiver clock drift | |
| 18 | Error of Gal. receiver clock bias |
| State | Description | Symbol |
|---|---|---|
| 19 | Dyn. tire radius error (front left) | |
| 20 | Dyn. tire radius error (front right) | |
| 21 | Dyn. tire radius error (rear left) | |
| 22 | Dyn. tire radius error (rear right) |
| Receiver | DCB Between L2C-L1 C/A and L1 C/A (in m) | DCB Between L5-L1 C/A and L1 C/A (in m) | DCB Between E5a-E1 and E1 (in m) | DCB Between E5b-E1 and E1 (in m) |
|---|---|---|---|---|
| JAVAD | 3.7/3.8/3.7 | −2.0/−2.0/−2.0 | −3.1/−3.0/−3.0 | 3.4/3.2/3.2 |
| TRIUMPH-LS #1 | 0.8/0.8/0.8 | 0.7/ 0.6/ 0.7 | 0.7/ 0.6/ 0.7 | 0.7/0.8/0.8 |
| JAVAD | 3.9/4.0/3.9 | −1.8/−1.9/−1.8 | −2.8/−2.9/−2.9 | 3.5/3.3/3.3 |
| TRIUMPH-LS #2 | 0.8/0.8/0.8 | 0.7/ 0.6/ 0.7 | 0.7/ 0.6/ 0.7 | 0.7/0.8/0.8 |
| #1 and #2 | 3.8 | −1.9 | −3.0 | 3.3 |
| combined | 0.8 | 0.7 | 0.7 | 0.8 |
| Receiver | Single-Epoch Solutions, Computed Including the Calibrated DCBs (in m) | Single-Epoch Solutions, Computed Without the Calibrated DCBs (in m) | Single-Epoch Solutions, Computed by RTKLIB with IF Combinations (in m) |
|---|---|---|---|
| JAVAD TRIUMPH-LS #1 | |||
| JAVAD TRIUMPH-LS #2 | |||
| All six data sets combined |
| Quantity | Unit | Data Set 1, | Data Set 1, | Data Set 2, | Data Set 2, |
|---|---|---|---|---|---|
| Odometry Off | Odometry On | Odometry Off | Odometry On | ||
| RMS of | |||||
| 50%/95% yaw | 0.2/1.1 | 0.2/0.8 | 0.3/0.8 | 0.1/0.4 | |
| error quantile | |||||
| RMS of | |||||
| 50%/95% hor. | 6/23 | 3/10 | 8/29 | 5/16 | |
| quantile of | |||||
| RMS of |
| Quantity | Data Set 1, | Data Set 1, | Data Set 2, | Data Set 2, |
|---|---|---|---|---|
| Odometry Off | Odometry On | Odometry Off | Odometry On | |
| Arithmetic mean of | ||||
| RMS of | ||||
| 50%/95% | 1.2/6.5 | 1.4/6.5 | 1.3/2.7 | 1.4/3.4 |
| horizontal | 1.3/8.2 | 1.3/4.4 | 1.0/2.7 | 1.2/3.0 |
| quantile of | 1.0/6.2 | 1.1/4.2 | 0.9/2.5 | 1.0/2.5 |
| Inertial Explorer Quality Number | Description | 3-D Accuracy of Ref. Solution (in m) |
|---|---|---|
| 1 | Fixed integer | 0.00–0.15 |
| 2 | Converged float or noisy fixed integer | 0.05–0.40 |
| 3 | Converging float | 0.20–1.00 |
| 4 | Converging float | 0.50–2.00 |
| 5 | DGNSS | 1.00–5.00 |
| 6 | DGNSS | 2.00–10.00 |
| Inertial Explorer Quality Number | Perc. of Epochs, Data Set 1 (in %) | RMS of , Data Set 1 (in m) | Perc. of Epochs, Data Set 2 (in %) | RMS of of , Data Set 2 (in m) |
|---|---|---|---|---|
| 1 | 36 | 50 | ||
| 2 | 24 | 20 | ||
| 3 | 23 | 22 | ||
| 4 | 11 | 5 | ||
| 5 | 5 | 2 | ||
| 6 | 1 | 1 | ||
| 1–6 | 100 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reuper, B.; Becker, M.; Leinen, S. Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm. Sensors 2018, 18, 3052. https://doi.org/10.3390/s18093052
Reuper B, Becker M, Leinen S. Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm. Sensors. 2018; 18(9):3052. https://doi.org/10.3390/s18093052
Chicago/Turabian StyleReuper, Björn, Matthias Becker, and Stefan Leinen. 2018. "Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm" Sensors 18, no. 9: 3052. https://doi.org/10.3390/s18093052
APA StyleReuper, B., Becker, M., & Leinen, S. (2018). Benefits of Multi-Constellation/Multi-Frequency GNSS in a Tightly Coupled GNSS/IMU/Odometry Integration Algorithm. Sensors, 18(9), 3052. https://doi.org/10.3390/s18093052




