Indoor Localization Based on Weighted Surfacing from Crowdsourced Samples
Abstract
:1. Introduction
2. Related Work and System Overview
2.1. Related Work
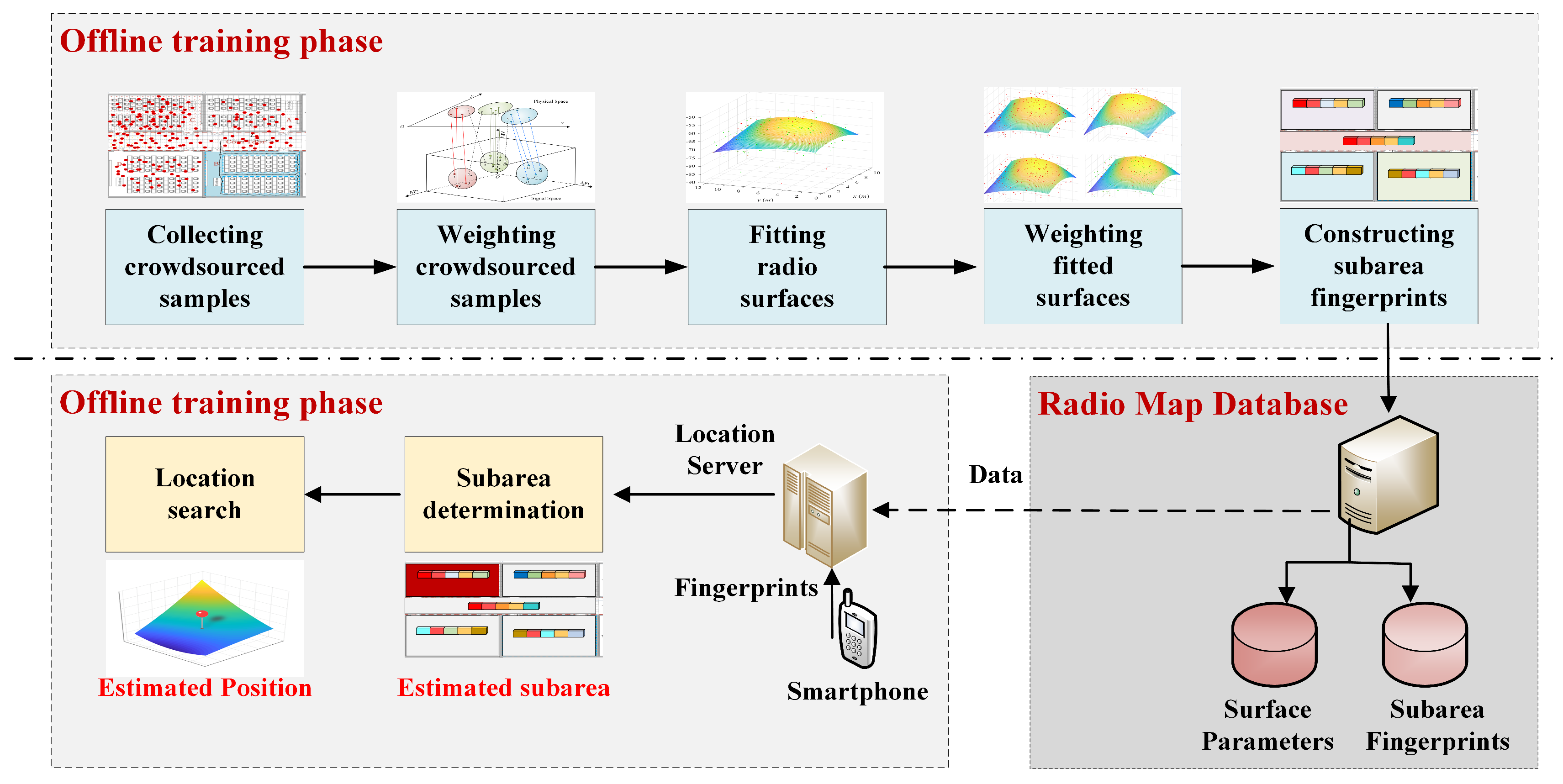
2.2. System Overview
3. The Offline Weighted Surfacing Algorithm
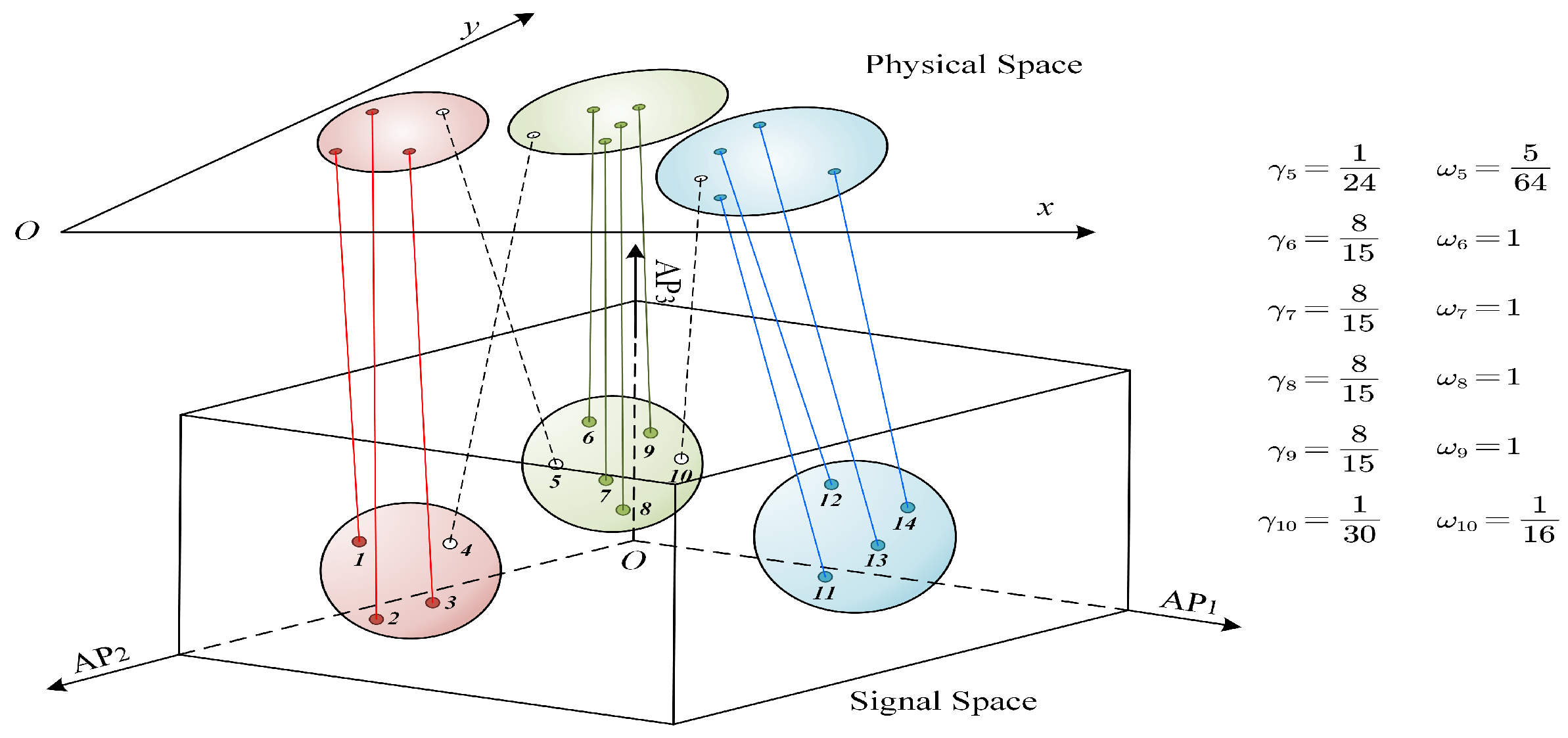
3.1. Weighting Crowdsourced Samples
3.2. Fitting Radio Surfaces
3.3. Weighting Fitted Surfaces
3.4. Constructing Subarea Fingerprints
4. The Online Positioning Algorithm
5. Field Measurements and Experiments
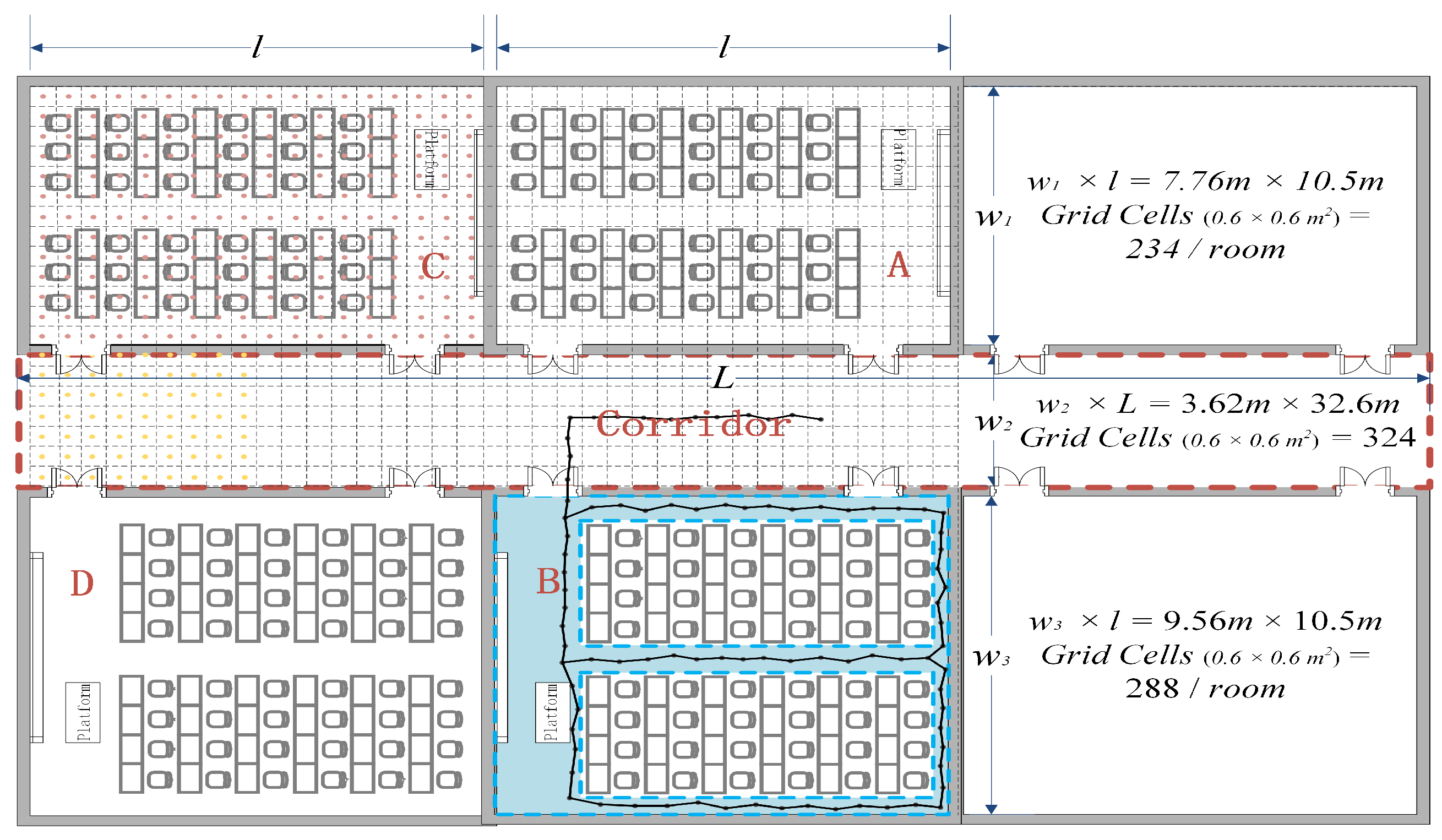
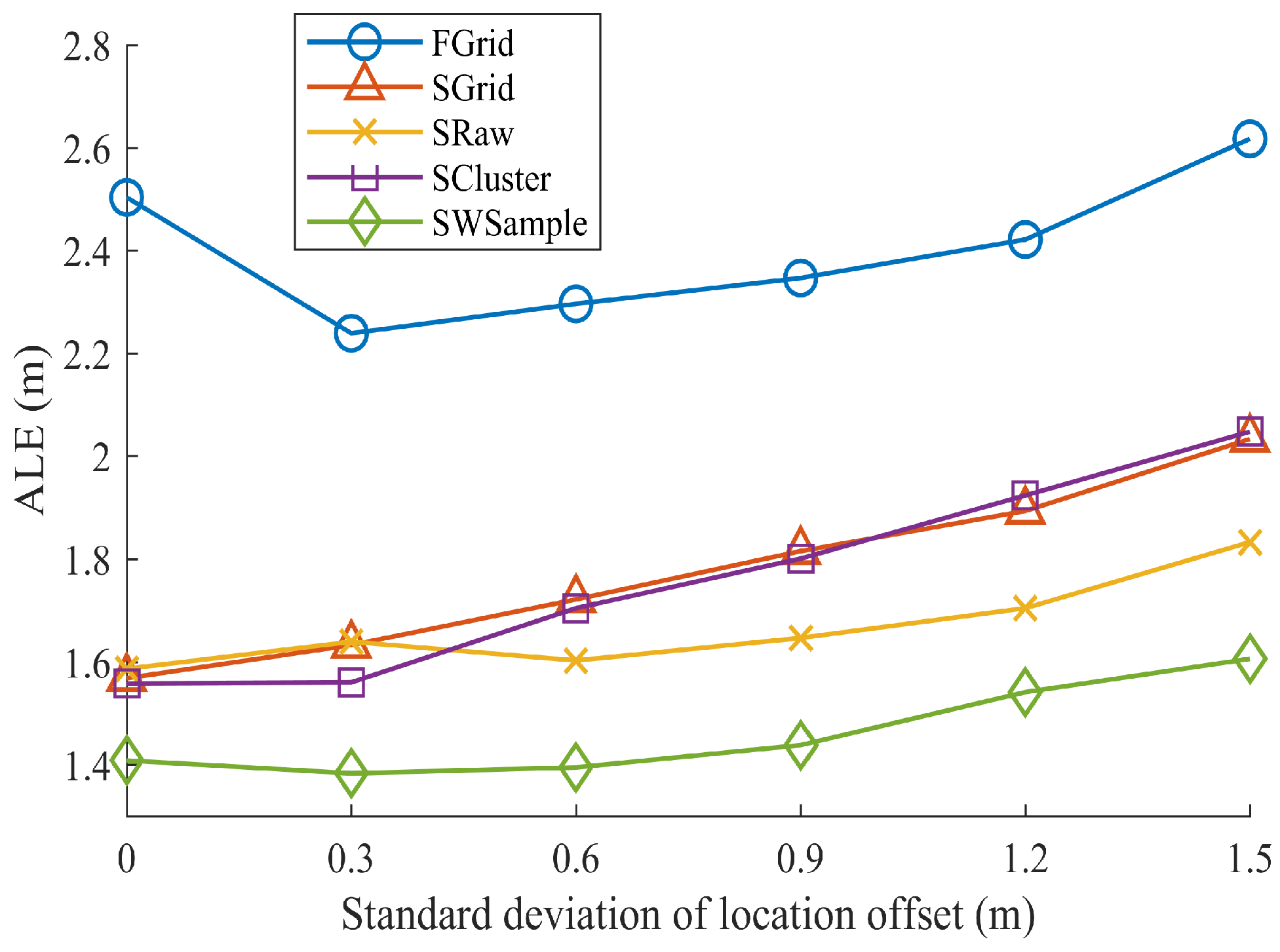
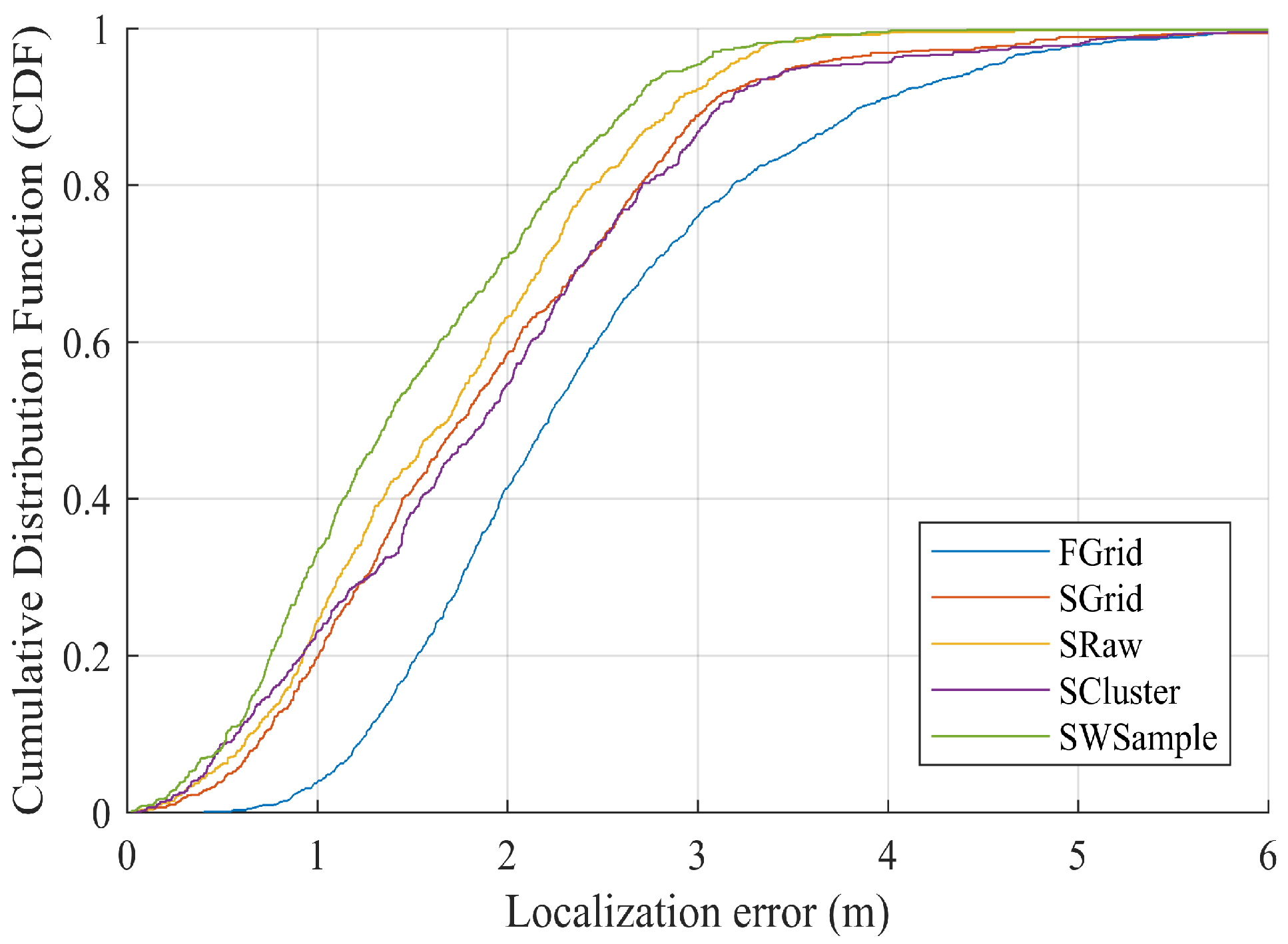
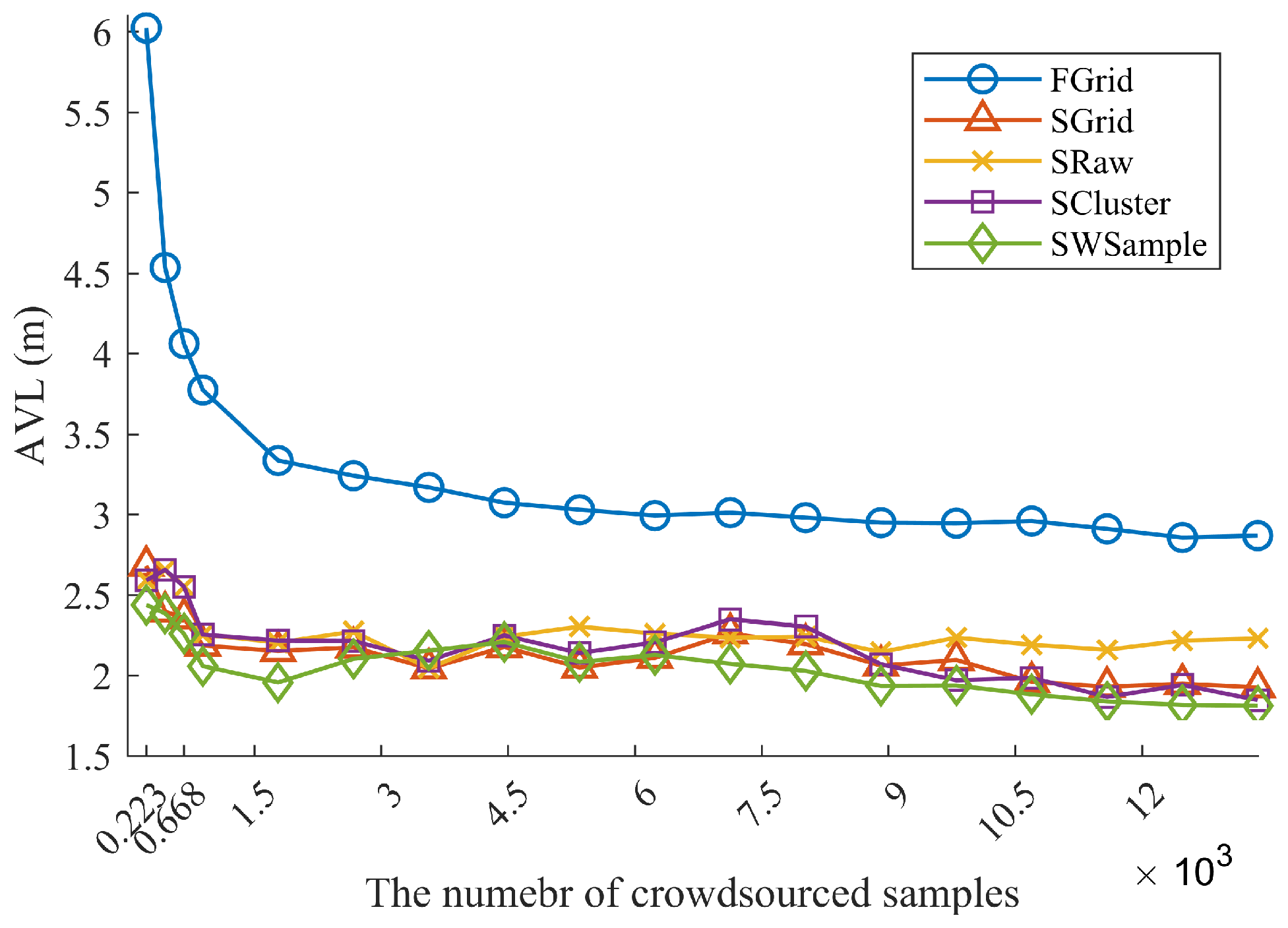
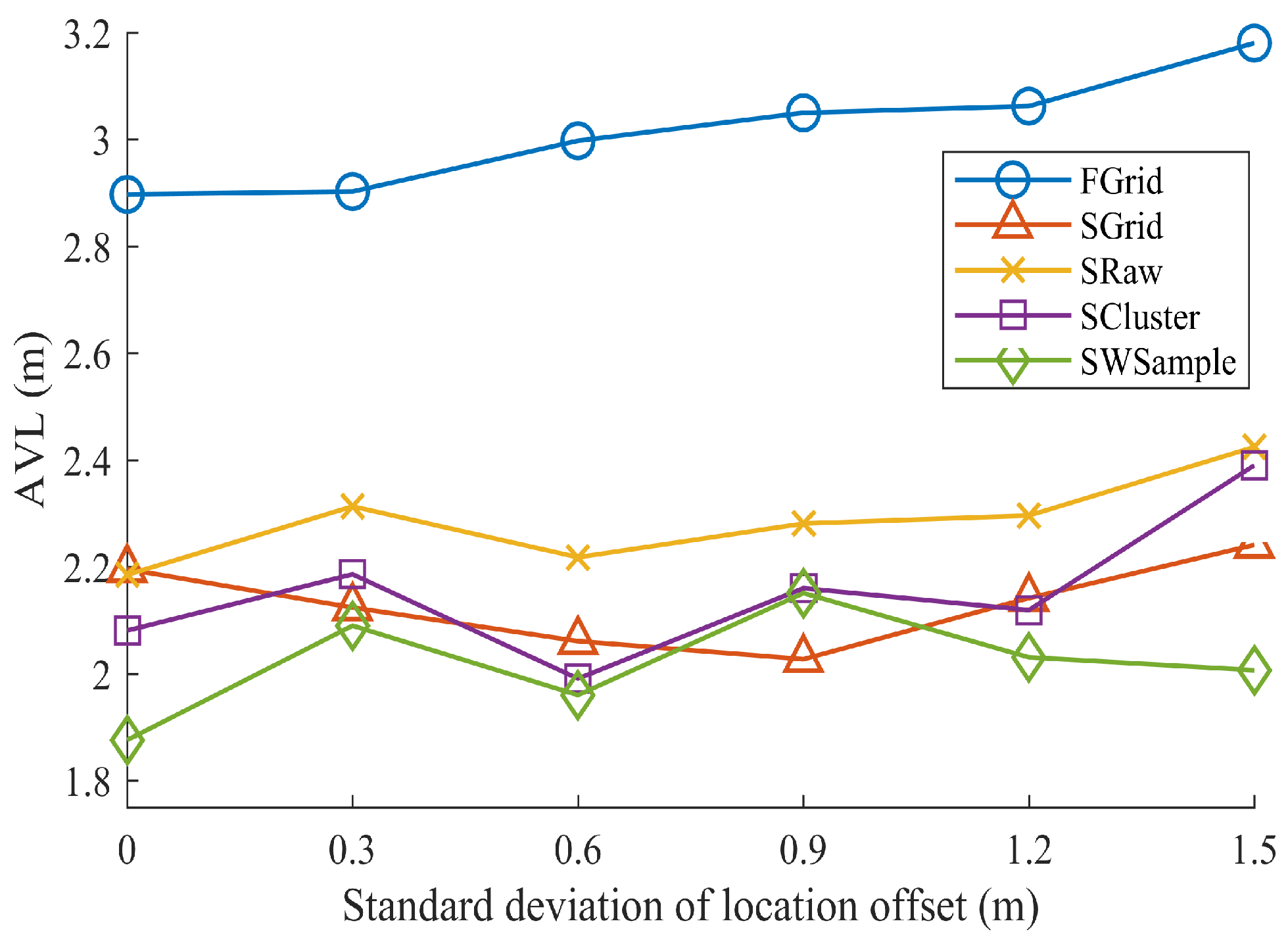
5.1. Experiment Settings
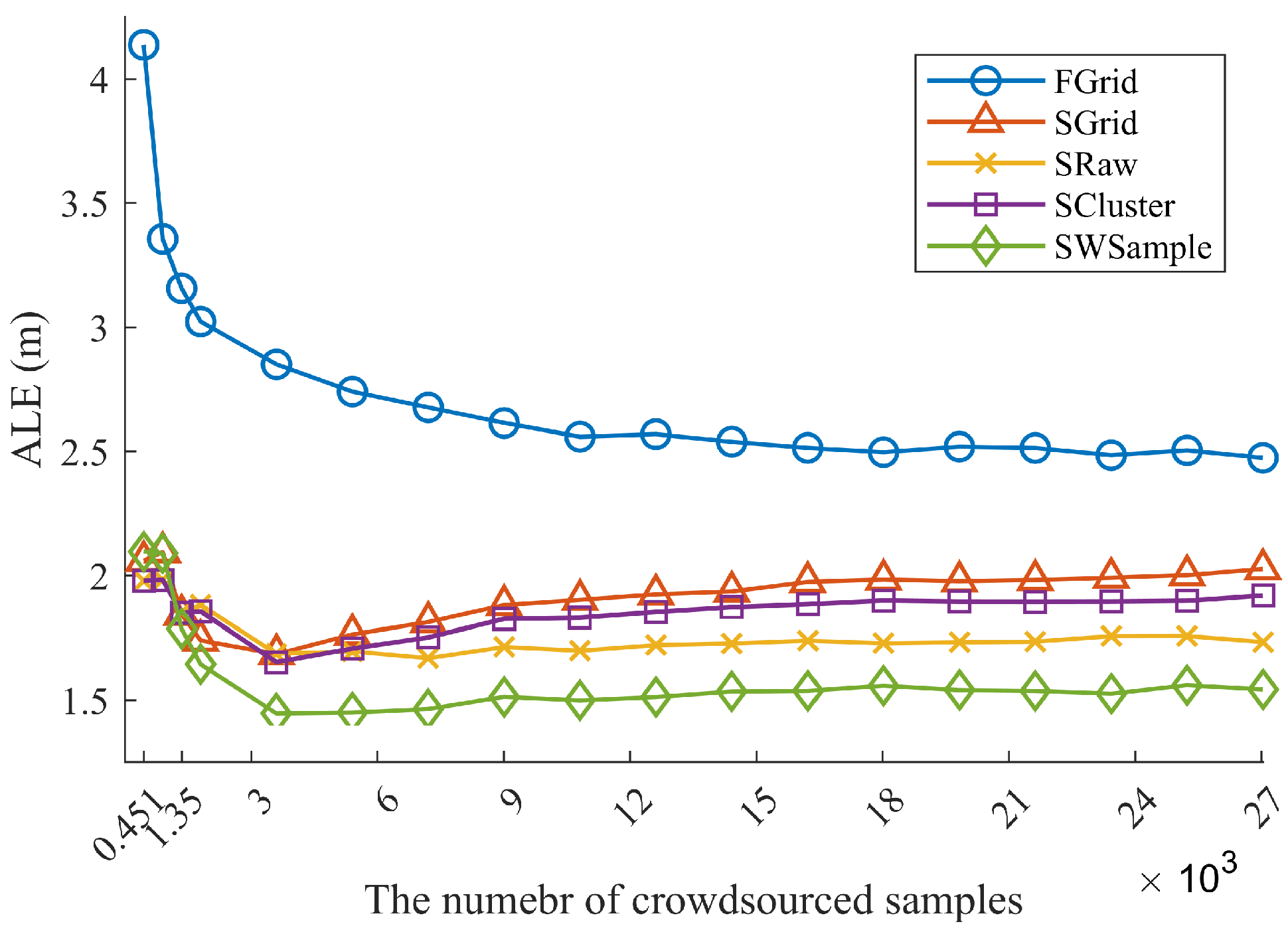
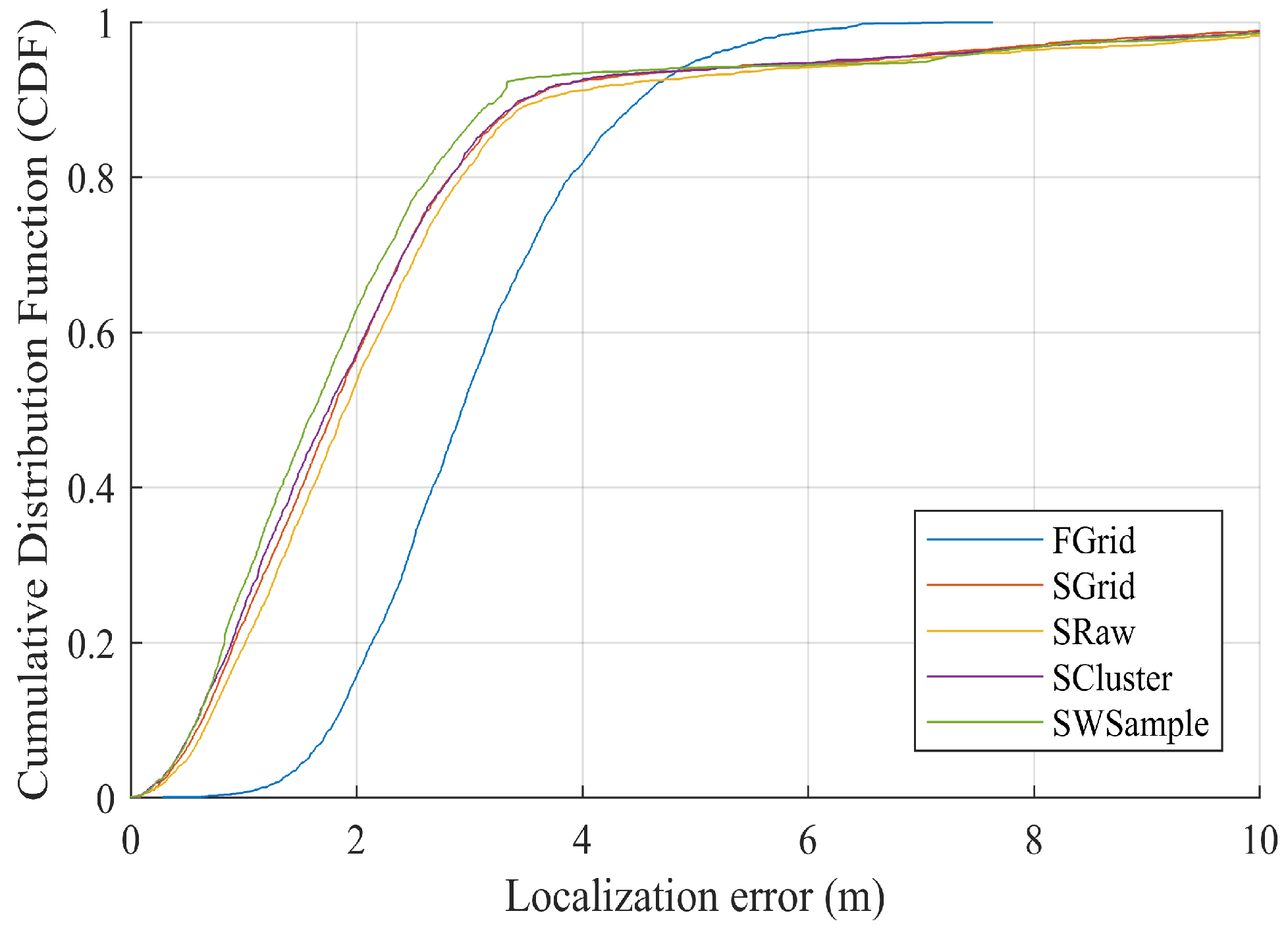
- FGrid emulates the traditional site-survey fingerprinting based on grid fingerprints, which divides the subarea into several non-overlapping grid cell to contain samples, and assigns each new sample into its nearest grid cell. For each grid cell, a grid fingerprint is composed by averaging all samples located within the grid cell, and the location of the grid fingerprint is annotated as the grid center. In the online phase, we used the nearest neighbor algorithm.
- SGrid is similar to the FGrid to obtain grid fingerprints. We then constructed surfaces based on these fingerprints in the offline phase. In the online phase, we used the same surface search method as the one in our proposed SWSample.
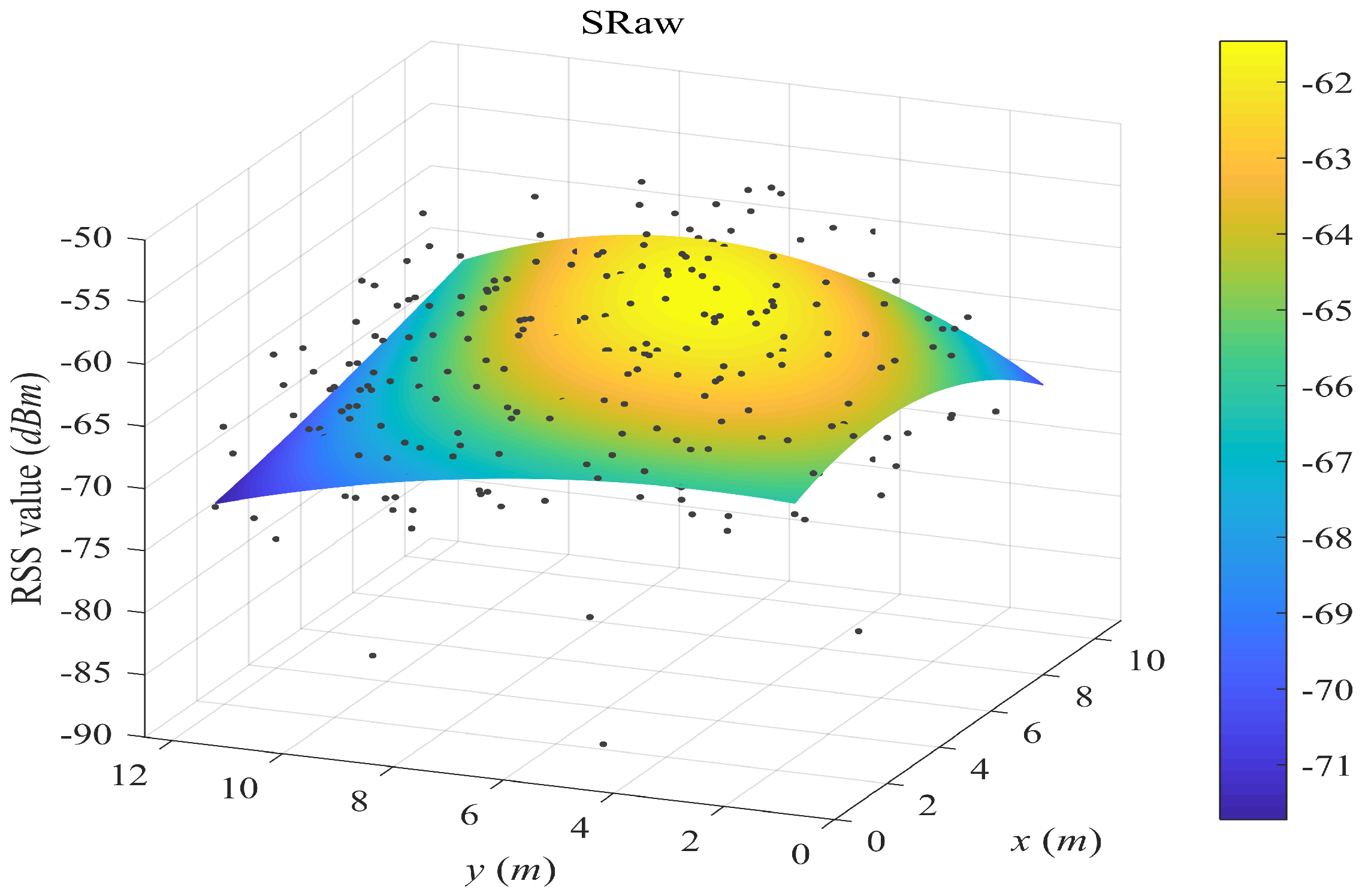
- SRaw retains the original position of every crowdsourced sample and fits propagation surfaces based on them. In the online phase, we used the same surface search method as the one in our proposed SWSample.
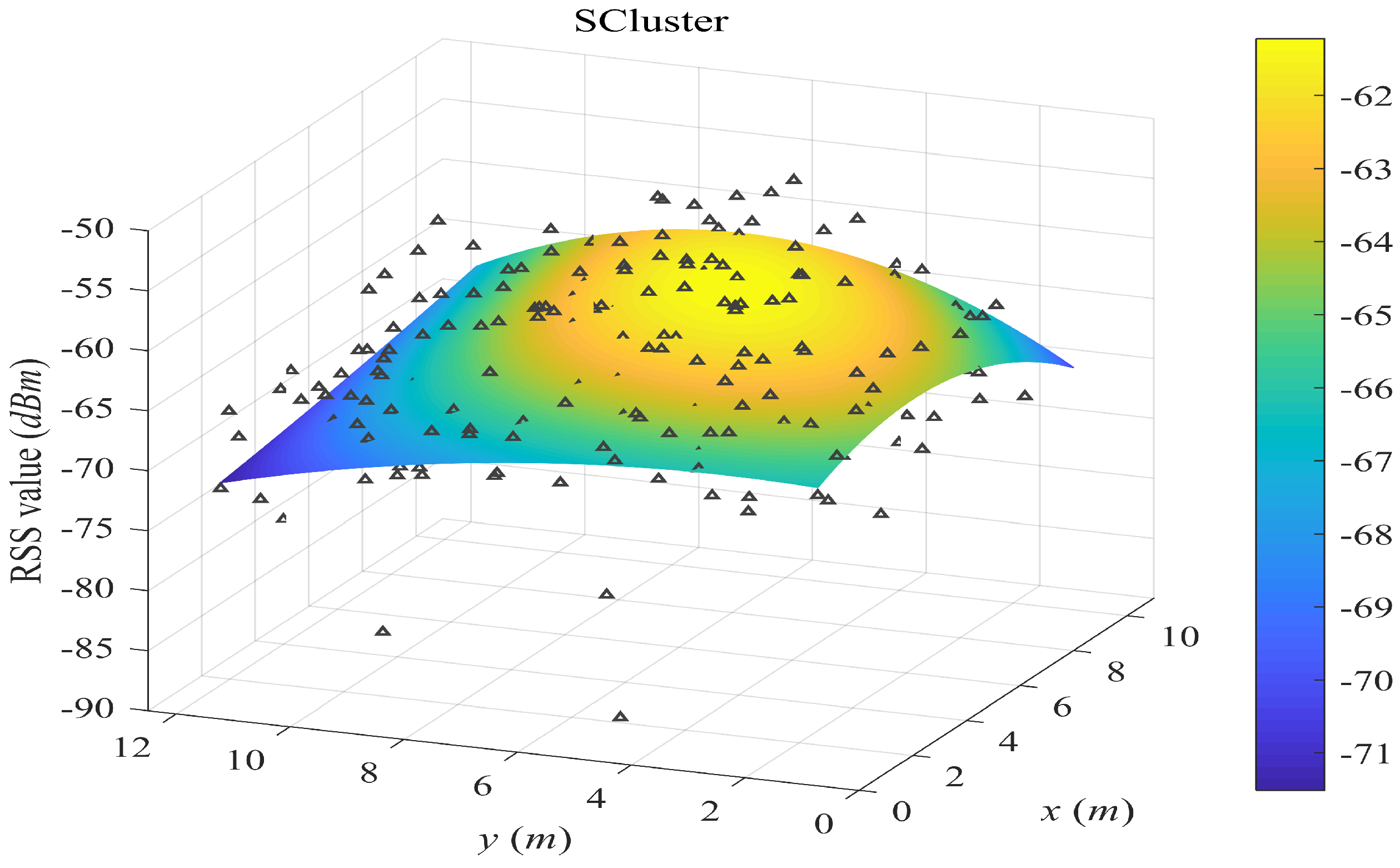
- SCluster clusters the samples in signal domain only. For each cluster, we obtained a cluster fingerprint, which is the average of its cluster members’ RSS vectors. The location of a cluster fingerprint is the geometric center of the cluster members. We fitted the propagation surfaces for every AP based on these cluster fingerprints. In the online phase, we used the surface search method the same as the one in our proposed SWSample.
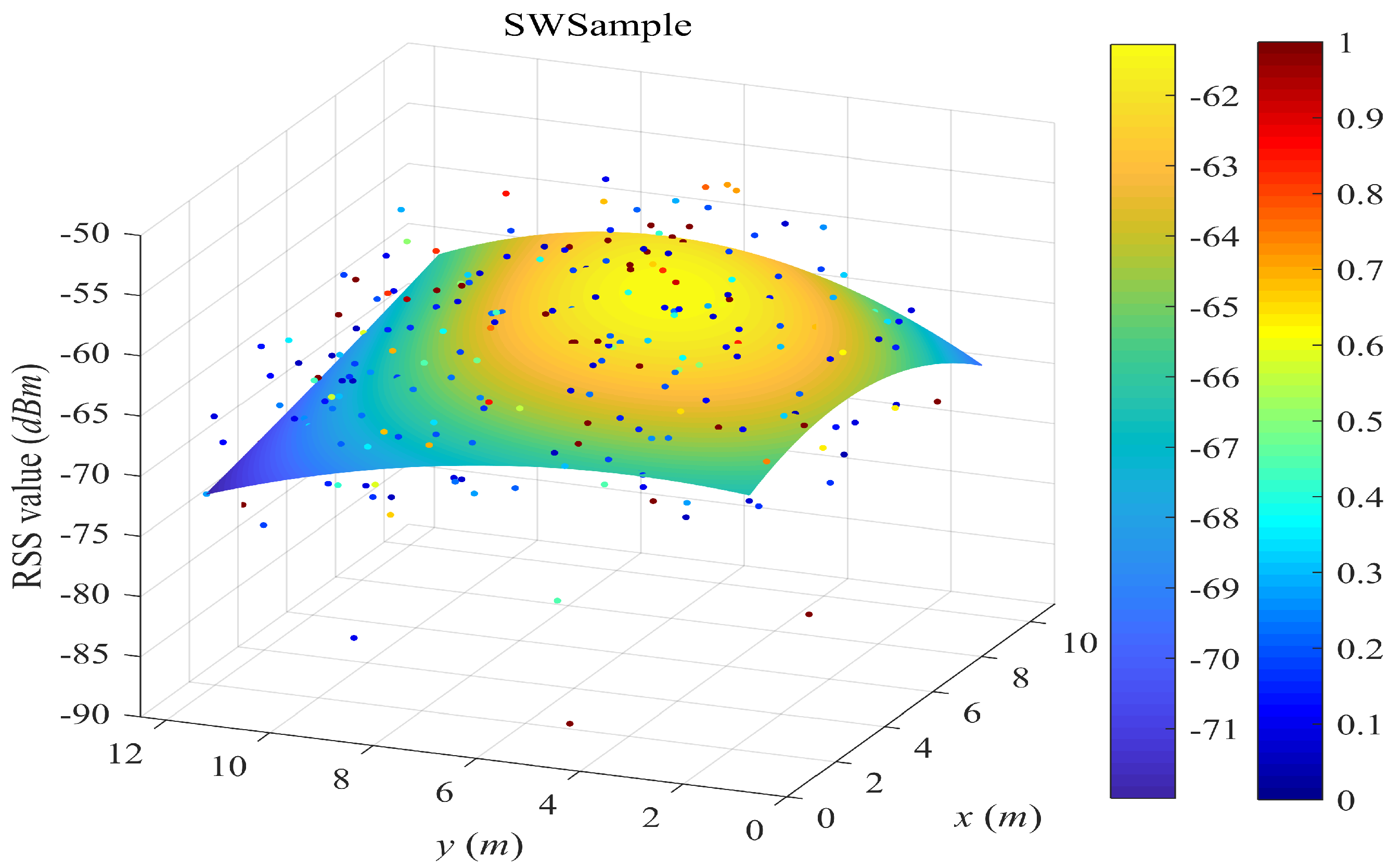
- SWSample is the proposed scheme.
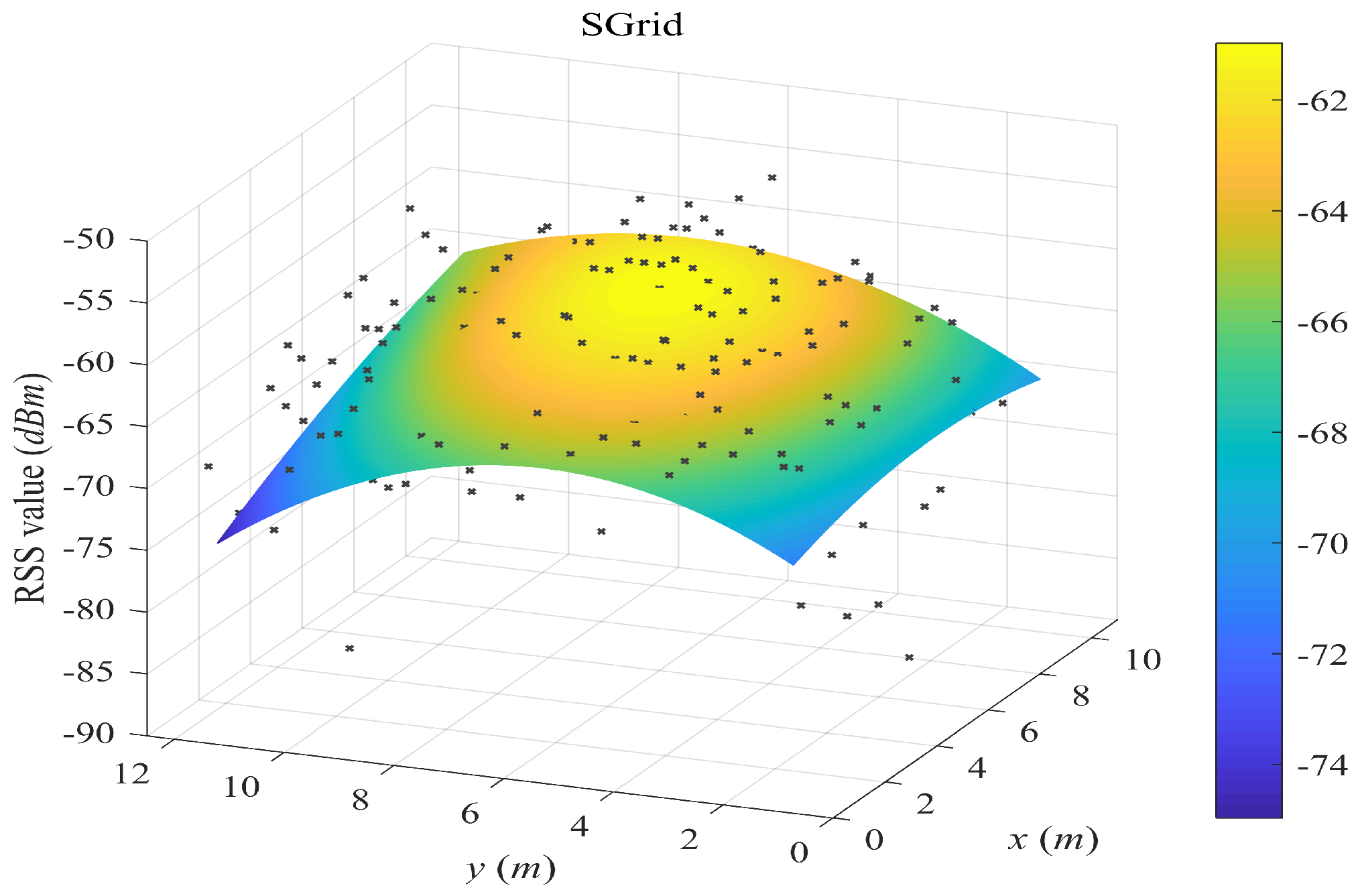
5.2. Surface Fitting Examples
5.3. Experiment Results
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. C 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent advances in indoor localization: A survey on theoretical approaches and applications. IEEE Commun. Surv. Tutor. 2016, 19, 1327–1346. [Google Scholar] [CrossRef]
- He, S.; Chan, S.-H.G. Wi-Fi fingerprint-based indoor positioning: Recent advances and comparisons. IEEE Commun. Surv. Tutor. 2016, 18, 466–490. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Liu, W.; Mo, Y. Indoor localization based on curve fitting and location search using received signal strength. IEEE Trans. Ind. Electron. 2015, 62, 572–582. [Google Scholar] [CrossRef]
- Bahl, P.; Padmanabhan, V.N. Radar: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM 2000. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No.00CH37064), Tel Aviv, Israel, 26–30 March 2000; Volume 2, pp. 775–784. [Google Scholar]
- Hossain, A.; Soh, W.-S. A survey of calibration-free indoor positioning systems. Comput. Commun. 2015, 66, 1–13. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Q.; Yang, L.T.; Chao, H.-C. Indoor smartphone localization via fingerprint crowdsourcing: Challenges and approaches. IEEE Wirel. Commun. 2016, 23, 82–89. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, T.; Guo, D.; Teng, X.; Yuan, B. From one to crowd: A survey on crowdsourcing-based wireless indoor localization. Front. Comput. Sci. 2018, 12, 423–450. [Google Scholar] [CrossRef]
- He, S.; Ji, B.; Chan, S.-H.G. Chameleon: Survey-free updating of a fingerprint database for indoor localization. IEEE Pervasive Comput. 2016, 15, 66–75. [Google Scholar] [CrossRef]
- Abdelnasser, H.; Mohamed, R.; Elgohary, A.; Alzantot, M.F.; Wang, H.; Sen, S.; Choudhury, R.R.; Youssef, M. Semanticslam: Using environment landmarks for unsupervised indoor localization. IEEE Trans. Mob. Comput. 2016, 15, 1770–1782. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q.; Wang, Y.; Tian, Z. Hotspot ranking based indoor mapping and mobility analysis using crowdsourced Wi-Fi signal. IEEE Access 2017, 5, 3594–3602. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Z.; Xiao, C. Automatic radio map adaptation for indoor localization using smartphones. IEEE Trans. Mob. Comput. 2018, 17, 517–528. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, B. Finccm: Fingerprint crowdsourcing, clustering and matching for indoor subarea localization. IEEE Wirel. Commun. Lett. 2015, 4, 677–680. [Google Scholar] [CrossRef]
- Liu, X.; Zhan, Y.; Cen, J. An energy-efficient crowd-sourcing-based indoor automatic localization system. IEEE Sens. J. 2018, 18, 6009–6022. [Google Scholar] [CrossRef]
- Chang, Q.; Li, Q.; Shi, Z.; Chen, W.; Wang, W. Scalable indoor localization via mobile crowdsourcing and gaussian process. Sensors 2016, 16, 381. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.; Moon, B.; Han, D. Unsupervised learning for crowdsourced indoor localization in wireless networks. IEEE Trans. Mob. Comput. 2016, 15, 2892–2906. [Google Scholar] [CrossRef]
- Zhou, M.; Tang, Y.; Tian, Z.; Geng, X. Semi-supervised learning for indoor hybrid fingerprint database calibration with low effort. IEEE Access 2017, 5, 4388–4400. [Google Scholar] [CrossRef]
- Jung, S.; Han, H. Automated construction and maintenance of Wi-Fi radio maps for crowdsourcing-based indoor positioning systems. IEEE Access 2017, 6, 1764–1777. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, H.; Chon, Y.; Cha, H. Crowdsensing-based Wi-Fi radio map management using a lightweight site survey. Comput. Commun. 2015, 60, 86–96. [Google Scholar] [CrossRef]
- Huang, Z.; Xia, J.; Yu, H.; Guan, Y.; Gan, X.; Liu, J. Fusing fixed and hint landmarks on crowd paths for automatically constructing Wi-Fi fingerprint database. China Commun. 2015, 12, 11–24. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Q.; Mao, Q.; Tu, W.; Zhang, X.; Chen, L. Alimc: Activity landmark-based indoor mapping via crowdsourcing. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2774–2785. [Google Scholar] [CrossRef]
- Yu, N.; Xiao, C.; Wu, Y.; Feng, R. A radio-map automatic construction algorithm based on crowdsourcing. Sensors 2016, 16, 504. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Li, Q.; Mao, Q.; Tu, W. A robust crowdsourcing-based indoor localization system. Sensors 2017, 17, 864. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wei, D.; Lai, Q.; Li, X.; Yuan, H. Geomagnetism-aided indoor Wi-Fi radio-map construction via smartphone crowdsourcing. Sensors 2018, 18, 1462. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Wang, Y.; Tian, Z.; Zhang, Q. Indoor pedestrian motion detection via spatial clustering and mapping. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Yang, L.T.; Mo, Y. Indoor positioning via subarea fingerprinting and surface fitting with received signal strength. Pervasive Mob. Comput. 2015, 23, 43–58. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, B. RMapCS: Radio map construction from crowdsourced samples for indoor localization. IEEE Access 2018, 6, 24224–24238. [Google Scholar] [CrossRef]
| Symbol | Definition |
|---|---|
| A set of crowdsourced samples in one subarea. | |
| M | The number of crowdsourced samples in , . |
| The ith crowdsourced sample in . | |
| The annotated location of the ith crowdsourced sample. | |
| The RSS vector of the ith crowdsourced sample. | |
| N | The maximum number of hearable AP in . |
| K | The number of clusters. |
| The set of clusters in the physical space. | |
| The set of clusters in the signal space. | |
| The cross-domain cluster coefficient of the ith sample. | |
| The reliability weight of the ith sample. | |
| The RSS surface function. | |
| The percentile threshold in sample selection method. | |
| The weight threshold in sample selection method. | |
| The increasing order of sample reliability weight. | |
| The reliability weight at the percentile in . | |
| The set of select samples. | |
| The set of hearable Aps by samples in . | |
| The surface coefficient of the RSS surface function. | |
| The set of RSS values from an AP in . | |
| The normalized elements in . | |
| The entropy-like quantity for each AP in . | |
| The surface weight of nth AP in for subarea determination. | |
| The surface weight of nth AP in for location search. | |
| Subarea fingerprint. | |
| The set of grid cells in one subarea. | |
| G | The number of grids in , . |
| The RSS vector of a test sample. | |
| The sth subarea fingerprint. | |
| The set of hearable APs by both and . | |
| The weighted signal distance between the test sample and a subarea. | |
| The number of grid cells. | |
| The standard deviation of location offset. | |
| The set of samples from site survey. | |
| The set of samples from pedestrian trajectories. |
| Error (m) | m | m | m | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 50% | 90% | Mean | 50% | 90% | Mean | 50% | 90% | ||
| Uni. | FGrid | 2.479 | 2.448 | 3.672 | 2.284 | 2.086 | 3.744 | 2.421 | 2.217 | 3.868 |
| SGrid | 1.571 | 1.353 | 2.595 | 1.726 | 1.630 | 2.884 | 1.898 | 1.757 | 3.048 | |
| SRaw | 1.575 | 1.370 | 2.645 | 1.618 | 1.524 | 2.694 | 1.711 | 1.688 | 2.873 | |
| SCluster | 1.552 | 1.364 | 2.550 | 1.708 | 1.657 | 2.875 | 1.916 | 1.879 | 3.111 | |
| SWSample | 1.373 | 1.124 | 2.413 | 1.374 | 1.243 | 2.470 | 1.513 | 1.366 | 2.640 | |
| Non-uni. | FGrid | 2.897 | 2.776 | 3.672 | 2.982 | 2.813 | 4.477 | 3.059 | 2.932 | 4.502 |
| SGrid | 2.164 | 1.691 | 3.522 | 2.086 | 1.679 | 3.402 | 2.169 | 1.795 | 3.499 | |
| SRaw | 2.155 | 1.713 | 3.459 | 2.221 | 1.732 | 3.594 | 2.322 | 1.898 | 3.647 | |
| SCluster | 2.063 | 1.602 | 3.497 | 2.009 | 1.584 | 3.287 | 2.144 | 1.752 | 3.477 | |
| SWSample | 1.854 | 1.497 | 3.172 | 1.951 | 1.472 | 3.217 | 2.043 | 1.625 | 3.242 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Wang, B.; Yang, G.; Zhou, M. Indoor Localization Based on Weighted Surfacing from Crowdsourced Samples. Sensors 2018, 18, 2990. https://doi.org/10.3390/s18092990
Lin J, Wang B, Yang G, Zhou M. Indoor Localization Based on Weighted Surfacing from Crowdsourced Samples. Sensors. 2018; 18(9):2990. https://doi.org/10.3390/s18092990
Chicago/Turabian StyleLin, Junhong, Bang Wang, Guang Yang, and Mu Zhou. 2018. "Indoor Localization Based on Weighted Surfacing from Crowdsourced Samples" Sensors 18, no. 9: 2990. https://doi.org/10.3390/s18092990
APA StyleLin, J., Wang, B., Yang, G., & Zhou, M. (2018). Indoor Localization Based on Weighted Surfacing from Crowdsourced Samples. Sensors, 18(9), 2990. https://doi.org/10.3390/s18092990






