Helical Structures Mimicking Chiral Seedpod Opening and Tendril Coiling
Abstract
1. Introduction
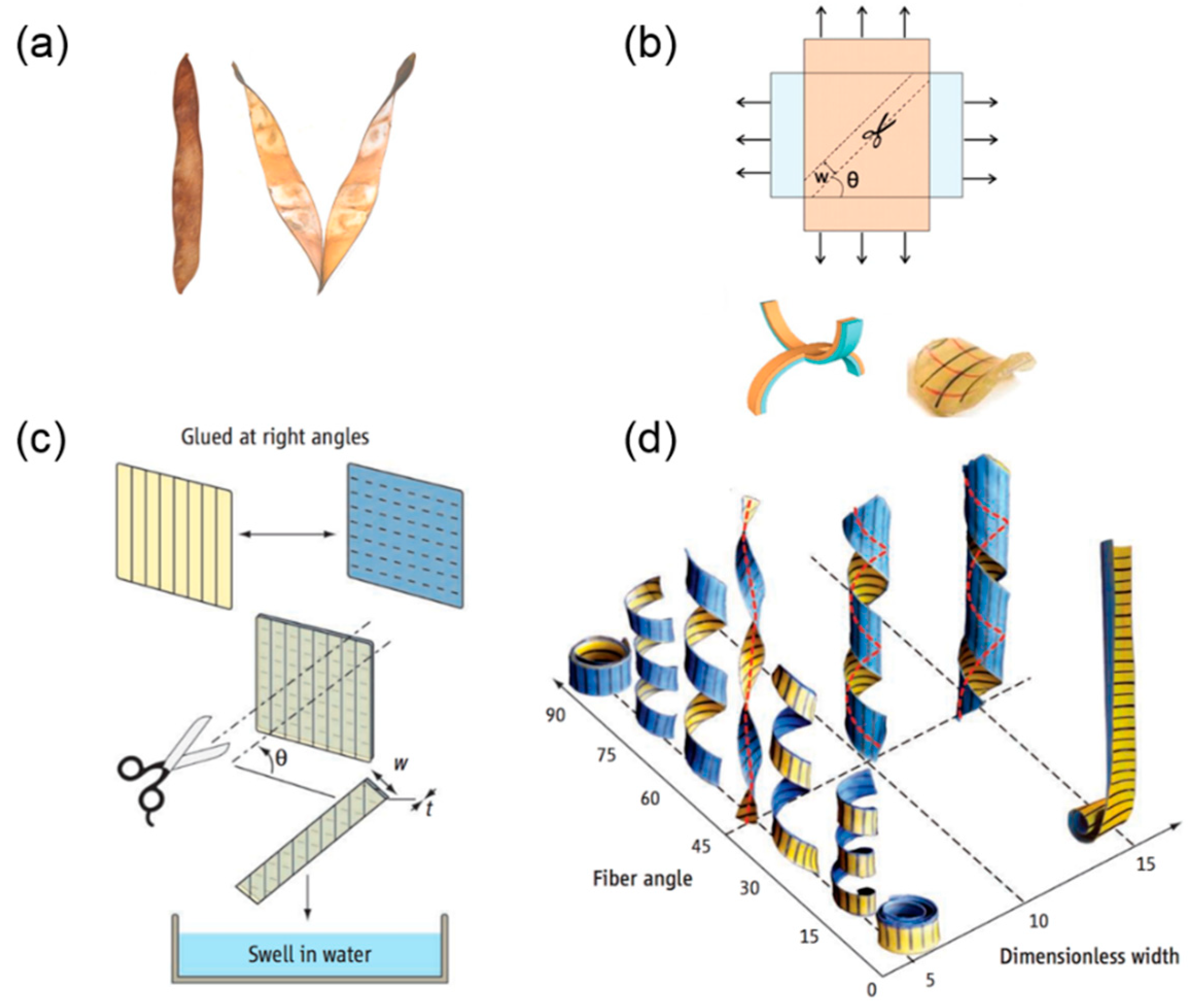
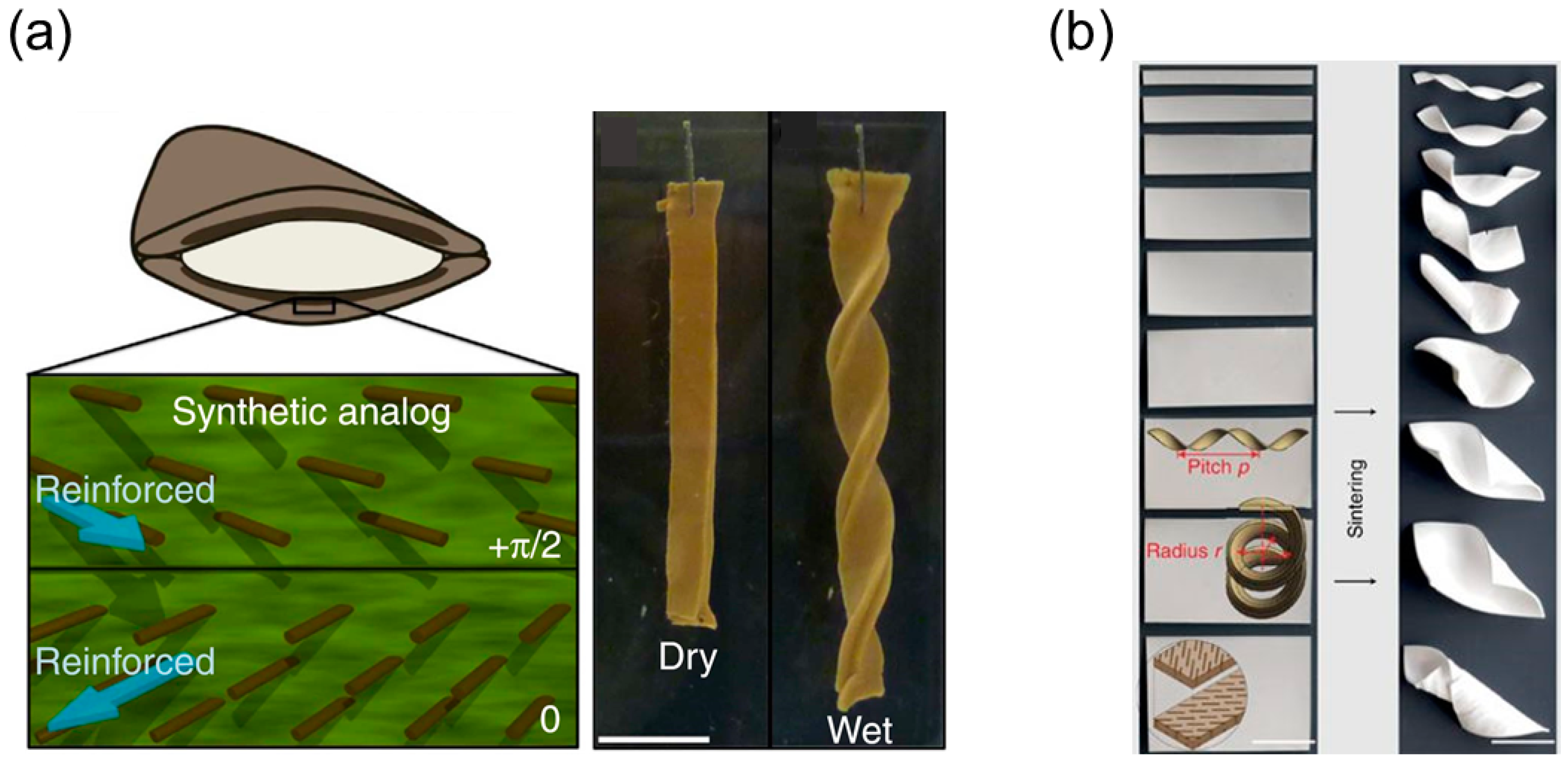
2. Helical Structures Mimicking the Opening of Bauhinia Variegata Pods
2.1. Opening Mechanism of Bauhinia Variegata Pods
2.1.1. Hygroscopic Motion in Plants
2.1.2. Transition from Pure Twisting to Helical Coiling During Pod Opening
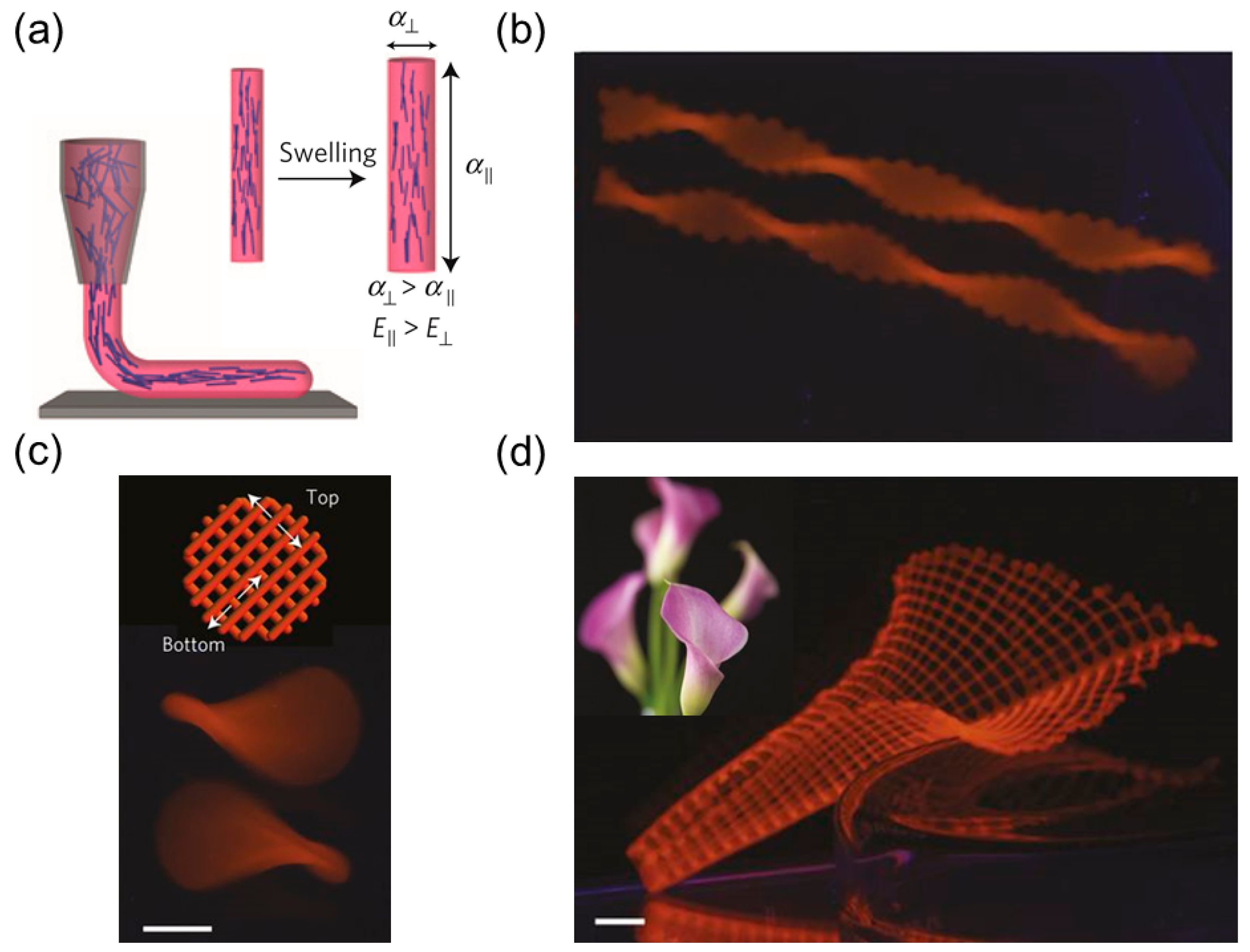
2.2. Biomimetic Helical Structures Based on Stimuli-Responsive Materials
2.2.1. Hydrogel-Based Helical Structures
Humidity-Responsive Hydrogels
Thermally Responsive Hydrogels
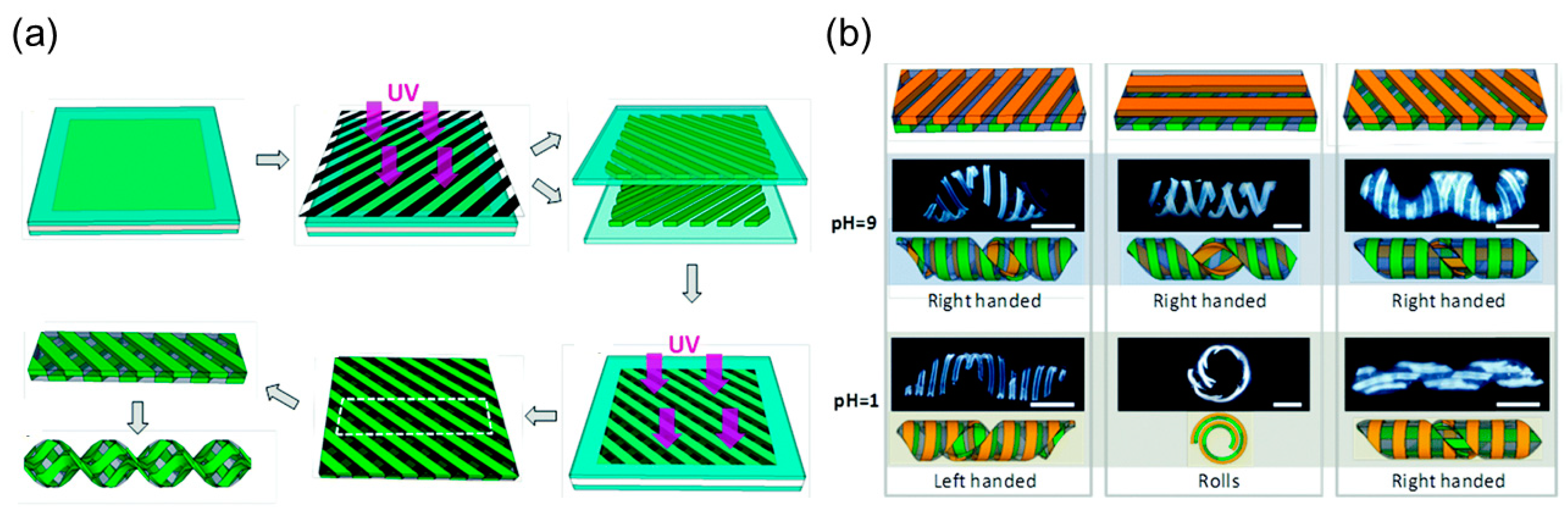
pH Responsive Hydrogels
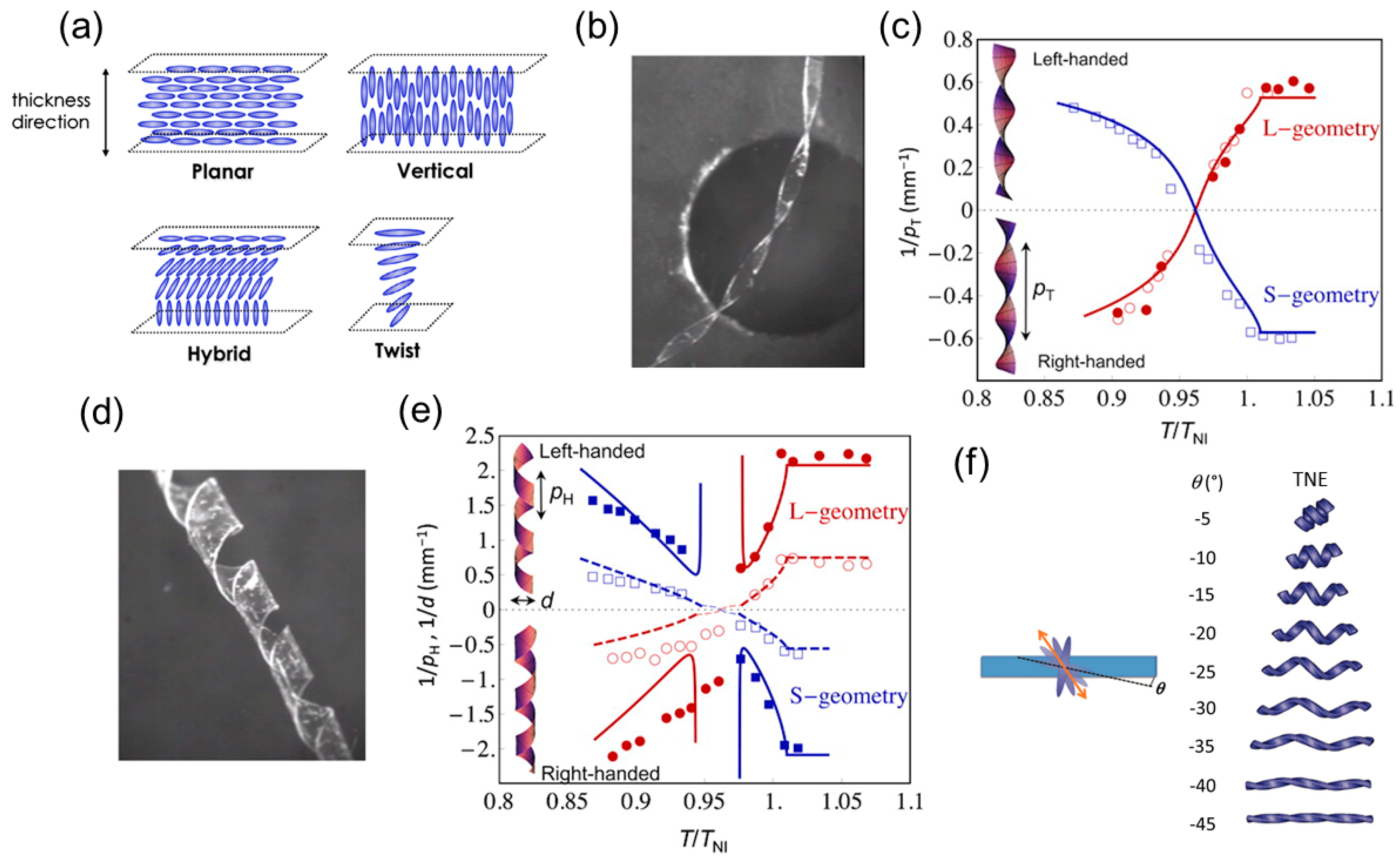
2.2.2. Liquid Crystal Networks or Elastomers-Based Helical Structures
Thermally Responsive LCNs or LCEs
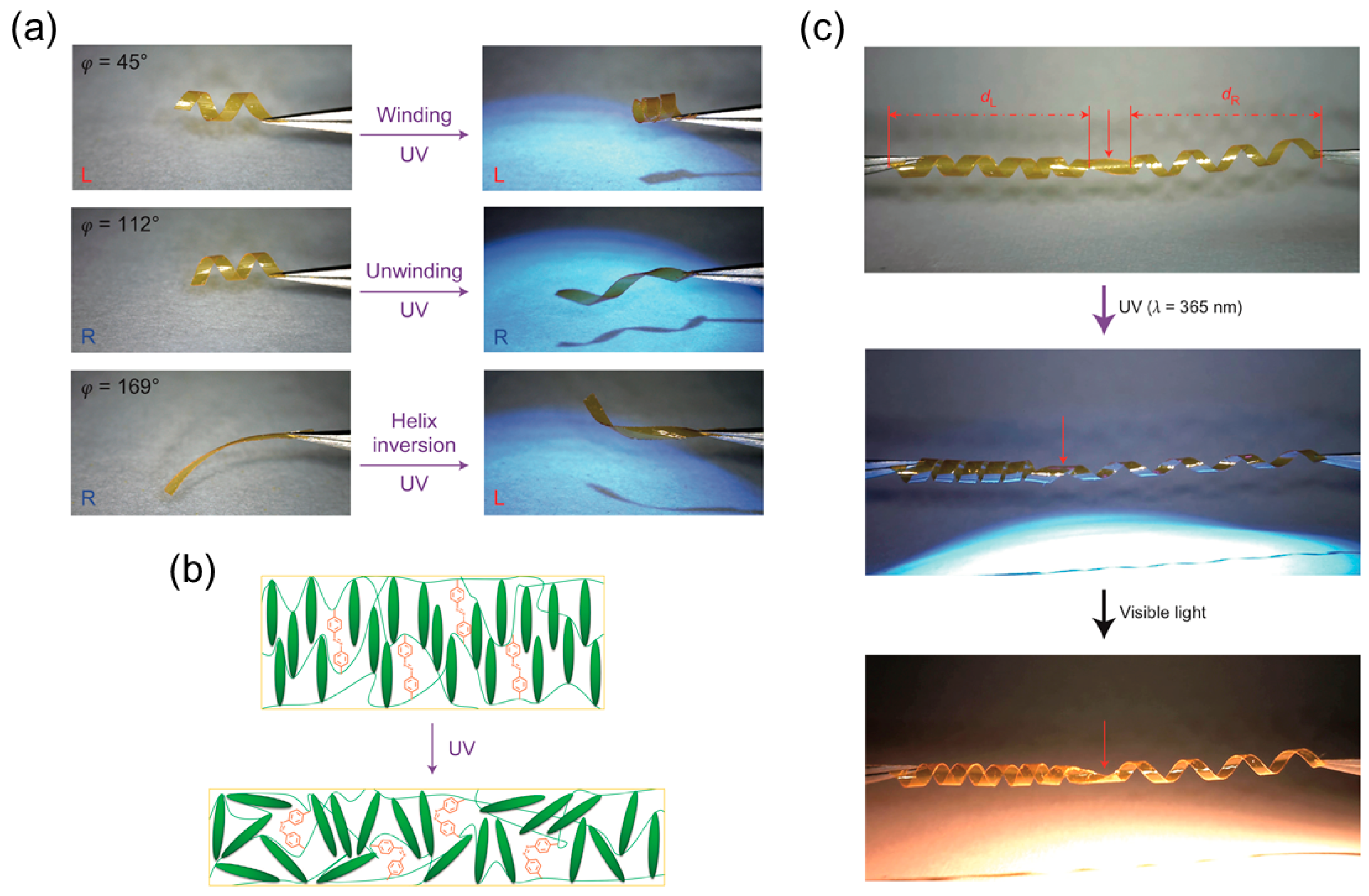
Light-Responsive LCNs or LCEs
Other Stimuli-Responsive LCNs or LCEs
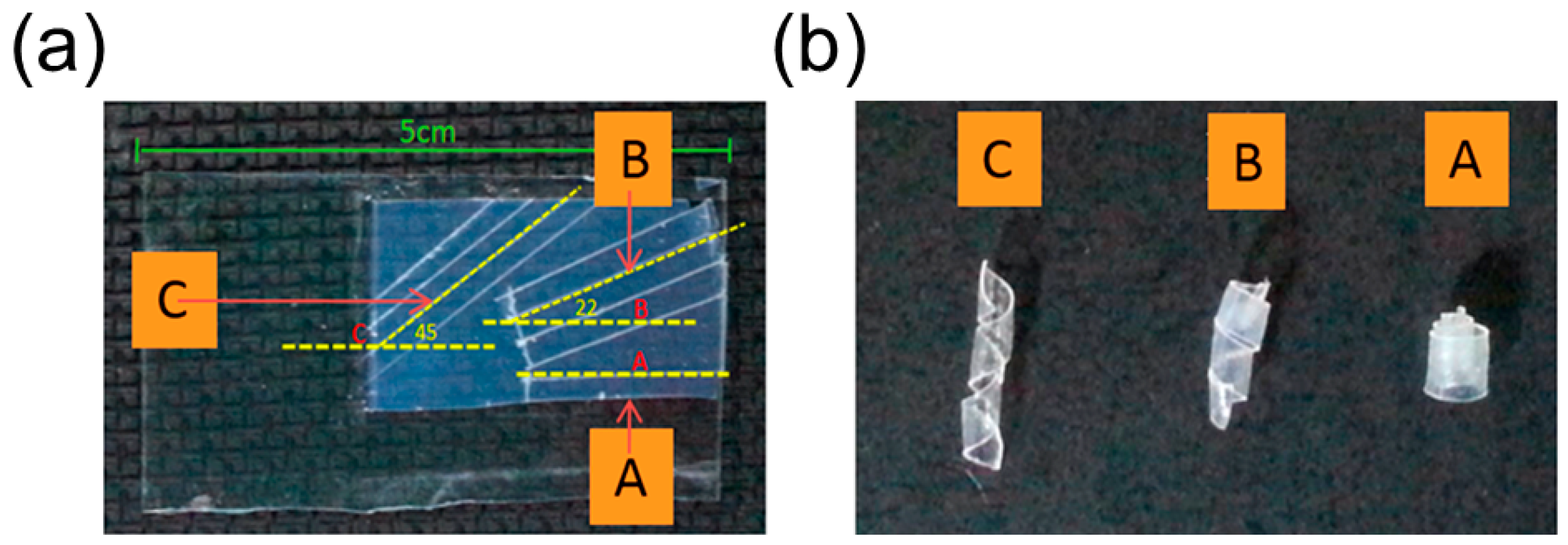
2.2.3. Shape Memory Polymers-Based Helical Structures
3. Helical Structures Mimicking Tendril’s Coiling
3.1. Coiling Mechanism of Tendrils
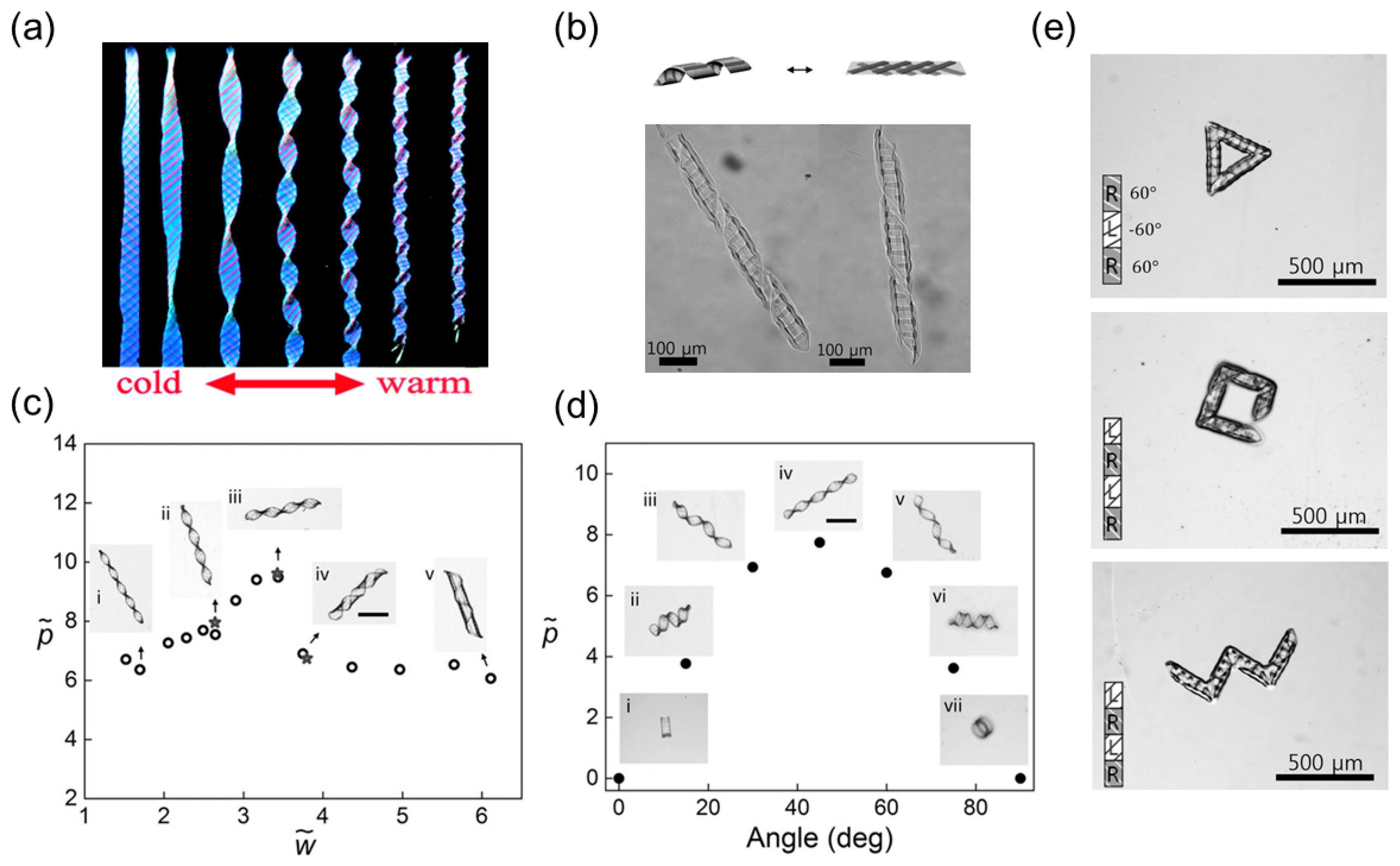
3.2. Helical Structures with Hierarchically Chiral Building Blocks
3.3. Helical Structures with Perversions
3.3.1. Bilayer Elastomers with Misfit Natural Length
Emergence of Multiple Perversions
Buckling Instability
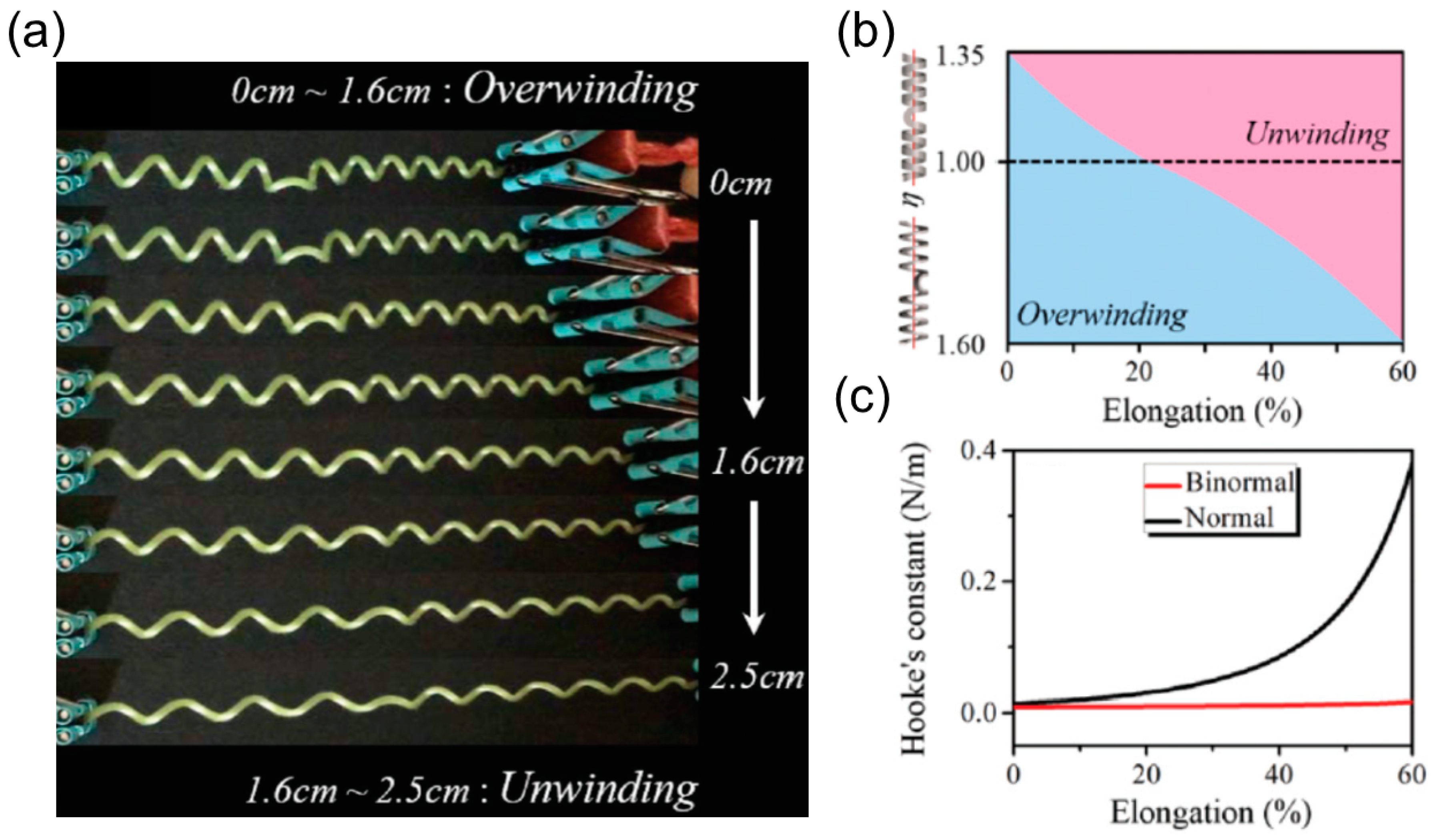
Over-Winding
Linear or Nonlinear Force-Extension Relationship
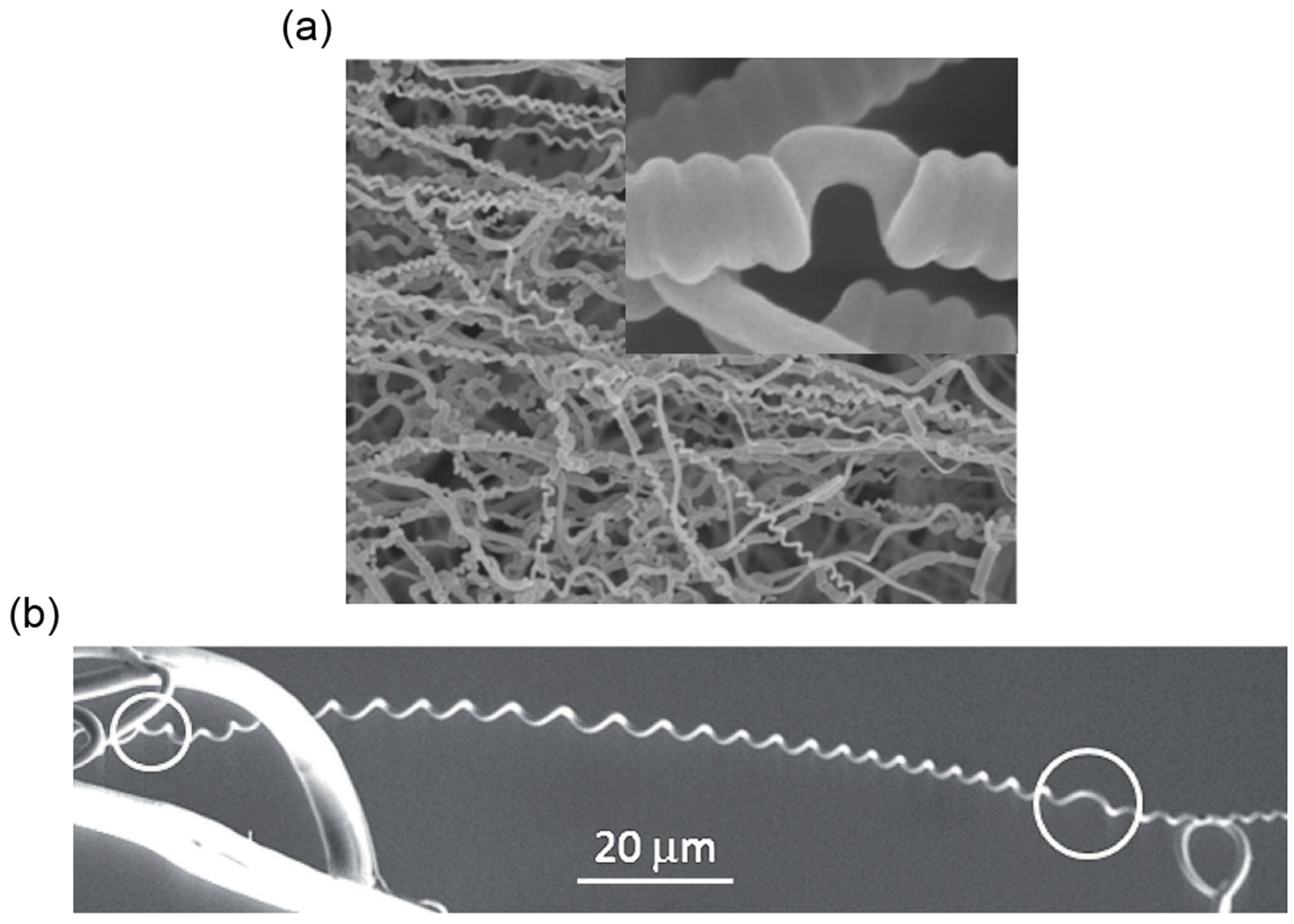
3.3.2. Helical Rods from Electrospinning
Bi-Component Electrospinning
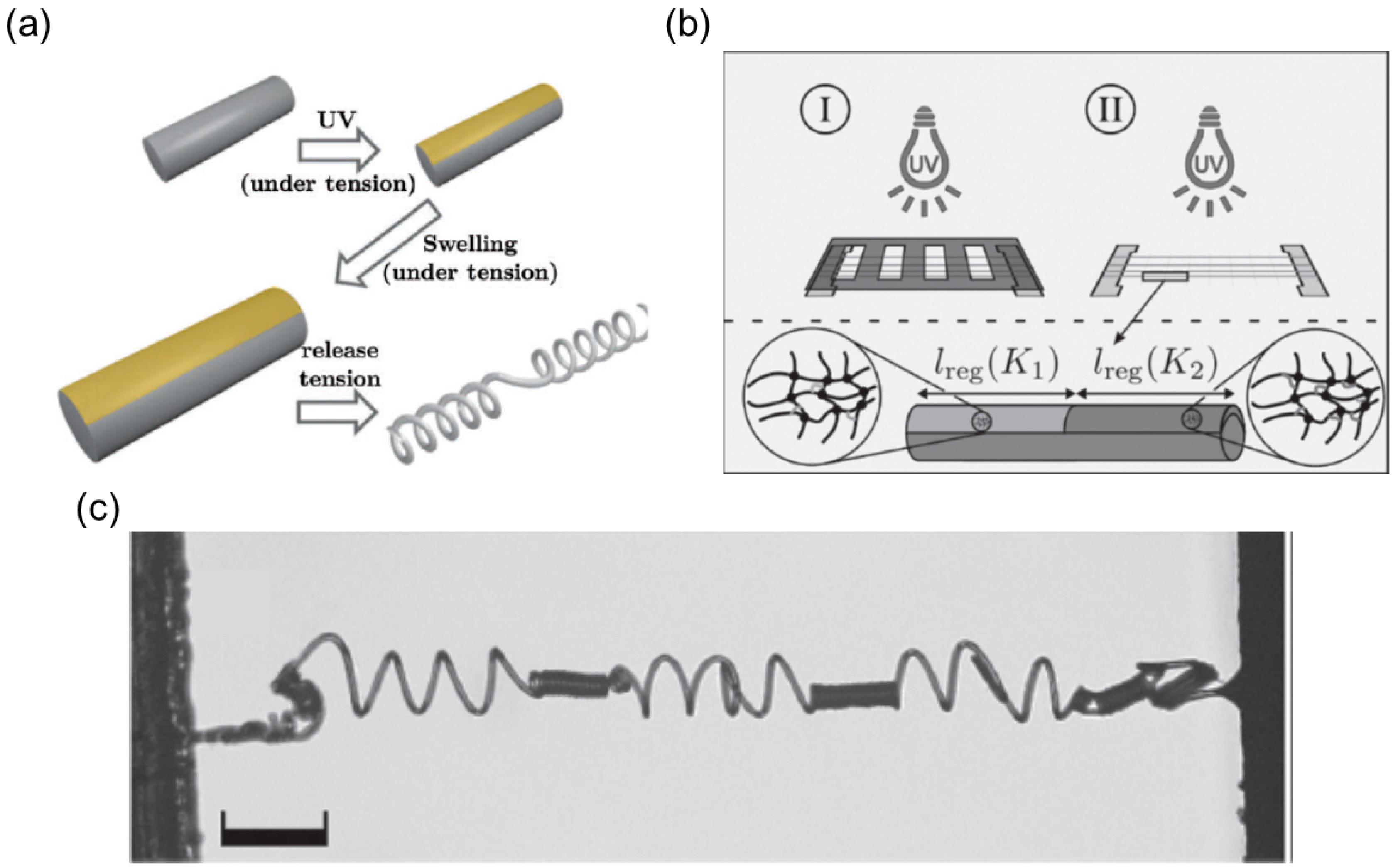
Electrospinning Liquid Crystalline Cellulose
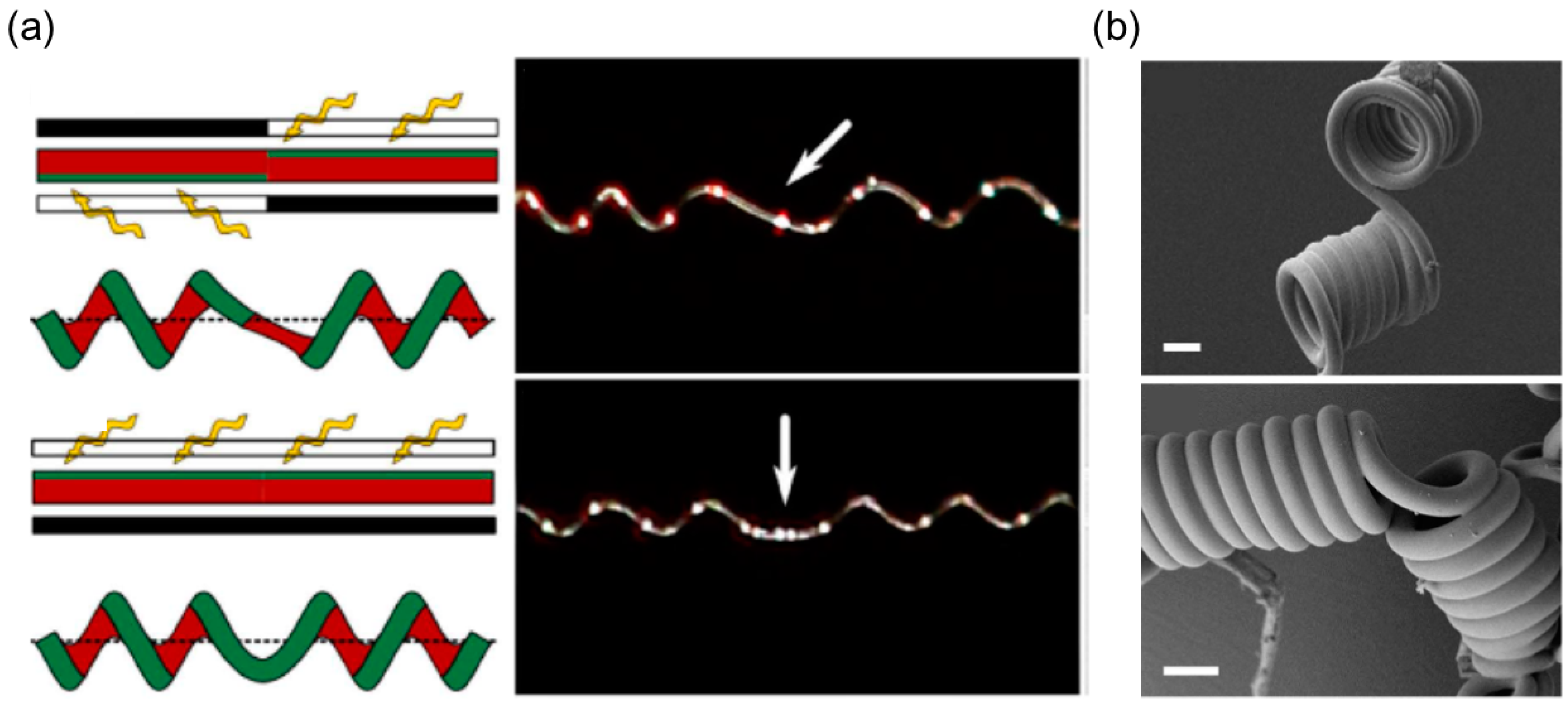
Selective UV Irradiation
4. Summary and Outlook
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Goldstein, R.E.; Goriely, A.; Huber, G.; Wolgemuth, C.W. Bistable Helices. Phy. Rev. Lett. 2000, 84, 1631–1634. [Google Scholar] [CrossRef] [PubMed]
- Goriely, A.; Tabor, M. Spontaneous Helix Hand Reversal and Tendril Perversion in Climbing Plants. Phys. Rev. Lett. 1998, 80, 1564–1567. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, Z.; Li, W.; Dai, P.; Ren, K.; Lin, J.; Taber, L.A.; Chen, W. Mechanics of tunable helices and geometric frustration in biomimetic seashells. EPL (Europhys. Lett.) 2014, 105, 64005. [Google Scholar] [CrossRef]
- Jung, W.; Choi, S.M.; Kim, W.; Kim, H.Y. Reduction of granular drag inspired by self-burrowing rotary seeds. Phys. Fluids 2017, 29, 041702. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Moldovan, R.; Yeung, C.; Wu, X.L. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA 2006, 103, 13712–13717. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Feng, X.; Pei, A.; Kane, C.R.; Tam, R.; Hennessy, C.; Wang, J. Bioinspired Helical Microswimmers Based on Vascular Plants. Nano Lett. 2014, 14, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Texier, B.D.; Ibarra, A.; Melo, F. Helical Locomotion in a Granular Medium. Phys. Rev. Lett. 2017, 119, 068003. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Yan, Z.; Jang, K.I.; Huang, W.; Fu, H.; Kim, J.; Wei, Z.; Flavin, M.; McCracken, J.; Wang, R.; et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 2015, 347, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Boone, C.; Roberts, M.; Savage, D.E.; Lagally, M.G.; Shaji, N.; Qin, H.; Blick, R.; Nairn, J.A.; Liu, F. Nanomechanical Architecture of Strained Bilayer Thin Films: From Design Principles to Experimental Fabrication. Adv. Mater. 2005, 17, 2860–2864. [Google Scholar] [CrossRef]
- Chen, Z.; Majidi, C.; Srolovitz, D.J.; Haataja, M. Tunable helical ribbons. Appl. Phys. Lett. 2011, 98, 011906. [Google Scholar] [CrossRef]
- Armon, S.; Efrati, E.; Kupferman, R.; Sharon, E. Geometry and Mechanics in the Opening of Chiral Seed Pods. Science 2011, 333, 1726–1730. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.S.; Wang, G.; Feng, X.Q.; Kitamura, T.; Kang, Y.L.; Yu, S.W.; Qin, Q.H. Hierarchical chirality transfer in the growth of Towel Gourd tendrils. Sci. Rep. 2013, 3, 3102. [Google Scholar] [CrossRef] [PubMed]
- Gerbode, S.J.; Puzey, J.R.; McCormick, A.G.; Mahadevan, L. How the Cucumber Tendril Coils and Overwinds. Science 2012, 337, 1087–1091. [Google Scholar] [CrossRef] [PubMed]
- Goriely, A. The Mathematics and Mechanics of Biological Growth; Springer: New York, NY, USA, 2017. [Google Scholar]
- McMillen, T.; Goriely, A. Tendril Perversion in Intrinsically Curved Rods. J. Nonlinear Sci. 2002, 12, 241–281. [Google Scholar] [CrossRef]
- Timoshenko, S. Analysis of Bi-Metal Thermostats. J. Opt. Soc. Am. 1925, 11, 233. [Google Scholar] [CrossRef]
- Forterre, Y.; Skotheim, J.M.; Dumais, J.; Mahadevan, L. How the Venus flytrap snaps. Nature 2005, 433, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Reyssat, E.; Mahadevan, L. Hygromorphs: From pine cones to biomimetic bilayers. J. R. Soc. Interface 2009, 6, 951–957. [Google Scholar] [CrossRef] [PubMed]
- Elbaum, R.; Zaltzman, L.; Burgert, I.; Fratzl, P. The Role of Wheat Awns in the Seed Dispersal Unit. Science 2007, 316, 884–886. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Wang, K.W. Plant-inspired adaptive structures and materials for morphing and actuation: A review. Bioinspir. Biomim. 2016, 12, 011001. [Google Scholar] [CrossRef] [PubMed]
- Efrati, E.; Sharon, E.; Kupferman, R. Elastic theory of unconstrained non-Euclidean plates. J. Mech. Phys. Solids 2009, 57, 762–775. [Google Scholar] [CrossRef]
- Forterre, Y.; Dumais, J. Generating Helices in Nature. Science 2011, 333, 1715–1716. [Google Scholar] [CrossRef] [PubMed]
- Pezzulla, M.; Smith, G.P.; Nardinocchi, P.; Holmes, D.P. Geometry and mechanics of thin growing bilayers. Soft Matter 2016, 12, 4435–4442. [Google Scholar] [CrossRef] [PubMed]
- Alben, S.; Balakrisnan, B.; Smela, E. Edge Effects Determine the Direction of Bilayer Bending. Nano Lett. 2011, 11, 2280–2285. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Mehta, A.K.; Grover, M.A.; Chen, W.; Lynn, D.G.; Chen, Z. Shape selection and multi-stability in helical ribbons. Appl. Phys. Lett. 2014, 104, 211901. [Google Scholar] [CrossRef]
- Sydney Gladman, A.; Matsumoto, E.A.; Nuzzo, R.G.; Mahadevan, L.; Lewis, J.A. Biomimetic 4D printing. Nat. Mater. 2016, 15, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Erb, R.M.; Sander, J.S.; Grisch, R.; Studart, A.R. Self-shaping composites with programmable bioinspired microstructures. Nat. Commun. 2013, 4, 1721. [Google Scholar] [CrossRef] [PubMed]
- Armon, S.; Aharoni, H.; Moshe, M.; Sharon, E. Shape selection in chiral ribbons: From seed pods to supramolecular assemblies. Soft Matter 2014, 10, 2733–2740. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.J.; Hayward, R.C. Reconfigurable Microscale Frameworks from Concatenated Helices with Controlled Chirality. Adv. Mater. 2017, 29, 1606111. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J.; Zhu, C.N.; Hong, W.; Wu, Z.L.; Zheng, Q. Programmed planar-to-helical shape transformations of composite hydrogels with bioinspired layered fibrous structures. J. Mater. Chem. B 2016, 4, 7075–7079. [Google Scholar] [CrossRef]
- Sawa, Y.; Ye, F.; Urayama, K.; Takigawa, T.; Gimenez-Pinto, V.; Selinger, R.L.B.; Selinger, J.V. Shape selection of twist-nematic-elastomer ribbons. Proc. Natl. Acad. Sci. USA 2011, 108, 6364–6368. [Google Scholar] [CrossRef] [PubMed]
- Sawa, Y.; Urayama, K.; Takigawa, T.; Gimenez-Pinto, V.; Mbanga, B.L.; Ye, F.; Selinger, J.V.; Selinger, R.L. Shape and chirality transitions in off-axis twist nematic elastomer ribbons. Biophys. Rev. E 2013, 88, 022502. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.M.; Bunning, T.J.; White, T.J. Autonomous, Hands-Free Shape Memory in Glassy, Liquid Crystalline Polymer Networks. Adv. Mater. 2012, 24, 2839–2843. [Google Scholar] [CrossRef] [PubMed]
- Wie, J.J.; Lee, K.M.; Ware, T.H.; White, T.J. Twists and Turns in Glassy, Liquid Crystalline Polymer Networks. Macromolecules 2015, 48, 1087–1092. [Google Scholar] [CrossRef]
- Agrawal, A.; Yun, T.; Pesek, S.L.; Chapman, W.G.; Verduzco, R. Shape-responsive liquid crystal elastomer bilayers. Soft Matter 2014, 10, 1411–1415. [Google Scholar] [CrossRef] [PubMed]
- Boothby, J.M.; Ware, T.H. Dual-responsive, shape-switching bilayers enabled by liquid crystal elastomers. Soft Matter 2017, 13, 4349–4356. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Geng, B.; Sayed, S.M.; Lin, B.P.; Keller, P.; Zhang, X.Q.; Sun, Y.; Yang, H. Single-layer dual-phase nematic elastomer films with bending, accordion-folding, curling and buckling motions. Chem. Commun. 2017, 53, 1844–1847. [Google Scholar] [CrossRef] [PubMed]
- Iamsaard, S.; Aßhoff, S.J.; Matt, B.; Kudernac, T.; Cornelissen, J.J.L.M.; Fletcher, S.P.; Katsonis, N. Conversion of light into macroscopic helical motion. Nat. Chem. 2014, 6, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Lin, B.P.; Yang, H. A plant tendril mimic soft actuator with phototunable bending and chiral twisting motion modes. Nat. Commun. 2016, 7, 13981. [Google Scholar] [CrossRef] [PubMed]
- Boothby, J.M.; Kim, H.; Ware, T.H. Shape changes in chemoresponsive liquid crystal elastomers. Sens. Actuators B Chem. 2017, 240, 511–518. [Google Scholar] [CrossRef]
- De Haan, L.T.; Verjans, J.M.N.; Broer, D.J.; Bastiaansen, C.W.M.; Schenning, A.P.H.J. Humidity-Responsive Liquid Crystalline Polymer Actuators with an Asymmetry in the Molecular Trigger That Bend, Fold, and Curl. J. Am. Chem. Soc. 2014, 136, 10585–10588. [Google Scholar] [CrossRef] [PubMed]
- Kamal, T.; Park, S. Shape-Responsive Actuator from a Single Layer of a Liquid-Crystal Polymer. ACS Appl. Mater. Interfaces 2014, 6, 18048–18054. [Google Scholar] [CrossRef] [PubMed]
- Mendez, J.; Annamalai, P.K.; Eichhorn, S.J.; Rusli, R.; Rowan, S.J.; Foster, E.J.; Weder, C. Bioinspired Mechanically Adaptive Polymer Nanocomposites with Water-Activated Shape-Memory Effect. Macromolecules 2011, 44, 6827–6835. [Google Scholar] [CrossRef]
- Robertson, J.M.; Torbati, A.H.; Rodriguez, E.D.; Mao, Y.; Baker, R.M.; Qi, H.J.; Mather, P.T. Mechanically programmed shape change in laminated elastomeric composites. Soft Matter 2015, 11, 5754–5764. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Guo, Q.; Majidi, C.; Chen, W.; Srolovitz, D.J.; Haataja, M.P. Nonlinear Geometric Effects in Mechanical Bistable Morphing Structures. Phys. Rev. Lett. 2012, 109, 114302. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.; Kasi, R.M.; Kim, S.C.; Sharma, N.; Zhou, Y. Stimuli-responsive polymer gels. Soft Matter 2008, 4, 1151–1157. [Google Scholar] [CrossRef]
- Jeon, S.J.; Hauser, A.W.; Hayward, R.C. Shape-Morphing Materials from Stimuli-Responsive Hydrogel Hybrids. Acc. Chem. Res. 2017, 50, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Ionov, L. Biomimetic Hydrogel-Based Actuating Systems. Adv. Funct. Mater. 2013, 23, 4555–4570. [Google Scholar] [CrossRef]
- Kim, J.; Hanna, J.A.; Hayward, R.C.; Santangelo, C.D. Thermally responsive rolling of thin gel strips with discrete variations in swelling. Soft Matter 2012, 8, 2375–2381. [Google Scholar] [CrossRef]
- Kim, J.; Hanna, J.A.; Byun, M.; Santangelo, C.D.; Hayward, R.C. Designing Responsive Buckled Surfaces by Halftone Gel Lithography. Science 2012, 335, 1201–1205. [Google Scholar] [CrossRef] [PubMed]
- Byun, M.; Santangelo, C.D.; Hayward, R.C. Swelling-driven rolling and anisotropic expansion of striped gel sheets. Soft Matter 2013, 9, 8264–8273. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, X.; Li, Y. Synthesis and Application of Modulated Polymer Gels. Science 1995, 269, 525–527. [Google Scholar] [CrossRef] [PubMed]
- Na, J.H.; Evans, A.A.; Bae, J.; Chiappelli, M.C.; Santangelo, C.D.; Lang, R.J.; Hull, T.C.; Hayward, R.C. Programming Reversibly Self-Folding Origami with Micropatterned Photo-Crosslinkable Polymer Trilayers. Adv. Mater. 2015, 27, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.L.; Moshe, M.; Greener, J.; Therien-Aubin, H.; Nie, Z.; Sharon, E.; Kumacheva, E. Three-dimensional shape transformations of hydrogel sheets induced by small-scale modulation of internal stresses. Nat. Commun. 2013, 4, 1586. [Google Scholar] [CrossRef] [PubMed]
- Thérien-Aubin, H.; Wu, Z.L.; Nie, Z.; Kumacheva, E. Multiple Shape Transformations of Composite Hydrogel Sheets. J. Am. Chem. Soc. 2013, 135, 4834–4839. [Google Scholar] [CrossRef] [PubMed]
- Thérien-Aubin, H.; Moshe, M.; Sharon, E.; Kumacheva, E. Shape transformations of soft matter governed by bi-axial stresses. Soft Matter 2015, 11, 4600–4605. [Google Scholar] [CrossRef] [PubMed]
- Pezzulla, M.; Stoop, N.; Jiang, X.; Holmes, D.P. Curvature-driven morphing of non-Euclidean shells. Proc. R. Soc. A 2017, 473, 20170087. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Zhang, L.; Hu, N.; Grover, H.; Huang, S.; Wang, D.; Chen, Z. Shape formation of helical ribbons induced by material anisotropy. Appl. Phys. Lett. 2017, 110, 091901. [Google Scholar] [CrossRef]
- Studart, A.R.; Erb, R.M. Bioinspired materials that self-shape through programmed microstructures. Soft Matter 2014, 10, 1284–1294. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chizhik, S.; Wen, Y.; Naumov, P. Directed Motility of Hygroresponsive Biomimetic Actuators. Adv. Funct. Mater. 2016, 26, 1040–1053. [Google Scholar] [CrossRef]
- Ge, Q.; Qi, H.J.; Dunn, M.L. Active materials by four-dimension printing. Appl. Phys. Lett. 2013, 103, 131901. [Google Scholar] [CrossRef]
- Erb, R.M.; Libanori, R.; Rothfuchs, N.; Studart, A.R. Composites Reinforced in Three Dimensions by Using Low Magnetic Fields. Science 2012, 335, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Takafuji, M.; Ihara, H.; Zhu, M.; Yang, M.; Gu, K.; Guo, W. Programmable responsive shaping behavior induced by visible multi-dimensional gradients of magnetic nanoparticles. Soft Matter 2012, 8, 3295–3299. [Google Scholar] [CrossRef]
- Morales, D.; Bharti, B.; Dickey, M.D.; Velev, O.D. Bending of Responsive Hydrogel Sheets Guided by Field-Assembled Microparticle Endoskeleton Structures. Small 2016, 12, 2283–2290. [Google Scholar] [CrossRef] [PubMed]
- Bargardi, F.L.; Le Ferrand, H.; Libanori, R.; Studart, A.R. Bio-inspired self-shaping ceramics. Nat. Commun. 2016, 7, 13912. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Duan, Z.; Yuan, P.; Li, Y.; Su, Y.; Zhang, X.; Pan, Y.; Dai, L.L.; Nuzzo, R.G.; Huang, Y.; et al. Electronically Programmable, Reversible Shape Change in Two- and Three-Dimensional Hydrogel Structures. Adv. Mater. 2013, 25, 1541–1546. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Hauser, A.W.; Bende, N.P.; Kuzyk, M.G.; Hayward, R.C. Waveguiding Microactuators Based on a Photothermally Responsive Nanocomposite Hydrogel. Adv. Funct. Mater. 2016, 26, 5447–5452. [Google Scholar] [CrossRef]
- Hauser, A.W.; Evans, A.A.; Na, J.H.; Hayward, R.C. Photothermally Reprogrammable Buckling of Nanocomposite Gel Sheets. Angew. Chem. Int. Ed. 2015, 54, 5434–5437. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Pint, C.L.; Lee, M.H.; Schubert, B.E.; Jamshidi, A.; Takei, K.; Ko, H.; Gillies, A.; Bardhan, R.; Urban, J.J.; et al. Optically- and Thermally-Responsive Programmable Materials Based on Carbon Nanotube-Hydrogel Polymer Composites. Nano Lett. 2011, 11, 3239–3244. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Lee, H.S.; Yoon, J. Highly bendable bilayer-type photo-actuators comprising of reduced graphene oxide dispersed in hydrogels. Sci. Rep. 2016, 6, 20921. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Desai, M.S.; Lee, S.W. Light-Controlled Graphene-Elastin Composite Hydrogel Actuators. Nano Lett. 2013, 13, 2826–2830. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Cho, Y.; Lee, S.Y.; Gong, X.; Kamien, R.D.; Yang, S.; Yodh, A.G. Topography-guided buckling of swollen polymer bilayer films into three-dimensional structures. Soft Matter 2017, 13, 956–962. [Google Scholar] [CrossRef] [PubMed]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef] [PubMed]
- Gu, W.; Wei, J.; Yu, Y. Thermo- and photo-driven soft actuators based on crosslinked liquid crystalline polymers. Chin. Phys. B 2016, 25, 096103. [Google Scholar] [CrossRef]
- Kularatne, R.S.; Kim, H.; Boothby, J.M.; Ware, T.H. Liquid crystal elastomer actuators: Synthesis, alignment, and applications. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 395–411. [Google Scholar] [CrossRef]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid Crystalline Elastomers as Actuators and Sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar] [CrossRef] [PubMed]
- Ionov, L. Polymeric Actuators. Langmuir 2015, 31, 5015–5024. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Huang, G.; Trase, I.; Han, X.; Mei, Y. Mechanical Self-Assembly of a Strain-Engineered Flexible Layer: Wrinkling, Rolling, and Twisting. Phys. Rev. Appl. 2016, 5, 017001. [Google Scholar] [CrossRef]
- De Haan, L.T.; Schenning, A.P.H.J.; Broer, D.J. Programmed morphing of liquid crystal networks. Polymer 2014, 55, 5885–5896. [Google Scholar] [CrossRef]
- Meng, H.; Li, G. Reversible switching transitions of stimuli-responsive shape changing polymers. J. Mater. Chem. A 2013, 1, 7838. [Google Scholar] [CrossRef]
- Meng, H.; Mohamadian, H.; Stubblefield, M.; Jerro, D.; Ibekwe, S.; Pang, S.S.; Li, G. Various shape memory effects of stimuli-responsive shape memory polymers. Smart Mater. Struct. 2013, 22, 093001. [Google Scholar] [CrossRef]
- Oliver, K.; Seddon, A.; Trask, R.S. Morphing in nature and beyond: A review of natural and synthetic shape-changing materials and mechanisms. Asian J. Mater. Sci. 2016, 51, 10663–10689. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Stimuli-Directing Self-Organized 3D Liquid-Crystalline Nanostructures: From Materials Design to Photonic Applications. Adv. Funct. Mater. 2016, 26, 10–28. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Wei, Z. Supramolecular Helices: Chirality Transfer from Conjugated Molecules to Structures. Adv. Mater. 2013, 25, 6039–6049. [Google Scholar] [CrossRef] [PubMed]
- Urayama, K. Switching shapes of nematic elastomers with various director configurations. React. Funct. Polym. 2013, 73, 885–890. [Google Scholar] [CrossRef]
- Mol, G.N.; Harris, K.D.; Bastiaansen, C.W.M.; Broer, D.J. Thermo-Mechanical Responses of Liquid-Crystal Networks with a Splayed Molecular Organization. Adv. Funct. Mater. 2005, 15, 1155–1159. [Google Scholar] [CrossRef]
- Tomassetti, G.; Varano, V. Capturing the helical to spiral transitions in thin ribbons of nematic elastomers. Meccanica 2017, 52, 3431–3441. [Google Scholar] [CrossRef]
- Teresi, L.; Varano, V. Modeling helicoid to spiral-ribbon transitions of twist-nematic elastomers. Soft Matter 2013, 9, 3081–3088. [Google Scholar] [CrossRef]
- Priimagi, A.; Barrett, C.J.; Shishido, A. Recent twists in photoactuation and photoalignment control. J. Mater. Chem. C 2014, 2, 7155–7162. [Google Scholar] [CrossRef]
- Iamsaard, S.; Villemin, E.; Lancia, F.; Aβhoff, S.J.; Fletcher, S.P.; Katsonis, N. Preparation of biomimetic photoresponsive polymer springs. Nat. Protoc. 2016, 11, 1788–1797. [Google Scholar] [CrossRef] [PubMed]
- Harris, K.D.; Cuypers, R.; Scheibe, P.; van Oosten, C.L.; Bastiaansen, C.W.M.; Lub, J.; Broer, D.J. Large amplitude light-induced motion in high elastic modulus polymer actuators. J. Mater. Chem. 2005, 15, 5043–5048. [Google Scholar] [CrossRef]
- Kaiser, A.; Winkler, M.; Krause, S.; Finkelmann, H.; Schmidt, A.M. Magnetoactive liquid crystal elastomer nanocomposites. J. Mater. Chem. 2009, 19, 538–543. [Google Scholar] [CrossRef]
- Winkler, M.; Kaiser, A.; Krause, S.; Finkelmann, H.; Schmidt, A.M. Liquid Crystal Elastomers with Magnetic Actuation. Macromol. Symp. 2010, 291, 186–192. [Google Scholar] [CrossRef]
- Zhou, Y.; Sharma, N.; Deshmukh, P.; Lakhman, R.K.; Jain, M.; Kasi, R.M. Hierarchically Structured Free-Standing Hydrogels with Liquid Crystalline Domains and Magnetic Nanoparticles as Dual Physical Cross-Linkers. J. Am. Chem. Soc. 2012, 134, 1630–1641. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.M.; Ding, Z.; Wang, C.C.; Wei, J.; Zhao, Y.; Purnawali, H. Shape memory materials. Mater. Today 2010, 13, 54–61. [Google Scholar] [CrossRef]
- Montero de Espinosa, L.; Meesorn, W.; Moatsou, D.; Weder, C. Bioinspired Polymer Systems with Stimuli-Responsive Mechanical Properties. Chem. Rev. 2017, 117, 12851–12892. [Google Scholar] [CrossRef] [PubMed]
- Janbaz, S.; Hedayati, R.; Zadpoor, A.A. Programming the shape-shifting of flat soft matter: From self-rolling/self-twisting materials to self-folding origami. Mater. Horiz. 2016, 3, 536–547. [Google Scholar] [CrossRef]
- Lendlein, A.; Kelch, S. Shape-Memory Polymers. Angew. Chem. Int. Ed. 2002, 41, 2034–2057. [Google Scholar] [CrossRef]
- Rong, Q.Q.; Cui, Y.H.; Shimada, T.; Wang, J.S.; Kitamura, T. Self-shaping of bioinspired chiral composites. Acta Mech. Sin. 2014, 30, 533–539. [Google Scholar] [CrossRef]
- Zhu, H.; Shimada, T.; Wang, J.; Kitamura, T.; Feng, X. Mechanics of Fibrous Biological Materials with Hierarchical Chirality. J. Appl. Mech. 2016, 83, 101010. [Google Scholar] [CrossRef]
- Abraham, Y.; Tamburu, C.; Klein, E.; Dunlop, J.W.C.; Fratzl, P.; Raviv, U.; Elbaum, R. Tilted cellulose arrangement as a novel mechanism for hygroscopic coiling in the stork’s bill awn. J. R. Soc. Interface 2012, 9, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Srigiriraju, S.V.; Powers, T.R. Model for polymorphic transitions in bacterial flagella. Phys. Rev. E 2006, 73, 011902. [Google Scholar] [CrossRef] [PubMed]
- Savin, T.; Kurpios, N.A.; Shyer, A.E.; Florescu, P.; Liang, H.; Mahadevan, L.; Tabin, C.J. On the growth and form of the gut. Nature 2011, 476, 57–62. [Google Scholar] [CrossRef] [PubMed]
- Sharon, E.; Roman, B.; Swinney, H.L. Geometrically driven wrinkling observed in free plastic sheets and leaves. Phys. Rev. E 2007, 75, 046211. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z. Geometric nonlinearity and mechanical anisotropy in strained helical nanoribbons. Nanoscale 2014, 6, 9443–9447. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Zhu, K.D.; Shen, W.; Huang, X.; Zhang, L.; Goriely, A. Controllable rotational inversion in nanostructures with dual chirality. Nanoscale 2018, 10, 6343–6348. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Zhang, X.; Li, R.; Zhao, J.; Xuan, X.; Wang, X.; Zou, J.; Li, Q. Electro-Induced Mechanical and Thermal Responses of Carbon Nanotube Fibers. Adv. Mater. 2014, 26, 2480–2485. [Google Scholar] [CrossRef] [PubMed]
- Foroughi, J.; Spinks, G.M.; Wallace, G.G.; Oh, J.; Kozlov, M.E.; Fang, S.; Mirfakhrai, T.; Madden, J.D.W.; Shin, M.K.; Kim, S.J.; et al. Torsional Carbon Nanotube Artificial Muscles. Science 2011, 334, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Ko, S.; Kwon, C.H.; Lima, M.D.; Baughman, R.H.; Kim, S.J. Carbon Nanotube Yarn-Based Glucose Sensing Artificial Muscle. Small 2016, 12, 2085–2091. [Google Scholar] [CrossRef] [PubMed]
- Lima, M.D.; Li, N.; Jung de Andrade, M.; Fang, S.; Oh, J.; Spinks, G.M.; Kozlov, M.E.; Haines, C.S.; Suh, D.; Foroughi, J.; et al. Electrically, Chemically, and Photonically Powered Torsional and Tensile Actuation of Hybrid Carbon Nanotube Yarn Muscles. Science 2012, 338, 928–932. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Kwon, C.H.; Park, K.; Mun, T.J.; Lepró, X.; Baughman, R.H.; Spinks, G.M.; Kim, S.J. Bio-inspired, Moisture-Powered Hybrid Carbon Nanotube Yarn Muscles. Sci. Rep. 2016, 6, 23016. [Google Scholar] [CrossRef] [PubMed]
- Haines, C.S.; Li, N.; Spinks, G.M.; Aliev, A.E.; Di, J.; Baughman, R.H. New twist on artificial muscles. Proc. Natl. Acad. Sci. USA 2016, 113, 11709–11716. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Xu, Y.; He, S.; Sun, X.; Pan, S.; Deng, J.; Chen, D.; Peng, H. Hierarchically arranged helical fibre actuators driven by solvents and vapours. Nat. Nanotechnol. 2015, 10, 1077–1083. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; He, S.; Xu, Y.; Sun, X.; Peng, H. Electromechanical Actuator Ribbons Driven by Electrically Conducting Spring-Like Fibers. Adv. Mater. 2015, 27, 4982–4988. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Xu, Y.; He, S.; Chen, P.; Bao, L.; Hu, Y.; Wang, B.; Sun, X.; Peng, H. Preparation of biomimetic hierarchically helical fiber actuators from carbon nanotubes. Nat. Protoc. 2017, 12, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Liu, C.; Zhao, F.; Sun, X.; Yang, Z.; Chen, T.; Chen, X.; Qiu, L.; Hu, X.; Peng, H. A Novel Electromechanical Actuation Mechanism of a Carbon Nanotube Fiber. Adv. Mater. 2012, 24, 5379–5384. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Xu, Y.; He, S.; Sun, X.; Guo, W.; Zhang, Z.; Qiu, L.; Li, J.; Chen, D.; Peng, H. Biologically Inspired, Sophisticated Motions from Helically Assembled, Conducting Fibers. Adv. Mater. 2015, 27, 1042–1047. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Huang, J.; Su, T.; Bertoldi, K.; Clarke, D.R. Structural Transition from Helices to Hemihelices. PLoS ONE 2014, 9, e93183. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Liu, J.; Kroll, B.; Bertoldi, K.; Clarke, D.R. Spontaneous and deterministic three-dimensional curling of pre-strained elastomeric bi-strips. Soft Matter 2012, 8, 6291–6300. [Google Scholar] [CrossRef]
- Liu, S.; Yao, Z.; Chiou, K.; Stupp, S.I.; Olvera de la Cruz, M. Emergent perversions in the buckling of heterogeneous elastic strips. Proc. Natl. Acad. Sci. USA 2016, 113, 7100–7105. [Google Scholar] [CrossRef] [PubMed]
- Silva, P.E.S.; Vistulo de Abreu, F.; Godinho, M.H. Shaping helical electrospun filaments: A review. Soft Matter 2017, 13, 6678–6688. [Google Scholar] [CrossRef] [PubMed]
- Ribe, N.M.; Habibi, M.; Bonn, D. Liquid Rope Coiling. Annu. Rev. Fluid Mech. 2012, 44, 249–266. [Google Scholar] [CrossRef]
- Chen, S.; Hou, H.; Hu, P.; Wendorff, J.H.; Greiner, A.; Agarwal, S. Polymeric Nanosprings by Bicomponent Electrospinning. Macromol. Mater. Eng. 2009, 294, 265–271. [Google Scholar] [CrossRef]
- Wu, H.; Zheng, Y.; Zeng, Y. Fabrication of Helical Nanofibers via Co-Electrospinning. Ind. Eng. Chem. Res. 2015, 54, 987–993. [Google Scholar] [CrossRef]
- Lin, T.; Wang, H.; Wang, X. Self-Crimping Bicomponent Nanofibers Electrospun from Polyacrylonitrile and Elastomeric Polyurethane. Adv. Mater. 2005, 17, 2699–2703. [Google Scholar] [CrossRef]
- Zhang, B.; Li, C.; Chang, M. Curled Poly (ethylene glycol terephthalate)/Poly (ethylene propanediol terephthalate) Nanofibers Produced by Side-by-side Electrospinning. Polym. J. 2009, 41, 252–253. [Google Scholar] [CrossRef]
- Chen, S.; Hou, H.; Hu, P.; Wendorff, J.H.; Greiner, A.; Agarwal, S. Effect of Different Bicomponent Electrospinning Techniques on the Formation of Polymeric Nanosprings. Macromol. Mater. Eng. 2009, 294, 781–786. [Google Scholar] [CrossRef]
- Godinho, M.H.; Canejo, J.P.; Pinto, L.F.V.; Borges, J.P.; Teixeira, P.I.C. How to mimic the shapes of plant tendrils on the nano and microscale: Spirals and helices of electrospun liquid crystalline cellulose derivatives. Soft Matter 2009, 5, 2772–2776. [Google Scholar] [CrossRef]
- Wu, J.; Liu, S.; He, L.; Wang, H.; He, C.; Fan, C.; Mo, X. Electrospun nanoyarn scaffold and its application in tissue engineering. Mater. Lett. 2012, 89, 146–149. [Google Scholar] [CrossRef]
- Canejo, J.P.; Borges, J.P.; Godinho, M.H.; Brogueira, P.; Teixeira, P.I.C.; Terentjev, E.M. Helical Twisting of Electrospun Liquid Crystalline Cellulose Micro- and Nanofibers. Adv. Mater. 2008, 20, 4821–4825. [Google Scholar] [CrossRef]
- Godinho, M.H.; Canejo, J.P.; Feio, G.; Terentjev, E.M. Self-winding of helices in plant tendrils and cellulose liquid crystal fibers. Soft Matter 2010, 6, 5965–5970. [Google Scholar] [CrossRef]
- Trindade, A.C.; Canejo, J.P.; Teixeira, P.I.C.; Patrício, P.; Godinho, M.H. First Curl, Then Wrinkle. Macromol. Rapid Commun. 2013, 34, 1618–1622. [Google Scholar] [CrossRef] [PubMed]
- Silva, P.E.S.; Godinho, M.H. Helical Microfilaments with Alternating Imprinted Intrinsic Curvatures. Macromol. Rapid Commun. 2017, 38, 1600700. [Google Scholar] [CrossRef] [PubMed]
- Silva, P.E.S.; Trigueiros, J.L.; Trindade, A.C.; Simoes, R.; Dias, R.G.; Godinho, M.H.; de Abreu, F.V. Perversions with a twist. Sci. Rep. 2016, 6, 23413. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.W.; Sakar, M.S.; Petruska, A.J.; Pané, S.; Nelson, B.J. Soft micromachines with programmable motility and morphology. Nat. Commun. 2016, 7, 12263. [Google Scholar] [CrossRef] [PubMed]
- Magdanz, V.; Medina-Sánchez, M.; Schwarz, L.; Xu, H.; Elgeti, J.; Schmidt, O.G. Spermatozoa as Functional Components of Robotic Microswimmers. Adv. Mater. 2017, 29, 1606301. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Dai, E.; Han, X.; Xie, S.; Chao, E.; Chen, Z. Fast nastic motion of plants and bioinspired structures. J. R. Soc. Interface 2015, 12, 20150598. [Google Scholar] [CrossRef] [PubMed]
- Gomez, M.; Moulton, D.E.; Vella, D. Critical slowing down in purely elastic ‘snap-through’ instabilities. Nature Physics 2017, 13, 142. [Google Scholar] [CrossRef]
- Pandey, A.; Moulton, D.E.; Vella, D.; Holmes, D.P. Dynamics of snapping beams and jumping poppers. EPL (Europhys. Lett.) 2014, 105, 24001. [Google Scholar] [CrossRef]

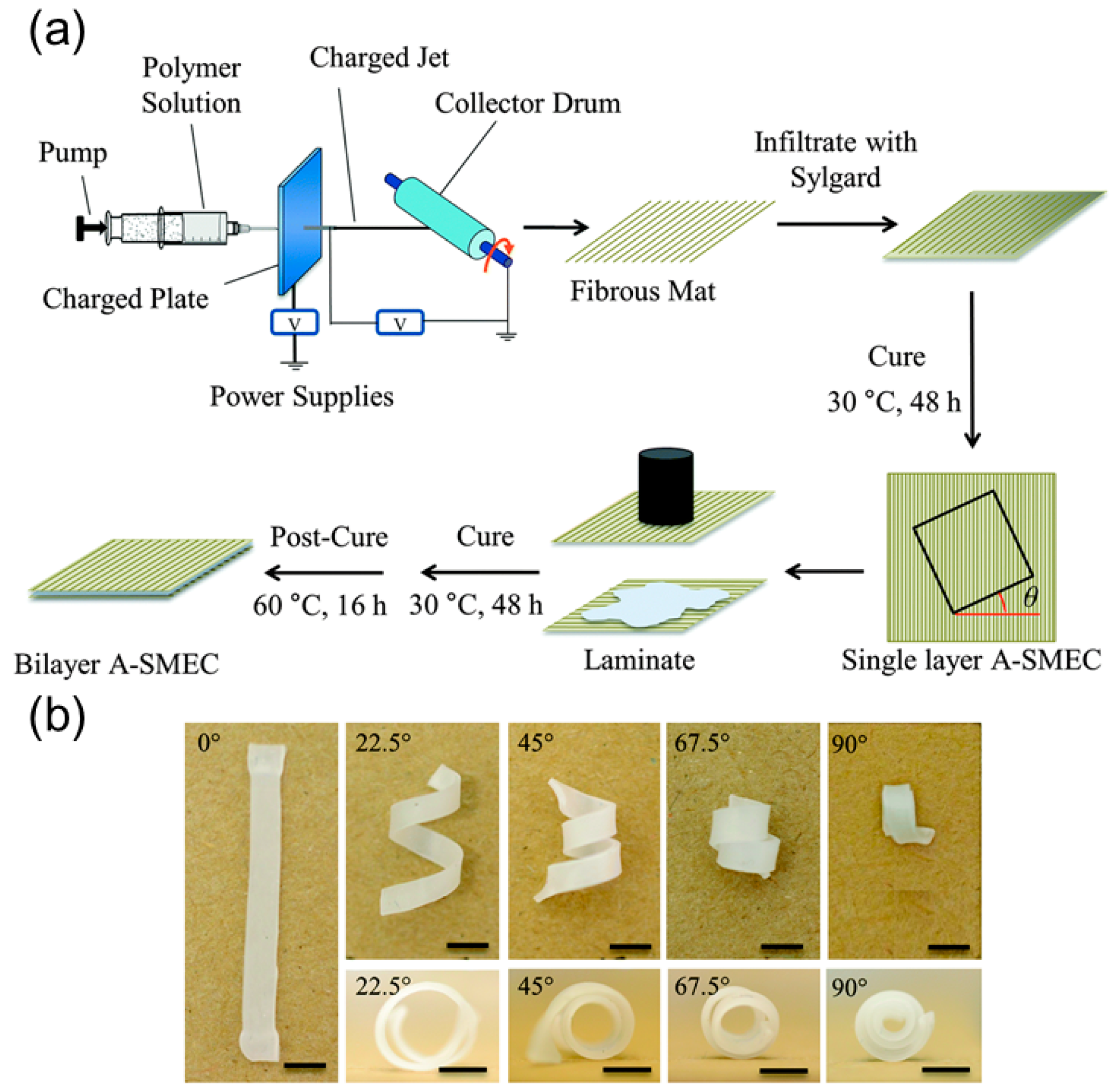
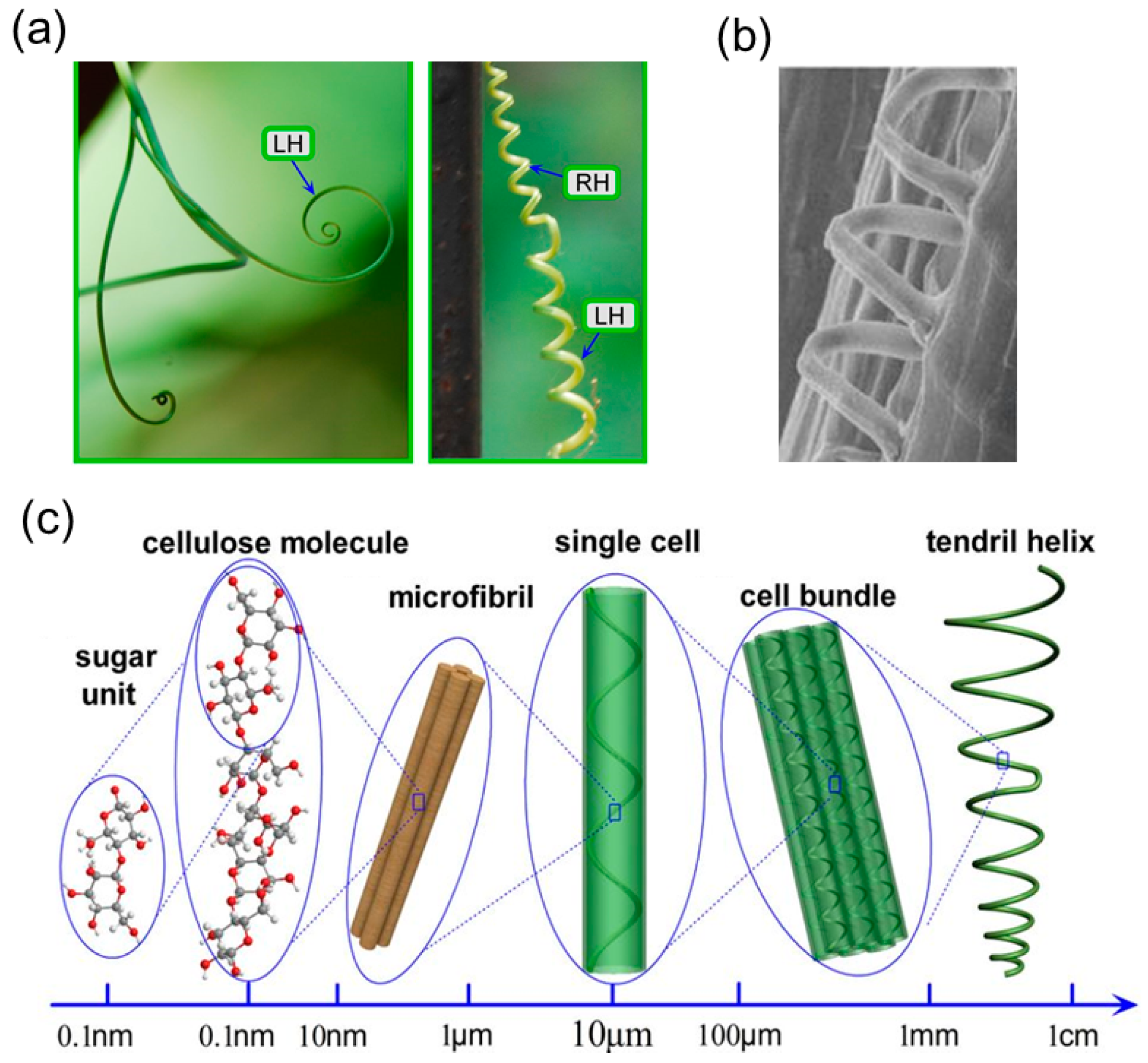

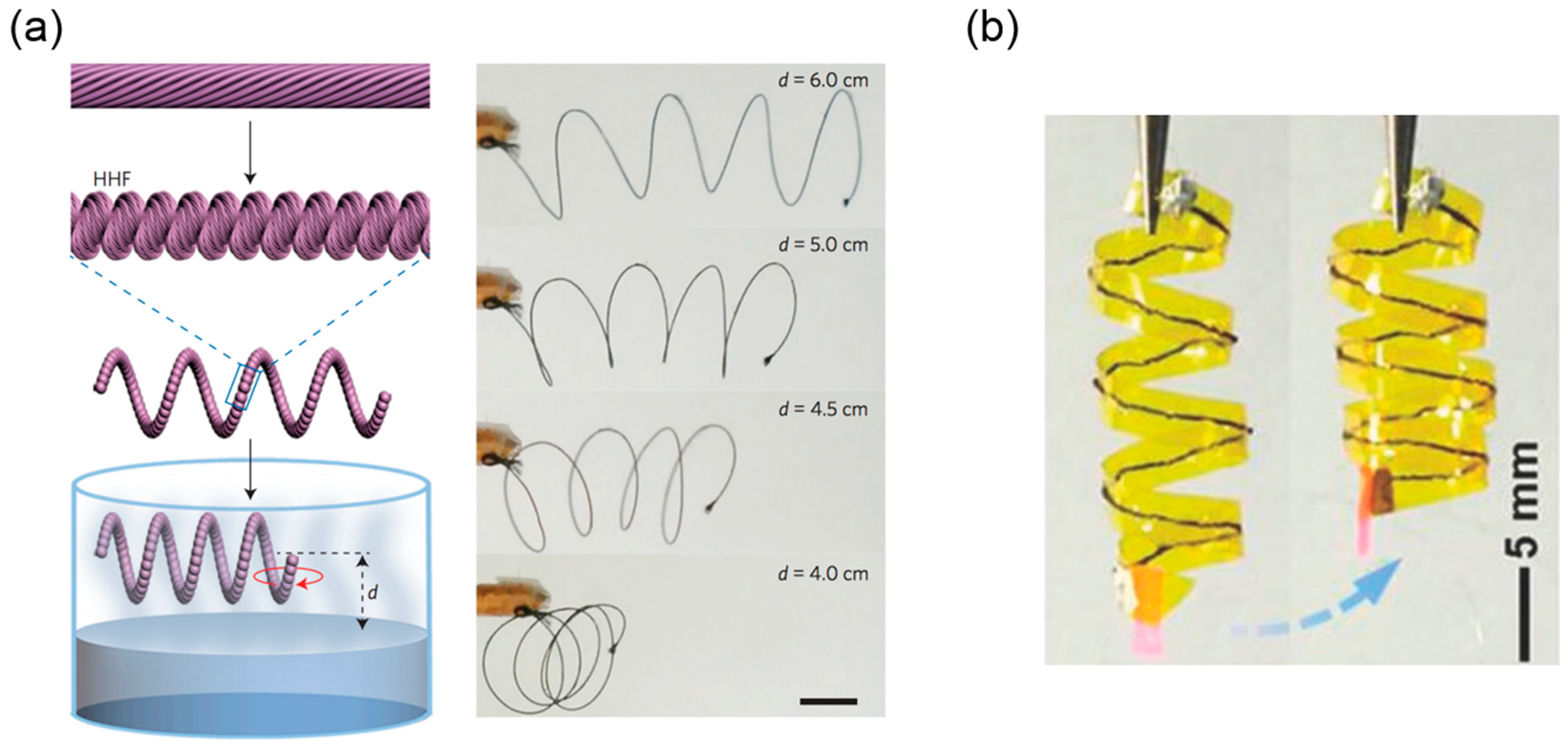
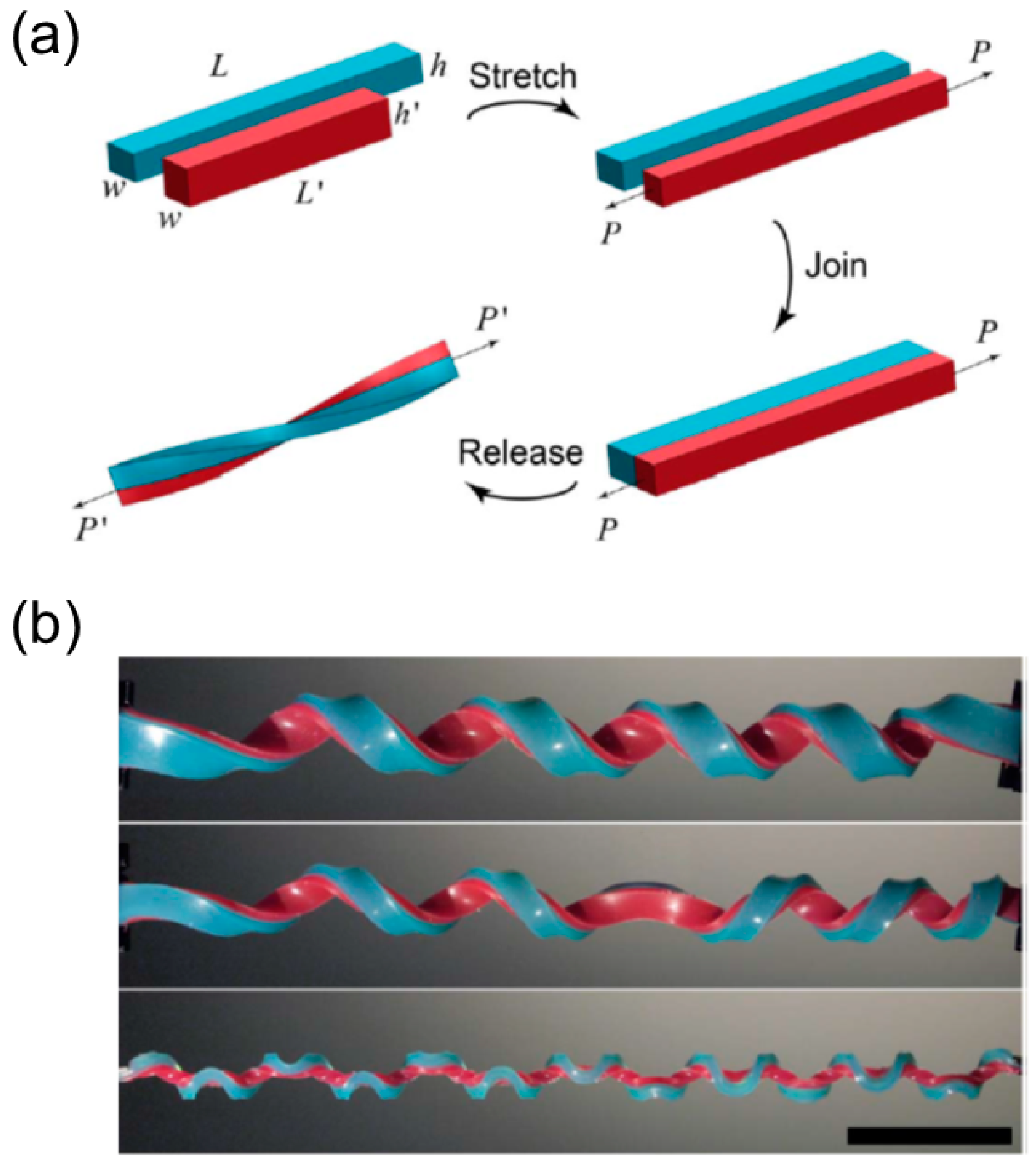

| Stimulus | Isotropic/Anisotropic | Approximate Size | Actuation Time | Reversible | |
|---|---|---|---|---|---|
| Hydrogels | humidity | isotropic: [26,27] | ~45mm [26,27] | >7 min [26] ~47 min [27] | yes |
| thermal | isotropic: [28,29] | several hundred micron (<1 mm) [29] | 2 min [29] | ||
| pH | isotropic [30] | 20–70 mm [30] | 1–30 min [30] | ||
| LCNs/LCEs | thermal | anisotropic: [31,32,33,34,35,36] Mix [37] | 5–25 mm [31,32,33,34,35,36,37] | unknown | yes [31,32,34,35,36] depending on cooling speed [33] |
| UV light | anisotropic [38,39,40,41,42] | 8–40 mm [38,39] | a few mins [38] 12 mins [39] | yes | |
| chemical | 10 mm [40] | 4–10 s [40] | |||
| humidity | 20 mm [41] | unknown | |||
| water/acetone | 20–30 mm [42] | =< 10 s [42] | |||
| SMPs | water | anisotropic [43,44] | 10–20 mm [43] | unknown [43] | no |
| thermal | 5–30 mm [44] | unknown [44] |
| Maximum Contractive Strain | Maximum Contractive Stress | Maximum Contractive Strain Rate | Maximum Contractive Stress Rate | Maximum Rotatory Speed | Reversibility | |
|---|---|---|---|---|---|---|
| Secondary Fiber | 15% | 1.5 Mpa | 330%/s | 8.0 MPa/s | 6361rpm | >30 cycles |
| Primary Fiber | 9% | <1.0 MPa | 30%/s | 2.5 MPa/s | 760 rpm | <15 cycles |
| Tensile Strength (MPa) | Elongation (%) | Toughness (MPa) | Maximum Storage Modulus (GPa) | |
|---|---|---|---|---|
| Helical Fiber | 151 | 97 | 102 | 6.70 |
| Straight Fiber | 202 | 33 | 59.0 | 5.15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, G.; Jin, C.; Trase, I.; Zhao, S.; Chen, Z. Helical Structures Mimicking Chiral Seedpod Opening and Tendril Coiling. Sensors 2018, 18, 2973. https://doi.org/10.3390/s18092973
Wan G, Jin C, Trase I, Zhao S, Chen Z. Helical Structures Mimicking Chiral Seedpod Opening and Tendril Coiling. Sensors. 2018; 18(9):2973. https://doi.org/10.3390/s18092973
Chicago/Turabian StyleWan, Guangchao, Congran Jin, Ian Trase, Shan Zhao, and Zi Chen. 2018. "Helical Structures Mimicking Chiral Seedpod Opening and Tendril Coiling" Sensors 18, no. 9: 2973. https://doi.org/10.3390/s18092973
APA StyleWan, G., Jin, C., Trase, I., Zhao, S., & Chen, Z. (2018). Helical Structures Mimicking Chiral Seedpod Opening and Tendril Coiling. Sensors, 18(9), 2973. https://doi.org/10.3390/s18092973





