Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence
Abstract
:1. Introduction
- We establish a novel matrix completion model employing the regularization technique for EDM recovery in WSNs. The model achieves a superior performance under pulse noise, as well as Gaussian noise and outlier noise.
- In order to maintain the low-rank character and sparsity of the matrix variables while improving the stability of the model, we propose a robust and efficient algorithm named LBDMC by introducing the linear Bregman iterative method. The experimental results show that LBDMC has high positioning accuracy and excellent scalability, which are superior to the existing localization algorithms.
- LBDMC can accurately acquire the location information contaminated by outliers and pulse noise in the observation matrix and then can determine the fault nodes, which can provide a basis for the fault diagnosis of the nodes in WSNs to a certain extent.
2. Related Work
2.1. Matrix Completion Technique
2.2. Bregman Divergence
- , in which, the Euclidean model .when , is the square of our most commonly used Euclidean distance.
- .when l = 1, is the Mahalanobis distance.
- .when l = 1, is the KL divergence.
3. Problem Formulation
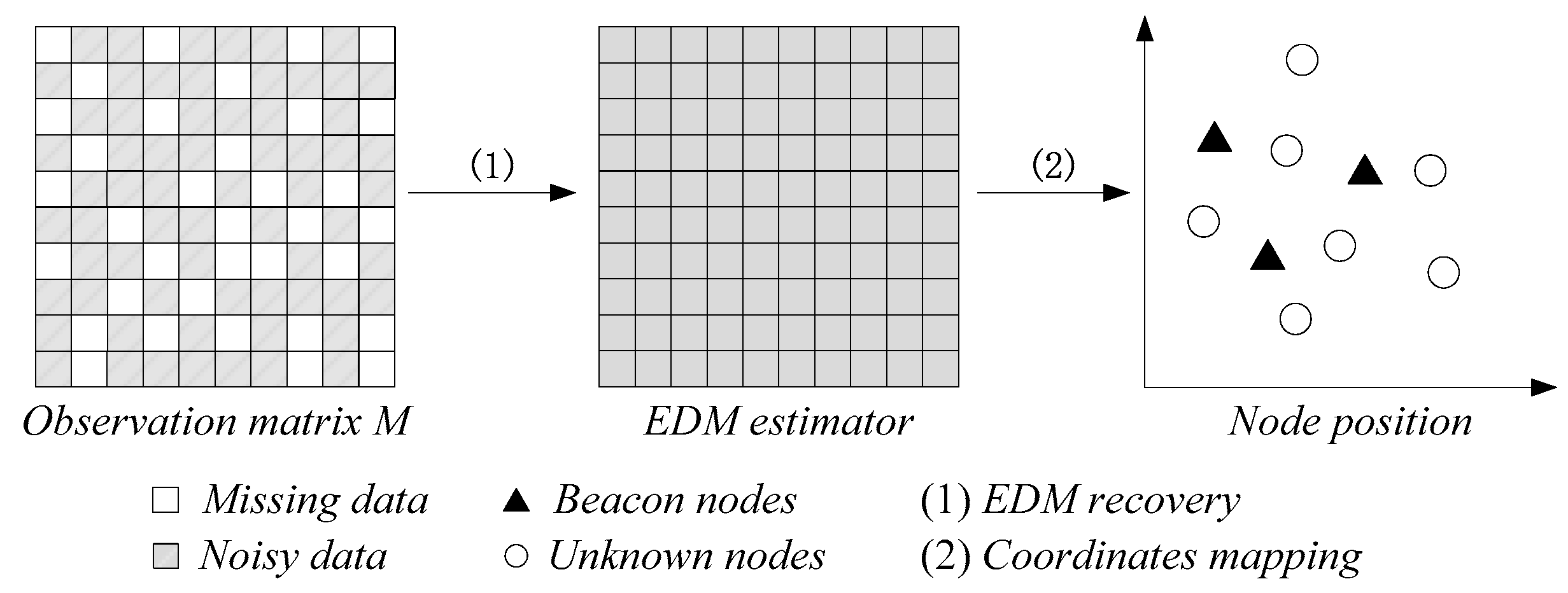
4. Localization Algorithm via Matrix Completion Based on Bregman Divergence
4.1. BDMC Algorithm
| Algorithm 1 Algorithmic description of the SBI-AM |
| Input:, the maximum number of iterations N |
| Output: |
| 1: Initialize , . |
| 2: for k = 0 to N |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: end for |
| 10: return |
- Step 1. Update RAccording to Definition 3 and Theorem 1, can be rewritten as:Let , and Equation (25) is simplified to:Meanwhile, we can deduce the iterative formula of :Furthermore, let:Obviously, the iterative formula of is:Then, Equation (26) can be reformulated as:According to Theorem 2:
- Step 2. Update OSimilar to Step 1, for outlier noise matrix :where .Let , and we can update as:Based on Theorem 3, the analytical solution of (34) is:
- Step 3. Update CSimilarly, for pulse noise matrices :where .Let , and we can update as:According to Theorem 4, Equation (39) can be solved as:
| Algorithm 2 Algorithmic description of BDMC |
| Input: , , the maximum number of iterations N |
| Output: |
| 1: Initialize , , . |
| 2: for k=0 to N |
| 3: . |
| 4: . |
| 5: . |
| 6: . |
| 7: . |
| 8: . |
| 9: end for |
| 10: return |
4.2. LBDMC Algorithm
| Algorithm 3 Algorithmic description of LBDMC |
| Input:, , the maximum number of iterations N, |
| the coordinates of the beacon nodes . |
| Output: the absolute coordinates of nodes in the entire WSN . |
| /* EDM recovery*/ |
| 1: Compute EDM estimator from data missing and noisy matrix based on BDMC. |
| /*Node positioning based on MDS method*/ |
| 2: |
| where , denotes the identity matrix. |
| 3: Generate relative coordinates. |
| where . |
| 4: Calculate the coordinates mapping matrix. |
| 5: Node coordinates mapping. |
| 6: return |
5. Numerical Experiments and Results Analysis
5.1. Evaluation Indicators
- EDM recovery errors :where denotes the EDM estimator obtained by the BDMC algorithm.
- Mean localization errors :where denotes the estimation of the node coordinate matrix .
- Localization errors variance :where denotes the localization errors of the node, , denote the coordinate of the node and its estimator, respectively.
- Localization errors cumulative distribution :where is a constant.
5.2. Comparison of Experiments
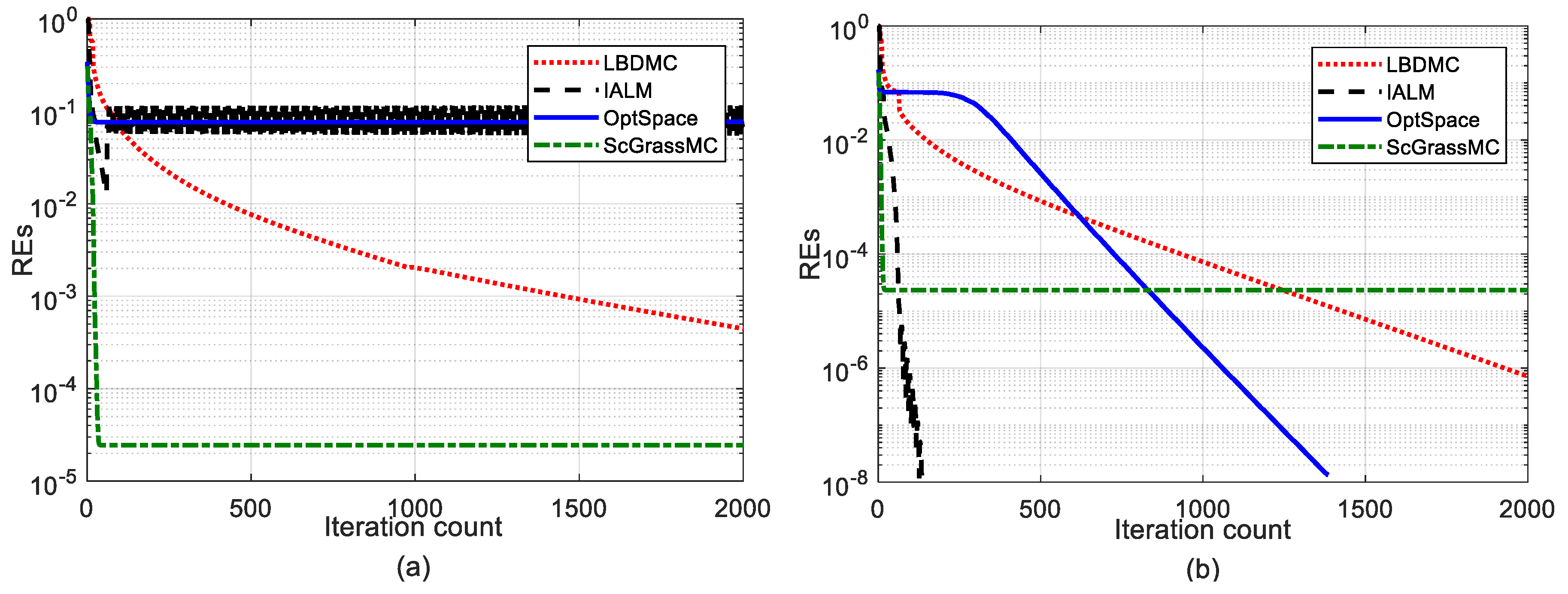
5.2.1. Comparison of Convergence
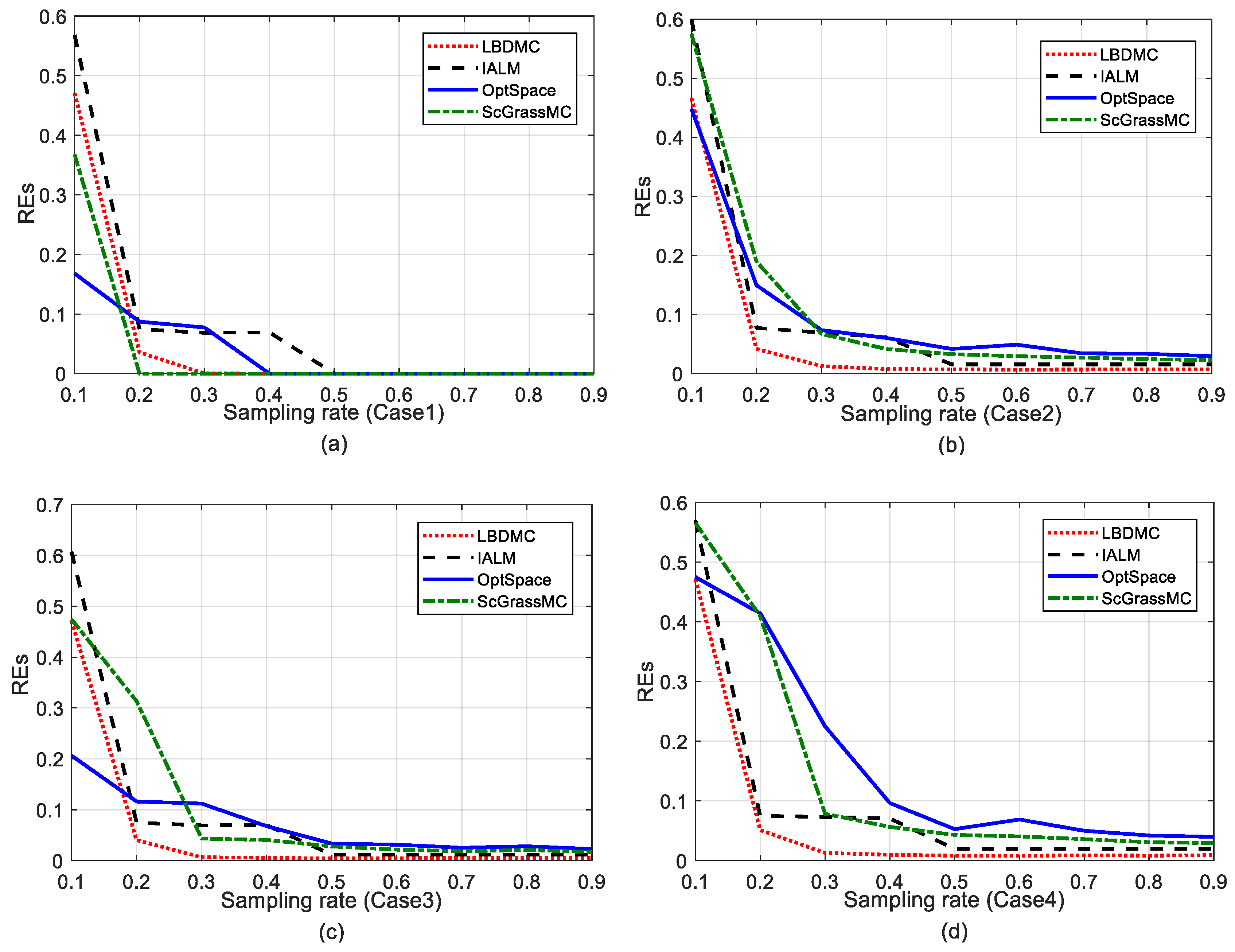
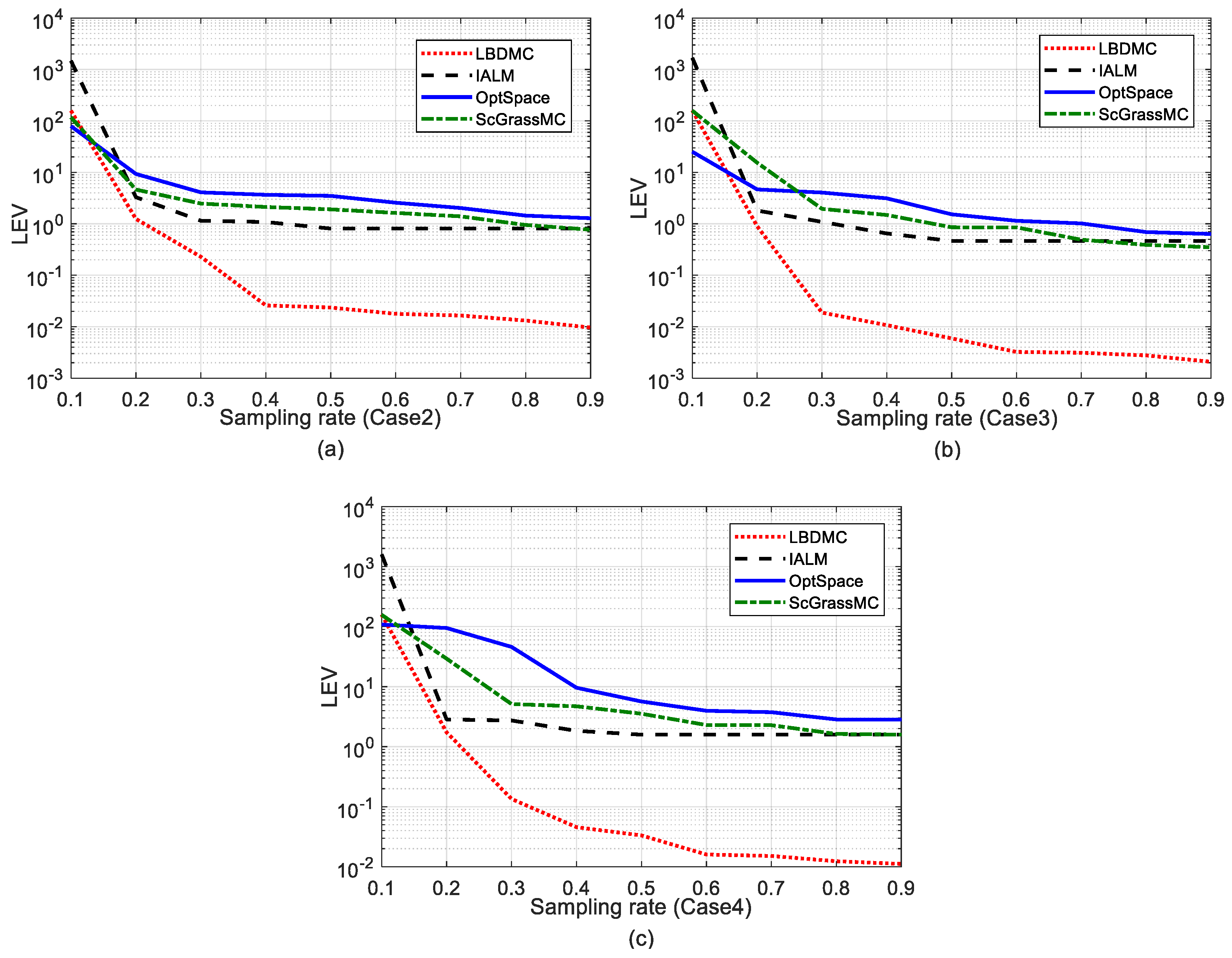
5.2.2. Comparison of the EDM Recovery Errors
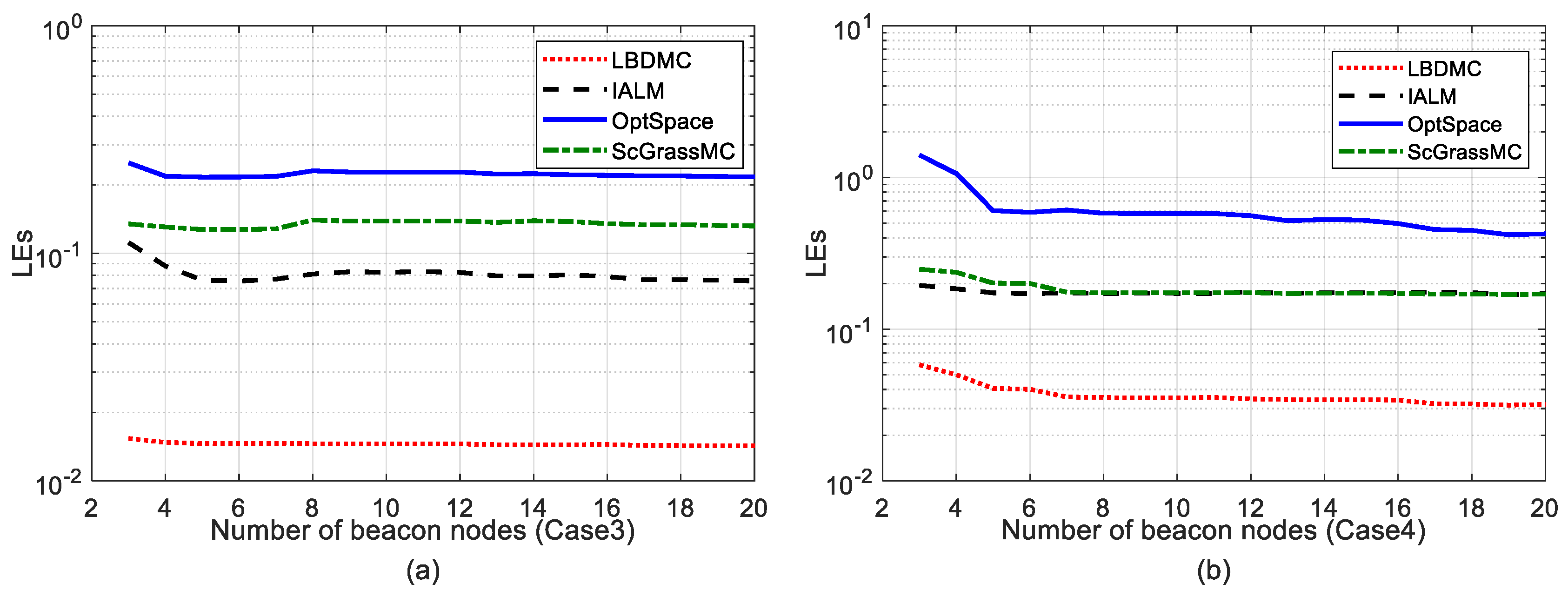
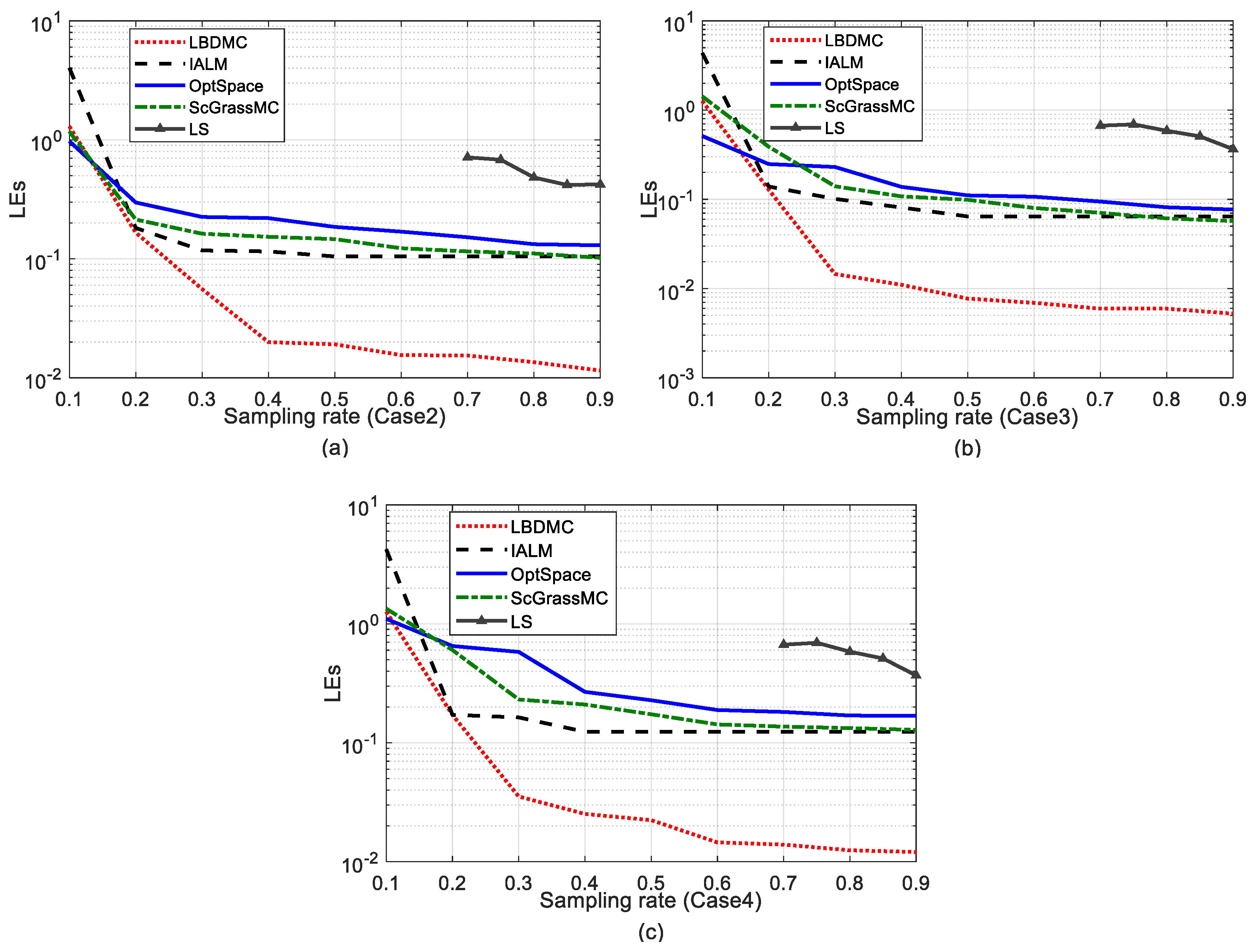
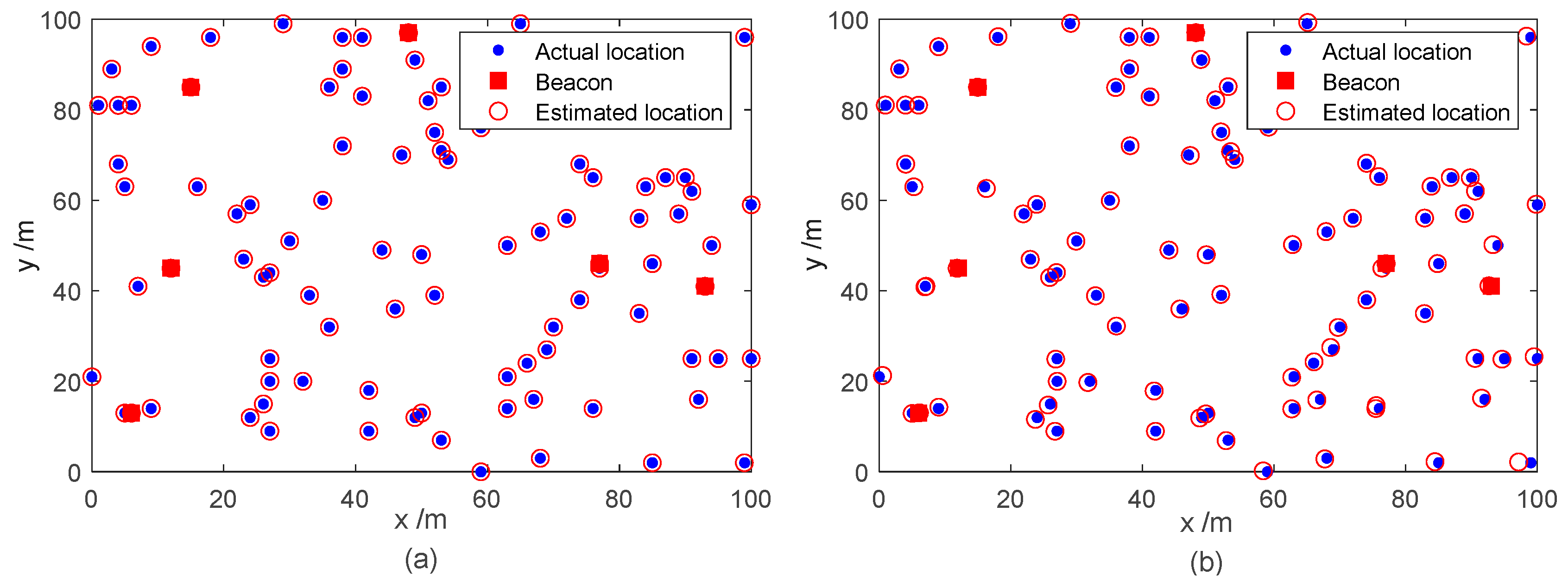
5.2.3. Comparison of Mean Localization Error and Error Variance
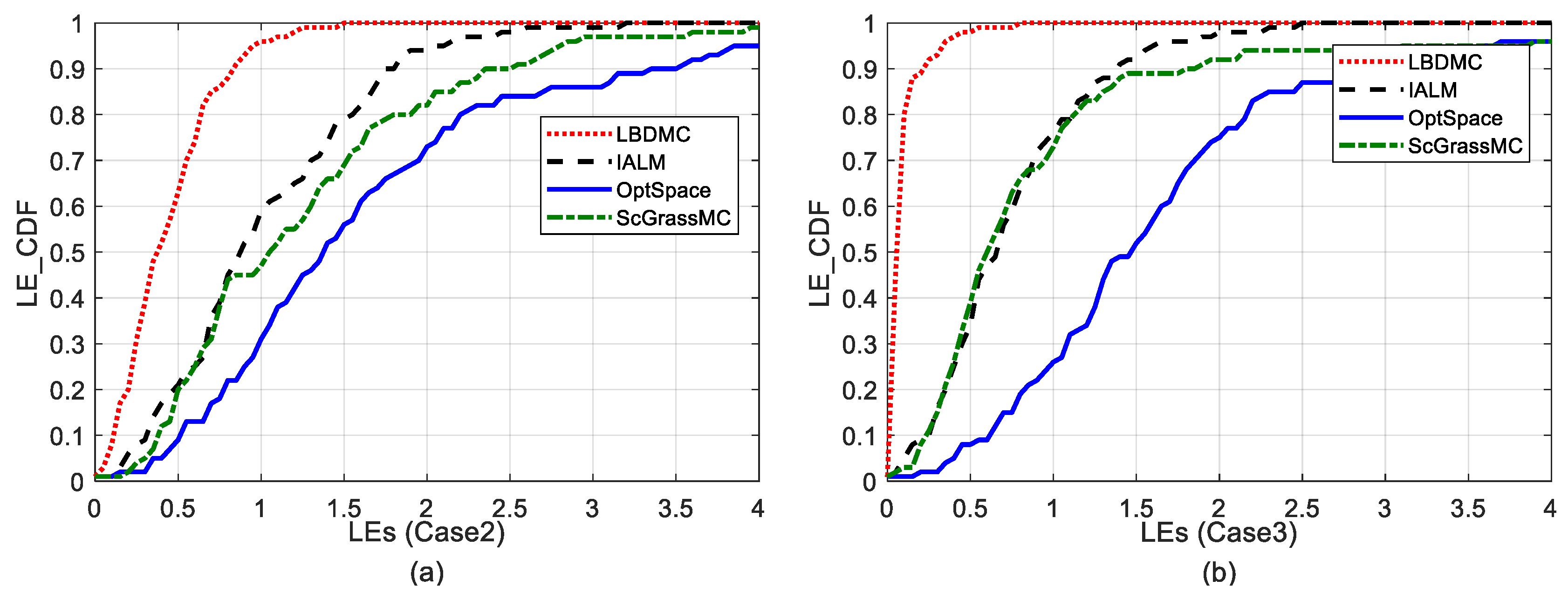
5.2.4. Comparison of the Localization Error Cumulative Distributions
5.2.5. Comparison of Performance with Different Noise Levels
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Assaf, A.E.; Zaidi, S.; Affes, S.; Kandil, N. Low-cost localization for multihop heterogeneous wireless sensor networks. IEEE Trans. Wirel. Commun. 2016, 15, 472–484. [Google Scholar] [CrossRef]
- Qian, H.; Fu, P.; Li, B.; Liu, J.; Yuan, X. A novel loss recovery and tracking scheme for maneuvering target in hybrid WSNs. Sensors 2018, 18, 341. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Liu, W.; Li, Z.; Chen, L.; Wang, R. Noise-tolerant wireless sensor networks localization via multinorms regularized matrix completion. IEEE Trans. Veh. Technol. 2018, 67, 2409–2419. [Google Scholar] [CrossRef]
- Wu, F.-J.; Hsu, H.-C.; Shen, C.-C.; Tseng, Y.-C. Range-free mobile actor relocation in a two-tiered wireless sensor and actor network. ACM Trans. Sens. Netw. 2016, 12, 1–40. [Google Scholar] [CrossRef]
- Nguyen, T.; Shin, Y. Matrix Completion optimization for localization in wireless sensor networks for intelligent IoT. Sensors 2016, 16, 722. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Ruml, W.; Zhang, Y.; Fromherz, M.P.J. Localization from mere connectivity. In Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking & Computing Pages, Annapolis, MD, USA, 1–3 June 2003; pp. 201–212. [Google Scholar]
- Fang, X.; Jiang, Z.; Nan, L.; Chen, L. Noise-aware localization algorithms for wireless sensor networks based on multidimensional scaling and adaptive Kalman filtering. Comput. Commun. 2017, 101, 57–68. [Google Scholar] [CrossRef]
- Bhaskar, S.A.; Bhaskar, S.A. Localization from connectivity: A 1-bit maximum likelihood approach. IEEEACM Trans. Netw. 2016, 24, 2939–2953. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Tian, X.; Wang, X. Temporal correlation of the RSS improves accuracy of fingerprinting localization. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Fang, X.; Jiang, Z.; Nan, L.; Chen, L. Optimal weighted K-nearest neighbour algorithm for wireless sensor network fingerprint localisation in noisy environment. IET Commun. 2018, 12, 1171–1177. [Google Scholar] [CrossRef]
- Guo, X.; Chu, L.; Ansari, N. Joint localization of multiple sources from incomplete noisy Euclidean distance matrix in wireless networks. Comput. Commun. 2018, 122, 20–29. [Google Scholar] [CrossRef]
- Singh, P.; Khosla, A.; Kumar, A.; Khosla, M. Computational intelligence based localization of moving target nodes using single anchor node in wireless sensor networks. Telecommun. Syst. 2018. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Node localization in wireless sensor networks using butterfly optimization algorithm. Arab. J. Sci. Eng. 2017, 42, 3325–3335. [Google Scholar] [CrossRef]
- Sahota, H.; Kumar, R. Maximum-likelihood sensor node localization using received signal strength in multimedia with multipath characteristics. IEEE Syst. J. 2018, 12, 506–515. [Google Scholar] [CrossRef]
- Feng, C.; Valaee, S.; Au, W.S.A.; Tan, Z. Localization of wireless sensors via nuclear norm for rank minimization. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010; pp. 1–5. [Google Scholar]
- Xiao, F.; Sha, C.; Chen, L.; Sun, L.; Wang, R. Noise-tolerant localization from incomplete range measurements for wireless sensor networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 2794–2802. [Google Scholar]
- Chan, F.; So, H.C. Efficient weighted multidimensional scaling for wireless sensor network localization. IEEE Trans. Signal Process. 2009, 57, 4548–4553. [Google Scholar] [CrossRef]
- Candes, E.J.; Recht, B. Exact low-rank matrix completion via convex optimization. In Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 23–26 September 2008; pp. 806–812. [Google Scholar]
- Cai, J.-F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv. 2009. Available online: https://arxiv.org/abs/1009.5055 (accessed on 26 September 2010).
- Ma, S.; Goldfarb, D.; Chen, L. Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 2011, 128, 321–353. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix completion from a few entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
- Ngo, T.; Saad, Y. Scaled gradients on Grassmann manifolds for matrix completion. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Carson City, NV, USA, 3–8 December 2012; pp. 1412–1420. [Google Scholar]
- Bi, D.; Xie, Y.; Ma, L.; Li, X.; Yang, X.; Zheng, Y.R. Multifrequency compressed sensing for 2-D near-field synthetic aperture radar image reconstruction. IEEE Trans. Instrum. Meas. 2017, 66, 777–791. [Google Scholar] [CrossRef]
- Cai, J.-F.; Osher, S.; Shen, Z. Linearized bregman iterations for frame-based image deblurring. SIAM J. Imaging Sci. 2009, 2, 226–252. [Google Scholar] [CrossRef]
- Hua, X.; Cheng, Y.; Wang, H. Geometric target detection based on total Bregman divergence. Digit. Signal Process. 2018, 3, 232–241. [Google Scholar] [CrossRef]
- Fischer, A. Quantization and clustering with Bregman divergences. J. Multivar. Anal. 2010, 101, 2207–2221. [Google Scholar] [CrossRef]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Fu, X.; Sha, C.; Lei, C.; Sun, L.J.; Wang, N.C. Localization algorithm for wireless sensor networks via norm regularized matrix completion. J. Res. Dev. 2016, 53, 216–227. [Google Scholar]
- Goldstein, T.; Osher, S. The split bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Parikh, N. Proximal algorithms. Found. Trends Optim. 2014, 1, 127–239. [Google Scholar] [CrossRef]
- Combettes, P.L.; Wajs, V.R. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- Bruckstein, A.M.; Donoho, D.L.; Elad, M. From sparse solutions of systems of s to sparse modeling of signals and images. SIAM Rev. 2009, 51, 34–81. [Google Scholar] [CrossRef]
- Gong, P.; Ye, J.; Zhang, C. Robust multi-task feature learning. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 895–903. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Shan, H.; Wang, B. Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence. Sensors 2018, 18, 2974. https://doi.org/10.3390/s18092974
Liu C, Shan H, Wang B. Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence. Sensors. 2018; 18(9):2974. https://doi.org/10.3390/s18092974
Chicago/Turabian StyleLiu, Chunsheng, Hong Shan, and Bin Wang. 2018. "Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence" Sensors 18, no. 9: 2974. https://doi.org/10.3390/s18092974
APA StyleLiu, C., Shan, H., & Wang, B. (2018). Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence. Sensors, 18(9), 2974. https://doi.org/10.3390/s18092974




