An Efficient ISAR Imaging of Targets with Complex Motions Based on a Quasi-Time-Frequency Analysis Bilinear Coherent Algorithm
Abstract
1. Introduction
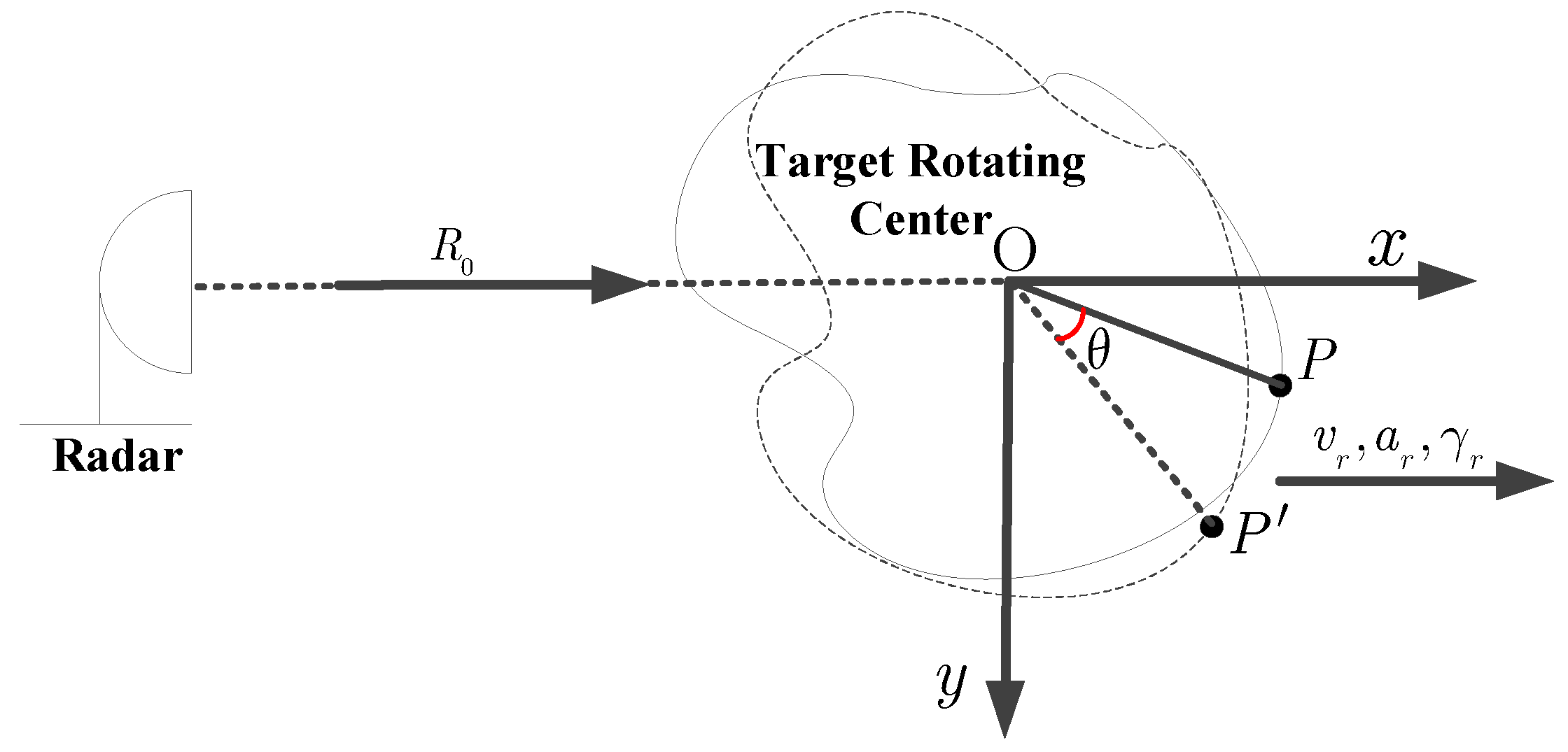
2. ISAR Imaging Model of Maneuvering Target
3. Proposed Algorithm Description
3.1. Description of the Proposed RCFT
- Remark 1:
- The RCFT employs the merits of both RCT and FT, and it not only has the same integration time as RCT but also works well as a useful tool for nonstationary signals.
- Remark 2:
- The bilinear cubic phase function in (5) utilizes only one time correlation, which is viewed as a signal energy preservation because each additional one time correlation loses about 4 –5 dB in the SNR threshold [17]. In addition to that, the 2-D coherent integration realized in the proposed RCFT will further enhance the SNR. Therefore, the proposed RCFT algorithm provides a good performance, especially when the SNR is low, see simulation section.
- Remark 3:
- the NUFFT speeds up the Fourier transform along the non-uniformly spaced lag-time axis, which is helpful for algorithm real-time realization.
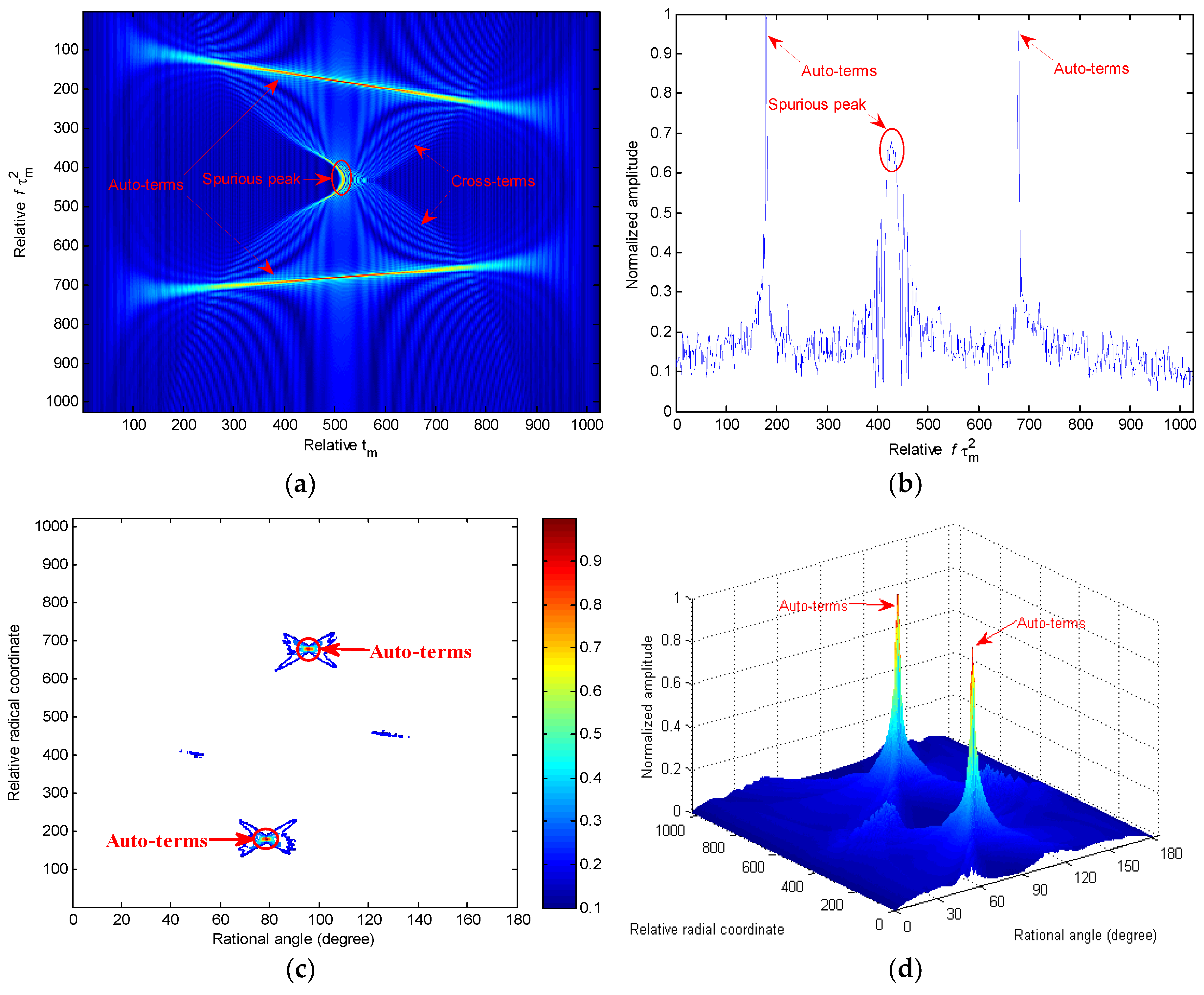
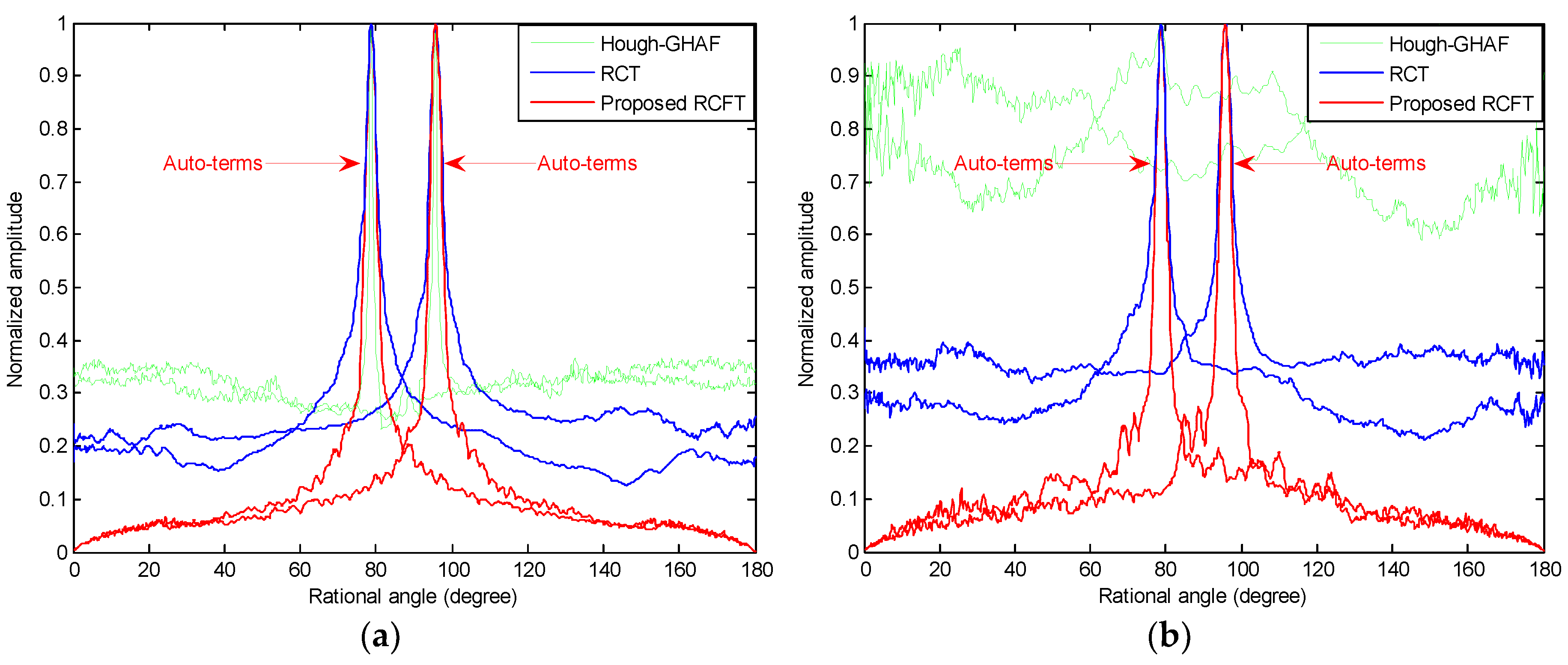
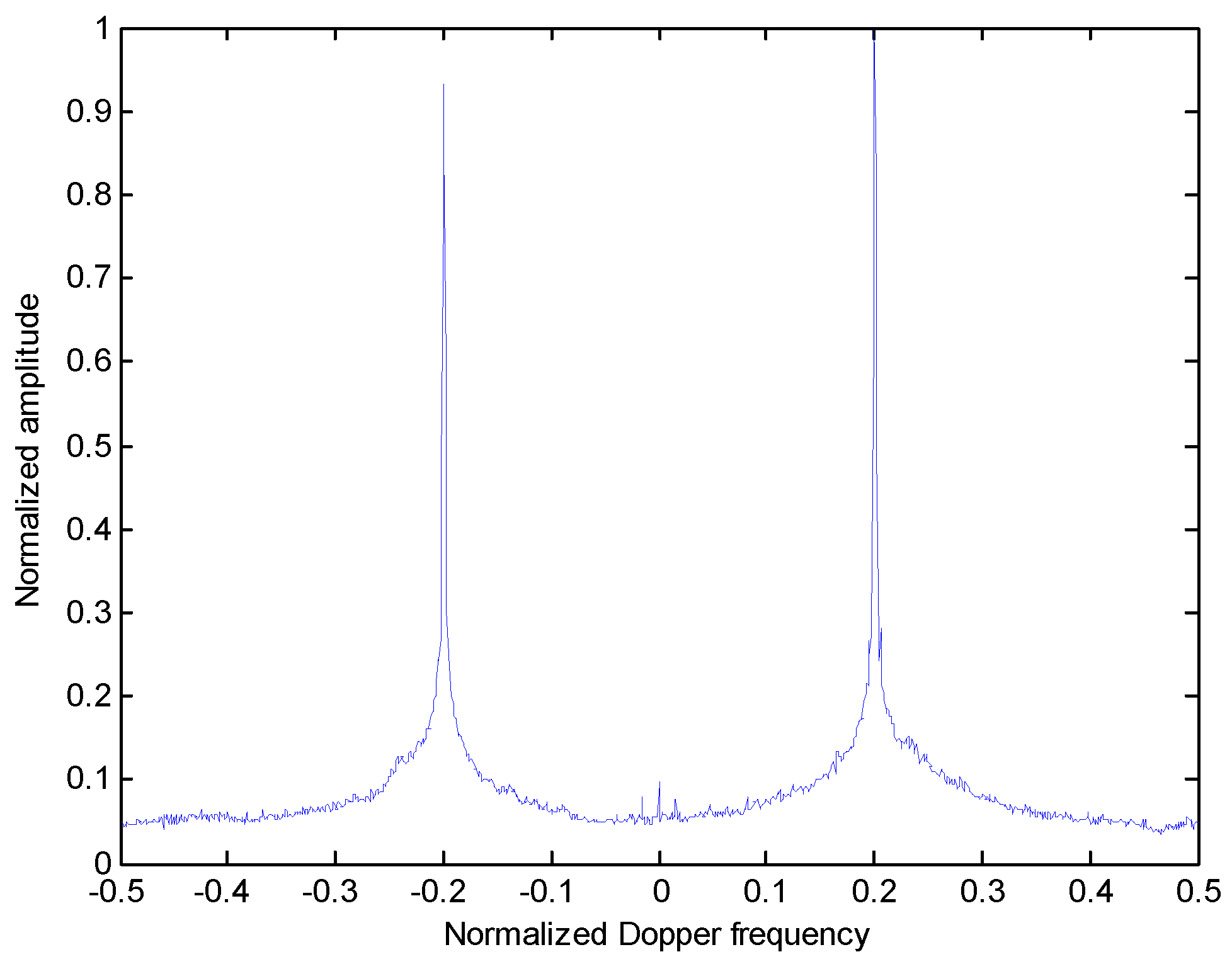
3.2. Numerical Study of RCFT
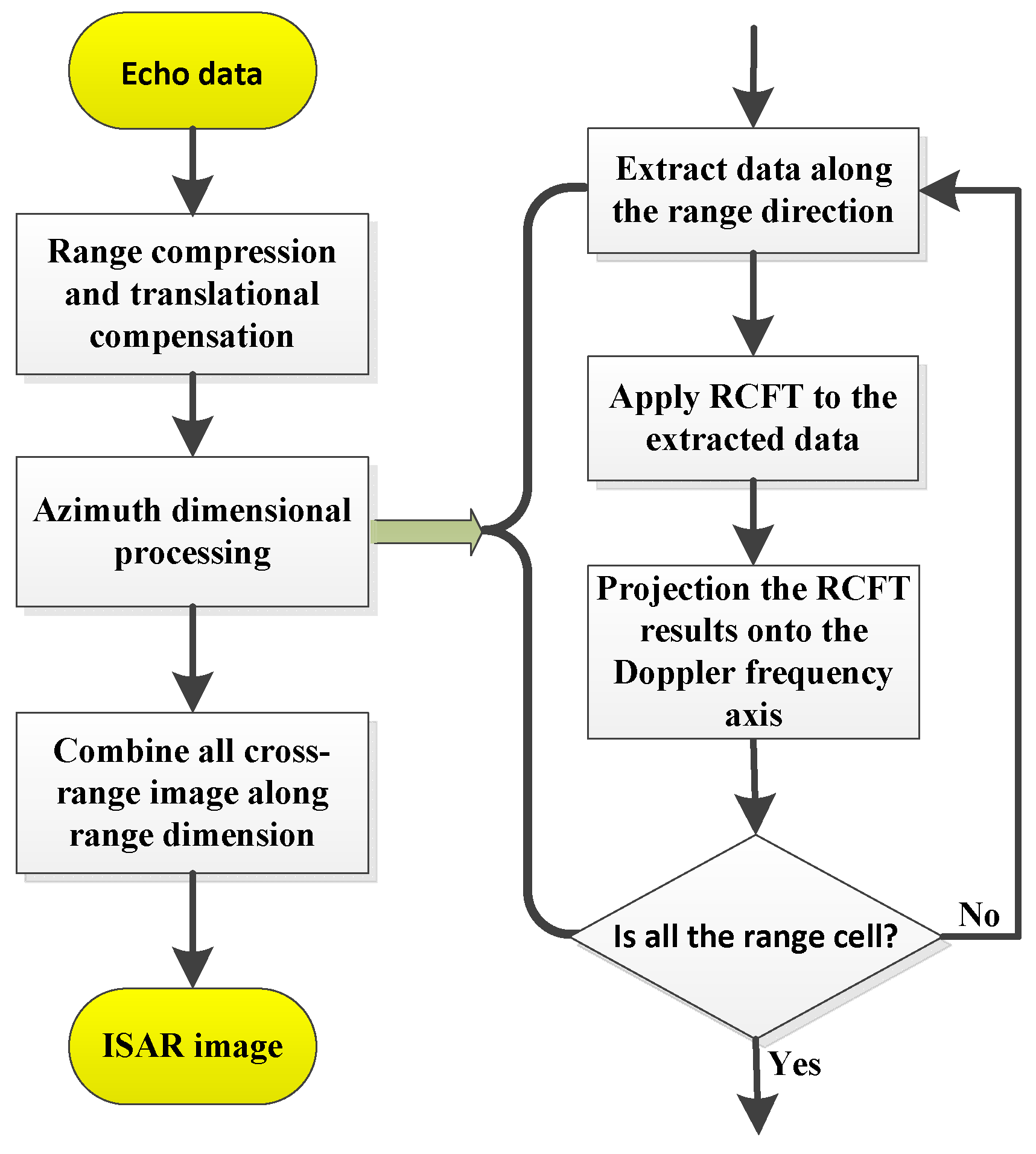
3.3. ISAR Imaging for Maneuvering Target Based on the Proposed RCFT Algorithm
- Step 1:
- Perform the range compression and the translational motion compensation including envelope alignment and phase autofocus.
- Step 2:
- Characterize the azimuth signal of a range cell after translational compensation as multi-component QFM signals , and perform NUFFT along the lag time variable to obtain CPF result .
- Step 3:
- Apply the proposed RCFT to the and obtain a three-dimensional data matrix in the Doppler Centroid -polar radius -polar angle domain.
- Step 4:
- Project the three-dimensional data matrix onto the Doppler frequency axis along the polar radius and polar angle , which is obtained by
- Step 5:
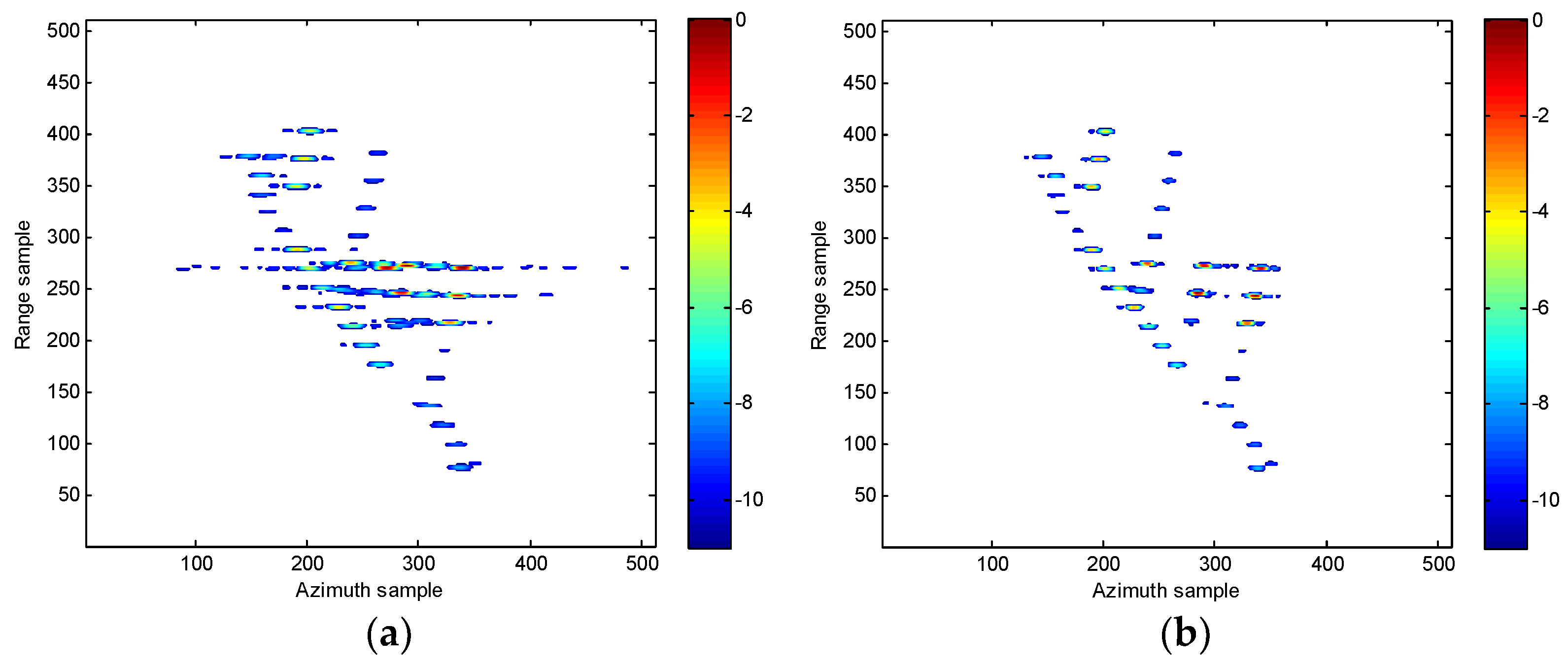
- Set a proper extraction threshold or a filter to suppress the residual cross terms and noise in the Doppler centroid frequency dimension. In practice, the threshold is usually determined by subtracting −3~−4.5 dB from the maximal energy.
- Step 6:
- Repeat the process of step 1–step 5 for all range cells, and the final high-resolution ISAR image is thus produced by regrouping all the range-Doppler frequency centroids. Since the proposed method does not require computations such as parameter estimation for each scatterer, it is computationally more efficient than the similar parameter estimation based algorithms. The flowchart of the proposed ISAR imaging algorithm is shown in Figure 6.
3.4. Components Computational Complexity Analysis
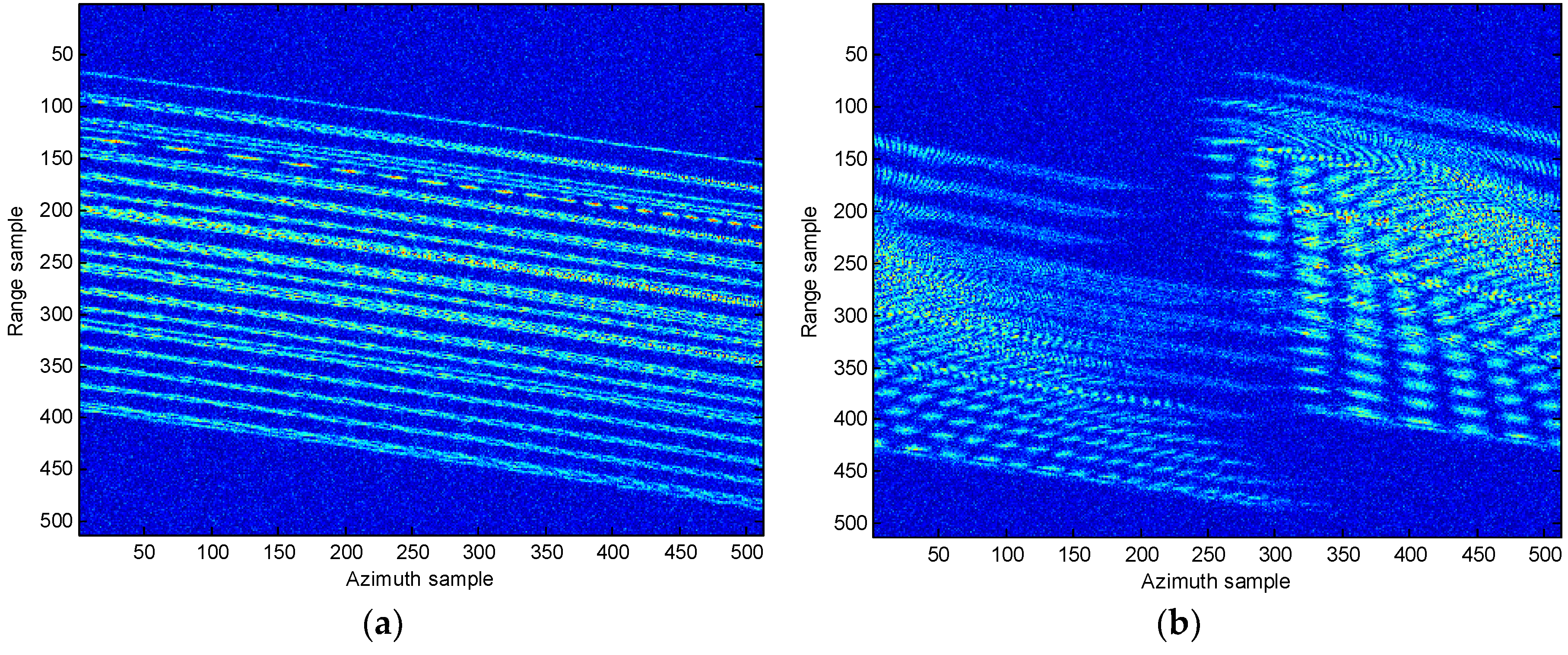
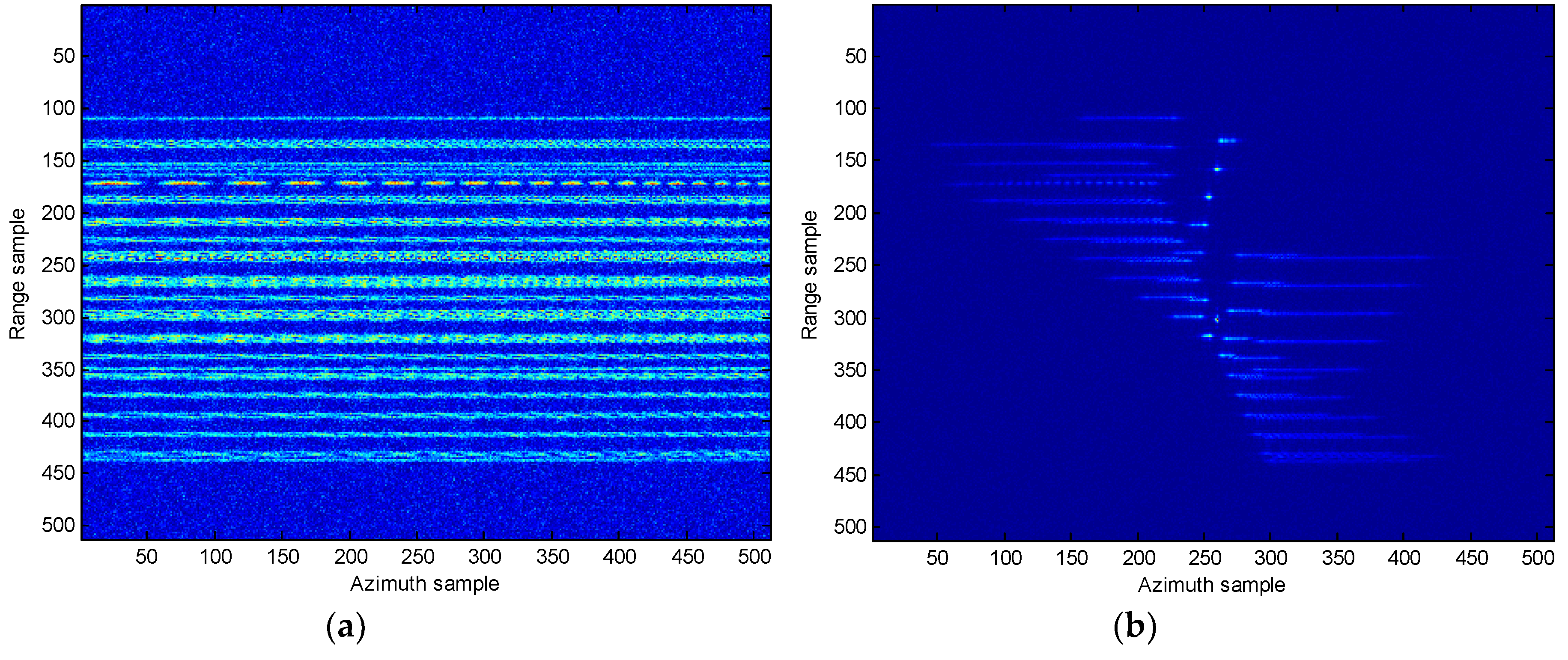
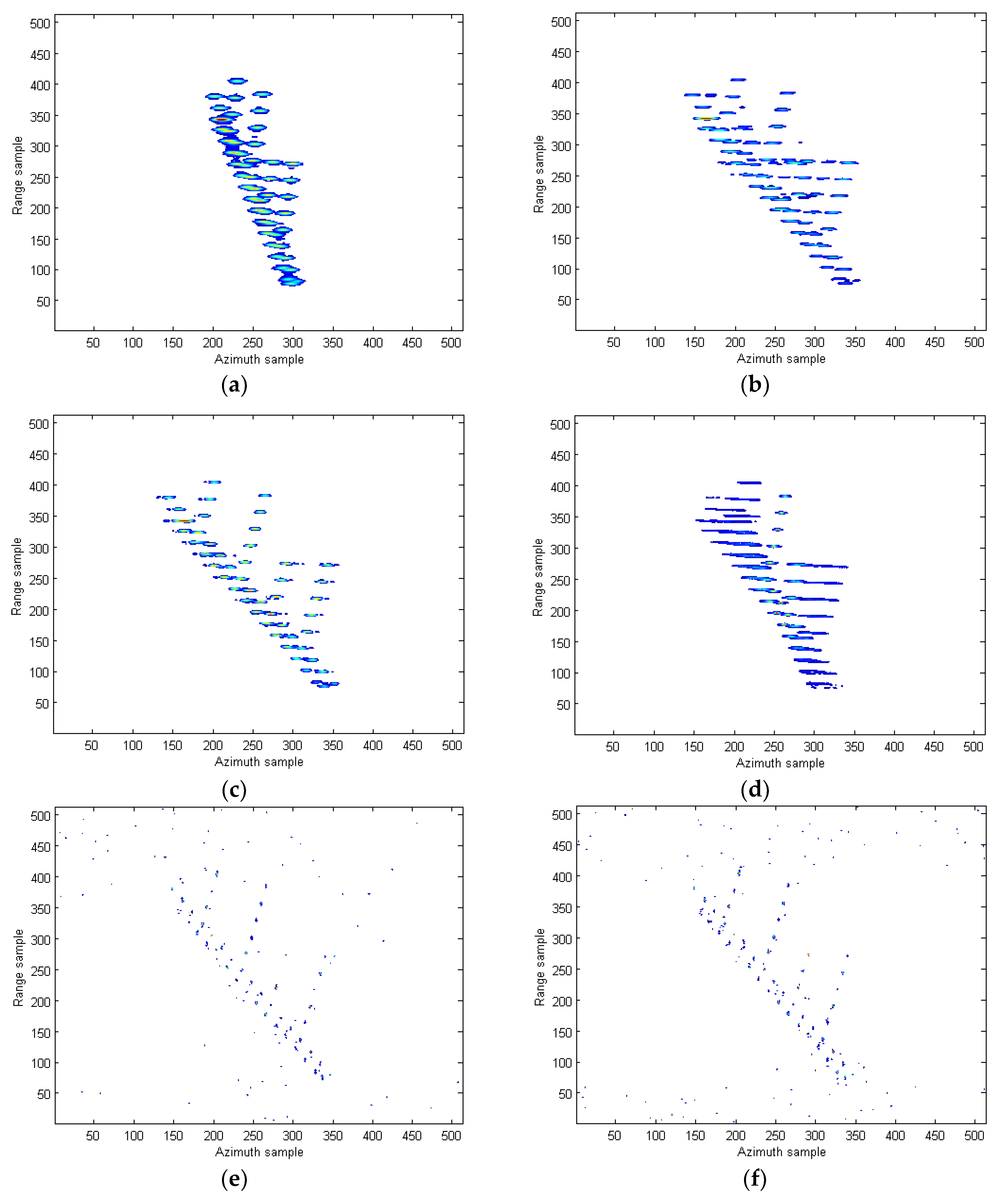
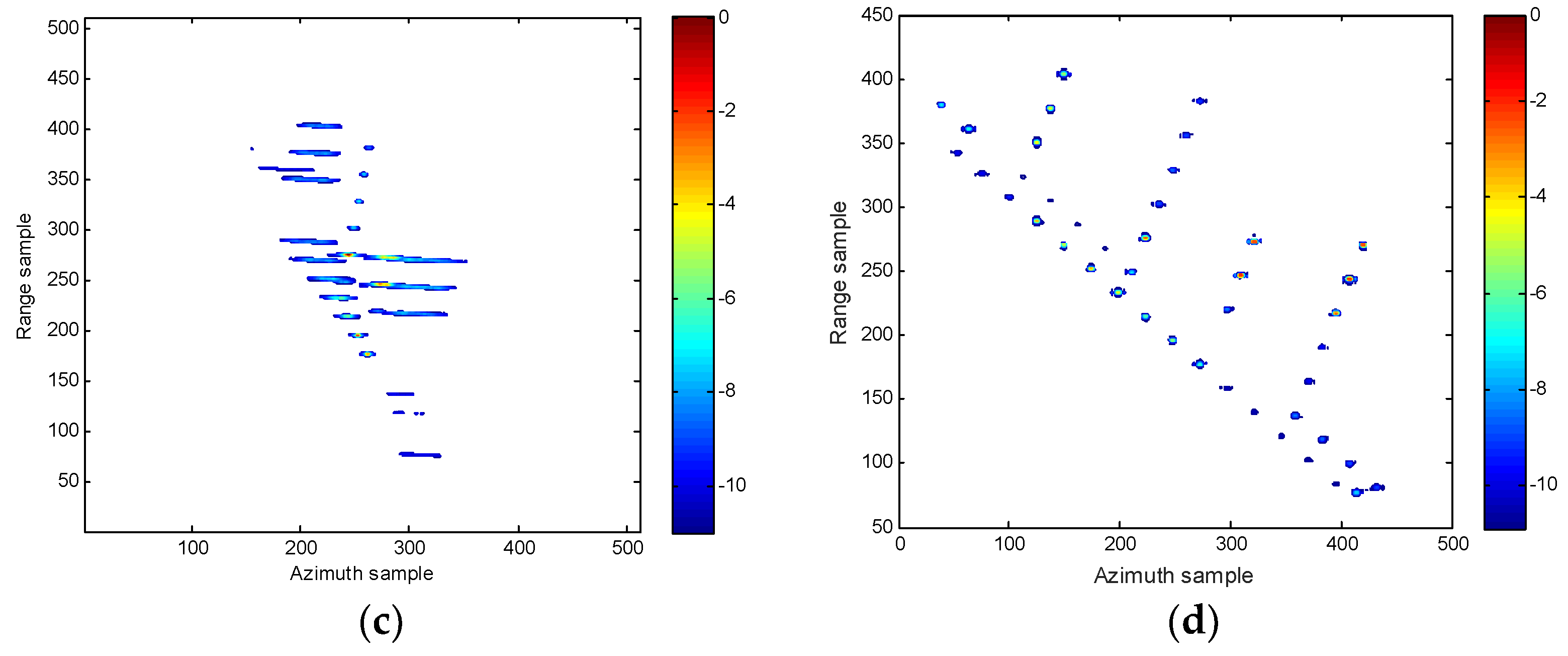
4. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Y.; Zhao, B. Inverse synthetic aperture radar imaging of nonuniformly rotating target based on the parameters estimation of multicomponent quadratic frequency-modulated signals. IEEE Sens. J. 2012, 15, 4053–4061. [Google Scholar] [CrossRef]
- Bai, X.R.; Zhou, F.; Xing, M.D.; Bao, Z. A novel method for imaging of group targets moving in a formation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 221–231. [Google Scholar] [CrossRef]
- Li, Y.Y.; Su, T.; Zheng, J.B.; He, X.H. ISAR imaging of targets with complex motions based on modified Lv’s distribution for cubic phase signal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4775–4784. [Google Scholar] [CrossRef]
- Sadjadi, F. New comparative experiments in range migration mitigation methods using polarimetric inverse synthetic aperture radar signatures of small boats. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0613–0616. [Google Scholar]
- Cohen, L. Time-frequency distributions-a review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef]
- Chen, V.C.; Qian, S. Joint time-frequency transform for radar range Doppler imaging. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 486–499. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, J.; Jiang, Y.C. ISAR imaging of maneuvering target based on the local polynomial Wigner distribution and integrated high-order ambiguity function for cubic phase signal model. IEEE J. Sel.Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2971–2991. [Google Scholar] [CrossRef]
- Zheng, J.B.; Su, T.; Zhu, W.T.; Zhang, L.; Liu, Z.; Liu, Q.H. ISAR imaging of nonuniformly rotating target based on a fast parameter estimation algorithm of cubic phase signal. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4727–4740. [Google Scholar] [CrossRef]
- Li, D.; Gui, X.G.; Liu, H.Q.; Su, J.; Xiong, H. An ISAR imaging algorithm for maneuvering targets with low SNR based on parameter estimation of multicomponent quadratic FM signals and nonuniform FFT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5688–5702. [Google Scholar] [CrossRef]
- Chen, V.C.; Miceli, W.J. Time-varying spectral analysis for radar imaging of maneuvering targets. IEEE Proc. Radar Sonar Navig. 1998, 145, 262–268. [Google Scholar] [CrossRef]
- Kim, K.T.; Choi, I.S.; Kim, H.T. Efficient radar target classification using adaptive joint time-frequency processing. IEEE Trans. Antennas Propag. 2000, 48, 1789–1801. [Google Scholar] [CrossRef]
- Bao, Z.; Sun, C.Y.; Xing, M.D. Time-frequency approaches to ISAR imaging of maneuvering targets and their limitations. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1091–1099. [Google Scholar] [CrossRef]
- Berizzi, F.; Mese, E.D.; Diani, M.; Martorella, M. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous Doppler technique: Modeling and performance analysis. IEEE Trans. Image Process. 2001, 10, 1880–1890. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jiang, Y.C. ISAR imaging of maneuvering targets based on the L-class of fourth-order complex-lag PWVD. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1518–1527. [Google Scholar] [CrossRef]
- Lv, X.L.; Xing, M.D.; Wan, C.R.; Zhang, S.H. ISAR imaging of maneuvering targets based on the range centroid Doppler technique. IEEE Trans. Image Process. 2010, 19, 141–153. [Google Scholar] [CrossRef] [PubMed]
- Xing, M.D.; Wu, R.; Li, Y.; Bao, Z. New ISAR imaging algorithm based on modified Wigner-Ville distribution. IET Radar Sonar Navig. 2009, 3, 70–80. [Google Scholar] [CrossRef]
- O’Shea, P. A fast algorithm for estimating the parameters of a quadratic FM signal. IEEE Trans. Signal Process. 2004, 52, 385–393. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J.Y. Parameter estimation of multicomponent quadratic FM signals using computationally efficient Radon-CPF transform. In Proceedings of the 14th European Signal Processing Conference, Florence, Italy, 4–8 September 2006; pp. 4–8. [Google Scholar]
- Nguyen, N.; Liu, Q.H. The regular Fourier matrices and nonuniform fast Fourier transforms. SIAM J. Sci. Comput. 1999, 21, 283–293. [Google Scholar] [CrossRef]
- Huang, P.H.; Liao, G.S.; Yang, Z.W.; Xia, X.G.; Ma, J.T. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order Keystone and generalized Hough-HAF transform. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1105–1117. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon–Fourier transform for radar target detection, I: Generalized Doppler filter bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; Liu, N.B.; He, Y. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, J.L.; Duan, J.; Xing, M.D.; Qiao, Z.J.; Bao, Z. Translational motion compensation for ISAR imaging under low SNR by minimum entropy. EURASIP J. Adv. Signal Process. 2013, 2013, 1–19. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, F.; Tao, M.L.; Sun, P.; Zhang, Z.J. Adaptive translational motion compensation method for ISAR imaging under low SNR based on particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5146–5157. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.Y.; Liu, H.Q.; Liao, G.S. A robust translational motion compensation method for ISAR imaging based on Keystone transform and fractional Fourier transform under low SNR environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Munoz-Ferreras, J.M.; Perez-Martinez, F.; Datcu, M. Generalization of inverse synthetic aperture radar autofocusing methods based on the minimization of the Renyi entropy. IET Radar Sonar Navig. 2010, 4, 586–594. [Google Scholar] [CrossRef]
- Martorella, M.; Berizzi, F.; Haywood, B. Contrast maximization based technique for 2-D. ISAR autofocusing. IET Proc. Radar Sonar Navig. 2005, 152, 253–262. [Google Scholar] [CrossRef]
- Liu, H.Q.; Li, D.; Zhou, Y.; Truong, T.-K. Simultaneous radio frequency and wideband interference suppression in SAR signals via sparsity exploitation in time-frequency Domain. IEEE Trans. Geosci. Remote Sens. 2018, 1–14. [Google Scholar] [CrossRef]


| Parameters Name | Value |
|---|---|
| Carrier frequency | 10 GHz |
| Transmit bandwidth | 200 MHz |
| Pulse repetition | 300 Hz |
| Wave length | 0.03 m |
| Range sample frequency | 300 MHz |
| Effective echo pluses | 512 |
| Translational coefficients velocity | 20 m/s |
| Translational coefficients acceleration | 2 m/s2 |
| Translational coefficients acceleration rate | 2 m/s3 |
| Effective rotational motion angular velocity | 0.018 rad/s |
| Effective rotational motion acceleration | 0.008 rad/s2 |
| Effective rotational motion acceleration rate | 0.002 rad/s3 |
| Methods | SNR = 5 dB | SNR = −3 dB | ||
|---|---|---|---|---|
| Figure | Entropy | Figure | Entropy | |
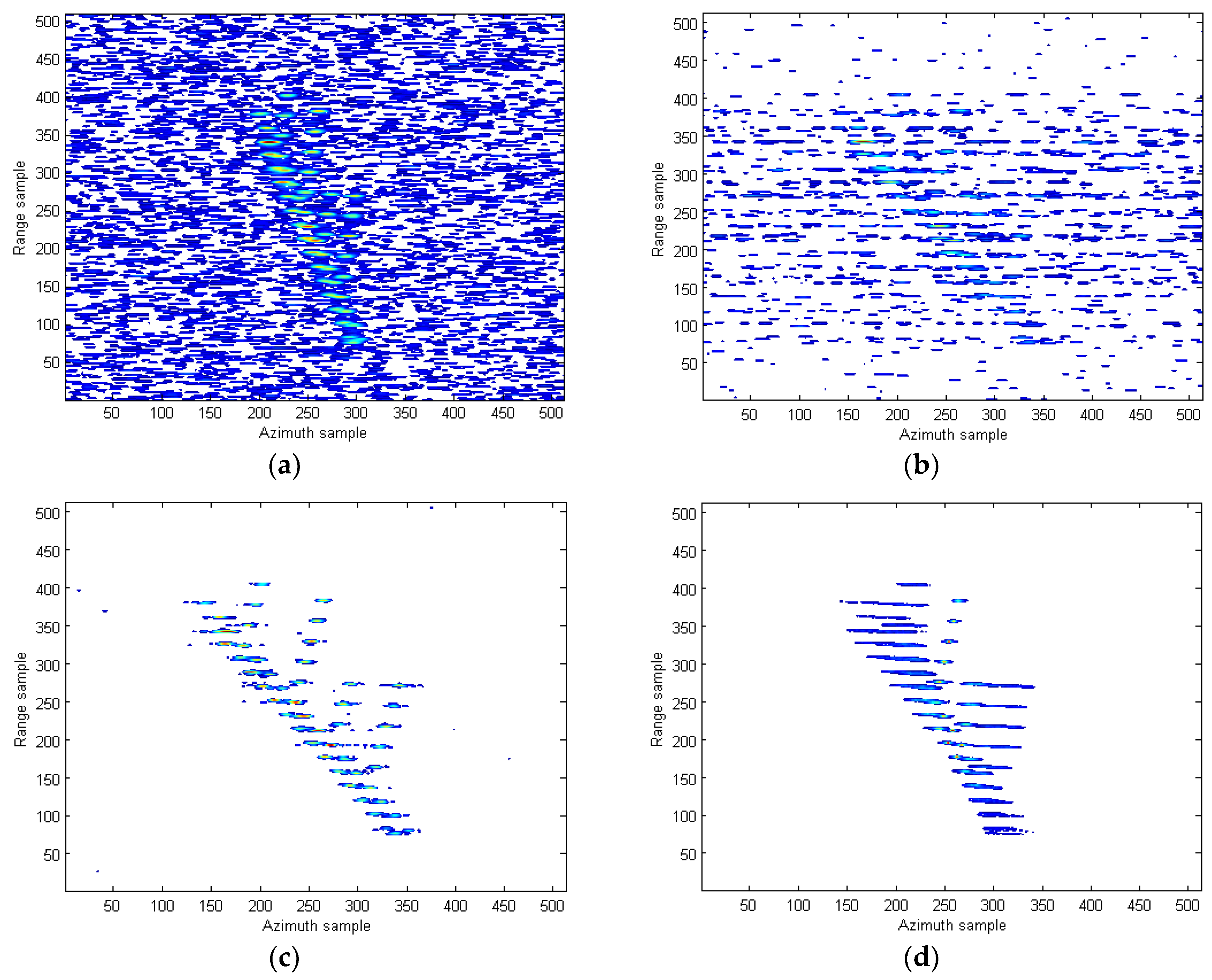
| STFT method in [10] | Figure 10a | 9.905 | Figure 11a | 11.623 |
| WVD method in [12] | Figure 10b | 9.170 | Figure 11b | 11.341 |
| SPWVD method in [13] | Figure 10c | 7.679 | Figure 11c | 9.208 |
| RCD method in [15] | Figure 10d | 7.418 | Figure 11d | 7.637 |
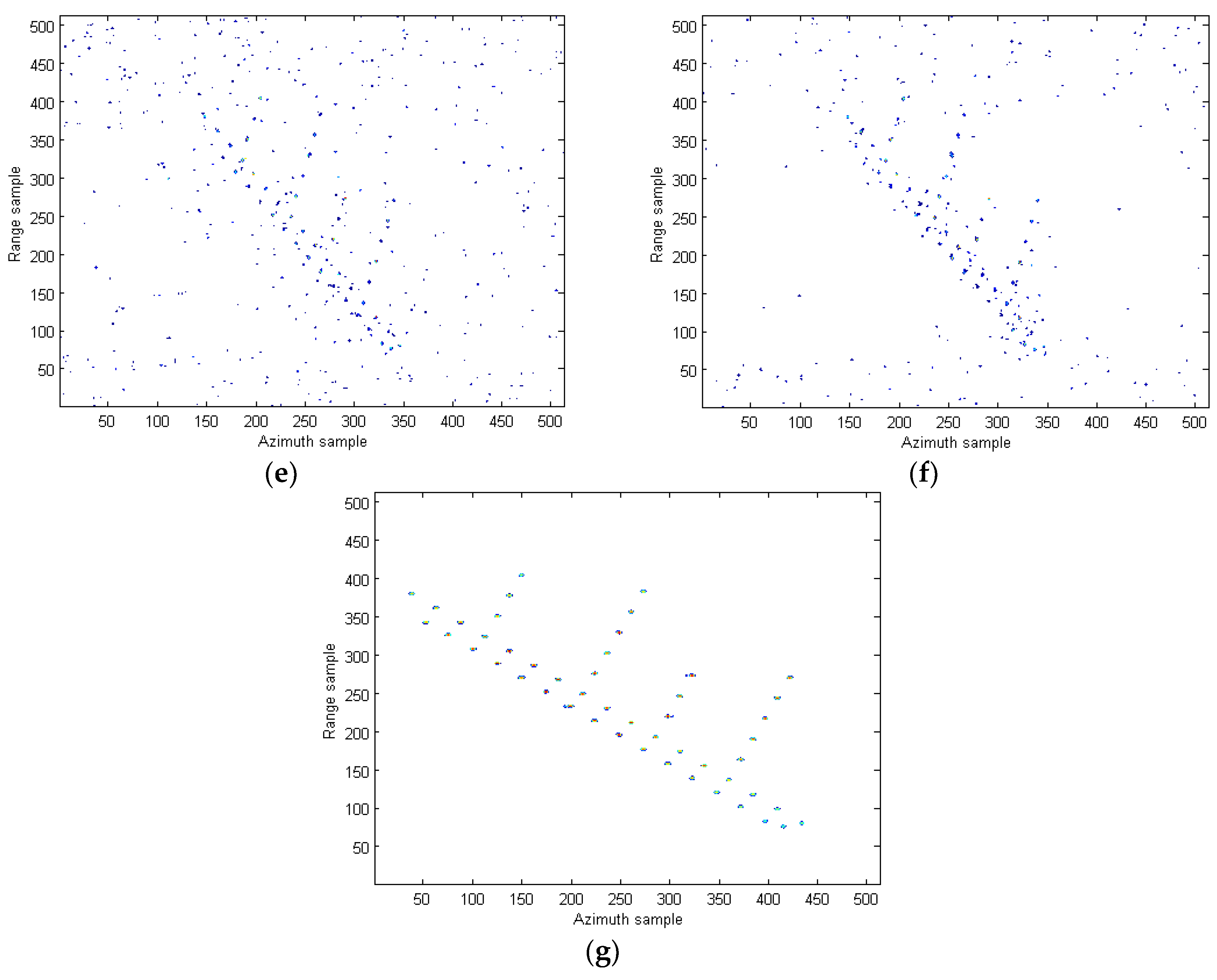
| IHAF-ICPF method in [7] | Figure 10e | 4.870 | Figure 11e | 5.619 |
| CIGCPF-CICPF method in [9] | Figure 10f | 4.513 | Figure 11f | 5.037 |
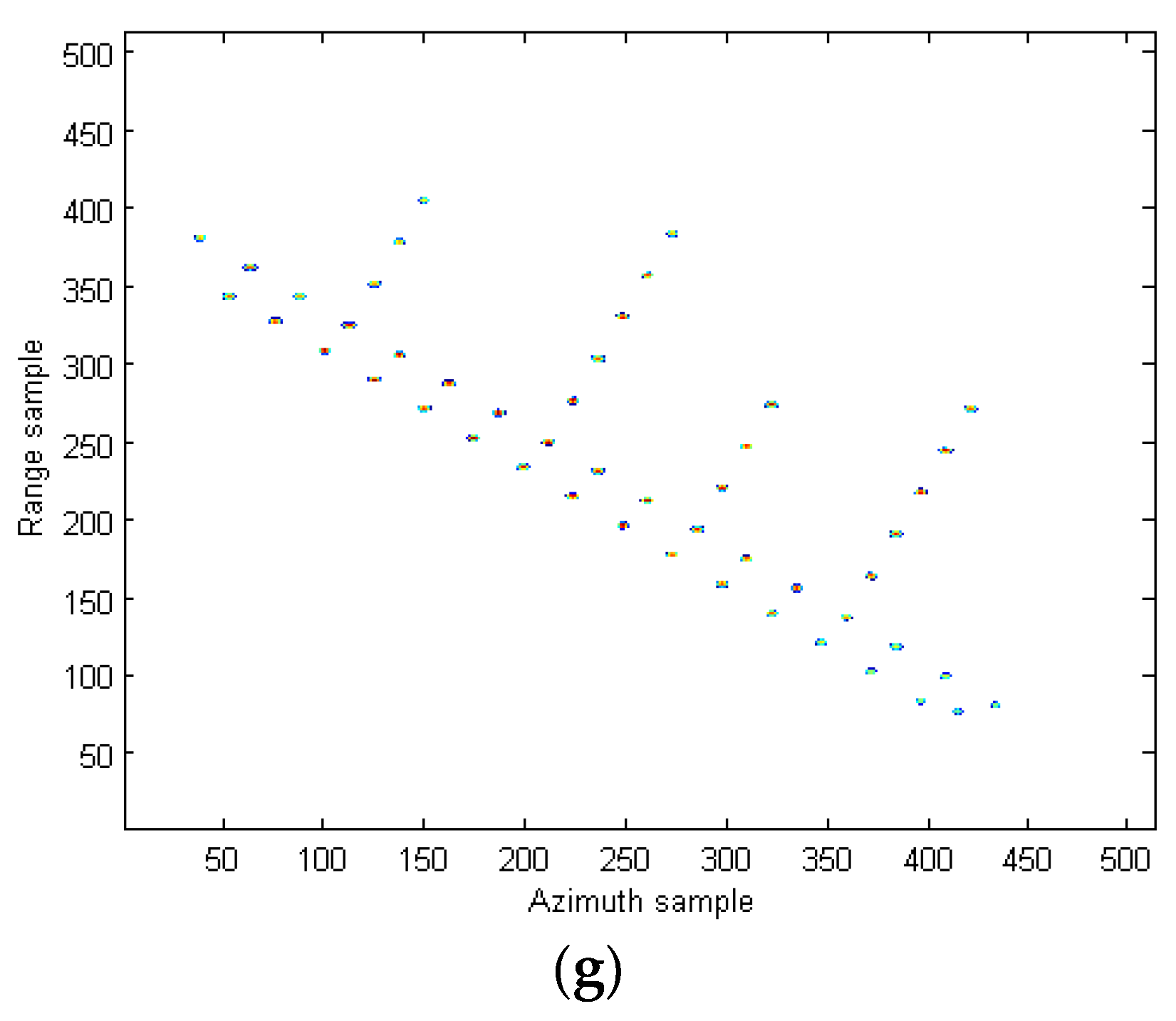
| Our proposed method | Figure 10g | 4.291 | Figure 11g | 4.372 |
| Methods | Runtime |
|---|---|
| RD algorithm | 0.50 m |
| STFT method | 1.24 m |
| WVD method | 1.56 m |
| SPWVD method | 2.73 m |
| RCD method | 5.04 m |
| IHAF-ICPF method | 56.23 m |
| CIGCPF-CICPF method | 41.78 m |
| Our proposed method | 8.35 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, C.; Qin, M.; Li, D.; Liu, H.; Chai, Y. An Efficient ISAR Imaging of Targets with Complex Motions Based on a Quasi-Time-Frequency Analysis Bilinear Coherent Algorithm. Sensors 2018, 18, 2814. https://doi.org/10.3390/s18092814
Zeng C, Qin M, Li D, Liu H, Chai Y. An Efficient ISAR Imaging of Targets with Complex Motions Based on a Quasi-Time-Frequency Analysis Bilinear Coherent Algorithm. Sensors. 2018; 18(9):2814. https://doi.org/10.3390/s18092814
Chicago/Turabian StyleZeng, Cao, Mengyi Qin, Dong Li, Hongqing Liu, and Yi Chai. 2018. "An Efficient ISAR Imaging of Targets with Complex Motions Based on a Quasi-Time-Frequency Analysis Bilinear Coherent Algorithm" Sensors 18, no. 9: 2814. https://doi.org/10.3390/s18092814
APA StyleZeng, C., Qin, M., Li, D., Liu, H., & Chai, Y. (2018). An Efficient ISAR Imaging of Targets with Complex Motions Based on a Quasi-Time-Frequency Analysis Bilinear Coherent Algorithm. Sensors, 18(9), 2814. https://doi.org/10.3390/s18092814







