A Hypergraph-Based Blockchain Model and Application in Internet of Things-Enabled Smart Homes
Abstract
:1. Introduction
- We propose a hypergraph-based blockchain model. The implementation of blockchain technology requires that all nodes in the network maintain synchronized data records, which will undoubtedly put a lot of pressure on data storage. Therefore, to a certain extent, reducing the number of nodes that synchronize data in the network can also guarantee the normal operation of the blockchain. We use hypergraph theory to partition the entire network into many hyperedges, and each hyperedge stores a part of transaction data to reduce the storage pressure.
- We discuss the additional security risks of the proposed model and put forward response strategies. The original blockchain technology is robust to single-point attacks. If a node is forged, the whole hash values in its blocks will be different from the others and it will be dropped from the network. If more than 51% of the nodes are forged, the false data alarm will take effect, but that is very difficult to implement in a network-scale environment [20]. In our model, the constraints are weakened, but we can reduce the risk to an acceptable level through the setting of network parameters, especially for IoT environments where security requirements are not very high.
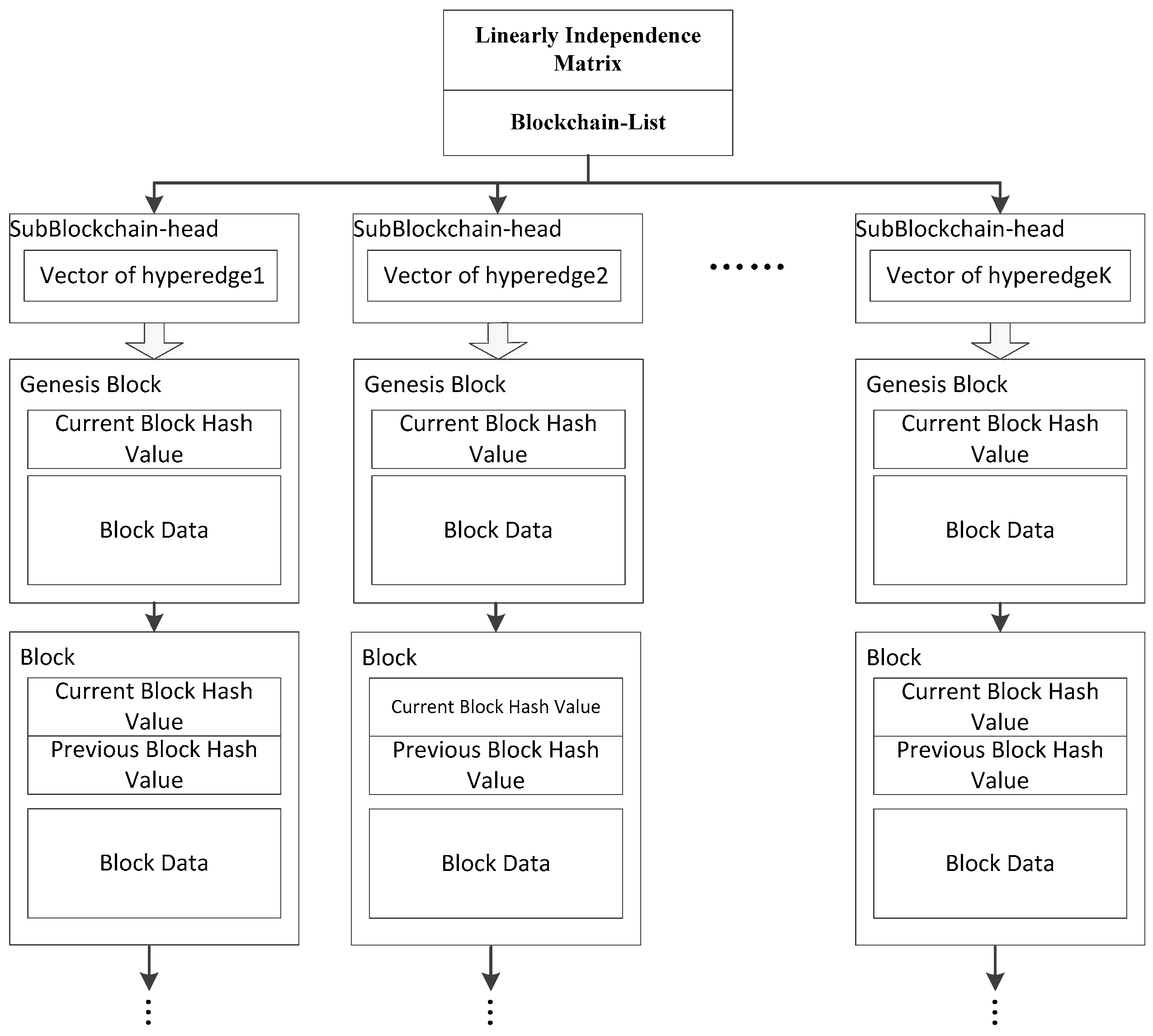
- We propose a dynamic network evolution algorithm. Considering the rapid expansion of IoT devices, IoT and smart home networks are growing at a geometric progression. When using hypergraph theory to partition blockchain networks, the algorithm takes the dynamic characteristics of the network into account, and due to the low power consumption and low processing capacity of IoT devices, the algorithm also needs to be designed relatively simply. An integer linear independence matrix is added to each node and each vector in the matrix map to a hyperedge. When the number of nodes increases or decreases, hyperedges can be easily split or aggregated according to the algorithm in order to guarantee the minimum cardinality of the graph.
2. Related Works
2.1. IoT and Smart Home
2.2. Blockchain
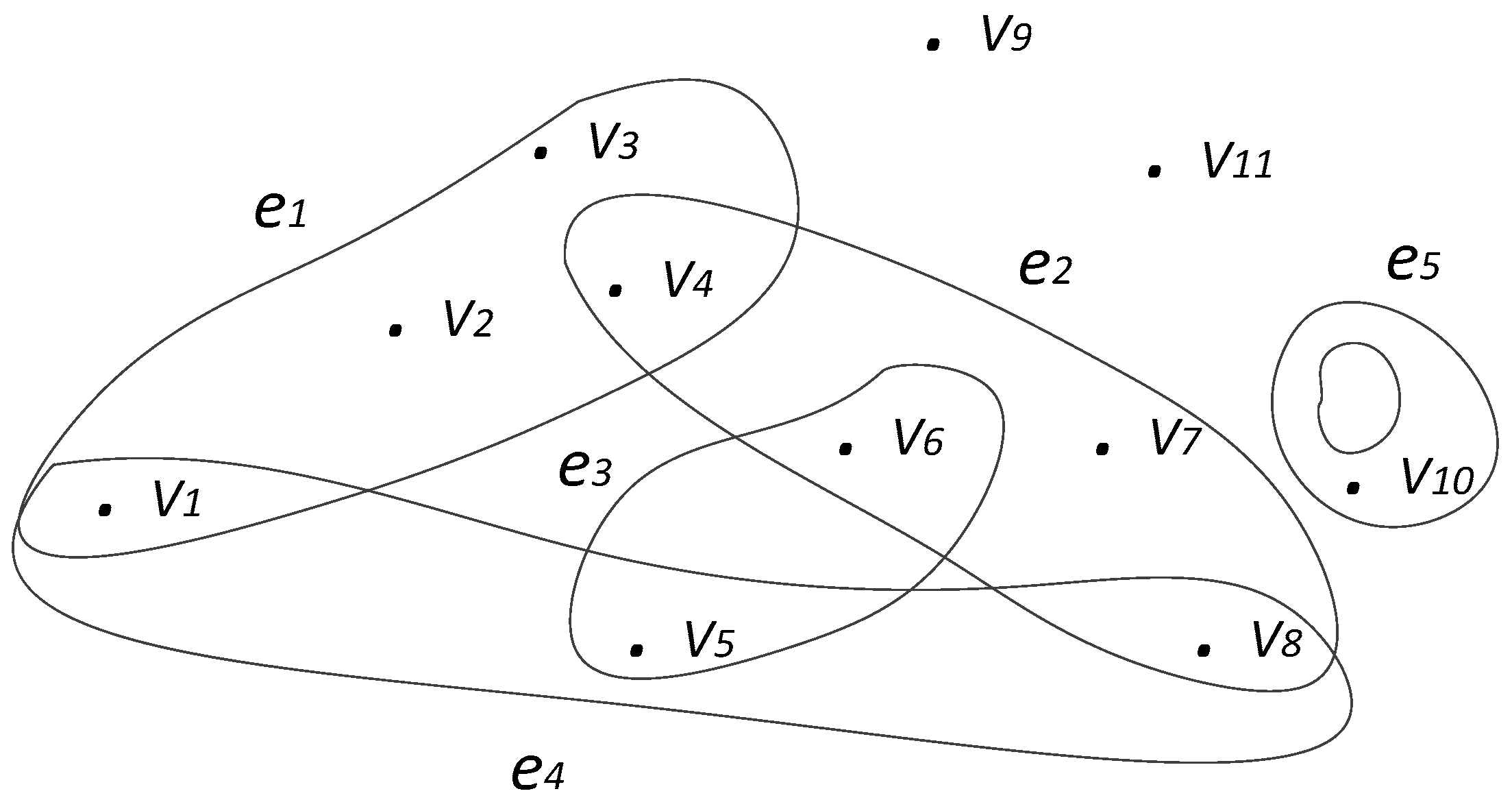
2.3. Hypergraph
3. Hypergraph Based Blockchain Model
3.1. Problem Statement
- The architecture of the model. In order to implement the proposed scheme, a structure is needed to support the blockchain networks, and only certain nodes are used to store a transaction record without affecting security and privacy or reducing security risks to acceptable conditions.
- How the scheme works. Under the designed structure, some mechanisms or algorithms are needed to support the structure to solve the problems caused by structural changes.
- The parameters set. In the support structure and the algorithm designed for this, a series of parameters needs to be adjusted so that they can achieve the desired purpose in an optimal way. The setting of these parameters needs to be adjusted through experiments and evaluations.
3.2. Architecture Overview
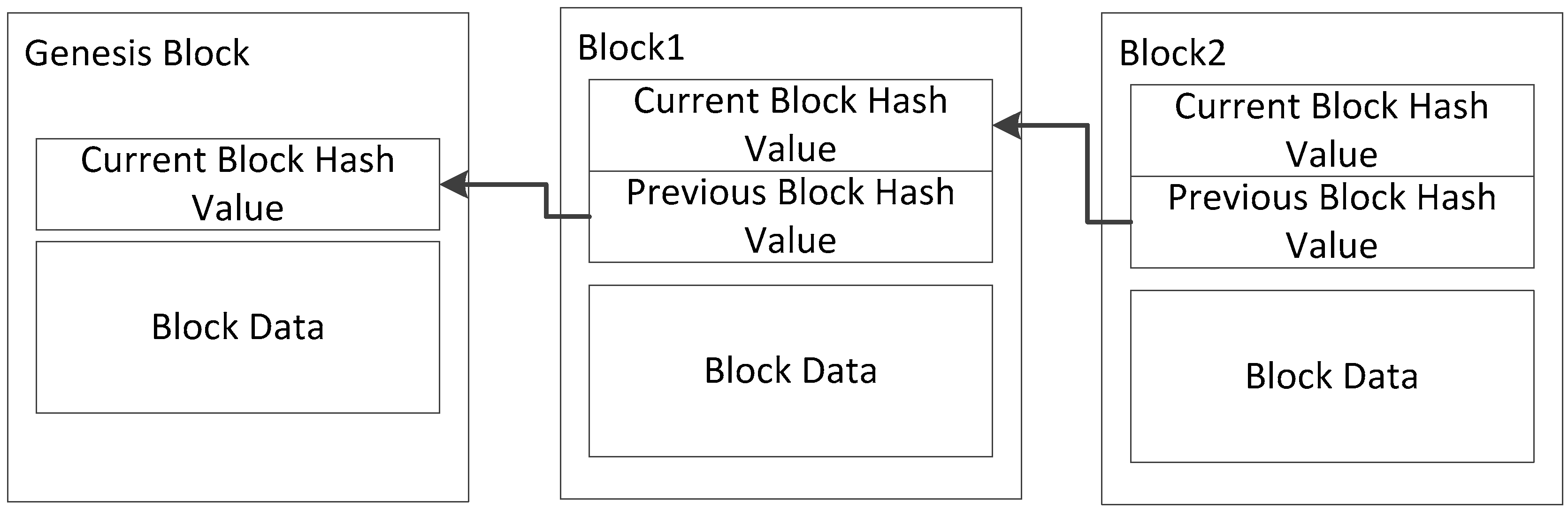
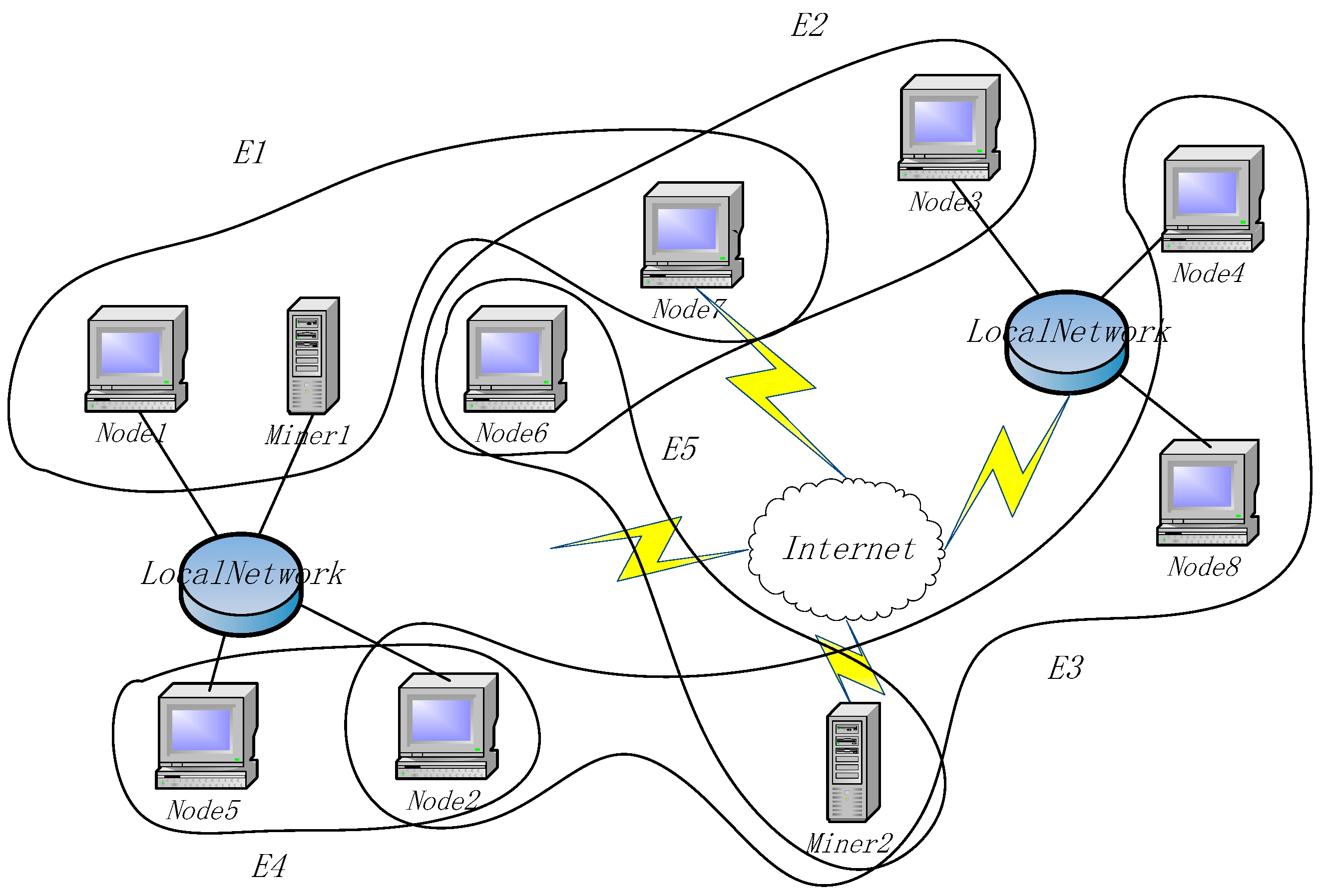
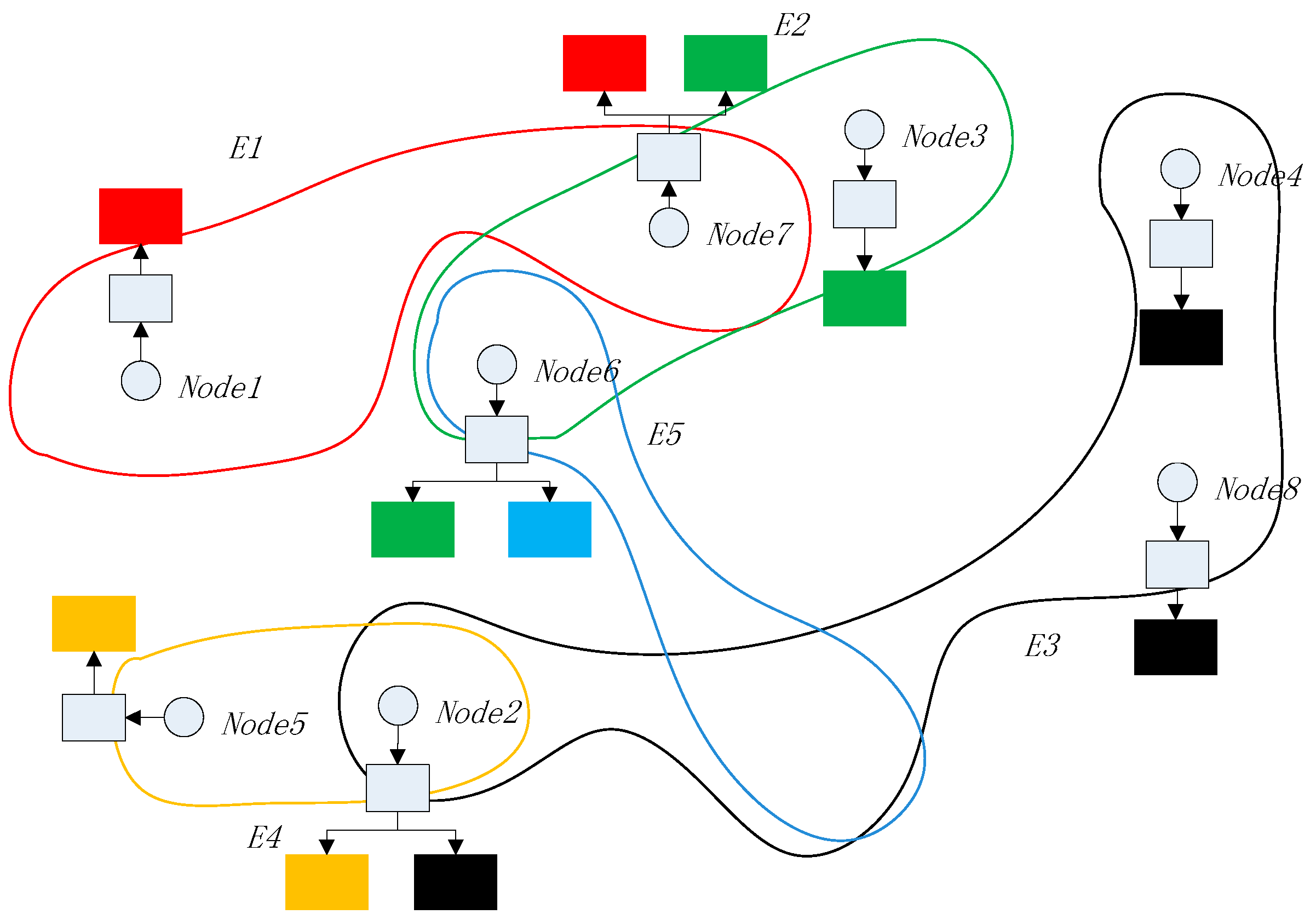
- Nodes: A node is a device with storage ability in a blockchain network. The route is reachable in the network and normal communication can be performed. Each node in the network belongs to at least one hyperedge and can belong to multiple hyperedges at the same time.
- Miners: Miners are devices for calculating encryption block hash keys in blockchain network, which is not much different from ordinary miners. However, in the designed architecture, miners also undertake the task of calculating the linear independence matrix (explained in Section 3.3.2) in the network, which is mainly used for the control of transaction data storage and network evolution.
- Hyperedge: A hyperedge is a set of nodes. All nodes on the same hyperedge have the same vector encoding that is independent of other hyperedges, and they have synchrony when storing transaction data.
3.3. Architecture Principal
3.3.1. Network Parameters
3.3.2. Node Blockchain
3.4. Working Mechanism
3.5. Security Discussion and Response Strategy
- Attacks on the storage nodes can be easier than in the original blockchain network;
- A verification attack will try to forge the legal message and increase the legal ratio;
- Attacks can occur from forging a new hyperedge and modifying the records only recorded by it.
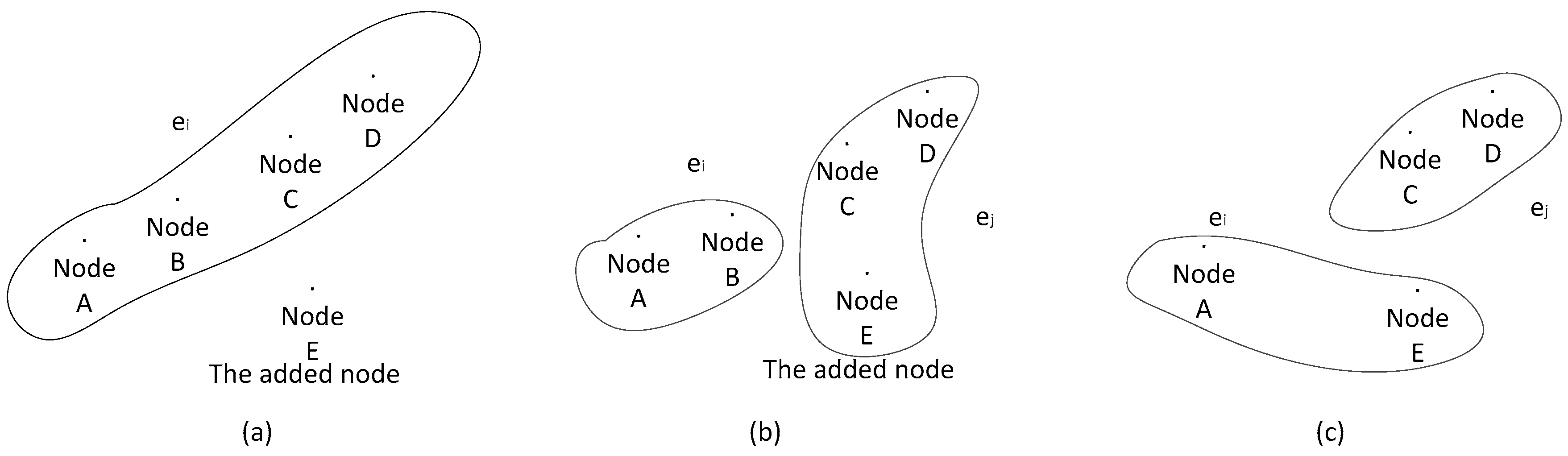
3.6. Hyperedge Splitting and Aggregation
| Algorithm 1 |
| Select a hyperedge ei randomly if |ei| < r insert the node n else split the r/2 of the nodes in ei to a new hyperedge ei” insert the node n to ei” and copy the synchronous SubBlockchain generate a new linear independence vector V’ for ei” for each node ni in the network add V’ to the linear independence matrix |
| Algorithm 2 |
| for each hyperedge ei that contains the deleted node n if |ei| < cr if exist a hyperedge ej and|ej| > cr and ei∩ej = Φ for each nk (k∈[cr, |ej|]) in ej move nk to ei and copy the SubBlockchain of ei else randomly select a hyperedge ek and combine it with ei |
4. Use Case in a Smart Home
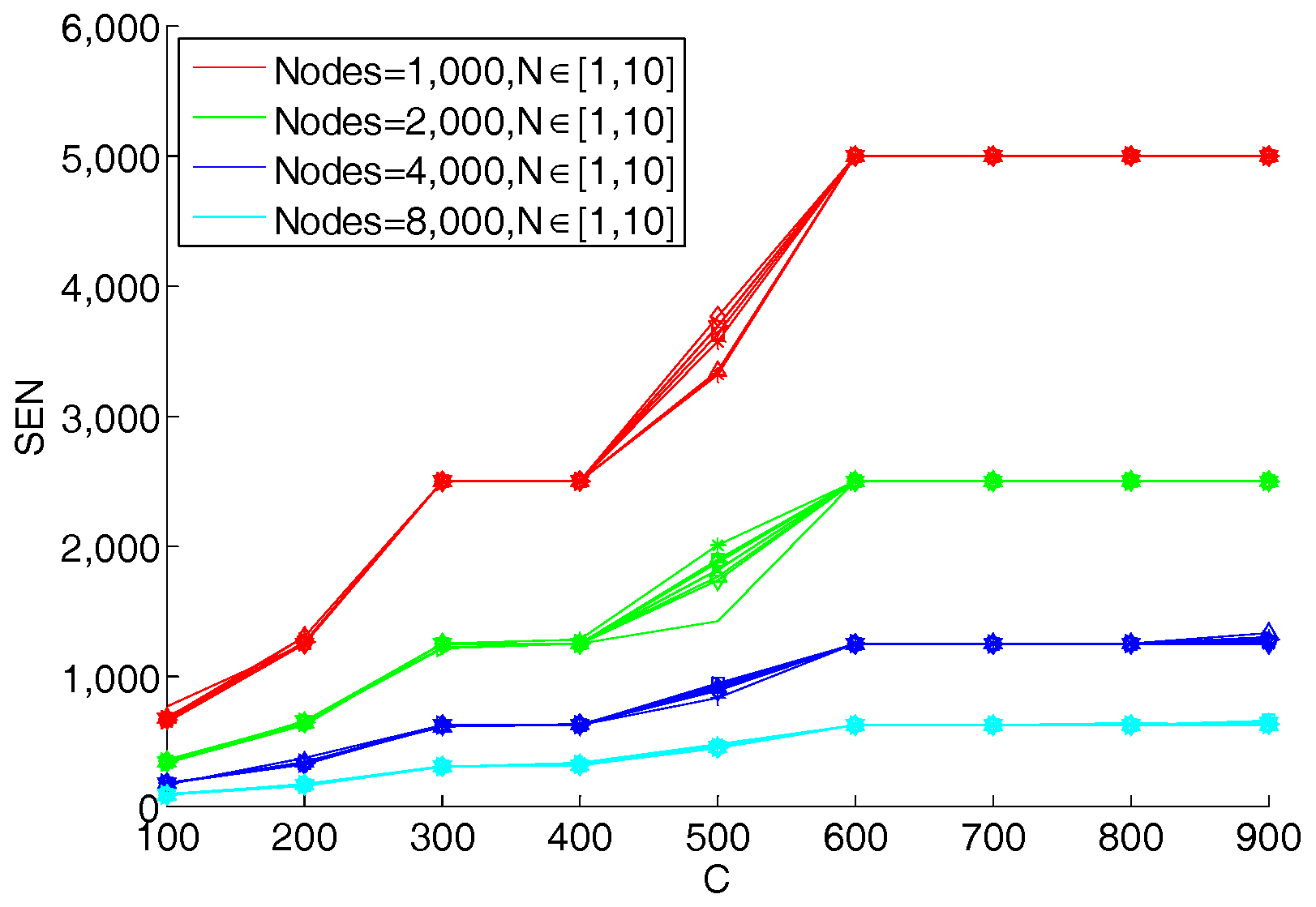
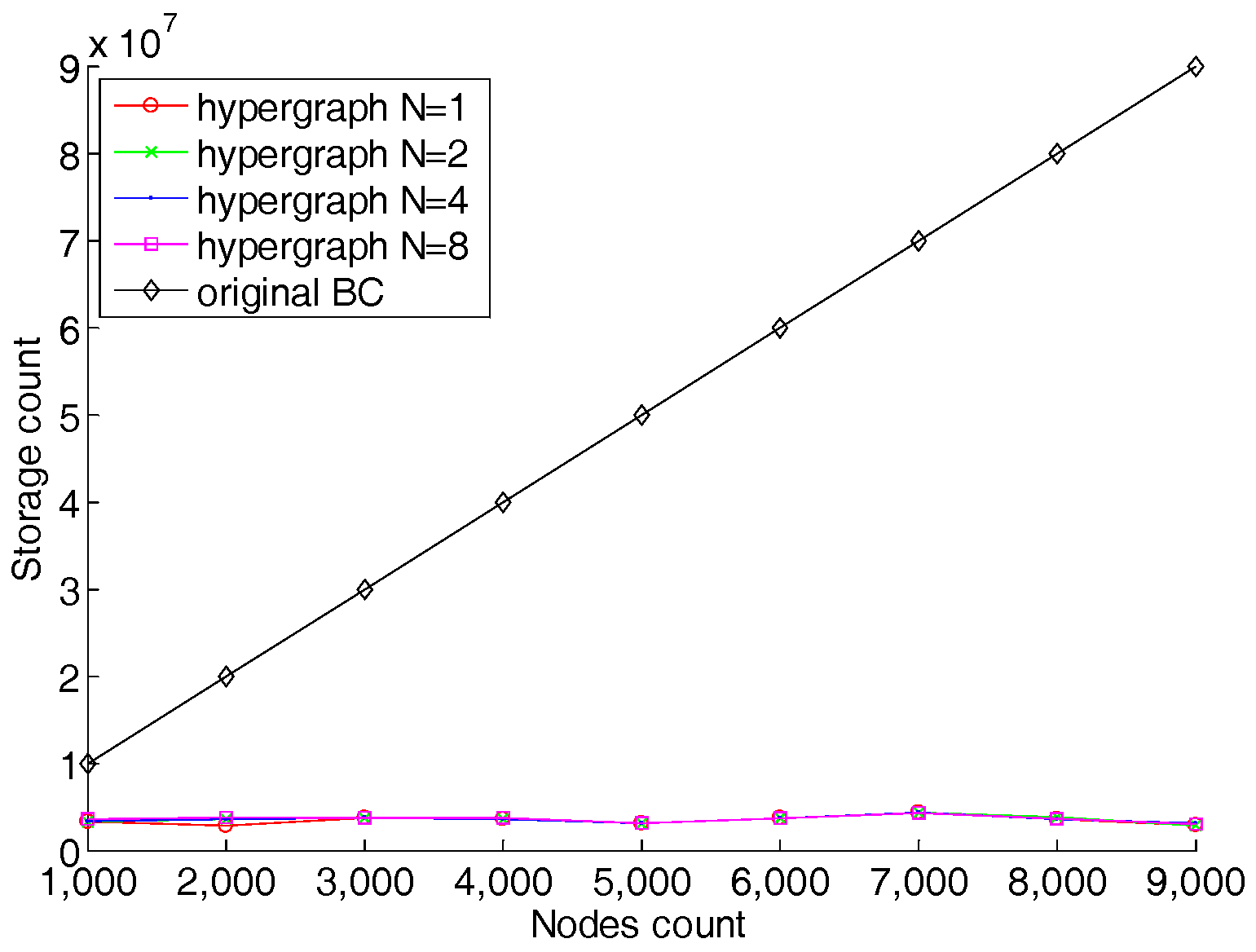
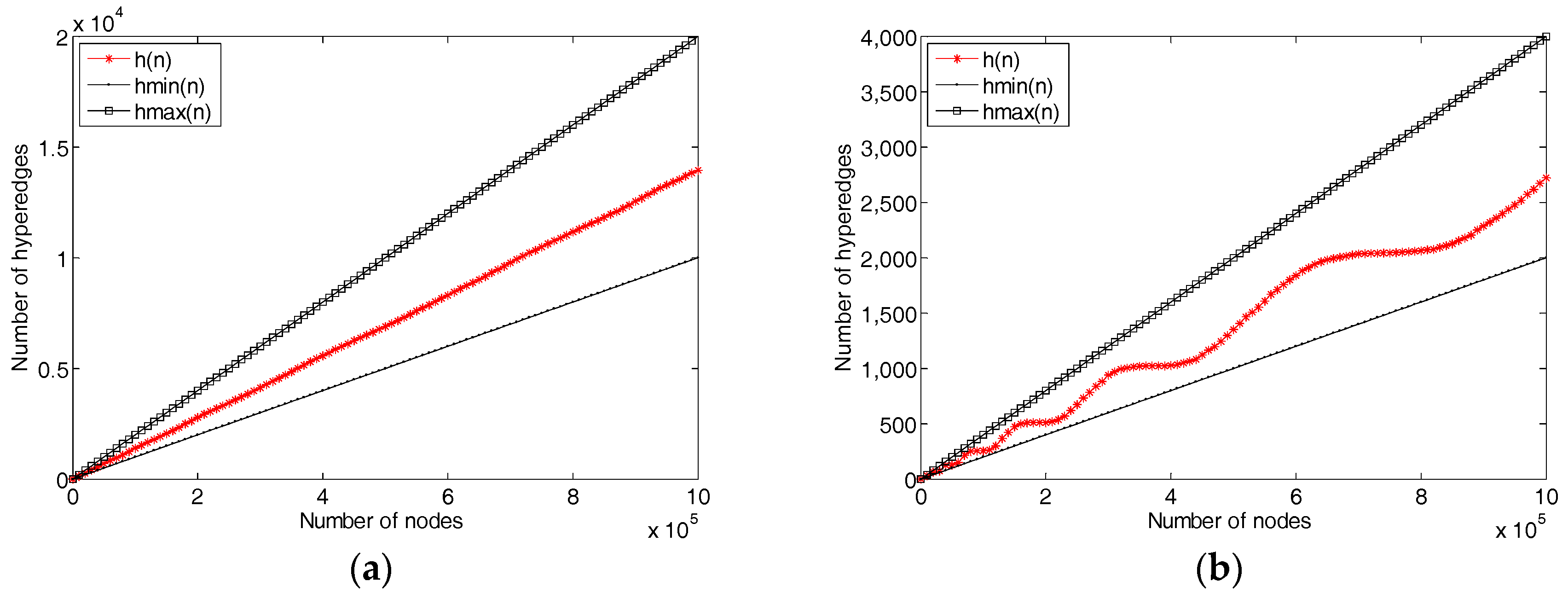
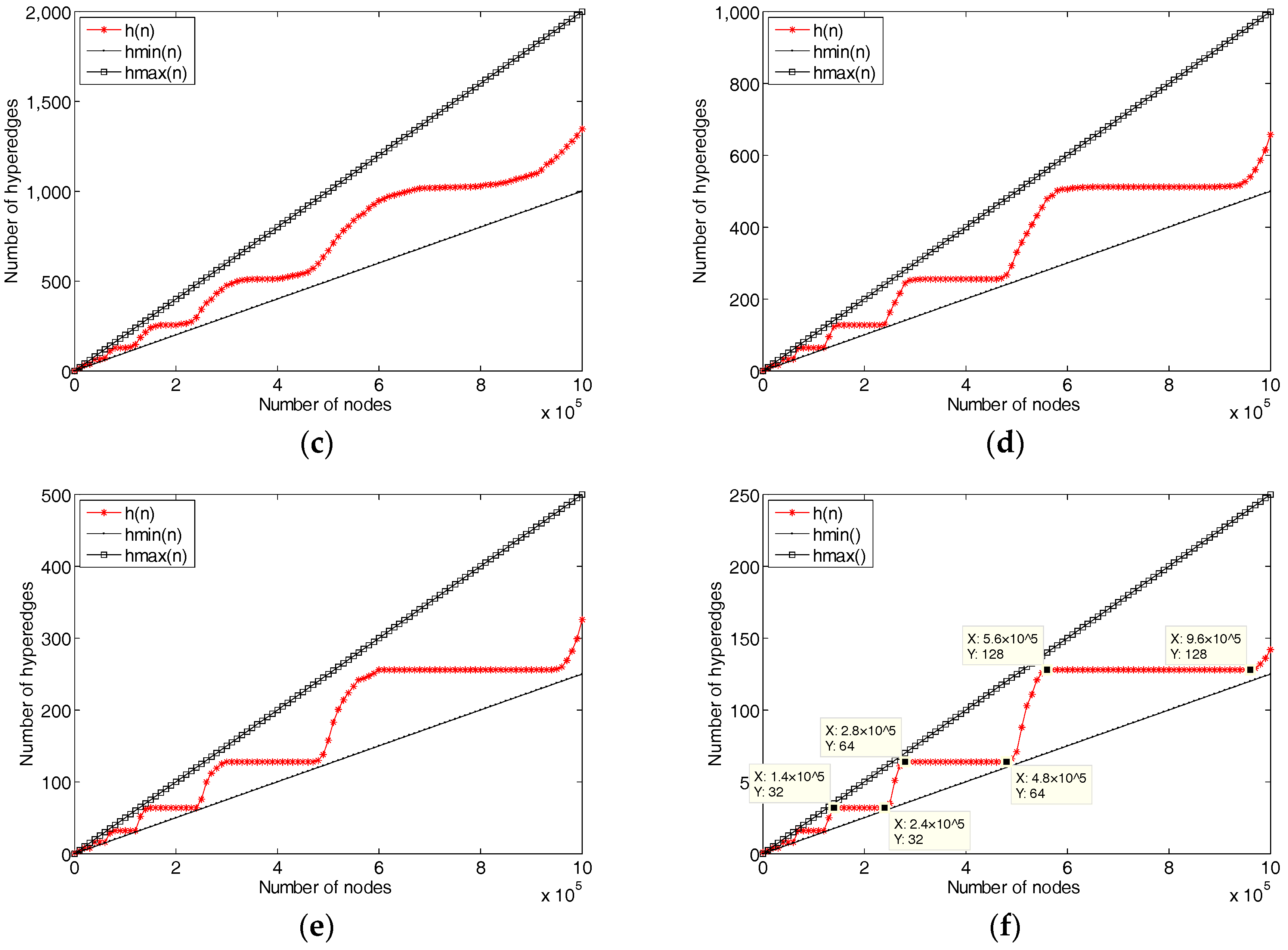
5. Experiments and Evolution
5.1. Storage Efficiency Analysis
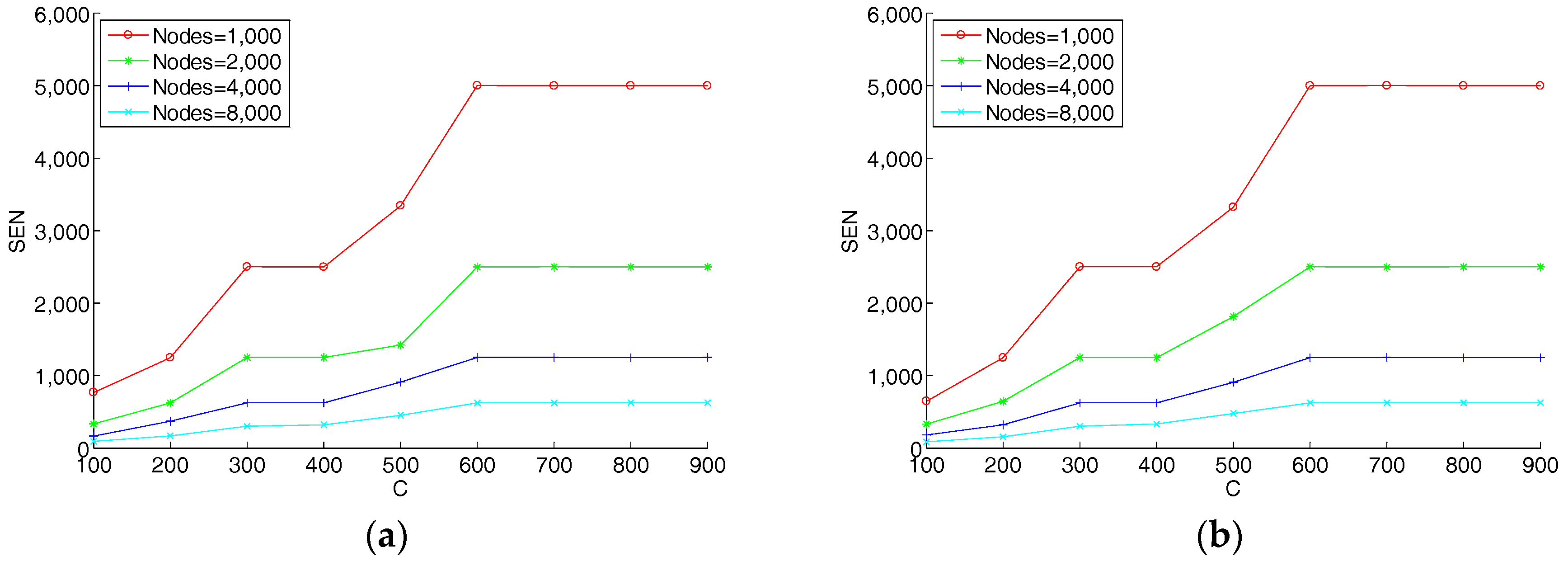
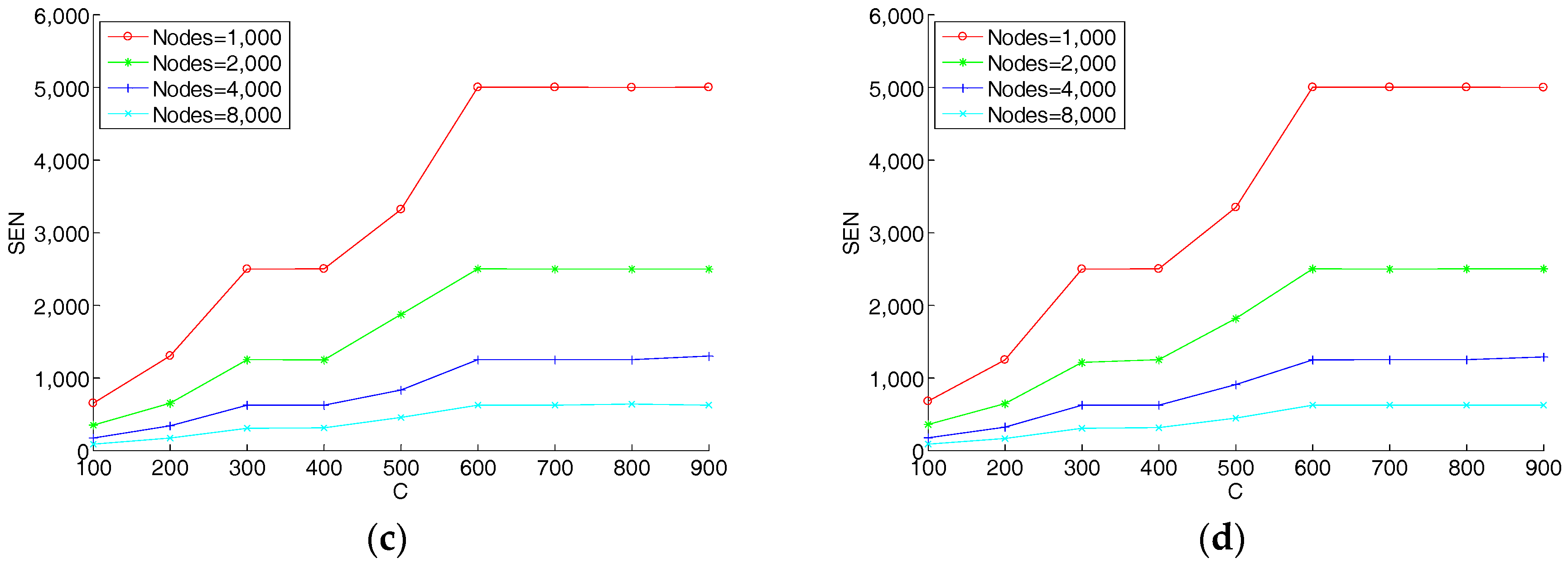
5.2. Network Evolution
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tao, M.; Zuo, J.; Liu, Z.; Castiglione, A.; Palmieri, F. Multi-layer cloud architectural model and ontology-based security service framework for IoT-based smart homes. Future Gener. Comput. Syst. 2018, 78, 1040–1051. [Google Scholar] [CrossRef]
- Li, H.; Tian, Y.; Liu, Y.; Li, T. UAI-IOT framework: A method of uniform interfaces to acquire information from heterogeneous enterprise information systems. In Proceedings of the IEEE International Conference on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber, Physical and Social Computing, Beijing, China, 20–23 August 2013; pp. 724–730. [Google Scholar]
- Xie, R.; He, C.L.; Xie, D.Q.; Gao, C.Z.; Zhang, X.J. A secure ciphertext retrieval scheme against insider kgas for mobile devices in cloud storage. Secur. Commun. Netw. 2018, 2018, 7254305. [Google Scholar] [CrossRef]
- Yang, H.; Yu, J.; Zo, H.; Choi, M. User acceptance of wearable devices: An extended perspective of perceived value. Telemat. Inform. 2016, 33, 256–269. [Google Scholar] [CrossRef]
- Sutar, S.H.; Koul, R.; Suryavanshi, R. Integration of smart phone and IOT for development of smart public transportation system. In Proceedings of the International Conference on Internet of Things and Applications, Pune, India, 22–24 June 2016; pp. 73–78. [Google Scholar]
- Tao, M.; Ota, K.; Dong, M. Ontology-based data semantic management and application in IoT- and cloud-enabled smart homes. Future Gener. Comput. Syst. 2017, 76, 528–539. [Google Scholar] [CrossRef]
- Chen, Z.H.; Zhang, F.G.; Zhang, P.; Liu, J.K.; Huang, J.W.; Zhao, H.B.; Shen, J. Verifiable keyword search for secure big data-based mobile healthcare networks with fine-grained authorization control. Future Gener. Comput. Syst. 2018, 87, 712–724. [Google Scholar] [CrossRef]
- Fernandes, E.; Jung, J.; Prakash, A. Security analysis of emerging smart home applications. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–26 May 2016; pp. 636–654. [Google Scholar]
- Kalofonos, D.N.; Shakhshir, S. Intuisec: A Framework for Intuitive User Interaction with Smart Home Security using Mobile Devices. In Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communication, Athens, Greece, 3–7 September 2007; pp. 1–5. [Google Scholar]
- Komninos, N.; Philippou, E.; Pitsillides, A. Survey in smart grid and smart home security: Issues, challenges and countermeasures. IEEE Commun. Surv. Tutor. 2014, 16, 1933–1954. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R.; Gauravaram, P. Blockchain for IoT security and privacy: The case study of a smart home. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications Workshops, Kona, HI, USA, 13–17 March 2017; pp. 618–623. [Google Scholar]
- Bertino, E. Data security and privacy in the IoT. In Proceedings of the 19th International Conference on Extending Database Technology, Bordeaux, France, 15–18 March 2016; pp. 1–3. [Google Scholar]
- Shafagh, H.; Burkhalter, L.; Hithnawi, A.; Duquennoy, S. Towards blockchain-based auditable storage and sharing of iot data. In Proceedings of the 2017 Cloud Computing Security Workshop, co-located with CCS 2017, Dallas, TX, USA, 3 November 2017; pp. 45–50. [Google Scholar]
- Treleaven, P.; Brown, R.G.; Yang, D. Blockchain technology in finance. Computer 2017, 50, 14–17. [Google Scholar] [CrossRef]
- Gatteschi, V.; Lamberti, F.; Demartini, C.; Pranteda, C.; Santamaría, V. To blockchain or not to blockchain: That is the question. IT Prof. 2018, 20, 62–74. [Google Scholar] [CrossRef]
- Laplante, P.A.; Amaba, B. Blockchain and the internet of things in the industrial sector. IT Prof. 2018, 20, 15–18. [Google Scholar] [CrossRef]
- Esposito, C.; Santis, A.D.; Tortora, G.; Chang, H.; Choo, K.K.R. Blockchain: A panacea for healthcare cloud-based data security and privacy? IEEE Cloud Comput. 2018, 5, 31–37. [Google Scholar] [CrossRef]
- Kshetri, N. Can blockchain strengthen the internet of things? IT Prof. 2017, 19, 68–72. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Towards an optimized blockchain for IoT. In Proceedings of the International Conference on Internet-Of-Things Design and Implementation, Pittsburgh, PA, USA, 18–20 April 2017; pp. 173–178. [Google Scholar]
- Jin, P.; Park, J. Blockchain security in cloud computing: Use cases, challenges, and solutions. Symmetry 2017, 9, 164. [Google Scholar]
- Ali, W.; Dustgeer, G.; Awais, M.; Shah, M.A. IoT based smart home: Security challenges, security requirements and solutions. In Proceedings of the International Conference on Automation and Computing, Huddersfield, UK, 7–8 September 2017; pp. 1–6. [Google Scholar]
- Chifor, B.C.; Bica, I.; Patriciu, V.V.; Pop, F. A security authorization scheme for smart home internet of things devices. Future Gener. Comput. Syst. 2018, 86, 740–749. [Google Scholar] [CrossRef]
- Khan, M.A.; Salah, K. IoT security: Review, blockchain solutions, and open challenges. Future Gener. Comput. Syst. 2018, 82, 395–411. [Google Scholar] [CrossRef]
- Qu, C.; Tao, M.; Zhang, J.; Hong, X.Y.; Yuan, R.F. Blockchain based credibility verification method for IoT entities. Secur. Commun. Netw. 2018, 2018, 7817614. [Google Scholar] [CrossRef]
- Gervais, A.; Karame, G.O.; Glykantzis, V.; Ritzdorf, H.; Capkun, S. On the security and performance of proof of work blockchains. In Proceedings of the ACM Sigsac Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 3–16. [Google Scholar]
- Swan, M. Blockchain: Blueprint for a New Economy, 1st ed.; O’Reilly: Sebastopol, CA, USA, 2015. [Google Scholar]
- Shen, J.; Wang, C.; Li, T.; Chen, X.F.; Huang, X.Y.; Zhan, Z.H. Secure data uploading scheme for a smart home system. Inf. Sci. 2018, 453, 186–197. [Google Scholar] [CrossRef]
- Christidis, K.; Devetsikiotis, M. Blockchains and smart contracts for the internet of things. IEEE Access 2016, 4, 2292–2303. [Google Scholar] [CrossRef]
- Huh, S.; Cho, S.; Kim, S. Managing IoT devices using blockchain platform. In Proceedings of the International Conference on Advanced Communication Technology, Bongpyeong, Korea, 19–22 February 2017; pp. 464–467. [Google Scholar]
- Ouaddah, A.; Elkalam, A.A.; Ouahman, A.A. Towards a novel privacy-preserving access control model based on blockchain technology in IoT. In Europe and MENA Cooperation Advances in Information and Communication Technologies; Springer: Berlin, Germany, 2017. [Google Scholar]
- Samaniego, M.; Deters, R. Blockchain as a service for IOT. In Proceedings of the IEEE International Conference on Internet of Things, Chengdu, China, 16–19 December 2017; pp. 433–436. [Google Scholar]
- Raman, R.K.; Varshney, L.R. Dynamic distributed storage for scaling blockchains. arXiv, 2017; arXiv:1711.07617. [Google Scholar]
- Bretto, A. Hypergraph Theory; Springer: Cham, Switzerlands, 2013. [Google Scholar]
- Jung, J.; Chun, S.; Lee, K.H. Hypergraph-based overlay network model for the internet of things. In Proceedings of the IEEE World Forum on Internet of Things, Milan, Italy, 14–16 December 2015; pp. 104–109. [Google Scholar]
- Yao, L.; Sheng, Q.Z.; Ngu, A.H.H.; Li, X. Things of interest recommendation by leveraging heterogeneous relations in the internet of things. ACM Trans. Internet Technol. 2016, 16, 1–25. [Google Scholar] [CrossRef]
- Rodrigues, B.; Bocek, T.; Stiller, B. Multi-domain ddos mitigation based on blockchains. In Proceedings of the 11th IFIP WG 6.6 International Conference on Autonomous Infrastructure, Management, and Security, AIMS, Zurich, Switzerland, 10–13 July 2017; pp. 185–190. [Google Scholar]
- Tosh, D.K.; Shetty, S.; Liang, X.; Kamhoua, C.A.; Kwiat, K.A.; Njilla, L.; IEEE. Security implications of blockchain cloud with analysis of block withholding attack. In Proceedings of the 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Madrid, Spain, 14–17 May 2017; pp. 458–467. [Google Scholar]
| Model | Storage | Blockchain Structure | Verification | Miners’ Function |
|---|---|---|---|---|
| Original blockchain | One node one copy | One chain | By node itself | POW |
| Hypergraph-based blockchain | Part nodes have a copy | Several subchains | By other nodes | POW and linear independence matrix |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, C.; Tao, M.; Yuan, R. A Hypergraph-Based Blockchain Model and Application in Internet of Things-Enabled Smart Homes. Sensors 2018, 18, 2784. https://doi.org/10.3390/s18092784
Qu C, Tao M, Yuan R. A Hypergraph-Based Blockchain Model and Application in Internet of Things-Enabled Smart Homes. Sensors. 2018; 18(9):2784. https://doi.org/10.3390/s18092784
Chicago/Turabian StyleQu, Chao, Ming Tao, and Ruifen Yuan. 2018. "A Hypergraph-Based Blockchain Model and Application in Internet of Things-Enabled Smart Homes" Sensors 18, no. 9: 2784. https://doi.org/10.3390/s18092784
APA StyleQu, C., Tao, M., & Yuan, R. (2018). A Hypergraph-Based Blockchain Model and Application in Internet of Things-Enabled Smart Homes. Sensors, 18(9), 2784. https://doi.org/10.3390/s18092784






