Optimal Particle Filter Weight for Bayesian Direct Position Estimation in a GNSS Receiver
Abstract
:1. Introduction
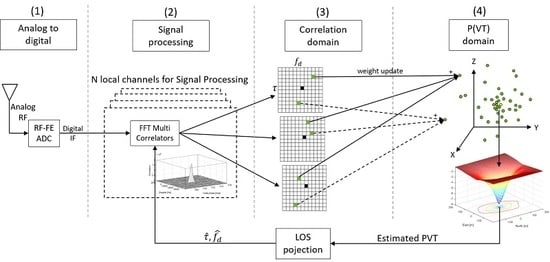
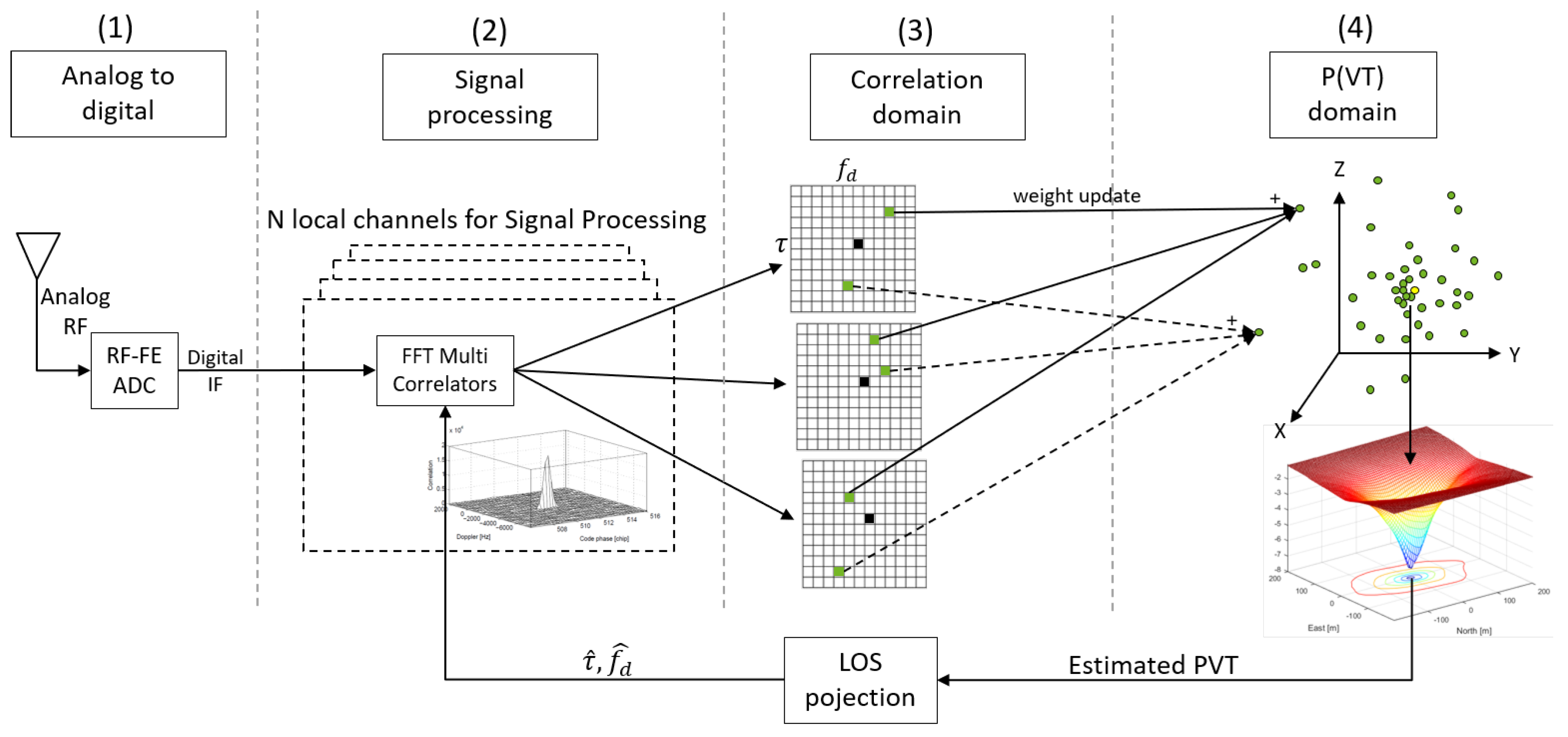
2. BDPE Receiver Architecture
3. Particle Filter
4. Derivation of the Optimal Particle Weight for Multiple GNSS Signals
5. Logarithmic Weight Update
6. Discussion of the Ranging Accuracy
7. Delay Bias as Gaussian Nuisance Parameter
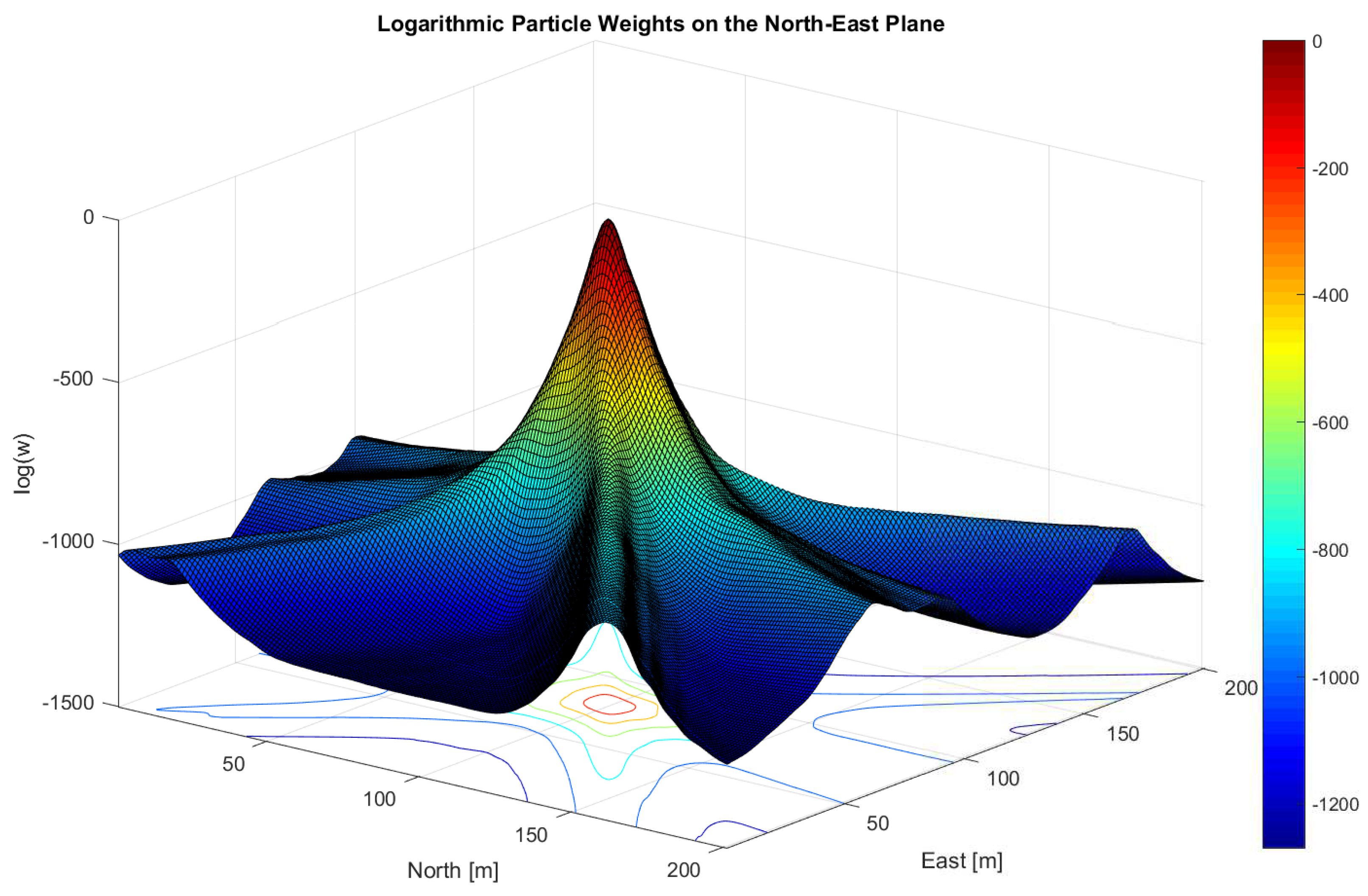
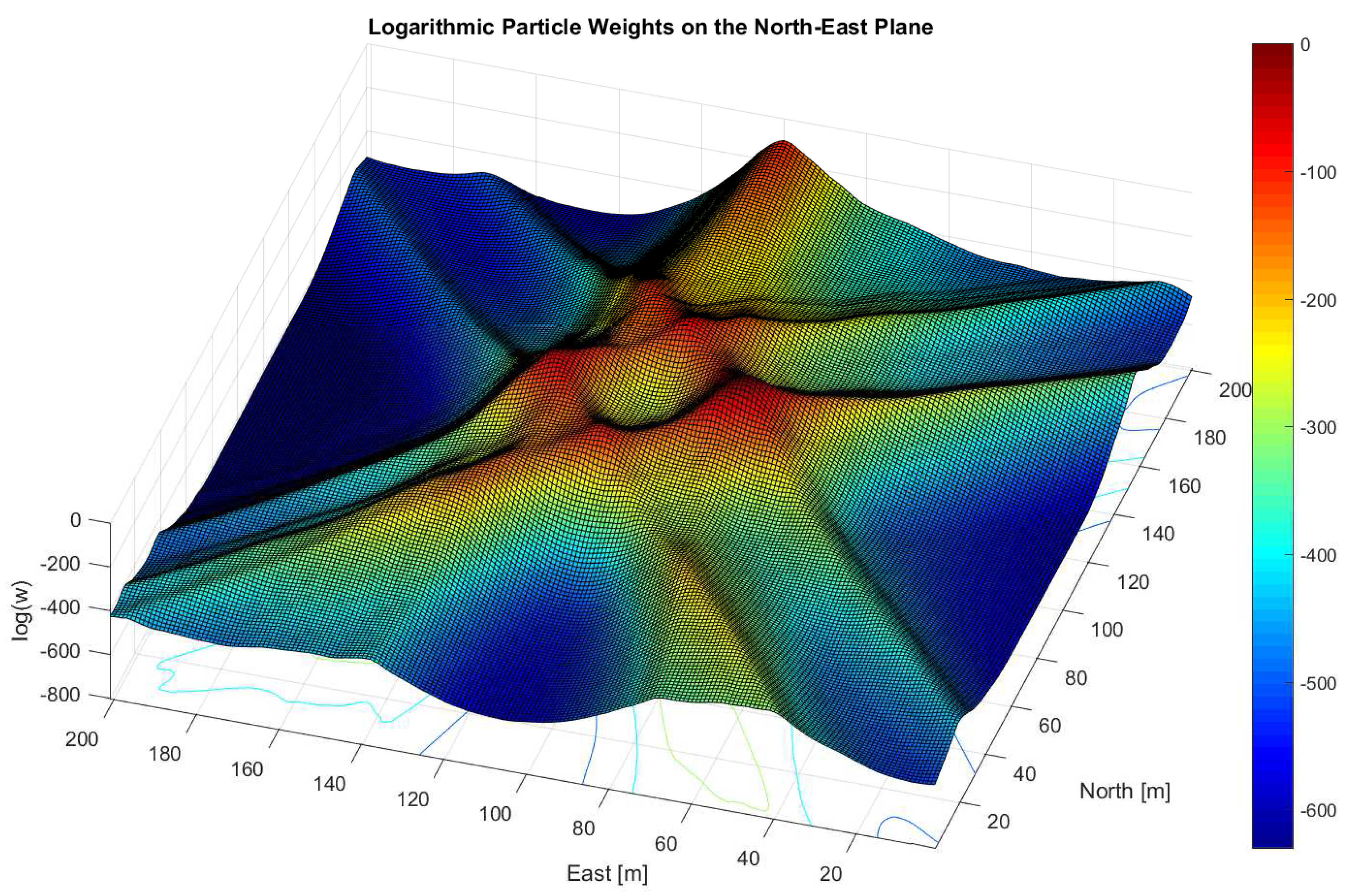
8. Simulations and Real-World Results
- different signal strengths,
- different code delay bias variances,
- constructive and destructive multipath,
- short, medium and far multipath,
- different multipath amplitudes,
- two significant real-world scenarios under open-sky and urban conditions.
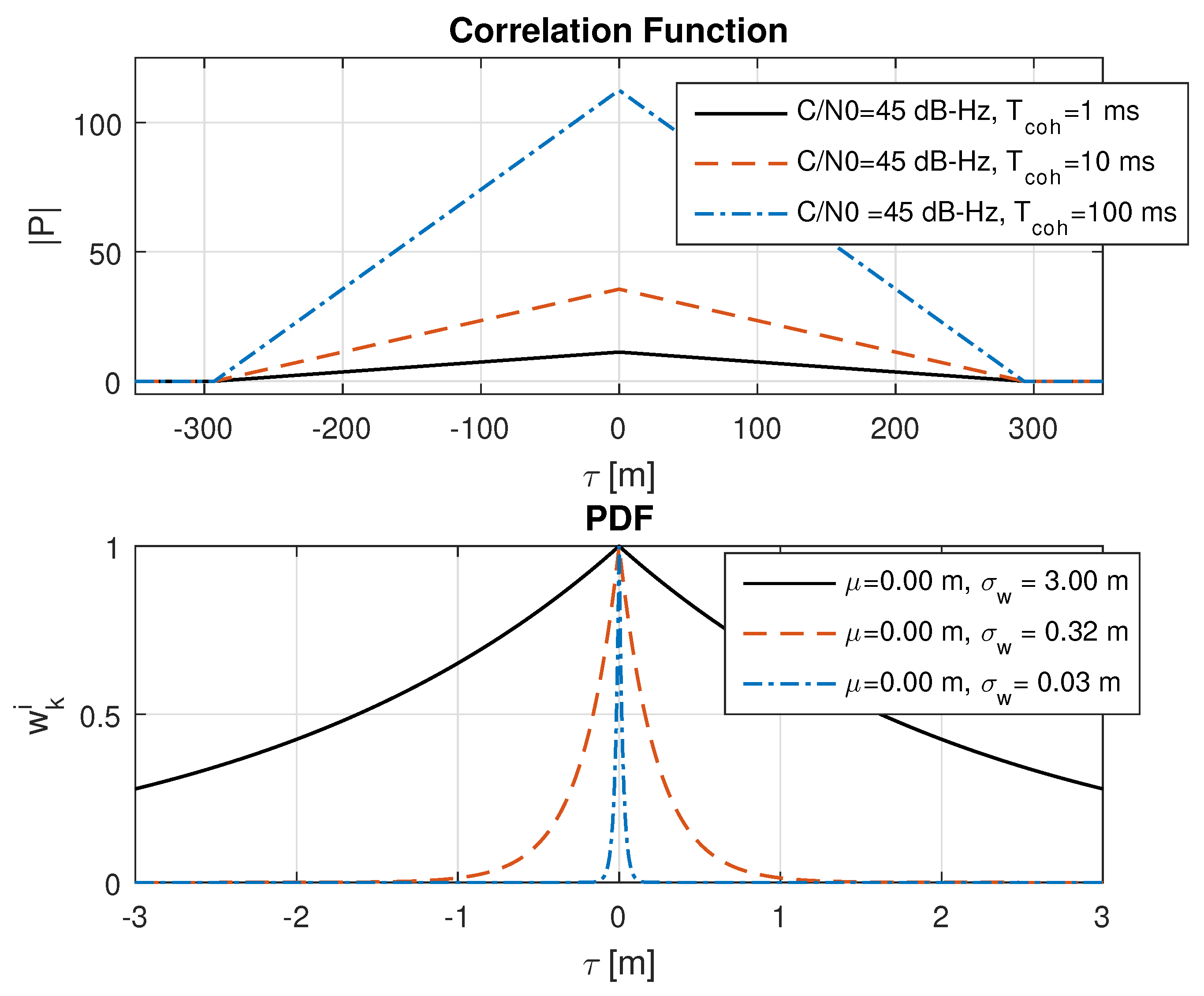
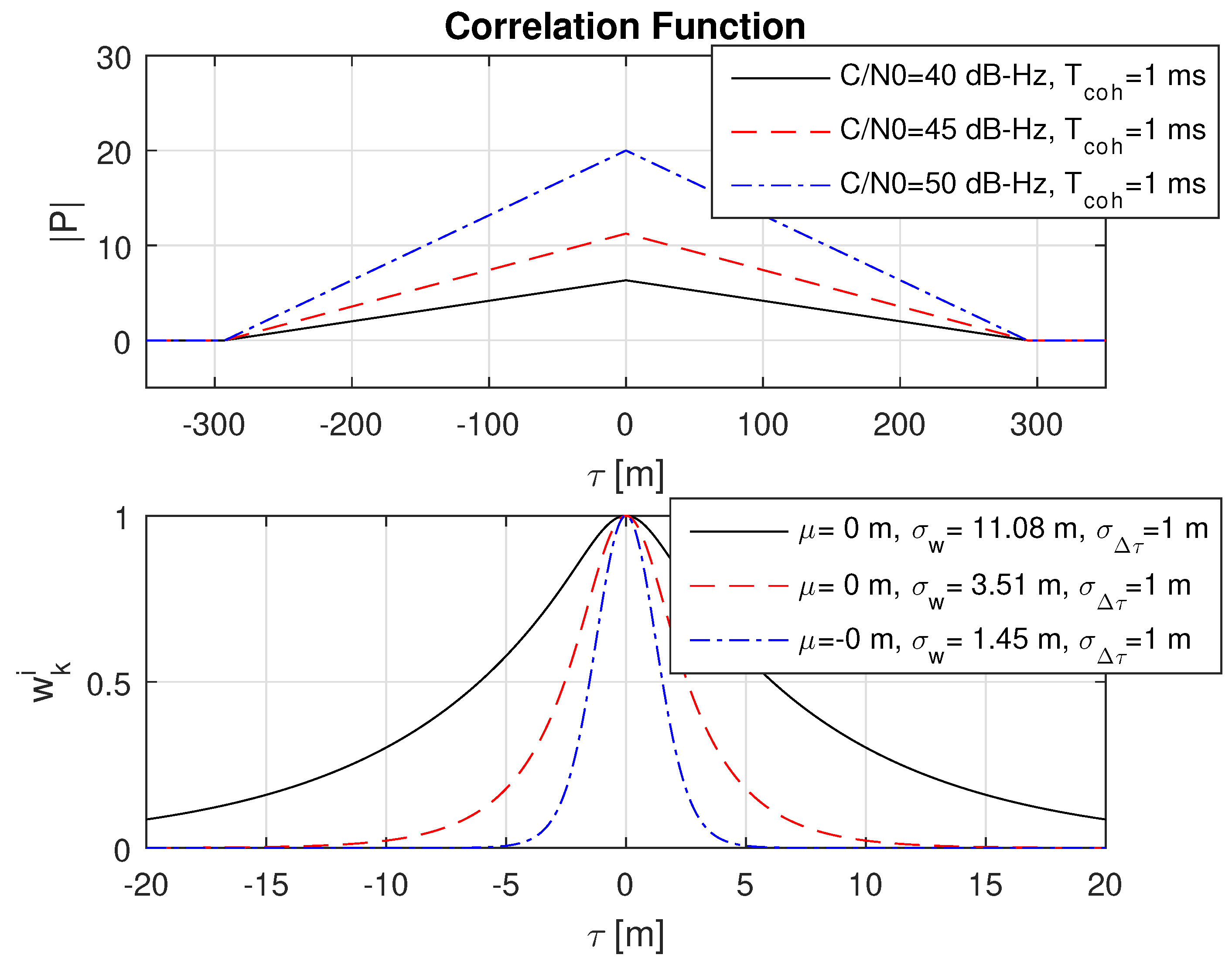
8.1. Impact of Different Signal Strengths
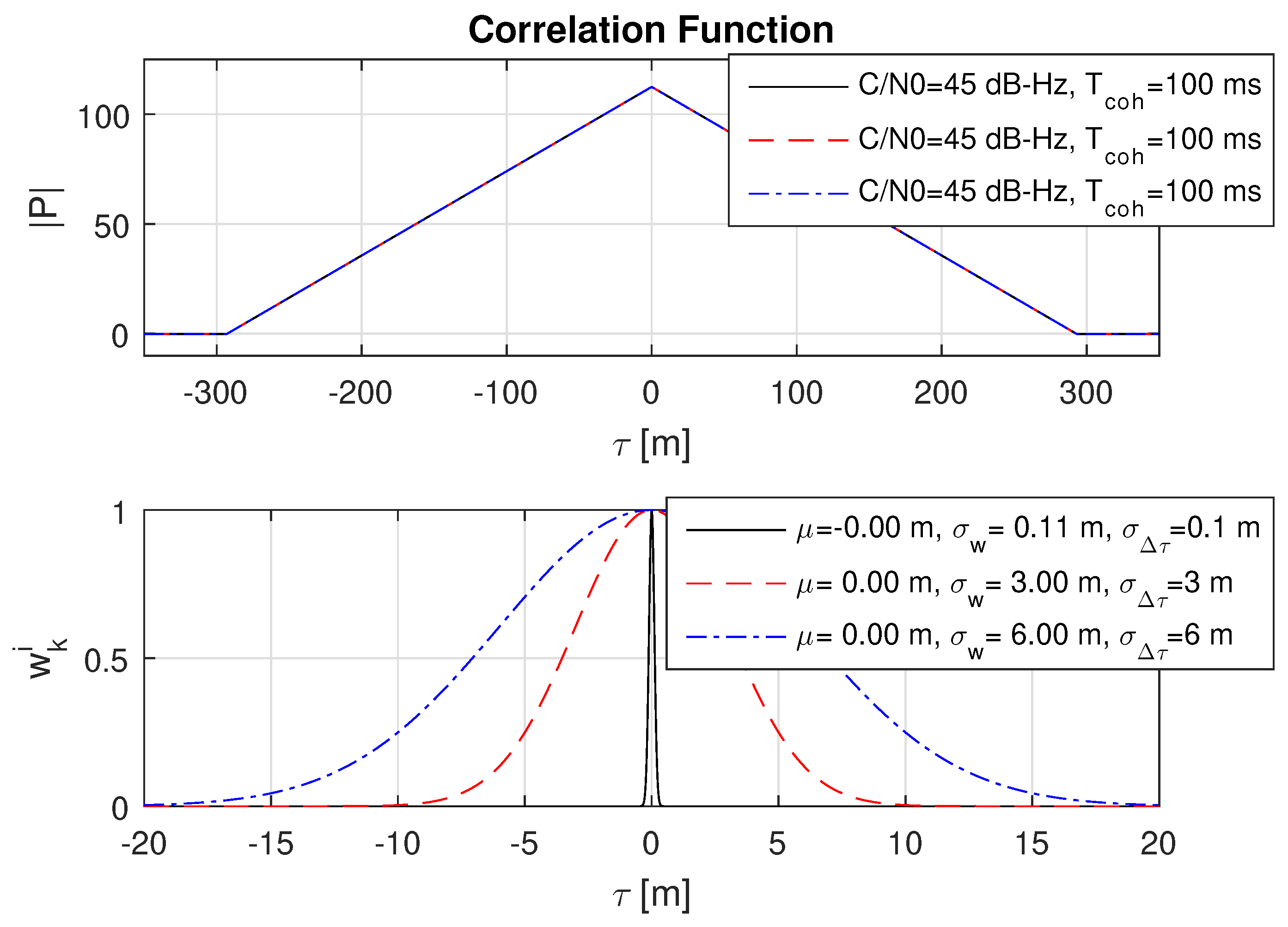
8.2. Impact of Different Code Delay Bias Variances
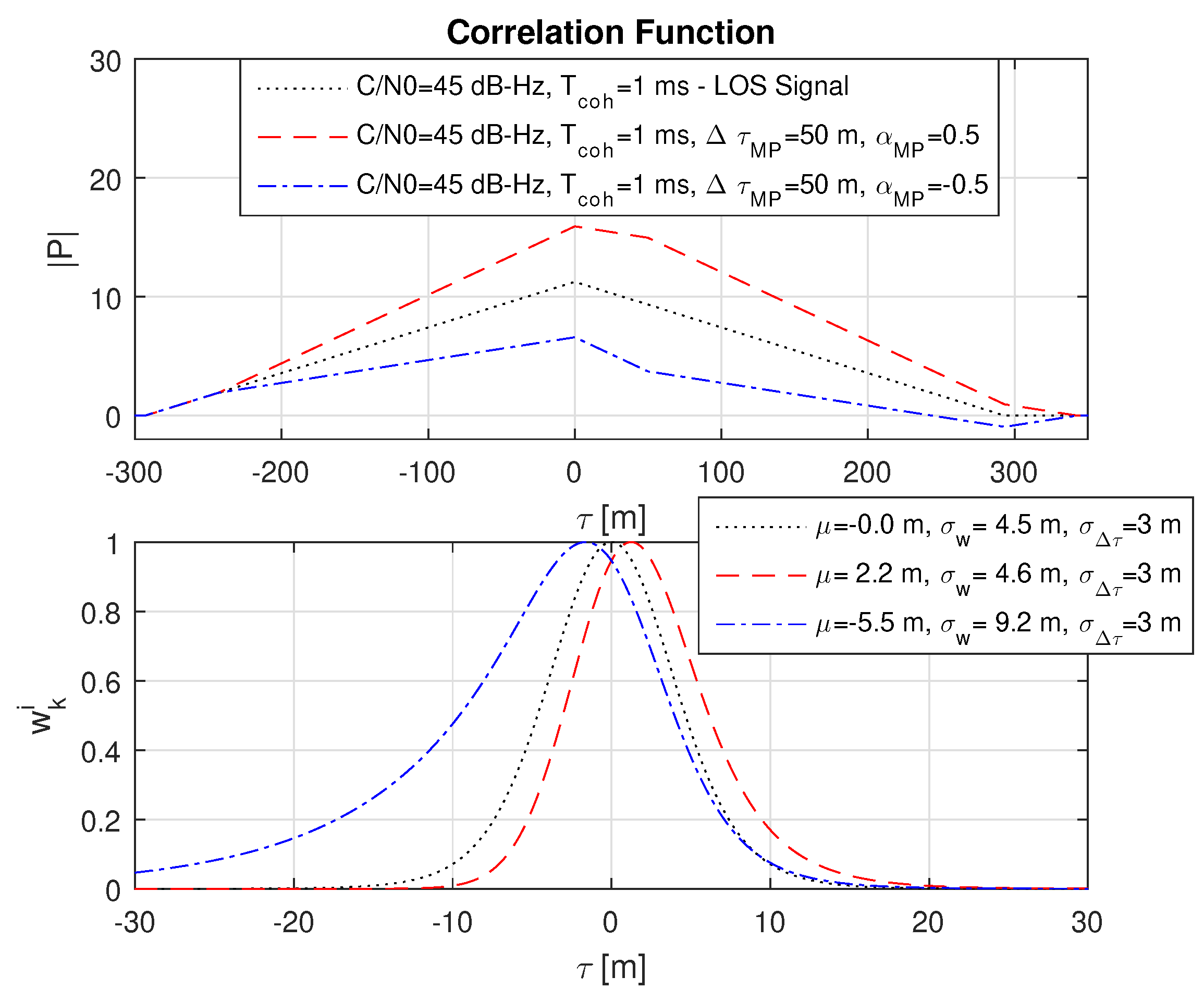
8.3. Impact of Constructive and Destructive Multipath
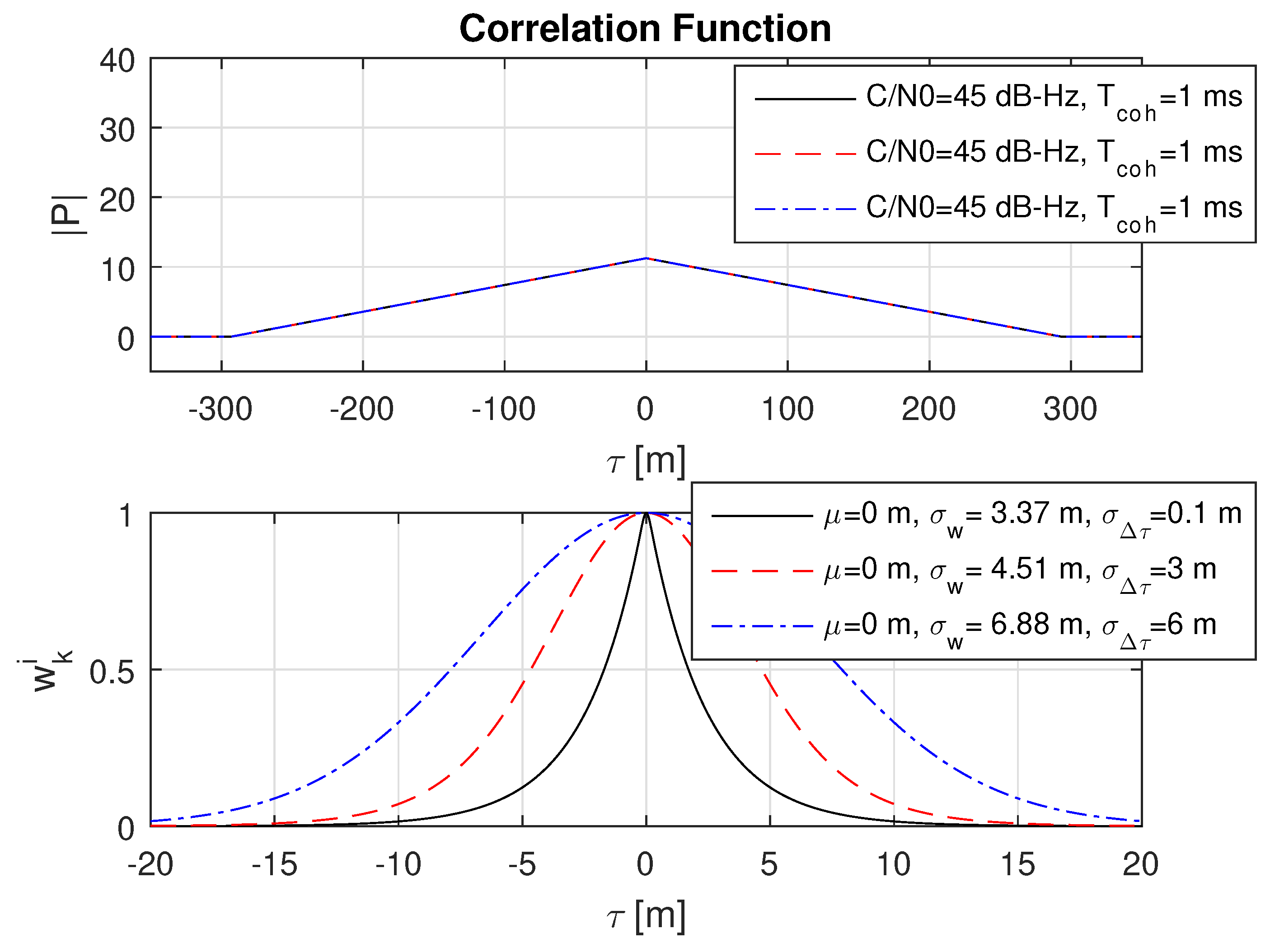
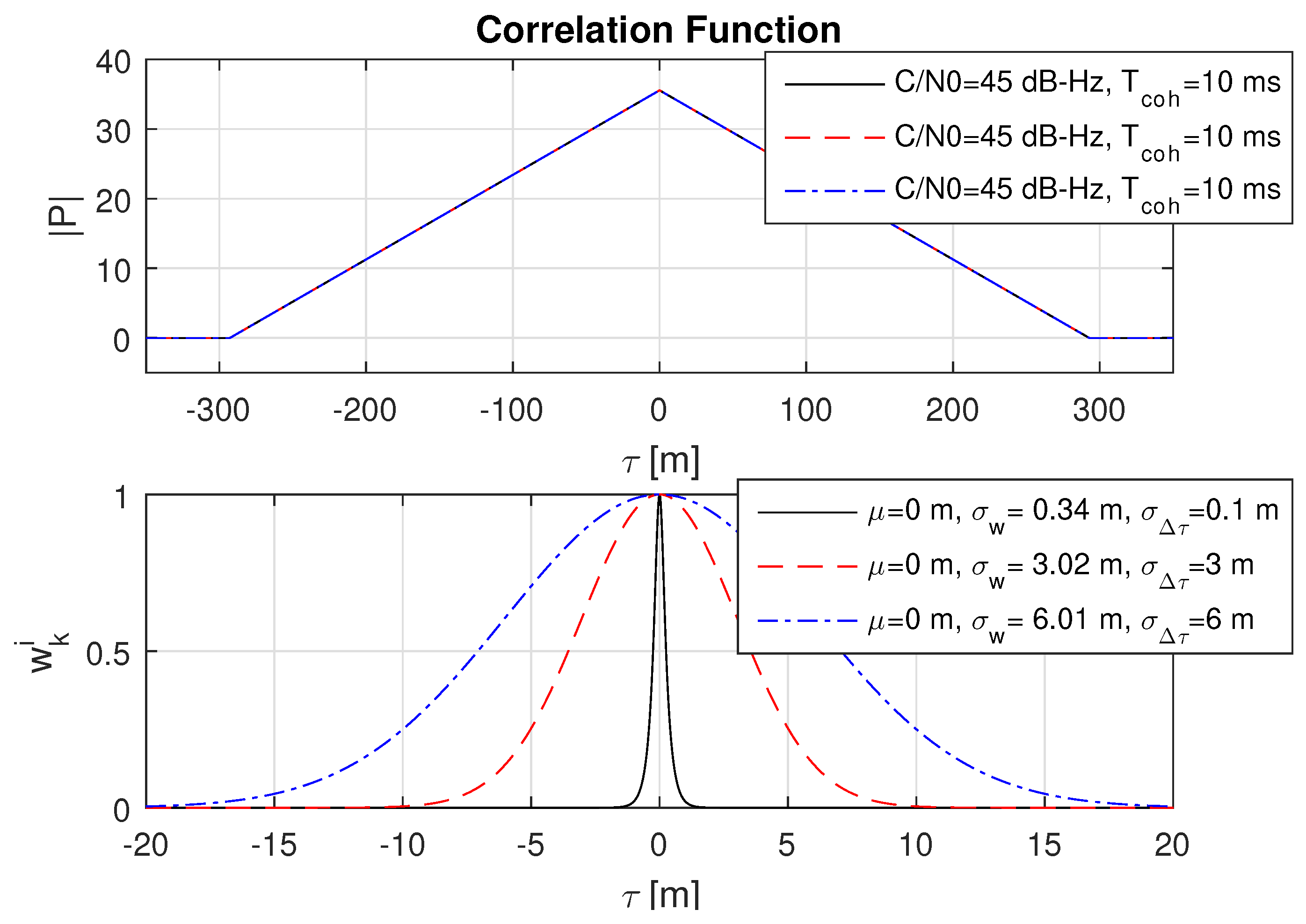
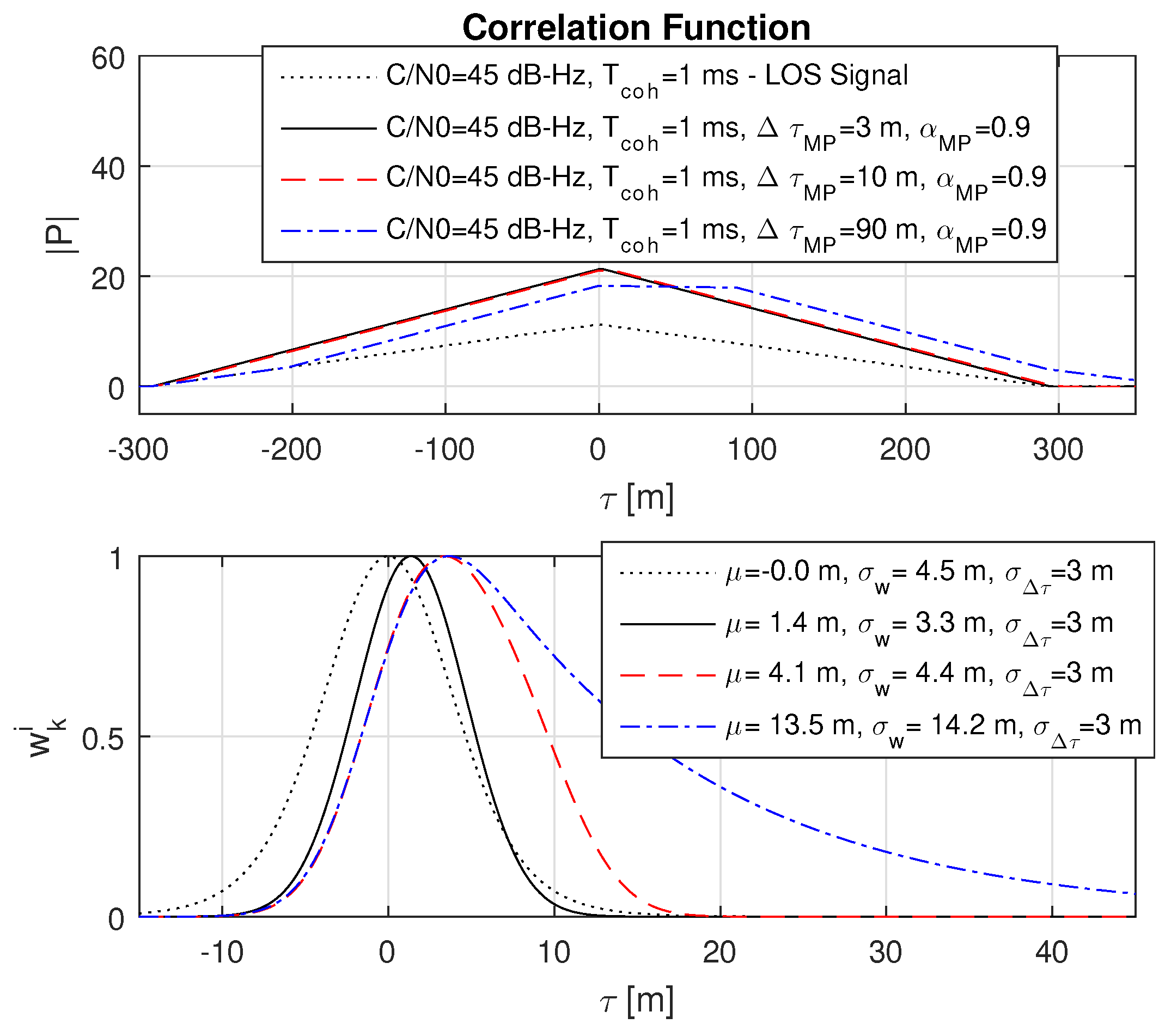
8.4. Impact of Short, Medium and Far Multipath
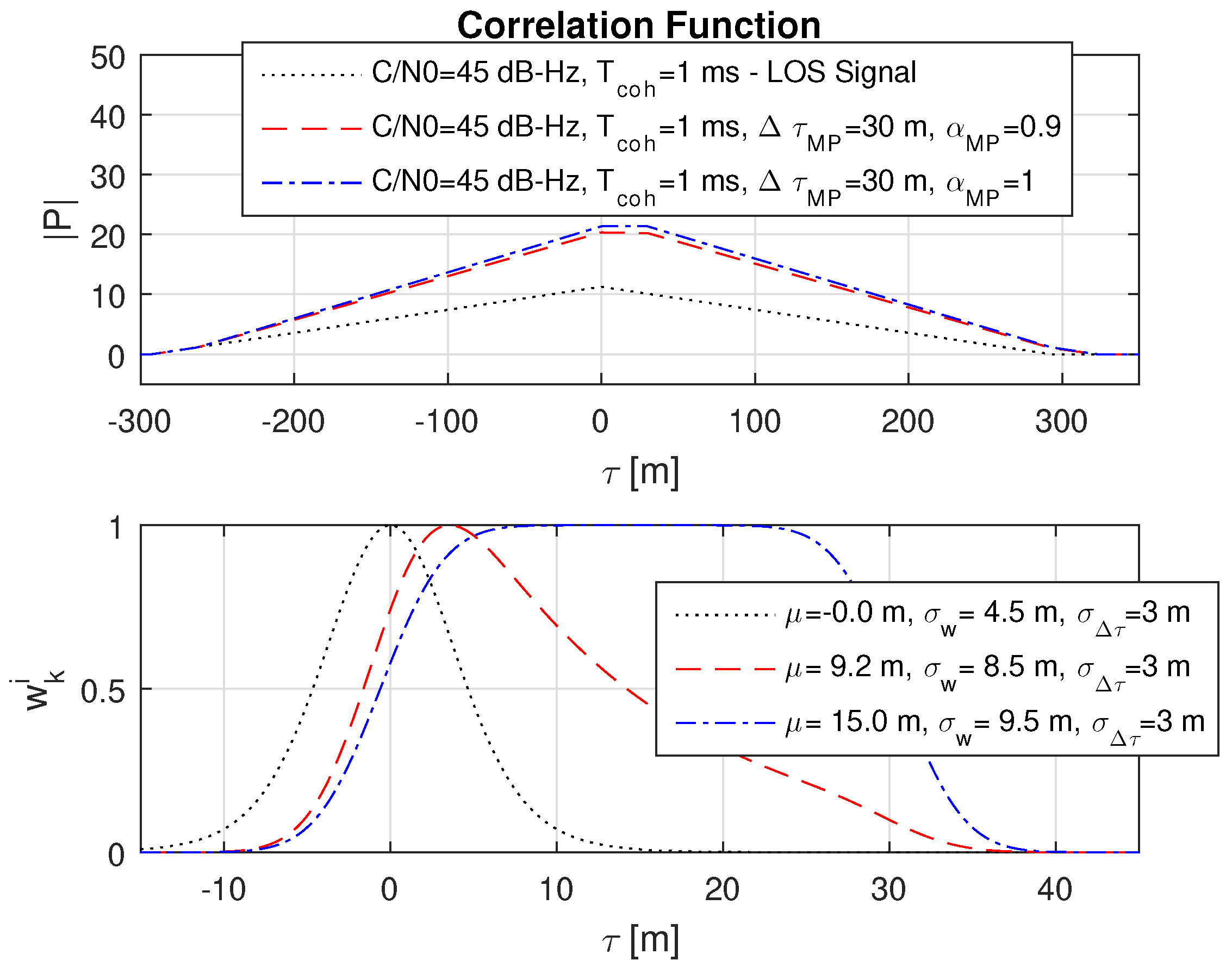
8.5. Impact of Different Multipath Amplitudes
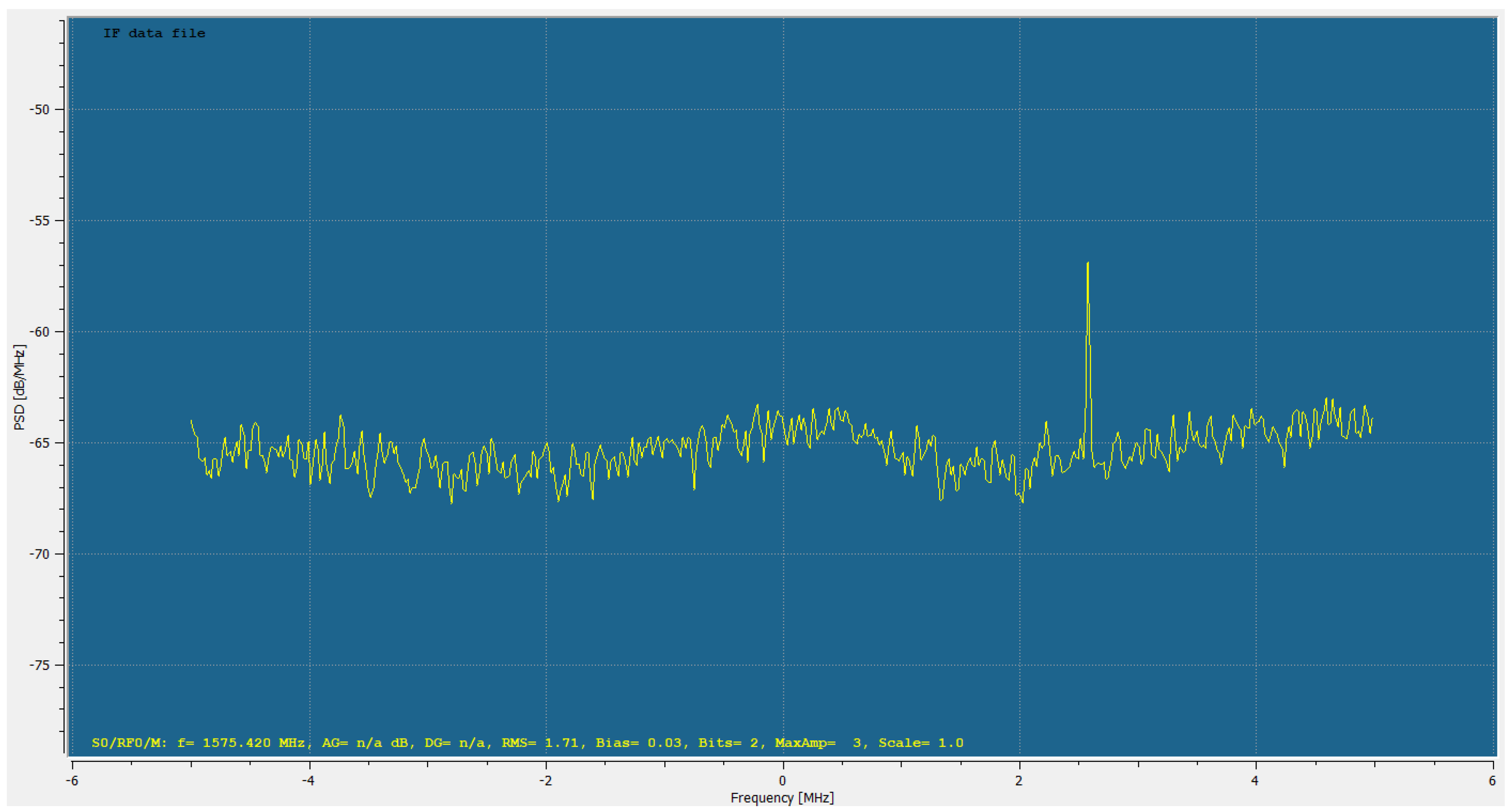
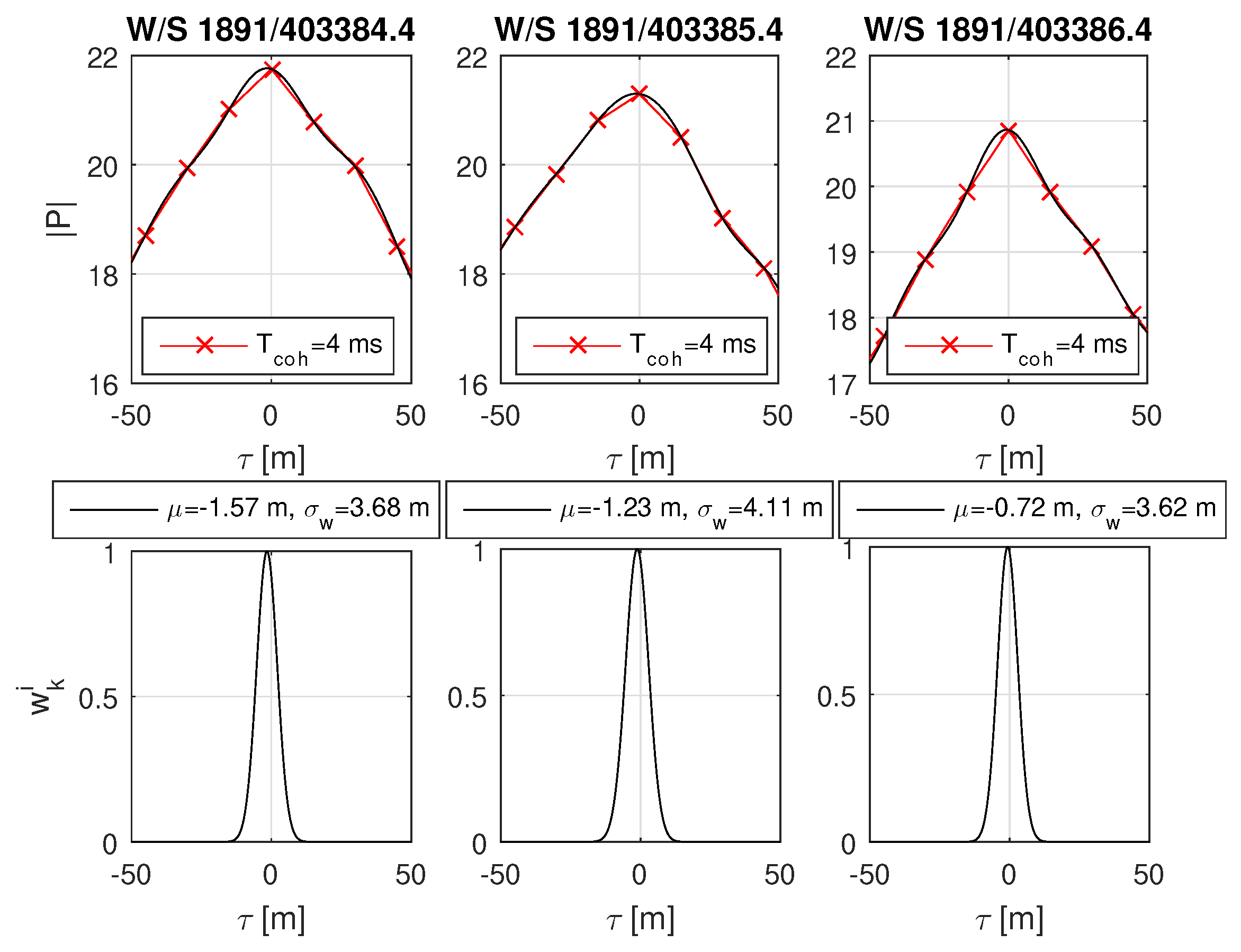
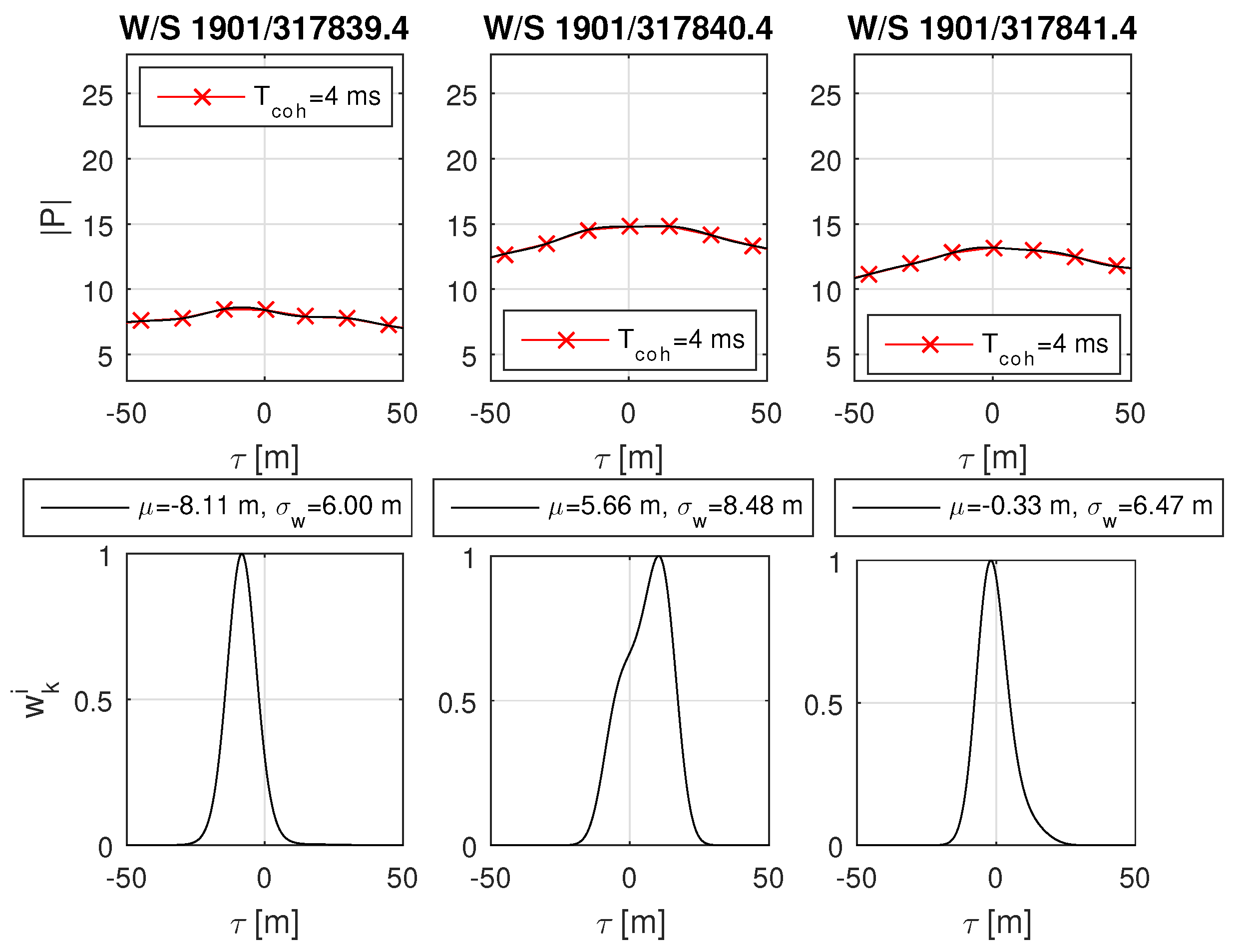
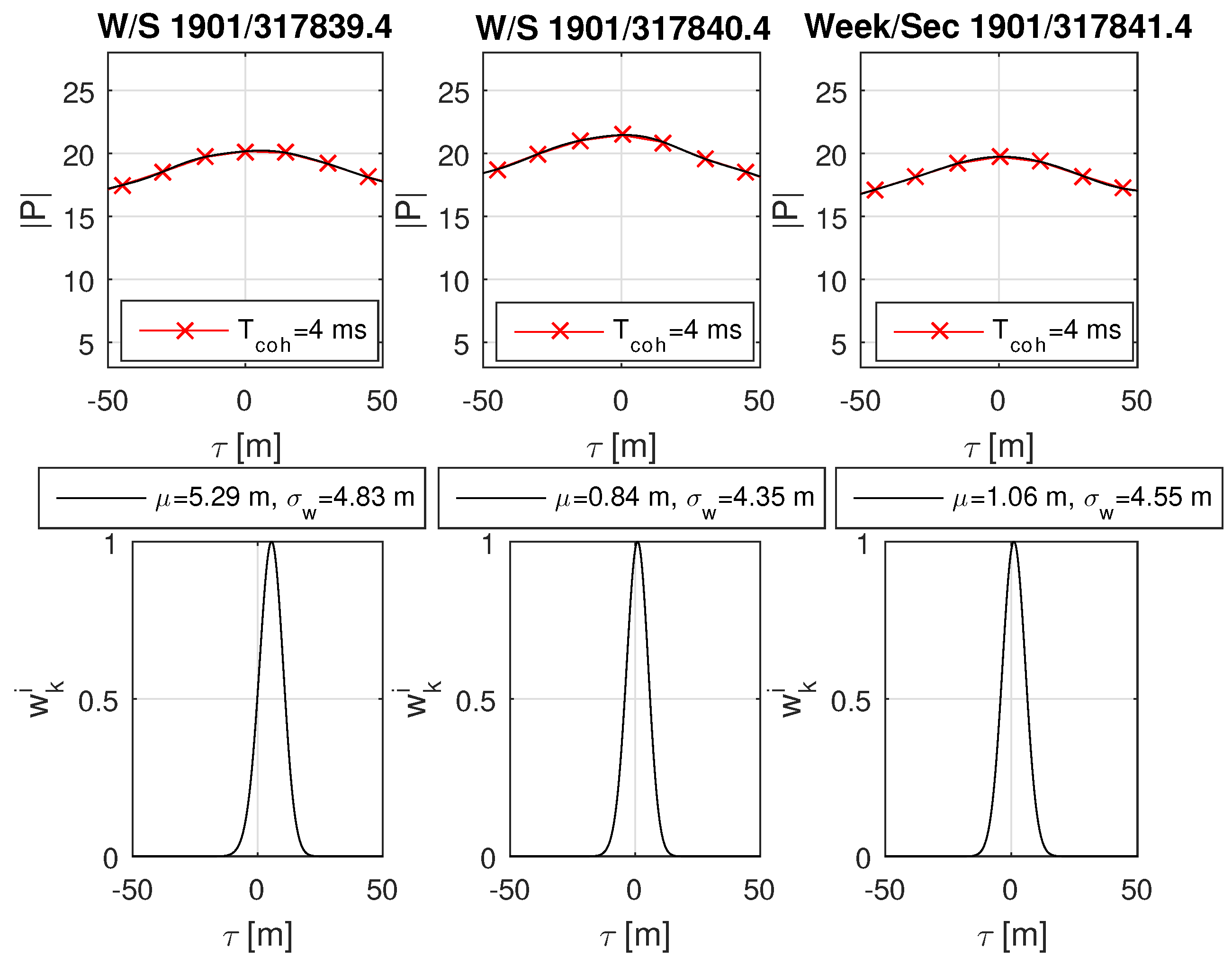
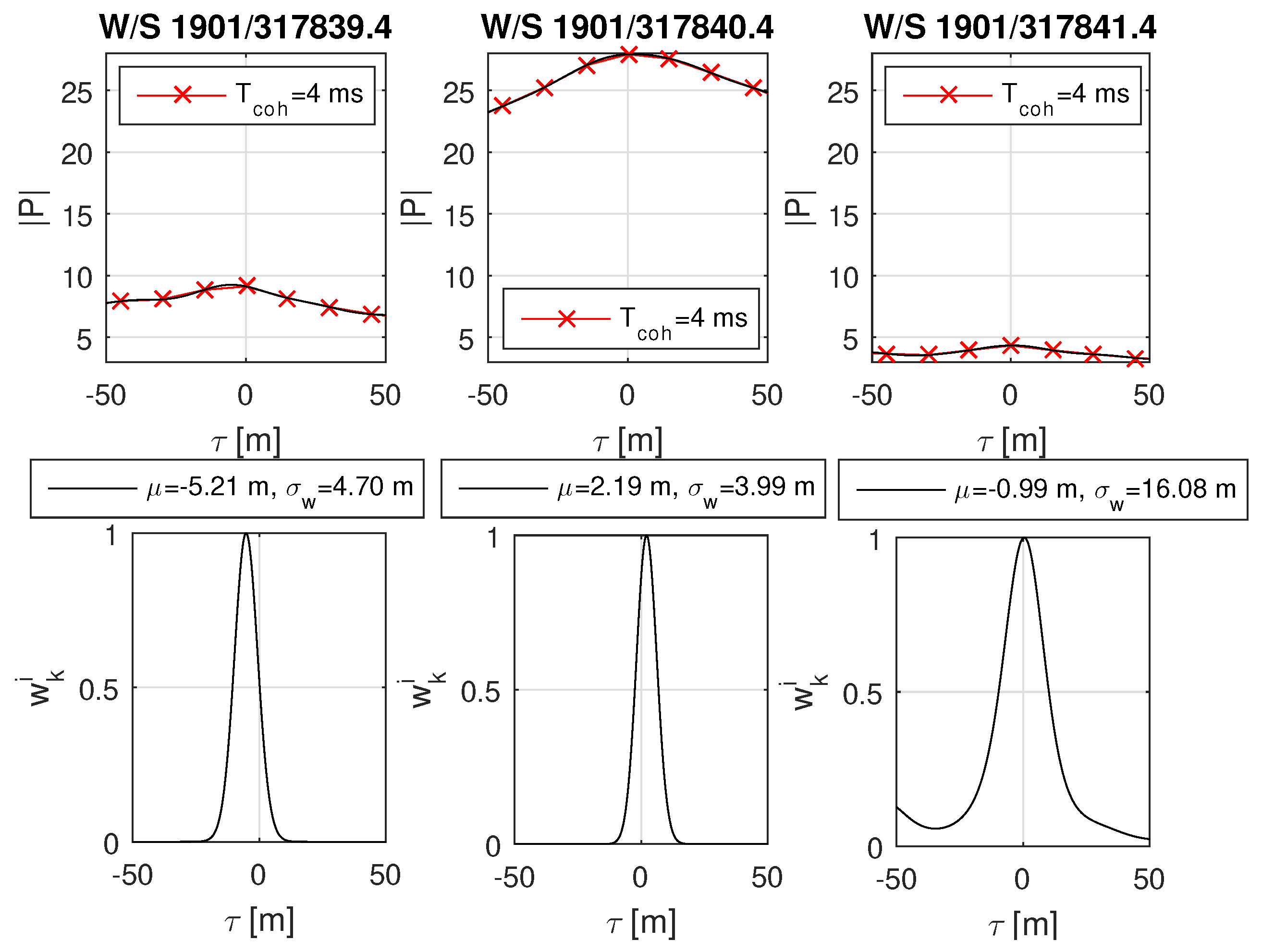
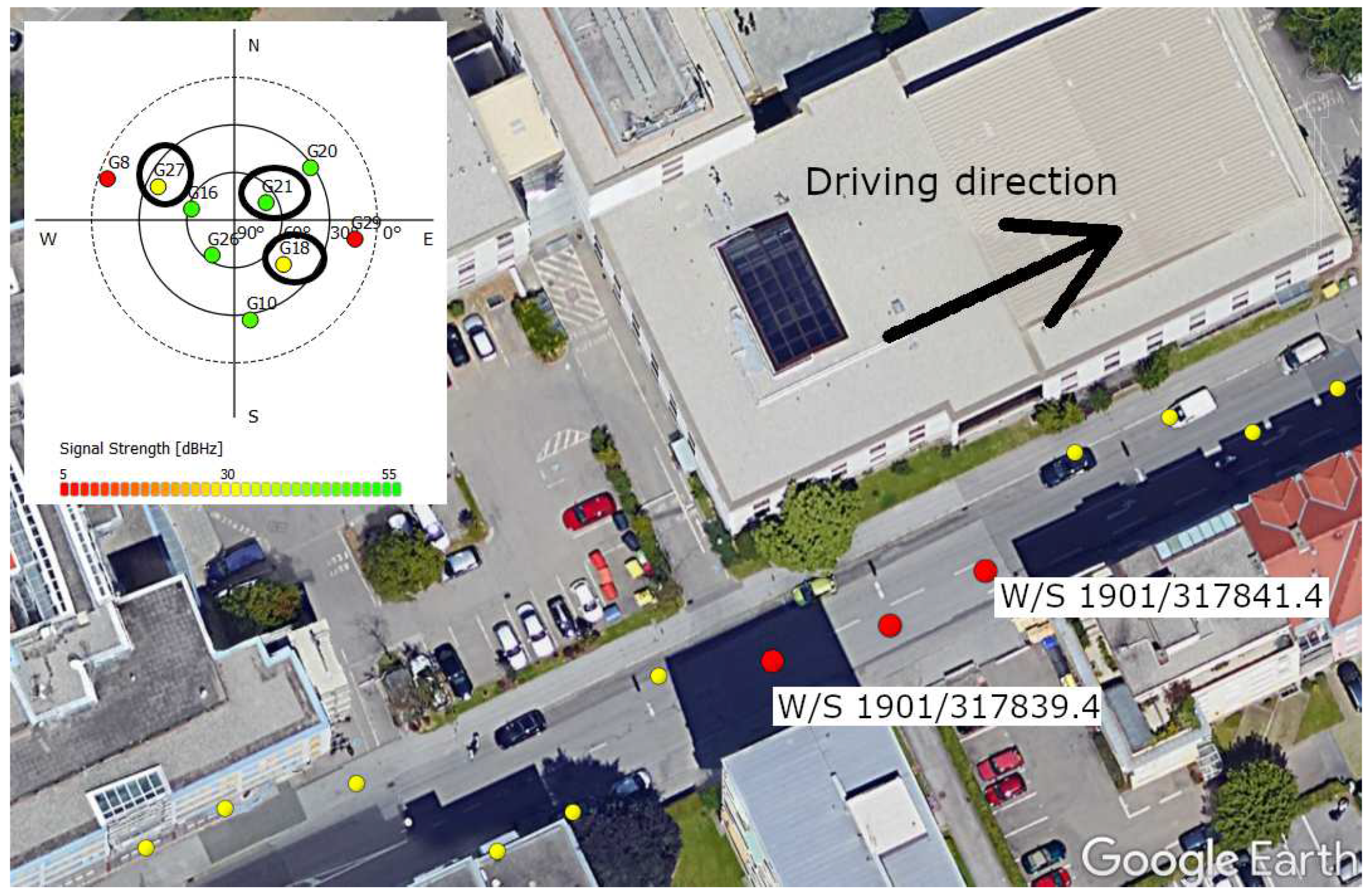
8.6. Real-World Open Sky and Urban Scenario
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DPE | Direct Position Estimation |
| BDPE | Bayesian Direct Position Estimation |
| GNSS | Global Navigation Satellite System |
| PVT | Position, Velocity and Time |
| BPSK(1) | Binary Phase Shift Keying (with 1.023 MHz code rate) |
| SMC | Sequential Monte Carlo |
| EKF | Extended Kalman Filter |
| LTE | Long-Term Evolution |
| LOS | Line of Sight |
| VTL | Vector Tracking Loop |
| MC | Multi-Correlator |
| GPS | Global Positioning System |
| PF | Particle Filter |
| C/A | Coarse/Acquisition codes |
| RF | Radio Frequency |
| IF | Intermediate Frequency |
| ADC | Analogue to Digital Converter |
| USB | Universal Serial Bus |
| FFT | Fast Fourier Transform |
| CRLB | Cramér–Rao Lower Bound |
| AGC | Automatic Gain Control |
| CW | Continuous Wave |
| BW | Bandwidth |
| LAT | Latitude |
| LON | Longitude |
| RMS | Root Mean Square |
| PRN | Pseudo-Random-Noise |
References
- Misra, P.; Enge, P. Global Positioning Systems: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2010. [Google Scholar]
- Van Diggelen, F. GPS Accuracy: Lies, Damn Lies, and Statistics; GPS World: Cleveland, OH, USA, 1998. [Google Scholar]
- Viandier, N.; Nahimana, D.; Marais, J.; Duflos, E. GNSS Performance Enhancement in Urban Environment Based on Pseudo-range Error Model. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5–8 May 2008; pp. 377–382. [Google Scholar] [CrossRef]
- Bin Ahmad, K.A.; Sahmoudi, M.; Macabiau, C. Characterization of GNSS Receiver Position Errors for User Integrity Monitoring in Urban Environments. In Proceedings of the ENC-GNSS 2014, European Navigation Conference, Rotterdam, The Netherlands, 14–17 April 2014. [Google Scholar]
- Zhu, N.; Marais, J.; Betaille, D.; Berbineau, M. GNSS Position Integrity in Urban Environments: A Review of Literature. IEEE Trans. Intell. Transp. Syst. 2018, 1–17. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte Carlo Filter and Smoother for Non-Gaussian Nonlinear State Space Models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Kanazawa, K.; Koller, D.; Russell, S. Stochastic simulation algorithms for dynamic probabilistic networks. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; pp. 346–351. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Gordon, N.; Salmond, D.; Smith, A. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F Radar Signal Process. 1993, 140, 107. [Google Scholar] [CrossRef]
- MacCormick, J.; Blake, A. A probabilistic exclusion principle for tracking multiple objects. In Proceedings of the Seventh IEEE Inernational Conference on Computer Vision(ICCV99), Kerkyra, Greece, 20–27 September 1999; pp. 572–578. [Google Scholar] [CrossRef]
- Roi, Y.; Boaz Ben, M. A Robust Shadow Matching Algorithm for GNSS Positioning. NAVIGATION J. Inst. Navig. 2014, 62, 95–109. [Google Scholar]
- Gentner, C.; Rawadi, J.M.; Muñoz Diaz, E.; Khider, M. Hybrid Positioning with 3GPP-LTE and GPS employing Particle Filters. In Proceedings of the ION GNSS 2012, Nashville, TN, USA, 17–21 September 2012; pp. 473–481. [Google Scholar]
- Hafner, P. Development of a Positioning Filter for the Smartphone-Based Navigation of Visually Impaired People. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2015. [Google Scholar]
- Closas, P.; Fernandez-Prades, C.; Bernal, D.; Fernandez–Rubio, J. Bayesian direct position estimation. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, Georgia, 16–19 September 2008; pp. 183–190. [Google Scholar]
- Closas, P. Bayesian Signal Processing Techniques for GNSS Receivers. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2009. [Google Scholar]
- Closas, P.; Gusi-Amigó, A. Direct Position Estimation of GNSS Receivers: Analyzing main results, architectures, enhancements, and challenges. IEEE Signal Process. Mag. 2017, 34, 72–84. [Google Scholar] [CrossRef]
- Axelrad, P.; Bradley, B.K.; Donna, J.; Mitchell, M.; Mohiuddin, S. Collective Detection and Direct Positioning Using Multiple GNSS Satellites. Navigation 2011, 58, 305–321. [Google Scholar] [CrossRef]
- He, Z.; Petovello, M. Joint Detection and Estimation of Weak GNSS Signals with Application to Coarse Time Navigation. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, Florida, 8–12 September 2014; pp. 1554–1567. [Google Scholar]
- Esteves, P.; Mohamed, S.; Ries, L. Collective Detection of Multi-GNSS Signals. Inside GNSS 2014, 54–65. [Google Scholar]
- Ng, Y.; Gao, G.X. Joint GPS and vision direct position estimation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, PLANS 2016, Savannah, GA, USA, 11–14 April 2016; pp. 380–385. [Google Scholar] [CrossRef]
- Ng, Y.; Member, S.; Gao, G.X.; Member, S. Robust GPS-Based Direct Time Estimation for PMUs. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 472–476. [Google Scholar]
- Ng, Y.; Gao, G.X. Mitigating jamming and meaconing attacks using direct GPS positioning. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, PLANS 2016, Savannah, GA, USA, 11–14 April 2016; pp. 1021–1026. [Google Scholar] [CrossRef]
- Dampf, J.; Witternigg, N.; Schwinzerl, M.; Lesjak, R.; Schönhuber, M.; Obertaxer, G.; Pany, T. Particle Filter Algorithms and Experiments for High Sensitivity GNSS Receivers. In Proceedings of the 6th International Colloquium—Scientific and Fundamental Aspects of GNSS/Galileo, Valencia, Spain, 25–27 October 2017. [Google Scholar]
- Massey, B. Fast perfect weighted resampling. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3457–3460. [Google Scholar] [CrossRef]
- Won, J.H.; Eissfeller, B.; Pany, T. Implementation, Test and Validation of a Vector-Tracking-Loop with the ipex Software Receiver. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011. [Google Scholar]
- Stöber, C.; Kneissel, F.; Eissfeller, B.; Pany, T. Analysis and Verification of Synthetic Multicorrelators. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 19–23 September 2011; pp. 2060–2069. [Google Scholar]
- Pany, T. Navigation Signal Processing for GNSS Software Receivers, 1st ed.; Artech House: Norwood, MA, USA, 2010; pp. 1–352. [Google Scholar]
- SX3 GNSS Software Receiver, Version 3.3.0, IFEN GmbH: Poing, Germany, 2018.
- Mathematica, Version 11.3, Wolfram Research Inc.: Champaign, IL, USA, 2018.
- Microsoft Developer Network (MSDN), Microsoft Corporation: Washington, DC, USA, 2018.
- MATLAB, Release 2015b, The MathWorks Inc.: Natick, MA, USA, 2018.
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dampf, J.; Frankl, K.; Pany, T. Optimal Particle Filter Weight for Bayesian Direct Position Estimation in a GNSS Receiver. Sensors 2018, 18, 2736. https://doi.org/10.3390/s18082736
Dampf J, Frankl K, Pany T. Optimal Particle Filter Weight for Bayesian Direct Position Estimation in a GNSS Receiver. Sensors. 2018; 18(8):2736. https://doi.org/10.3390/s18082736
Chicago/Turabian StyleDampf, Jürgen, Kathrin Frankl, and Thomas Pany. 2018. "Optimal Particle Filter Weight for Bayesian Direct Position Estimation in a GNSS Receiver" Sensors 18, no. 8: 2736. https://doi.org/10.3390/s18082736
APA StyleDampf, J., Frankl, K., & Pany, T. (2018). Optimal Particle Filter Weight for Bayesian Direct Position Estimation in a GNSS Receiver. Sensors, 18(8), 2736. https://doi.org/10.3390/s18082736