High-Precision Detection of Defects of Tire Texture Through X-ray Imaging Based on Local Inverse Difference Moment Features
Abstract
1. Introduction
2. Background and Related Works
3. Proposed Texture Descriptor Based on GLCM
3.1. Texture Feature Extraction Based on GLCM
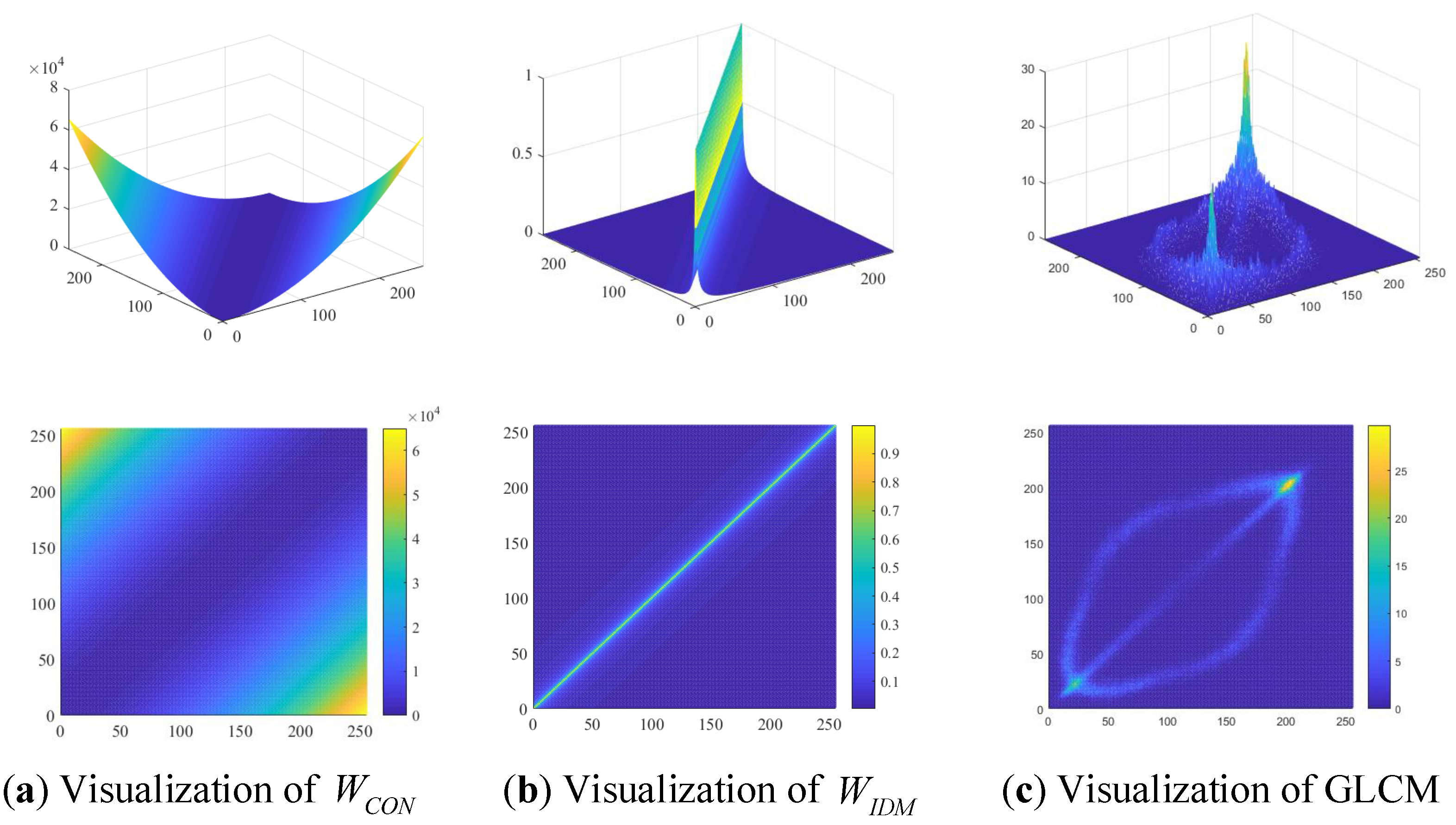
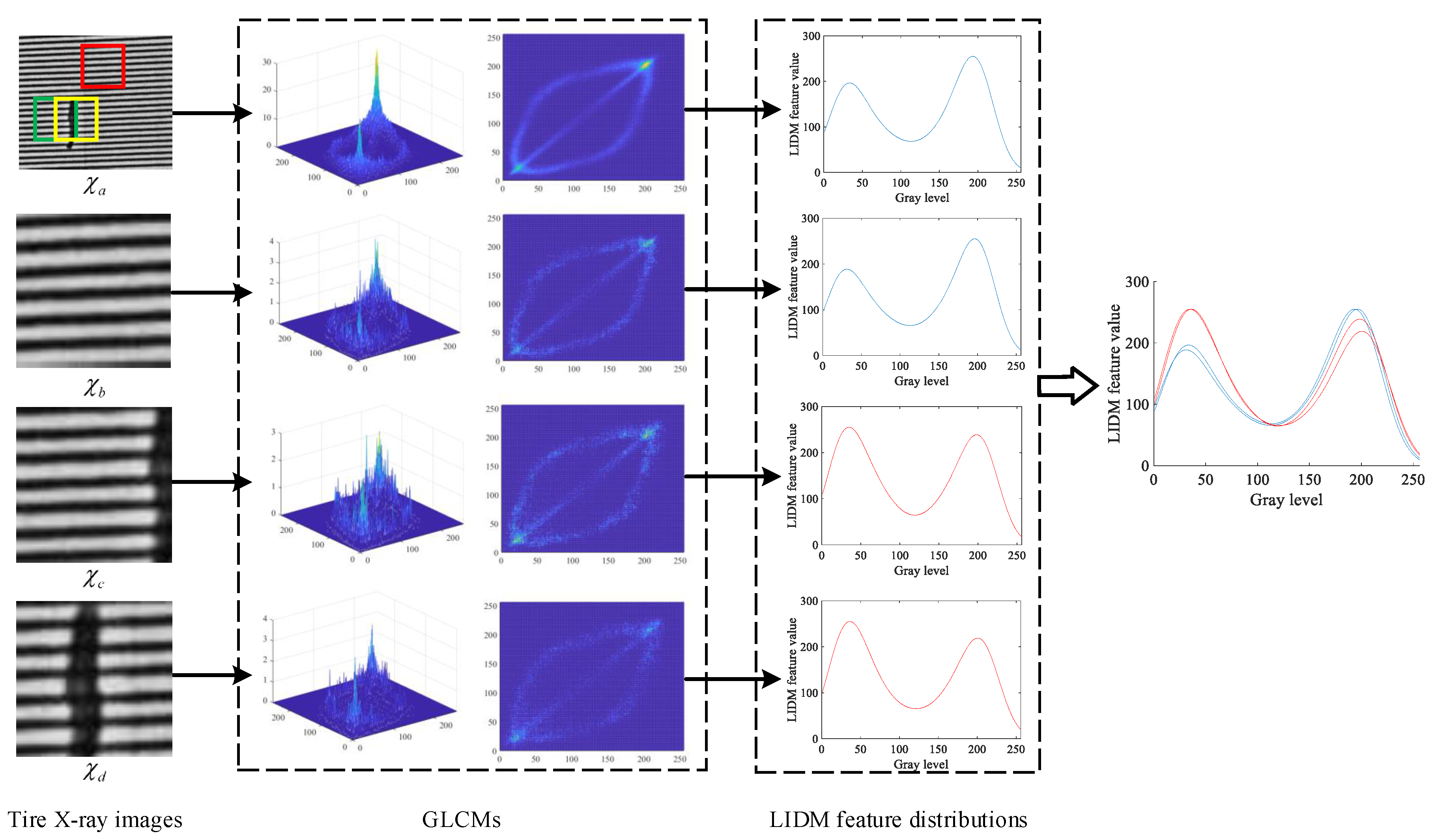
3.2. Visualization and Characteristic Analysis of GLCM
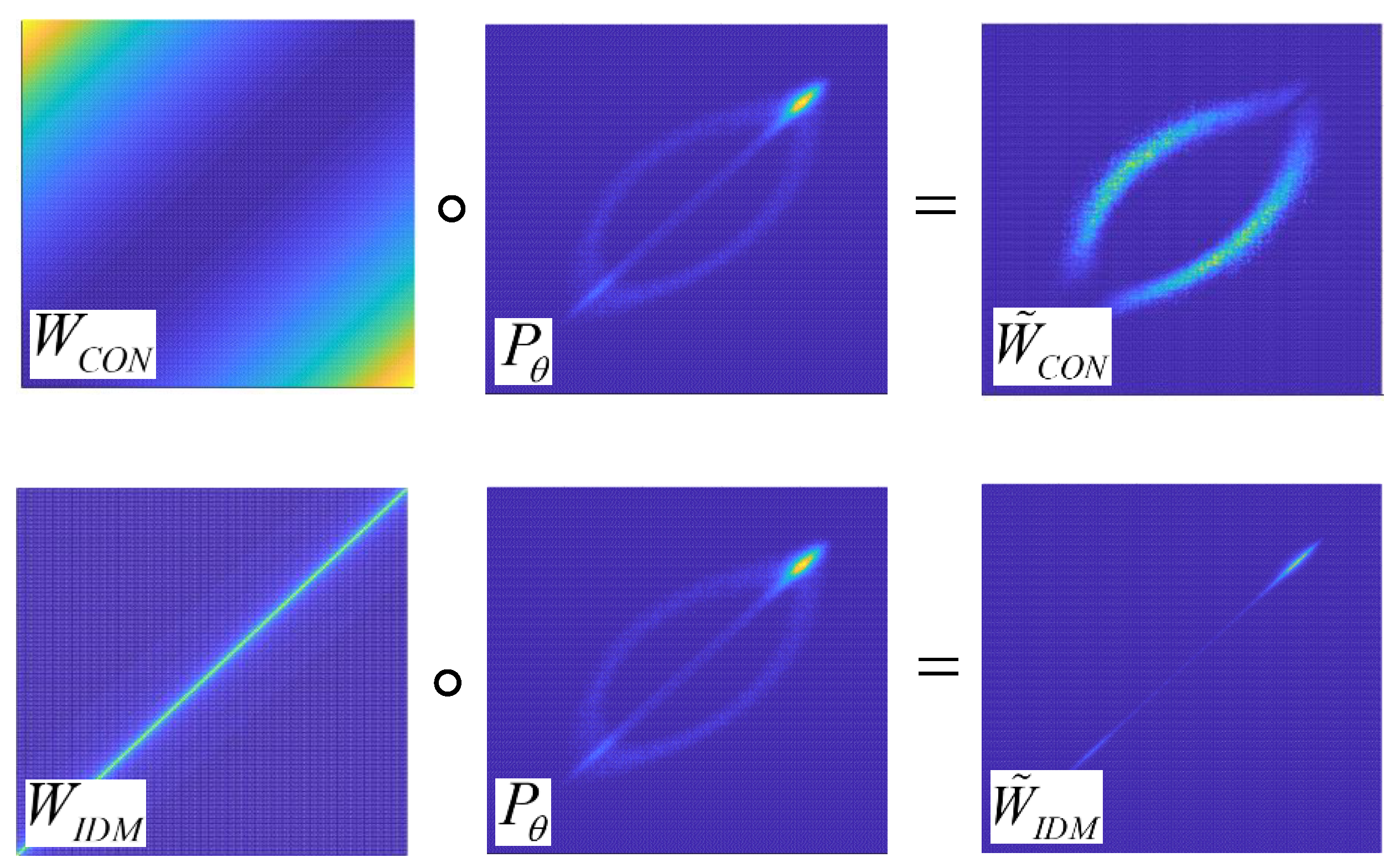
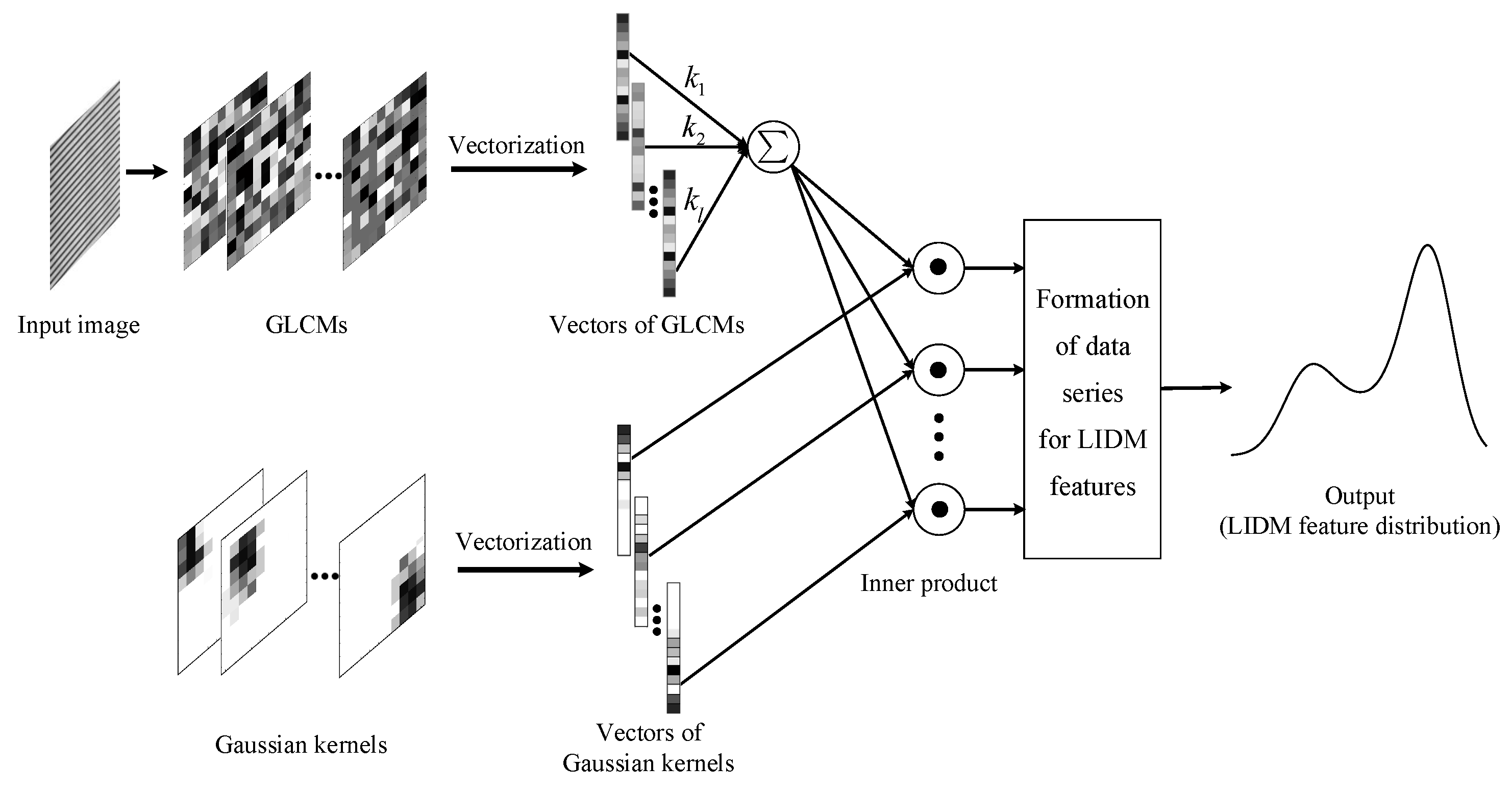
3.3. Texture Descriptor of Tire X-ray Image Based on LIDM Feature
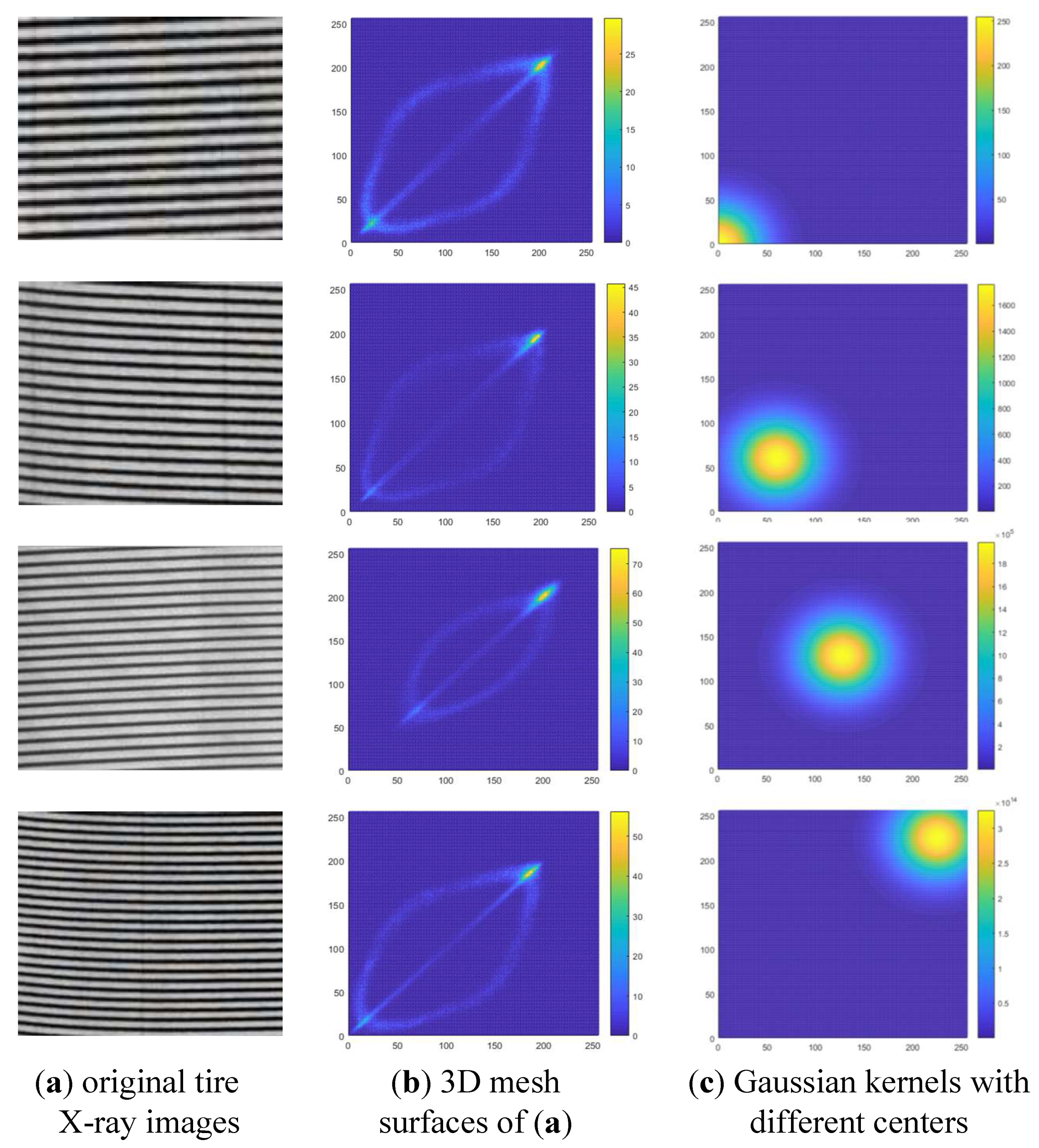
3.4. Representing Characteristics of Defects in Proposed Texture Descriptor
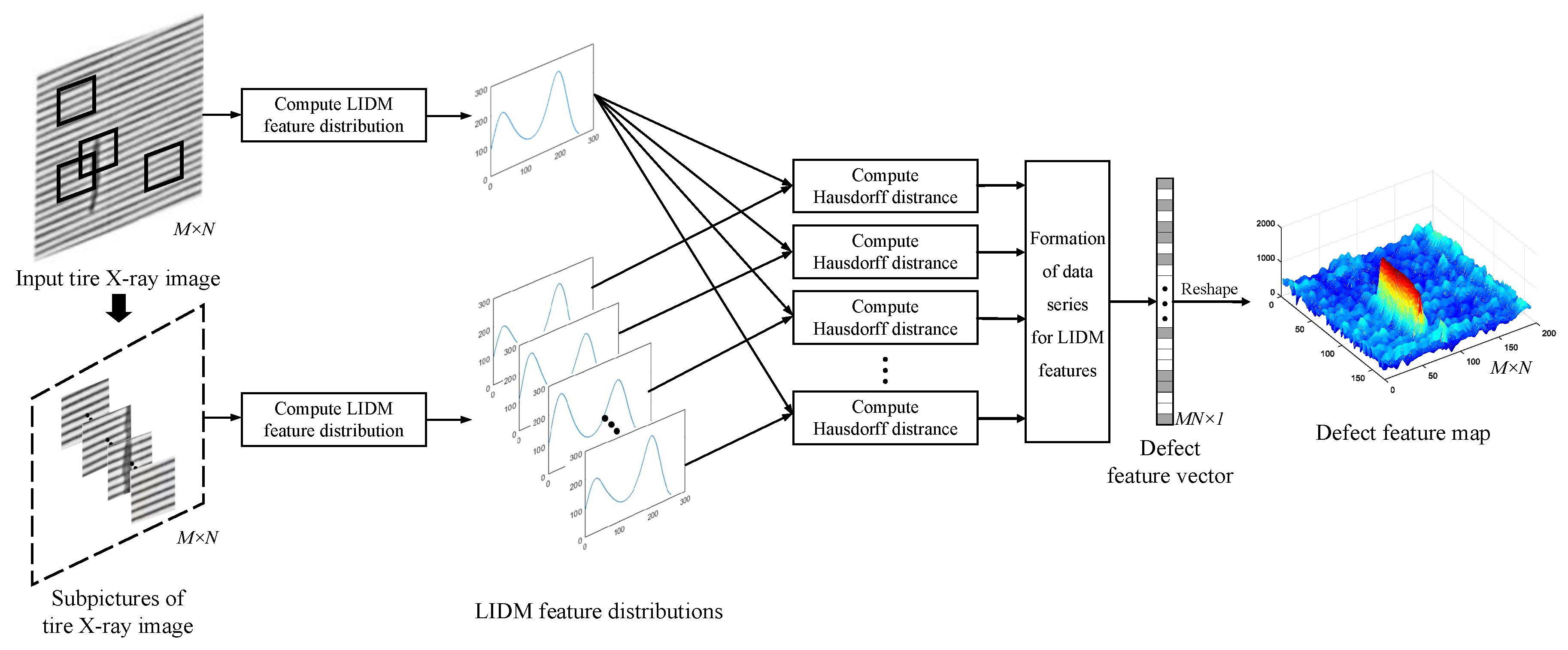
4. Detection Algorithm of Tire Texture Defects
4.1. Construction of Defect Feature Map Based on Texture Descriptor
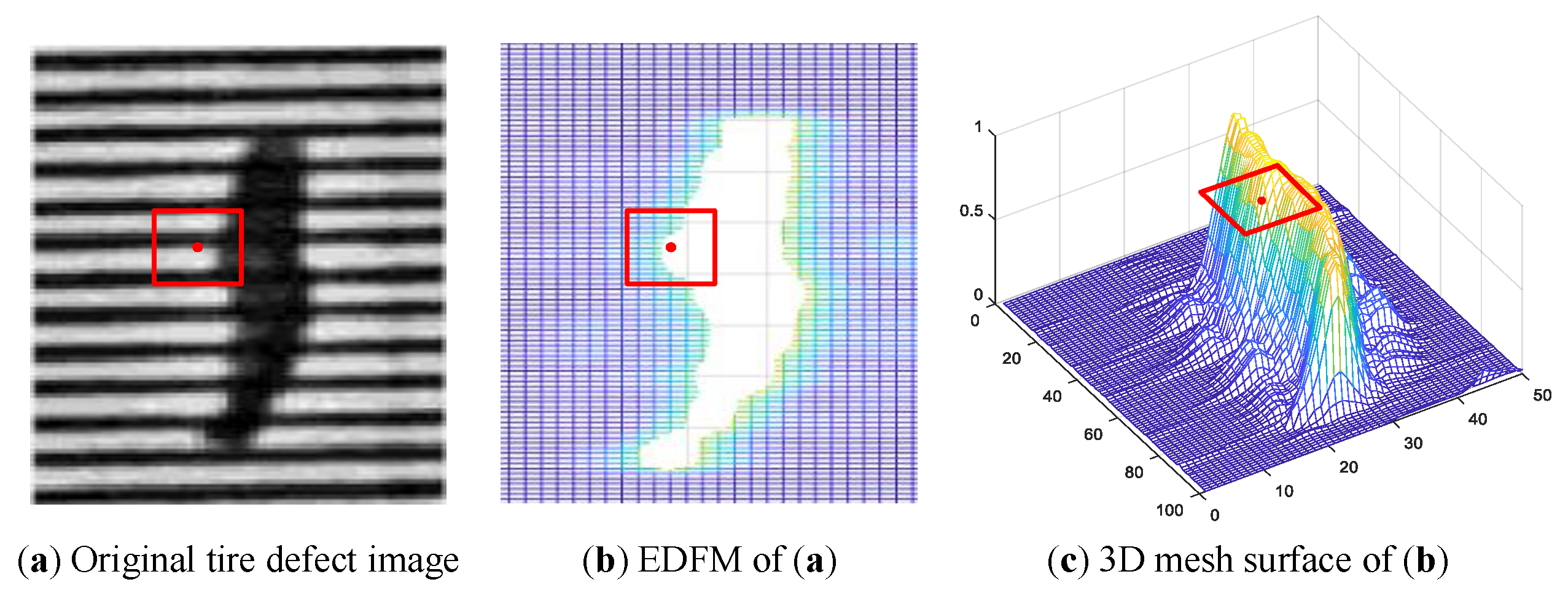
4.2. Enhancement of Defect Features Based on Background Suppression
- (1)
- The feature values of defects are always much greater than that of background, except that some feature values in the background are great enough to affect the performance of detection algorithm.
- (2)
- The feature values in the background always fluctuate in a large range, but most of these feature values are distributed below a certain level, which is marked by the red line in Figure 7.
- (3)
- The defect region makes up only a small portion of the whole tire X-ray image, on the contrary, the background takes up most of the tire X-ray image.
4.3. Detection Algorithm of Defects with Defect Feature Map
| Algorithm 1 Detection algorithm of defects of tire X-ray image |
| Input: Original tire X-ray image I, defect feature map Output: Mask result of defect detection algorithm Method:
|
4.4. Performance Analysis and Comments
5. Experimental Results and Assessment
5.1. Experiment Scheme and Parameters Setting
5.2. Experimental Results and Comparative Analysis
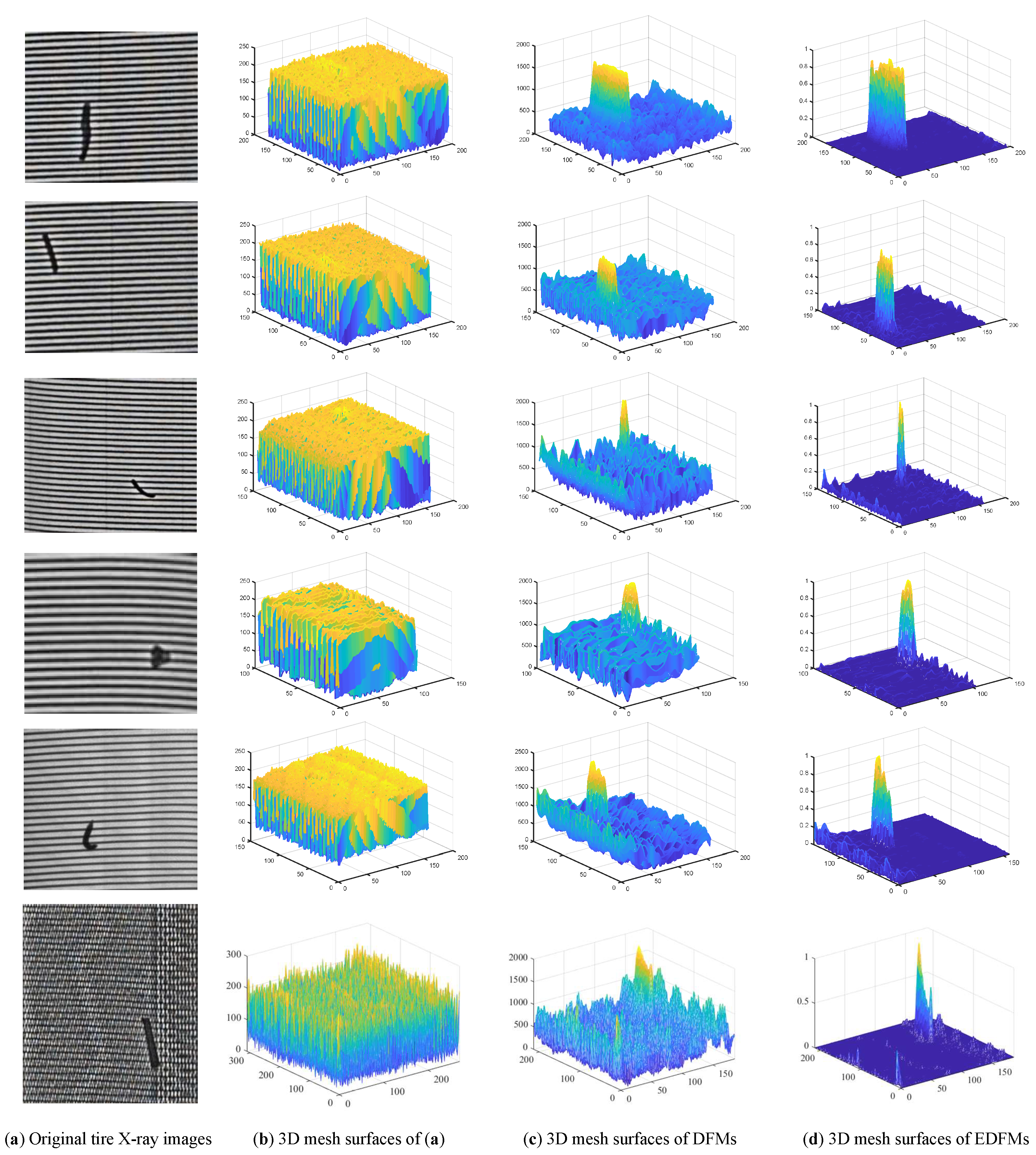
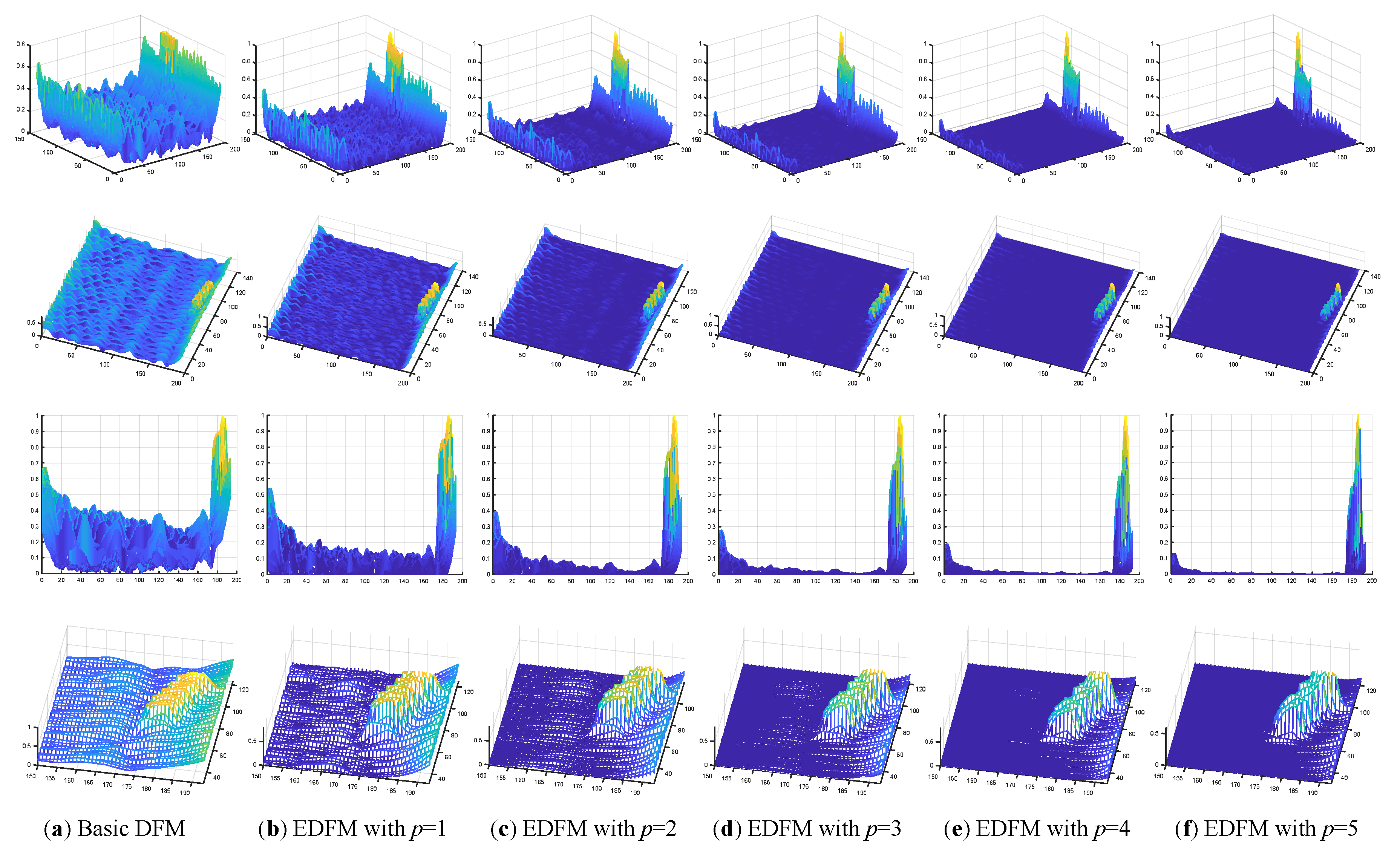
5.2.1. Experiment Towards Construction of Defect Feature Map
5.2.2. Experiment Towards Detection Performance of Defects
5.2.3. Comparative Analysis and Remarks
5.3. Evaluation Metrics and Performance Assessment
5.4. Comparative Experiments with State-of-the-Art Methods
6. Discussion and Comments
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Guo, Q.; Zhang, C.; Liu, H.; Zhang, X. Defect Detection in Tire X-Ray Images Using Weighted Texture Dissimilarity. J. Sens. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Aryan, P.; Sampath, S.; Sohn, H. An Overview of Non-Destructive Testing Methods for Integrated Circuit Packaging Inspection. Sensors 2018, 18, 7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lefebvre, D.; Li, Q. Automatic Detection of Defects in Tire Radiographic Images. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1378–1386. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K. Computer Classification of Reservoir Sandstones. IEEE Trans. Geosci. Electron. 1973, 11, 171–177. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, T.W.; Pahk, H.J. Robust defect detection method for a non-periodic TFT-LCD pad area. Int. J. Precis. Eng. Manuf. 2017, 18, 1093–1102. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Yan, Y.H.; Song, K.C. Vision-based automatic detection of steel surface defects in the cold rolling process: considering the influence of industrial liquids and surface textures. Int. J. Adv. Manuf. Technol. 2017, 90, 1665–1678. [Google Scholar] [CrossRef]
- Zhu, D.; Pan, R.; Gao, W.; Zhang, J. Yarn-Dyed Fabric Defect Detection Based On Autocorrelation Function And GLCM. Autex Res. J. 2015, 15, 226–232. [Google Scholar] [CrossRef]
- Amet, A.L.; Ertuzun, A.; Ercil, A. Texture defect detection using subband domain co-occurrence matrices. In Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation, Tucson, AZ, USA, 5–7 April 1998; pp. 205–210. [Google Scholar]
- Raheja, J.L.; Kumar, S.; Chaudhary, A. Fabric defect detection based on GLCM and Gabor filter: A comparison. Optik 2013, 124, 6469–6474. [Google Scholar] [CrossRef]
- Chaudhuri, B.B.; Sarkar, N. An efficient approach to compute fractal dimension in texture image. In Proceedings of the 11th IAPR International Conference on Pattern Recognition, Hague, The Netherlands, 30 August–3 September 1992; pp. 358–361. [Google Scholar]
- Tsai, D.M.; Lin, C.P. Fast Defect Detection in Textured Surfaces Using 1D Gabor Filters. Int. J. Adv. Manuf. Technol. 2002, 20, 664–675. [Google Scholar] [CrossRef]
- Bissi, L.; Baruffa, G.; Placidi, P.; Ricci, E.; Scorzoni, A.; Valigi, P. Automated defect detection in uniform and structured fabrics using Gabor filters and PCA. J. Vis. Commun. Image Represent. 2013, 24, 838–845. [Google Scholar] [CrossRef]
- Chan, H.; Raju, C.; SariSarraf, H.; Hequet, E.F. A general approach to defect detection in textured materials using a wavelet domain model and level sets. Proc. SPIE Int. Soc. Opt. Eng. 2005, 6001, 309–310. [Google Scholar]
- Li, Y.; Zhao, W.; Pan, J. Deformable Patterned Fabric Defect Detection with Fisher Criterion-Based Deep Learning. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1256–1264. [Google Scholar] [CrossRef]
- Mei, S.; Wang, Y.; Wen, G. Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model. Sensors 2018, 18, 1064. [Google Scholar] [CrossRef] [PubMed]
- Bennamoun, M.; Bodnarova, A. Automatic visual inspection and flaw detection in textile materials: Past, present and future. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 14 October 1998; pp. 4340–4343. [Google Scholar]
- Zhou, J.; Wang, J.; Bu, H. Fabric Defect Detection Using a Hybrid and Complementary Fractal Feature Vector and FCM-based Novelty Detector. Fibres Text. East. Eur. 2017, 25, 46–52. [Google Scholar] [CrossRef]
- Gururajan, A.; Hequet, E.F.; Sari-Sarraf, H. Objective Evaluation of Soil Release in Fabrics. Text. Res. J. 2008, 78, 782–795. [Google Scholar] [CrossRef]
- Ngan, H.Y.T.; Pang, G.K.H.; Yung, N.H.C. Review article: Automated fabric defect detection—A review. Image Vis. Comput. 2011, 29, 442–458. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 39, 640–651. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Szegedy, C.; Toshev, A.; Erhan, D. Deep Neural Networks for object detection. Adv. Neural Inf. Process. Syst. 2013, 26, 2553–2561. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Weimer, D.; Scholz-Reiter, B.; Shpitalni, M. Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection. CIRP Ann. Manuf. Technol. 2016, 65, 417–420. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y.; Qiao, M.; Snoussi, H. A fast and robust convolutional neural network-based defect detection model in product quality control. Int. J. Adv. Manuf. Technol. 2018, 94, 3465–3471. [Google Scholar] [CrossRef]
- Park, S.; Kim, B.; Lee, J.; Jin, M.G.; Shin, Y.G. GGO Nodule Volume-Preserving Nonrigid Lung Registration Using GLCM Texture Analysis. IEEE Trans. Biomed. Eng. 2011, 58, 2885–2894. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Yan, G.R.; Sun, M.; Di, T.T.; Wang, S.; Zhai, J.; Zhao, Z. The Effects of GLCM parameters on LAI estimation using texture values from Quickbird Satellite Imagery. Sci. Rep. 2017, 7, 7366. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Thomas, G.; Williams, D. Detection of Ice on Power Cables Based on Image Texture Features. IEEE Trans. Instrum. Meas. 2018, 67, 497–504. [Google Scholar] [CrossRef]
- Ou, X.; Pan, W.; Xiao, P. In vivo skin capacitive imaging analysis by using grey level co-occurrence matrix (GLCM). Int. J. Pharm. 2014, 460, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Gan, Y.; Lin, B.; Zhang, Q.; Chang, H. An active contour model based on fused texture features for image segmentation. Neurocomputing 2015, 151, 1133–1141. [Google Scholar] [CrossRef]
- Zhang, X.; Cui, J.; Wang, W.; Lin, C. A Study for Texture Feature Extraction of High-Resolution Satellite Images Based on a Direction Measure and Gray Level Co-Occurrence Matrix Fusion Algorithm. Sensors 2017, 17, 1474. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Kao, C.Y.; Gore, J.C.; Ding, Z. Implicit Active Contours Driven by Local Binary Fitting Energy. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–7. [Google Scholar]
- Jia, L.; Chen, C.; Liang, J.; Hou, Z. Fabric defect inspection based on lattice segmentation and Gabor filtering. Neurocomputing 2017, 238, 84–102. [Google Scholar] [CrossRef]




| Distance | LIDM Features | ||||
|---|---|---|---|---|---|
| LIDM Features | |||||
| 0 | 130.35 | 474.59 | 536.70 | ||
| 130.35 | 0 | 494.25 | 545.76 | ||
| 474.59 | 494.25 | 0 | 164.43 | ||
| 536.70 | 545.76 | 164.43 | 0 | ||
| Detection Time (sec) | Image | Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | Image 6 |
|---|---|---|---|---|---|---|---|
| Different Algorithms | |||||||
| DFM + ACWE [36] | 13.54 | 45.94 | 55.97 | 5.3 | 32.25 | 13.99 | |
| DFM + LBFACM [37] | 45 | 52.18 | 19.03 | 9.75 | 21.87 | 18.57 | |
| DFM + TSWD | 1.12 | 0.81 | 0.77 | 0.35 | 0.74 | 1.39 | |
| EDFM + ACWE [36] | 13.95 | 45.61 | 54.5 | 5.21 | 7.88 | 13.32 | |
| EDFM + LBFACM [37] | 17.01 | 3.24 | 8.31 | 3.56 | 11.2 | 14.17 | |
| EDFM + TSWD | 1.18 | 0.78 | 0.76 | 0.34 | 0.75 | 1.33 | |
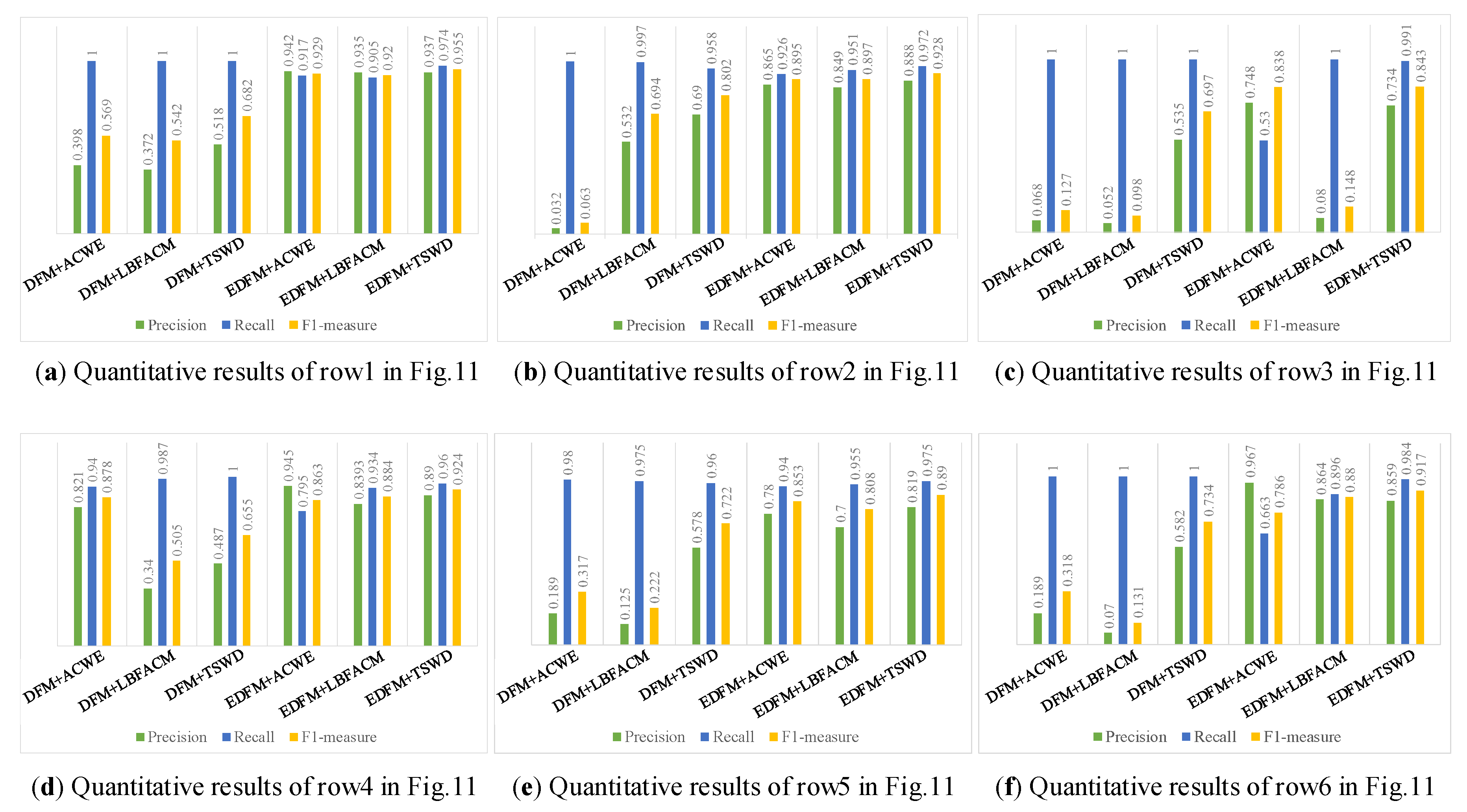
| Results | Performance Index | Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | Image 6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Different Algorithms | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | |
| DFM + ACWE [36] | 39.8 | 100 | 56.9 | 3.20 | 100 | 6.30 | 6.80 | 100 | 12.7 | 82.1 | 94.0 | 87.8 | 18.9 | 100 | 31.8 | 18.9 | 100 | 31.8 | |
| DFM + LBFACM [37] | 37.2 | 100 | 54.2 | 53.2 | 99.7 | 69.4 | 5.20 | 100 | 9.80 | 34.0 | 98.7 | 50.5 | 12.5 | 97.5 | 22.2 | 7.00 | 100 | 13.1 | |
| DFM + TSWD | 51.8 | 100 | 68.2 | 69.0 | 95.8 | 80.2 | 53.5 | 100 | 69.7 | 48.7 | 100 | 65.5 | 57.8 | 96.0 | 72.2 | 58.2 | 100 | 73.4 | |
| EDFM + ACWE [36] | 94.2 | 91.7 | 92.9 | 86.5 | 92.6 | 89.5 | 74.8 | 53.0 | 83.8 | 94.5 | 79.5 | 86.3 | 78.0 | 94.0 | 85.3 | 96.7 | 66.3 | 78.6 | |
| EDFM + LBFACM [37] | 93.5 | 90.5 | 92.0 | 84.9 | 95.1 | 89.7 | 8.00 | 100 | 14.8 | 83.9 | 93.4 | 88.4 | 70.0 | 95.5 | 80.8 | 86.4 | 89.6 | 88.0 | |
| EDFM + TSWD | 93.7 | 97.4 | 95.5 | 88.8 | 97.2 | 92.8 | 73.4 | 99.1 | 84.3 | 89.0 | 96.0 | 92.4 | 81.9 | 97.5 | 89.0 | 85.9 | 98.4 | 91.7 | |
| Results | Performance Index | Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | Image 6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Different Algorithms | P (%) | R(%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | P (%) | R (%) | F (%) | |
| LSG [38] | 46.4 | 100 | 63.4 | 40.3 | 94.7 | 56.6 | 24.7 | 82.4 | 38.0 | 34.5 | 97.5 | 51.0 | 76.4 | 92.1 | 83.5 | 42.6 | 100 | 59.8 | |
| Faster RCNN [25] | 59.5 | 98.4 | 74.2 | 42.3 | 100 | 59.5 | 25.7 | 96.2 | 40.1 | 41.9 | 100 | 59.0 | 63.5 | 100 | 77.6 | 37.3 | 100 | 54.4 | |
| EDFM + TSWD | 93.7 | 97.4 | 95.5 | 88.8 | 97.2 | 92.8 | 73.4 | 99.1 | 84.3 | 89.0 | 96.0 | 92.4 | 81.9 | 97.5 | 89.0 | 85.9 | 98.4 | 91.7 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Qin, S. High-Precision Detection of Defects of Tire Texture Through X-ray Imaging Based on Local Inverse Difference Moment Features. Sensors 2018, 18, 2524. https://doi.org/10.3390/s18082524
Zhao G, Qin S. High-Precision Detection of Defects of Tire Texture Through X-ray Imaging Based on Local Inverse Difference Moment Features. Sensors. 2018; 18(8):2524. https://doi.org/10.3390/s18082524
Chicago/Turabian StyleZhao, Guo, and Shiyin Qin. 2018. "High-Precision Detection of Defects of Tire Texture Through X-ray Imaging Based on Local Inverse Difference Moment Features" Sensors 18, no. 8: 2524. https://doi.org/10.3390/s18082524
APA StyleZhao, G., & Qin, S. (2018). High-Precision Detection of Defects of Tire Texture Through X-ray Imaging Based on Local Inverse Difference Moment Features. Sensors, 18(8), 2524. https://doi.org/10.3390/s18082524




