Estimation of Cough Peak Flow Using Cough Sounds
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Participants
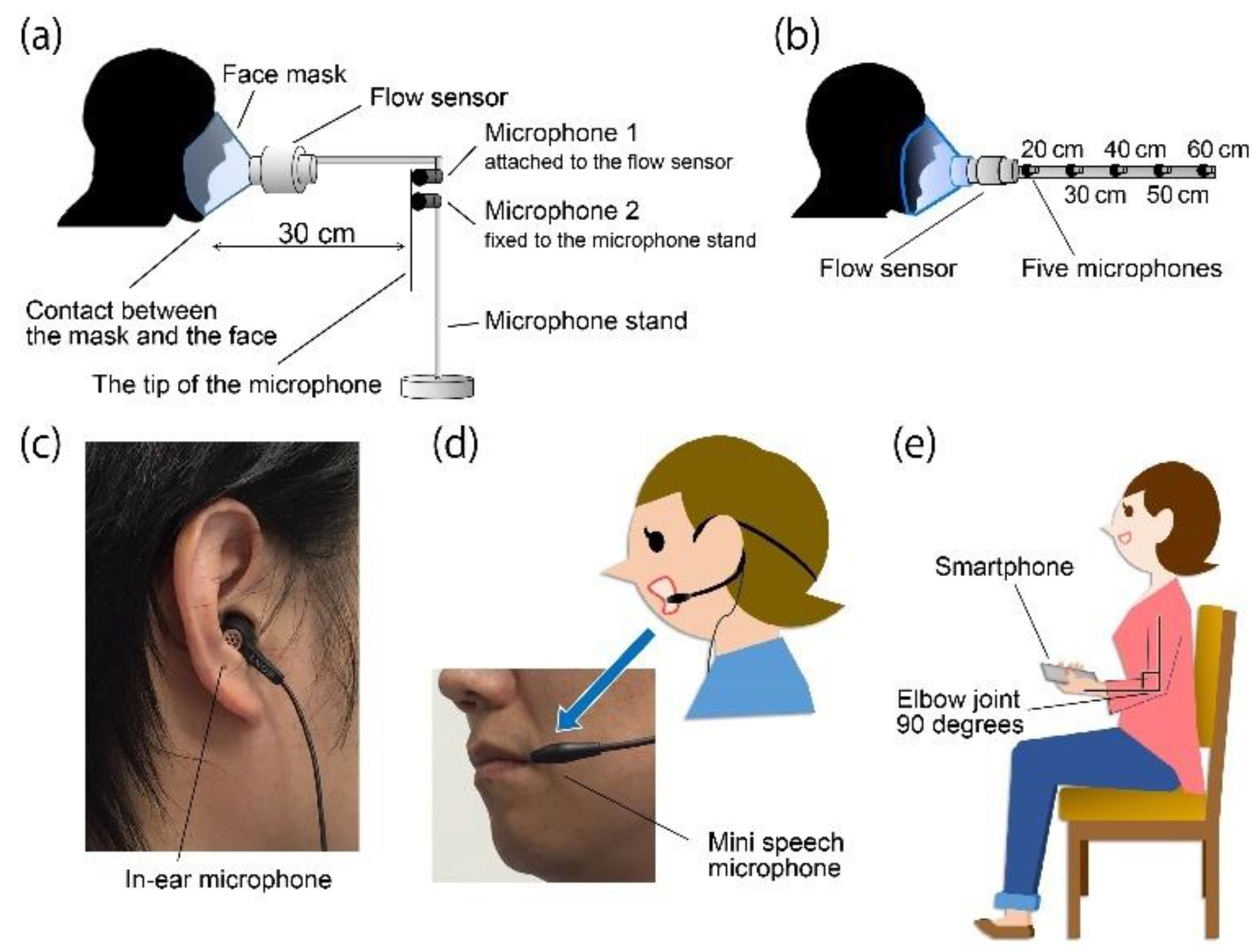
2.3. Cough Flow Measurements
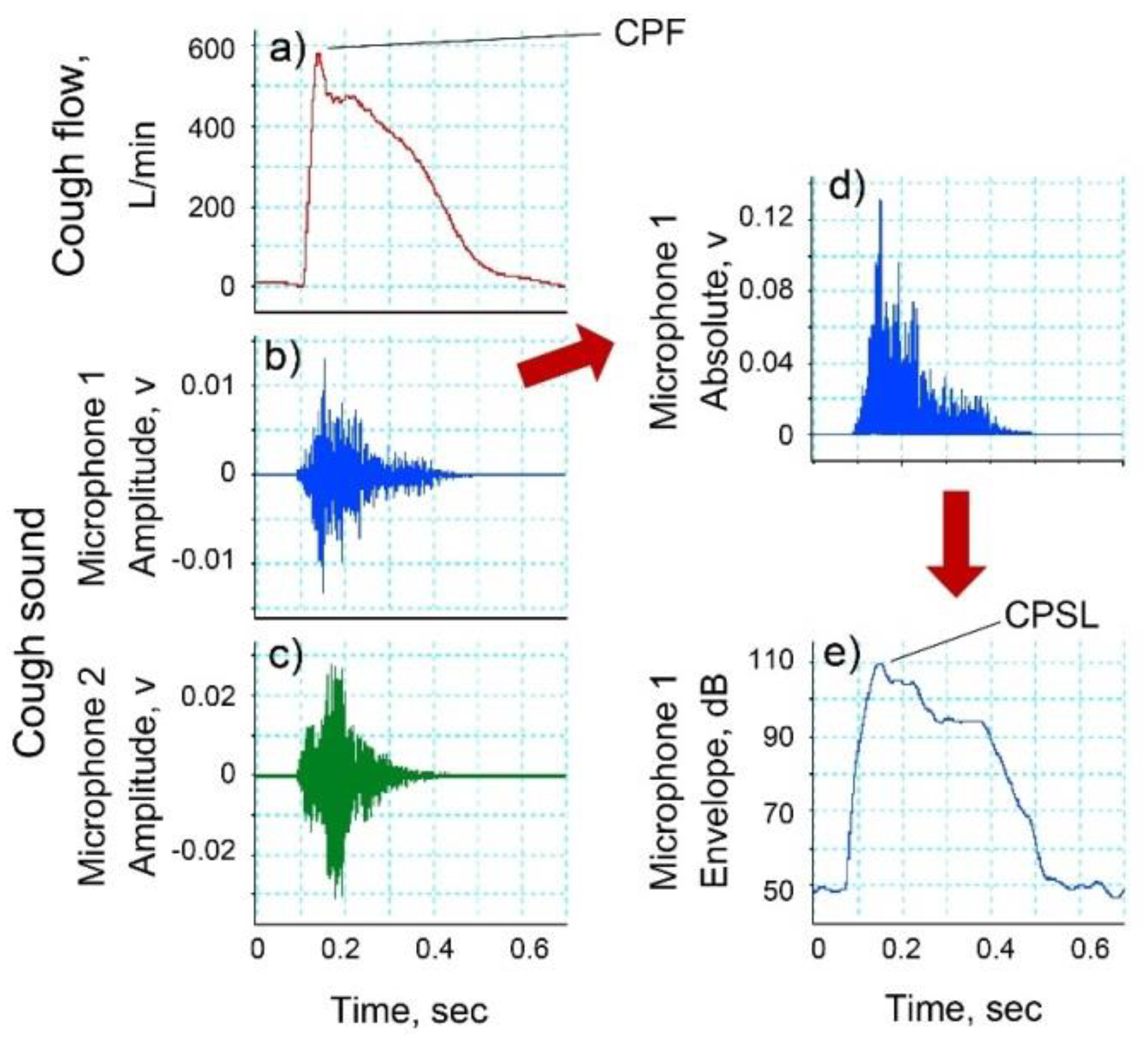
2.4. Cough Sound Measurements
2.5. Experimental Protocols
2.6. Statistical Analysis
3. Results
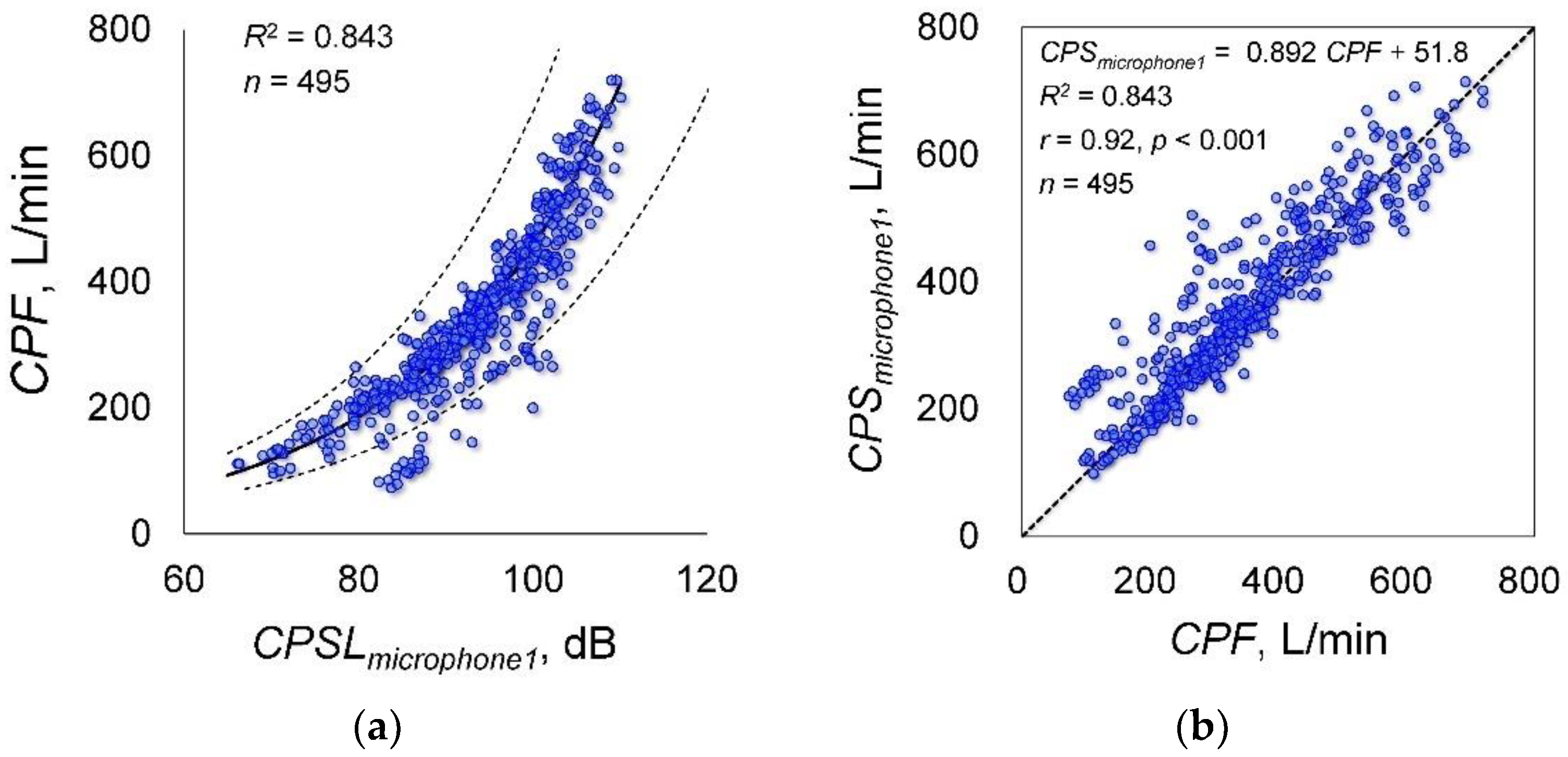
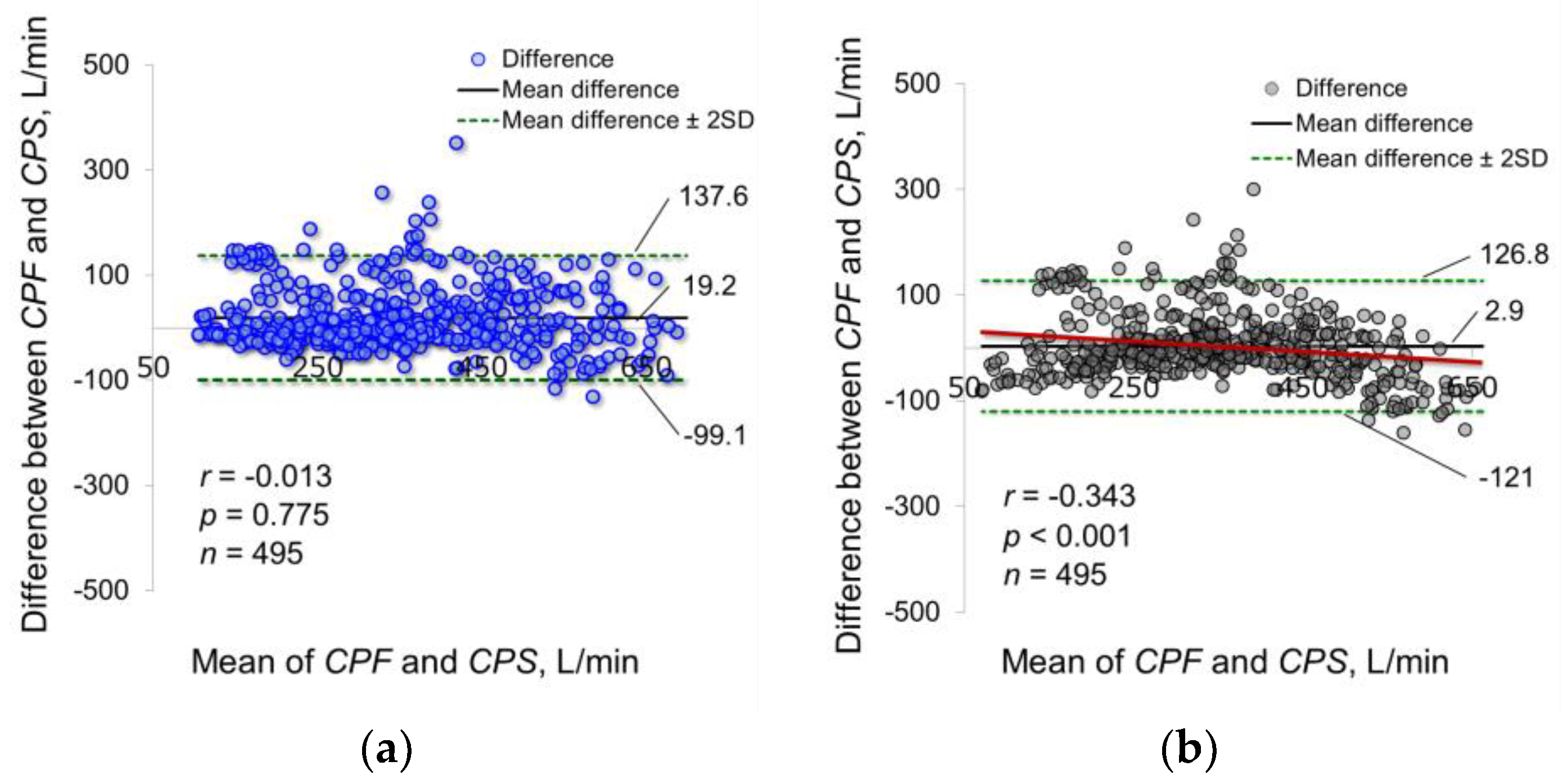
3.1. Experiment 1: Relationships between CPF and CPSL and Verification of the Microphone Installation Method
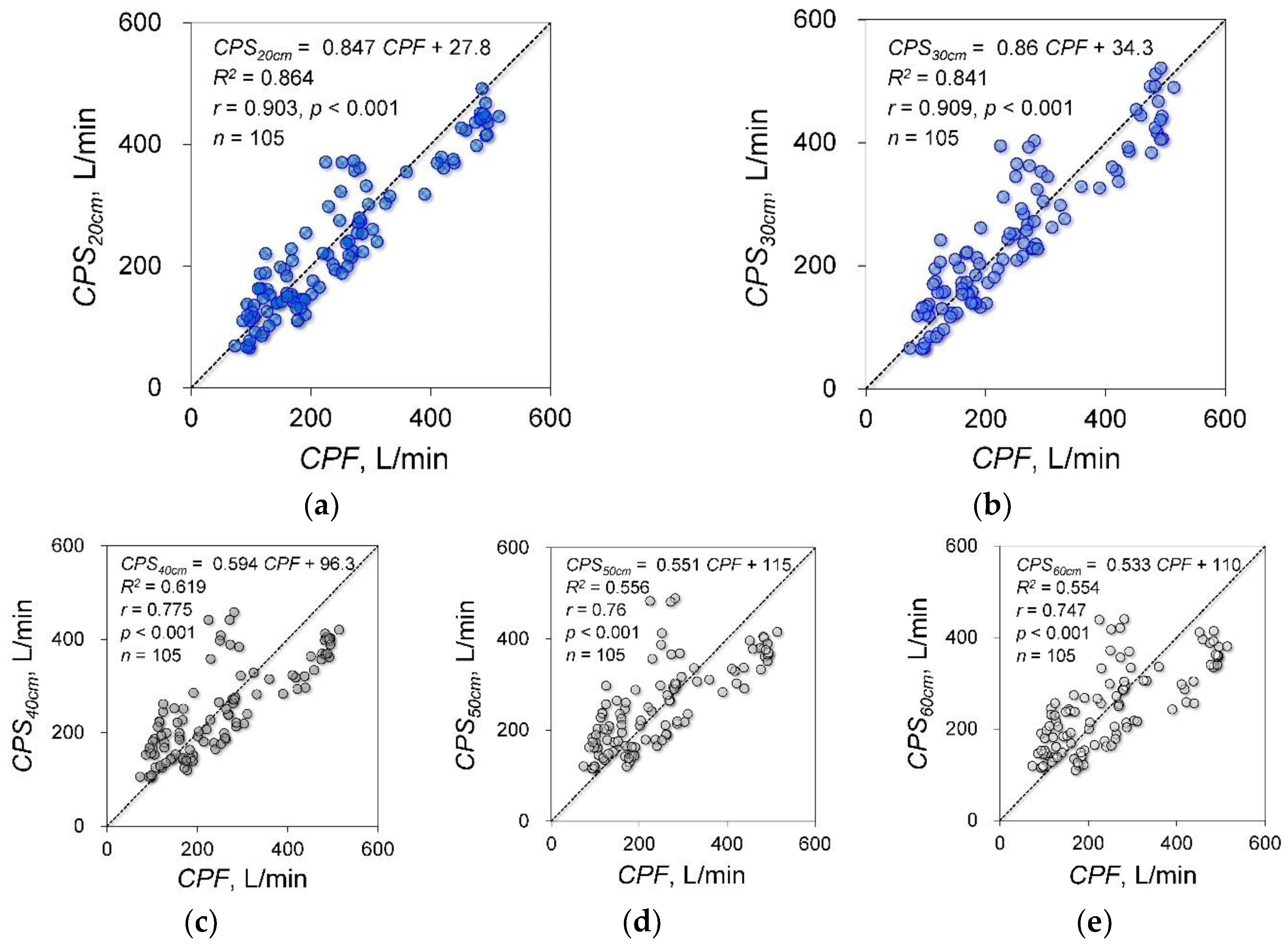
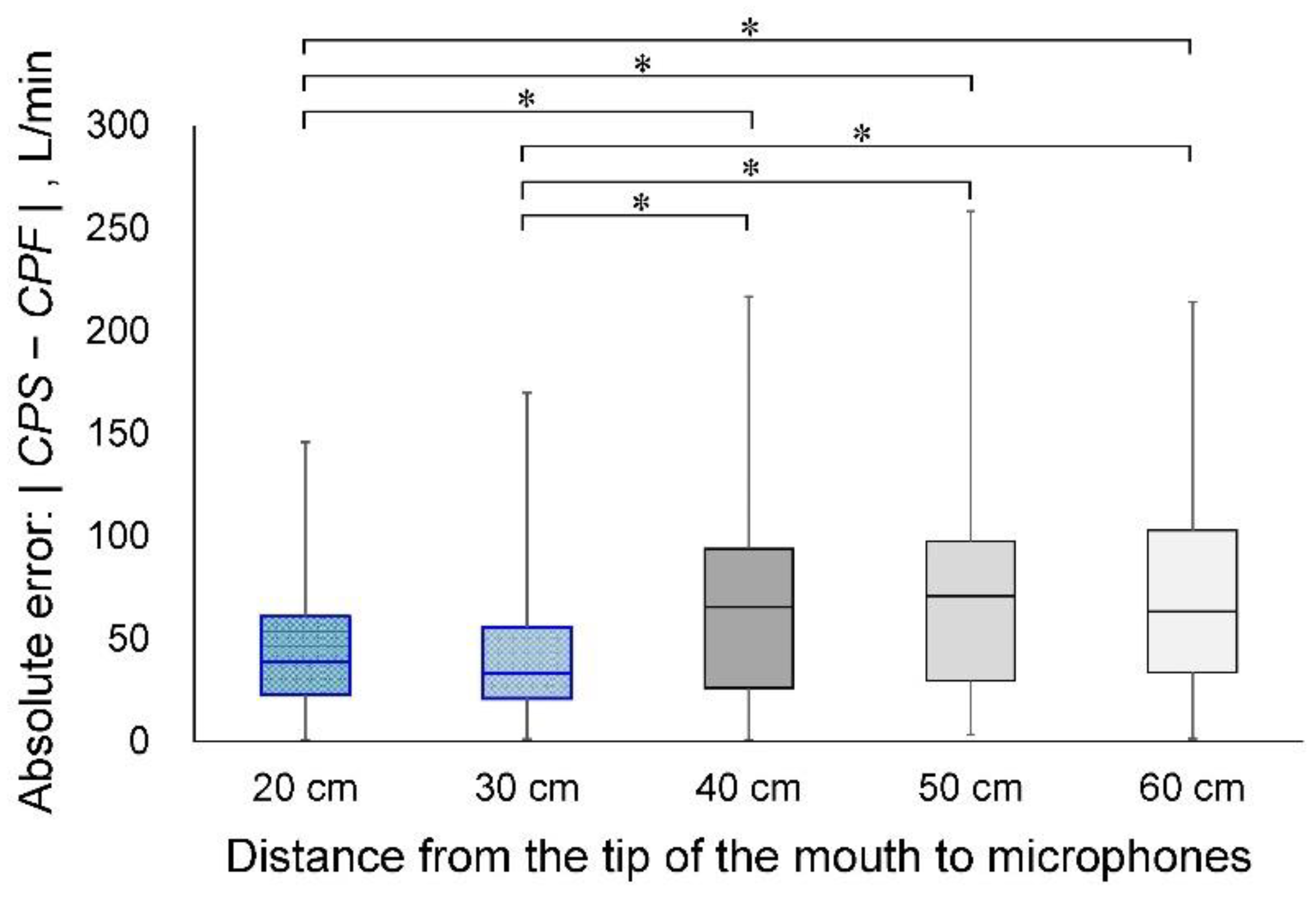
3.2. Experiment 2: Effects of Microphone Distance from the Sound Source on Estimation Accuracy
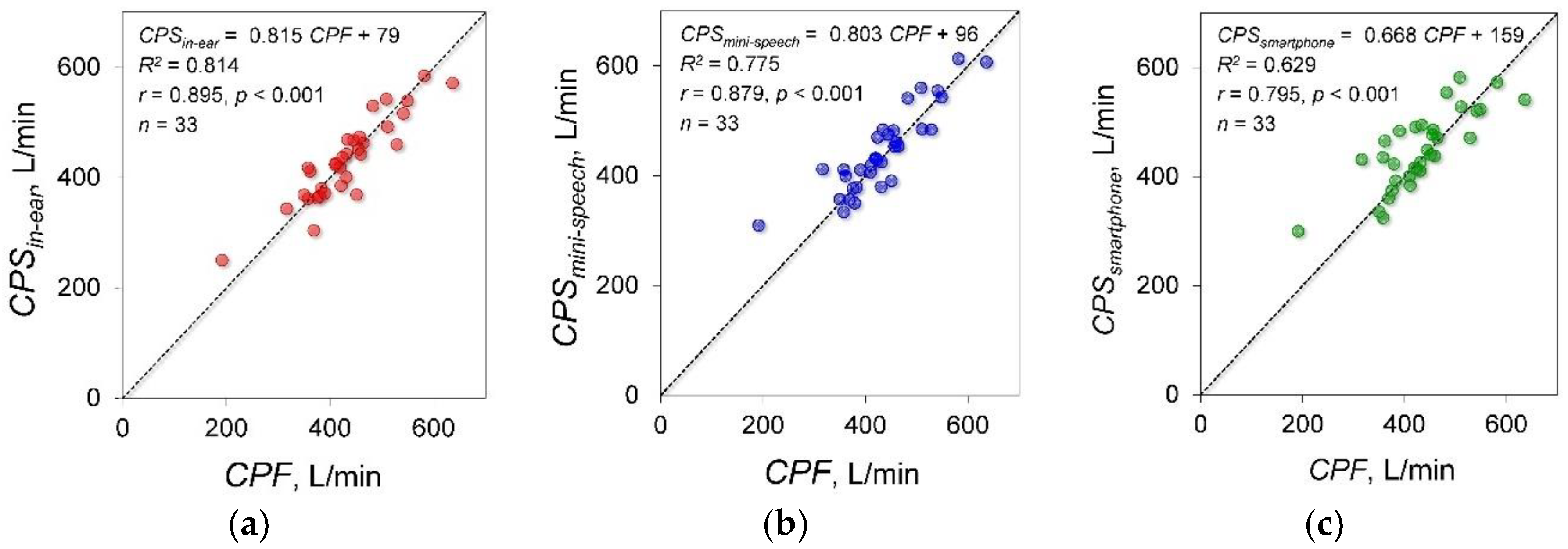
3.3. Experiment 3: Effects of Microphone Type on Estimation Accuracy
3.4. Effects of Participant’s Height on Estimation Accuracy
3.5. Effects of Gender on Estimation Accuracy
3.6. Comparison between the Proposed Model and Polynomial Functions
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chatwin, M.; Toussaint, M.; Goncalves, M.R.; Sheers, N.; Mellies, U.; Gonzales-Bermejo, J.; Sancho, J.; Fauroux, B.; Andersen, T.; Hov, B.; et al. Airway clearance techniques in neuromuscular disorders: A state of the art review. Respir. Med. 2018, 136, 98–110. [Google Scholar] [CrossRef] [PubMed]
- Srour, N.; LeBlanc, C.; King, J.; McKim, D.A. Lung volume recruitment in multiple sclerosis. PLoS ONE 2013, 8, e56676. [Google Scholar] [CrossRef] [PubMed]
- LoMauro, A.; Aliverti, A.; Mastella, C.; Arnoldi, M.T.; Banfi, P.; Baranello, G. Spontaneous breathing pattern as respiratory functional outcome in children with spinal muscular atrophy (SMA). PLoS ONE 2016, 11, e0165818. [Google Scholar] [CrossRef] [PubMed]
- Benditt, J.O.; Boitano, L.J. Pulmonary issues in patients with chronic neuromuscular disease. Am. J. Respir. Crit. Care Med. 2013, 187, 1046–1055. [Google Scholar] [CrossRef] [PubMed]
- Sancho, J.; Servera, E.; Diaz, J.; Marin, J. Predictors of ineffective cough during a chest infection in patients with stable amyotrophic lateral sclerosis. Am. J. Respir. Crit. Care Med. 2007, 175, 1266–1271. [Google Scholar] [CrossRef] [PubMed]
- Finder, J.D.; Birnkrant, D.; Carl, J.; Farber, H.J.; Gozal, D.; Iannaccone, S.T.; Kovesi, T.; Kravitz, R.M.; Panitch, H.; Schramm, C.; et al. Respiratory care of the patient with duchenne muscular dystrophy: ATS consensus statement. Am. J. Respir. Crit. Care Med. 2004, 170, 456–465. [Google Scholar] [PubMed]
- Bach, J.R.; Saporito, L.R. Criteria for extubation and tracheostomy tube removal for patients with ventilatory failure. A different approach to weaning. Chest 1996, 110, 1566–1571. [Google Scholar] [CrossRef] [PubMed]
- Su, W.L.; Chen, Y.H.; Chen, C.W.; Yang, S.H.; Su, C.L.; Perng, W.C.; Wu, C.P.; Chen, J.H. Involuntary cough strength and extubation outcomes for patients in an icu. Chest 2010, 137, 777–782. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Zhou, L.; Xiao, M.; Liu, J.; Yang, X. Semiquantitative cough strength score for predicting reintubation after planned extubation. Am. J. Crit. Care 2015, 24, e86–e90. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Liu, J.; Xiao, M.; Yang, X.; Wu, J.; Zhou, L. Voluntary is better than involuntary cough peak flow for predicting re-intubation after scheduled extubation in cooperative subjects. Respir. Care 2014, 59, 1643–1651. [Google Scholar] [CrossRef] [PubMed]
- Smailes, S.T.; McVicar, A.J.; Martin, R. Cough strength, secretions and extubation outcome in burn patients who have passed a spontaneous breathing trial. Burns 2013, 39, 236–242. [Google Scholar] [CrossRef] [PubMed]
- Bach, J.R. Amyotrophic lateral sclerosis: Predictors for prolongation of life by noninvasive respiratory aids. Arch. Phys. Med. Rehabil. 1995, 76, 828–832. [Google Scholar] [CrossRef]
- Bach, J.R.; Ishikawa, Y.; Kim, H. Prevention of pulmonary morbidity for patients with duchenne muscular dystrophy. Chest 1997, 112, 1024–1028. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Duan, J. Use of cough peak flow measured by a ventilator to predict re-intubation when a spirometer is unavailable. Respir. Care 2017, 62, 566–571. [Google Scholar] [CrossRef] [PubMed]
- Larson, S.; Comina, G.; Gilman, R.H.; Tracey, B.H.; Bravard, M.; Lopez, J.W. Validation of an automated cough detection algorithm for tracking recovery of pulmonary tuberculosis patients. PLoS ONE 2012, 7, e46229. [Google Scholar] [CrossRef] [PubMed]
- Morice, A.H.; Fontana, G.A.; Belvisi, M.G.; Birring, S.S.; Chung, K.F.; Dicpinigaitis, P.V.; Kastelik, J.A.; McGarvey, L.P.; Smith, J.A.; Tatar, M.; et al. ERS guidelines on the assessment of cough. Eur. Respir. J. 2007, 29, 1256–1276. [Google Scholar] [CrossRef] [PubMed]
- Sumner, H.; Woodcock, A.; Kolsum, U.; Dockry, R.; Lazaar, A.L.; Singh, D.; Vestbo, J.; Smith, J.A. Predictors of objective cough frequency in chronic obstructive pulmonary disease. Am. J. Respir. Crit. Care Med. 2013, 187, 943–949. [Google Scholar] [CrossRef] [PubMed]
- Ing, A.J.; Ngu, M.C.; Breslin, A.B. Pathogenesis of chronic persistent cough associated with gastroesophageal reflux. Am. J. Respir. Crit. Care Med. 1994, 149, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.K.; Matos, S.; Evans, D.H.; White, P.; Pavord, I.D.; Birring, S.S. A longitudinal assessment of acute cough. Am. J. Respir. Crit. Care Med. 2013, 187, 991–997. [Google Scholar] [CrossRef] [PubMed]
- Birring, S.S.; Matos, S.; Patel, R.B.; Prudon, B.; Evans, D.H.; Pavord, I.D. Cough frequency, cough sensitivity and health status in patients with chronic cough. Respir. Med. 2006, 100, 1105–1109. [Google Scholar] [CrossRef] [PubMed]
- Birring, S.S.; Fleming, T.; Matos, S.; Raj, A.A.; Evans, D.H.; Pavord, I.D. The leicester cough monitor: Preliminary validation of an automated cough detection system in chronic cough. Eur. Respir. J. 2008, 31, 1013–1018. [Google Scholar] [CrossRef] [PubMed]
- Spinou, A.; Birring, S.S. An update on measurement and monitoring of cough: What are the important study endpoints? J. Thorac. Dis. 2014, 6, S728–S734. [Google Scholar] [PubMed]
- Umayahara, Y.; Soh, Z.; Ozaki, T.; Murakami, T.; Otsuka, A.; Tsuji, T. Ability to cough can be evaluated through cough sounds: An experimental investigation of effects of microphone type on accuracy. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 936–941. [Google Scholar]
- Japanease Ministry of Health, Labor and Welfare. National Health in 2016 and Nutritional Investigation Report. Available online: https://www.mhlw.go.jp/bunya/kenkou/eiyou/dl/h28-houkoku-05.pdf (accessed on 7 July 2018).
- Toop, L.J.; Dawson, K.P.; Thorpe, C.W. A portable system for the spectral analysis of cough sounds in asthma. J. Asthma 1990, 27, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Murata, A.; Ohota, N.; Shibuya, A.; Ono, H.; Kudoh, S. New non-invasive automatic cough counting program based on 6 types of classified cough sounds. Intern. Med. 2006, 45, 391–397. [Google Scholar] [CrossRef] [PubMed]
- Dosani, R.; Kraman, S.S. Lung sound intensity variability in normal men. A contour phonopneumographic study. Chest 1983, 83, 628–631. [Google Scholar] [CrossRef] [PubMed]
- Taylor, T.E.; Lacalle Muls, H.; Costello, R.W.; Reilly, R.B. Estimation of inhalation flow profile using audio-based methods to assess inhaler medication adherence. PLoS ONE 2018, 13, e0191330. [Google Scholar] [CrossRef] [PubMed]
- Shafieian, M.; Kashani, F.H. Effect of diffusive and nondiffusive surfaces combinations on sound diffusion. Acoust. Phys. 2010, 56, 342–347. [Google Scholar] [CrossRef]
- Baldwin, E.D.; Cournand, A.; Richards, D.W., Jr. Pulmonary insufficiency; physiological classification, clinical methods of analysis, standard values in normal subjects. Medicine 1948, 27, 243–278. [Google Scholar] [CrossRef] [PubMed]
- Berglund, E.; Birath, G.; Bjure, J.; Grimby, G.; Kjellmer, I.; Sandqvist, L.; Soderholm, B. Spirometric studies in normal subjects. I. Forced expirograms in subjects between 7 and 70 years of age. Acta Med. Scand. 1963, 173, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, C.; Baiardi, P. Cough peak flows: Standard values for children and adolescents. Am. J. Phys. Med. Rehabil. 2008, 87, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Kraman, S.S. The relationship between airflow and lung sound amplitude in normal subjects. Chest 1984, 86, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Reyes, B.A.; Reljin, N.; Chon, K.H. Tracheal sounds acquisition using smartphones. Sensors 2014, 14, 13830–13850. [Google Scholar] [CrossRef] [PubMed]
- Shykoff, B.E.; Ploysongsang, Y.; Chang, H.K. Airflow and normal lung sounds. Am. Rev. Respir. Dis. 1988, 137, 872–876. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.K.; Matos, S.; Ward, K.; Rafferty, G.F.; Moxham, J.; Evans, D.H.; Birring, S.S. Sound: A non-invasive measure of cough intensity. BMJ Open Respir. Res. 2017, 4, e000178. [Google Scholar] [CrossRef] [PubMed]
| Variable | Experiment 1 (n = 33) | Experiment 2 (n = 7) | Experiment 3 (n = 33) |
|---|---|---|---|
| Age, years | 20.7 ± 1.0 | 22.0 ± 2.8 | 21.3 ± 0.4 |
| Male gender, n | 21 | 5 | 20 |
| Height, cm | 167 ± 7.9 | 167 ± 7.5 | 165 ± 8.4 |
| Body weight, kg (male, female) | 61.5 ± 12 (66.0 ± 12, 53.7 ± 5.4) | 58.7 ± 9 (61.0 ± 7.6, 53.0 ± 11.3) | 58.5 ± 11 (64.5 ± 11.3, 51.0 ± 6.2) |
| BMI, kg/m2 (male, female) | 21.9 ± 3.2 (22.4 ± 3.6, 21 ± 2.1) | 22.0 ± 2.8 (21.2 ± 2.0, 20.3 ± 2.2) | 21.3 ± 0.5 (21.4 ± 0.6, 20.9 ± 0.5) |
| Estimation Equation | Coefficient | Estimated Value | Standard Error | 95% CI | Determination Coefficient | |
|---|---|---|---|---|---|---|
| Lower | Upper | |||||
| Equation (3) | α3 | 3.819 | 0.053 | 3.714 | 3.923 | 0.373 |
| Equation (4) | α4 | 0.117 | 0.003 | 0.111 | 0.124 | 0.822 |
| α5 | −7.288 | 0.317 | −7.910 | −6.665 | ||
| Equation (5) | α6 | 0.002 | 0.000 | 0.002 | 0.003 | 0.843 |
| α7 | −0.326 | 0.054 | −0.431 | −0.220 | ||
| α8 | 13.013 | 2.2485 | 8.132 | 17.895 | ||
| Equation (6) | α9 | 0.019 | 0.000 | −0.015 | 0.052 | 0.844 |
| α10 | −0.005 | 0.007 | −0.019 | 0.008 | ||
| α11 | 0.355 | 0.617 | −0.858 | 1.567 | ||
| α12 | −7.198 | 18.431 | −43.412 | 29.016 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umayahara, Y.; Soh, Z.; Sekikawa, K.; Kawae, T.; Otsuka, A.; Tsuji, T. Estimation of Cough Peak Flow Using Cough Sounds. Sensors 2018, 18, 2381. https://doi.org/10.3390/s18072381
Umayahara Y, Soh Z, Sekikawa K, Kawae T, Otsuka A, Tsuji T. Estimation of Cough Peak Flow Using Cough Sounds. Sensors. 2018; 18(7):2381. https://doi.org/10.3390/s18072381
Chicago/Turabian StyleUmayahara, Yasutaka, Zu Soh, Kiyokazu Sekikawa, Toshihiro Kawae, Akira Otsuka, and Toshio Tsuji. 2018. "Estimation of Cough Peak Flow Using Cough Sounds" Sensors 18, no. 7: 2381. https://doi.org/10.3390/s18072381
APA StyleUmayahara, Y., Soh, Z., Sekikawa, K., Kawae, T., Otsuka, A., & Tsuji, T. (2018). Estimation of Cough Peak Flow Using Cough Sounds. Sensors, 18(7), 2381. https://doi.org/10.3390/s18072381





