Huber’s Non-Linearity for GNSS Interference Mitigation †
Abstract
:1. Introduction
2. Signal and System Model
2.1. Standard Processing
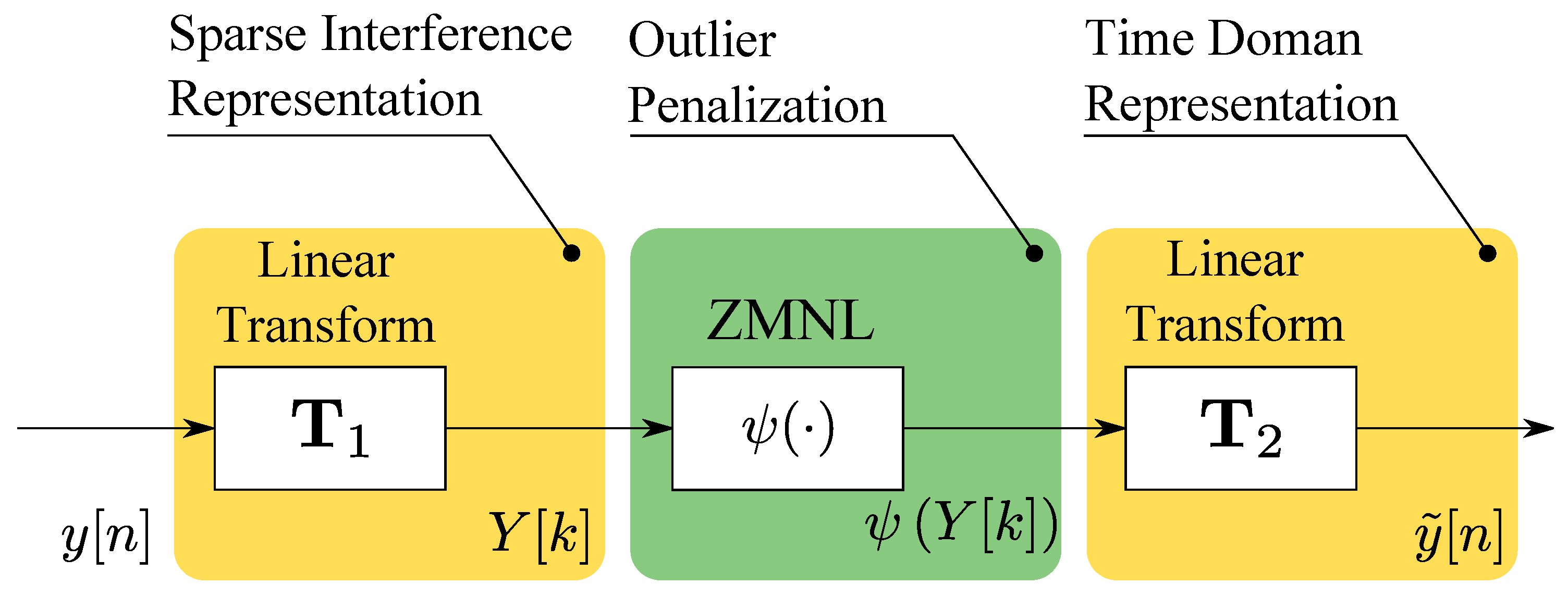
2.2. Robust Interference Mitigation
- Time domain processing: when is a low pass-filter and is the identity operator. In narrowband receivers, low-pass filtering is not needed. and can be replaced by the identity operator,
- TD processing: and are inverse operators and
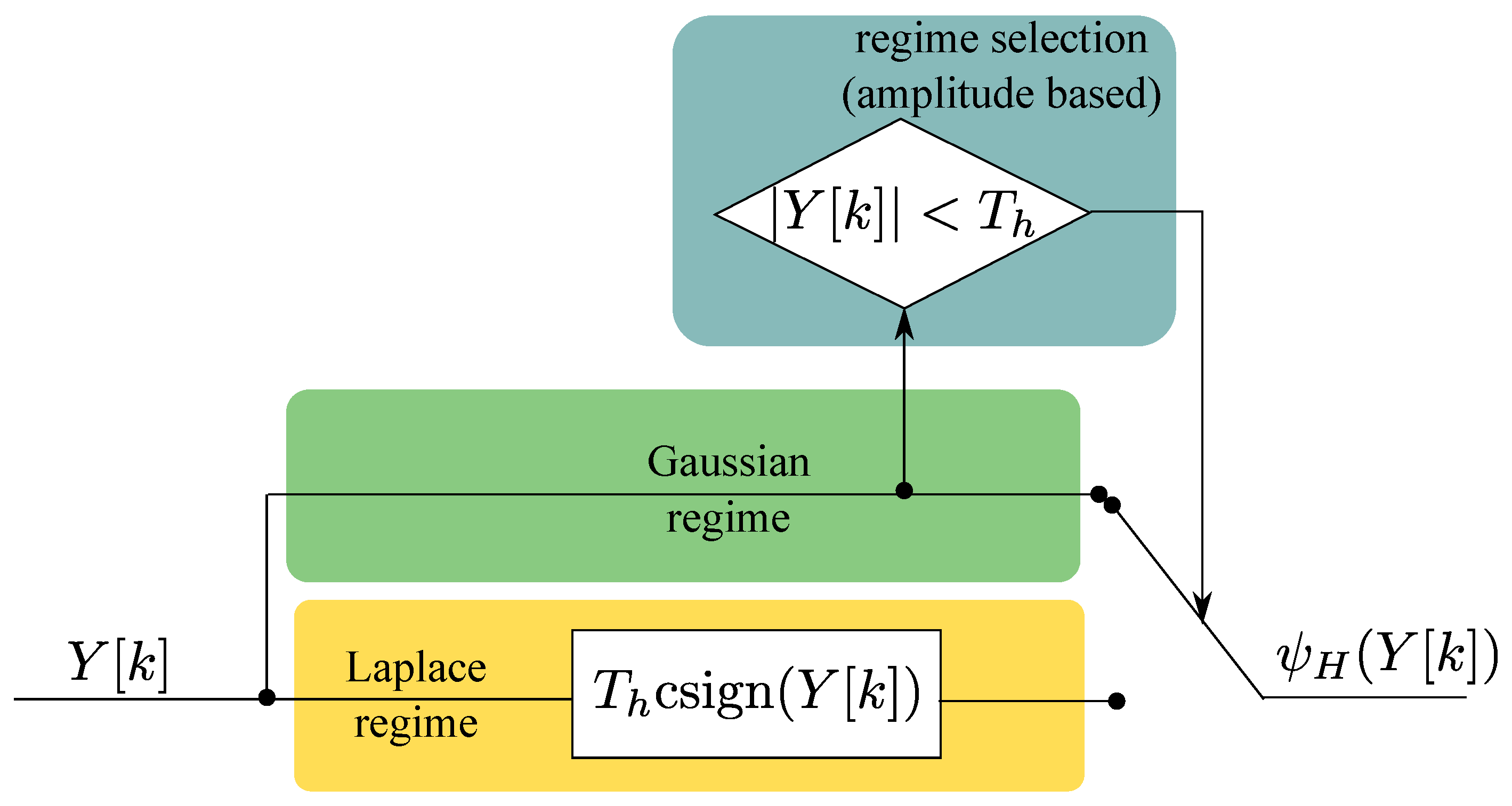
3. Huber’s Non-Linearity
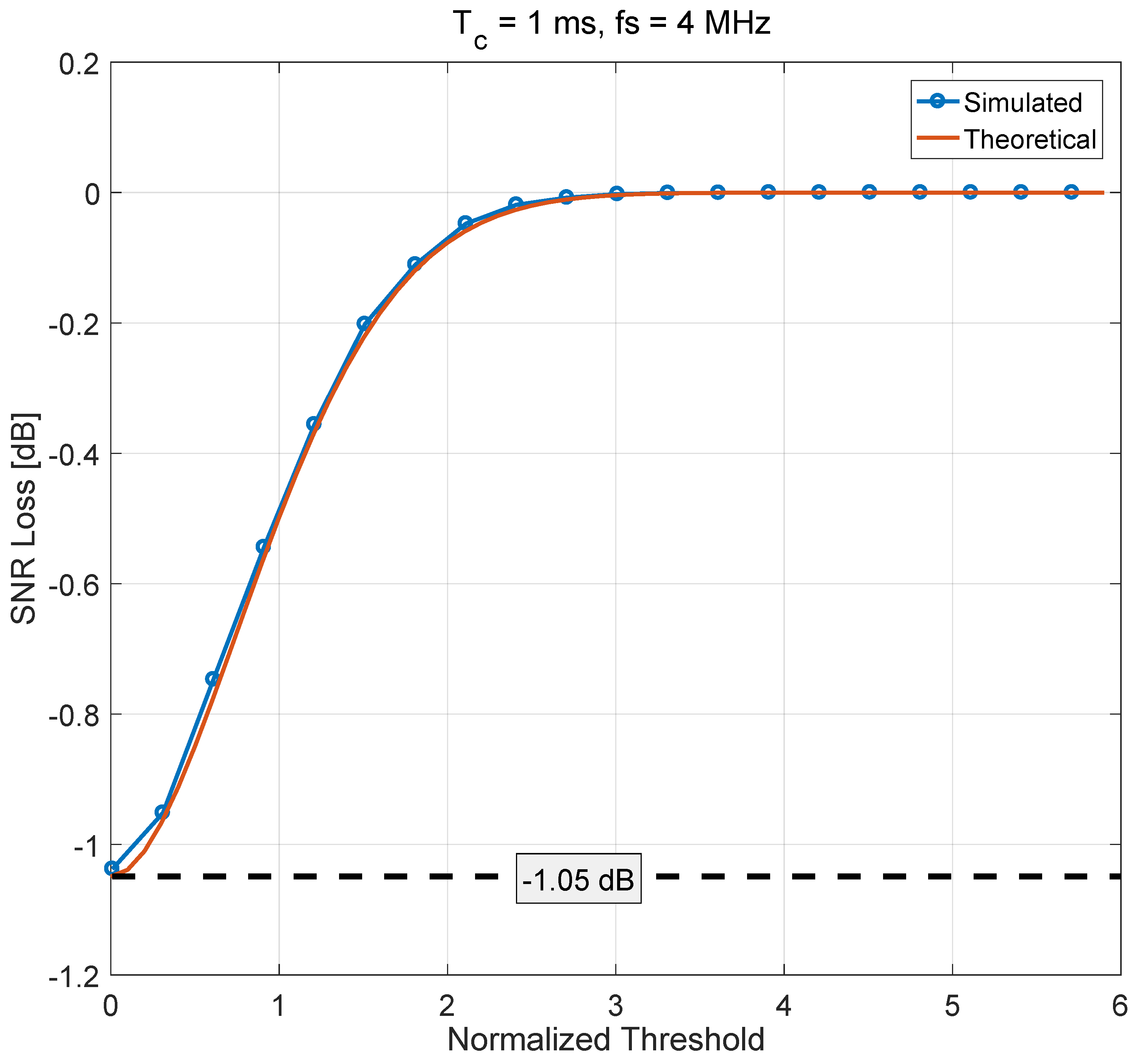
4. Efficiency Analysis
Validation through Simulations
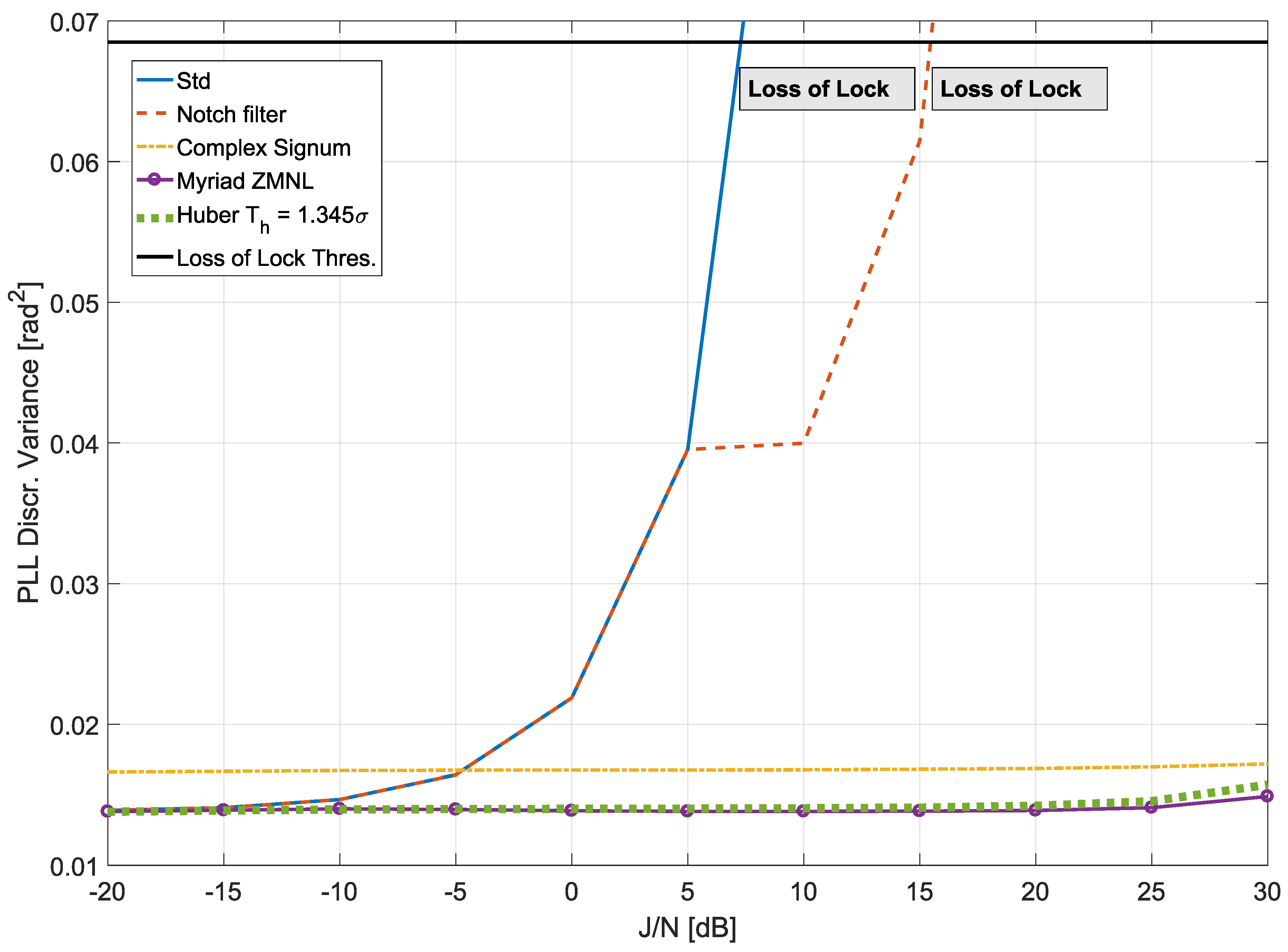
5. Simulation Analysis
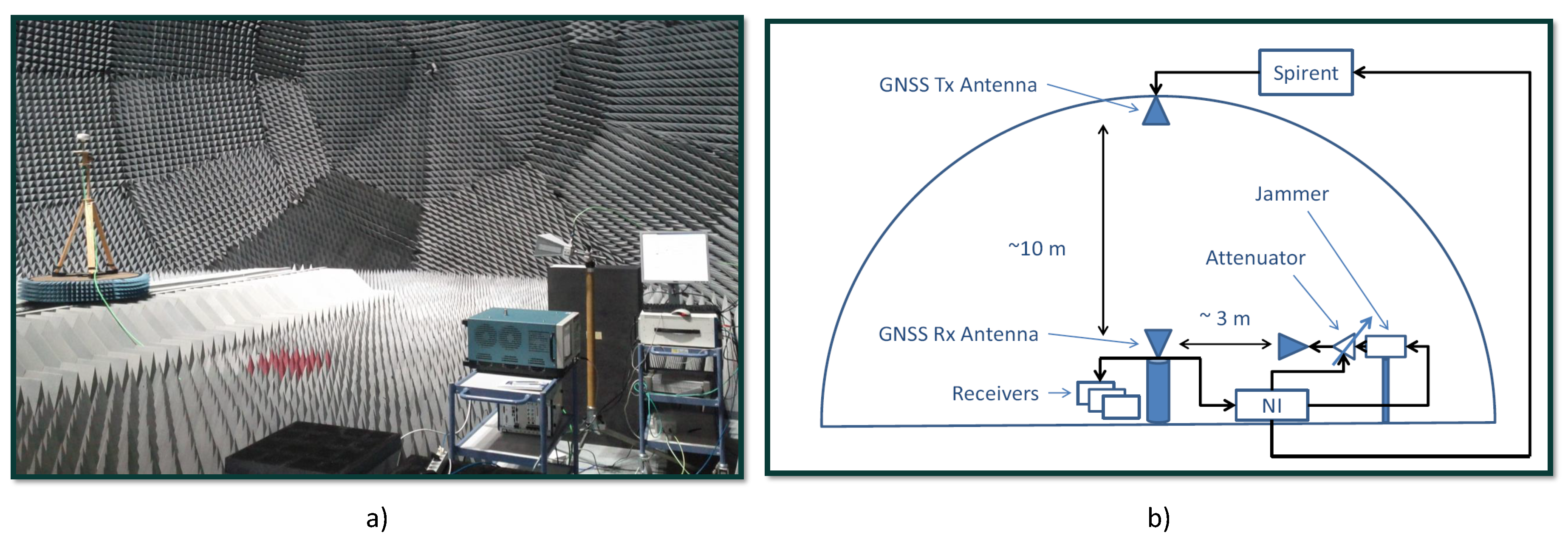
6. Experimental Setup
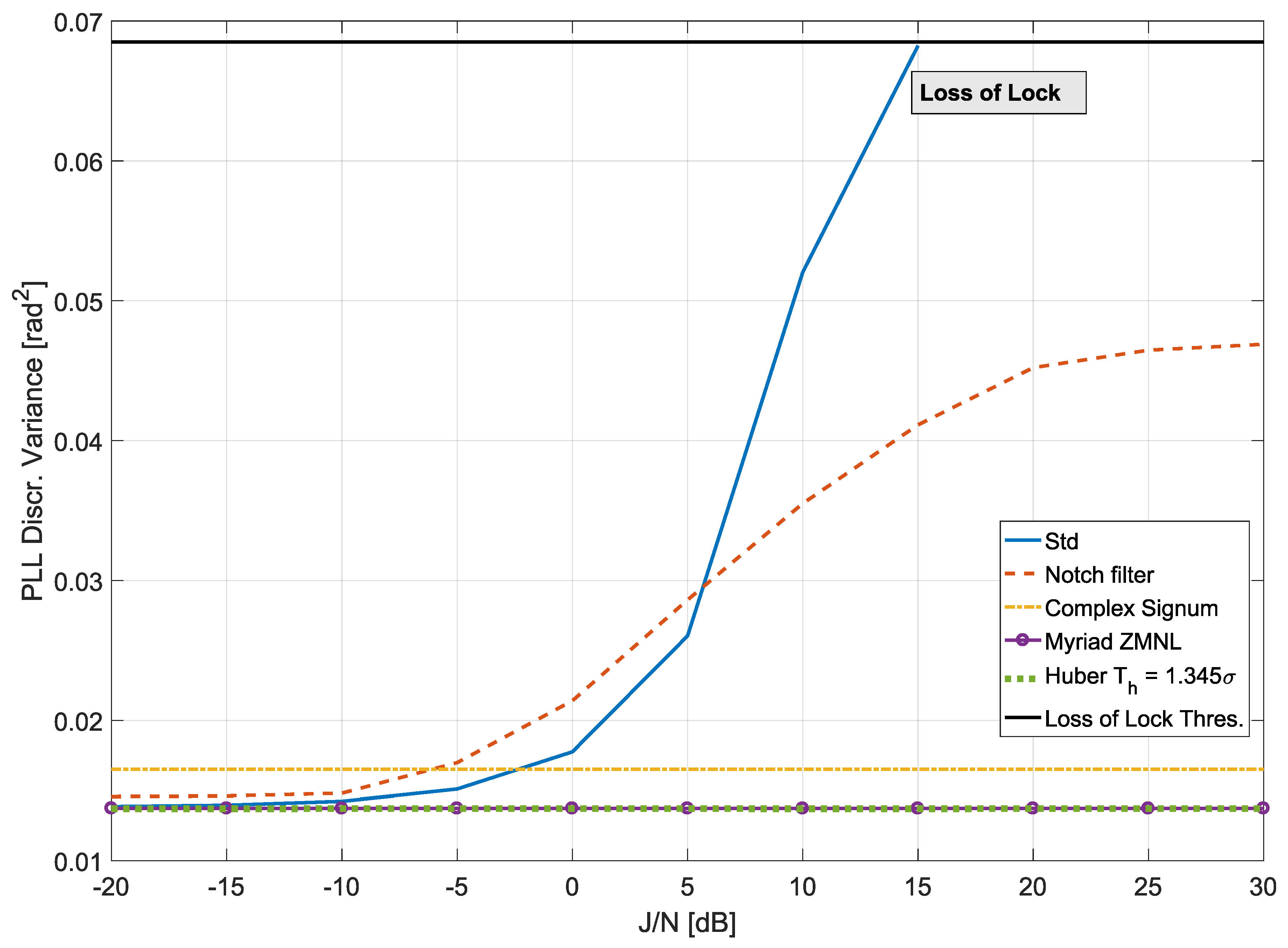
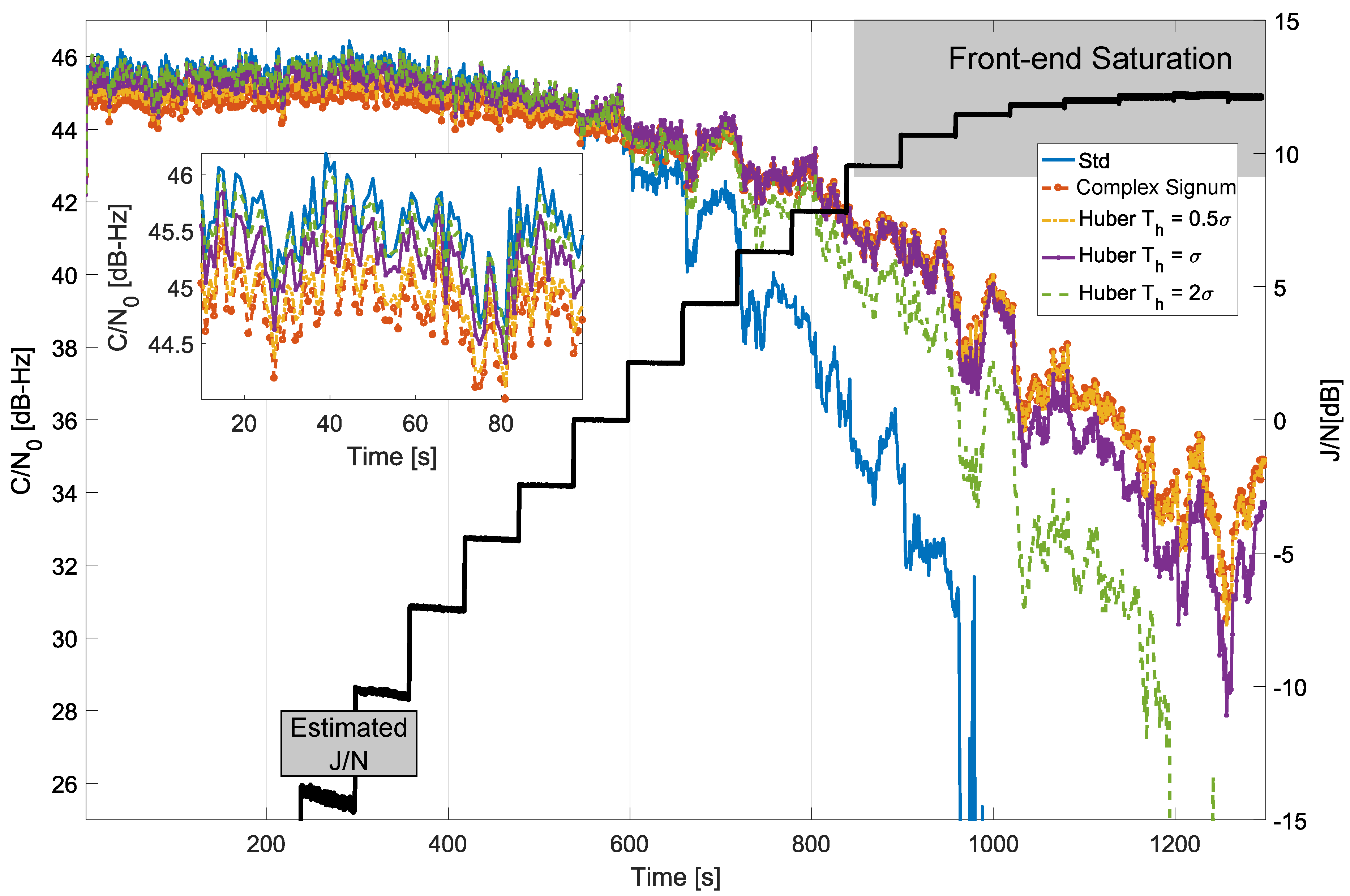
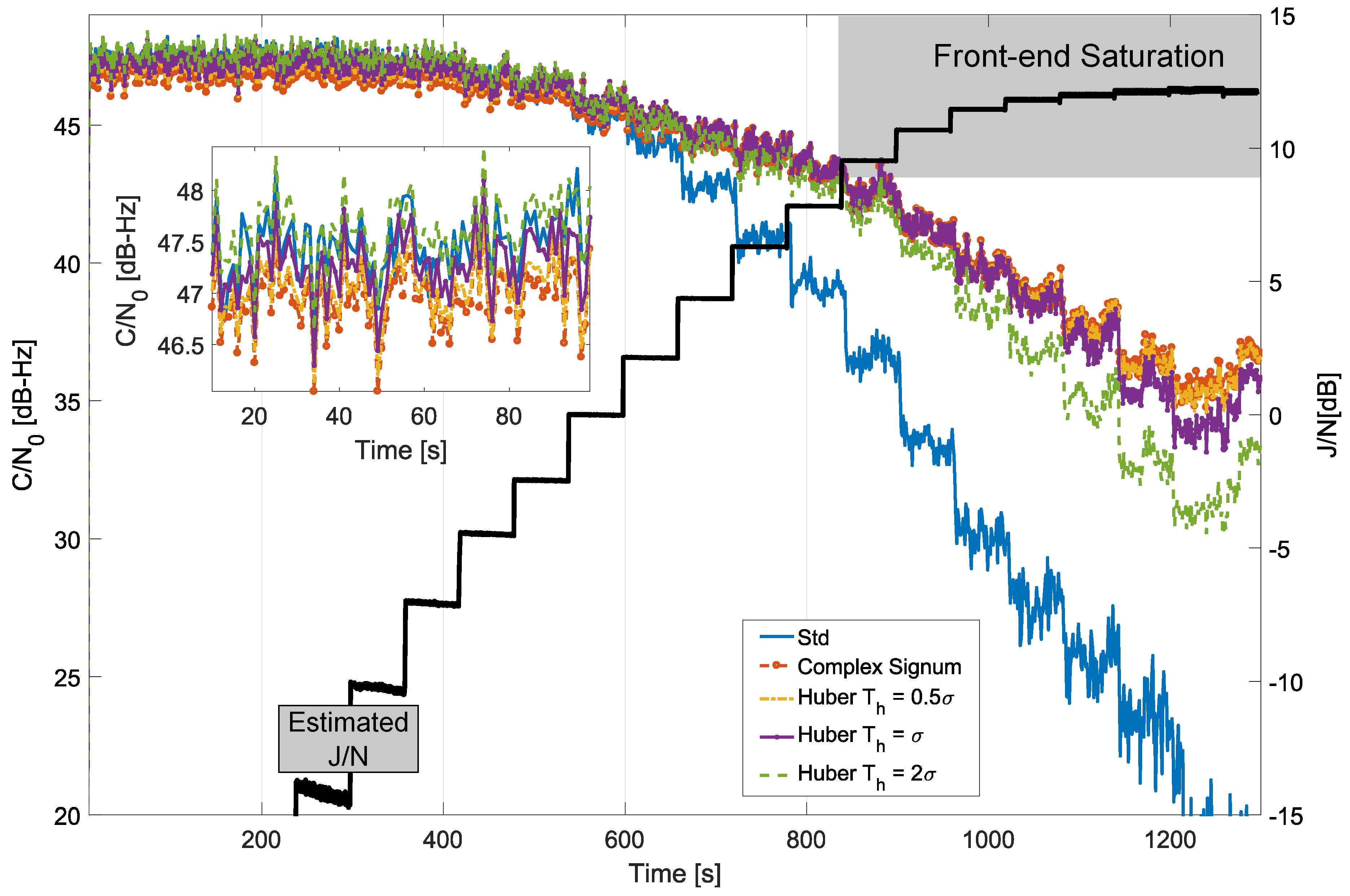
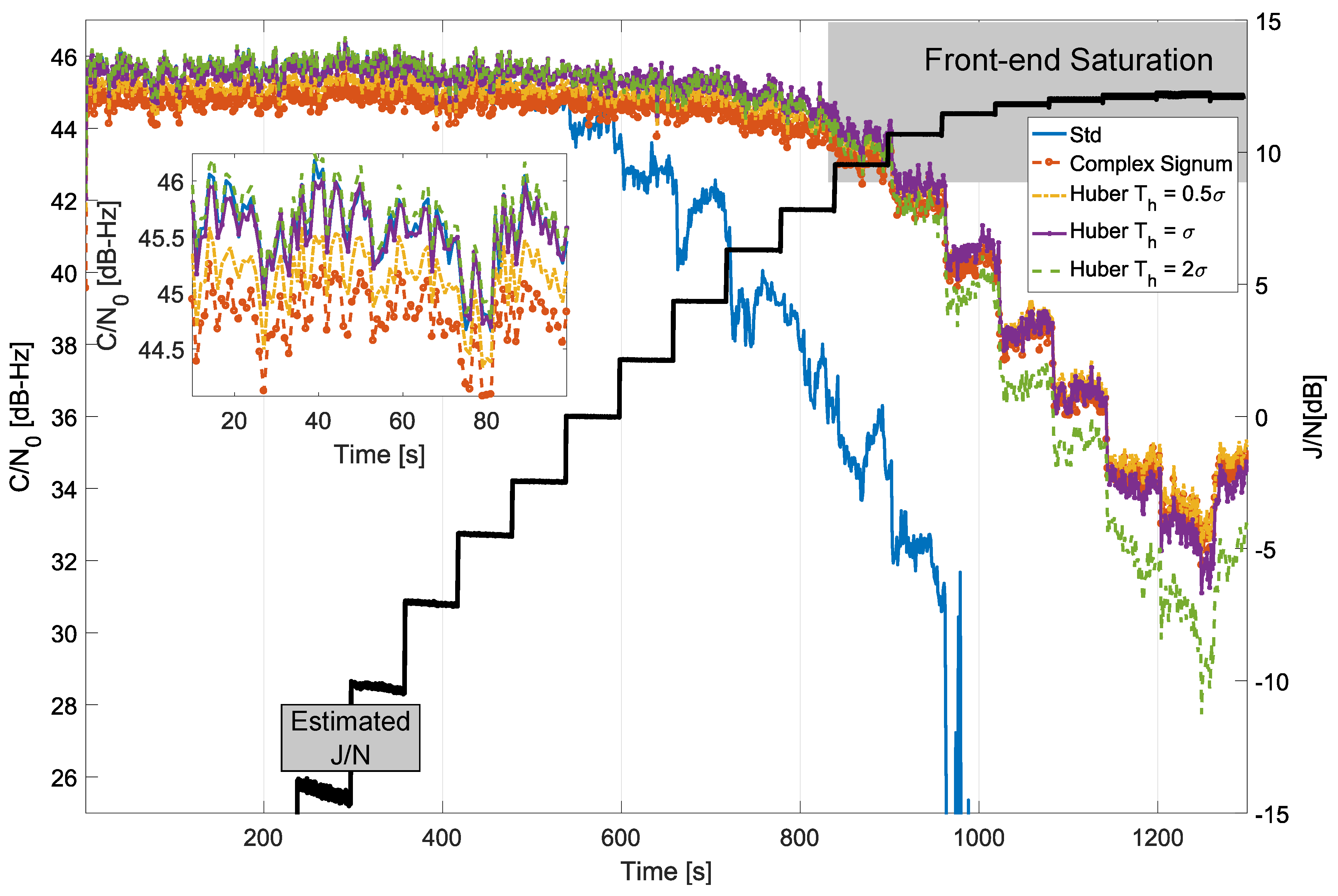
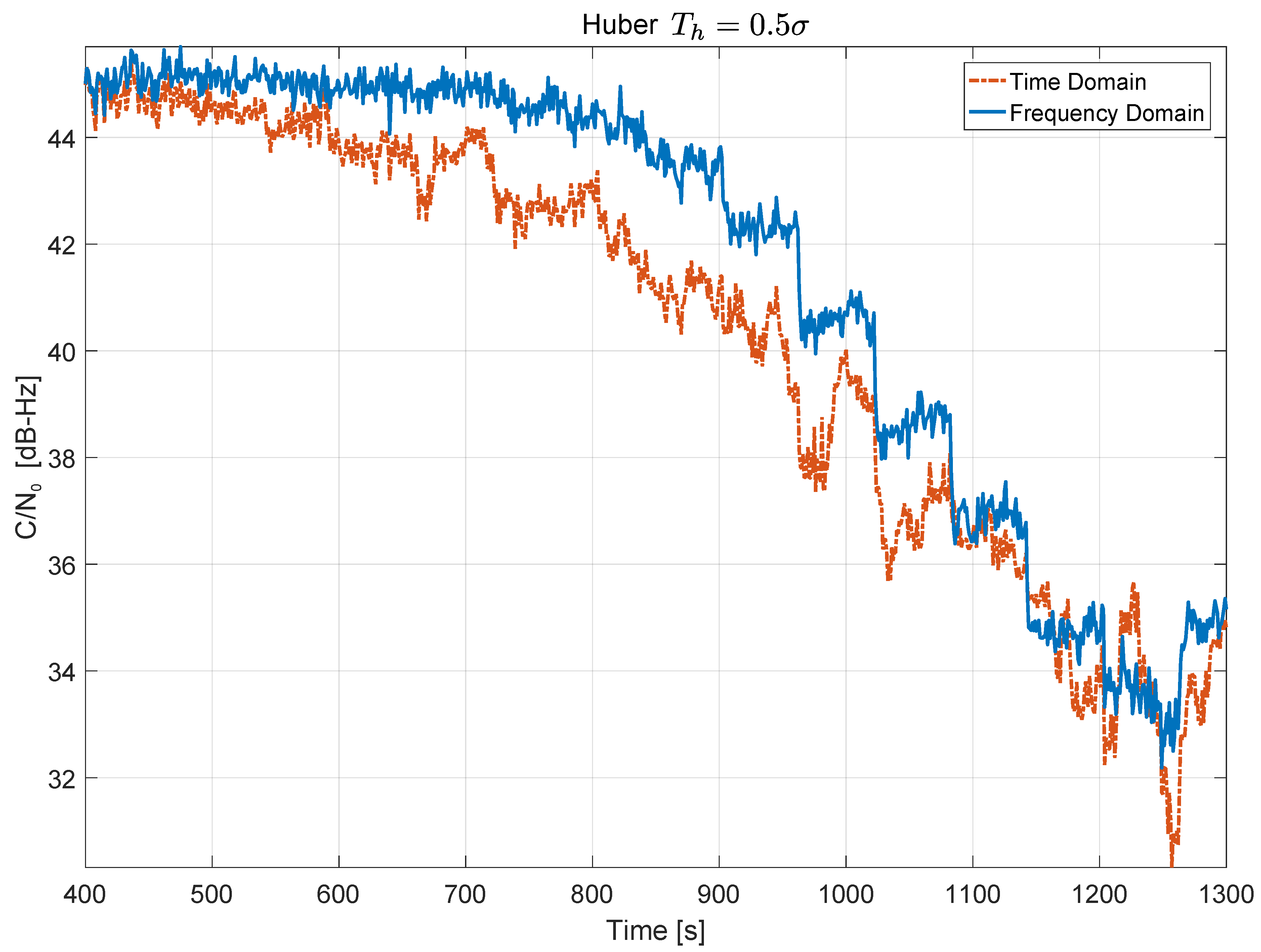
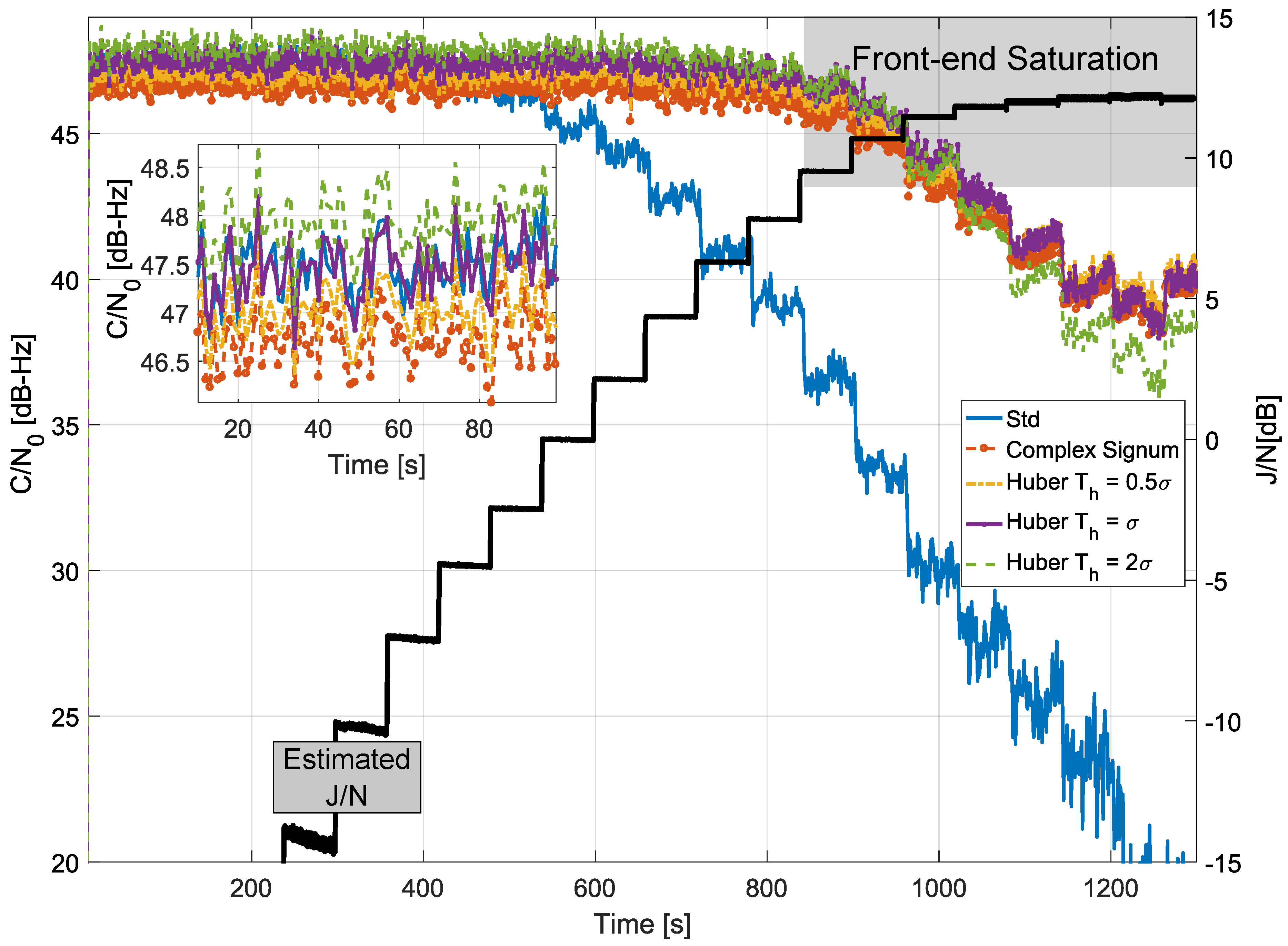
7. Experimental Results
7.1. Time Domain Processing
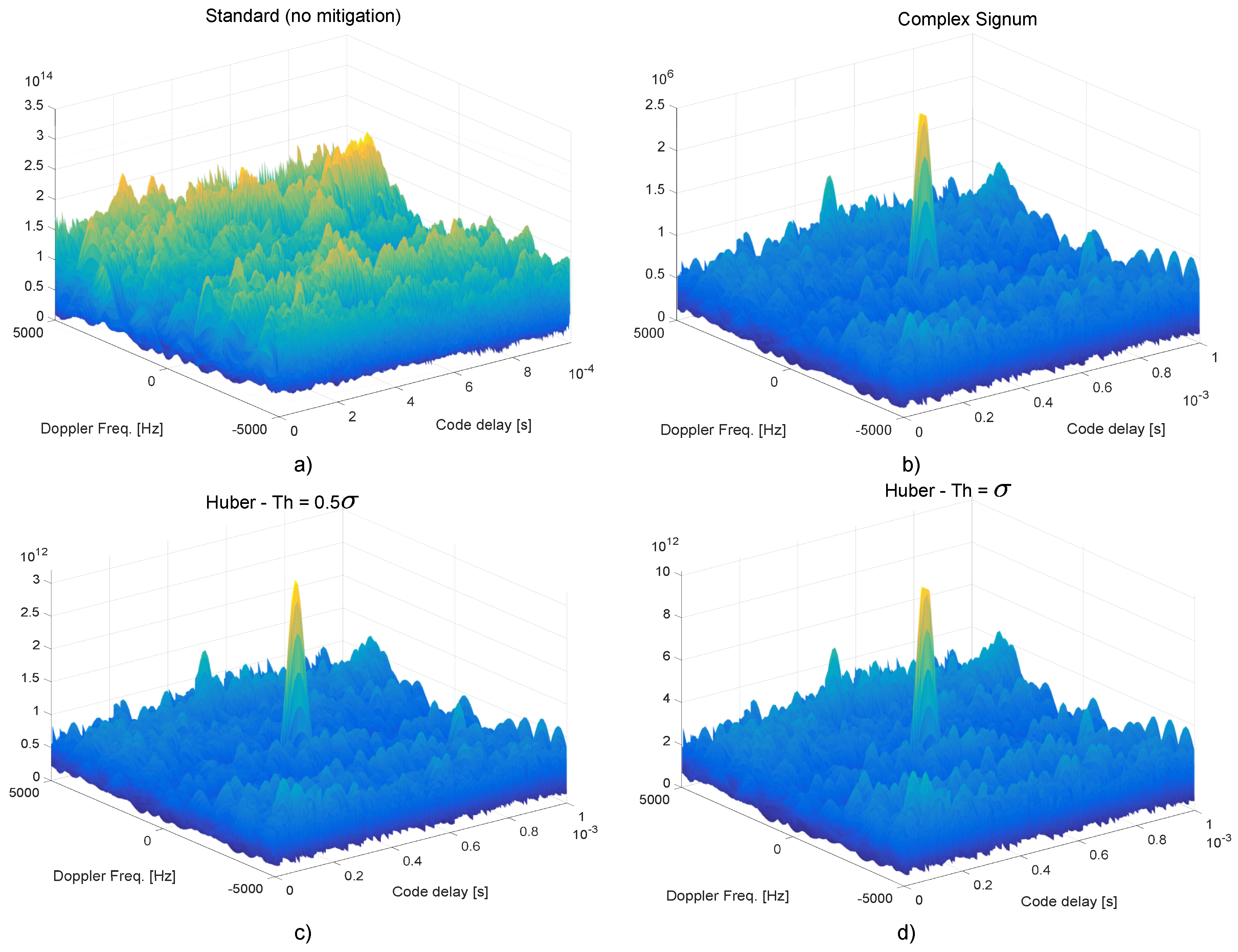
7.2. Frequency Domain Processing
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Moments of the Samples Processed with Huber’s Non-Linearity
References
- Dardari, D.; Closas, P.; Djurić, P.M. Indoor tracking: Theory, methods, and technologies. IEEE Trans. Veh. Technol. 2015, 64, 1263–1278. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C. (Eds.) Understanding GPS: Principles and Applications, 2nd ed.; Artech House Publishers: Norwood, MA, USA, 2005. [Google Scholar]
- Borre, K.; Akos, D.; Bertelsen, N.; Rinder, P.; Jensen, S. A Software–Defined GPS and Galileo Receiver. A Single–Frequency Approach; Birkhäuser: Boston, MA, USA, 2007. [Google Scholar]
- Pany, T. Navigation Signal Processing for GNSS Software Receivers; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Ioannides, R.T.; Pany, T.; Gibbons, G. Known Vulnerabilities of Global Navigation Satellite Systems, Status, and Potential Mitigation Techniques. Proc. IEEE 2016, 104, 1174–1194. [Google Scholar] [CrossRef]
- Gao, G.X.; Sgammini, M.; Lu, M.; Kubo, N. Protecting GNSS Receivers From Jamming and Interference. Proc. IEEE 2016, 104, 1327–1338. [Google Scholar] [CrossRef]
- Borio, D.; Dovis, F.; Kuusniemi, H.; Presti, L.L. Impact and Detection of GNSS Jammers on Consumer Grade Satellite Navigation Receivers. Proc. IEEE 2016, 104, 1233–1245. [Google Scholar] [CrossRef]
- Graham, A. Communications, Radar and Electronic Warfare; John Wiley & Sons: Hoboken, NJ, USA, 2011; p. 378. [Google Scholar]
- Pullen, S.; Gao, G. GNSS Jamming in the Name of Privacy. Inside GNSS 2012, 7, 34–43. [Google Scholar]
- Borio, D.; Cano, E. Optimal Global Navigation Satellite System pulse blanking in the presence of signal quantisation. IET Signal Process. 2013, 7, 400–410. [Google Scholar] [CrossRef]
- Borio, D.; Camoriano, L.; Lo Presti, L. Two-Pole and Multi-Pole Notch Filters: A Computationally Effective Solution for GNSS Interference Detection and Mitigation. IEEE Syst. J. 2008, 2, 38–47. [Google Scholar] [CrossRef]
- A Fresh Look at GNSS Anti-Jamming. Available online: https://ec.europa.eu/jrc/en/publication/fresh-look-gnss-anti-jamming (accessed on 9 July 2018).
- Zoubir, A.; Koivunen, V.; Chakhchoukh, Y.; Muma, M. Robust estimation in signal processing: A tutorial-style treatment of fundamental concepts. IEEE Signal Process. Mag. 2012, 29, 61–80. [Google Scholar] [CrossRef]
- Borio, D. Myriad Non-Linearity for GNSS Robust Signal Processing. IET Radar Sonar Navig. 2017, 11, 1467–1476. [Google Scholar] [CrossRef]
- Borio, D.; Closas, P. Complex Signum Non-Linearity for Robust GNSS Signal Processing. IET Radar Sonar Navig. 2018, 1–9. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Musumeci, L.; Dovis, F. Use of the Wavelet Transform for Interference Detection and Mitigation in Global Navigation Satellite Systems. Int. J. Navig. Obs. 2014, 2014, 262186. [Google Scholar] [CrossRef]
- Chien, Y.R.; Chen, P.Y.; Fang, S.H. Novel Anti-Jamming Algorithm for GNSS Receivers Using Wavelet-Packet-Transform-Based Adaptive Predictors. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, E100-A, 602–610. [Google Scholar] [CrossRef]
- Borio, D.; Li, H.; Closas, P. Huber’s Non-linearity for Robust Transformed Domain GNSS Signal Processing. In Proceedings of the 31st International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+), Miami, FL, USA, 24–28 September 2018; pp. 1–9, Accepted for presentation. [Google Scholar]
- Mitch, R.H.; Dougherty, R.C.; Psiaki, M.L.; Powell, S.P.; O’Hanlon, B.W.; Bhatti, J.A.; Humphreys, T.E. Signal Characteristics of Civil GPS Jammers. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION/GNSS), Portland, OR, USA, 20–23 September 2011; pp. 1907–1919. [Google Scholar]
- Borio, D.; O’Driscoll, C.; Fortuny, J. GNSS Jammers: Effects and countermeasures. In Proceedings of the 6th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012; pp. 1–7. [Google Scholar]
- Borio, D.; Closas, P. Robust Transform Domain Signal Processing for GNSS. Navigation 2018, 1–12, under review. [Google Scholar]
- Borio, D. Robust signal processing for GNSS. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 150–158. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Wang, X.; Poor, H.V. Robust multiuser detection in non-Gaussian channels. IEEE Trans. Signal Process. 1999, 47, 289–305. [Google Scholar] [CrossRef]
- Bechman, G.; Narici, L. Functional Analysis, 2nd ed.; Dover Publications: Mineola, NY, USA, 1998. [Google Scholar]
- Arce, G.R. Nonlinear Signal Processing: A Statistical Approach; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Theory; Pearson Education: London, UK, 1998; Volume 2. [Google Scholar]
- Fox, J.; Sanford, H. Robust regression. In An R and S-Plus Companion to Applied Regression; Sage: Newcastle upon Tyne, UK, 2002. [Google Scholar]
- Betz, J.W. Effect of Partial-Band Interference on Receiver Estimation of C/N0: Theory. In Proceedings of the National Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 22–24 January 2001; pp. 817–828. [Google Scholar]
- Betz, J.W. Effect of narrowband interference on GPS code tracking accuracy. In Proceedings of the National Technical Meeting of the Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 16–27. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Borio, D.; O’Driscoll, C.; Fortuny, J. Fast and Flexible Tracking and Mitigating a Jamming Signal with an Adaptive Notch Filter. Inside GNSS 2014, 9, 67–73. [Google Scholar]
- Borio, D. Loop analysis of adaptive notch filters. IET Signal Process. 2016, 10, 659–669. [Google Scholar] [CrossRef]
- Borio, D. Swept GNSS jamming mitigation through pulse blanking. In Proceedings of the European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016; pp. 1–8. [Google Scholar]
- Rügamer, A.; Joshi, S.; van der Merwe, J.R.; Garzia, F.; Felber, W.; Wendel, J.; Schubert, F.M. Chirp Mitigation for Wideband GNSS Signals with Filter Bank Pulse Blanking. In Proceedings of the 30th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+), Portland, OR, USA, 25–29 September 2017; pp. 3924–3940. [Google Scholar]
- Cuntz, M.; Konovaltsev, A.; Sgammini, M.; Hattich, C.; Kappen, G.; Meurer, M.; Hornbostel, A.; Dreher, A. Field Test: Jamming the DLR Adaptive Antenna Receiver. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS), Portland, OR, USA, 20–23 September 2011; pp. 384–392. [Google Scholar]
- De Lorenzo, D.S.; Antreich, F.; Denks, H.; Hornbostel, A.; Weber, C.; Enge, P. Testing of Adaptive Beamsteering for Interference Rejection in GNSS Receivers. Proc. ENC 2007, 2007, 1277–1287. [Google Scholar]
- Simon, M.K. Probability Distributions Involving Gaussian Random Variables: A Handbook for Engineers, Scientists and Mathematicians; Springer: Secaucus, NJ, USA, 2006. [Google Scholar]
| Parameter | Value |
|---|---|
| Sampling Frequency | MHz |
| Signal | GPS L1 C/A |
| Integration Time | 1 ms |
| 40 dB-Hz | |
| DFT size | 4000 samples |
| No. of Simulation Runs |
| Parameter | Value |
|---|---|
| Centre Frequency | 1575.42 MHz |
| Sampling Frequency | 10 MHz |
| Sampling Type | Complex I&Q |
| Number of bits | 16 |
| Parameter | GPS L1 C/A | Galileo E1c |
|---|---|---|
| Coherent integration time | 1 ms | 4 ms |
| Coherent integration time after bit/secondary code synchronization | 20 ms | 20 ms |
| DLL order | 2 | 2 |
| DLL bandwidth | 5 Hz | 5 Hz |
| PLL order | 3 | 3 |
| PLL bandwidth | 10 Hz | 10 Hz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borio, D.; Li, H.; Closas, P. Huber’s Non-Linearity for GNSS Interference Mitigation †. Sensors 2018, 18, 2217. https://doi.org/10.3390/s18072217
Borio D, Li H, Closas P. Huber’s Non-Linearity for GNSS Interference Mitigation †. Sensors. 2018; 18(7):2217. https://doi.org/10.3390/s18072217
Chicago/Turabian StyleBorio, Daniele, Haoqing Li, and Pau Closas. 2018. "Huber’s Non-Linearity for GNSS Interference Mitigation †" Sensors 18, no. 7: 2217. https://doi.org/10.3390/s18072217
APA StyleBorio, D., Li, H., & Closas, P. (2018). Huber’s Non-Linearity for GNSS Interference Mitigation †. Sensors, 18(7), 2217. https://doi.org/10.3390/s18072217





