Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model
Abstract
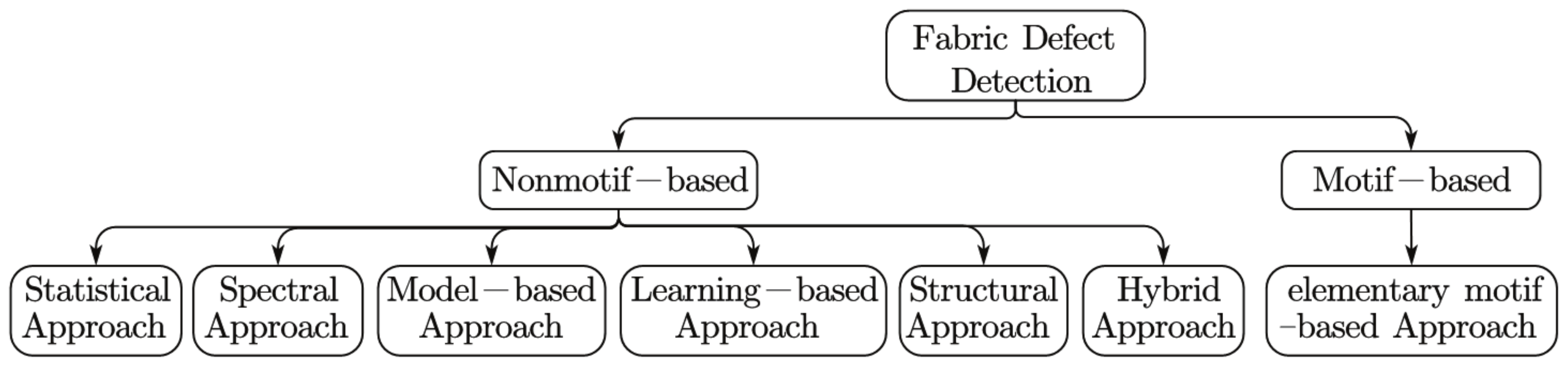
1. Introduction
- We proposed a new non-motif-based method MSCDAE which has the advantage of good compatibility for fabric defect detection. This method is a learning-based model that is suitable for the p1 and non-p1 types of fabrics. Experimental results have verified its good performance.
- The multi-pyramid and CDAE architectures in this model are novel and subtle. Specifically, processing in a multi-scale manner with pyramids may ensure the capture of sufficient textural properties, which are often data independent. In addition, applying the CDAE network can distinguish defective and defect-free patches easily through the use of reconstruction residual maps, which are more intuitive.
- This model is conducted in an unsupervised way, and no labeled ground truth or human intervention is needed. Furthermore, only defect-free samples are required for the training of this model. All these properties make it easier to apply the method in practice.
2. Related Works and Foundations
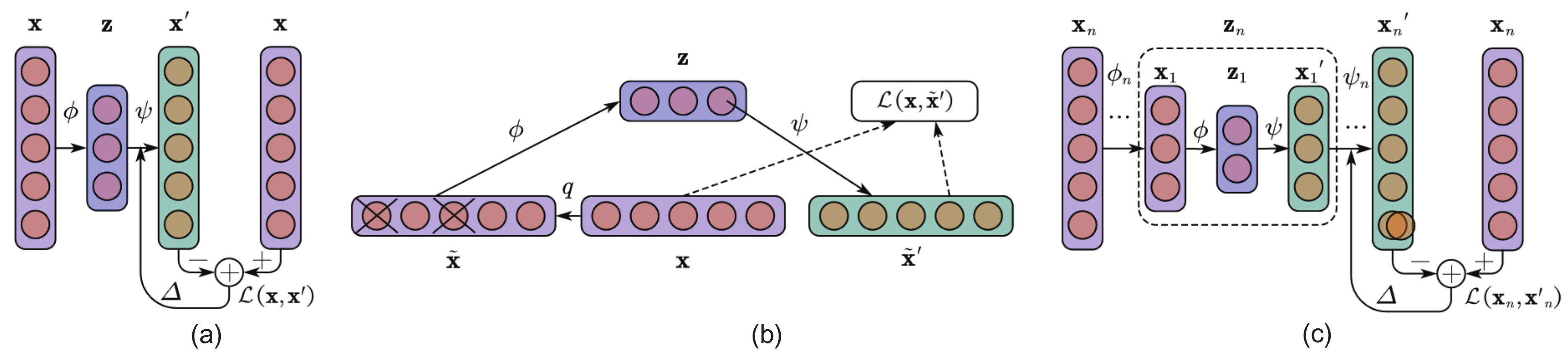
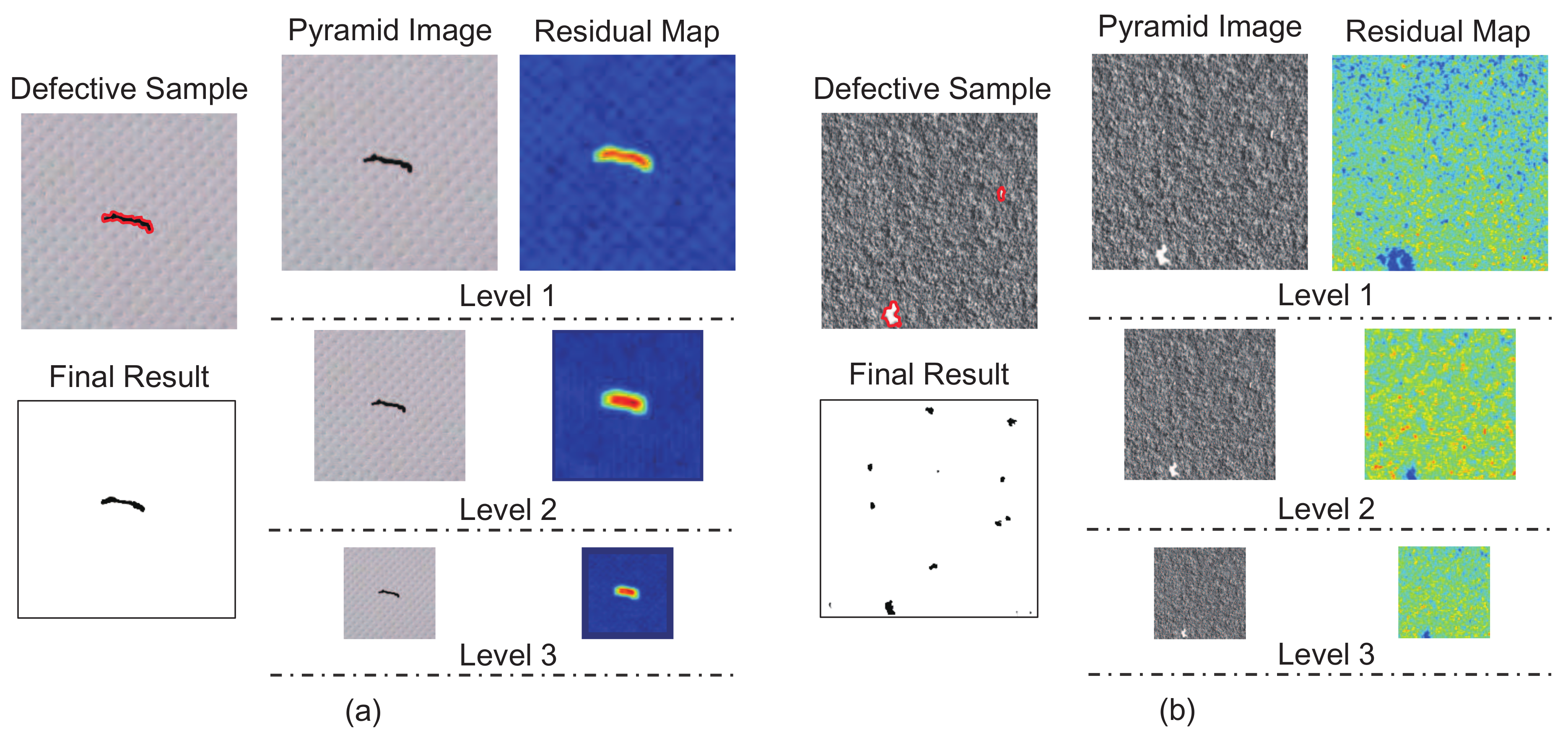
3. Proposed Methods
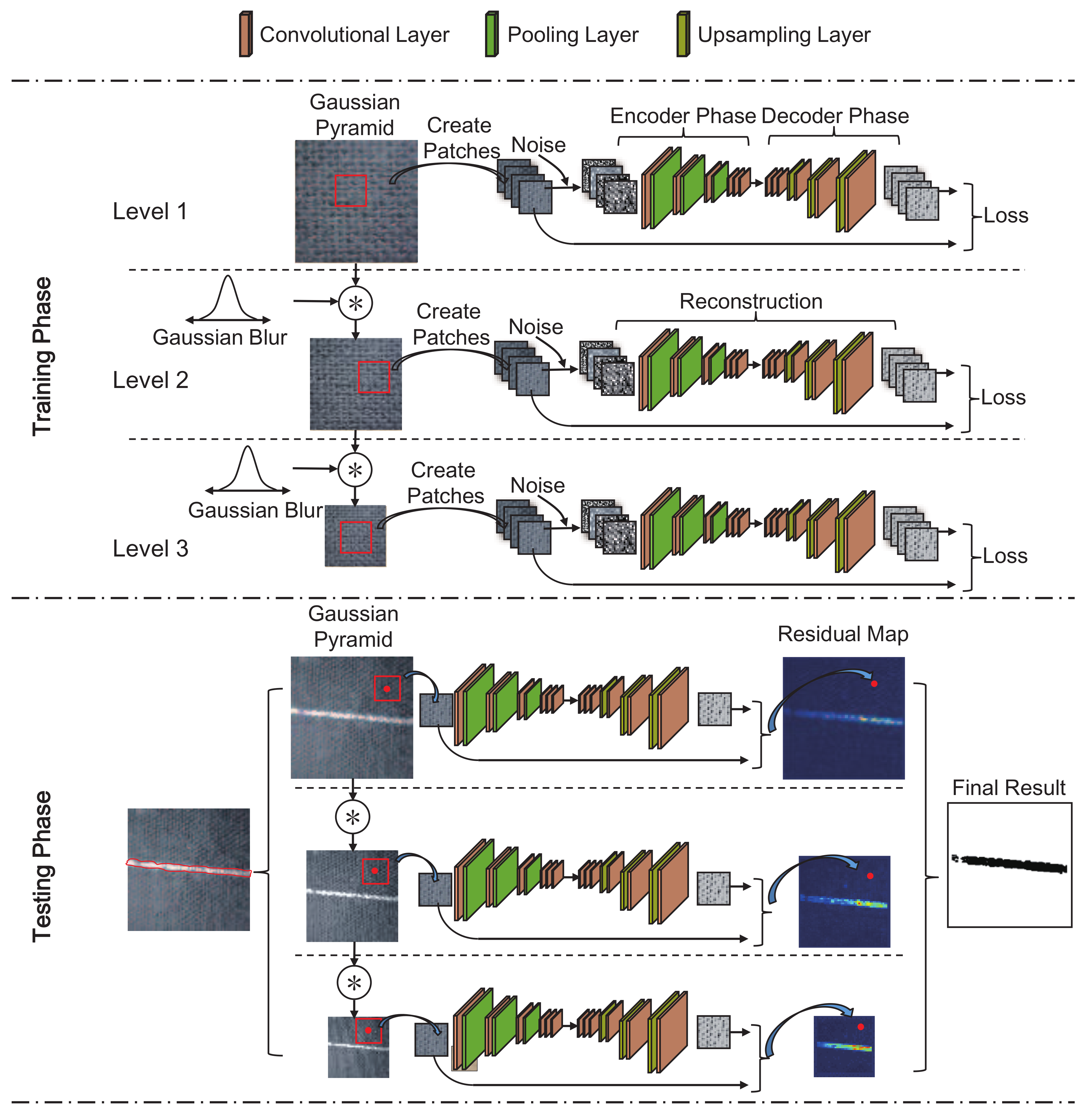
3.1. MSCDAE Model Training
3.1.1. Image Preprocessing
3.1.2. Patch Extraction
3.1.3. Model Training
| Step 1: , set |
| Step 2: for to m, |
| a. Calculate the partial derivatives and |
| b. Partial differential superposition: |
| Step 3: Update weight parameters: |
| a. Renew , ; |
| b. Disrupt the order of patches in the dataset and finish the current iteration epoch; |
3.1.4. Threshold Determination
3.2. MSCDAE Model Testing
3.2.1. Image Preprocessing
3.2.2. Patch Extraction
3.2.3. Residual Map Construction
3.2.4. Defect Segmentation
3.2.5. Result Synthesization
4. Experiments and Discussion
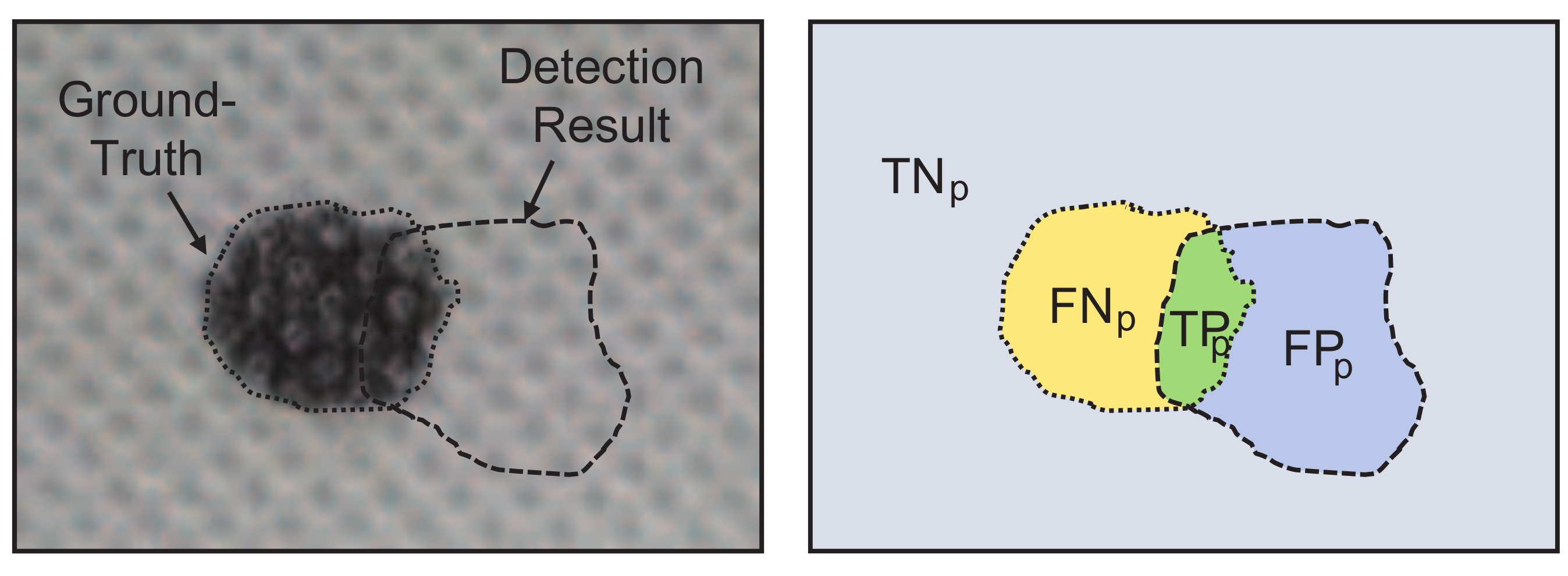
4.1. Datasets and Evaluation Criteria
4.2. Analysis of the Defect Detection Principle
4.3. Evaluation of Defect Detection Performance
4.4. Comparison of Defect Detection Performances
5. Implementation Details
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AE | Autoencoder |
| AOI | Automatic optical inspection |
| CAE | Convolutional autoencoder |
| CCD | Charge coupled device |
| CDAE | Convolutional denoising autoencoder |
| DCT | Discrete cosine transform |
| GPU | Graphics processing unit |
| MSCDAE | Multi-scale convolutional denoising autoencoder |
| NLSR | Nonlocal sparse representation |
| PCA | Principal component analysis |
| PHOT | Phase only transform |
| WLD | Weber local descriptor |
References
- Wikipedia. Fabric (Disambiguation). Available online: https://en.wikipedia.org/wiki/Fabric_(disambiguation) (accessed on 1 January 2018).
- Ngan, H.Y.; Pang, G.K.; Yung, N.H. Automated fabric defect detection—A review. Image Vis. Comput. 2011, 29, 442–458. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, J. Unsupervised fabric defect segmentation using local patch approximation. J. Text. Inst. 2016, 107, 800–809. [Google Scholar] [CrossRef]
- Hangzhou Chixiao Technology Co. Ltd. Fabric Surface Defect Online. Available online: https://chixiaotech.com/ (accessed on 1 January 2018).
- Joyce, D.E. Walpaper Groups. Available online: https://en.wikipedia.org/wiki/Wallpaper_group (accessed on 1 January 2018).
- Yapi, D.; Allili, M.S.; Baaziz, N. Automatic Fabric Defect Detection Using Learning-Based Local Textural Distributions in the Contourlet Domain. IEEE Trans. Autom. Sci. Eng. 2017, 99, 1–13. [Google Scholar] [CrossRef]
- Ng, M.K.; Ngan, H.Y.; Yuan, X.; Zhang, W. Patterned fabric inspection and visualization by the method of image decomposition. IEEE Trans. Autom. Sci. Eng. 2014, 11, 943–947. [Google Scholar] [CrossRef]
- Mak, K.L.; Peng, P.; Yiu, K. Fabric defect detection using morphological filters. Image Vis. Comput. 2009, 27, 1585–1592. [Google Scholar] [CrossRef]
- Lin, J.J. Applying a co-occurrence matrix to automatic inspection of weaving density for woven fabrics. Text. Res. J. 2002, 72, 486–490. [Google Scholar] [CrossRef]
- Aiger, D.; Talbot, H. The phase only transform for unsupervised surface defect detection. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 295–302. [Google Scholar]
- Liu, J.; Zuo, B. Identification of fabric defects based on discrete wavelet transform and back-propagation neural network. J. Text. Inst. 2007, 98, 355–362. [Google Scholar]
- Tilocca, A.; Borzone, P.; Carosio, S.; Durante, A. Detecting fabric defects with a neural network using two kinds of optical patterns. Text. Res. J. 2002, 72, 545–550. [Google Scholar] [CrossRef]
- Bissi, L.; Baruffa, G.; Placidi, P.; Ricci, E.; Scorzoni, A.; Valigi, P. Automated defect detection in uniform and structured fabrics using Gabor filters and PCA. J. Vis. Commun. Image Represent. 2013, 24, 838–845. [Google Scholar] [CrossRef]
- Harinath, D.; Babu, K.R.; Satyanarayana, P.; Murthy, M.R. Defect Detection in Fabric using Wavelet Transform and Genetic Algorithm. Trans. Mach. Learn. Artif. Intell. 2016, 3, 10. [Google Scholar] [CrossRef]
- Qu, T.; Zou, L.; Zhang, Q.; Chen, X.; Fan, C. Defect detection on the fabric with complex texture via dual-scale over-complete dictionary. J. Text. Inst. 2016, 107, 743–756. [Google Scholar] [CrossRef]
- Ngan, H.Y.; Pang, G.K.; Yung, S.; Ng, M.K. Wavelet based methods on patterned fabric defect detection. Pattern Recognit. 2005, 38, 559–576. [Google Scholar] [CrossRef]
- Jia, L.; Chen, C.; Liang, J.; Hou, Z. Fabric defect inspection based on lattice segmentation and Gabor filtering. Neurocomputing 2017, 238, 84–102. [Google Scholar] [CrossRef]
- Li, Y.; Ai, J.; Sun, C. Online Fabric Defect Inspection Using Smart Visual Sensors. Sensors 2013, 13, 4659–4673. [Google Scholar] [CrossRef] [PubMed]
- Madrigal, C.A.; Branch, J.W.; Restrepo, A.; Mery, D. A Method for Automatic Surface Inspection Using a Model-Based 3D Descriptor. Sensors 2017, 17, 2262. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhao, W.; Pan, J. Deformable patterned fabric defect detection with Fisher criterion-based deep learning. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1256–1264. [Google Scholar] [CrossRef]
- Yapi, D.; Mejri, M.; Allili, M.S.; Baaziz, N. A learning-based approach for automatic defect detection in textile images. IFAC-PapersOnLine 2015, 48, 2423–2428. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Lin, Y. Combining Fisher criterion and deep learning for patterned fabric defect inspection. IEICE Trans. Inf. Syst. 2016, 99, 2840–2842. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Wang, H.; Núñez, A.; Han, Z. Automatic defect detection of fasteners on the catenary support device using deep convolutional neural network. IEEE Trans. Instrum. Meas. 2018, 67, 257–269. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, X.; Bai, S.; Yao, C.; Bai, X. Deep learning representation using autoencoder for 3D shape retrieval. Neurocomputing 2016, 204, 41–50. [Google Scholar] [CrossRef]
- Malek, S.; Melgani, F.; Mekhalfi, M.L.; Bazi, Y. Real-Time Indoor Scene Description for the Visually Impaired Using Autoencoder Fusion Strategies with Visible Cameras. Sensors 2017, 17, 2641. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Ji, K.; Leng, X.; Xing, X.; Zou, H. Synthetic aperture radar target recognition with feature fusion based on a stacked autoencoder. Sensors 2017, 17, 192. [Google Scholar] [CrossRef] [PubMed]
- Gu, F.; Flórez-Revuelta, F.; Monekosso, D.; Remagnino, P. Marginalised stacked denoising autoencoders for robust representation of real-time multi-view action recognition. Sensors 2015, 15, 17209–17231. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Jia, P.; Qiao, S.; Duan, S. Self-Taught Learning Based on Sparse Autoencoder for E-Nose in Wound Infection Detection. Sensors 2017, 17, 2279. [Google Scholar] [CrossRef] [PubMed]
- Zeiler, M.D.; Taylor, G.W.; Fergus, R. Adaptive deconvolutional networks for mid and high level feature learning. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2018–2025. [Google Scholar]
- Klein, S.; Pluim, J.P.; Staring, M.; Viergever, M.A. Adaptive stochastic gradient descent optimisation for image registration. Int. J. Comput. Vis. 2009, 81, 227–239. [Google Scholar] [CrossRef]
- Wang, B.; Li, W.; Yang, W.; Liao, Q. Illumination normalization based on weber’s law with application to face recognition. IEEE Signal Process. Lett. 2011, 18, 462–465. [Google Scholar] [CrossRef]
- Chen, J.; Shan, S.; He, C.; Zhao, G.; Pietikainen, M.; Chen, X.; Gao, W. WLD: A robust local image descriptor. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1705–1720. [Google Scholar] [CrossRef] [PubMed]
- Leo Breiman, P.S. Submodel Selection and Evaluation in Regression. The X-Random Case. Int. Stat. Rev. 1992, 60, 291–319. [Google Scholar] [CrossRef]
- Mei, S.; Yang, H.; Yin, Z. Unsupervised-Learning-Based Feature-Level Fusion Method for Mura Defect Recognition. IEEE Trans. Semicond. Manuf. 2017, 30, 105–113. [Google Scholar] [CrossRef]
- Kim, W.; Kim, C. Total variation flow-based multiscale framework for unsupervised surface defect segmentation. Opt. Eng. 2012, 51, 127201. [Google Scholar] [CrossRef]
- Escofet, J.; Navarro, R.; Pladellorens, J.; Garcia-Verela, M.S.M. Detection of local defects in textile webs using Gabor filters. Opt. Eng. 1998, 37, 2297–2307. [Google Scholar]
- Kampouris, C.; Zafeiriou, S.; Ghosh, A.; Malassiotis, S. Fine-Grained Material Classification Using Micro-Geometry and Reflectance. In Proceedings of the European Conference on Computer Vision–ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 778–792. [Google Scholar]
- Fritz, M.; Eric Hayman, B.C.; Eklundh, J.O. THE KTH-TIPS Database. Available online: http://www.nada.kth.se/cvap/databases/kth-tips/doc/ (accessed on 20 January 2018).
- Kylberg, G. The Kylberg Texture Dataset v. 1.0. In External Report (Blue Series) 35, Centre for Image Analysis; Swedish University of Agricultural Sciences and Uppsala University: Uppsala, Sweden, 2011. [Google Scholar]
- Lin, H.D. Tiny surface defect inspection of electronic passive components using discrete cosine transform decomposition and cumulative sum techniques. Image Vis. Comput. 2008, 26, 603–621. [Google Scholar] [CrossRef]
- Tong, L.; Wong, W.; Kwong, C. Fabric Defect Detection for Apparel Industry: A Nonlocal Sparse Representation Approach. IEEE Access 2017, 5, 5947–5964. [Google Scholar] [CrossRef]
- Chollet, F. Keras: The Python Deep Learning library. Available online: https://keras.io/#support (accessed on 25 January 2018).






| Criterion(%) | (a) Series | (b) Series | (c) Series | (d) Series | (e) Series | (f) Series | (g) Series | (h) Series |
|---|---|---|---|---|---|---|---|---|
| Recall | 0.5316 | 0.6102 | 0.9177 | 0.8366 | 0.9098 | 0.7936 | 0.9521 | 0.9355 |
| Precision | 0.6531 | 0.7349 | 0.6453 | 0.7573 | 0.4251 | 0.6517 | 0.3758 | 0.3942 |
| F1-Measure | 0.5861 | 0.6667 | 0.7578 | 0.7950 | 0.5794 | 0.7157 | 0.5389 | 0.5547 |
| Criterion(%) | |||
|---|---|---|---|
| Fabrics (62 samples) | 87.5 (21/24) | 18.4 (7/38) | 83.8 |
| KTH-TIPS (128 samples) | 84.1 (37/44) | 14.3 (12/84) | 85.2 |
| Kylberg Texture (132 samples) | 85.3 (29/34) | 21.4 (21/98) | 80.3 |
| ms-Texture (50 samples) | 84.6 (11/13) | 16.2 (6/37) | 84.0 |
| Criteria | Recall | Precision | F1-Measure | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples | DCT | PHOT | NLSR | Ours | DCT | PHOT | NLSR | Ours | DCT | PHOT | NLSR | Ours | |
| (a) series | 0.7352 | 0.6131 | 0.9325 | 0.9256 | 0.8985 | 0.2417 | 0.7148 | 0.8353 | 0.8087 | 0.0.3467 | 0.8093 | 0.8781 | |
| (b) series | 0.7912 | 0.5484 | 0.7743 | 0.7959 | 0.3251 | 0.7254 | 0.4487 | 0.6584 | 0.4608 | 0.6246 | 0.5682 | 0.7206 | |
| (c) series | 0.8359 | 0.5495 | 0.7018 | 0.7347 | 0.1025 | 0.8571 | 0.4497 | 0.8953 | 0.1826 | 0.6697 | 0.5482 | 0.8071 | |
| (d) series | 0.8547 | 0.6988 | 0.8416 | 0.9451 | 0.8222 | 0.6134 | 0.5491 | 0.8121 | 0.8381 | 0.6533 | 0.6646 | 0.8736 | |
| (e) series | 0.3035 | 0.4862 | 0.5351 | 0.4795 | 0.1032 | 0.2142 | 0.1749 | 0.6024 | 0.1540 | 0.2974 | 0.2636 | 0.5540 | |
| (f) series | 0.2435 | 0.5101 | 0.7482 | 0.8353 | 0.1759 | 0.1016 | 0.5412 | 0.6333 | 0.2043 | 0.1694 | 0.6281 | 0.7204 | |
| (g) series | 0.8912 | 0.1117 | 0.6381 | 0.6479 | 0.3540 | 0.1984 | 0.2264 | 0.3951 | 0.5067 | 0.1429 | 0.3342 | 0.4909 | |
| (h) series | 0.7781 | 0.5426 | 0.4105 | 0.7414 | 0.1684 | 0.1158 | 0.3003 | 0.6357 | 0.2769 | 0.1909 | 0.3469 | 0.6845 | |
| Accuracy (%) | DCT | PHOT | NLSR | Ours |
|---|---|---|---|---|
| Fabrics (62 samples) | 71.0 | 62.9 | 79.0 | 83.8 |
| KTH-TIPS (128 samples) | 69.5 | 64.8 | 75.8 | 85.2 |
| Kylberg Texture (132 samples) | 76.5 | 68.2 | 81.1 | 80.3 |
| ms-Texture (50 samples) | 78 | 54.0 | 68.0 | 84.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, S.; Wang, Y.; Wen, G. Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model. Sensors 2018, 18, 1064. https://doi.org/10.3390/s18041064
Mei S, Wang Y, Wen G. Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model. Sensors. 2018; 18(4):1064. https://doi.org/10.3390/s18041064
Chicago/Turabian StyleMei, Shuang, Yudan Wang, and Guojun Wen. 2018. "Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model" Sensors 18, no. 4: 1064. https://doi.org/10.3390/s18041064
APA StyleMei, S., Wang, Y., & Wen, G. (2018). Automatic Fabric Defect Detection with a Multi-Scale Convolutional Denoising Autoencoder Network Model. Sensors, 18(4), 1064. https://doi.org/10.3390/s18041064





