Polar Cooperative Navigation Algorithm for Multi-Unmanned Underwater Vehicles Considering Communication Delays
Abstract
1. Introduction
2. Polar Cooperative Navigation System
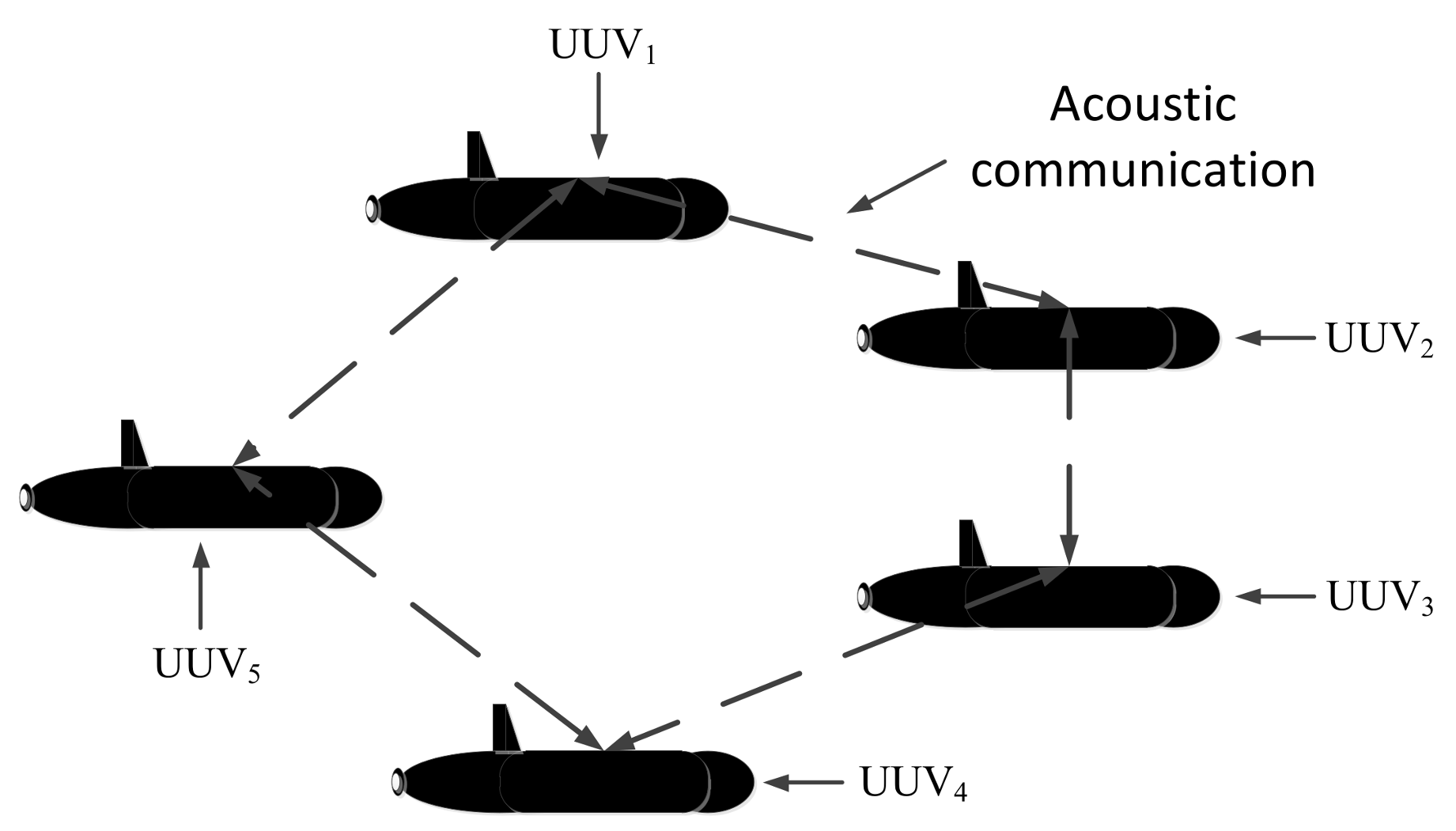
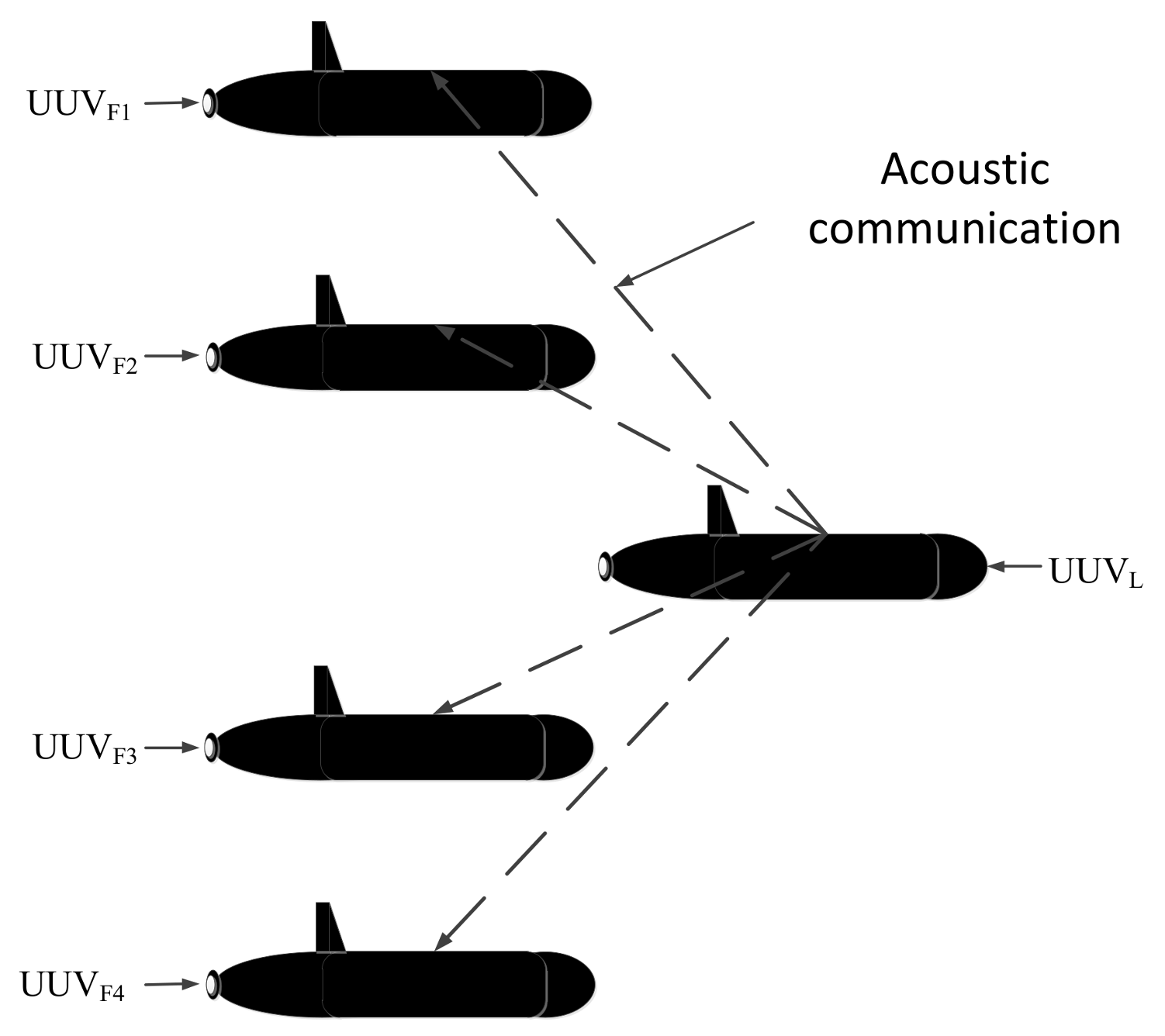
2.1. Formation Configuration
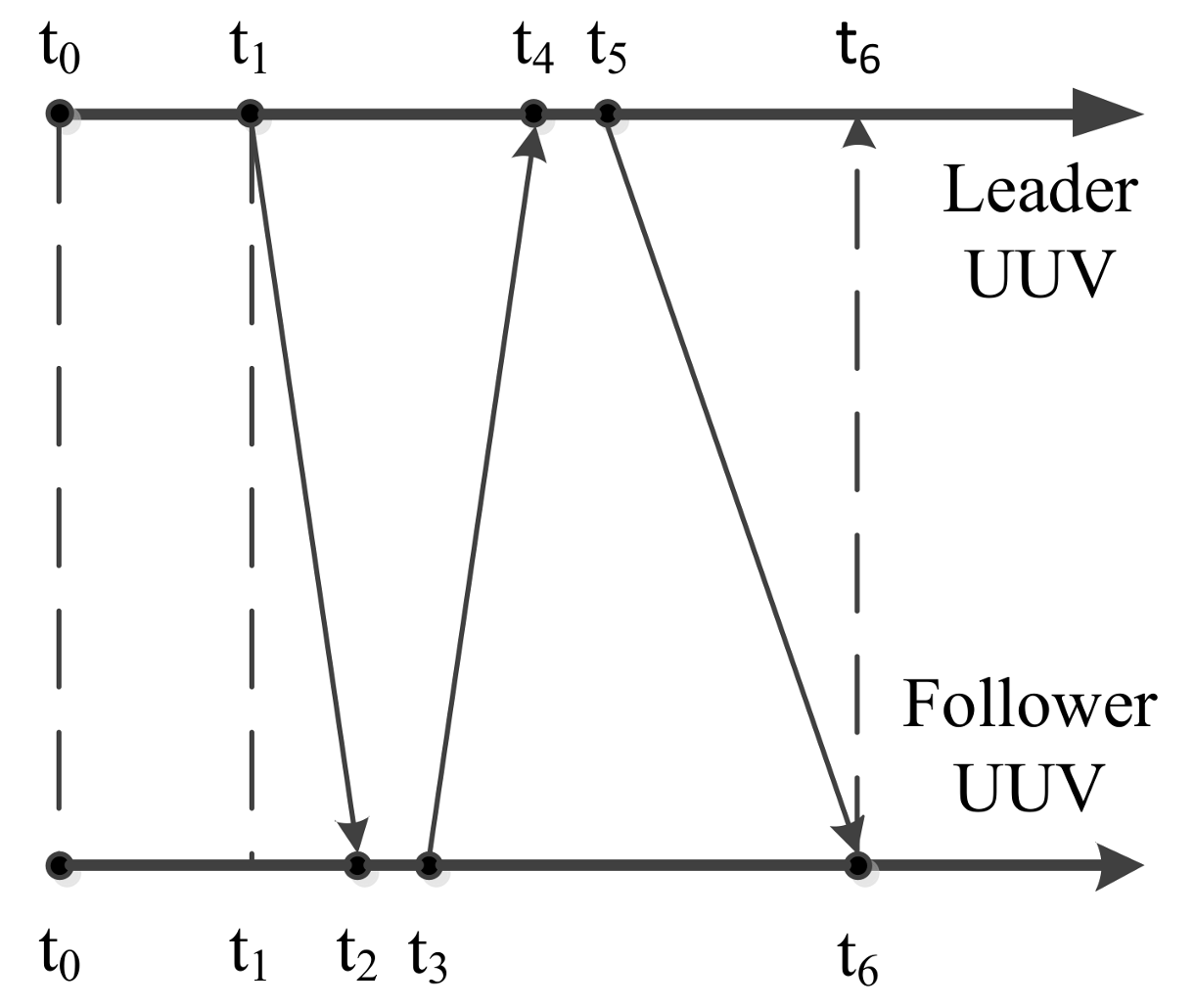
2.2. Underwater Acoustic Communication Delay
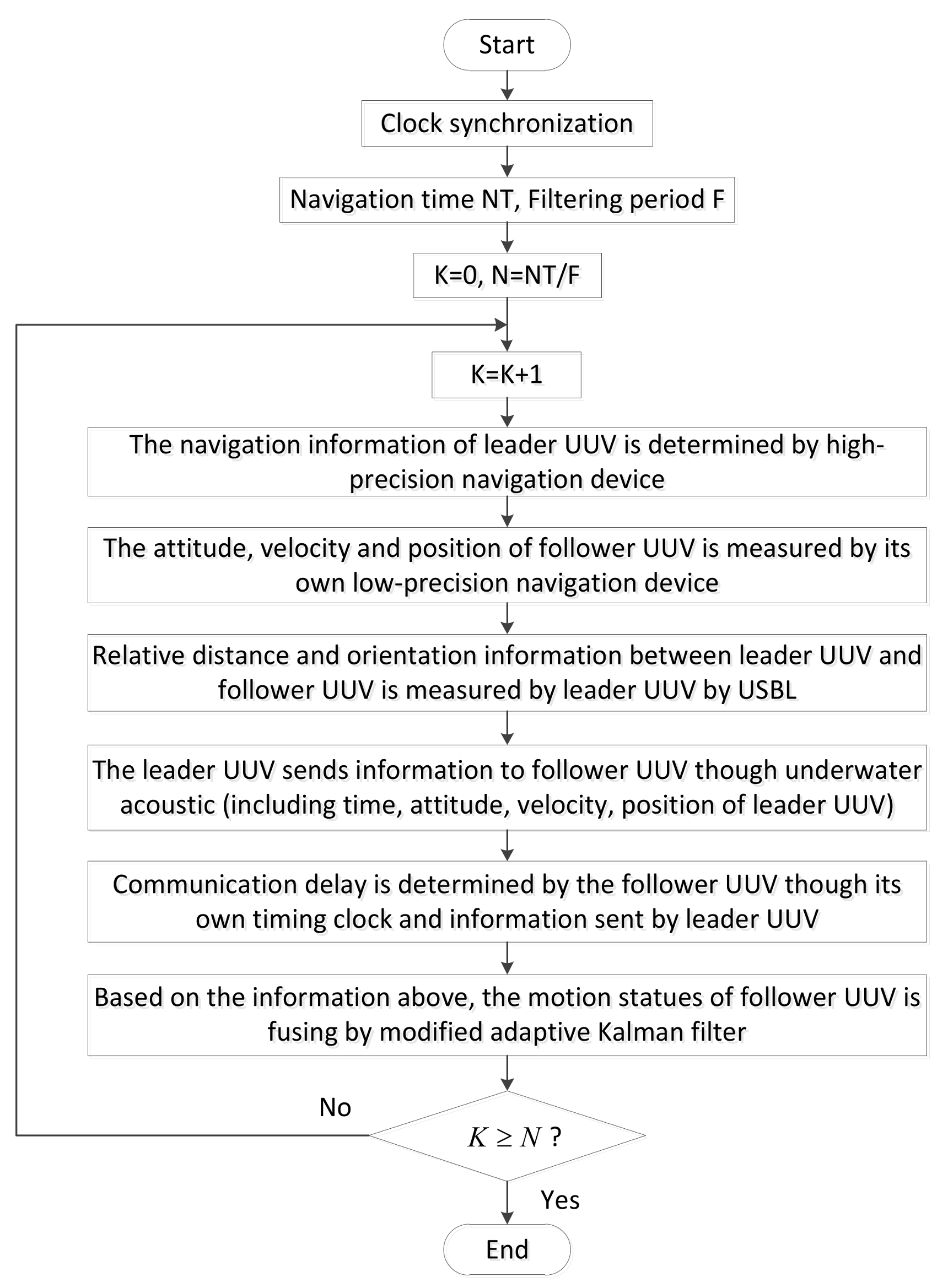
2.3. Overall Process of the Polar Cooperative Navigation Algorithm
3. Error Equations of the Polar Cooperative Navigation Algorithm
- Inertial frame— frame;
- Navigation frame— frame;
- Body frame of UUV— frame;
- Geographic frame— frame;
- Earth centered earth fixed frame— frame;
- Grid frame— frame;
- Body frame of DVL— frame;
- Acoustic array frame of USBL— frame.
3.1. Attitude Error Equation of a Follower UUV
3.2. Velocity Error Equation of a Follower UUV
3.3. Position Error Equation of the Follower UUV
3.4. Error Model of DVL in the Follower UUV
3.5. Error Model of USBL
4. Filter Models of the Follower UUV in the Polar Cooperative Navigation Algorithm
4.1. Dynamic Model
4.2. Observation Model
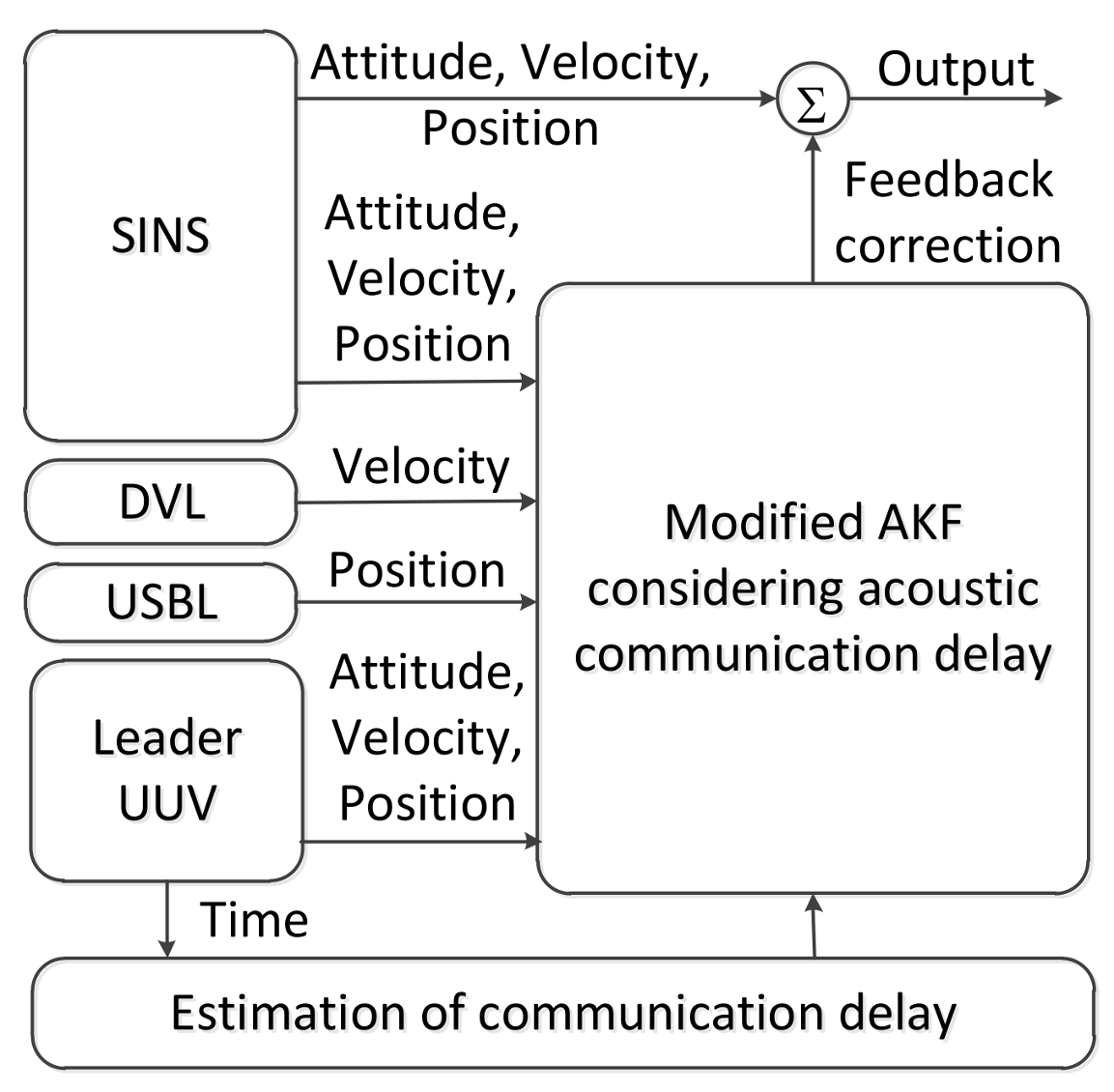
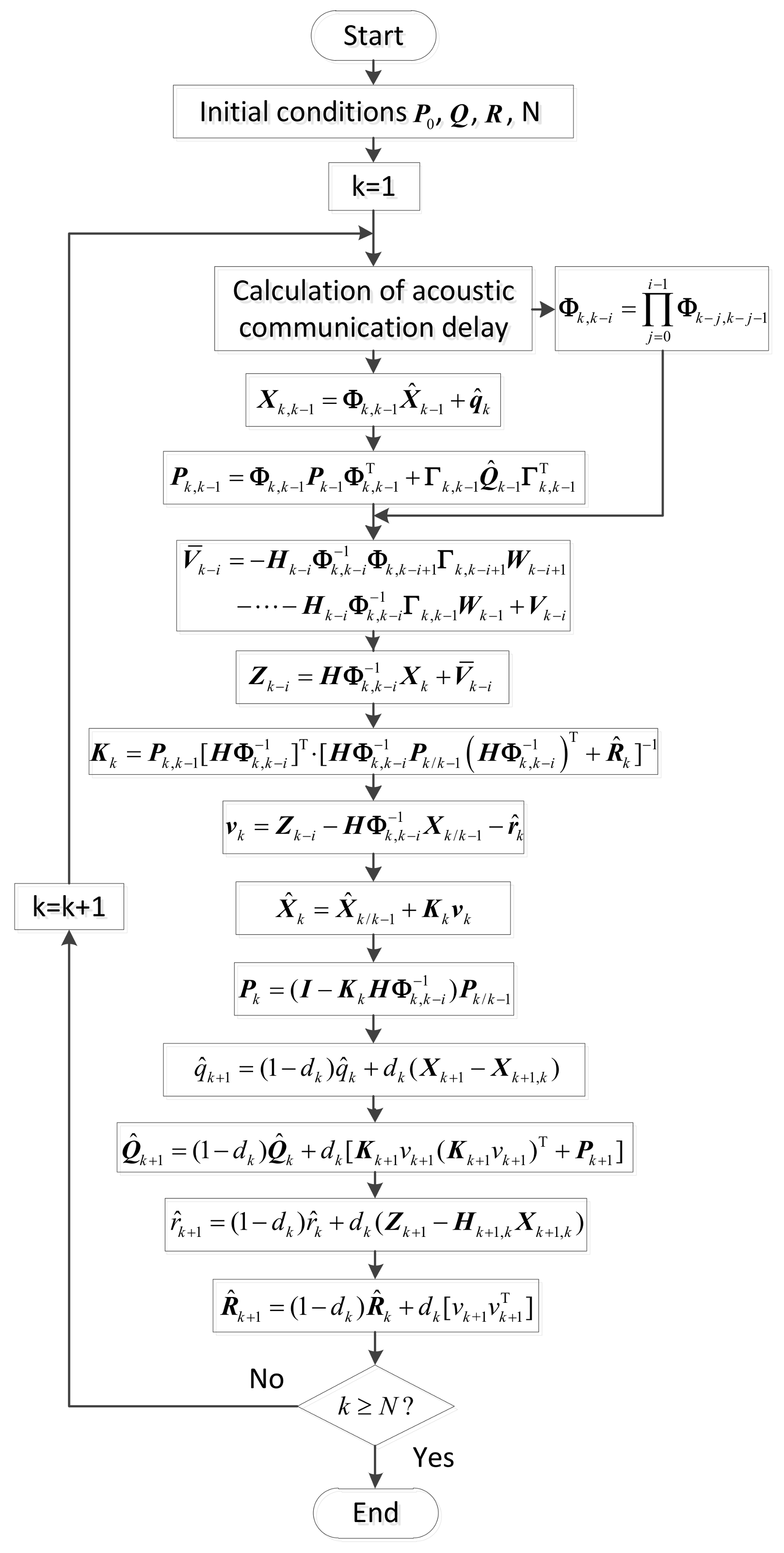
5. Modified Adaptive Kalman Filter Considering Communication Delays
5.1. Conventional Adaptive Kalman Filter
5.2. Underwater Acoustic Communication Delay in AKF
5.3. Modified Adaptive Kalman Filter Considering Communication Delays
6. Results and Discussion
6.1. Simulation Results and Analyses
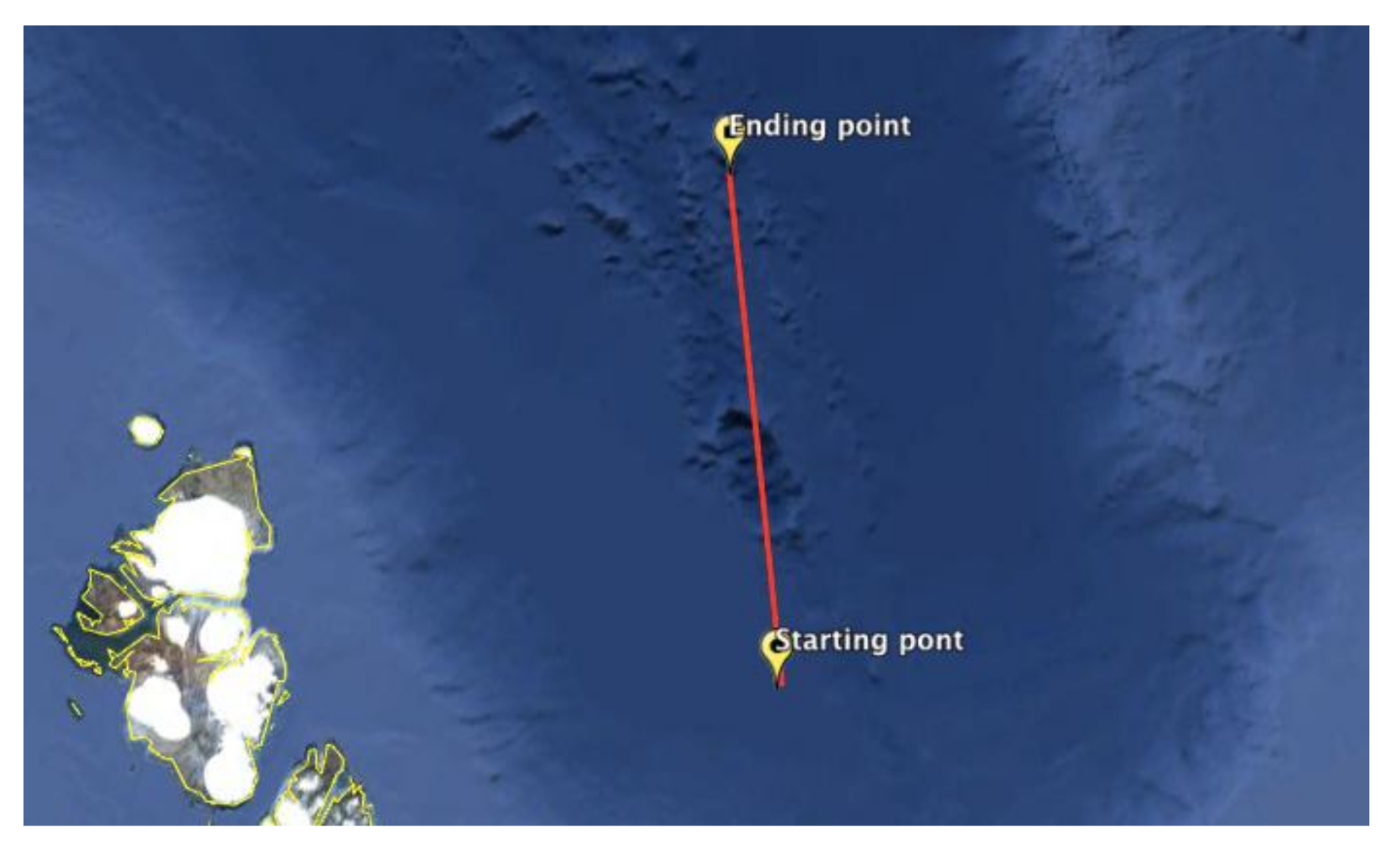
6.2. Experiment Results and Analyses
6.3. Discussions
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jacobi, M. Autonomous inspection of underwater structures. Robot. Auton. Syst. 2015, 67, 80–86. [Google Scholar] [CrossRef]
- Wynn, R.B.; Huvenne, V.A.I.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Cao, X.; Zhu, D.Q.; Simon, X.Y. Multi-AUV Target Search Based on Bioinspired Neurodynamics Model in 3-D Underwater Environments. IEEE Trans. Neural Netw. Learn. Syst. 2016, 21, 2364–2374. [Google Scholar] [CrossRef] [PubMed]
- Gerigk, M.K. Modeling of Combined Phenomena Affecting an AUV Stealth Vehicle. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2016, 10, 665–669. [Google Scholar] [CrossRef]
- Zhou, Q. All-Earth Inertial Navigation Algorithm for Large Aircraft. Northwest. Polytech. Univ. 2013, 10, 156–161. (In Chinese) [Google Scholar]
- Zhou, Q.; Qin, Y.Y.; Fu, Q.W.; Yue, Y.Z. Grid mechanization in Inertial Navigation Syatem for Transpolar Aircraft. J. Northwest. Polytech. Univ. 2013, 31, 210–217. (In Chinese) [Google Scholar]
- Cheng, J.H.; Wang, T.D.; Guan, D.X.; Li, M.L. Polar transfer alignment of shipborne SINS with a large misalignment angle. Meas. Sci. Technol. 2016, 27, 035101. [Google Scholar] [CrossRef]
- Xu, B.; Bai, J.L.; Hao, Y.L.; Gao, W.; Liu, Y.L. The research status and progress of cooperative navigation for multiple AUVs. Acta Autom. Sin. 2015, 41, 445–461. (In Chinese) [Google Scholar] [CrossRef]
- Liu, M.Y. Cooperative Navigation Technology for Underwater Vehicles, 1st ed.; National Defense Industry Press: Beijing, China, 2014; pp. 14–15. [Google Scholar]
- Matos, A.; Cruz, N. AUV navigation and guidance in a moving acoustic network. Proc. IEEE/MTS OCEANS Conf. Exhib. 2005, 1, 680–685. [Google Scholar]
- Vaganay, J.; Leonard, J.; Curcio, J.; Willcox, J.S. Experimental validation of the moving long base line navigation concept. Proc. IEEE/OES AUV Conf. 2004, 59–65. [Google Scholar] [CrossRef]
- Liu, J.; Cai, B.G.; Wang, J. Cooperative localization of connected vehicles: Integrating GNSS with DSRC using a robust cubature Kalman filter. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2111–2125. [Google Scholar] [CrossRef]
- Manzoor, S.; Lee, S.; Choi, Y. A Coordinated navigation strategy for multi-robots to capture a target moving with unknown speed. J. Intell. Robot. Syst. 2017, 87, 627–641. [Google Scholar] [CrossRef]
- Scheggi, S.; Aggravi, M.; Prattichizzo, D. Cooperative navigation for mixed human-robot teams using haptic feedback. IEEE Trans. Hum. Mach. Syst. 2017, 47, 462–473. [Google Scholar] [CrossRef]
- Xiao, G.D.; Wang, S.T.; Wang, B.; Deng, Z.H. A cooperative navigation method based on USBL. In Proceedings of the 2016 China International Conference on Inertial Technology and Navigation, Beijing, China, 1 November 2016; pp. 586–590. [Google Scholar]
- Xiao, G.D.; Wang, B.; Deng, Z.H.; Fu, M.; Ling, Y. An Acoustic Communication Time Delays Compensation Approach for Master-Slave AUV Cooperative Navigation. IEEE Sens. J. 2017, 17, 504–513. [Google Scholar] [CrossRef]
- Allotta, B.; Caiti, A.; Costanzi, R.; Di Corato, F.; Fenucci, D.; Monni, N.; Pugi, L. Cooperative navigation of AUVs via acoustic communication networking: Field experience with the Typhoon vehicles. Auton. Robots 2016, 40, 1229–1244. [Google Scholar] [CrossRef]
- Gao, W.; Yang, J.; Liu, J.; Xu, B.; Shi, H.Y. Cooperative location of multiple UUVs based on hydro-acoustic communication delay. Syst. Eng. Electron. 2014, 36, 539–545. (In Chinese) [Google Scholar] [CrossRef]
- Yan, Z.P.; Wang, L.; Zhang, W.; Zhou, J.; Wang, M. Polar Grid Navigation Algorithm for Unmanned Underwater Vehicles. Sensors 2017, 17, 01599. [Google Scholar] [CrossRef]
- Thong, Y.K.; Woolfson, M.S.; Crowe, J.A.; Hayes-Gill, B.R.; Challis, R.E. Dependence of inertial measurements of distance on accelerometer noise. Meas. Sci. Technol. 2002, 13, 1163–1172. [Google Scholar] [CrossRef]
- Bian, H.W.; Jin, Z.H.; Tian, W.F. Study on GPS attitude determination system aided INS using adaptive Kalman filter. Meas. Sci. Technol. 2005, 16, 2072–2079. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G. Robust Student’s t-Based Stochastic Cubature Filter for Nonlinear Systems With Heavy-Tailed Process and Measurement Noises. IEEE Access. 2017, 5, 7964–7974. [Google Scholar] [CrossRef]
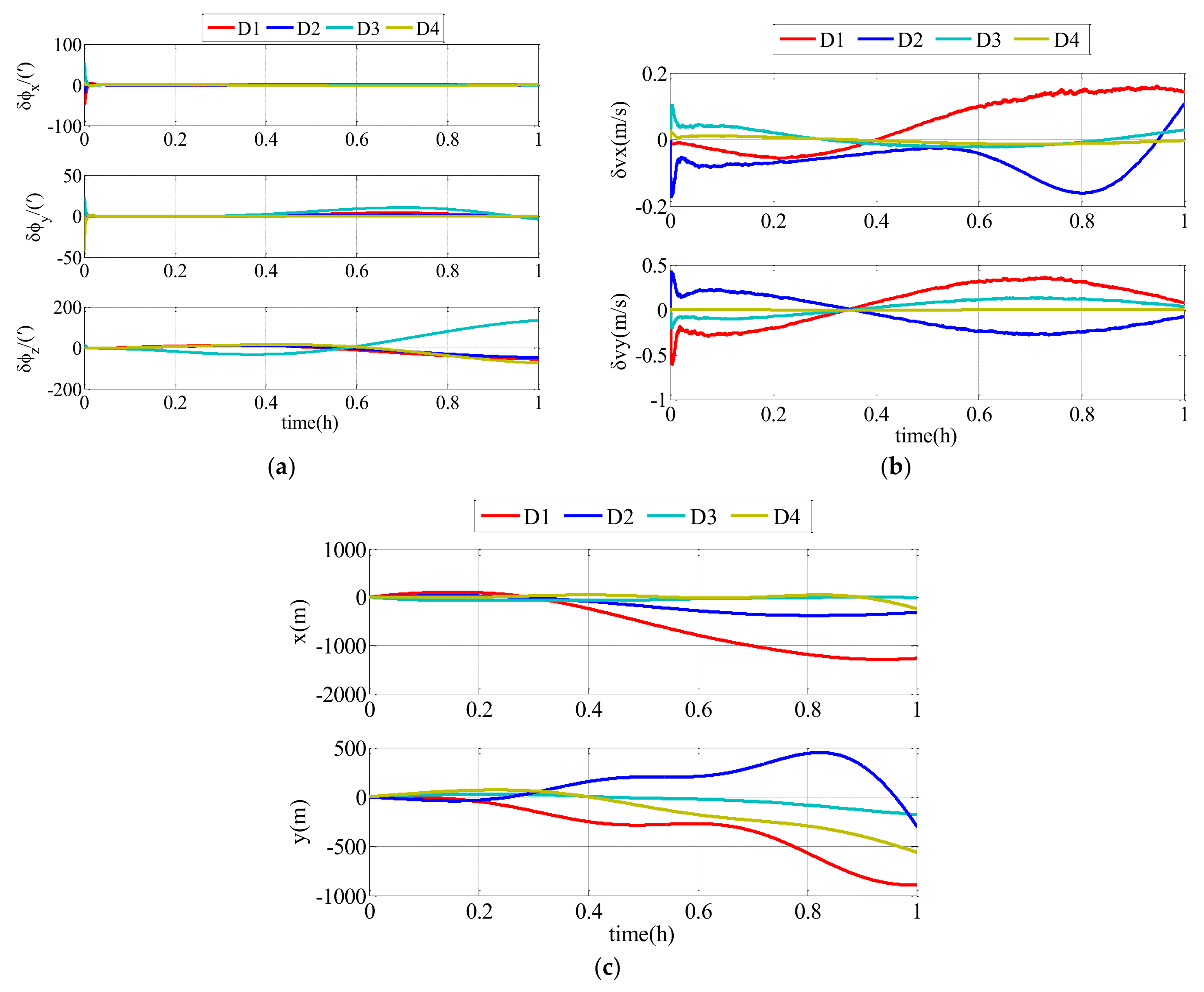
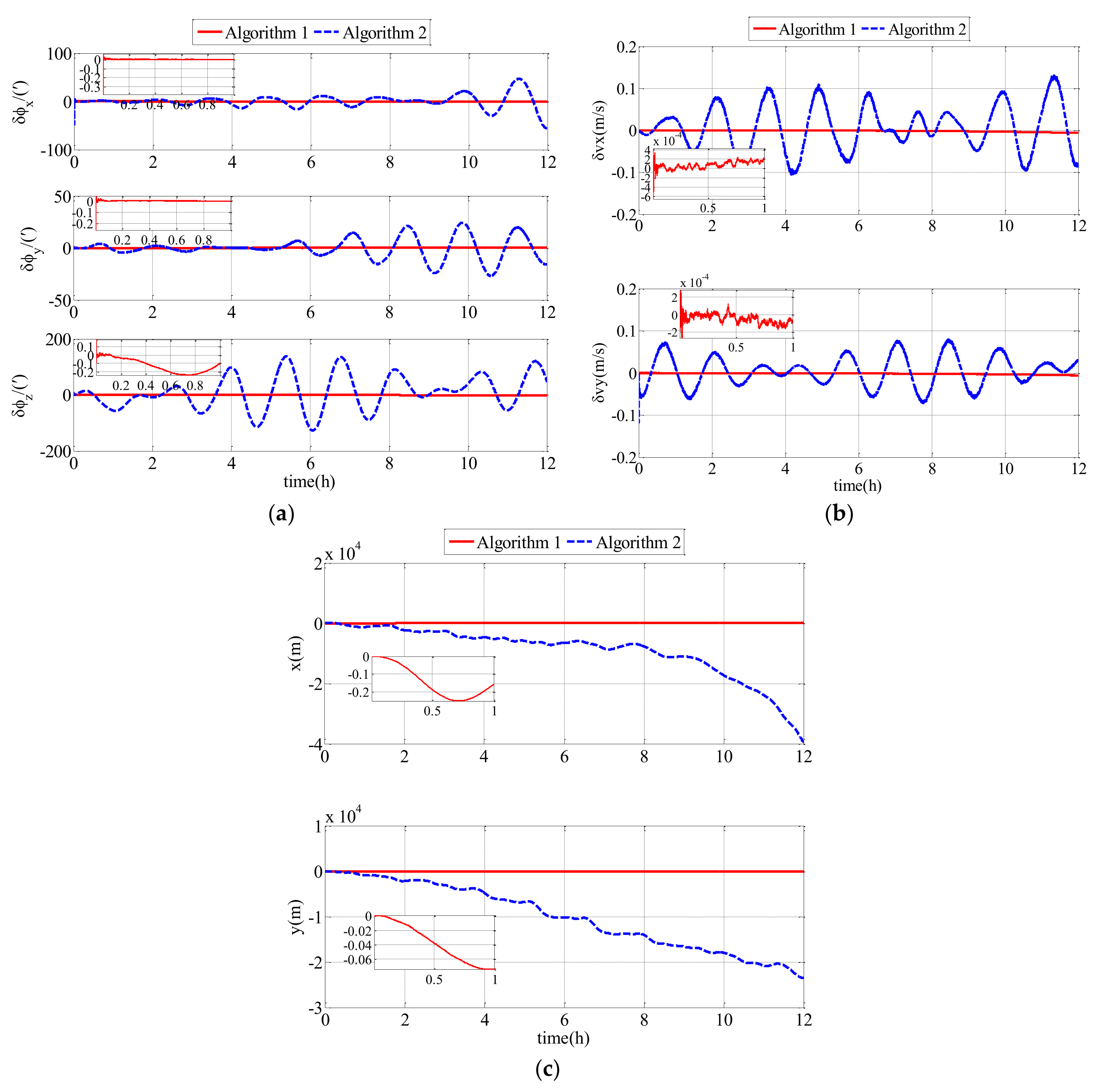

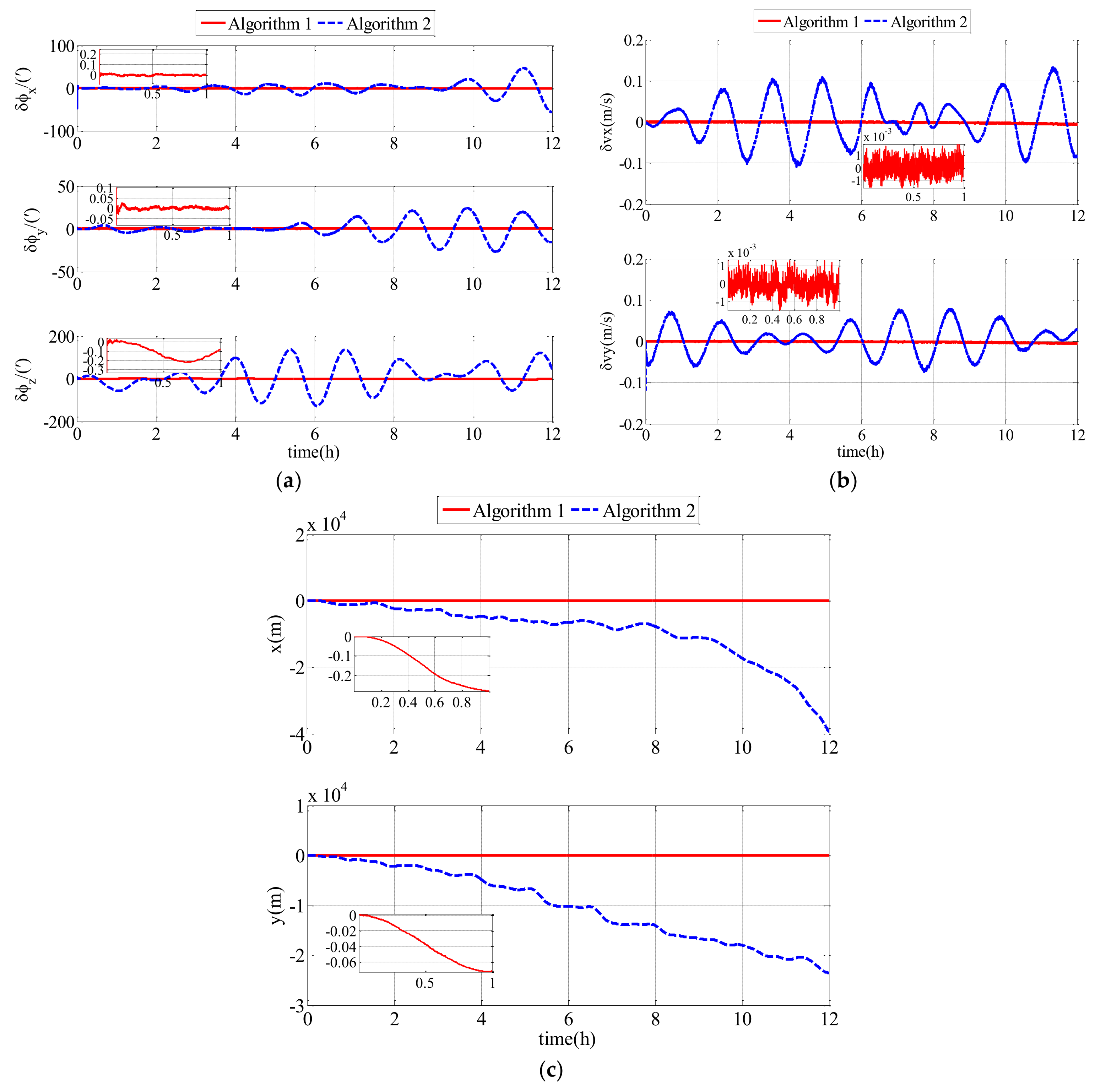
| Parameters | D1 | D2 | D3 | D4 |
|---|---|---|---|---|
| /(′) | 0.9893 | 0.3130 | 0.0474 | 0.0734 |
| /(′) | 0.0646 | 0.1698 | 0.2496 | 0.1341 |
| /(′) | 3.0777 | 1.5085 | 0.8161 | 0.8719 |
| /(m/s) | 0.0045 | 0.0083 | 0.0150 | 0.0202 |
| /(m/s) | 0.0520 | 0.0184 | 0.0401 | 0.0028 |
| /(m) | 63.667 | 40.433 | 21.188 | 3.120 |
| /(m) | 28.437 | 21.082 | 13.080 | 4.240 |
| Parameters | Algorithm 1 | Algorithm 2 |
|---|---|---|
| /(′) | 0.0229 | 13.5681 |
| /(′) | 0.0291 | 10.1113 |
| /(′) | 1.2218 | 62.1246 |
| /(m/s) | 0.0021 | 0.0550 |
| /(m/s) | 0.0022 | 0.0355 |
| /(m) | 37.3563 | 1252.2 |
| /(m) | 9.5654 | 1244.7 |
| Parameters | Algorithm 1 | Algorithm 2 |
|---|---|---|
| /(′) | 0.0242 | 13.5848 |
| /(′) | 0.0266 | 10.1178 |
| /(′) | 1.2140 | 62.1555 |
| /(m/s) | 0.0021 | 0.0551 |
| /(m/s) | 0.0022 | 0.0355 |
| /(m) | 37.1366 | 1253.2 |
| /(m) | 9.4960 | 1244.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Wang, L.; Wang, T.; Yang, Z.; Chen, T.; Xu, J. Polar Cooperative Navigation Algorithm for Multi-Unmanned Underwater Vehicles Considering Communication Delays. Sensors 2018, 18, 1044. https://doi.org/10.3390/s18041044
Yan Z, Wang L, Wang T, Yang Z, Chen T, Xu J. Polar Cooperative Navigation Algorithm for Multi-Unmanned Underwater Vehicles Considering Communication Delays. Sensors. 2018; 18(4):1044. https://doi.org/10.3390/s18041044
Chicago/Turabian StyleYan, Zheping, Lu Wang, Tongda Wang, Zewen Yang, Tao Chen, and Jian Xu. 2018. "Polar Cooperative Navigation Algorithm for Multi-Unmanned Underwater Vehicles Considering Communication Delays" Sensors 18, no. 4: 1044. https://doi.org/10.3390/s18041044
APA StyleYan, Z., Wang, L., Wang, T., Yang, Z., Chen, T., & Xu, J. (2018). Polar Cooperative Navigation Algorithm for Multi-Unmanned Underwater Vehicles Considering Communication Delays. Sensors, 18(4), 1044. https://doi.org/10.3390/s18041044




