Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications
Abstract
1. Introduction
2. Correlator Architecture
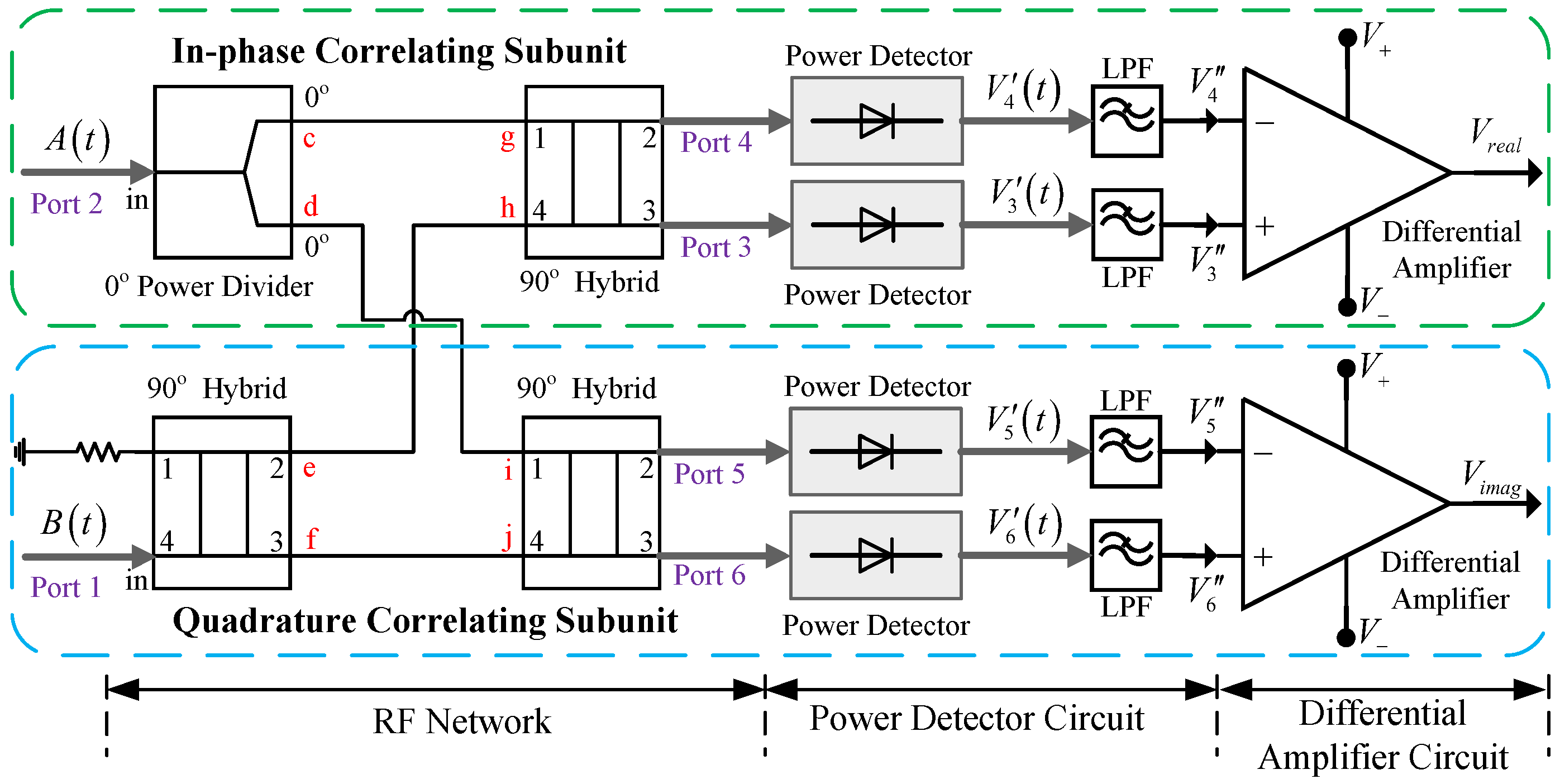
2.1. Diode-Based Analog Complex Cross-Correlator
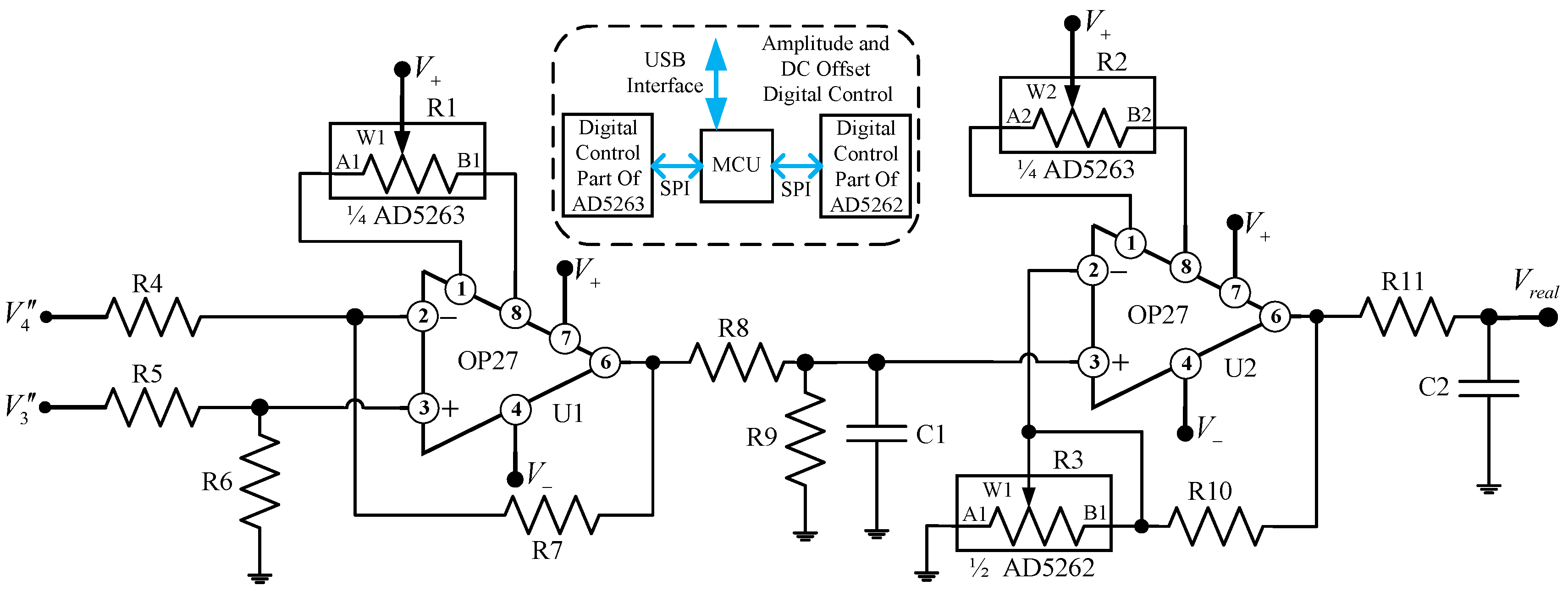
2.2. Digital Tunable Readout Electronics
3. Calibration of the Correlator
3.1. Hardware Calibration Scheme
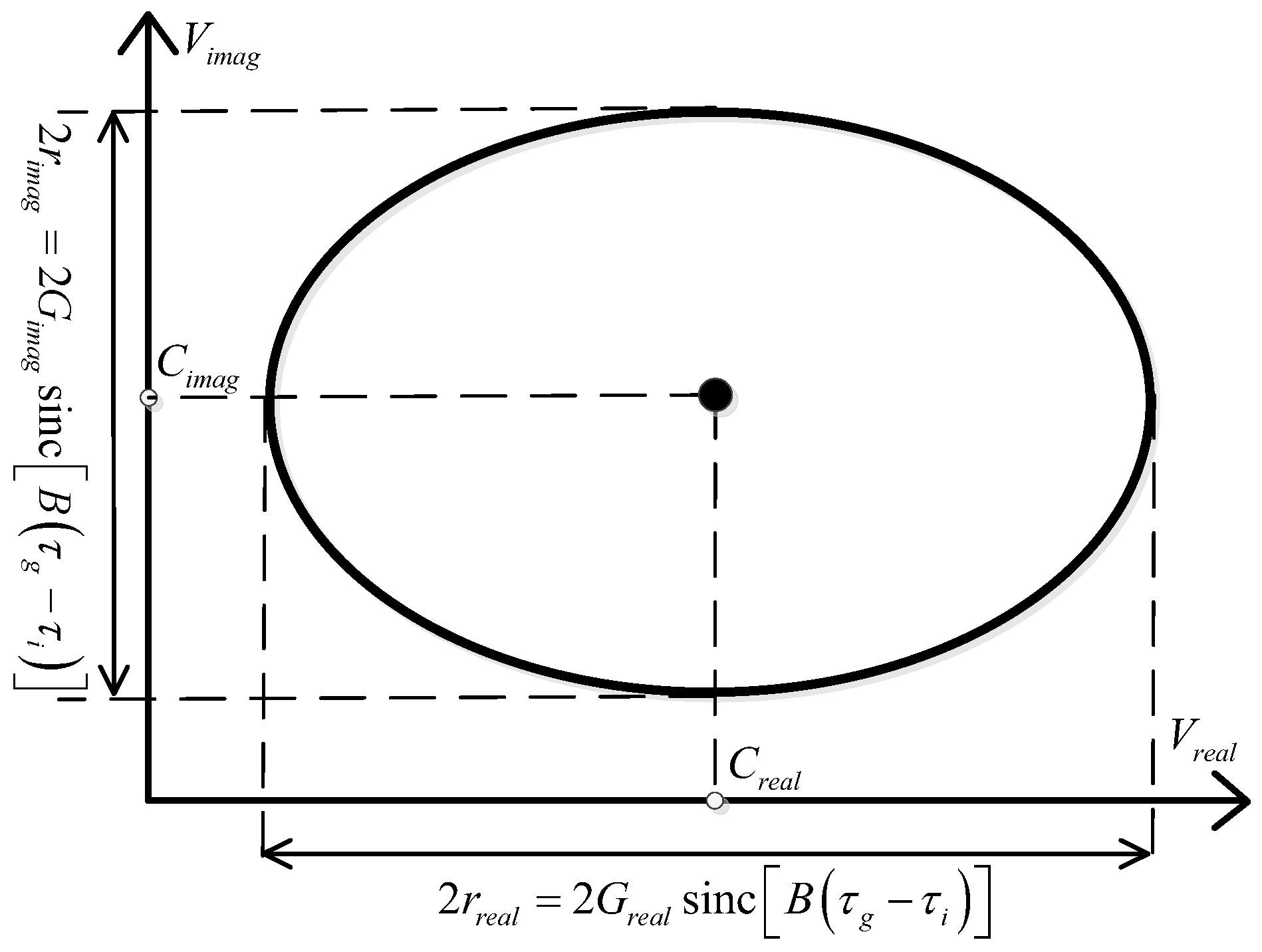
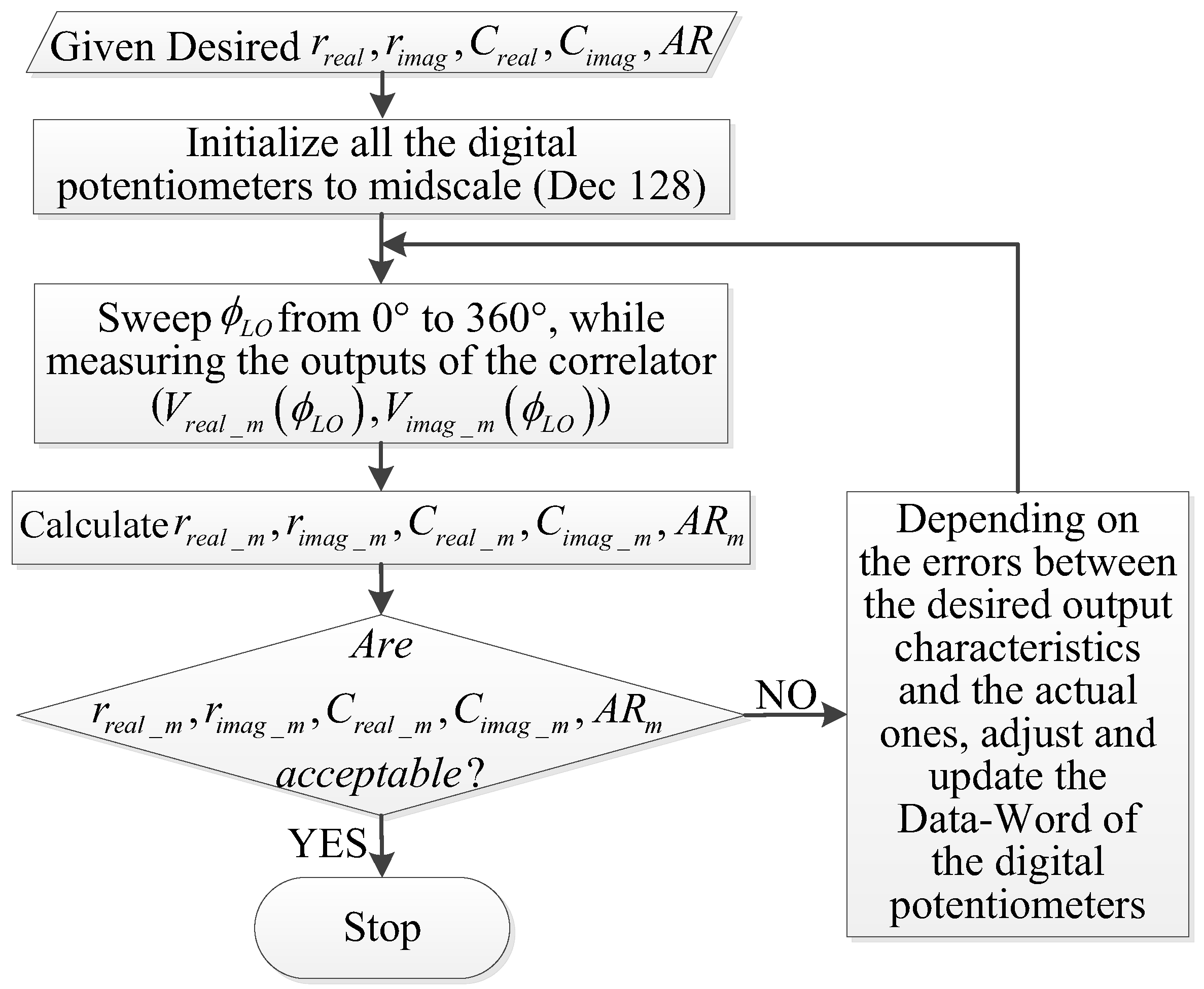
3.2. Quadrature Errors and Residual DC Offsets Calibration Algorithm
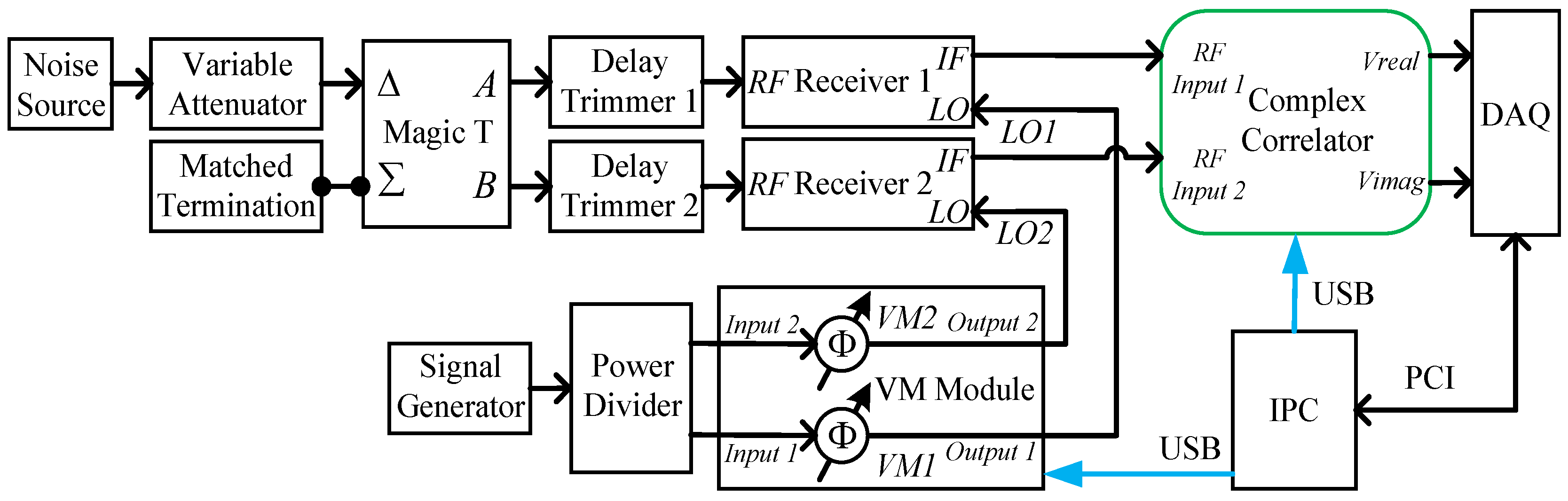
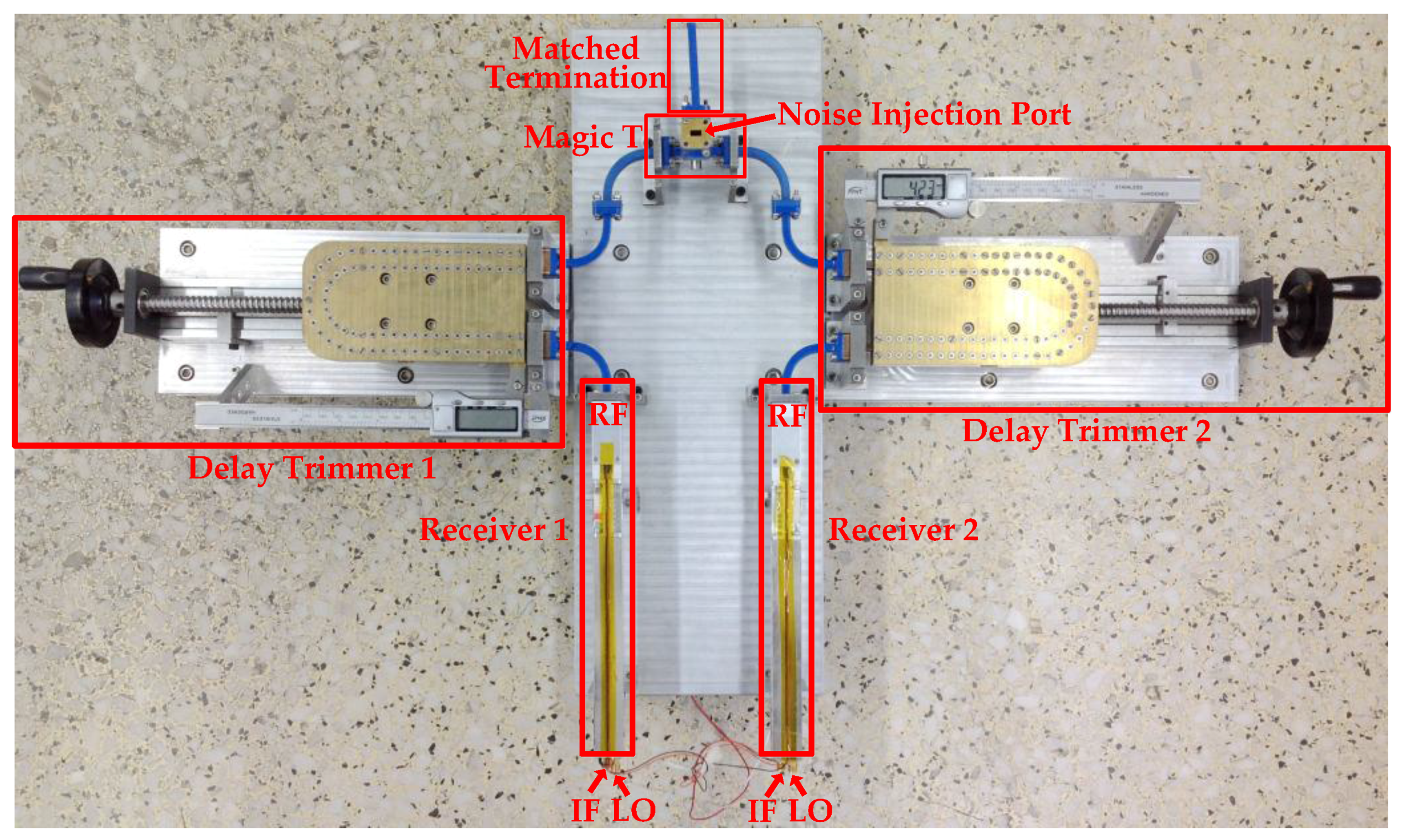
4. Experimental Realization
4.1. Experimental Analog Complex Cross-Correlator
4.2. Experimental System
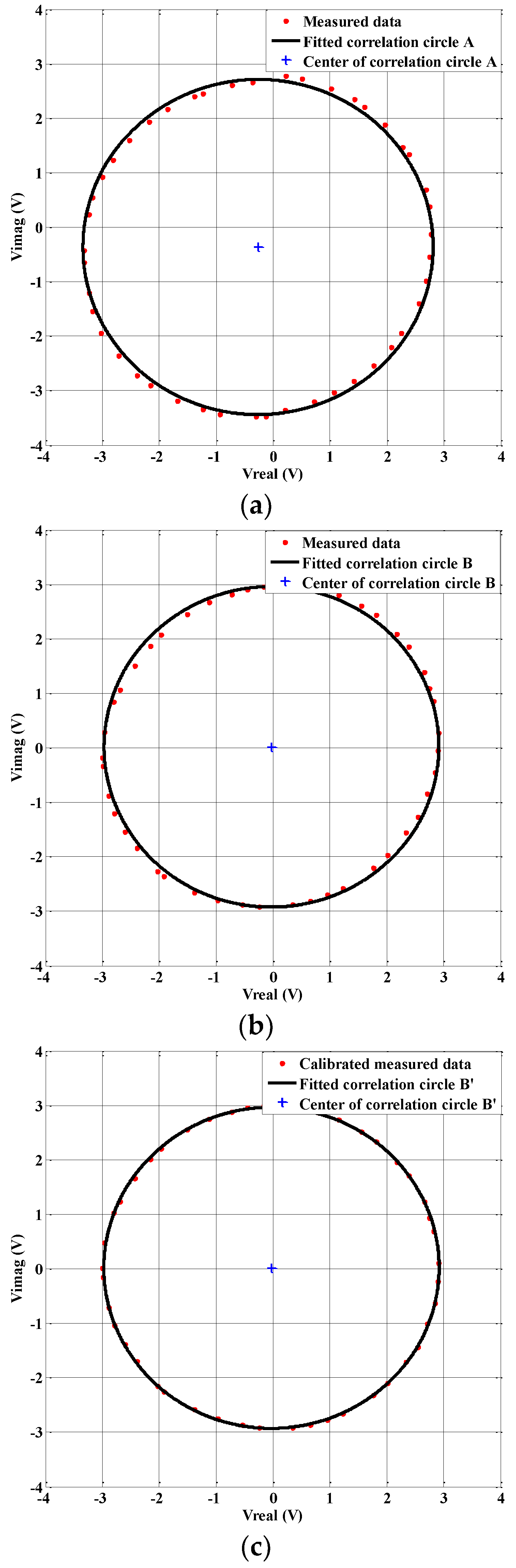
4.3. Hardware Calibration of the Outputs Amplitudes and DC Offsets
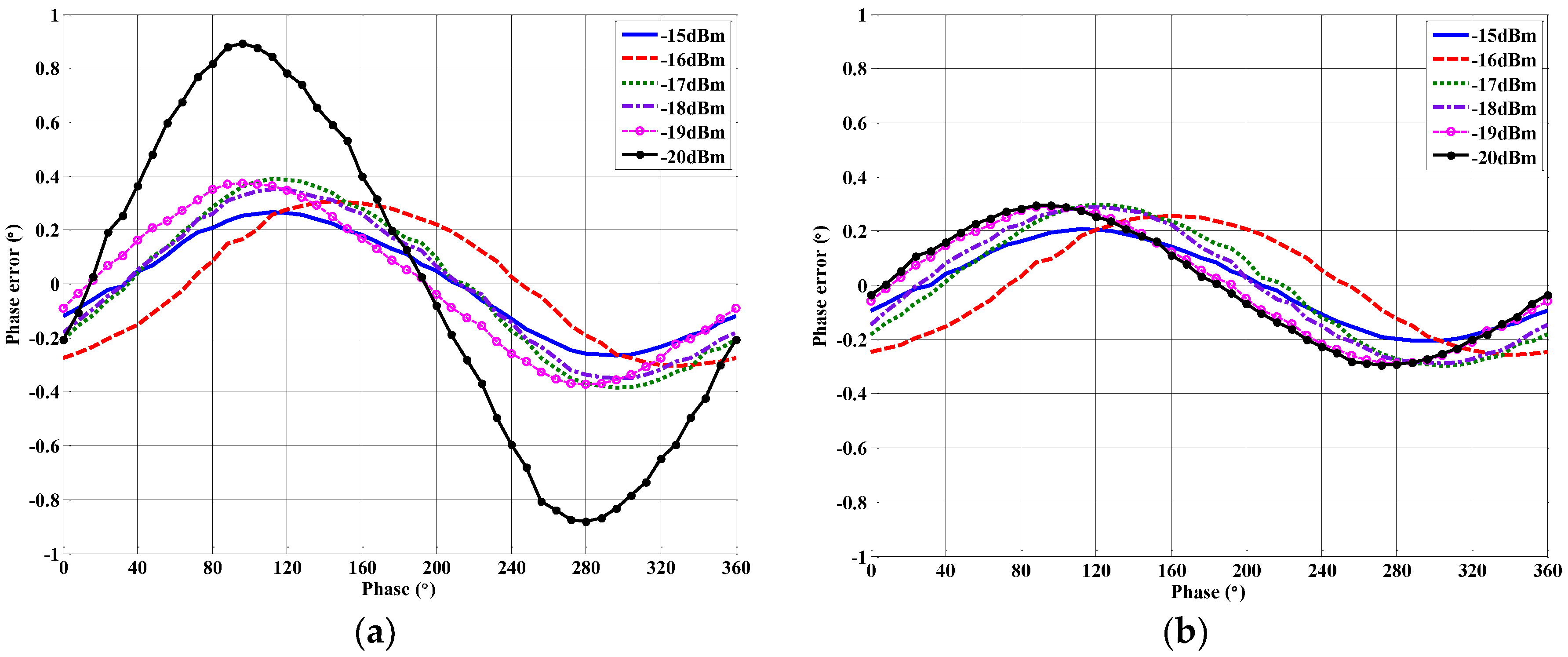
4.4. Calibration of the Quadrature Errors and Residual DC Offsets
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Le Vine, D.M. The sensitivity of synthetic aperture radiometers for remote sensing applications from space. Radio Sci. 1990, 25, 441–453. [Google Scholar] [CrossRef]
- Le Vine, D.M. Synthetic aperture radiometer systems. IEEE Trans. Microw. Theory Tech. 1999, 47, 2228–2236. [Google Scholar] [CrossRef]
- Weber, J.C.; Pospieszalski, M.W. Microwave instrumentation for radio astronomy. IEEE Trans. Microw. Theory Tech. 2002, 50, 986–995. [Google Scholar] [CrossRef]
- Thompson, A.R.; Moran, J.M.; Swenson, G.W., Jr. Interferometry and Synthesis in Radio Astronomy; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Yujiri, L.; Shoucri, M.; Moffa, P. Passive millimeter wave imaging. IEEE Microw. Mag. 2003, 4, 39–50. [Google Scholar] [CrossRef]
- Appleby, R.; Wallace, H.B. Standoff detection of weapons and contraband in the 100 GHz to 1 THz region. IEEE Trans. Antennas Propag. 2007, 55, 2944–2956. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Schiessl, A.; Gumbmann, F.; Tiebout, M.; Methfessel, S.; Schmidt, L.P. Advanced microwave imaging. IEEE Microw. Mag. 2012, 13, 26–43. [Google Scholar] [CrossRef]
- Patel, V.M.; Mait, J.N.; Prather, D.W.; Hedden, A.S. Computational millimeter wave imaging: Problems, progress and prospects. IEEE Signal Process. Mag. 2016, 33, 109–118. [Google Scholar] [CrossRef]
- Nanzer, J.A. Microwave and Millimeter-Wave Remote Sensing for Security Applications; Artech House: Norwood, MA, USA, 2012. [Google Scholar]
- Corbella, I.; Camps, A.; Torres, F.; Bara, J. Analysis of noise-injection networks for interferometric-radiometer calibration. IEEE Trans. Microw. Theory Tech. 2000, 48, 545–552. [Google Scholar] [CrossRef]
- Zheng, C.; Yao, X.; Hu, A.; Miao, J. Closed form calibration of 1 bit/2 level correlator used for synthetic aperture interferometric radiometer. Prog. Electromagn. Res. M 2013, 29, 193–205. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Yao, X.; Zheng, C.; Zhang, J.; Li, Z.; Miao, J. Analysis of uncertainty in visibilty samples via average correlation in a synthetic aperture interferometric radiometer. Int. J. Remote Sens. 2014, 35, 7795–7814. [Google Scholar] [CrossRef]
- Holler, C.M.; Jones, M.E.; Taylor, A.C.; Harris, A.I.; Maas, S.A. A 2-20-GHz analog lag correlator for radio interferometry. IEEE Trans. Instrum. Meas. 2012, 61, 2253–2261. [Google Scholar] [CrossRef]
- Wang, C.; Xin, X.; Kashif, M.; Miao, J. A Compact Analog Complex Cross-Correlator for Passive Millimeter-Wave Imager. IEEE Trans. Instrum. Meas. 2017, 66, 2997–3006. [Google Scholar] [CrossRef]
- Li, C.T.; Kubo, D.Y.; Wilson, W.; Lin, K.Y.; Chen, M.T.; Ho, P.T.P.; Chen, C.C.; Han, C.C.; Oshiro, P.; Martin-Cocher, P.; et al. AMiBA wideband analog correlator. Astrophys. J. 2010, 716, 746–757. [Google Scholar] [CrossRef]
- Ruf, C.S. Digital correlators for synthetic aperture interferometric radiometry. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1222–1229. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhu, S.; Li, Y. A Robust Reweighted L1-Minimization Imaging Algorithm for Passive Millimeter Wave SAIR in Near Field. Sensors 2015, 15, 24945–24960. [Google Scholar] [CrossRef] [PubMed]
- Holler, C.M.; Kaneko, T.; Jones, M.E.; Grainge, K.; Scott, P. A 6-12 GHz analogue lag-correlator for radio interferometry. Astron. Astrophys. 2007, 464, 795–806. [Google Scholar] [CrossRef]
- Koistinen, O.; Lahtinen, J.; Hallikainen, M.T. Comparison of analog continuum correlators for remote sensing and radio astronomy. IEEE Trans. Instrum. Meas. 2002, 51, 227–234. [Google Scholar] [CrossRef]
- Padin, S. A wideband analog continuum correlator for radio astronomy. IEEE Trans. Instrum. Meas. 1994, 43, 782–785. [Google Scholar] [CrossRef]
- Li, C.T.; Kubo, D.; Han, C.C.; Chen, C.C.; Chen, M.T.; Lien, C.H.; Wang, H.; Wei, R.M.; Yang, C.H.; Chiueh, T.D.; et al. A wideband analog correlator system for AMiBA. Proc. SPIE Millim. Submillim. Detect. Astron. II 2004, 5498, 455–463. [Google Scholar]
- Zheng, C.; Yao, X.; Hu, A.; Miao, J. A Passive Millimeter-Wave Imager used for Concealed Weapon Detection. Prog. Electromagn. Res. B 2013, 46, 379–397. [Google Scholar] [CrossRef]
- Padin, S.; Cartwright, J.K.; Shepherd, M.C.; Yamasaki, J.K.; Holzapfel, W.L. A wideband analog correlator for microwave background observations. IEEE Trans. Instrum. Meas. 2001, 50, 1234–1240. [Google Scholar] [CrossRef]
- Zwart, J.T.L.; Barker, R.W.; Biddulph, P.; Bly, D.; Boysen, R.C.; Brown, A.R.; Clementson, C.; Crofts, M.; Culverhouse, T.L.; Czeres, J.; et al. The arcminute microkelvin imager. Mon. Not. R. Astron. Soc. 2008, 391, 1545–1558. [Google Scholar] [CrossRef]
- Toonen, R.C.; Haselby, C.C.; Blick, R.H. An Ultrawideband Cross-Correlation Radiometer for Mesoscopic Experiments. IEEE Trans. Instrum. Meas. 2008, 57, 2874–2879. [Google Scholar] [CrossRef]
- Ryle, M. A New Radio Interferometer and Its Application to the Observation of Weak Radio Stars. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1952, 211, 351–375. [Google Scholar] [CrossRef]
- Peng, J.; Ruf, C.S. Covariance Statistics of Fully Polarimetric Brightness Temperature Measurements. IEEE Geosci. Remote Sens. Lett. 2010, 7, 460–463. [Google Scholar] [CrossRef]
- Mirzavand, R.; Mohammadi, A.; Ghannouchi, F.M. Five-port microwave receiver architectures and applications. IEEE Commun. Mag. 2010, 48, 30–36. [Google Scholar] [CrossRef]
- AN-1291: Digital Potentiometers: Frequently Asked Questions, Analog Devices. Available online: http://www.analog.com/media/en/technical-documentation/application-notes/AN-1291.pdf (accessed on 7 December 2017).
- Ruf, C.S.; Li, J. A correlated noise calibration standard for interferometric, polarimetric, and autocorrelation microwave radiometers. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2187–2196. [Google Scholar] [CrossRef]
- Wang, C.; Miao, J. Implementation and broadband calibration of a multichannel vector modulator module. IET Sci. Meas. Technol. 2016, 11, 155–163. [Google Scholar] [CrossRef]
- Harris, A.I.; Zmuidzinas, J. A wideband lag correlator for heterodyne spectroscopy of broad astronomical and atmospheric spectral lines. Rev. Sci. Instrum. 2001, 72, 1531–1538. [Google Scholar] [CrossRef][Green Version]
- Mickelson, R.L.; Swenson, G.W., Jr. A comparison of two correlation schemes. IEEE Trans. Instrum. Meas. 1991, 40, 816–819. [Google Scholar] [CrossRef]

| Module | Parameter | Specification |
|---|---|---|
| Receiver | Center frequency | 34 GHz |
| LO frequency | 32 GHz | |
| IF frequency | 1.5–2.5 GHz | |
| Receiver type | Heterodyne, SSB (Ka-band) | |
| RF Delay Trimmer | Delay range | 1275 ps |
| Delay increment | 0.17 ps | |
| Complex Correlator | Operating frequency range | 1.5–2.5 GHz |
| Output voltage range | −5~+5 V | |
| Noise Source | Output frequency range | Ka-band |
| ENR | 15 dB | |
| DAQ | Part number | PCI-1715U (Advantech) |
| Description | 500 kS/s, 12-bit, 32-ch Analog Input PCI Card |
| Circle No. | A (Hardware Uncalibrated) | B (Hardware Calibrated) | B’ (Quadrature Errors Calibrated) |
|---|---|---|---|
| Correlation Circle Origin Offset (mV) | (−265.576,−363.641) | (−25.855,18.831) | (−25.567,19.312) |
| Correlation Circle RMS Fitting Error | 0.02743 | 0.02383 | 0.00163 |
| Circle Radius (V) | 3.075 | 2.942 | 2.946 |
| Axial Ratio | 0.9751 | 1.0047 | 1.0023 |
| Quadrature Amplitude Error (dB) | −0.22 | 0.041 | 0.02 |
| Comments | Unacceptable DC offsets, axial ratio, and quadrature amplitude error | Acceptable for our application | Acceptable for our application |
| Power (dBm) | −20 | −19 | −18 | −17 | −16 | −15 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Uncal | Cal | Uncal | Cal | Uncal | Cal | Uncal | Cal | Uncal | Cal | Uncal | Cal | |
| Correlation Circle RMS Fitting Error | 0.02860 | 0.01231 | 0.02424 | 0.00190 | 0.02383 | 0.00163 | 0.01912 | 0.00100 | 0.02190 | 0.00287 | 0.02060 | 0.00317 |
| Mean Phase Error (°) | −0.0063 | −0.0013 | −0.0026 | −0.0018 | −0.0033 | −0.0028 | −0.0061 | −0.0053 | −0.0064 | −0.0057 | −0.0031 | −0.0024 |
| Peak-Peak Phase Error (°) | 1.7725 | 0.5905 | 0.7471 | 0.5755 | 0.7017 | 0.5786 | 0.7738 | 0.5946 | 0.6094 | 0.5120 | 0.5314 | 0.4110 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Xin, X.; Liang, B.; Li, Z.; Miao, J. Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications. Sensors 2018, 18, 677. https://doi.org/10.3390/s18020677
Wang C, Xin X, Liang B, Li Z, Miao J. Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications. Sensors. 2018; 18(2):677. https://doi.org/10.3390/s18020677
Chicago/Turabian StyleWang, Chao, Xin Xin, Bingyuan Liang, Zhiping Li, and Jungang Miao. 2018. "Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications" Sensors 18, no. 2: 677. https://doi.org/10.3390/s18020677
APA StyleWang, C., Xin, X., Liang, B., Li, Z., & Miao, J. (2018). Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications. Sensors, 18(2), 677. https://doi.org/10.3390/s18020677




