Development of a Micro/Nano Probing System Using Double Elastic Mechanisms
Abstract
1. Introduction
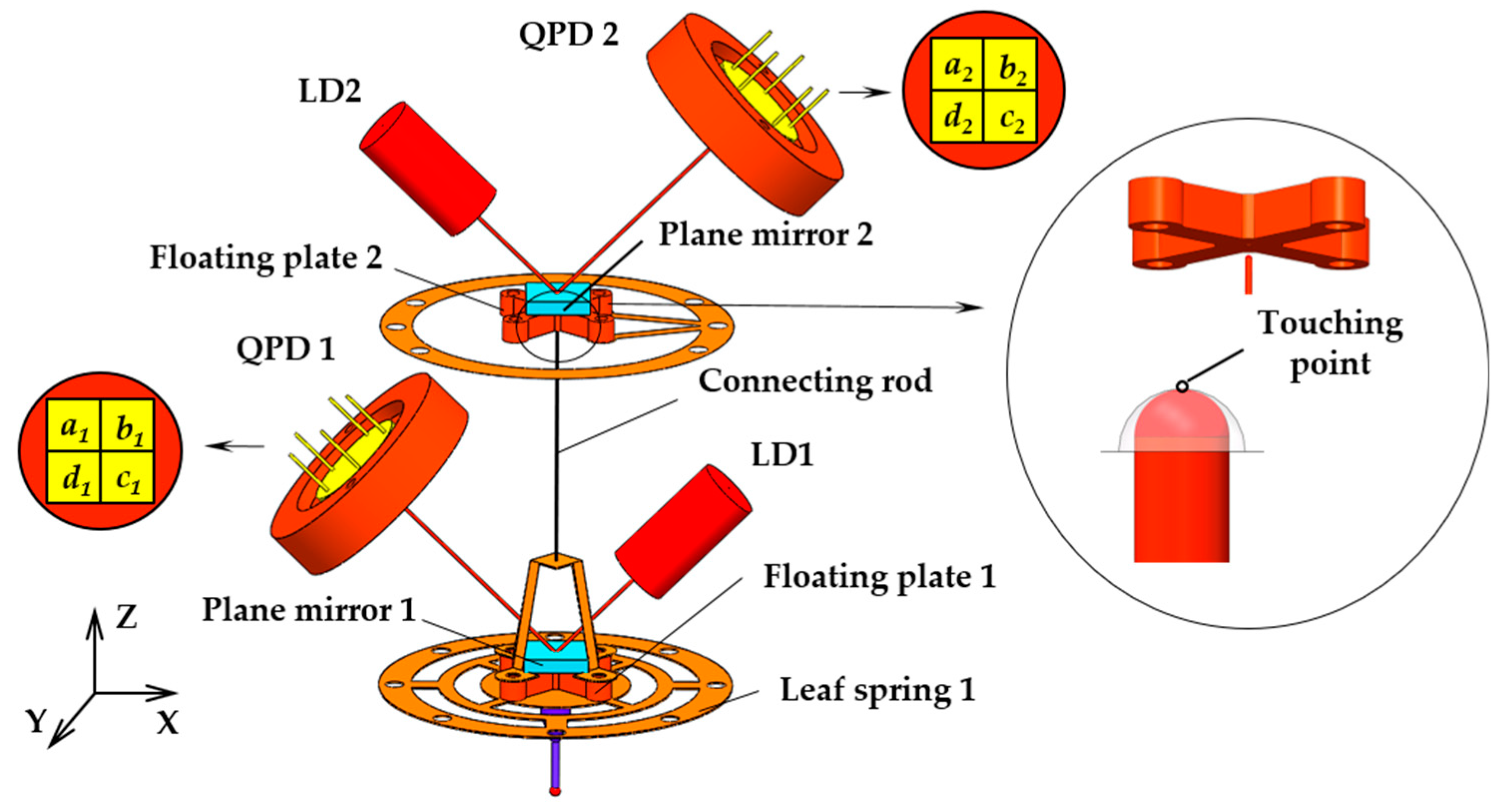
2. Probe Principle and Design
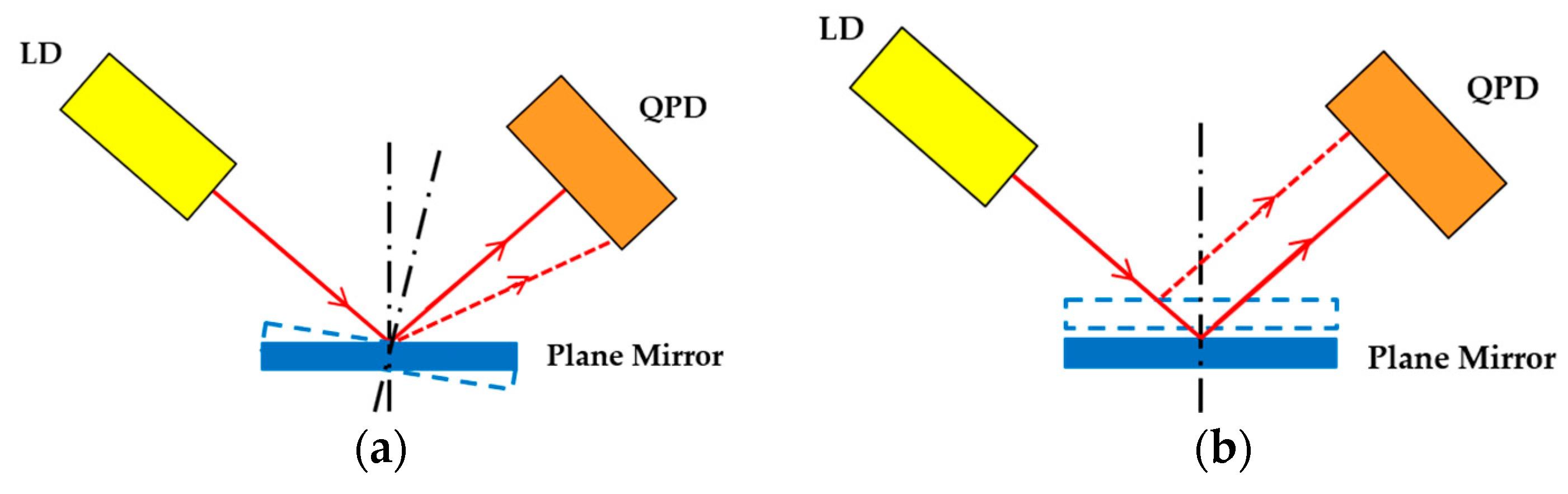
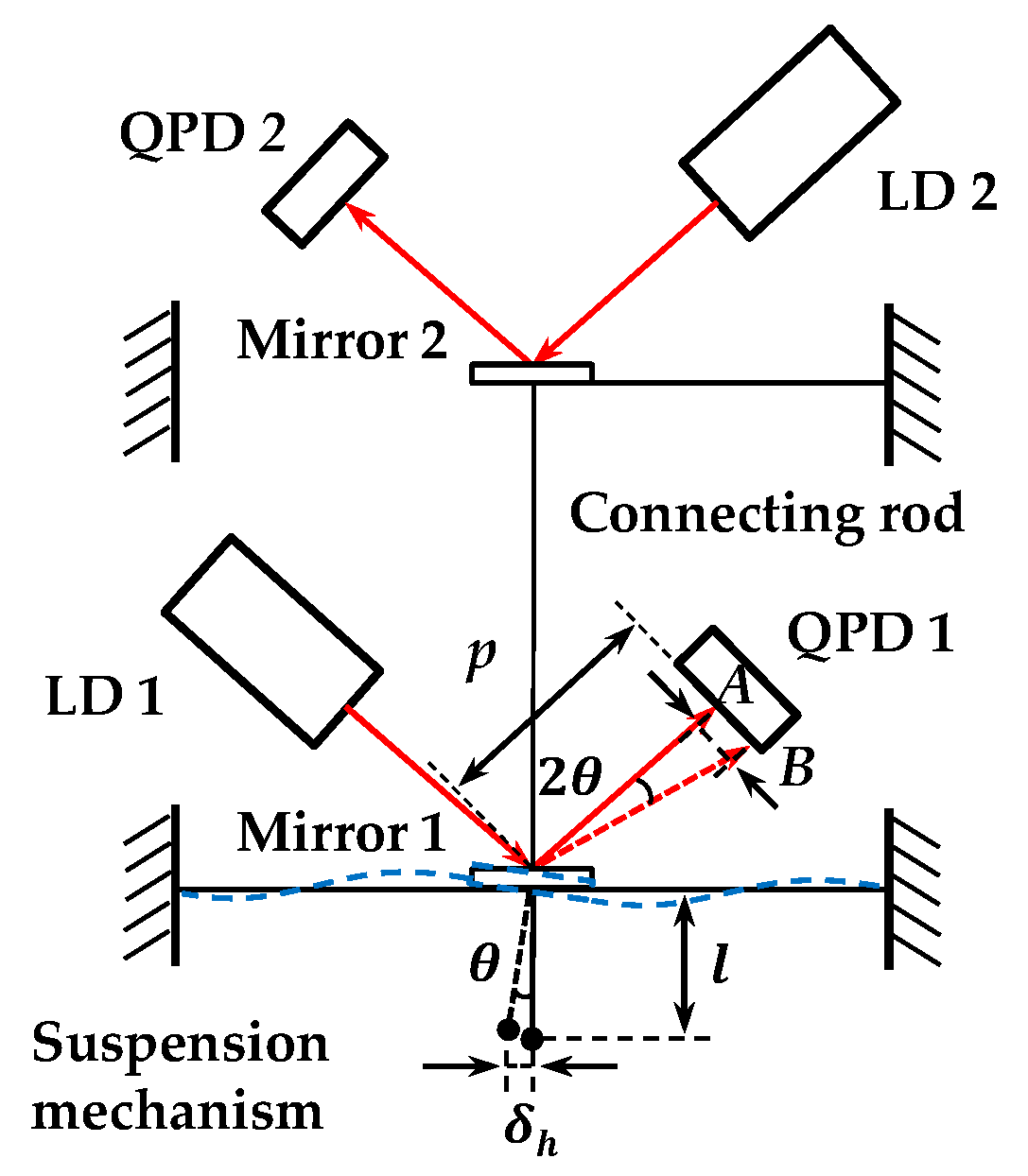
2.1. Principle of the Microprobe
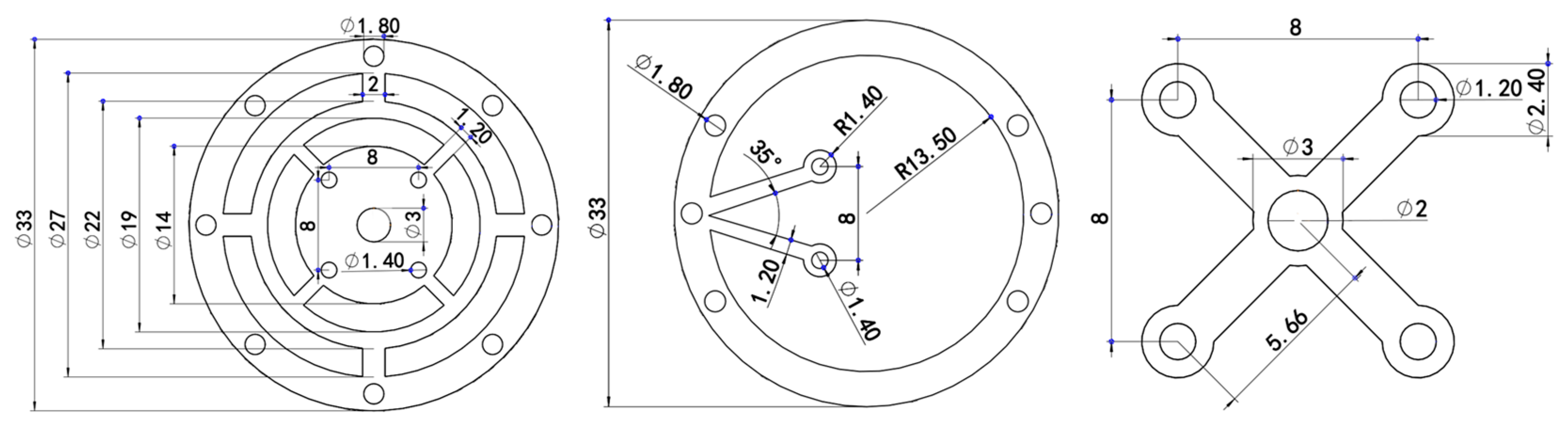
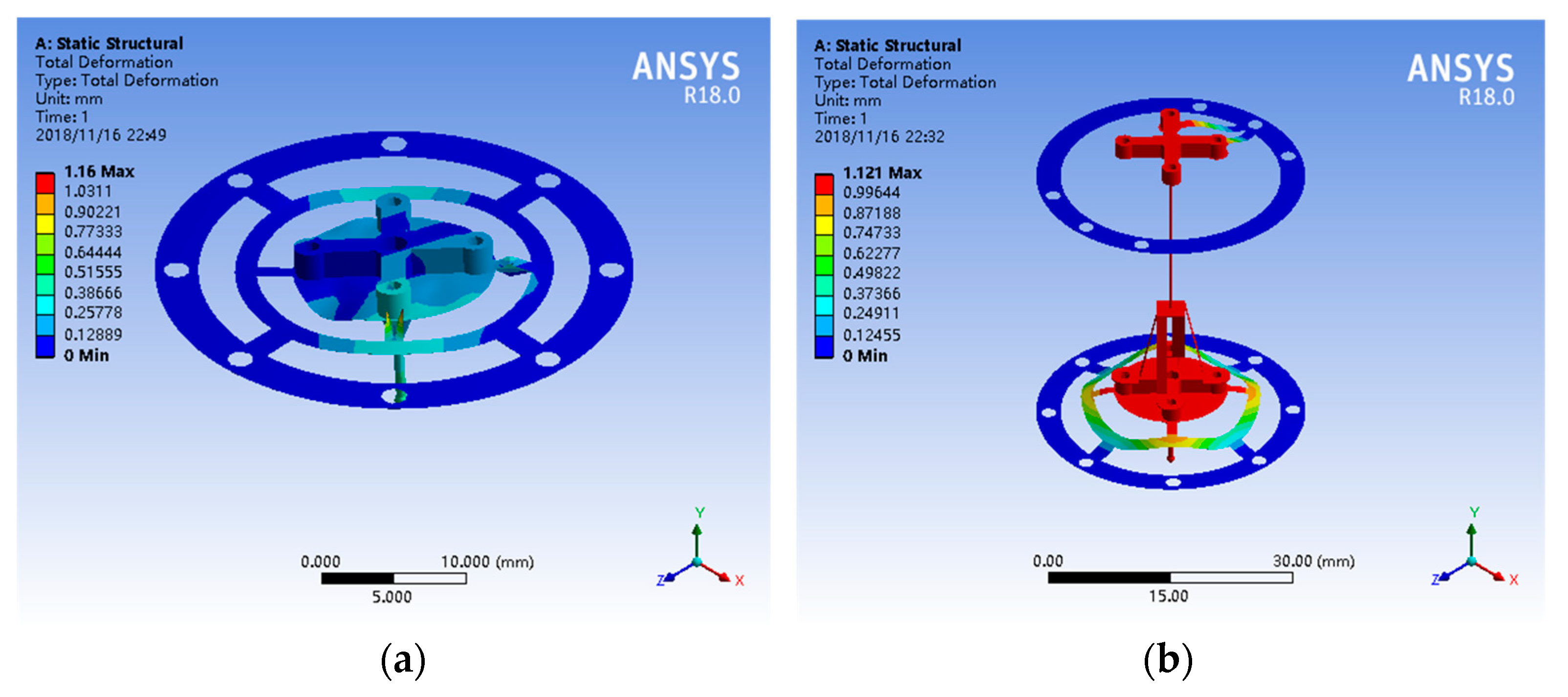
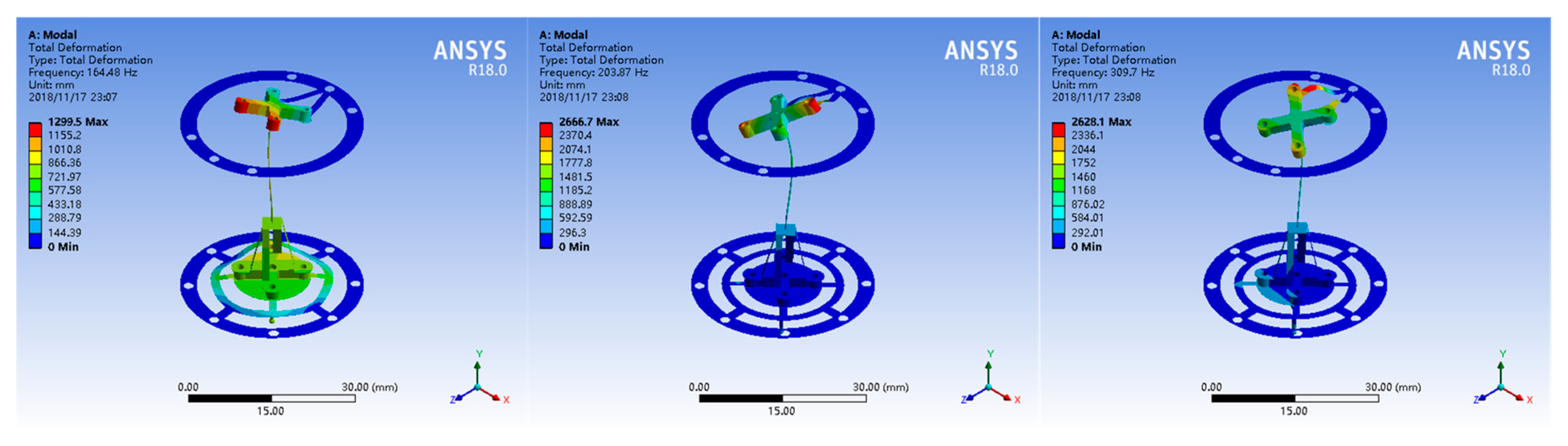
2.2. Uniform Stiffness
2.3. Sensitivity Analysis
3. Experiments
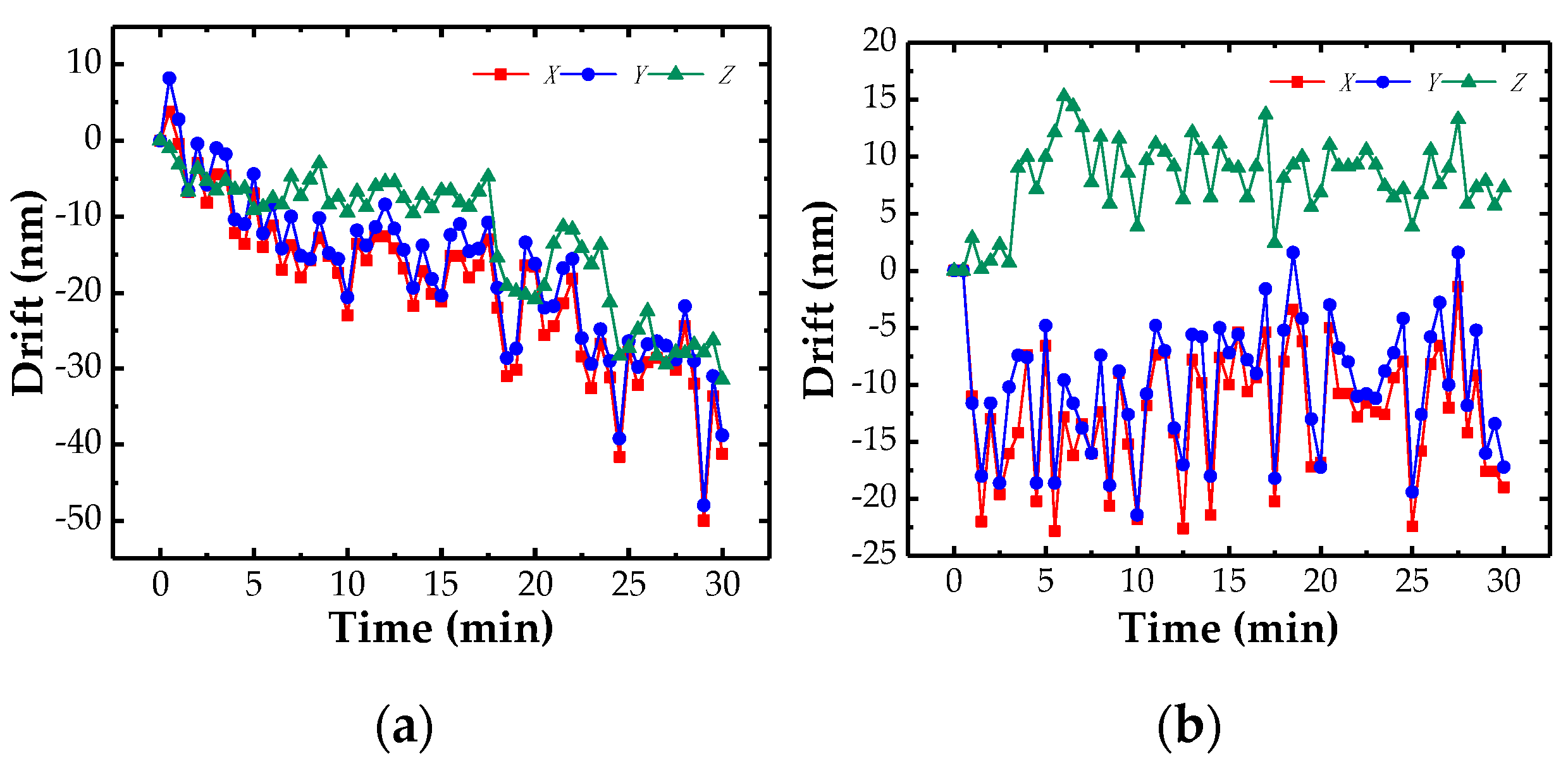
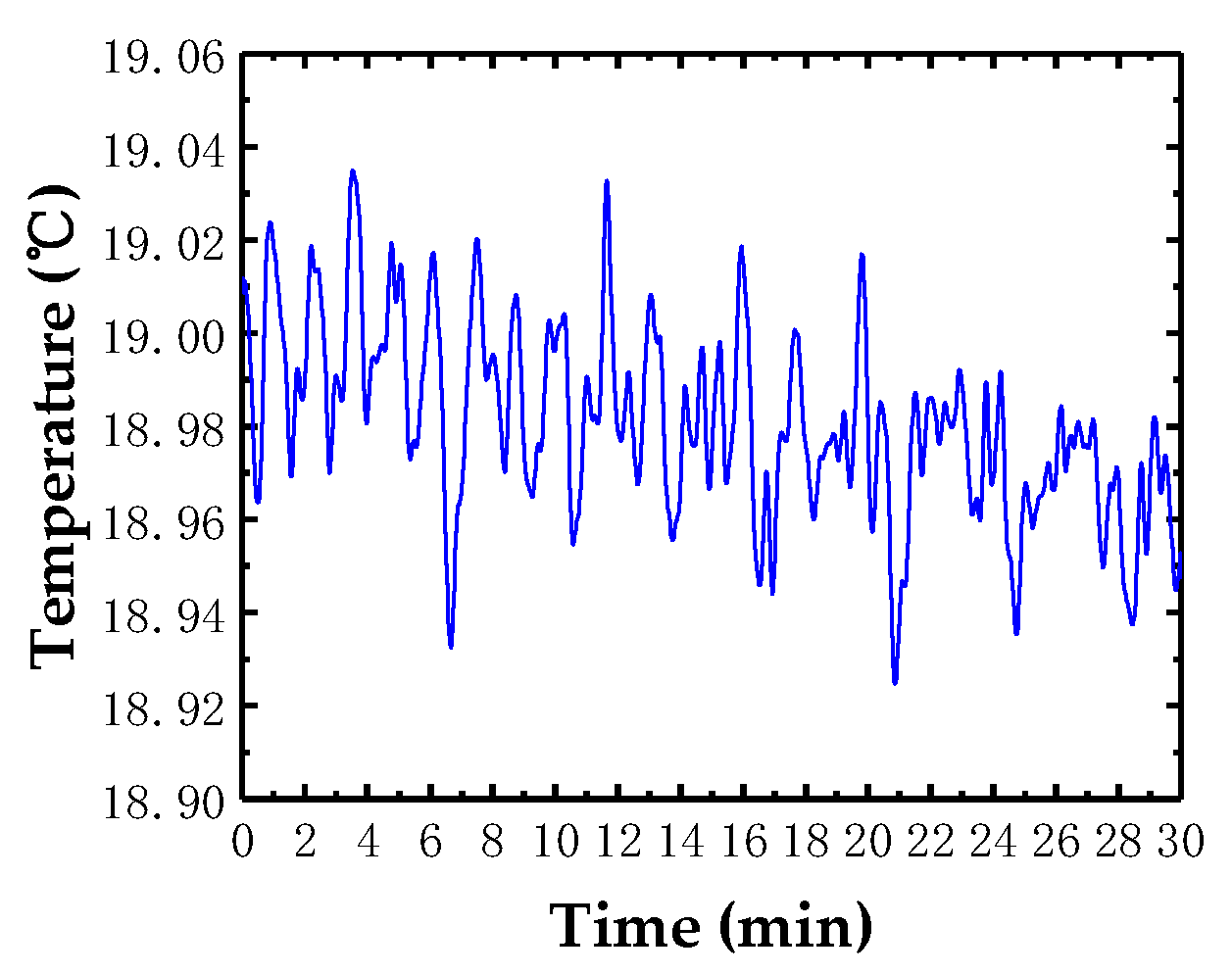
3.1. Drift
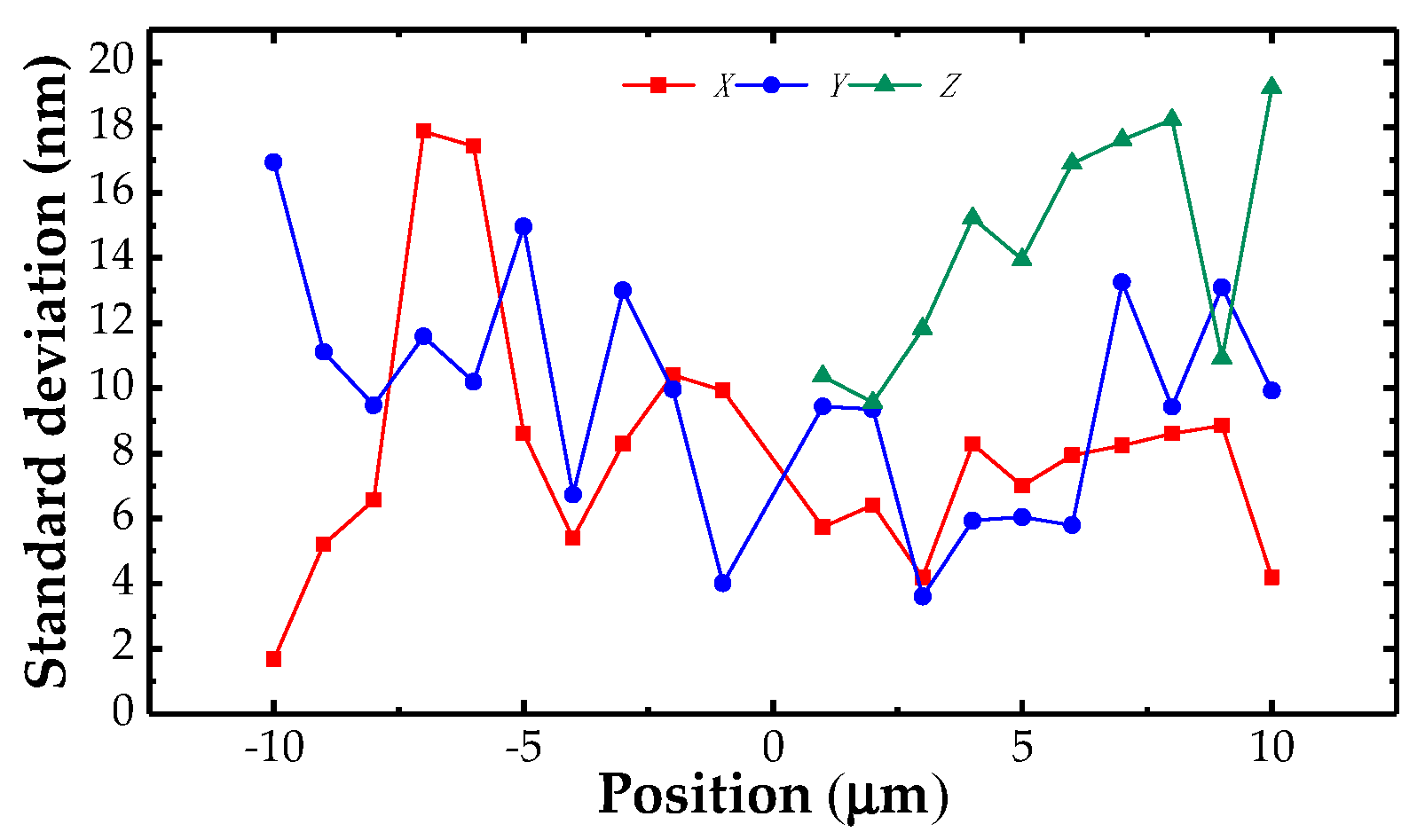
3.2. Repeatability
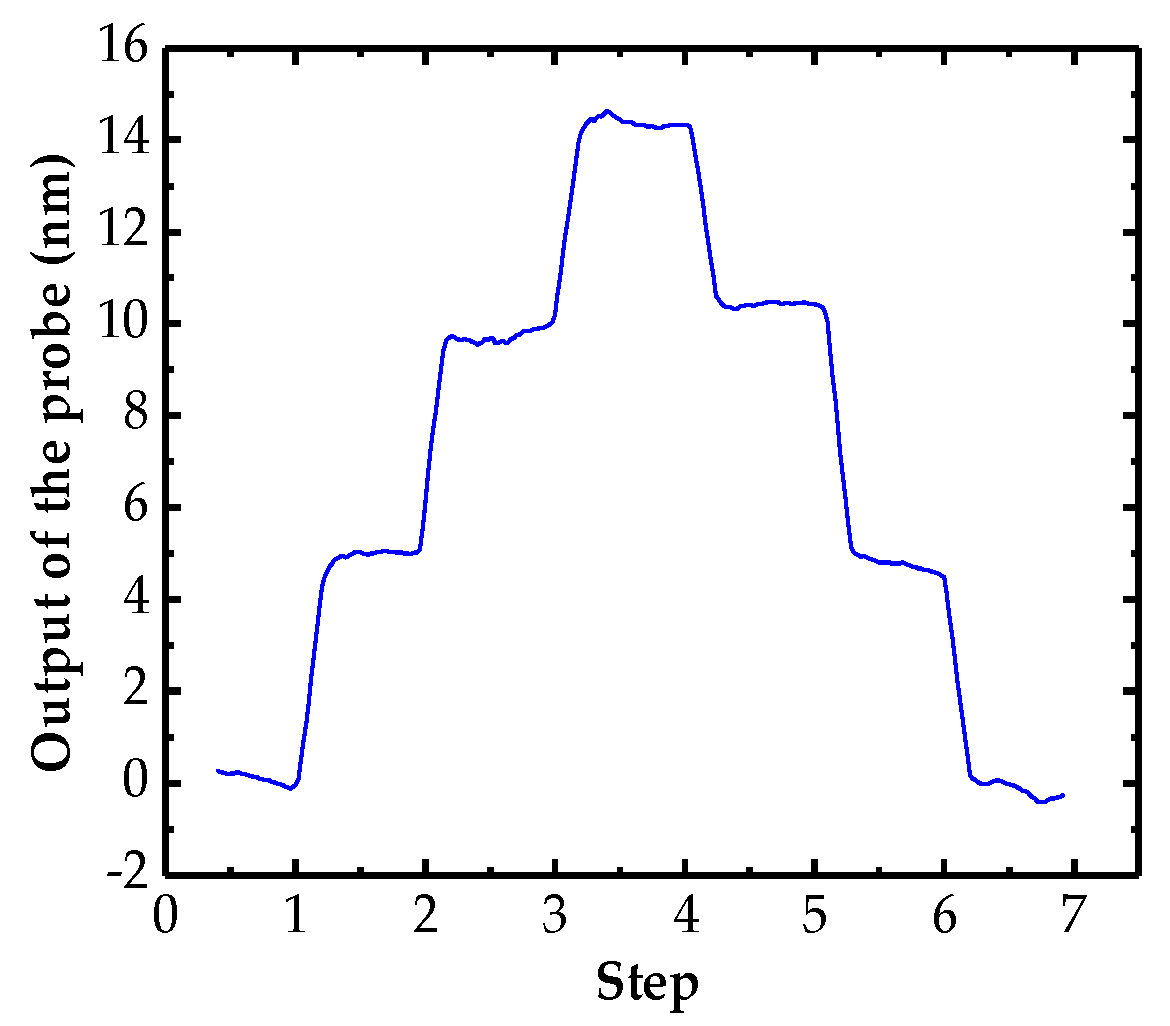
3.3. Resolution
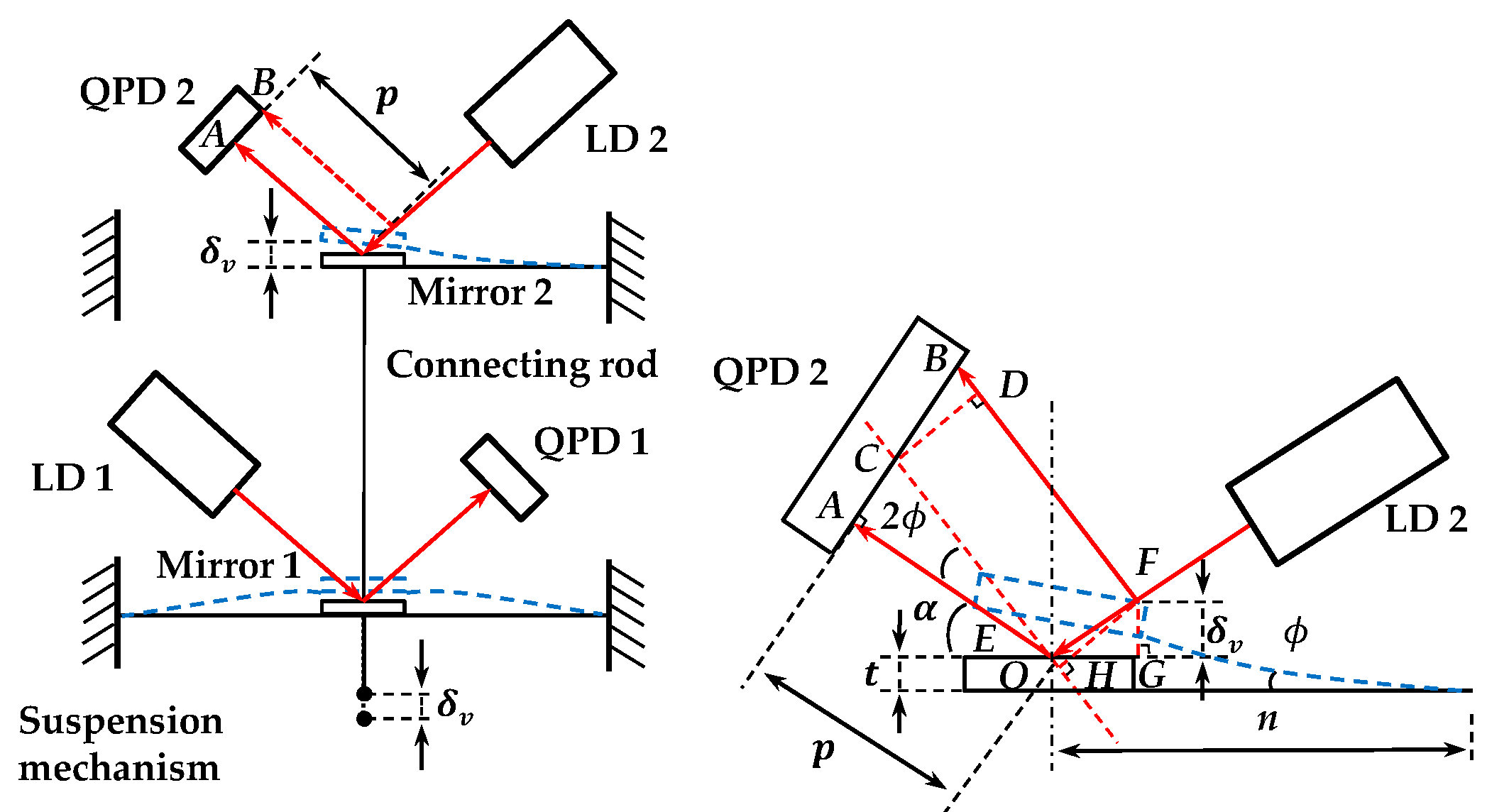
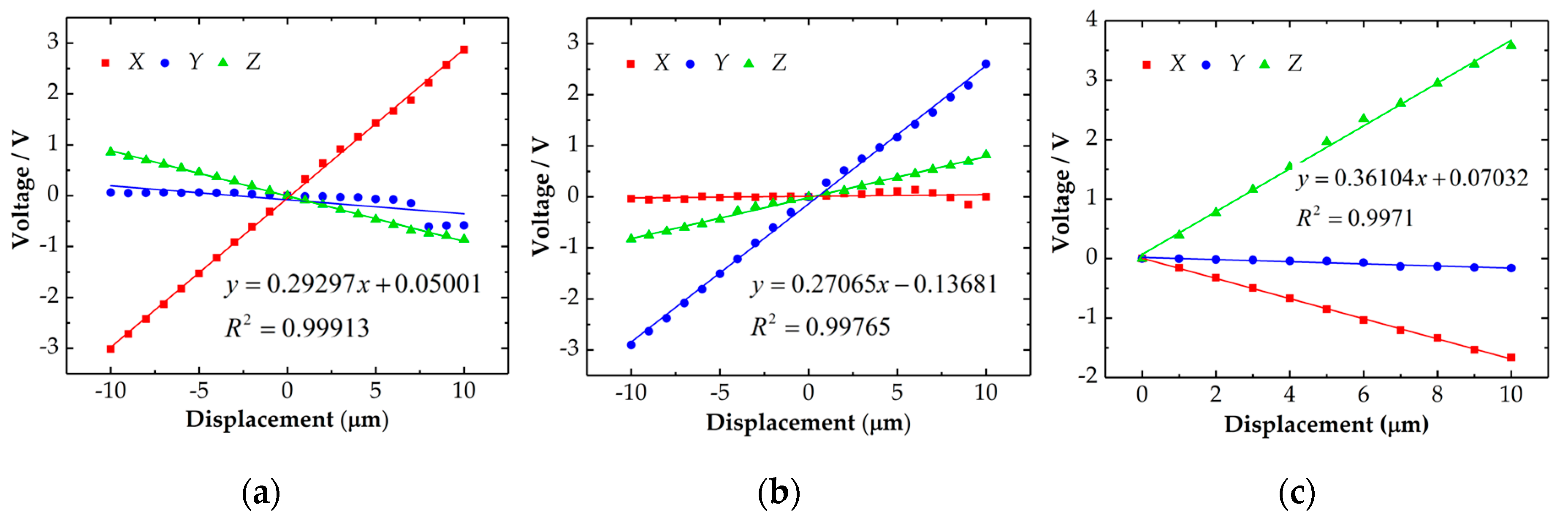
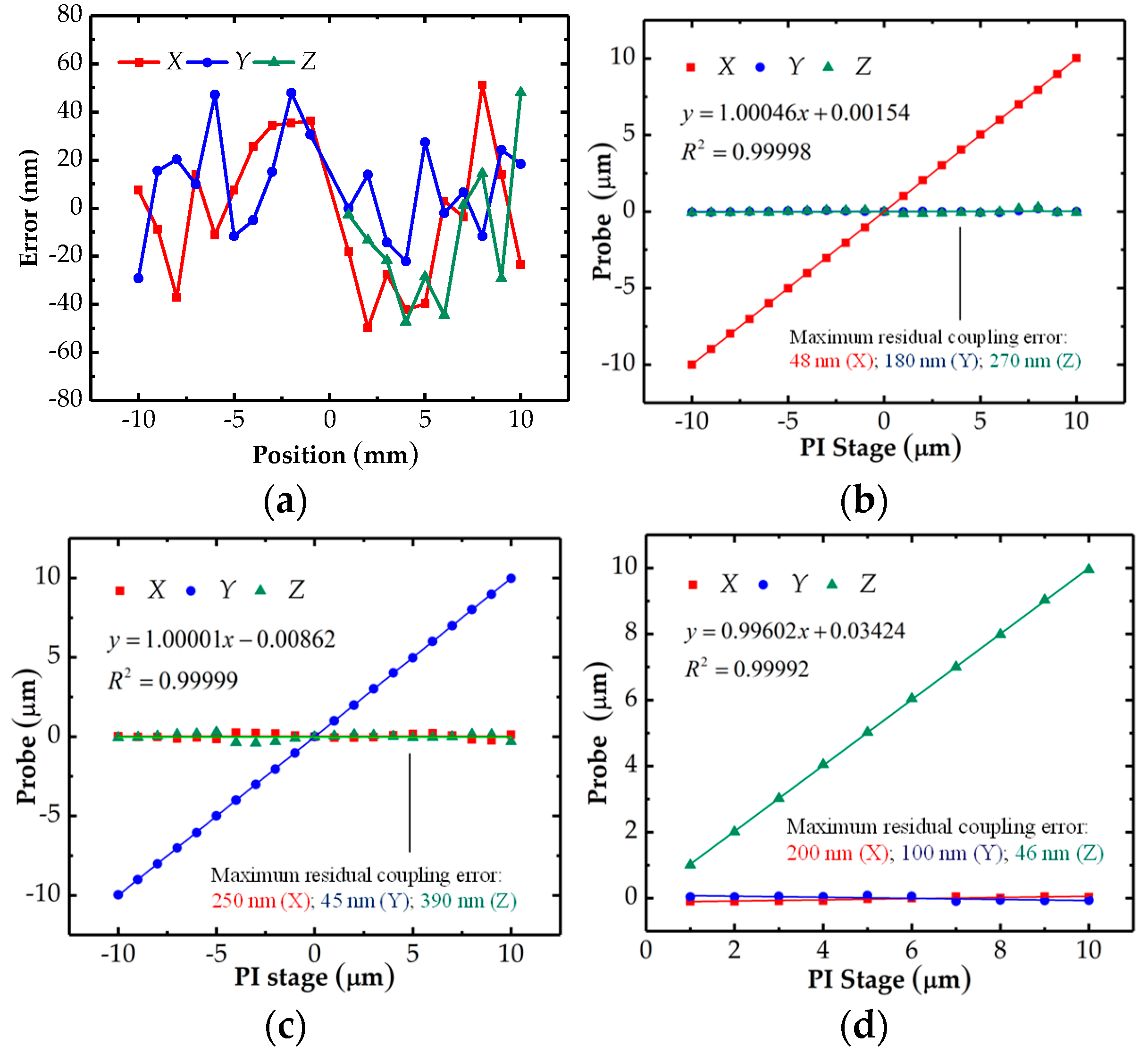
4. Decoupling of the Cross-Talk Errors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alshehri, A.; Kraft, M.; Gardonio, P. Two-mass MEMS velocity sensor: Internal feedback loop design. IEEE Sens. J. 2013, 13, 1003–1011. [Google Scholar] [CrossRef]
- Woźniak, A.; Dobosz, M. Influence of measured objects parameters on CMM touch trigger probe accuracy of probing. Precis. Eng. 2005, 29, 290–297. [Google Scholar] [CrossRef]
- Weckenmann, A.; Estler, T.; Peggs, G.; McMurtry, D. Probing systems in dimensional metrology. CIRP Ann. 2004, 53, 657–684. [Google Scholar] [CrossRef]
- Guilun, J.; Schwenke, H.; Trapet, E. Opto-tactile sensor for measuring small structures on coordinate measuring machines. Proc. ASPE 1998, 18, 25–28. [Google Scholar] [CrossRef]
- Van Vliet, W.P.; Schellekens, P.H. Development of a fast mechanical probe for coordinate measuring machines. Precis. Eng. 1998, 22, 141–152. [Google Scholar] [CrossRef]
- Kim, S.W.; Yang, D.Y. New design of precision CMM based upon volumetric phase-measuring interferometry. CIRP Ann. 2001, 50, 357–360. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Stone, J.A.; Stoup, J.R. Fiber deflection probe for small hole metrology. Precis. Eng. 2006, 30, 154–164. [Google Scholar] [CrossRef]
- Cui, J.W.; Li, L.; Tan, J.B. Optical fiber probe based on spherical coupling of light energy for inner-dimension measurement of microstructures with high aspect ratios. Opt. Lett. 2011, 36, 4689–4691. [Google Scholar] [CrossRef]
- Ettemeyer, A. New three-dimensional fiber probe for multisensory coordinate measurement. Opt. Eng. 2012, 51, 1502. [Google Scholar] [CrossRef]
- Fan, K.C.; Cheng, F.; Wang, W.; Chen, Y.J.; Lin, J.Y. A scanning contact probe for a micro-coordinate measuring machine (CMM). Meas. Sci. Technol. 2010, 21, 054002. [Google Scholar] [CrossRef]
- Enami, K.; Kuo, C.C.; Nogami, T. Development of nano-probe system using optical sensing. In Proceedings of the IMEKO-XV World Congress, Wien, Austria, 25–28 September 2000. [Google Scholar]
- Liebrich, T.; Knapp, W. New concept of a 3D-probing system for micro-components. CIRP Ann. 2010, 59, 513–516. [Google Scholar] [CrossRef]
- Yang, W.; Liu, X.; Lu, W.; Yu, N.; Chen, L.; Zhou, L.; Chang, S. A novel white light interference based AFM head. J. Lightwave Technol. 2017, 35, 3604–3610. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, X.; Zhao, L.; Chen, L.; Li, Q.; Yuan, T.; Lu, W. A novel 3D stitching method for WLI based large range surface topography measurement. Opt. Commun. 2016, 359, 435–447. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, X.; Chen, L.; Lu, W.; Chang, S. A novel surface recovery algorithm in white light interferometry. Measurement 2016, 80, 1–11. [Google Scholar] [CrossRef]
- Buetefisch, S.; Dai, G.; Danzebrink, H.U. Novel design for an ultra high precision 3D micro probe for CMM applications. Procedia Eng. 2010, 5, 705–712. [Google Scholar] [CrossRef]
- Peiner, E.; Balke, M.; Doering, L. Tactile probes for dimensional metrology with microcomponents at nanometre resolution. Meas. Sci. Technol. 2008, 19, 064001. [Google Scholar] [CrossRef]
- Tibrewala, A.; Phataralaoha, A.; Büttgenbach, S. Development, fabrication and characterization of a 3D tactile sensor. J. Micromech. Microeng. 2009, 19, 125005. [Google Scholar] [CrossRef]
- Pril, W. Development of High Precision Mechanical Probes for Coordinate Measuring Machines. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2002. [Google Scholar]
- Haitjema, H.; Pril, W.O.; Schellekens, P.H.J. Development of a silicon-based nanoprobe system for 3-D measurements. CIRP Ann. 2001, 50, 365–368. [Google Scholar] [CrossRef]
- Yuan, L. Study of MEMS Piezo-Resistance 3D Micro Tactile Probe and Application in NMM. Ph.D. Thesis, Tianjing University of Technology, Tianjing, China, 2007. [Google Scholar]
- Murphy, J.; Leach, R. The design of coordinate measuring probe for characterising truly three-dimensional micro-structures. In Proceedings of the 4th Euspen International Conference: European Society for Precision Engineering and Nanotechnology, Glasgow, UK, 31 May–2 June 2004. [Google Scholar]
- Peggs, G.N.; Lewis, A.J.; Oldfield, S. Design for a compact high-accuracy CMM. CIRP Ann. 1999, 48, 417–420. [Google Scholar] [CrossRef]
- Meli, F.; Küng, A.; Thalmann, R. Ultraprecision micro-CMM using a low force 3D touch probe. Meas. Sci. Technol. 2005, 18. [Google Scholar] [CrossRef]
- Thalmann, R.; Meli, F.; Küng, A. State of the art of tactile micro coordinate metrology. Appl. Sci. 2016, 6, 150. [Google Scholar] [CrossRef]
- Masuzawa, T.; Hamasaki, Y.; Fujino, M. Vibroscanning method for nondestructive measurement of small holes. CIRP Ann. 1993, 42, 589–592. [Google Scholar] [CrossRef]
- Kim, B.; Masuzawa, T.; Bourouina, T. The vibroscanning method for the measurement of micro-hole profiles. Meas. Sci. Technol. 1999, 10, 697. [Google Scholar] [CrossRef]
- Claverley, J.D.; Leach, R.K. A vibrating micro-scale CMM probe for measuring high aspect ratio structures. Microsyst. Technol. 2010, 16, 1507–1512. [Google Scholar] [CrossRef]
- Claverley, J.D.; Georgi, A.; Leach, R.K. Modelling the interaction forces between an ideal measurement surface and the stylus tip of a novel vibrating micro-scale CMM probe. In Proceedings of the 5th International Precision Assembly Seminar, Chamonix, France, 14–17 February 2010; Volume 315, pp. 131–138. [Google Scholar]
- Li, R.J.; Fan, K.C.; Huang, Q.X.; Qian, J.Z.; Gong, W.; Wang, Z.W. Design of a large-scanning-range contact probe for nano-coordinate measurement machines. Opt. Eng. 2012, 51, 081503. [Google Scholar] [CrossRef]
- Li, R.J.; Fan, K.C.; Miao, J.W.; Huang, Q.X.; Tao, S.; Gong, E.M. An analogue contact probe using a compact 3D optical sensor for micro/nano coordinate measuring machines. Meas. Sci. Technol. 2014, 25, 094008. [Google Scholar] [CrossRef]
- Li, R.J.; Wang, P.Y.; Li, D.D.; Fan, K.C.; Liu, F.F.; Chen, L.J.; Huang, Q.X. Precision Manufacturing of Patterned Beryllium Bronze Leaf Springs via Chemical Etching. Appl. Sci. 2018, 8, 1476. [Google Scholar] [CrossRef]
- Li, R.J.; Fan, K.C.; Huang, Q.X.; Zhou, H.; Gong, E.M.; Xiang, M. A long-stroke 3D contact scanning probe for micro/nano coordinate measuring machine. Precis. Eng. 2016, 43, 220–229. [Google Scholar] [CrossRef]
- Li, R.J.; Xiang, M.; He, Y.X.; Fan, K.C.; Cheng, Z.Y.; Huang, Q.X.; Zhou, B. Development of a high-precision touch-trigger probe using a single sensor. Appl. Sci. 2016, 6, 86. [Google Scholar] [CrossRef]
- Feng, J.; Li, R.J.; Fan, K.C.; Zhou, H.; Zhang, H. Development of a low-cost and vibration-free constant-temperature chamber for precision measurement. Sens. Mater. 2015, 27, 329–340. [Google Scholar] [CrossRef]
- Park, J.; Kwon, K.; Cho, N. Development of a coordinate measuring machine (CMM) touch probe using a multi-axis force sensor. Meas. Sci. Technol. 2006, 17, 2380. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Material of the leaf spring | Beryllium–copper alloy |
| Young’s modulus of the leaf spring (Gpa) | 130 |
| Material of the floating plate | Aluminum alloy |
| Weight of the floating plate (g) | 1.5 |
| Thickness (mm) | 2 |
| Young’s modulus of the floating plate (Gpa) | 71 |
| Material of the stylus | Tungsten stylus with a ruby ball tip |
| Length of the stylus (mm) | 10 |
| Diameter of the probe ball (mm) | 1 |
| Young’s modulus of the stylus (Gpa) | 193 |
| Distance between the two leaf springs (mm) | 34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.-J.; Xu, P.; Wang, P.-Y.; Fan, K.-C.; Cheng, R.-J.; Huang, Q.-X. Development of a Micro/Nano Probing System Using Double Elastic Mechanisms. Sensors 2018, 18, 4229. https://doi.org/10.3390/s18124229
Li R-J, Xu P, Wang P-Y, Fan K-C, Cheng R-J, Huang Q-X. Development of a Micro/Nano Probing System Using Double Elastic Mechanisms. Sensors. 2018; 18(12):4229. https://doi.org/10.3390/s18124229
Chicago/Turabian StyleLi, Rui-Jun, Peng Xu, Peng-Yu Wang, Kuang-Chao Fan, Rong-Jun Cheng, and Qiang-Xian Huang. 2018. "Development of a Micro/Nano Probing System Using Double Elastic Mechanisms" Sensors 18, no. 12: 4229. https://doi.org/10.3390/s18124229
APA StyleLi, R.-J., Xu, P., Wang, P.-Y., Fan, K.-C., Cheng, R.-J., & Huang, Q.-X. (2018). Development of a Micro/Nano Probing System Using Double Elastic Mechanisms. Sensors, 18(12), 4229. https://doi.org/10.3390/s18124229






