A Handheld Real-Time Photoacoustic Imaging System for Animal Neurological Disease Models: From Simulation to Realization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Light Propagation Simulation in Scattering Medium
2.2. Simulation of PA Wave Propagation Using COMSOL
- (i)
- Light diffusion/propagation in the scattering medium (calculated in the previous section). We used the acquired fluence intensities (based on different illumination angles and intervals) at 10 mm depth as the fluence input for calculating the PA wave generation.
- (ii)
- Heat generation and transfer inside the target and medium. For nanosecond laser pulse radiation, the temperature T was calculated using the following equation [26,27,28]:where C and k are the heat capacity and thermal conductivity, respectively. ρ is the density of the selected material. Q is the heat source, and it can be represented by the absorbed fluence times a yield Y (i.e., Q = ϕμaY).
- (iii)
- Target stress-strain distribution. We also considered how the strain and stress of the target would change due to the transient temperature rise. The solid stress-strain model was used to evaluate this thermal expansion characteristic [15,27]:where ɛ is the changed strain, and β represents the thermal expansion coefficient. Tref is the reference temperature. The mechanical properties of the material were also included as inputs for this calculation, such as Young’s modulus and Poisson’s ratio.
- (iv)
- Thermal expansion and PA wave generation/propagation. Thermal expansion was modeled using the boundary acceleration between the target and surrounding medium. The dominant equation is shown below:where p is the response PA wave. The propagation of the PA wave in a medium follows the equation [15,22,27]:where cs is the sound velocity [16,27]. Based on the above equations, we could simulate a complete procedure of PA wave generation for evaluating the proposed strategies of the PA imaging system design. Note that a schematic of simulation procedures using the FEM method is shown in Figure S1 (Supplementary Materials) to illustrate the simulation strategy in details.
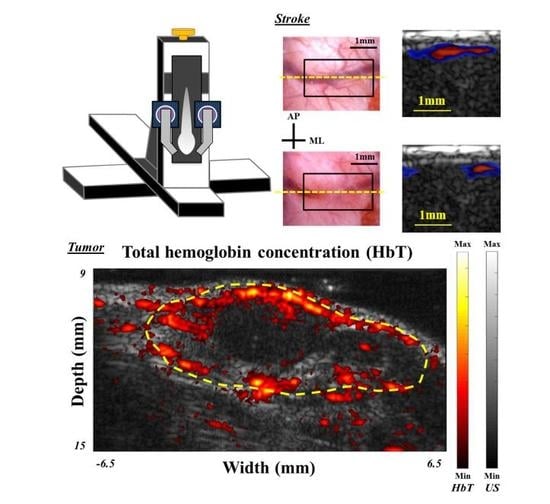
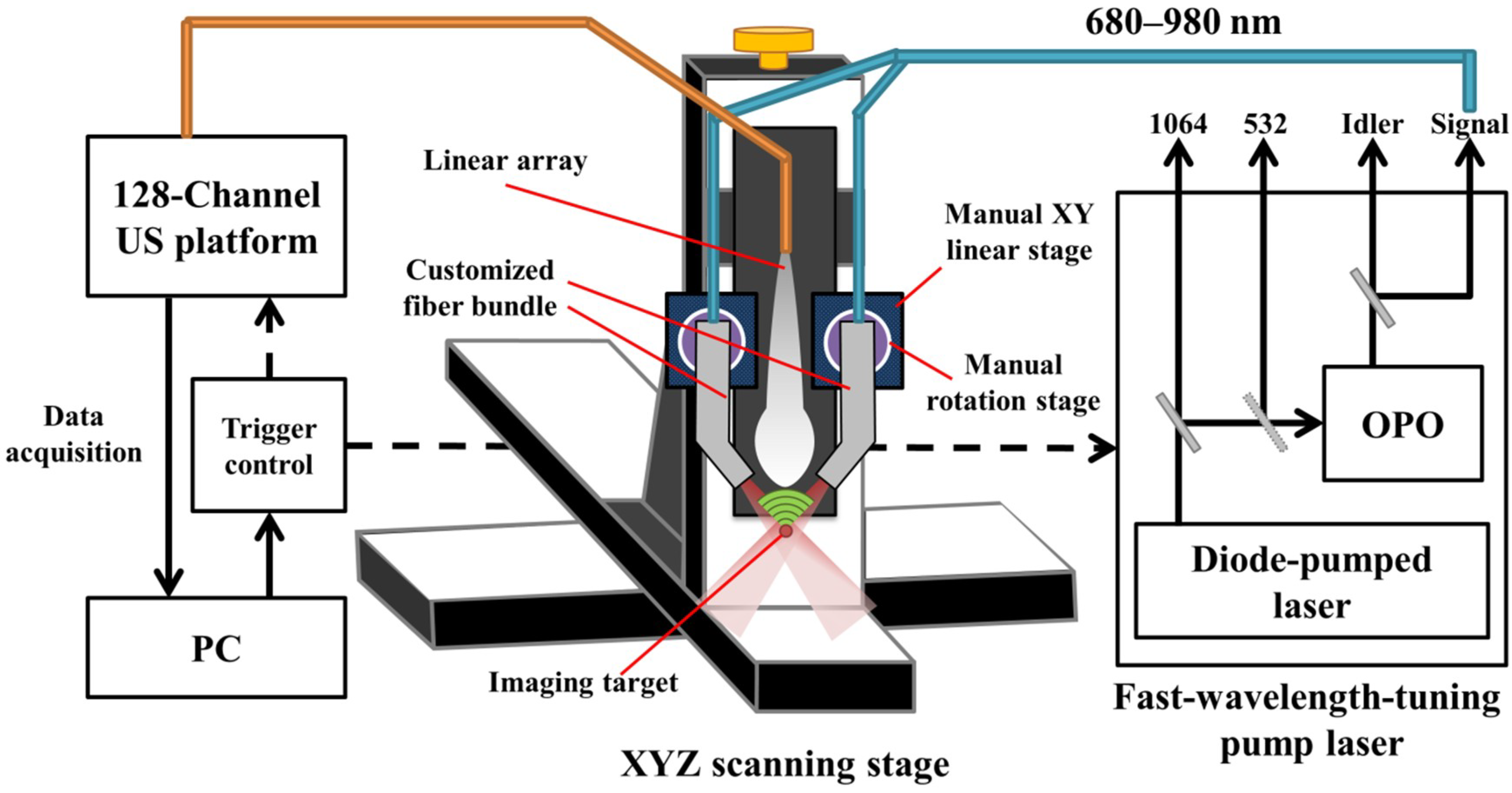
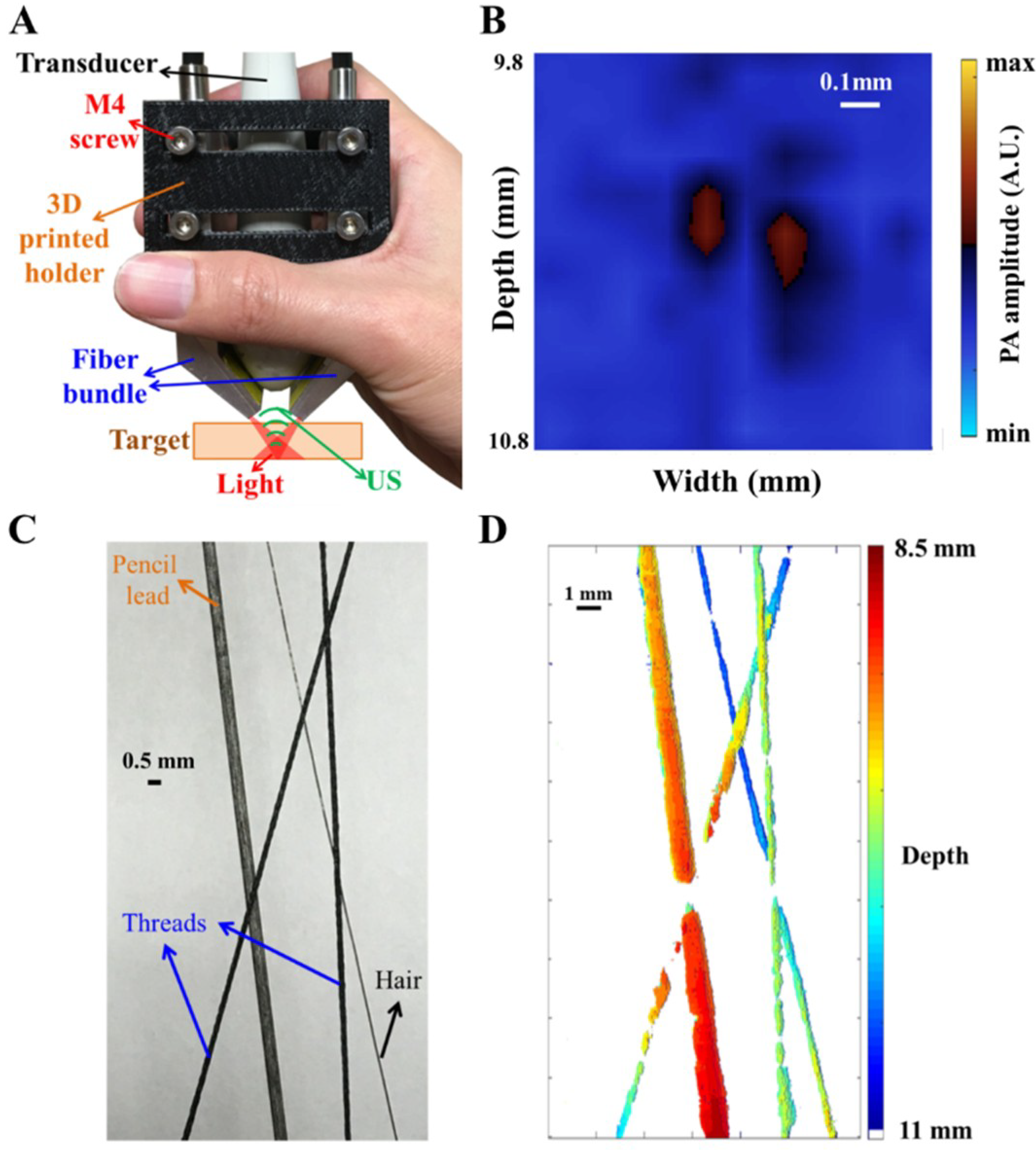
2.3. Handheld, Real-Time Photoacoustic Imaging System
2.4. Animal Experiments
3. Results
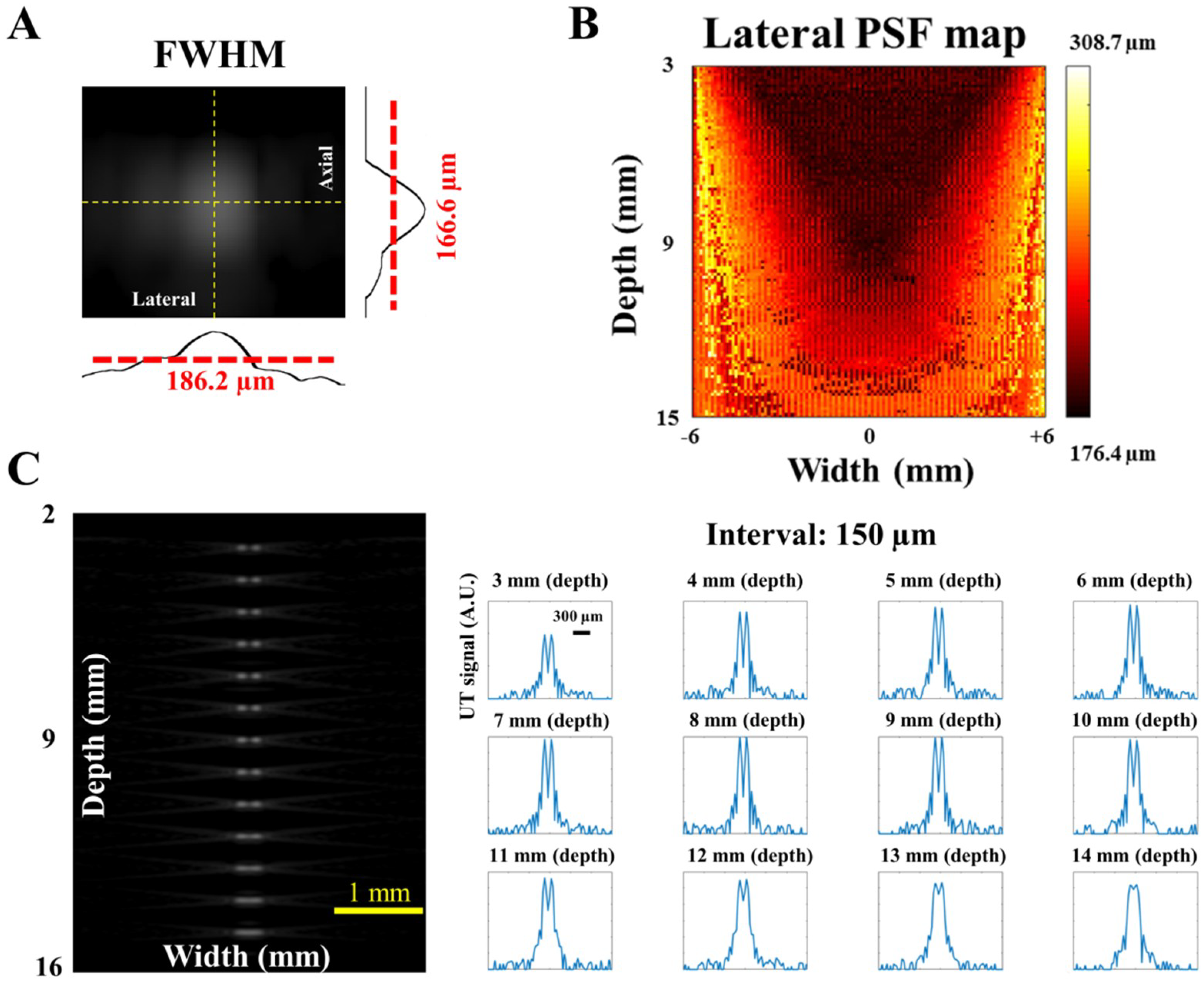
3.1. Simulation Results—Ultrasound Response Based on Vantage Software
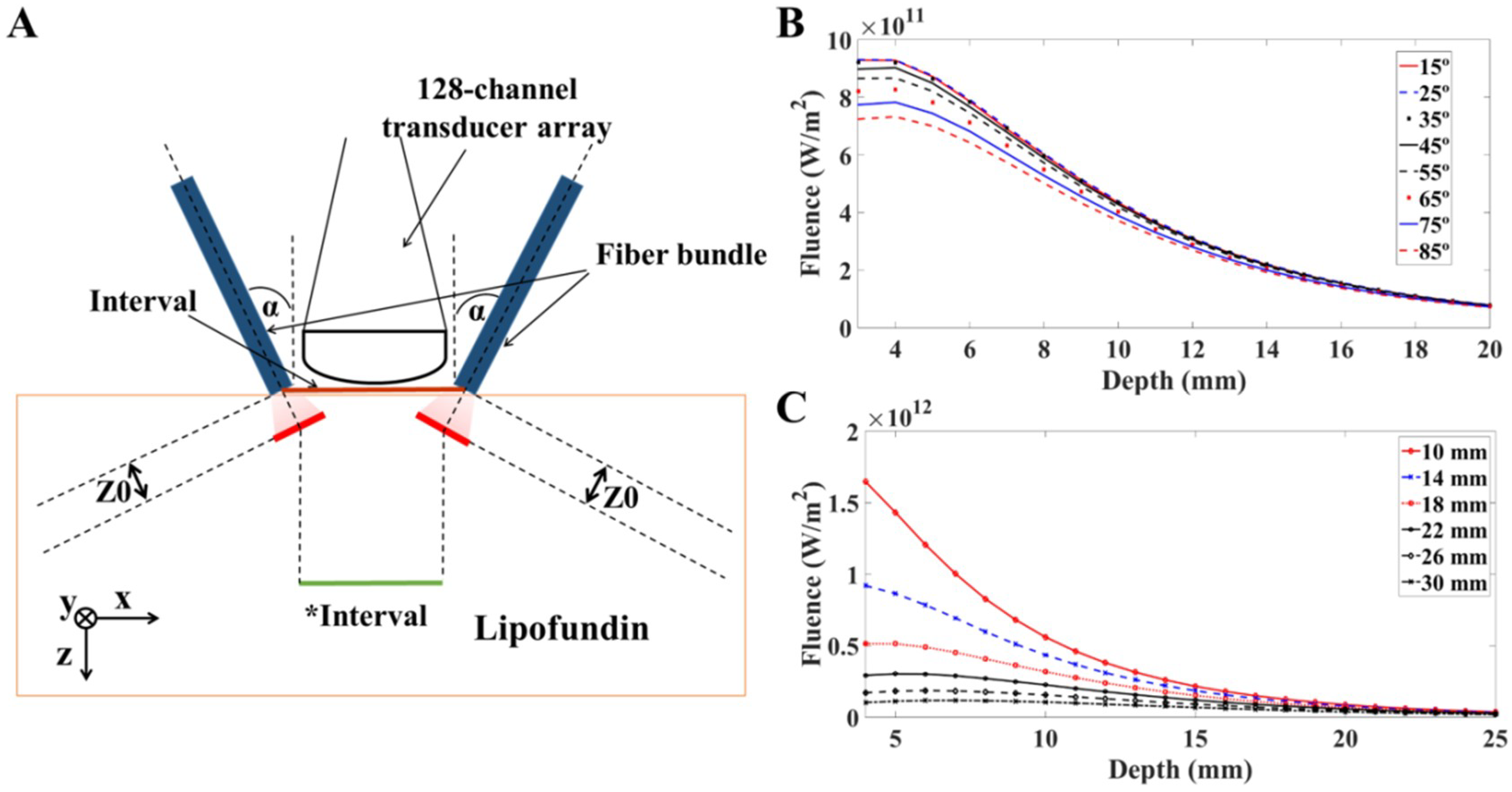
3.2. Simulation Results—Light Propagation in Scattering Medium
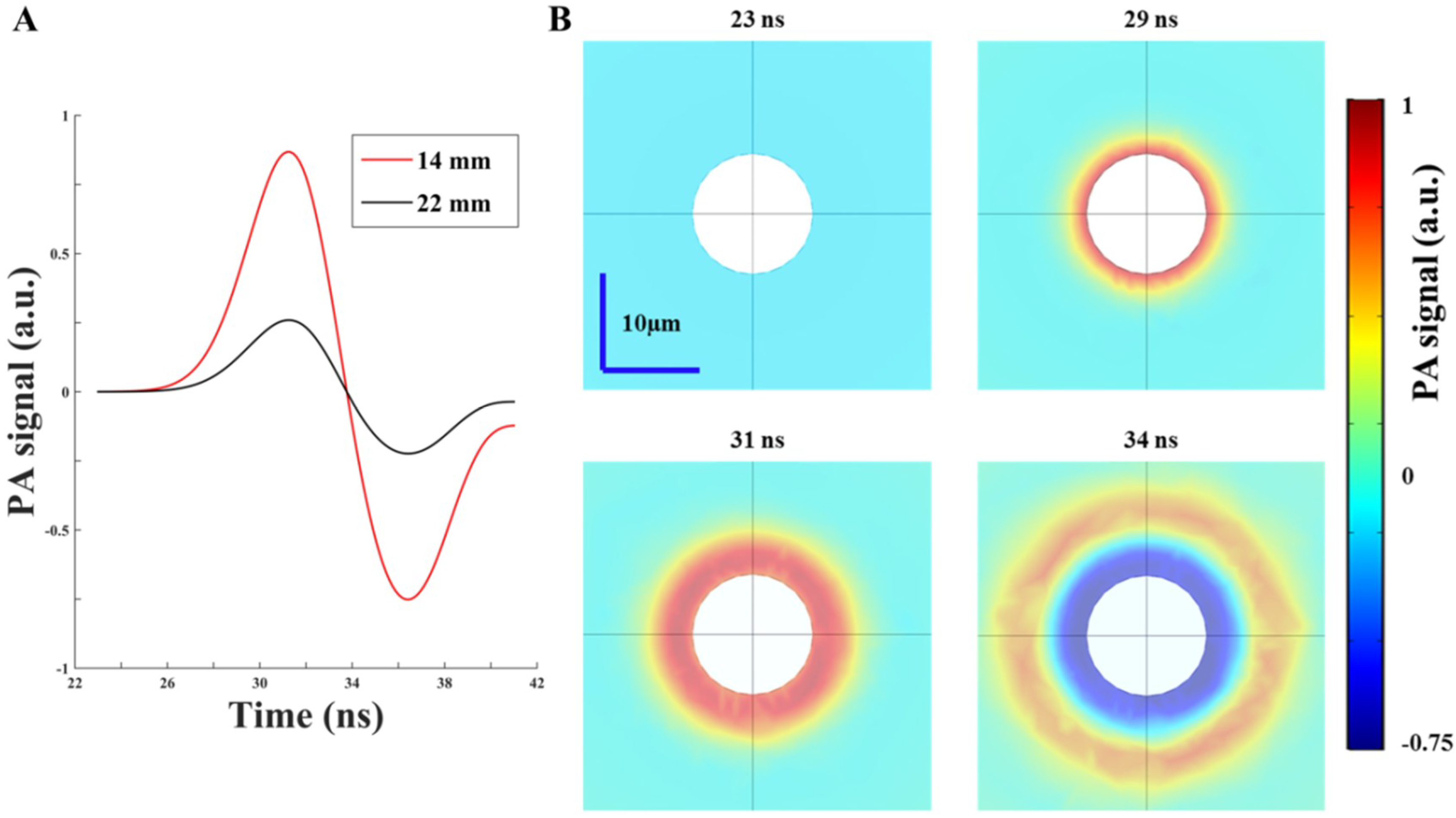
3.3. Simulation Results—PA Wave Propagation in Scattering Medium
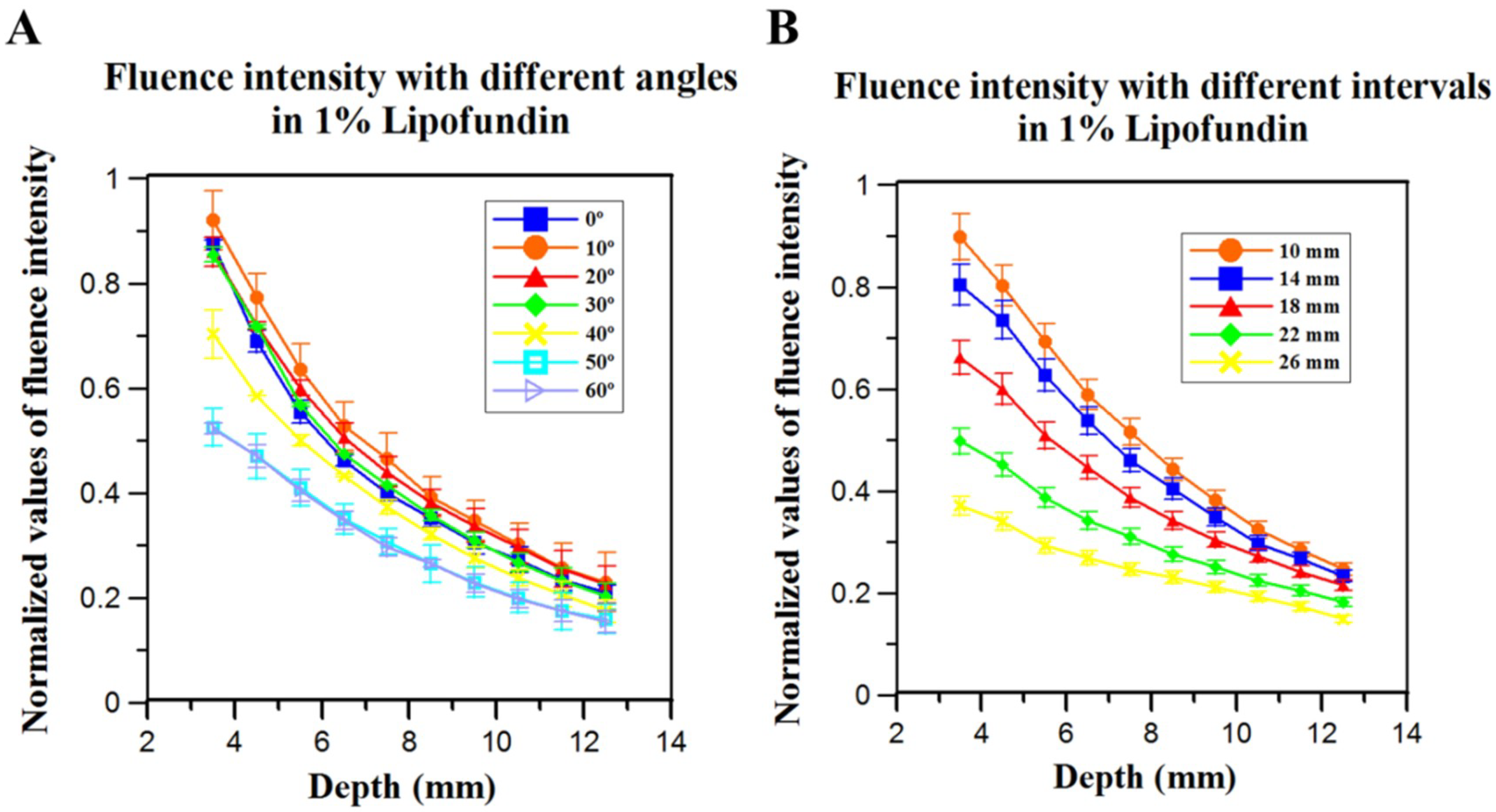
3.4. Evaluation of Fluence Changes in 1% Lipofundin at Different Depths
3.5. PA Image Assessment Based on Phantom Targets
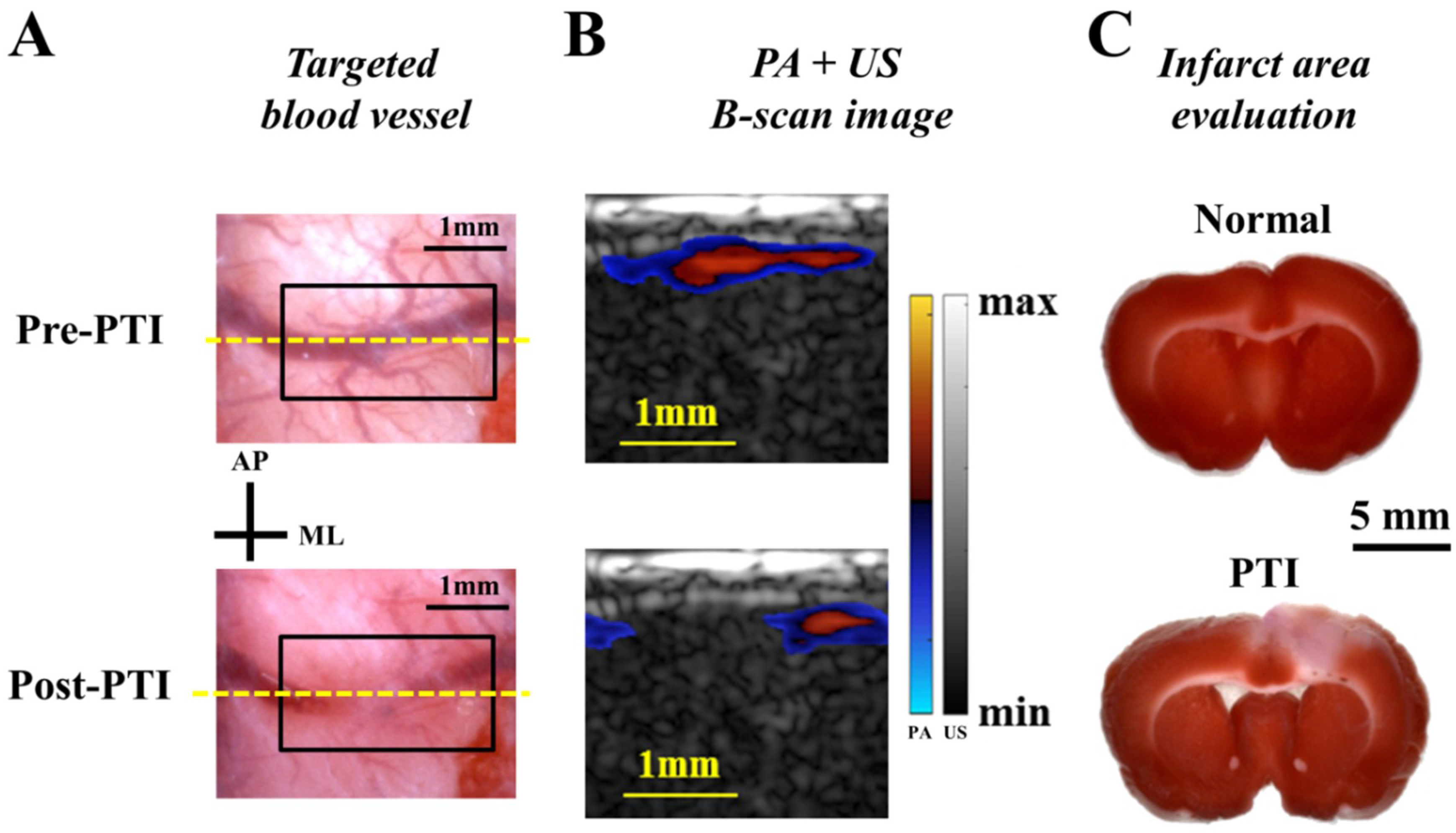
3.6. Performance Evaluation of the PA Imaging System Based on the PTI Model
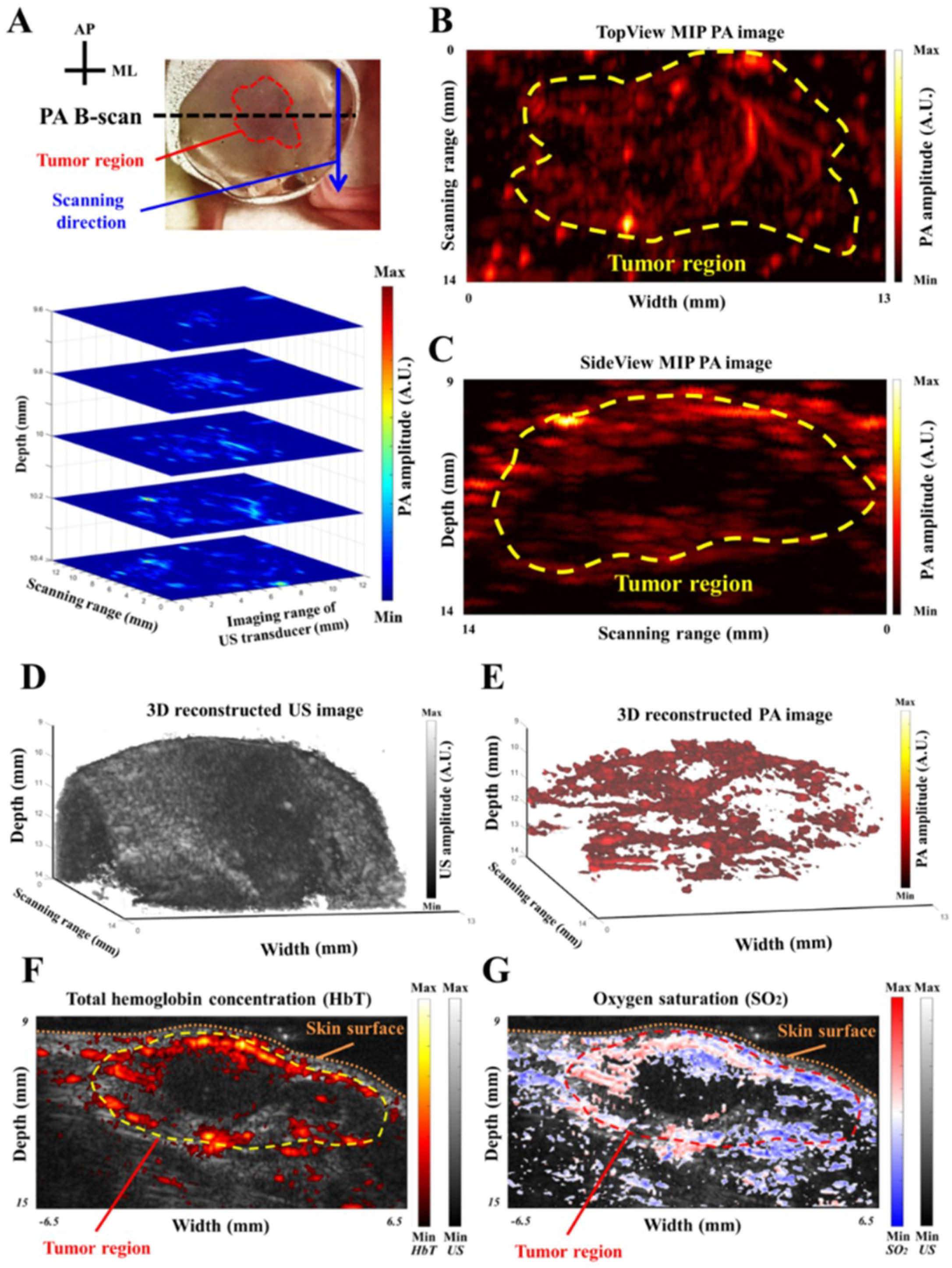
3.7. Performance Evaluation of the PA Imaging System Based on the Subcutaneous Tumor Model
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Ethical Statements
References
- Daoudi, K.; van den Berg, P.J.; Rabot, O.; Kohl, A.; Tisserand, S.; Brands, P.; Steenbergen, W. Handheld probe integrating laser diode and ultrasound transducer array for ultrasound/photoacoustic dual modality imaging. Opt. Express 2014, 22, 26365–26374. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.D.; Liu, Y.H.; Lai, H.Y.; Bandla, A.; Shih, Y.Y.; Chen, Y.Y.; Thakor, N.V. Rescue of cortical neurovascular functions during the hyperacute phase of ischemia by peripheral sensory stimulation. Neurobiol. Dis. 2015, 75, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Liao, L.D.; Tan, S.S.; Kwon, K.Y.; Ling, J.M.; Bandla, A.; Shih, Y.I.; Tan, E.T.; Li, W.; Ng, W.H.; et al. Assessment of neurovascular dynamics during transient ischemic attack by the novel integration of micro-electrocorticography electrode array with functional photoacoustic microscopy. Neurobiol. Dis. 2015, 82, 455–465. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Li, G.; Zhu, L.; Li, C.; Cornelius, L.A.; Wang, L.V. Handheld photoacoustic probe to detect both melanoma depth and volume at high speed in vivo. J. Biophotonics 2015, 8, 961–967. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Tripathi, S.V.; Rosman, I.; Ma, J.; Hai, P.; Linette, G.P.; Council, M.L.; Fields, R.C.; Wang, L.V.; Cornelius, L.A. Noninvasive determination of melanoma depth using a handheld photoacoustic probe. J. Investig. Dermatol. 2017, 137, 1370–1372. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Xing, W.; Maslov, K.I.; Cornelius, L.A.; Wang, L.V. Handheld photoacoustic microscopy to detect melanoma depth in vivo. Opt. Lett. 2014, 39, 4731–4734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Park, S.; Jung, Y.; Chang, S.; Park, J.; Zhang, Y.; Lovell, J.F.; Kim, C. Programmable real-time clinical photoacoustic and ultrasound imaging system. Sci. Rep. 2016, 6, 35137. [Google Scholar] [CrossRef] [PubMed]
- Toi, M.; Asao, Y.; Matsumoto, Y.; Sekiguchi, H.; Yoshikawa, A.; Takada, M.; Kataoka, M.; Endo, T.; Kawaguchi-Sakita, N.; Kawashima, M.; et al. Visualization of tumor-related blood vessels in human breast by photoacoustic imaging system with a hemispherical detector array. Sci. Rep. 2017, 7, 41970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, D.; Wang, Y.; Wang, W.; Luo, D.; Chitgupi, U.; Geng, J.; Zhou, Y.; Wang, L.; Lovell, J.F.; Xia, J. Deep tissue photoacoustic computed tomography with a fast and compact laser system. Biomed. Opt. Express 2017, 8, 112–123. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.A.; Rasheed, N.; Chitnis, P.V.; Sikdar, S. Photoacoustic imaging of muscle oxygenation during exercise. J. Acoust. Soc. Am. 2016, 139, 2176. [Google Scholar] [CrossRef]
- Yao, J.; Wang, L.V. Photoacoustic Brain Imaging: From Microscopic to Macroscopic Scales. Neurophotonics 2014, 1, 011033. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.K.A.; Steenbergen, W.; Manohar, S. Handheld Probe-Based Dual Mode Ultrasound/Photoacoustics for Biomedical Imaging. In Frontiers in Biophotonics for Translational Medicine: In the Celebration of Year of Light (2015); Olivo, M., Dinish, U.S., Eds.; Springer: Singapore, 2016; pp. 209–247. [Google Scholar]
- Schellenberg, M.W.; Hunt, H.K. Hand-held optoacoustic imaging: A review. Photoacoustics 2018, 11, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhao, H.; Ren, Q.; Li, C. Simulation of light delivery for photoacoustic breast imaging using the handheld probe. Chin. Opt. Lett. 2014, 12, 051703. [Google Scholar] [CrossRef]
- Wang, Z.; Ha, S.; Kim, K. A new design of light illumination scheme for deep tissue photoacoustic imaging. Opt. Express 2012, 20, 22649–22659. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Ha, S.; Kim, K. Evaluation of finite-element-based simulation model of photoacoustics in biological tissues. In Proceedings of the Medical Imaging 2012: Ultrasonic Imaging, Tomography, and Therapy, San Diego, CA, USA, 25 February 2012. [Google Scholar]
- Flock, S.T.; Patterson, M.S.; Wilson, B.C.; Wyman, D.R. Monte Carlo modeling of light propagation in highly scattering tissues. I. Model predictions and comparison with diffusion theory. IEEE Trans. Biomed. Eng. 1989, 36, 1162–1168. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 050902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwon, K.; Son, T.; Lee, K.-J.; Jung, B. Enhancement of light propagation depth in skin: Cross-validation of mathematical modeling methods. Lasers Med. Sci. 2009, 24, 605–615. [Google Scholar] [CrossRef] [PubMed]
- Paltauf, G.; Viator, J.; Prahl, S.; Jacques, S. Iterative reconstruction algorithm for optoacoustic imaging. J. Acoust. Soc. Am. 2002, 112, 1536–1544. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Jiang, H. Finite-element-based photoacoustic tomography in time domain. J. Opt. A Pure Appl. Opt. 2009, 11, 085301. [Google Scholar] [CrossRef]
- Strohm, E.M.; Gorelikov, I.; Matsuura, N.; Kolios, M.C. Modeling photoacoustic spectral features of micron-sized particles. Phys. Med. Biol. 2014, 59, 5795. [Google Scholar] [CrossRef] [PubMed]
- Valdes, C.P.; Varma, H.M.; Kristoffersen, A.K.; Dragojevic, T.; Culver, J.P.; Durduran, T. Speckle contrast optical spectroscopy, a non-invasive, diffuse optical method for measuring microvascular blood flow in tissue. Biomed. Opt. Express 2014, 5, 2769–2784. [Google Scholar] [CrossRef] [PubMed]
- Zhen, X.; Feng, X.; Xie, C.; Zheng, Y.; Pu, K. Surface engineering of semiconducting polymer nanoparticles for amplified photoacoustic imaging. Biomaterials 2017, 127, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Godavarty, A.; Hawrysz, D.; Roy, R.; Sevick-Muraca, E.; Eppstein, M. Influence of the refractive index-mismatch at the boundaries measured in fluorescenceenhanced frequency-domain photon migration imaging. Opt. Express 2002, 10, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Baffou, G.; Quidant, R.; García de Abajo, F.J. Nanoscale control of optical heating in complex plasmonic systems. ACS Nano 2010, 4, 709–716. [Google Scholar] [CrossRef] [PubMed]
- Hatef, A.; Darvish, B.; Dagallier, A.; Davletshin, Y.R.; Johnston, W.; Kumaradas, J.C.; Rioux, D.; Meunier, M. Analysis of photoacoustic response from gold–silver alloy nanoparticles irradiated by short pulsed laser in water. J. Phys. Chem. C 2015, 119, 24075–24080. [Google Scholar] [CrossRef]
- Gould, T.; Wang, Q.; Pfefer, T.J. Optical-thermal light-tissue interactions during photoacoustic breast imaging. Biomed. Opt. Express 2014, 5, 832–847. [Google Scholar] [CrossRef] [PubMed]
- Bok, T.H.; Hysi, E.; Kolios, M.C. Simultaneous assessment of red blood cell aggregation and oxygen saturation under pulsatile flow using high-frequency photoacoustics. Biomed. Opt. Express 2016, 7, 2769–2780. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xie, X.; Ku, G.; Wang, L.V.; Stoica, G. Noninvasive imaging of hemoglobin concentration and oxygenation in the rat brain using high-resolution photoacoustic tomography. J. Biomed. Opt. 2006, 11, 024015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bove, K.; Lincoln, D.W.; Tsan, M.F. Effect of resveratrol on growth of 4T1 breast cancer cells in vitro and in vivo. Biochem. Biophys. Res. Commun. 2002, 291, 1001–1005. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Chan, S.J.; Pan, H.C.; Bandla, A.; King, N.K.K.; Wong, P.T.H.; Chen, Y.Y.; Ng, W.H.; Thakor, N.V.; Liao, L.D. Integrated treatment modality of cathodal-transcranial direct current stimulation with peripheral sensory stimulation affords neuroprotection in a rat stroke model. Neurophotonics 2017, 4, 045002. [Google Scholar] [CrossRef] [PubMed]
- Fantini, S.; Franceschini, M.A.; Gratton, E. Semi-infinite-geometry boundary problem for light migration in highly scattering media: A frequency-domain study in the diffusion approximation. J. Opt. Soc. Am. B 1994, 11, 2128–2138. [Google Scholar] [CrossRef]
- Carroll, L.; Humphreys, T.R. LASER-tissue interactions. Clin. Dermatol. 2006, 24, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Li, M.L.; Oh, J.T.; Xie, X.; Ku, G.; Wang, W.; Li, C.; Lungu, G.; Stoica, G.; Wang, L.V. Simultaneous molecular and hypoxia imaging of brain tumors in vivo using spectroscopic photoacoustic tomography. Proc. IEEE 2008, 96, 481–489. [Google Scholar]
- Wang, K.K.-H.; Zhu, T.C. Reconstruction of Optical Properties Using a Diffusion Model for Interstitial Diffuse Optical Tomography. In Proceedings of the Optical Methods for Tumor Treatment and Detection: Mechanisms and Techniques in Photodynamic Therapy XVIII, San Jose, CA, USA, 18 February 2009. [Google Scholar]
- Sheng, Y.; Liao, L.-D.; Bandla, A.; Liu, Y.-H.; Thakor, N.; Tan, M.C. Size and Shell Effects on the Photoacoustic and Luminescence Properties of Dual Modal Rare-Earth-Doped Nanoparticles for Infrared Photoacoustic Imaging. ACS Biomater. Sci. Eng. 2016, 2, 809–817. [Google Scholar] [CrossRef]
- Sheng, Y.; Liao, L.D.; Bandla, A.; Liu, Y.H.; Yuan, J.; Thakor, N.; Tan, M.C. Enhanced near-infrared photoacoustic imaging of silica-coated rare-earth doped nanoparticles. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 70, 340–346. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-H.; Xu, Y.; Liao, L.-D.; Chan, K.C.; Thakor, N.V. A Handheld Real-Time Photoacoustic Imaging System for Animal Neurological Disease Models: From Simulation to Realization. Sensors 2018, 18, 4081. https://doi.org/10.3390/s18114081
Liu Y-H, Xu Y, Liao L-D, Chan KC, Thakor NV. A Handheld Real-Time Photoacoustic Imaging System for Animal Neurological Disease Models: From Simulation to Realization. Sensors. 2018; 18(11):4081. https://doi.org/10.3390/s18114081
Chicago/Turabian StyleLiu, Yu-Hang, Yu Xu, Lun-De Liao, Kim Chuan Chan, and Nitish V. Thakor. 2018. "A Handheld Real-Time Photoacoustic Imaging System for Animal Neurological Disease Models: From Simulation to Realization" Sensors 18, no. 11: 4081. https://doi.org/10.3390/s18114081
APA StyleLiu, Y.-H., Xu, Y., Liao, L.-D., Chan, K. C., & Thakor, N. V. (2018). A Handheld Real-Time Photoacoustic Imaging System for Animal Neurological Disease Models: From Simulation to Realization. Sensors, 18(11), 4081. https://doi.org/10.3390/s18114081