Correntropy Based Divided Difference Filtering for the Positioning of Ships
Abstract
1. Introduction
2. Preliminaries
2.1. Correntropy
2.2. DD1 Filter
2.3. DD2 Filter
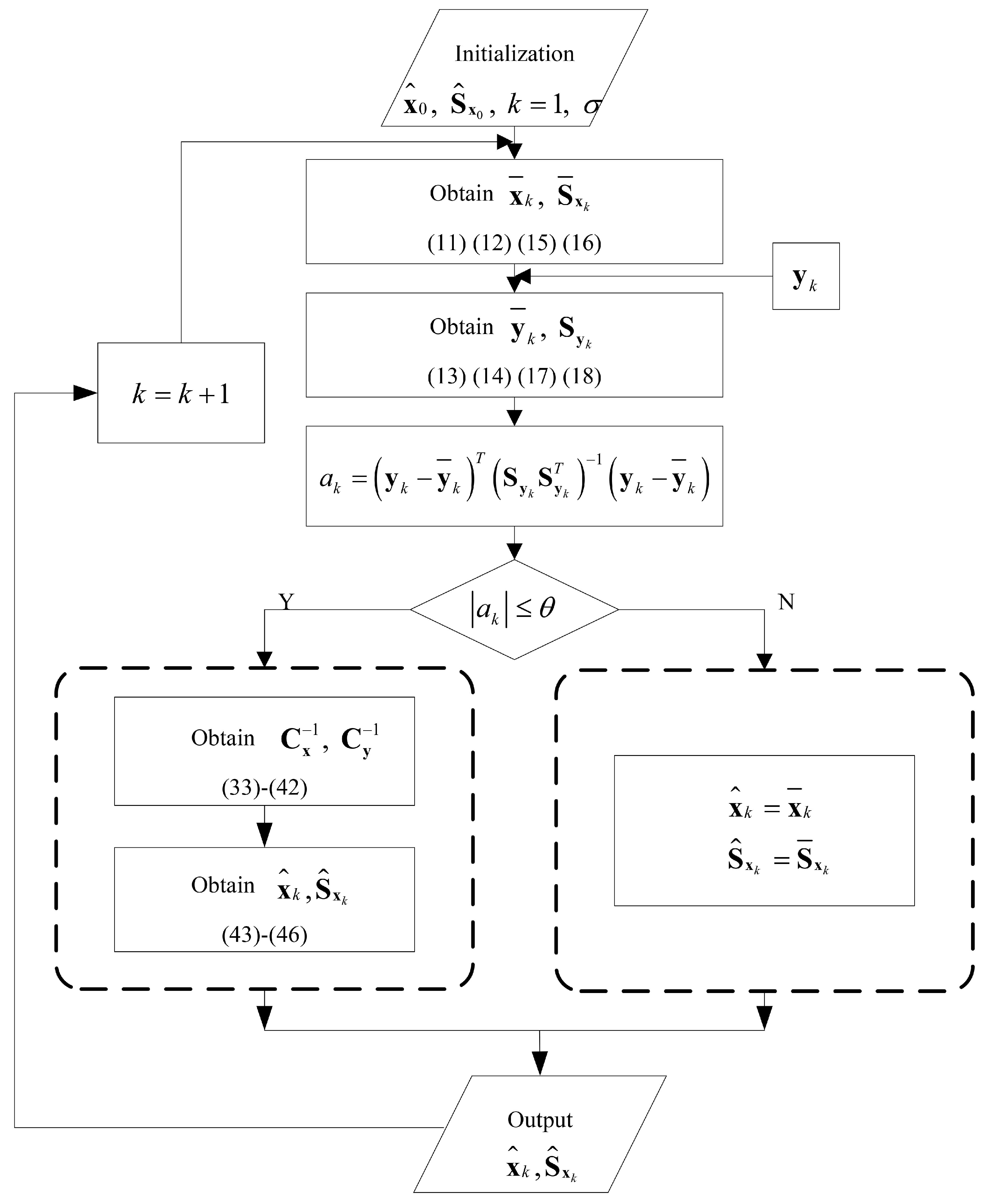
3. Correntropy-Based DDF
4. Positioning of Ships
4.1. The State and Measurement Models
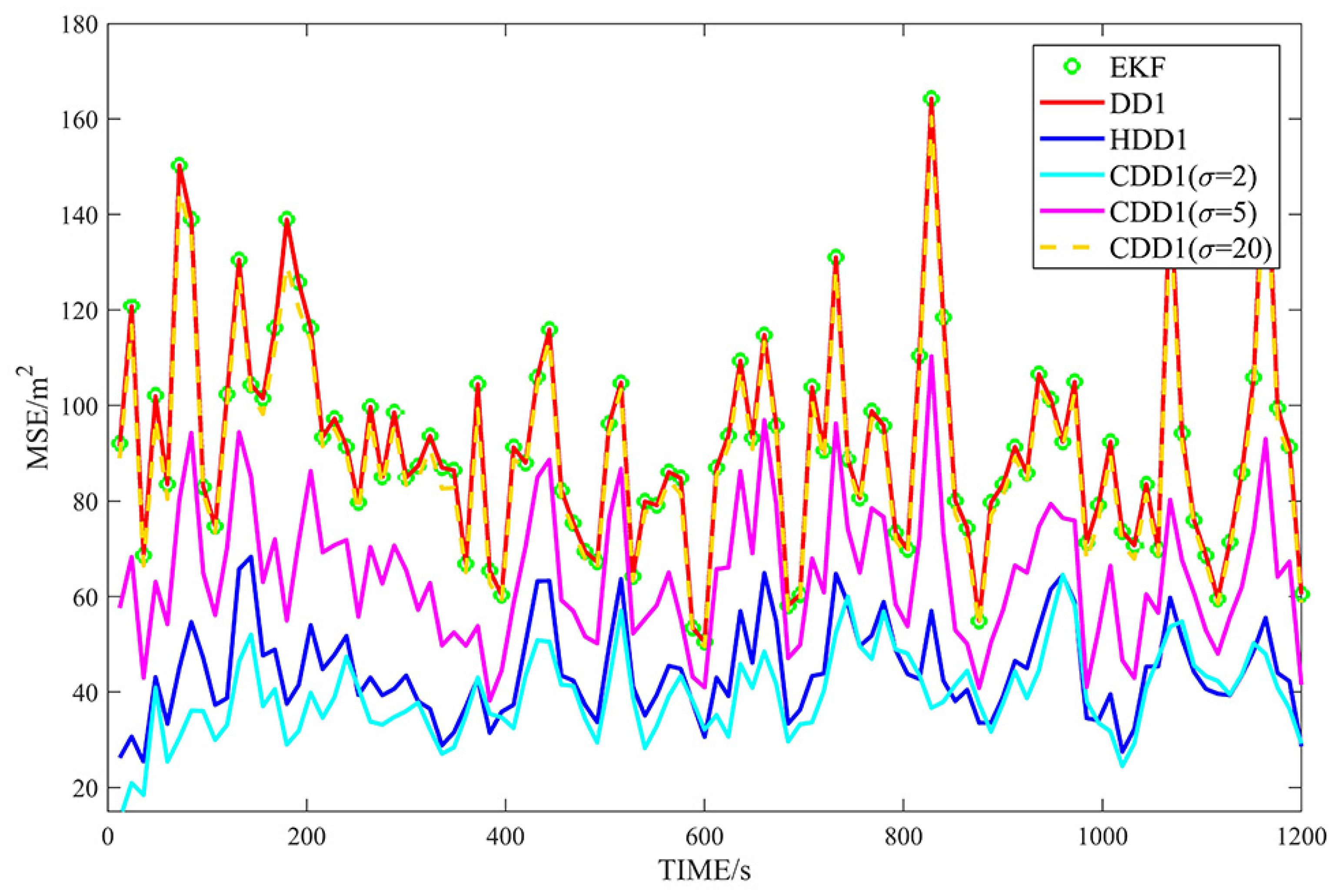
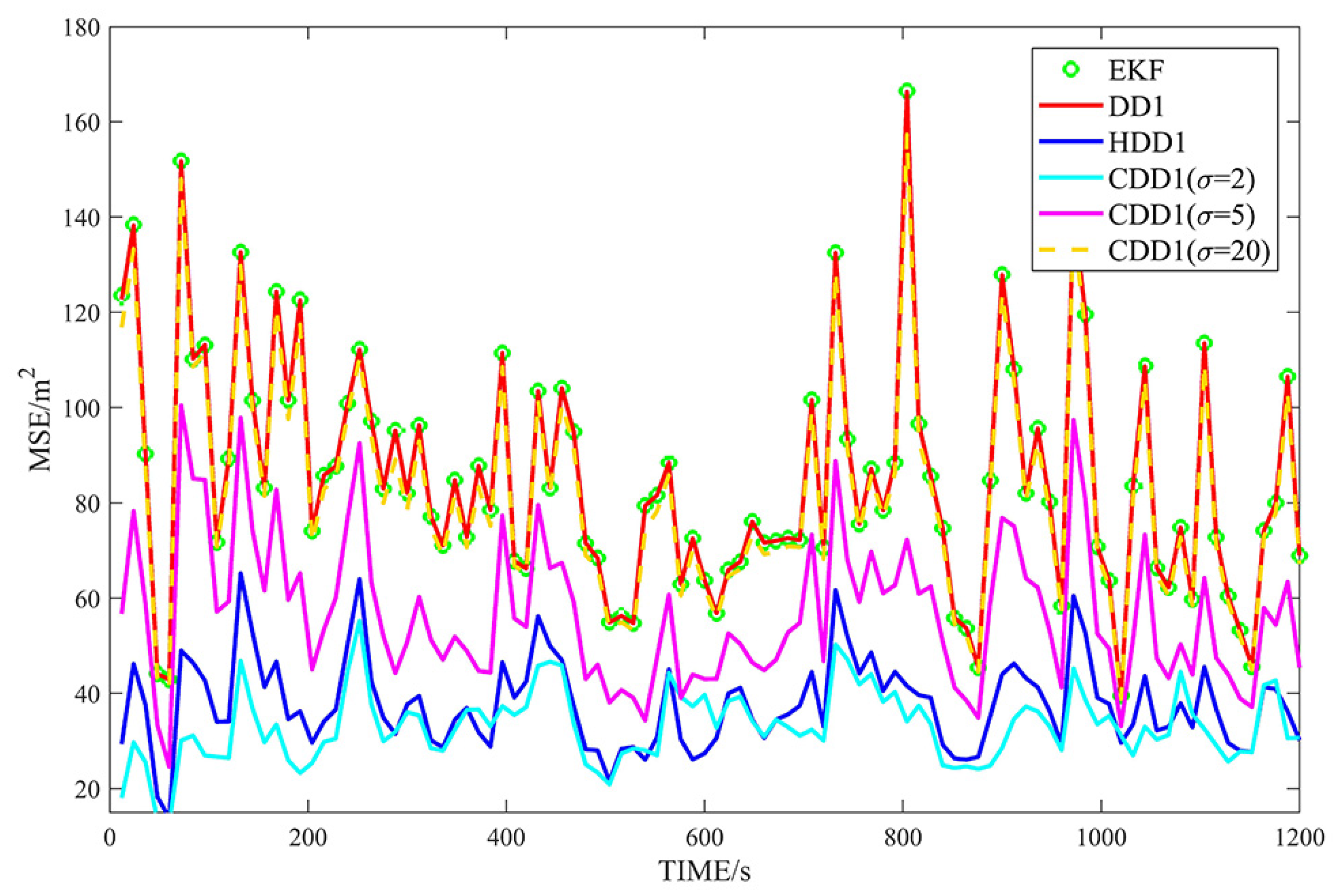
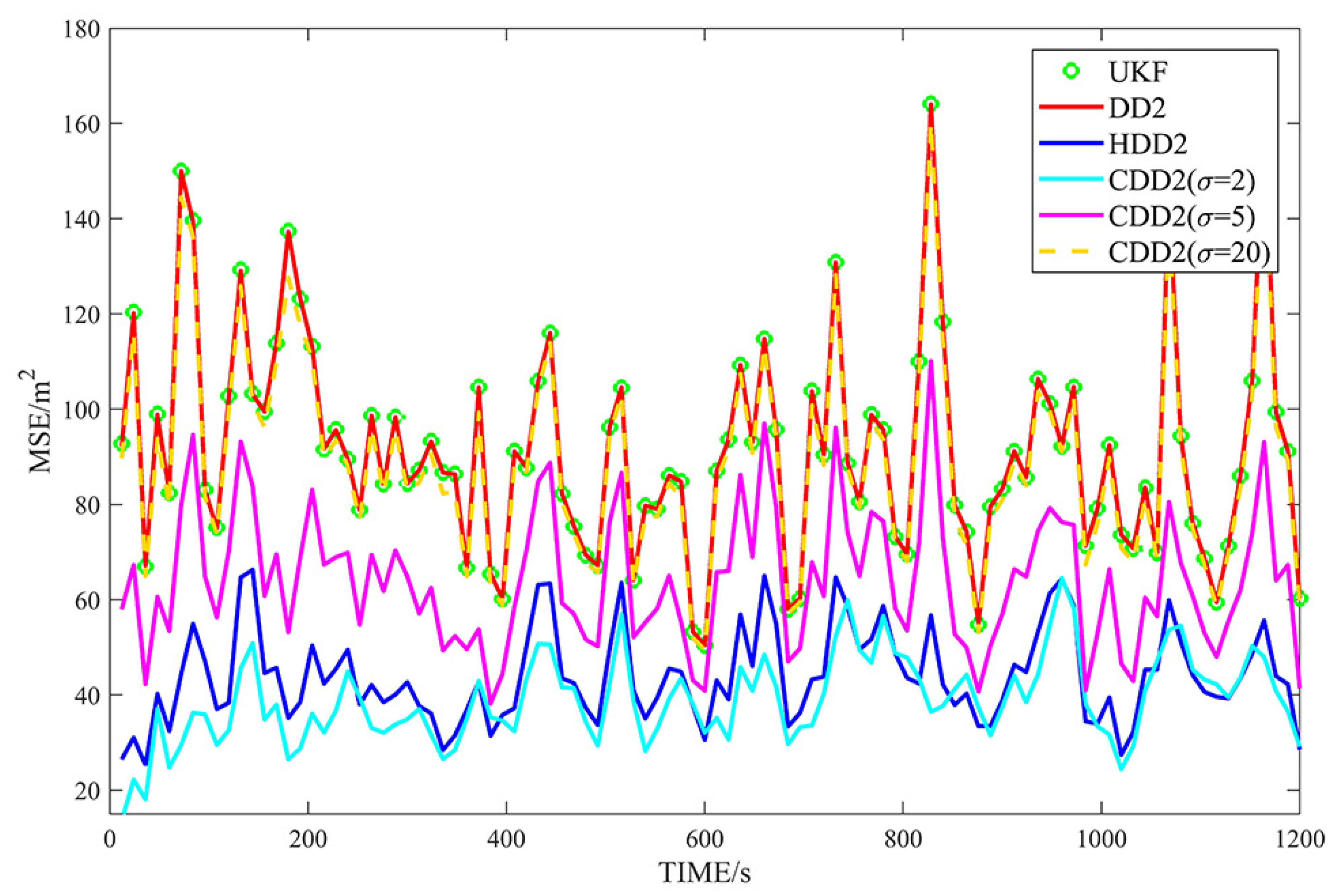
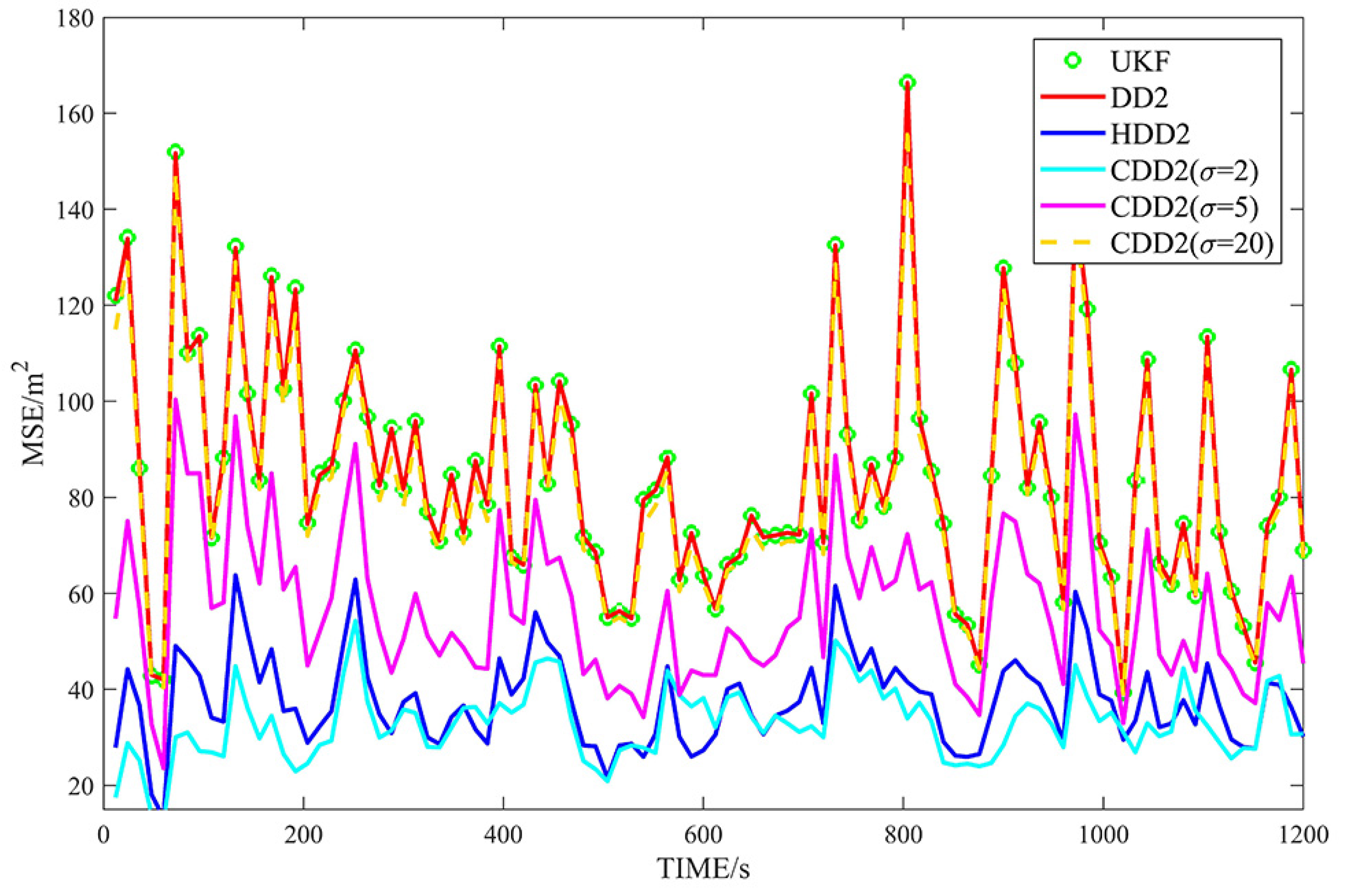
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Q.; Gao, Z.; Wan, D. An adaptive information fusion method to vehicle integrated navigation. In Proceedings of the 2002 IEEE Position Location and Navigation Symposium, Palms Springs, CA, USA, 15–18 April 2002; pp. 248–253. [Google Scholar]
- Zhao, L.; Ochieng, W.Y.; Quddus, M.A.; Noland, R.B. An Extended Kalman Filter Algorithm for Integrating GPS and Low Cost Dead Reckoning System Data for Vehicle Performance and Emissions Monitoring. J. Navig. 2003, 56, 257–275. [Google Scholar] [CrossRef]
- Parkinson, B.; Spilker, J.; Axelrad, P.; Enge, P. Global Positioning System: Theory and Applications, Volume II; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1996. [Google Scholar]
- Han, S.; Wang, J. Integrated GPS/INS navigation system with dual-rate Kalman Filter. GPS Solut. 2012, 16, 389–404. [Google Scholar] [CrossRef]
- Xiong, H.; Tang, J.; Xu, H.; Zhang, W.; Du, Z. A Robust Single GPS Navigation and Positioning Algorithm Based on Strong Tracking Filtering. IEEE Sens. J. 2018, 18, 290–298. [Google Scholar] [CrossRef]
- Jo, K.; Lee, M.; Sunwoo, M. Fast GPS-DR Sensor Fusion Framework: Removing the Geodetic Coordinate Conversion Process. IEEE Trans. Intell. Transp. 2016, 17, 2008–2013. [Google Scholar] [CrossRef]
- Wang, S.; Deng, Z.; Yin, G. An Accurate GPS-IMU/DR Data Fusion Method for Driverless Car Based on a Set of Predictive Models and Grid Constraints. Sensors 2016, 16, 280. [Google Scholar] [CrossRef] [PubMed]
- Jirawimut, R.; Ptasinski, P.; Garaj, V.; Cecelja, F.; Balachandran, W. A method for dead reckoning parameter correction in pedestrian navigation system. IEEE Trans. Instrum. Meas. 2003, 52, 209–215. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME-J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Nahi, N.E. Estimation Theory and Applications; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Anderson, B.; Moore, J. Optimal Filtering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Ameid, T.; Menacer, A.; Talhaoui, H.; Harzelli, I. Rotor resistance estimation using Extended Kalman filter and spectral analysis for rotor bar fault diagnosis of sensorless vector control induction motor. Measurement 2017, 111, 243–259. [Google Scholar] [CrossRef]
- Sabet, M.T.; Sarhadi, P.; Zarini, M. Extended and Unscented Kalman filters for parameter estimation of an autonomous underwater vehicle. Ocean Eng. 2014, 91, 329–339. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Lee, J.S.; Choi, I.Y.; Kim, S.; Moon, D.S. Kinematic modeling of a track geometry using an Unscented Kalman Filter. Measurement 2016, 94, 707–716. [Google Scholar] [CrossRef]
- Gao, B.; Gao, S.; Hu, G.; Zhong, Y.; Gu, C. Maximum likelihood principle and moving horizon estimation based adaptive unscented Kalman filter. Aerosp. Sci. Technol. 2018, 73, 184–196. [Google Scholar] [CrossRef]
- Nørgaard, M.; Poulsen, N.K.; Ravn, O. New developments in state estimation for nonlinear systems. Automatica 2000, 36, 1627–1638. [Google Scholar] [CrossRef]
- Subrahmanya, N.; Shin, Y.C. Adaptive divided difference filtering for simultaneous state and parameter estimation. Automatica 2009, 45, 1686–1693. [Google Scholar] [CrossRef]
- Schick, I.; Mitter, S. Robust Recursive Estimation in the Presence of Heavy-Tailed Observation Noise. Ann. Stat. 1994, 22, 1045–1080. [Google Scholar] [CrossRef]
- Huber, P.; Ronchetti, E. Robust Statistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Karlgaard, C.D. Huber-Based Divided Difference Filtering. J. Guid. Control Dyn. 2007, 30, 885–891. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.; Duan, D. Improved robust Huber-based divided difference filtering. Proc. Inst. Mech. Eng. G J. Aerosp. 2014, 228, 2123–2129. [Google Scholar] [CrossRef]
- Roth, M.; Özkan, E.; Gustafsson, F. A Student’s t filter for heavy tailed process and measurement noise. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 5770–5774. [Google Scholar]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. Robust Student’s t Based Nonlinear Filter and Smoother. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2586–2596. [Google Scholar] [CrossRef]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar]
- Chen, B.; Zhu, Y.; Hu, J.; Principe, J.C. System Parameter Identification: Information Criteria and Algorithms; Elsevier Inc.: London, UK, 2013. [Google Scholar]
- Liu, W.; Pokharel, P.P.; Principe, J.C. Correntropy: Properties, and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- He, R.; Zheng, W.; Hu, B. Maxinum correntropy criterion for robust face recognition. IEEE Trans. Pattern Anal. 2011, 33, 1561–1576. [Google Scholar]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Mandanas, F.D.; Kotropoulos, C.L. Robust Multidimensional Scaling Using a Maximum Correntropy Criterion. IEEE Trans. Signal Process. 2017, 65, 919–932. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, Y.Y.; Li, L. Correntropy Matching Pursuit With Application to Robust Digit and Face Recognition. IEEE Trans. Cybern. 2017, 47, 1354–1366. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Principe, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum Correntropy Kalman Filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Kulikova, M.V. Square-root algorithms for maximum correntropy estimation of linear discrete-time systems in presence of non-Gaussian noise. Syst. Control Lett. 2017, 108, 8–15. [Google Scholar] [CrossRef]
- Izanloo, R.; Fakoorian, S.A.; Yazdi, H.S.; Simon, D. Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise. In Proceedings of the Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 500–505. [Google Scholar]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P.; Wang, M. Maximum Correntropy Unscented Kalman Filter for Spacecraft Relative State Estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Li, N.; Zhang, Y. Maximum correntropy unscented Kalman and information filters for non-Gaussian measurement noise. J. Frankl. Inst. 2017, 354, 8659–8677. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Y.; Wang, G.; Gao, W. A Maximum Correntropy Divided Difference Filter for Cooperative Localization. IEEE Access 2018, 6, 41720–41727. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Principe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Zhang, H.; Mao, X. Fuzzy-based Kalman Filter for Ship Navigation. In Proceedings of the International Conference on Mechatronics and Automation (ICMA), Changchun, China, 9–12 August 2009; pp. 2388–2392. [Google Scholar]
| Parameter | Value |
|---|---|
| 27,780/s | |
| 12 |
| Parameter | Value |
|---|---|
| 1 | |
| 1 | |
| 10.289 | |
| 0 |
| Filter | sof | sof |
|---|---|---|
| EKF | 10.3197 | 11.1708 |
| DD1 | 10.3196 | 11.1707 |
| HDD1 | 12.1968 | 13.1074 |
| CDD1 | 23.8353 | 22.6151 |
| CDD1 | 10.4517 | 11.2693 |
| CDD1 | 10.3215 | 11.1690 |
| UKF | 10.3093 | 11.1557 |
| DD2 | 10.3086 | 11.1549 |
| HDD2 | 12.1613 | 13.0604 |
| CDD2 | 23.8503 | 22.3792 |
| CDD2 | 10.4366 | 11.2484 |
| CDD2 | 10.3102 | 11.1529 |
| Filter | sof | sof |
|---|---|---|
| EKF | 91.7839 | 84.7678 |
| DD1 | 91.7776 | 84.7557 |
| HDD1 | 44.2747 | 37.6608 |
| CDD1 | 39.4284 | 33.0989 |
| CDD1 | 64.5026 | 56.9180 |
| CDD1 | 89.3531 | 82.3220 |
| UKF | 91.4480 | 84.5617 |
| DD2 | 91.4269 | 84.5294 |
| HDD2 | 43.8700 | 37.4722 |
| CDD2 | 39.0126 | 32.8825 |
| CDD2 | 64.1485 | 56.7222 |
| CDD2 | 89.0010 | 82.0980 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Chen, B.; Wang, S.; Du, S. Correntropy Based Divided Difference Filtering for the Positioning of Ships. Sensors 2018, 18, 4080. https://doi.org/10.3390/s18114080
Liu X, Chen B, Wang S, Du S. Correntropy Based Divided Difference Filtering for the Positioning of Ships. Sensors. 2018; 18(11):4080. https://doi.org/10.3390/s18114080
Chicago/Turabian StyleLiu, Xi, Badong Chen, Shiyuan Wang, and Shaoyi Du. 2018. "Correntropy Based Divided Difference Filtering for the Positioning of Ships" Sensors 18, no. 11: 4080. https://doi.org/10.3390/s18114080
APA StyleLiu, X., Chen, B., Wang, S., & Du, S. (2018). Correntropy Based Divided Difference Filtering for the Positioning of Ships. Sensors, 18(11), 4080. https://doi.org/10.3390/s18114080






