Stackelberg Dynamic Game-Based Resource Allocation in Threat Defense for Internet of Things
Abstract
1. Introduction
- Firstly, we research a cyber-security IoT system, which consists of one defender and attackers. The defender tries to find the optimal allocated resources for threat defense, and the attackers try to use their resources to attack the IoT system.
- Secondly, a Stackelberg dynamic game model is proposed to formulate the resource allocation problem in threat defense for the Internet of Things. The Stackelberg game is a one-leader-many-followers game, where the defender is the leader and the attackers are the followers.
- For the dynamic game, we use the risk level as the system state. The objectives for the defender and attackers are to optimize the cost during the threat defense to find the optimal allocated resources for both the defender and attackers.
- Finally, the open-loop control solutions and the feedback control solutions for both the defender and attackers are given based on Bellman dynamic programming.
2. System Model and Problem Formulation
3. Game Analysis
3.1. Open-Loop Nash Equilibrium Solutions
3.1.1. Open-Loop Solutions for the Attackers
3.1.2. Open-Loop Solutions for the Defender
3.1.3. Open-Loop Control Algorithm
| Algorithm 1. Open-loop control algorithm for the attackers and defender. |
| Start algorithm |
| Step 1. Set up the parameter for the attackers and defender; |
| Step 2. The defender controls its initial strategy for resource allocation for threat defense; |
| Step 3. Start the open-loop control of the attackers and the defender; |
| Step 4. Start to calculate the open-loop control solutions for the attackers, Step 4.1. Set up the objective function for the attackers; Step 4.2. Calculate the solutions for the attackers. |
| Step 5. Get the open-loop solutions of the attackers for the defender; |
| Step 6. Start to calculate the open-loop control solutions for the defender; Step 6.1. Set up the objective function for the defender; Step 6.2. Calculate the solutions for the defender. |
| Algorithm End |
3.2. Feedback Nash Equilibrium Solutions
3.2.1. Feedback Solutions for the Attackers
3.2.2. Feedback Solutions for the Defender
3.2.3. Feedback Control Algorithm
| Algorithm 2. Feedback control algorithm for the attackers and defender. |
| Start algorithm |
| Step 1. Set up the parameter for the attackers and defender; |
| Step 2. The defender control its initial strategy for resource allocation for threat defense; |
| Step 3. Start the feedback control of the attackers and the defender; |
| Step 4. Start to calculate the feedback control solutions for the attackers, Step 4.1. Set up the objective function for the attackers; Step 4.2. Calculate the solutions for the attackers. |
| Step 5. Get the feedback solutions of the attackers for the defender; |
| Step 6. Start to calculate the feedback control solutions for the defender; Step 6.1. Set up the objective function for the defender; Step 6.2. Calculate the solutions for the defender. |
| Algorithm End |
4. Numerical Simulations
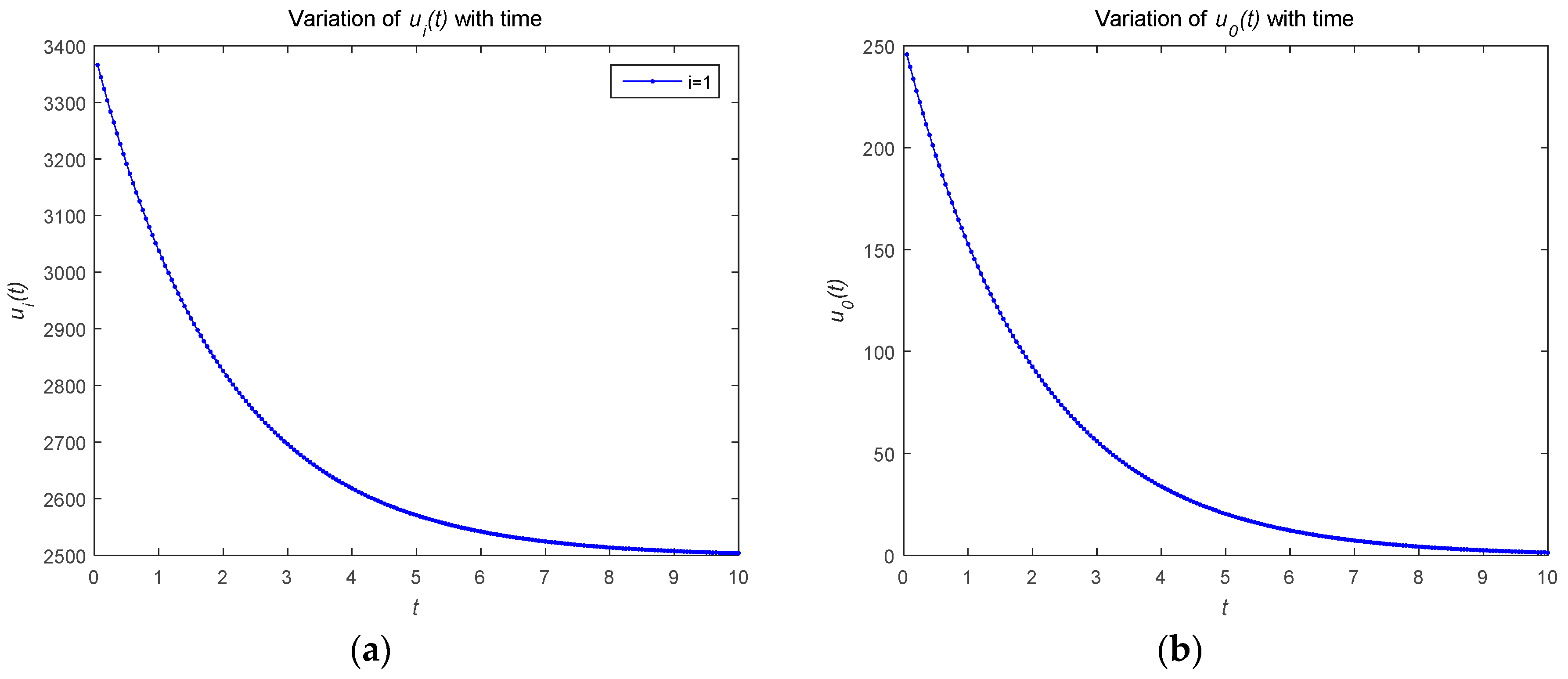
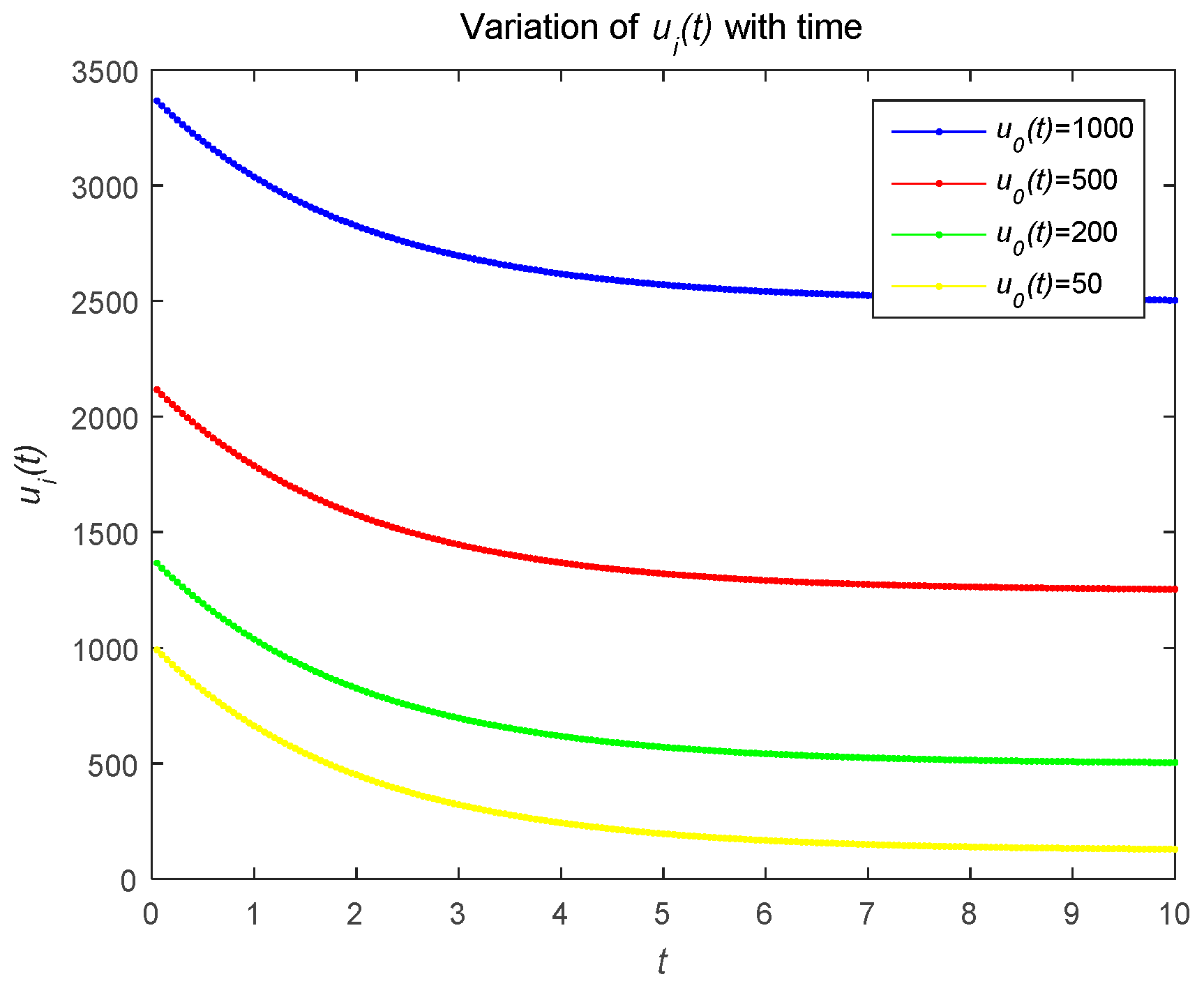
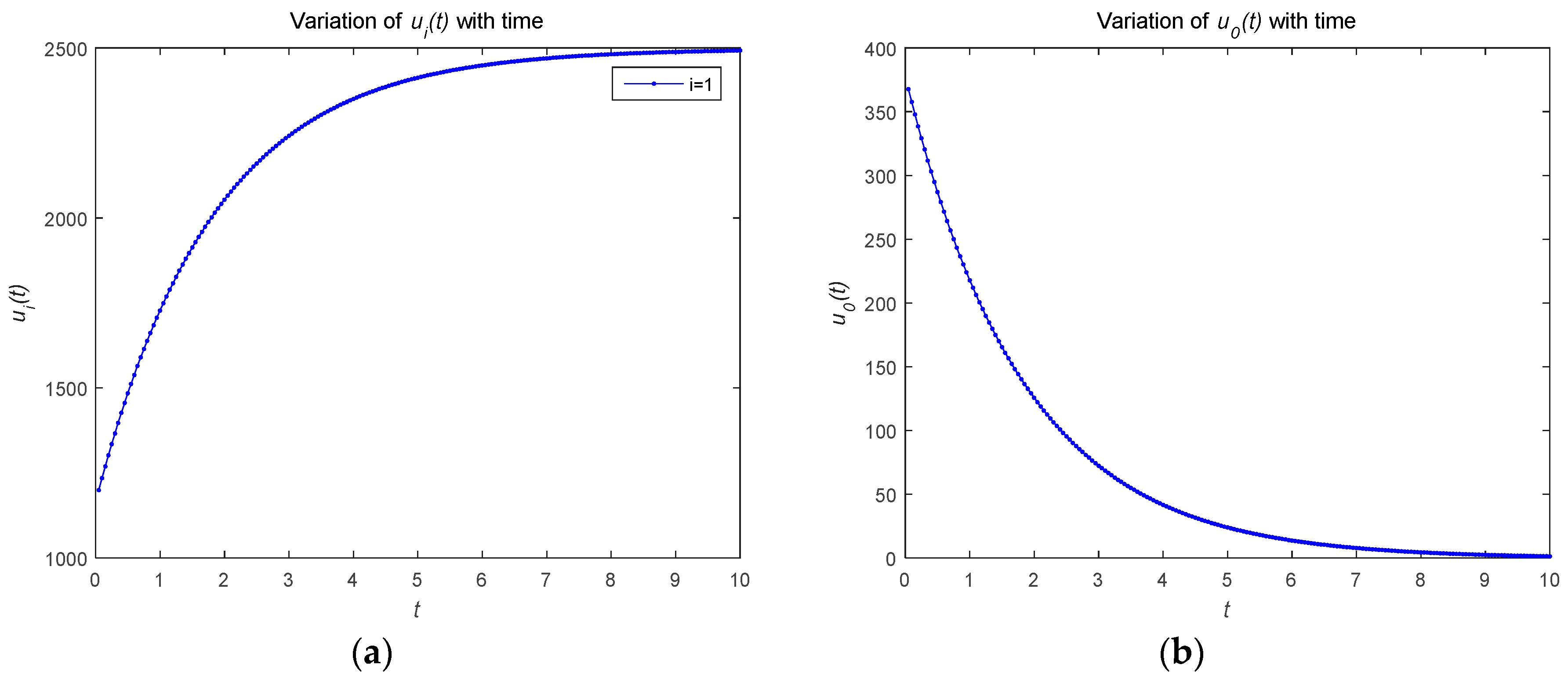
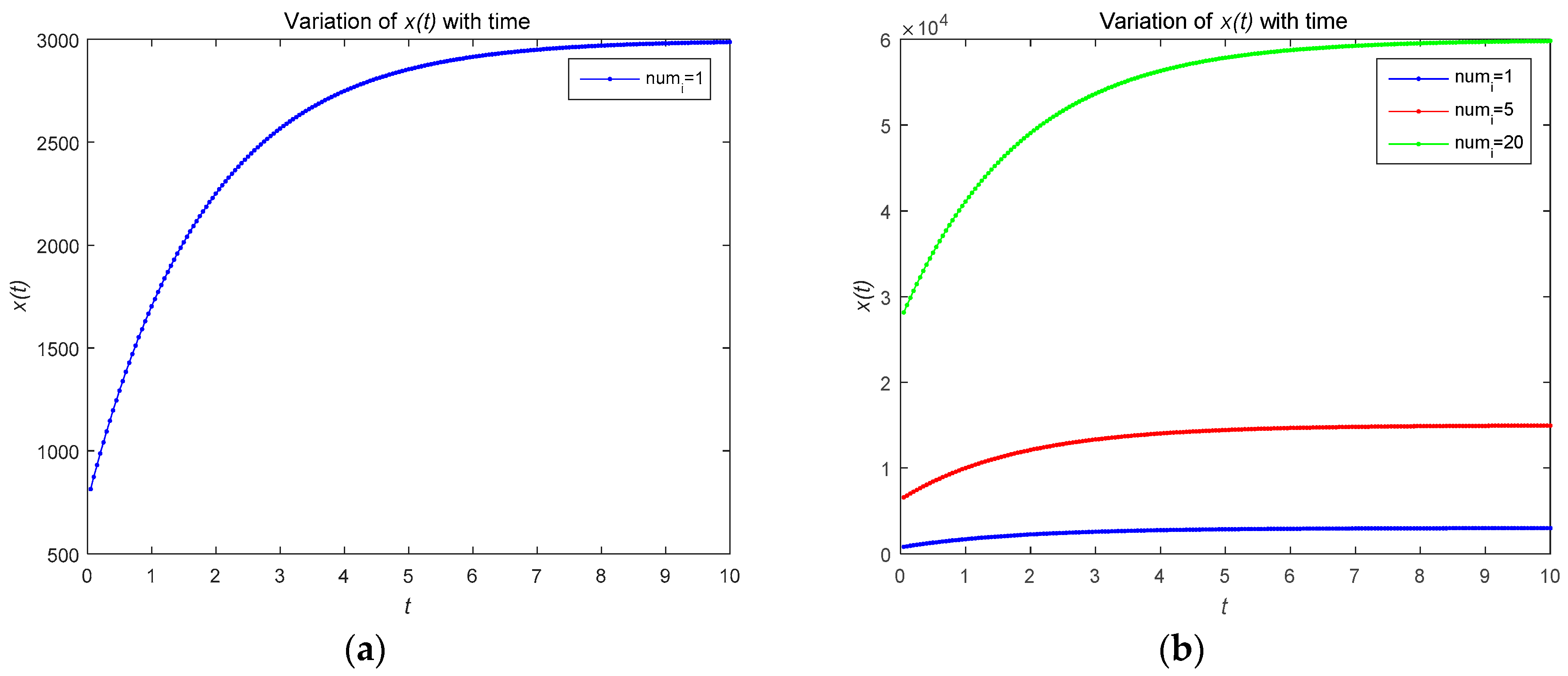
4.1. Numerical Simulations of Open-Loop Nash Equilibrium Solutions
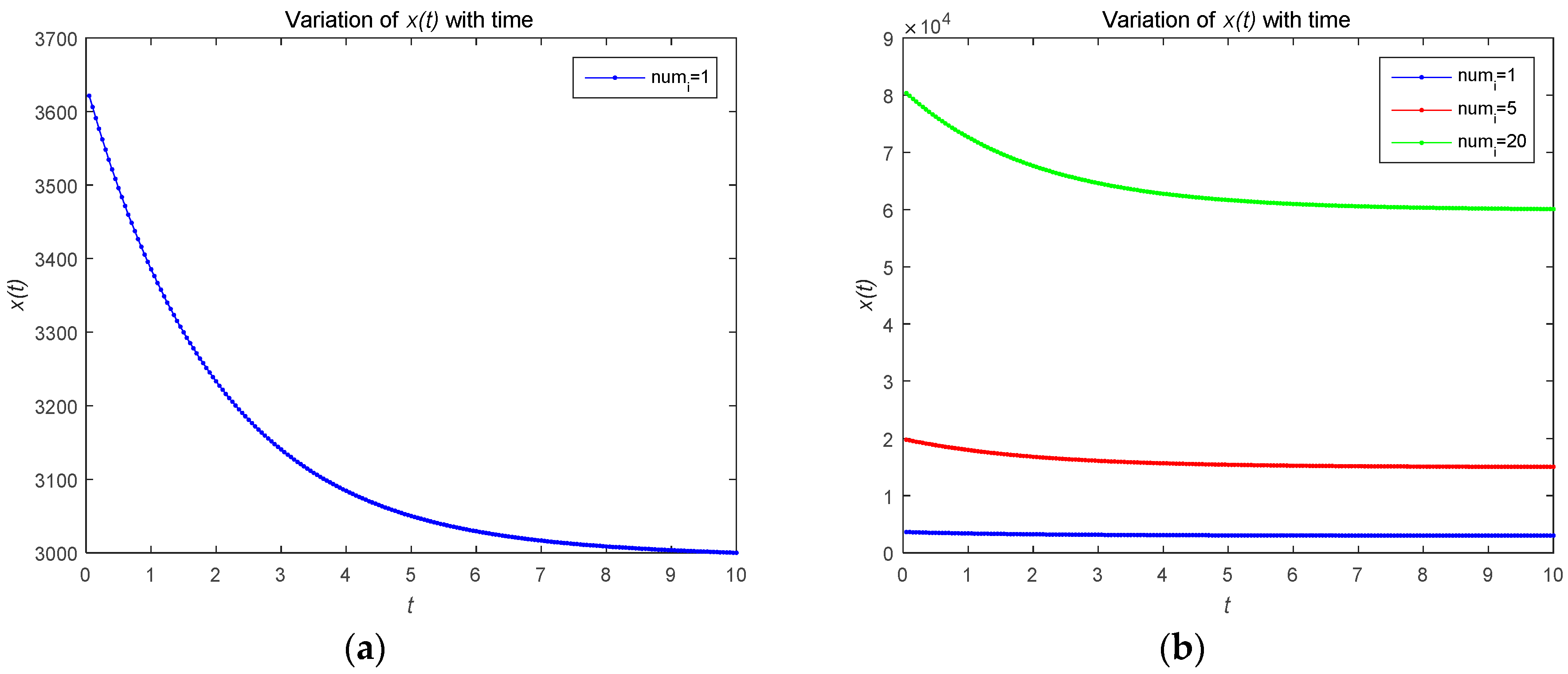
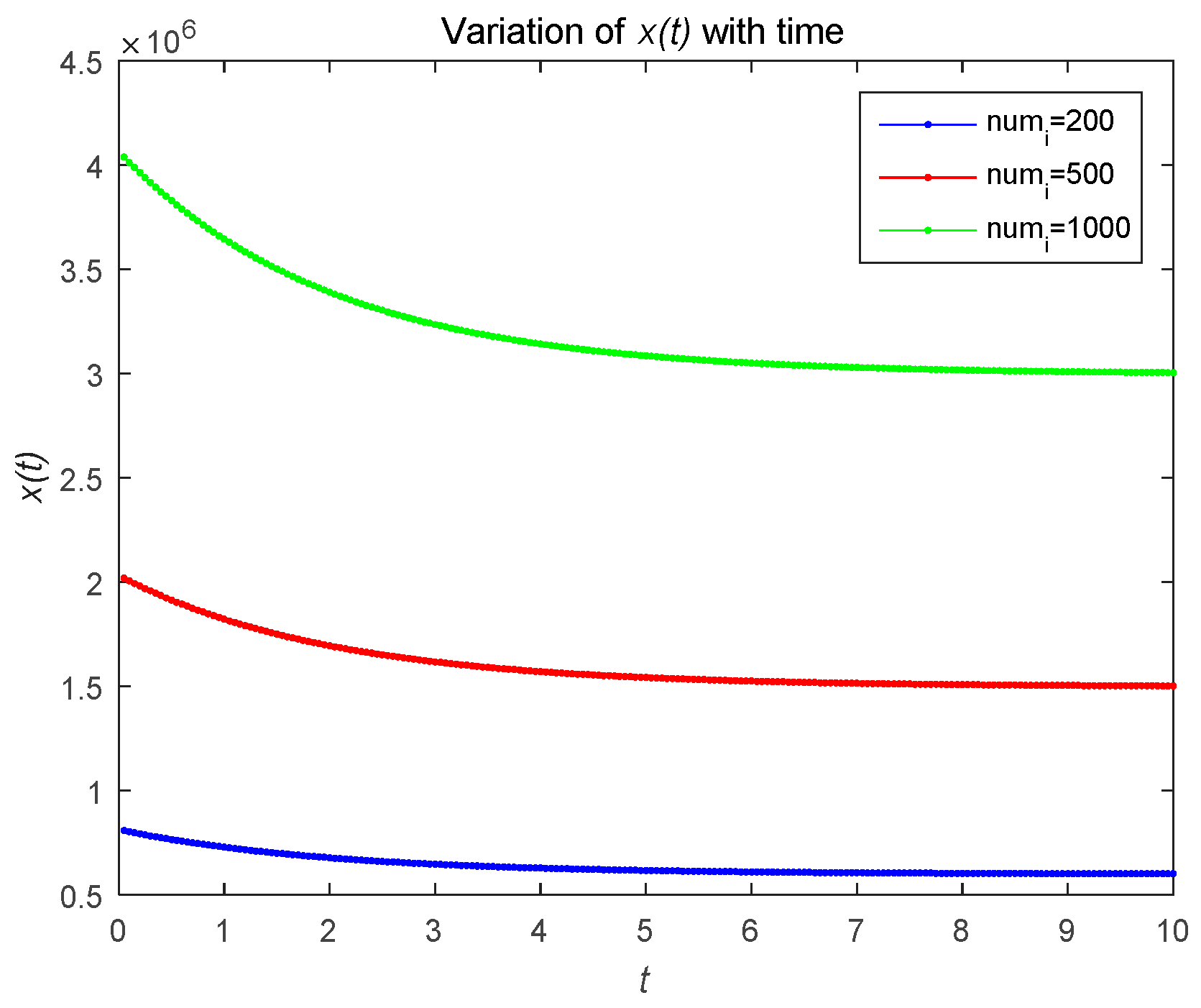
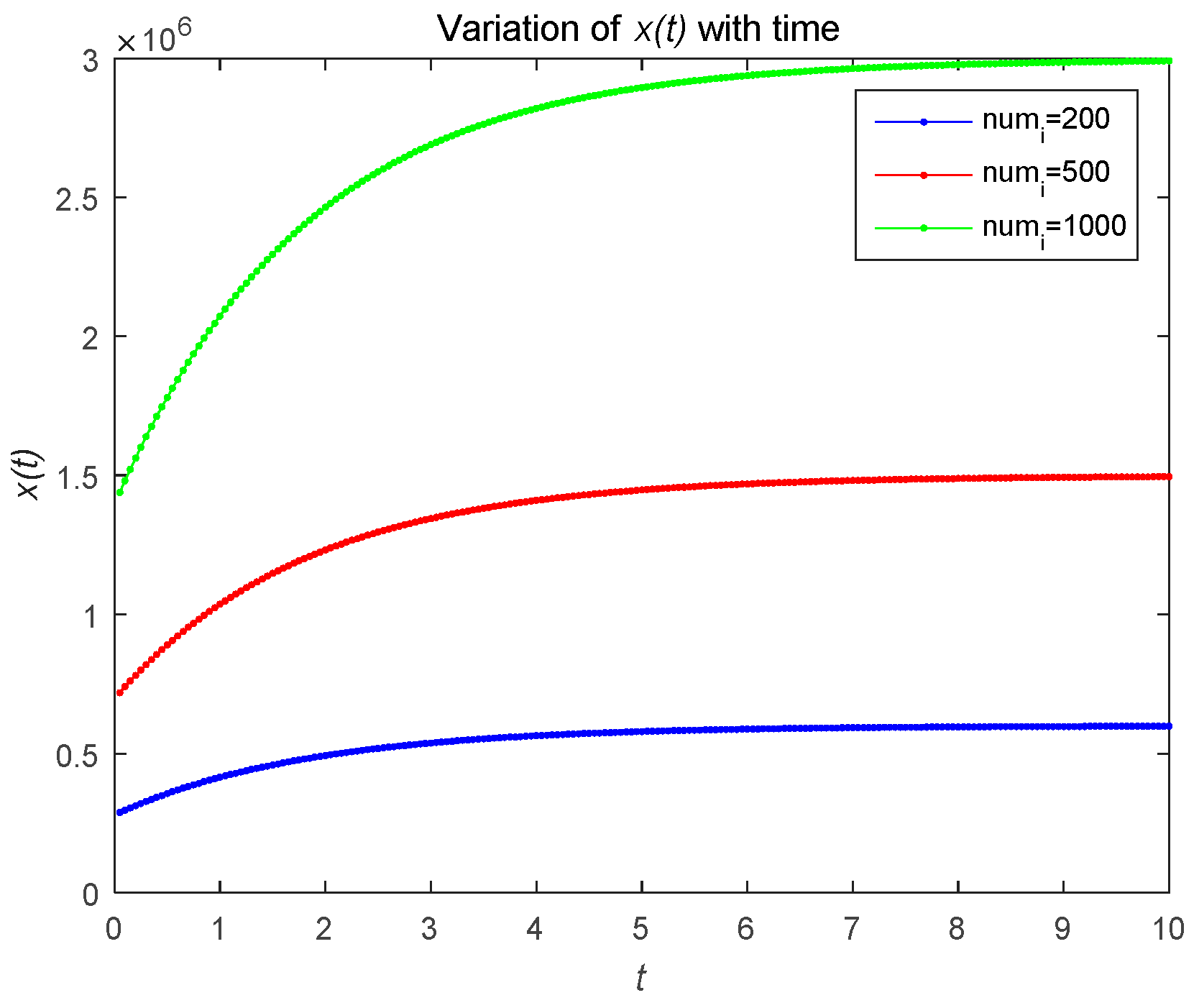
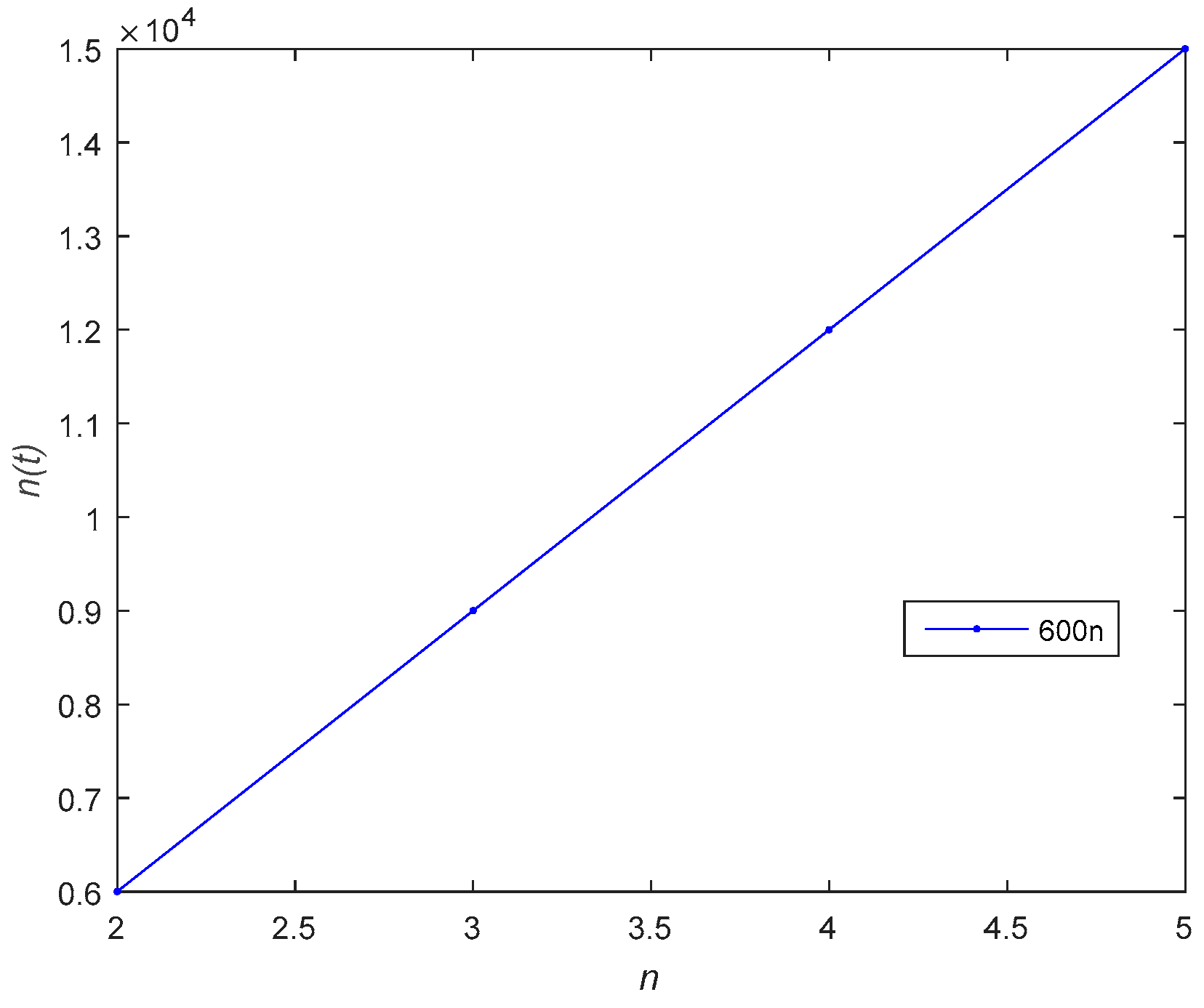
4.2. Numerical Simulations of Feedback Nash Equilibrium Solutions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
Proof of Lemma 1.
Appendix B.
Proof of Lemma 2.
References
- Keoh, S.L.; Kumar, S.S.; Tschofenig, H. Securing the Internet of Things: A Standardization Perspective. IEEE Internet Things J. 2014, 1, 265–275. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Baras, J.S.; Papavassiliou, S.; Qu, G. On the Mitigation of Interference Imposed by Intruders in Passive RFID Networks. In Proceedings of the International Conference on Decision and Game Theory for Security, New York, NY, USA, 2–4 November 2016. [Google Scholar]
- Alaba, F.A.; Othman, M.; Hashem, I.A.T.; Alotaibi, F. Internet of things Security: A Survey. J. Netw. Comput. Appl. 2017, 88, 10–28. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. The Internet of Things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Miorandi, D.; Sicari, S.; De Pellegrini, F.; Chlamtac, I. Internet of things. Ad Hoc Netw. 2012, 10, 1497–1516. [Google Scholar] [CrossRef]
- An, X.; Su, J.; Lü, X.; Lin, F. Hypergraph clustering model-based association analysis of DDOS attacks in fog computing intrusion detection system. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 249. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.D.; Zhao, S. The Internet of Things: A Survey; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2015; pp. 243–259. [Google Scholar]
- Oleshchuk, V. Internet of things and privacy preserving technologies. In Proceedings of the 2009 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace & Electronic Systems Technology, Aalborg, Denmark, 17–20 May 2009; pp. 336–340. [Google Scholar]
- An, X.; Zhou, X.; Xing, L.; Lin, F.; Yang, L. Sample Selected Extreme Learning Machine Based Intrusion Detection in Fog Computing and MEC. Wirel. Commun. Mob. Comput. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Lin, F.; Lü, X.; You, I.; Zhou, X. A novel utility based resource management scheme in vehicular social edge computing. IEEE Access 2018. [Google Scholar] [CrossRef]
- Mavropoulos, O.; Mouratidis, H.; Fish, A.; Panaousis, E.; Kalloniatis, C. A conceptual model to support security analysis in the internet of things. Comput. Sci. Inf. Syst. 2017, 14, 557–578. [Google Scholar] [CrossRef]
- Yang, J.C.; Fang, B.X. Security model and key technologies for the Internet of things. J. China Univ. Posts Telecommun. 2011, 18, 109–112. [Google Scholar] [CrossRef]
- Lin, F.; Zhou, Y.; An, X.; You, I.; Choo, K.R. Fair Resource Allocation in an Intrusion-Detection System for Edge Computing: Ensuring the Security of Internet of Things Devices. IEEE Consum. Electron. Mag. 2018, 7, 45–50. [Google Scholar] [CrossRef]
- Zhang, B.; Zou, Z.; Liu, M. Evaluation on security system of internet of things based on Fuzzy-AHP method. In Proceedings of the 2011 International Conference on E-Business and E-Government (ICEE), Shanghai, China, 6–8 May 2011; pp. 1–5. [Google Scholar]
- Leusse, P.D.; Periorellis, P.; Dimitrakos, T.; Nair, S.K. Self Managed Security Cell, a Security Model for the Internet of Things and Services. In Proceedings of the 2009 First International Conference on Advances in Future Internet, Athens, Greece, 18–23 June 2009; pp. 47–52. [Google Scholar]
- Acharya, R.; Asha, K. Data integrity and intrusion detection in Wireless Sensor Networks. In Proceedings of the 2008 16th IEEE International Conference on Networks, New Delhi, India, 12–14 December 2008; pp. 1–5. [Google Scholar]
- Yuan, X. Key Management Schemes for Distributed Sensor Networks; University of Western Ontario: London, ON, Canada, 2008. [Google Scholar]
- Tague, P.; Slater, D.; Rogers, J.; Poovendran, R. Vulnerability of Network Traffic under Node Capture Attacks Using Circuit Theoretic Analysis. In Proceedings of the IEEE INFOCOM 2008—The 27th Conference on Computer Communications, Phoenix, Arizona, 13–18 April 2008; pp. 161–165. [Google Scholar]
- Choi, Y.S.; Shin, S.H. A Study on Sensor Node Capture Defense Protocol for Ubiquitous Sensor Network; InTech: Vienna, Austria, 2007. [Google Scholar]
- Ho, J.W. Distributed Detection of Node Capture Attacks in Wireless Sensor Networks; InTech: Vienna, Austria, 2010; pp. 661–666. [Google Scholar]
- Tague, P.; Poovendran, R. Modeling adaptive node capture attacks in multi-hop wireless networks. Ad Hoc Netw. 2007, 5, 801–814. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Zhang, H. A Novel Approach to IoT Security Based on Immunology. In Proceedings of the 2013 Ninth International Conference on Computational Intelligence and Security, E’Mei Mountain, China, 14–15 December 2013; pp. 771–775. [Google Scholar]
- An, X.; Lin, F.; Xu, S.; Miao, L.; Gong, C. A Novel Differential Game Model-Based Intrusion Response Strategy in Fog Computing. Secur. Commun. Netw. 2018. [Google Scholar] [CrossRef]
- Zhang, C.; Green, R. Communication security in internet of thing: preventive measure and avoid DDoS attack over IoT network. In Proceedings of the 18th Symposium on Communications & Networking, San Jose, CA, USA, 11–13 December 2015; pp. 8–15. [Google Scholar]
- Tsiropoulou, E.E.; Vamvakas, P.; Papavassiliou, S. Joint utility-based uplink power and rate allocation in wireless networks: A non-cooperative game theoretic framework. Phys. Commun. 2013, 9, 299–307. [Google Scholar] [CrossRef]
- Kastrinogiannis, T.; Tsiropoulou, E.; Papavassiliou, S. Utility-based uplink power control in CDMA wireless networks with real-time services. In International Conference on Ad-Hoc; Springer: New York, NY, USA, 2008; pp. 307–320. [Google Scholar]
- Bloem, M.; Alpcan, T. A Stackelberg Game for Power Control and Channel Allocation. In Proceedings of the International Conference on Performance Evaluation Methodolgies & Tools, Nantes, France, 22–27 October 2007; pp. 1–9. [Google Scholar]
- Daoud, A.A.; Alpcan, T.; Agarwal, S.; Alanyali, M. A stackelberg game for pricing uplink power in wide-band cognitive radio networks. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 1422–1427. [Google Scholar]
- Basar, T.; Srikant, R. Revenue-maximizing pricing and capacity expansion in a many-users regim. In Proceedings of the Joint Conference of the IEEE Computer & Communications Societies, New York, NY, USA, 23–27 June 2002; pp. 294–301. [Google Scholar]
- Zhu, Q.; Basar, T. Game-Theoretic Methods for Robustness, Security, and Resilience of Cyberphysical Control Systems: Games-in-Games Principle for Optimal Cross-Layer Resilient Control Systems. IEEE Control Syst. 2015, 35, 46–65. [Google Scholar]
- Manshaei, M.; Zhu, Q.; Alpcan, T.; Tamer, B.; Jean-Pierre, H. Game Theory Meets Network Security and Privacy. ACM Comput. Surv. 2013, 45, 1–39. [Google Scholar] [CrossRef]
- Liu, R.; Zhai, F. Model Identification of Risk Management System. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar]
- Yeung, D.W.K.; Petrosyan, L.A. Cooperative Stochastic Differential Games; Springer: New York, NY, USA, 2006; p. 256. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Interscience Publishers: New York, NY, USA, 1962. [Google Scholar]
| Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | −0.85 | 0.6 | −0.5 | 0.3 | 0.5 | 0.2 | 0.1 | 0.5 | 0.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Xu, H.; Zhou, X. Stackelberg Dynamic Game-Based Resource Allocation in Threat Defense for Internet of Things. Sensors 2018, 18, 4074. https://doi.org/10.3390/s18114074
Liu B, Xu H, Zhou X. Stackelberg Dynamic Game-Based Resource Allocation in Threat Defense for Internet of Things. Sensors. 2018; 18(11):4074. https://doi.org/10.3390/s18114074
Chicago/Turabian StyleLiu, Bingjie, Haitao Xu, and Xianwei Zhou. 2018. "Stackelberg Dynamic Game-Based Resource Allocation in Threat Defense for Internet of Things" Sensors 18, no. 11: 4074. https://doi.org/10.3390/s18114074
APA StyleLiu, B., Xu, H., & Zhou, X. (2018). Stackelberg Dynamic Game-Based Resource Allocation in Threat Defense for Internet of Things. Sensors, 18(11), 4074. https://doi.org/10.3390/s18114074






