Designing a Robust Kelvin Probe Setup Optimized for Long-Term Surface Photovoltage Acquisition
Abstract
1. Introduction
- light intensity,
- time (SPV transients), or
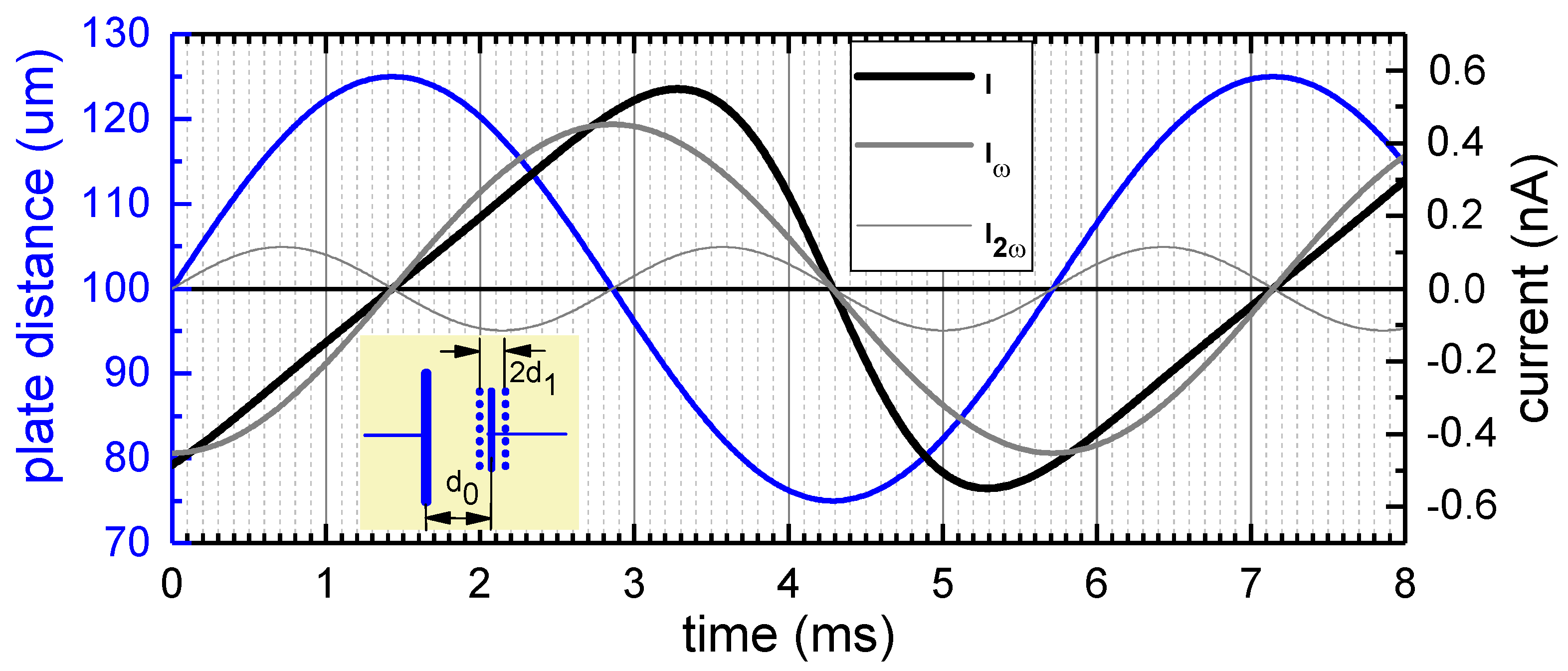
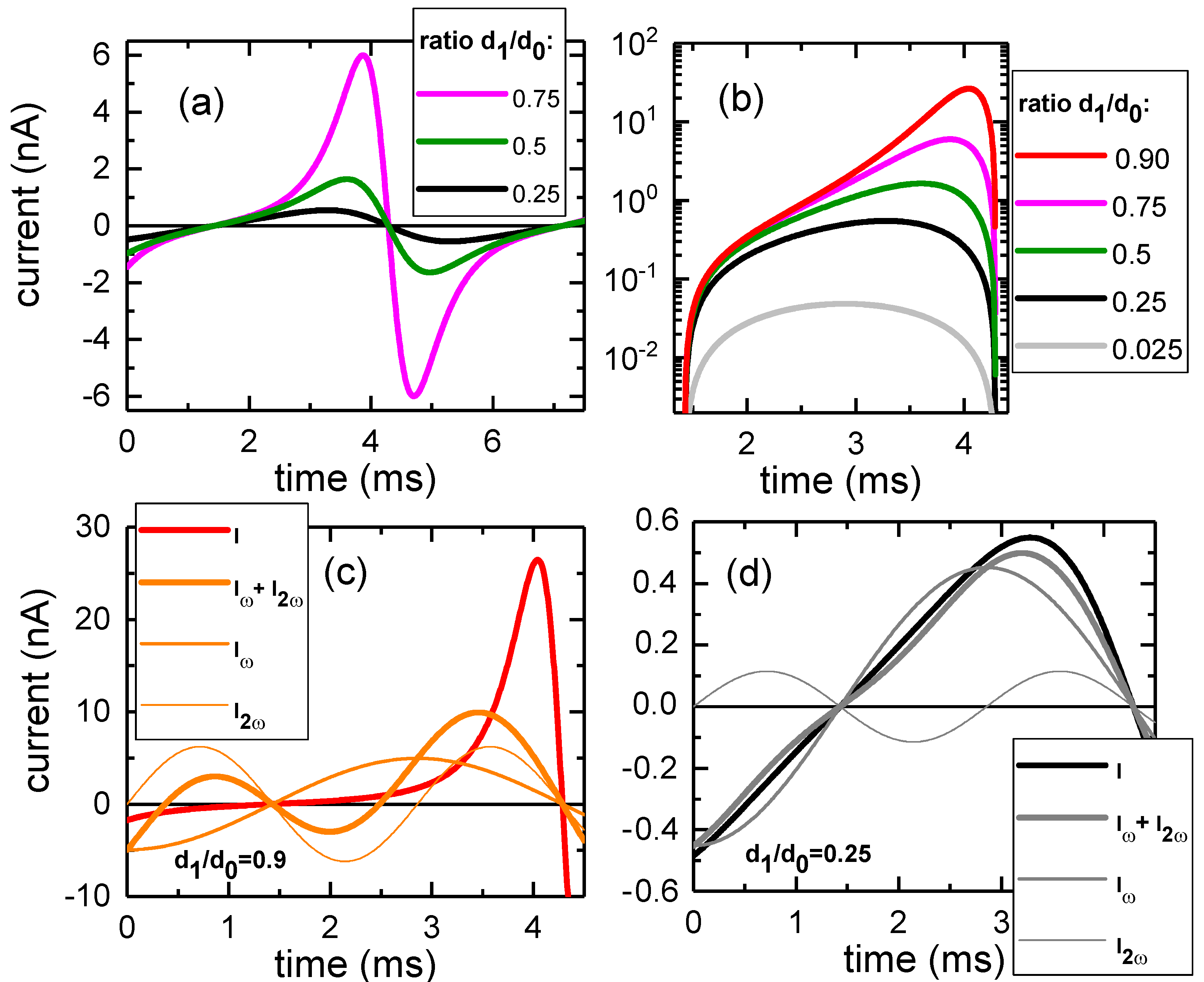
2. Theoretical Considerations
3. Design Description
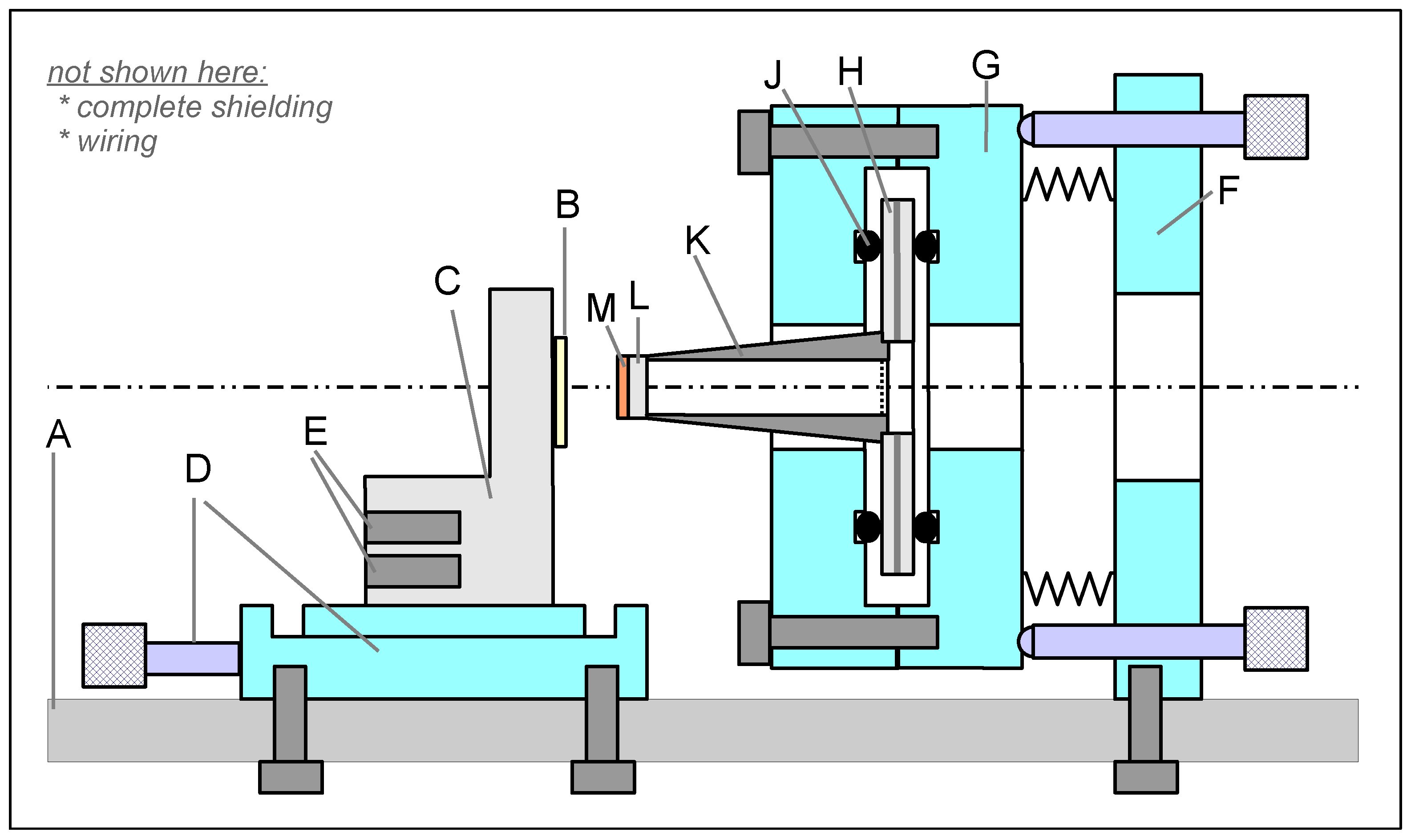
3.1. Mechanical Construction
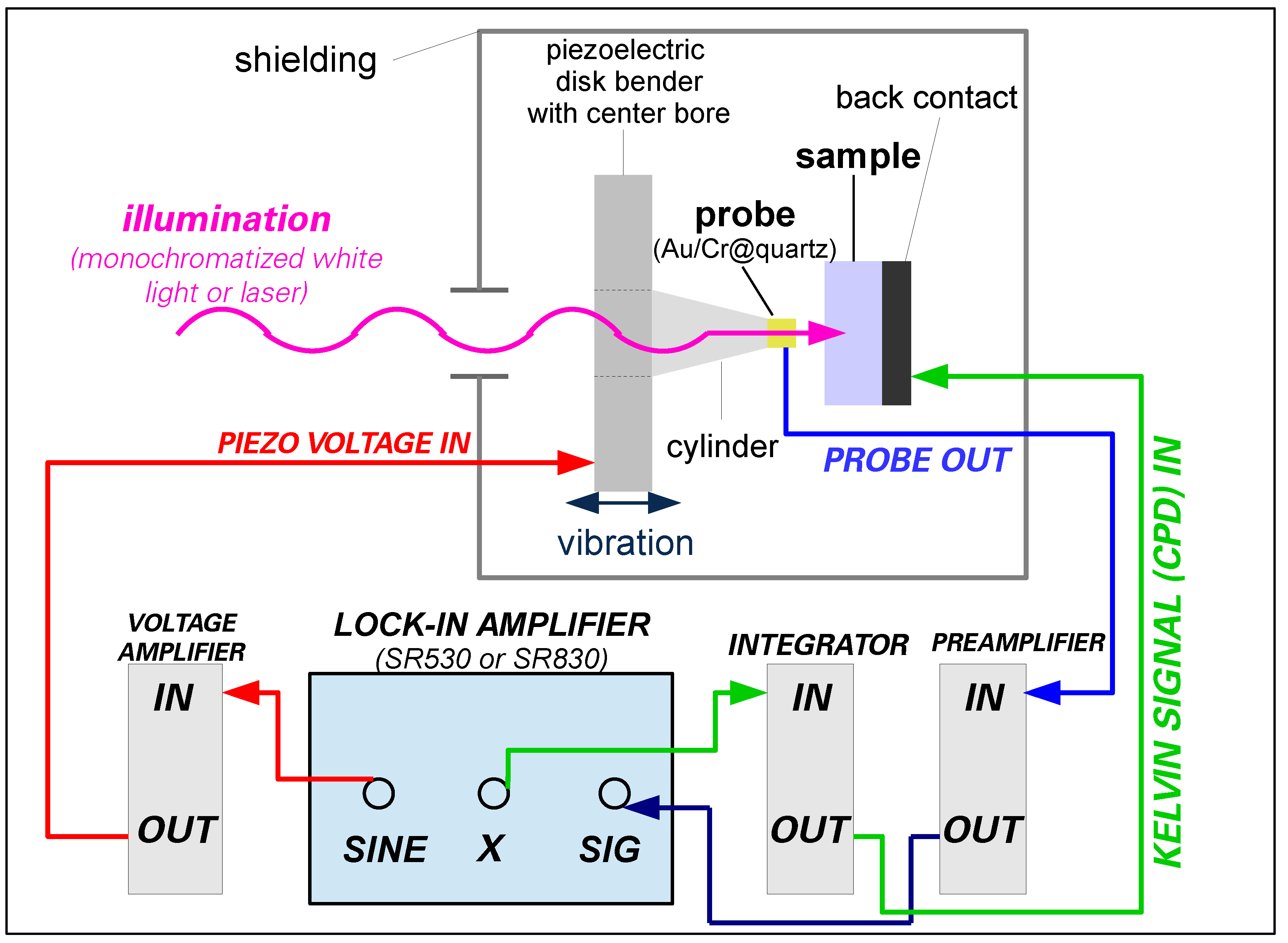
3.2. Electrical Circuitry
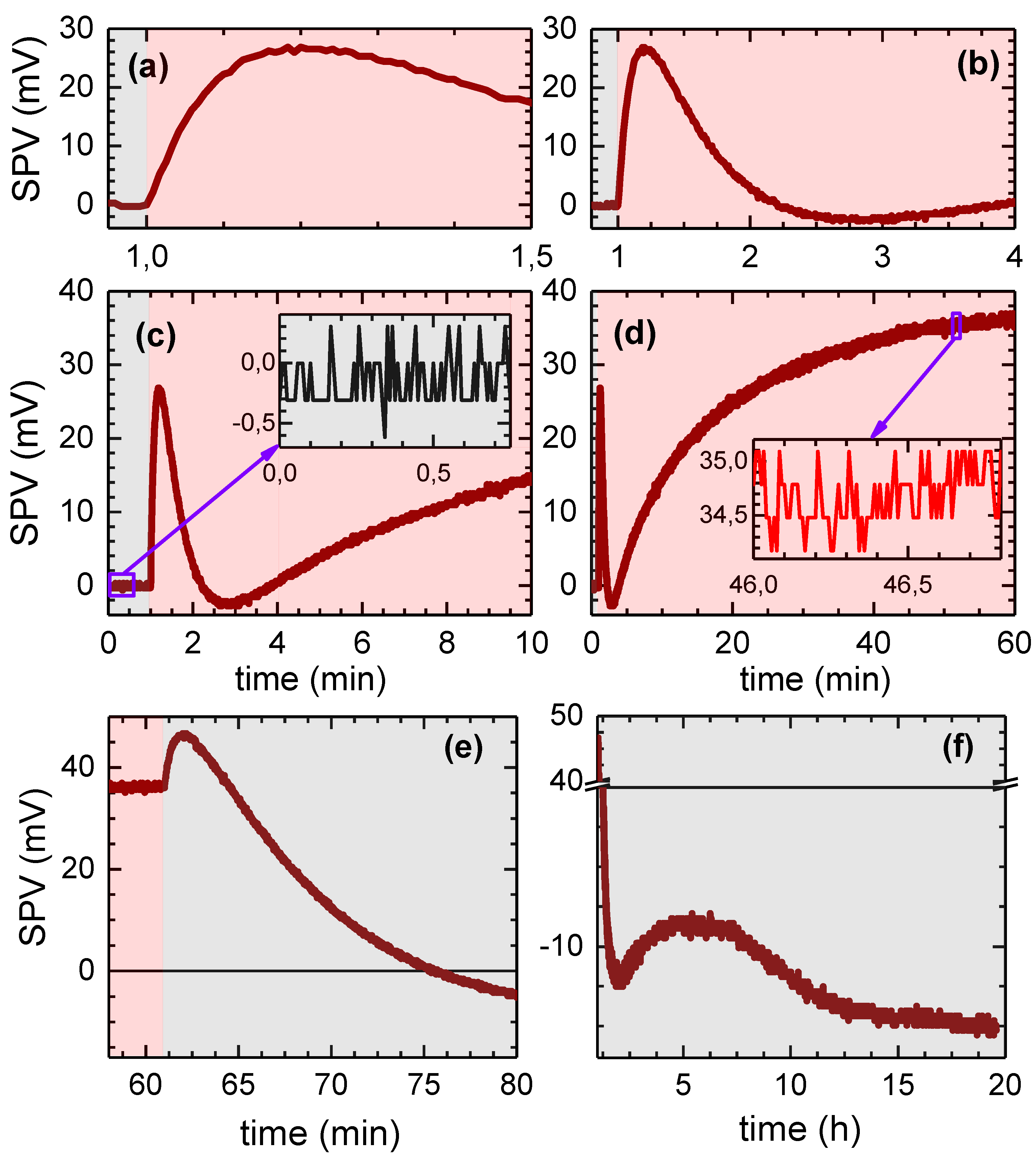
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lorenz, M.; Rao, M.S.R.; Venkatesan, T.; Fortunato, E.; Barquinha, P.; Branquinho, R.; Salgueiro, D.; Martins, R.; Carlos, E.; Liu, A.; et al. The 2016 oxide electronic materials and oxide interfaces roadmap. J. Phys. D Appl. Phys. 2016, 49, 433001. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zubko, P.; Gariglio, S.; Gabay, M.; Ghosez, P.; Triscone, J.M. Interface Physics in Complex Oxide Heterostructures. Annu. Rev. Condens. Matter Phys. 2011, 2, 141–165. [Google Scholar] [CrossRef]
- Liu, Q.; Ruda, H.E. Role of deep-level trapping on the surface photovoltage of semi-insulating GaAs. Phys. Rev. B 1997, 55, 10541–10548. [Google Scholar] [CrossRef]
- Kronik, L.; Shapira, Y. Surface photovoltage phenomena: Theory, experiment, and applications. Surf. Sci. Rep. 1999, 37, 1–206. [Google Scholar] [CrossRef]
- Gatos, H.; Lagowski, J. Surface Photovoltage Spectroscopy—A New Approach to the Study of High-Gap Semiconductor Surfaces. J. Vac. Sci. Technol. 1973, 10, 130–135. [Google Scholar] [CrossRef]
- Kronik, L.; Shapira, Y. Surface photovoltage spectroscopy of semiconductor structures: At the crossroads of physics, chemistry and electrical engineering. Surf. Interface Anal. 2001, 31, 954–965. [Google Scholar] [CrossRef]
- Huang, Y.S.; Pollak, F.H. Non-destructive, room temperature characterization of wafer-sized III-V semiconductor device structures using contactless electromodulation and wavelength-modulated surface photovoltage spectroscopy. Phys. Status Solidi A 2005, 202, 1193–1207. [Google Scholar] [CrossRef]
- Lang, D.V. Deep-level transient spectroscopy: A new method to characterize traps in semiconductors. J. Appl. Phys. 1974, 45, 3023–3032. [Google Scholar] [CrossRef]
- Lagowski, J.; Morawski, A.; Edelman, P. Non-Contact, No Wafer Preparation Deep Level Transient Spectroscopy Based on Surface Photovoltage. Jpn. J. Appl. Phys. 1992, 31, L1185. [Google Scholar] [CrossRef]
- Lägel, B.; Baikie, I.D.; Petermann, U. A novel detection system for defects and chemical contamination in semiconductors based upon the Scanning Kelvin Probe. Surf. Sci. 1999, 433–435, 622–626. [Google Scholar] [CrossRef]
- Dittrich, T.; Fengler, S.; Franke, M. Transient surface photovoltage measurement over 12 orders of magnitude in time. Rev. Sci. Instrum. 2017, 88, 053904. [Google Scholar] [CrossRef] [PubMed]
- Kwoka, M.; Borysiewicz, M.A.; Tomkiewicz, P.; Piotrowska, A.; Szuber, J. A Novel Type Room Temperature Surface Photovoltage Gas Sensor Device. Sensors 2018, 18, 2919. [Google Scholar] [CrossRef] [PubMed]
- Kelvin, L. Contact Electricity of Metals. Philos. Mag. 1898, 46, 82–120. [Google Scholar] [CrossRef]
- Zisman, W.A. A new method of measuring contact potential differences in metals. Rev. Sci. Instrum. 1932, 3, 367–370. [Google Scholar] [CrossRef]
- Maltby, J.R.; Reed, C.E.; Scott, C.G. An improved apparatus for clean surface studies of high resistivity photoconductors. J. Phys. E Sci. Instrum. 1972, 5, 584–586. [Google Scholar] [CrossRef]
- Dix, M.J.; Wood, R.; Slater, D.H. An integrated, high vacuum, beam modulation device. J. Phys. E Sci. Instrum. 1973, 6, 1099–1100. [Google Scholar] [CrossRef]
- Hölzl, J.; Schrammen, P. A New Pendulum Device to Measure Contact Potential Differences. Appl. Phys. 1974, 3, 353–357. [Google Scholar] [CrossRef]
- Besocke, K.; Berger, S. Piezoelectric driven Kelvin probe for contact potential difference studies. Rev. Sci. Instrum. 1976, 47, 840–842. [Google Scholar] [CrossRef]
- Harris, L.B.; Fiasson, J. Vibrating capacitor measurement of surface charge. J. Phys. E Sci. Instrum. 1984, 17, 788–792. [Google Scholar] [CrossRef]
- Germanova, K.; Hardalov, C.; Strashilov, V.; Georgiev, B. An improved apparatus for surface photovoltage studies with a bimorphous piezoelectric Kelvin probe. J. Phys. E Sci. Instrum. 1987, 20, 273–276. [Google Scholar] [CrossRef]
- Germanova, K.; Nikolov, L.; Hardalov, C. Highly sensitive automated setup for measuring surface photovoltage spectra. Rev. Sci. Instrum. 1989, 60, 746–748. [Google Scholar] [CrossRef]
- Baikie, I.D.; van der Werf, K.O.; Oerbekke, H.; Broeze, J.; van Silfhout, A. Automatic Kelvin probe compatible with ultrahigh vacuum. Rev. Sci. Instrum. 1989, 60, 930–934. [Google Scholar] [CrossRef]
- Baikie, I.D.; Mackenzie, S.; Estrup, P.J.Z.; Meyer, J.A. Noise and the Kelvin method. Rev. Sci. Instrum. 1991, 62, 1326. [Google Scholar] [CrossRef]
- Suresh Kumar, C.; Subrahmanyam, A.; Majhi, J. Automated reed-type Kelvin probe for work function and surface photovoltage studies. Rev. Sci. Instrum. 1996, 67, 805–807. [Google Scholar] [CrossRef]
- Schmidt, M.; Nohlen, M.; Bermes, G.; Böhmer, M.; Wandelt, K. A versatile Kelvin probe for dynamic work function change measurements during gas adsorption and in situ film growth experiments. Rev. Sci. Instrum. 1997, 68, 3866–3871. [Google Scholar] [CrossRef]
- Kronik, L.; Shapira, Y. New approach to quantitative surface photovoltage spectroscopy analysis. J. Vac. Sci. Technol. A 1993, 11, 3081–3084. [Google Scholar] [CrossRef]
- Kronik, L.; Leibovitch, M.; Fefer, E.; Burstein, L.; Shapira, Y. Quantitative surface photovoltage spectroscopy of semiconductor interfaces. J. Electron. Mater. 1995, 24, 379–385. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Foussekis, M.; Baski, A.A. Surface photovoltage in undoped n-type GaN. J. Appl. Phys. 2010, 107, 113535. [Google Scholar] [CrossRef]
- McNamara, J.D.; Baski, A.A.; Reshchikov, M.A. Temperature-dependent Kelvin probe studies on GaN from 80 to 600 K. Phys. Status Solidi C 2014, 11, 726–729. [Google Scholar] [CrossRef]
- Beyreuther, E.; Becherer, J.; Thiessen, A.; Grafström, S.; Eng, L. Electronic surface properties of SrTiO3 derived from a surface photovoltage study. Surf. Sci. 2013, 612, 1–9. [Google Scholar] [CrossRef]
- Ivanov, T.; Donchev, V.; Germanova, K.; Kirilov, K. A vector model for analysing the surface photovoltage amplitude and phase spectra applied to complicated nanostructures. J. Phys. D Appl. Phys. 2009, 42, 135302. [Google Scholar] [CrossRef]
- Beyreuther, E.; Thiessen, A.; Grafström, S.; Eng, L.M.; Dekker, M.C.; Dörr, K. Large photoconductivity and light-induced recovery of the insulator-metal transition in ultrathin La0.7Ce0.3MnO3−δ films. Phys. Rev. B 2009, 80, 075106. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beyreuther, E.; Grafström, S.; Eng, L.M. Designing a Robust Kelvin Probe Setup Optimized for Long-Term Surface Photovoltage Acquisition. Sensors 2018, 18, 4068. https://doi.org/10.3390/s18114068
Beyreuther E, Grafström S, Eng LM. Designing a Robust Kelvin Probe Setup Optimized for Long-Term Surface Photovoltage Acquisition. Sensors. 2018; 18(11):4068. https://doi.org/10.3390/s18114068
Chicago/Turabian StyleBeyreuther, Elke, Stefan Grafström, and Lukas M. Eng. 2018. "Designing a Robust Kelvin Probe Setup Optimized for Long-Term Surface Photovoltage Acquisition" Sensors 18, no. 11: 4068. https://doi.org/10.3390/s18114068
APA StyleBeyreuther, E., Grafström, S., & Eng, L. M. (2018). Designing a Robust Kelvin Probe Setup Optimized for Long-Term Surface Photovoltage Acquisition. Sensors, 18(11), 4068. https://doi.org/10.3390/s18114068




