Validation of Finite Element Model by Smart Aggregate-Based Stress Monitoring
Abstract
1. Introduction
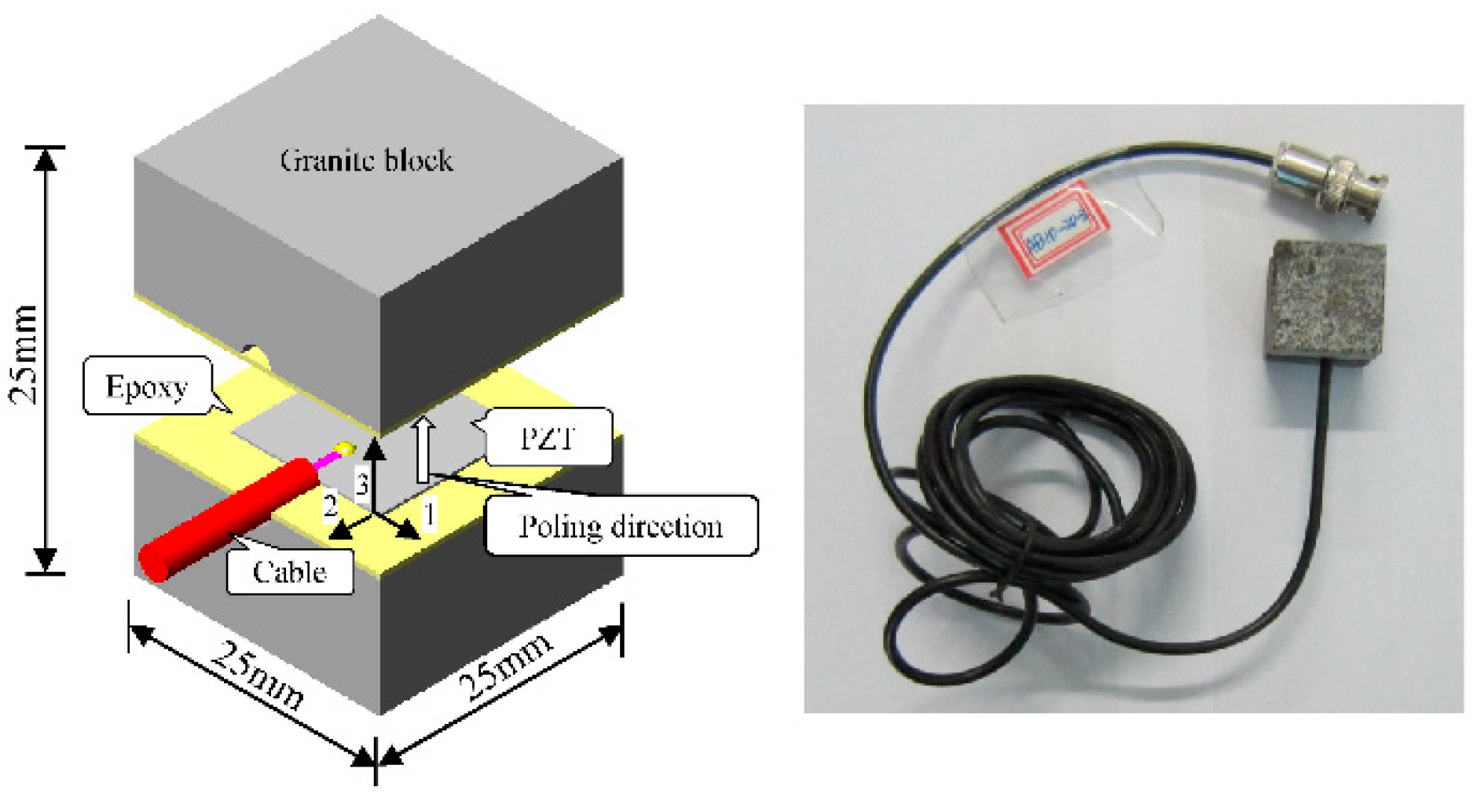
2. SA Sensor
3. Simulation of the RC Column Test
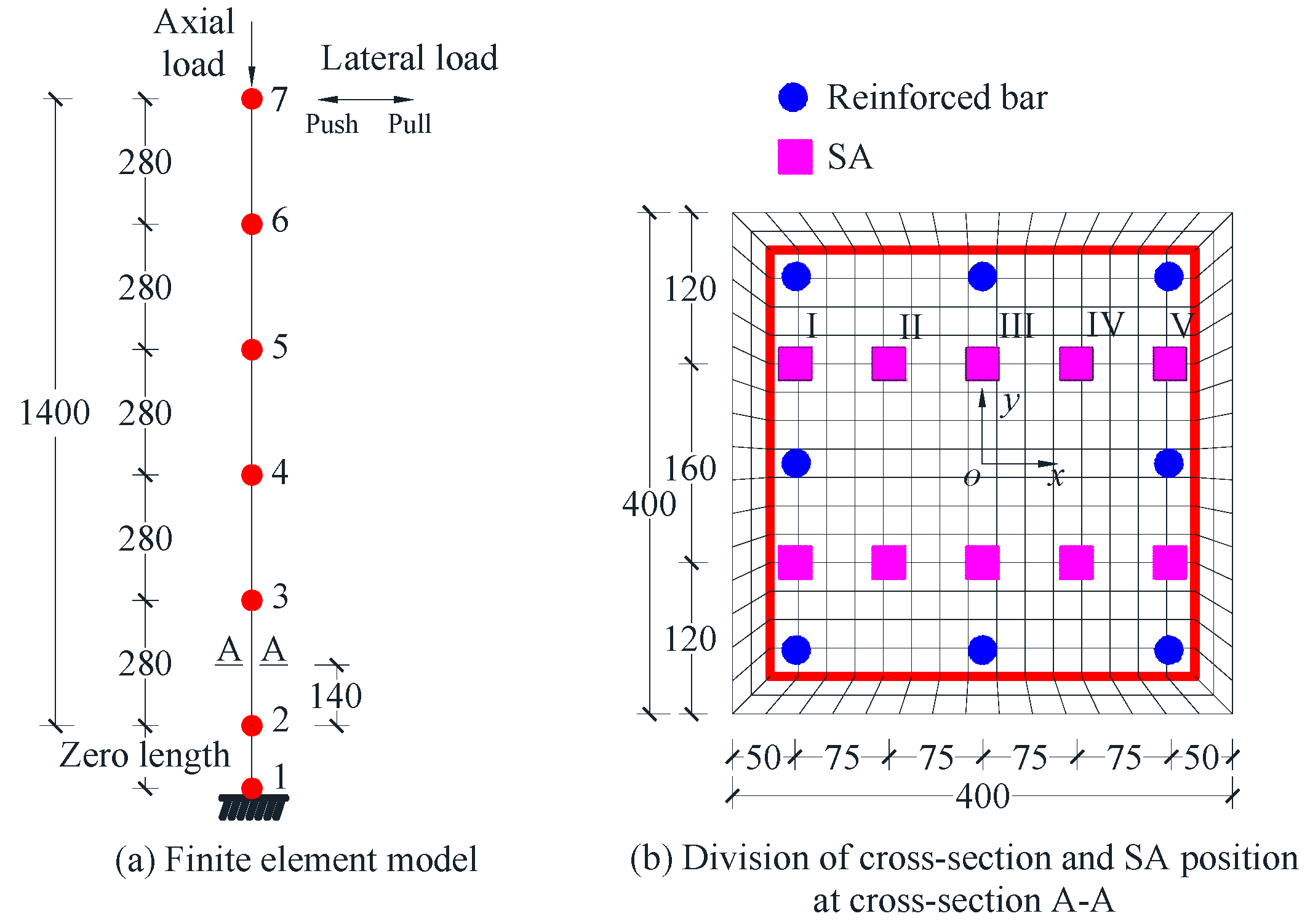
3.1. Description of the Finite Element Model
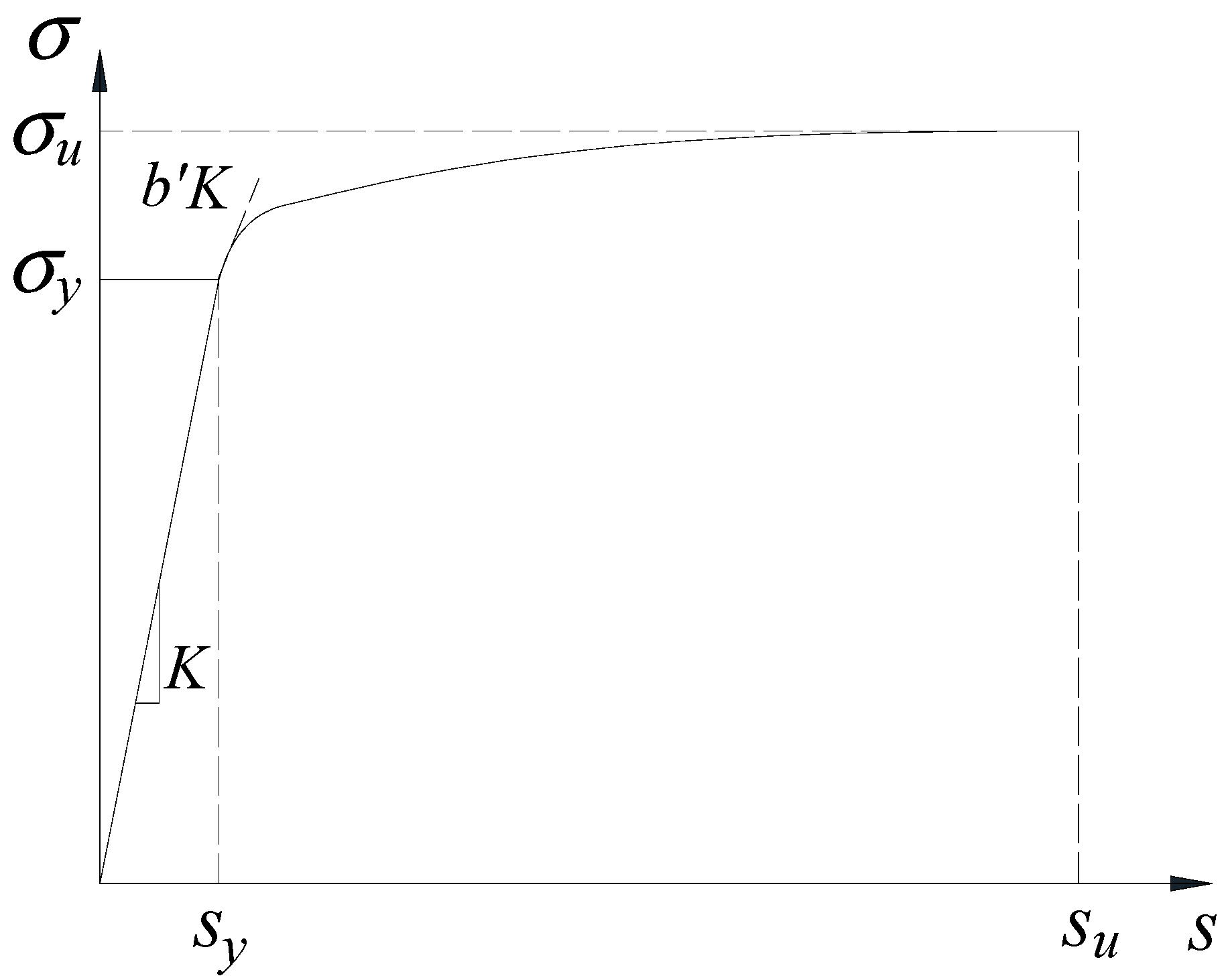
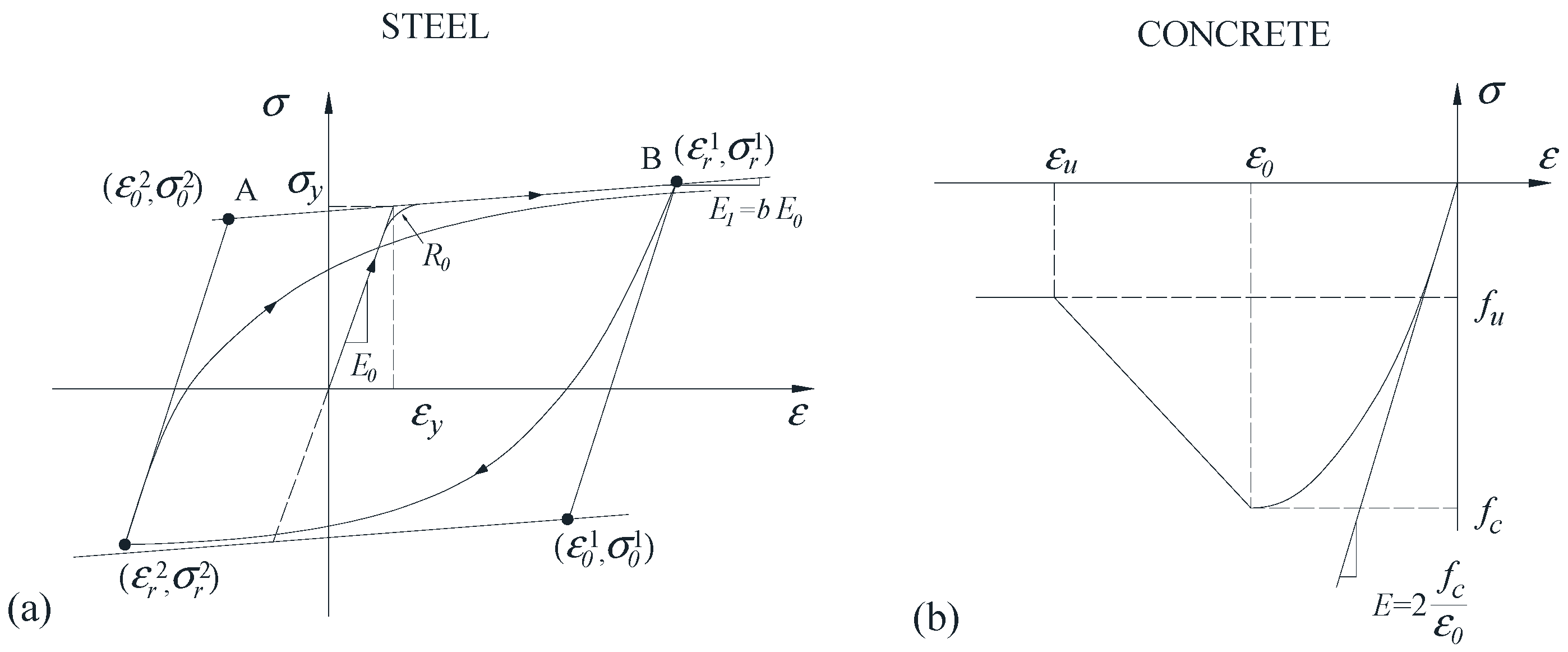
3.2. Section and Material Properties
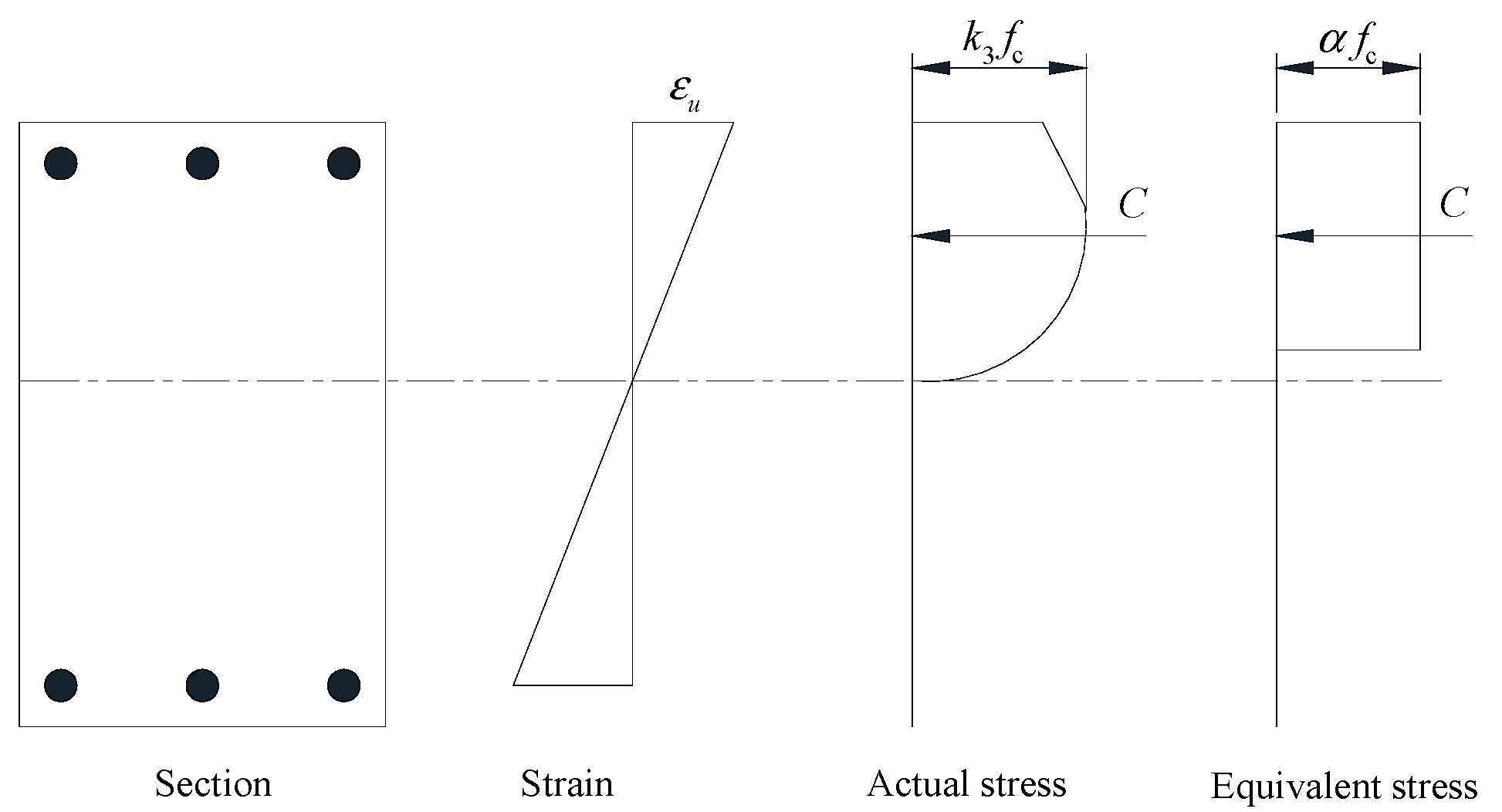
3.3. Concrete Strength Selection
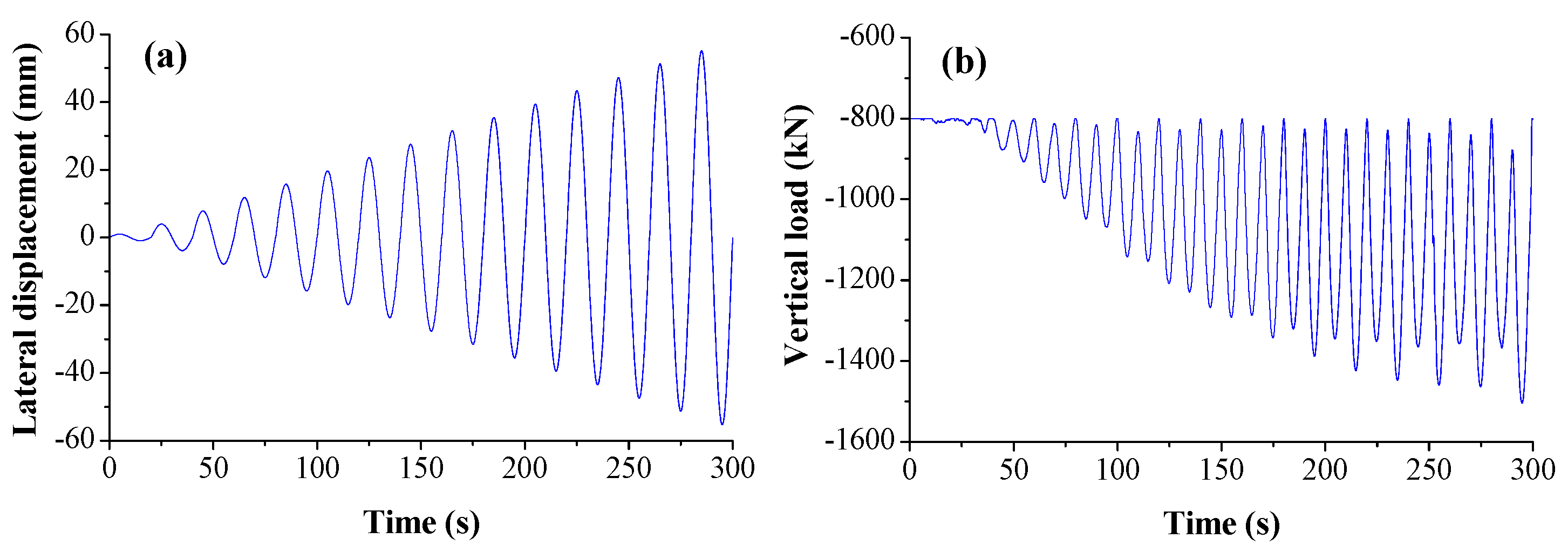
3.4. Loading Scheme
4. Results and Discussion
4.1. Global Response
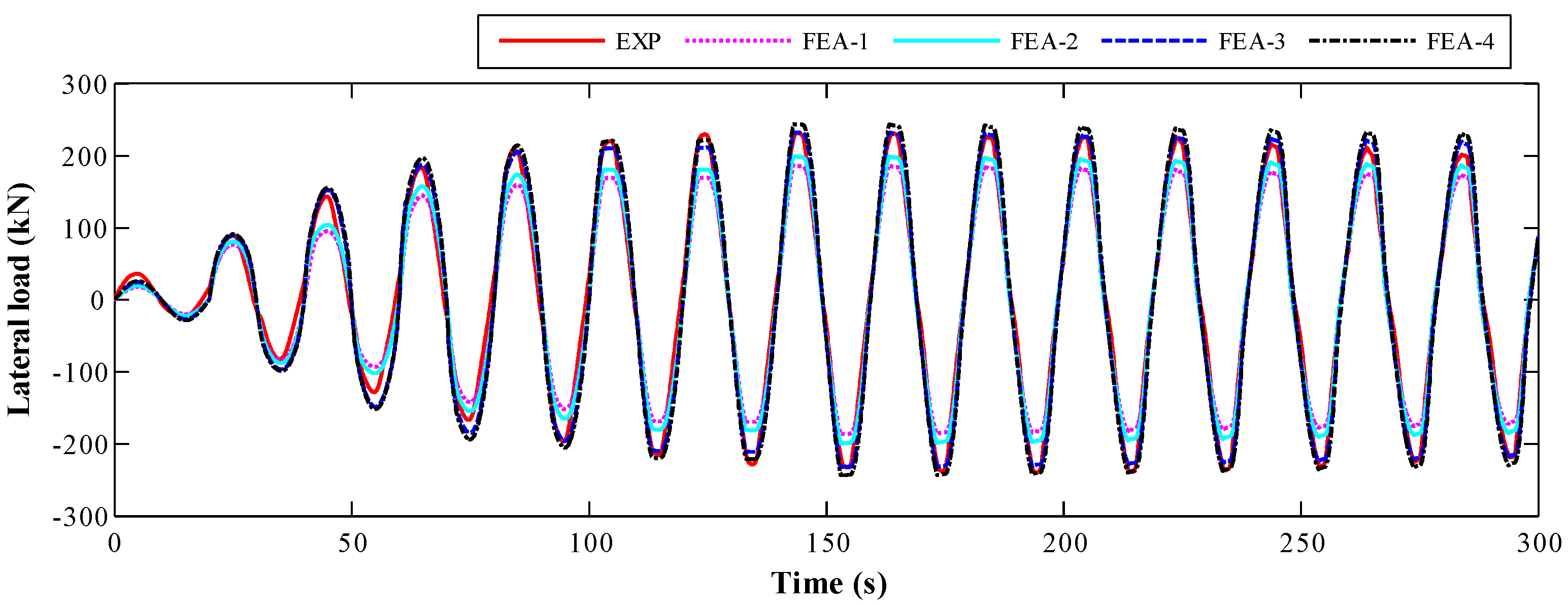
4.1.1. Lateral Load
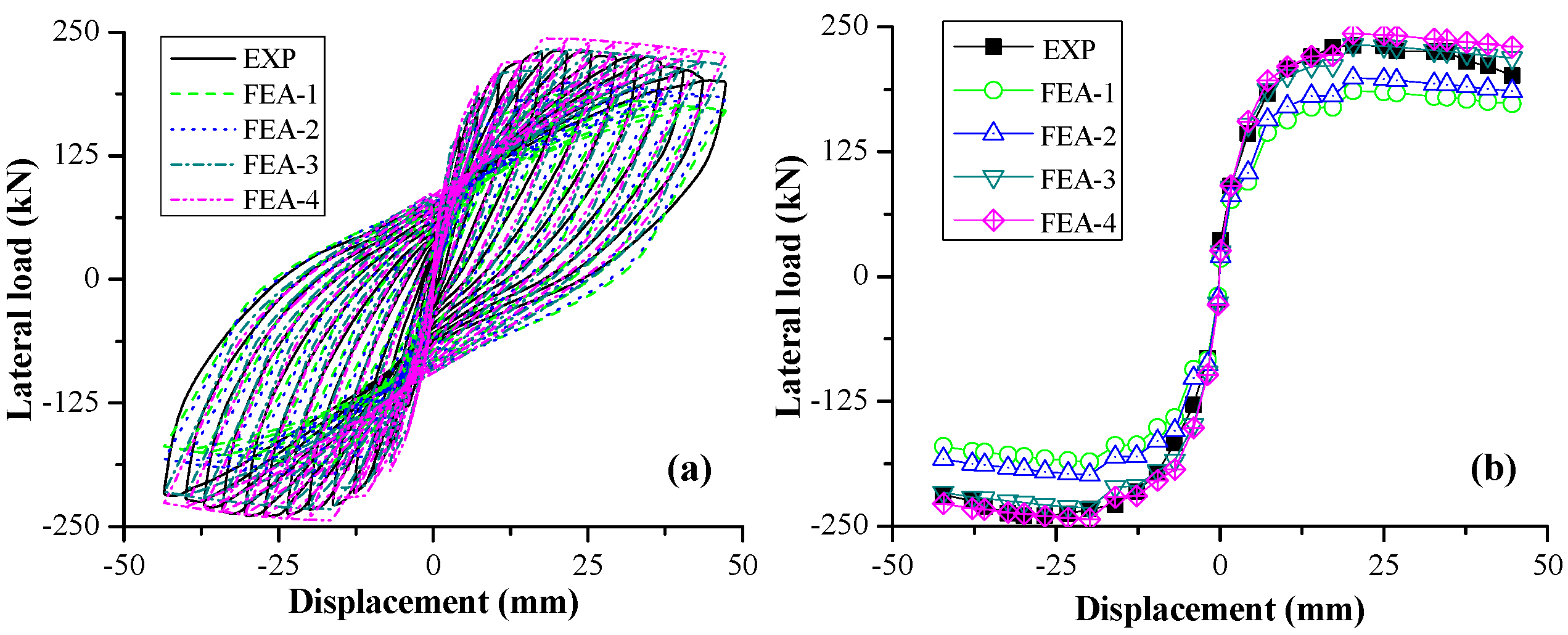
4.1.2. Hysteretic Loop
4.2. Local Response
4.2.1. Concrete Stress
4.2.2. Rebar Strain
4.2.3. Cross-Section Moment
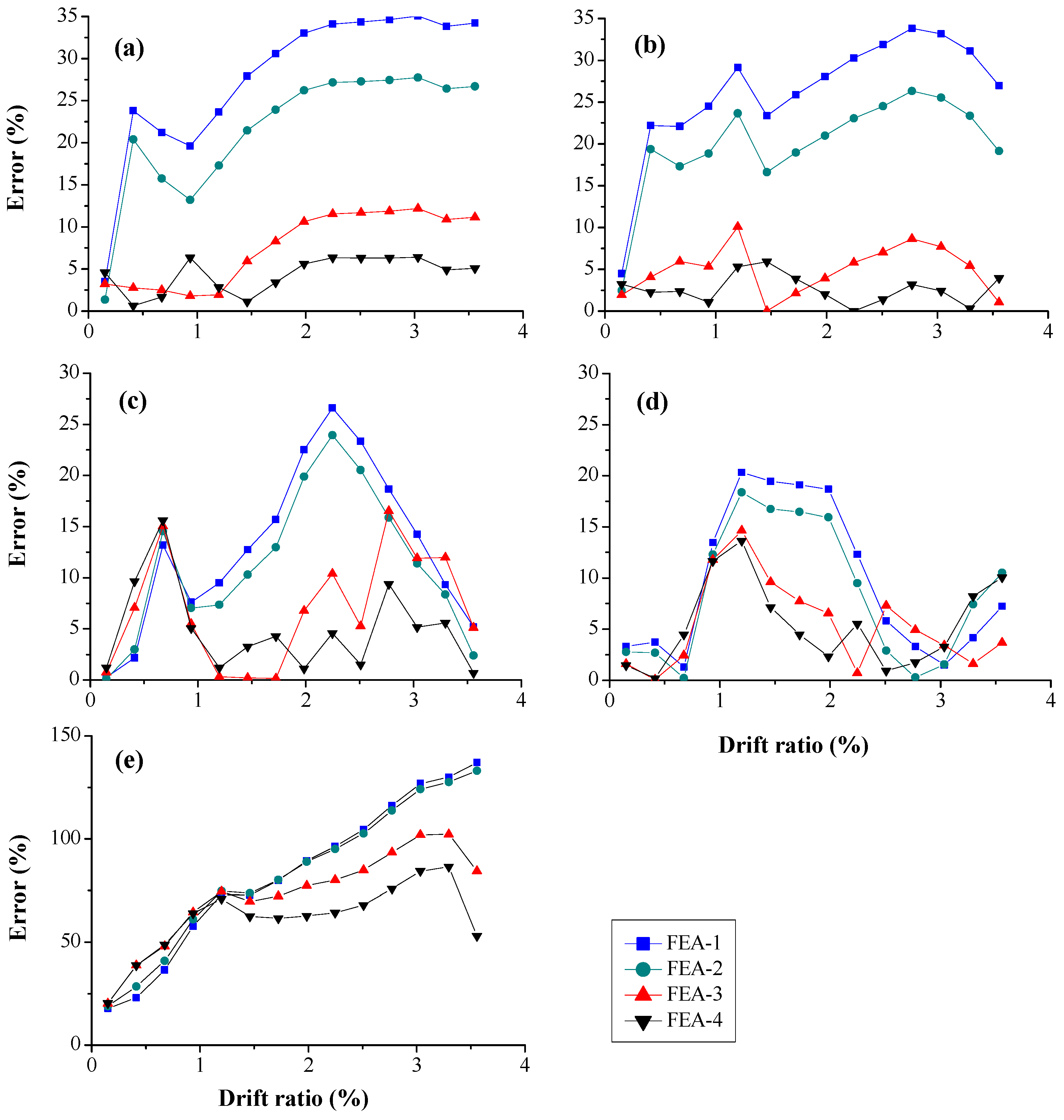
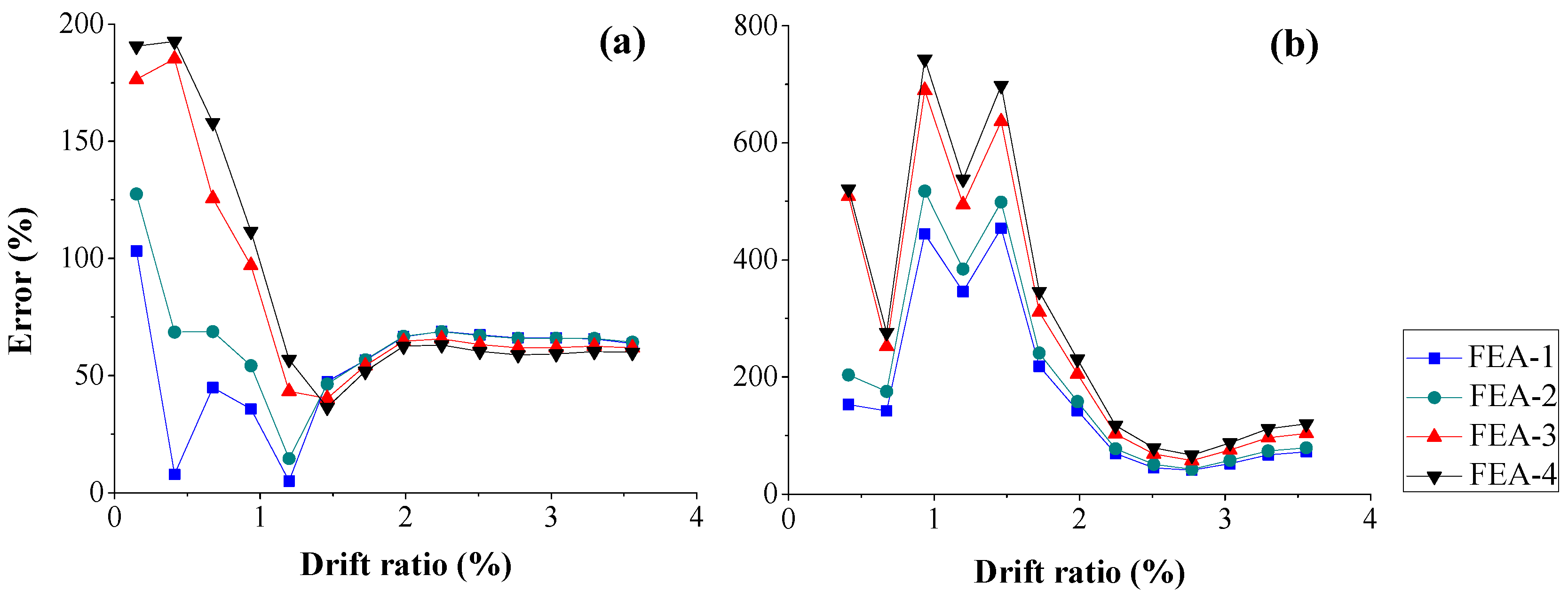
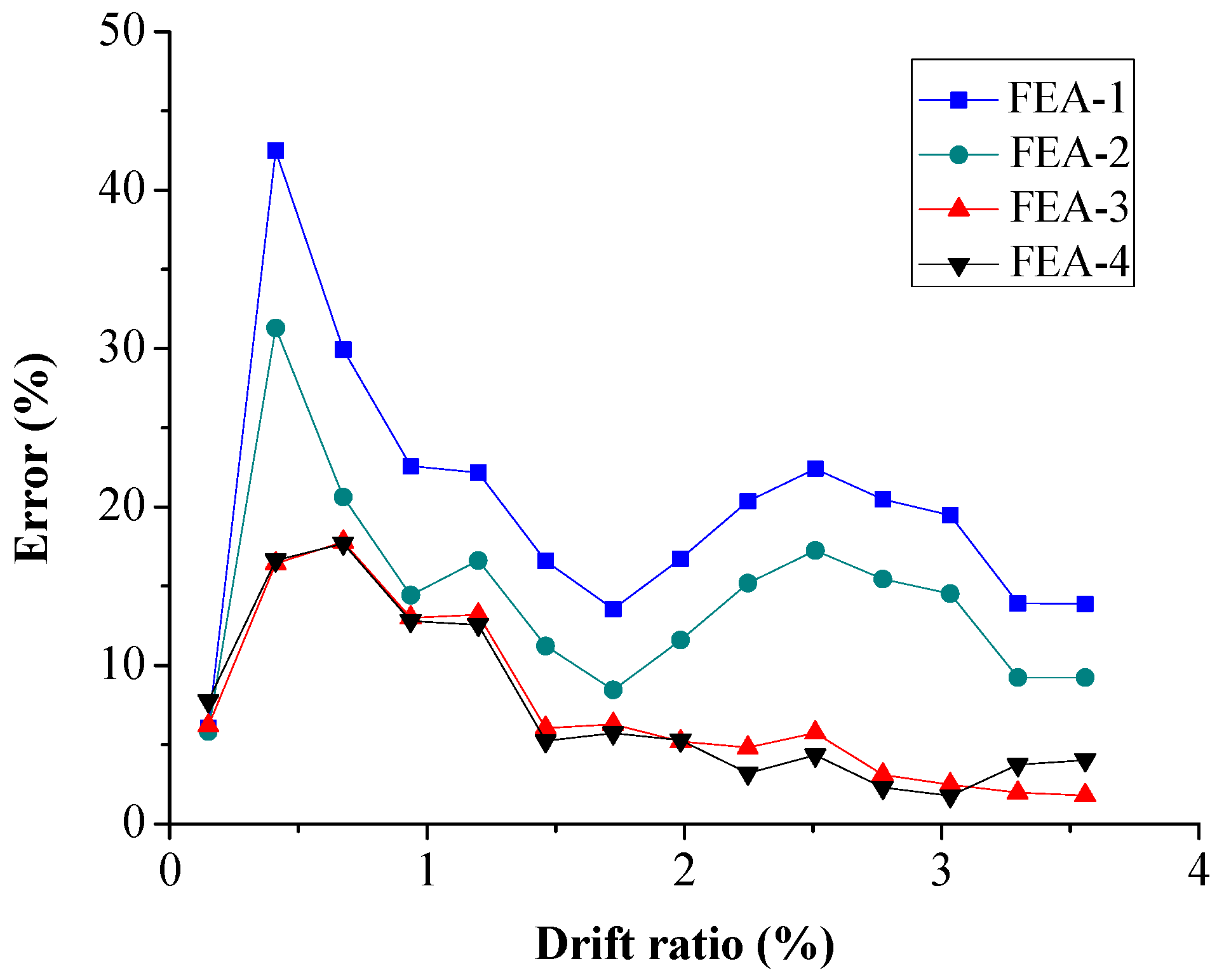
5. Error Analysis
5.1. Global Response
5.2. Local Response
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ACI Committee. ACI 318-11: Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2011. [Google Scholar]
- China Architecture & Building Press. GB 50010-2010: The Code for Design of Concrete Structure, Ministry of Housing and Urban-Rural Development of the People’s Republic of China; China Architecture & Building Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Pereira, N.; Romão, X. Assessment of the concrete strength in existing buildings using a finite population approach. Constr. Build. Mater. 2016, 110, 106–116. [Google Scholar] [CrossRef]
- Bartlett, M.; Macgregor, J.G. Statistical analysis of the compressive strength of concrete structures. ACI Mater. J. 1996, 93, 158–168. [Google Scholar]
- Drysdale, R.G. Variation of concrete strength in existing buildings. Mag. Concr. Res. 1973, 25, 201–207. [Google Scholar] [CrossRef]
- Stewart, M.G. Workmanship and its influence on probabilistic models of concrete compressive strength. ACI Mater. J. 1995, 92, 361–372. [Google Scholar]
- Shang, H.S.; Song, Y.P. Experimental study of strength and deformation of plain concrete under biaxial compression after freezing and thawing cycles. Cem. Concr. Res. 2006, 36, 1857–1864. [Google Scholar] [CrossRef]
- Glasser, F.P.; Marchand, J.; Samson, E. Durability of concrete—Degradation phenomena involving detrimental chemical reactions. Cem. Concr. Res. 2008, 38, 226–246. [Google Scholar] [CrossRef]
- Khoury, G.A. Effect of fire on concrete and concrete structures. Prog. Struct. Eng. Mater. 2001, 2, 429–447. [Google Scholar] [CrossRef]
- Masi, A.; Vona, M. Estimation of the in-situ concrete strength: Provisions of the European and Italian seismic codes and possible improvements. In Eurocode 8 Perspectives from the Italian Standpoint Workshop; Doppiavoce: Naples, Italy, 2009; pp. 67–77. [Google Scholar]
- Breysse, D.; Martínez-Fernández, J.L. Assessing concrete strength with rebound hammer: Review of key issues and ideas for more reliable conclusions. Mater. Struct. 2014, 47, 1589–1604. [Google Scholar] [CrossRef]
- Alwash, M.; Breysse, D.; Sbartaï, Z.M.; Szilágyi, K.; Borosnyói, A. Factors affecting the reliability of assessing the concrete strength by rebound hammer and cores. Constr. Build. Mater. 2017, 140, 354–363. [Google Scholar] [CrossRef]
- Szilágyi, K.; Borosnyói, A.; Zsigovics, I. Rebound surface hardness of concrete: Introduction of an empirical constitutive model. Constr. Build. Mater. 2011, 25, 2480–2487. [Google Scholar] [CrossRef]
- Szilágyi, K.; Borosnyói, A. 50 years of experience with the schmidt rebound hammer. Concr. Struct. 2009, 10, 46–56. [Google Scholar]
- Popovics, J. Ultrasonic testing of concrete structures. Mater. Eval. 2005, 63, 50–55. [Google Scholar]
- Amini, K.; Jalalpour, M.; Delatte, N. Advancing concrete strength prediction using non-destructive testing: Development and verification of a generalizable model. Constr. Build. Mater. 2016, 102, 762–768. [Google Scholar] [CrossRef]
- Yıldırım, H.; Sengul, O. Modulus of elasticity of substandard and normal concretes. Constr. Build. Mater. 2011, 25, 1645–1652. [Google Scholar] [CrossRef]
- Qasrawi, H.Y. Concrete strength by combined nondestructive methods simply and reliably predicted. Cem. Concr. Res. 2000, 30, 739–746. [Google Scholar] [CrossRef]
- Teodoru, G.V. The use of simultaneous nondestructive tests to predict the compressive strength of concrete. ACI Spec. Publ. 1989, 112, 137–152. [Google Scholar]
- ACI Committee. ACI 228.1R-03: In-Place Methods to Estimate Concrete Strength; American Concrete Institute: Famington Hills, MI, USA, 2003. [Google Scholar]
- Li, W.; Kong, Q.; Ho, S.C.M.; Lim, I.; Mo, Y.L.; Song, G. Feasibility study of using smart aggregates as embedded acoustic emission sensors for health monitoring of concrete structures. Smart Mater. Struct. 2016, 25, 115031. [Google Scholar] [CrossRef]
- Li, Z.; Qin, L.; Huang, S. Embedded piezo-transducer in concrete for property diagnosis. J. Mater. Civ. Eng. 2009, 21, 643–647. [Google Scholar] [CrossRef]
- Karaiskos, G.; Deraemaeker, A.; Aggelis, D.G.; Van Hemelrijck, D. Monitoring of concrete structures using the ultrasonic pulse velocity method. Smart Mater. Struct. 2015, 24, 113001. [Google Scholar] [CrossRef]
- Dumoulin, C.; Karaiskos, G.; Carette, J.; Staquet, S.; Deraemaeker, A. Monitoring of the ultrasonic P-wave velocity in early-age concrete with embedded piezoelectric transducers. Smart Mater. Struct. 2012, 21, 047001. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.; Dhonde, H.; Zhu, R.R.H. Health monitoring of a concrete structure using piezoceramic materials. In Smart Structures and Materials 2005: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; SPIE: Bellingham, WA, USA, 2005; Volume 5765, pp. 108–119. [Google Scholar]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregate for compressive seismic stress monitoring. Smart Mater. Struct. 2012, 21, 105035. [Google Scholar] [CrossRef]
- Kong, Q.Z.; Hou, S.; Ji, Q.; Mo, Y.L.; Song, G. Very early age concrete hydration characterization monitoring using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22, 085025. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2006, 15, 1837. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.C.; Mo, Y.L. Smart aggregates: Multi-functional sensors for concrete structures—A tutorial and a review. Smart Mater. Struct. 2008, 17, 033001. [Google Scholar] [CrossRef]
- Feng, Q.; Kong, Q.; Huo, L.; Song, G. Crack detection and leakage monitoring on reinforced concrete pipe. Smart Mater. Struct. 2015, 24, 115020. [Google Scholar] [CrossRef]
- Yan, S.; Ma, H.; Li, P.; Song, G.; Wu, J. Development and application of a structural health monitoring system based on wireless smart aggregates. Sensors 2017, 17, 1641. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Sun, W.; Song, G.; Gu, H.; Huo, L.S.; Liu, B.; Zhang, Y.G. Health monitoring of reinforced concrete shear walls using smart aggregates. Smart Mater. Struct. 2009, 18, 047001. [Google Scholar] [CrossRef]
- Moslehy, Y.; Gu, H.; Belarbi, A.; Mo, Y.L.; Song, G. Smart aggregate based damage detection of circular RC columns under cyclic combined loading. Smart Mater. Struct. 2010, 19, 065021. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Du, G.; Song, G. Damage detection of L-shaped concrete filled steel tube (L-CFST) columns under cyclic loading using embedded piezoceramic transducers. Sensors 2018, 18, 2171. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Deng, Q.; Cai, L.; Ho, S.; Song, G. Damage detection of a concrete column subject to blast loads using embedded piezoceramic transducers. Sensors 2018, 18, 1377. [Google Scholar] [CrossRef] [PubMed]
- Zou, D.J.; Li, W.J.; Liu, T.J.; Teng, J. Two-dimensional water seepage monitoring in concrete structures using smart aggregates. Struct. Monitor. Maint. 2018, 5, 313–323. [Google Scholar]
- Zou, D.J.; Liu, T.J.; Huang, Y.C.; Zhang, F.Y.; Du, C.C.; Li, B. Feasibility of water seepage monitoring in concrete with embedded smart aggregates by P-wave travel time measurement. Smart Mater. Struct. 2014, 23, 067003. [Google Scholar] [CrossRef]
- Liu, T.J.; Huang, Y.C.; Zou, D.J.; Teng, J.; Li, B. Exploratory study on water seepage monitoring of concrete structures using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22, 065002. [Google Scholar] [CrossRef]
- Song, G.; Olmi, C.; Gu, H. An overheight vehicle-bridge collision monitoring system using piezoelectric transducers. Smart Mater. Struct. 2007, 16, 462. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregate for seismic shear stress monitoring. Smart Mater. Struct. 2013, 22, 065012. [Google Scholar] [CrossRef]
- Zhang, H.B.; Hou, S.; Ou, J.P. Smart aggregate-based seismic stress monitoring system using a specially designed charge amplifier. J. Intell. Mater. Syst. Struct. 2016, 27, 418–426. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. SA-based concrete seismic stress monitoring: A case study for normal strength concrete. Smart Mater. Struct. 2016, 25, 095041. [Google Scholar] [CrossRef]
- Zhang, H.B.; Hou, S.; Ou, J.P. Feasibility of SA-based concrete seismic stress monitoring for high-strength concrete. J. Intell. Mater. Syst. Struct. 2017, 28, 2428–2436. [Google Scholar] [CrossRef]
- Zhang, H.B.; Hou, S.; Ou, J.P. Smart aggregates for monitoring stress in structural lightweight concrete. Measurement 2018, 122, 257–263. [Google Scholar] [CrossRef]
- Du, G.; Zhang, J.; Zhang, J.; Song, G. Experimental study on stress monitoring of sand-filled steel tube during impact using piezoceramic smart aggregates. Sensors 2017, 17, 1930. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Sritharan, S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures. ACI Struct. J. 2007, 104, 133–141. [Google Scholar]
- Comite Euro-International du Beton. CEB-FIP Model Code 1990: Design Code; Comite Euro-International du Beton: London, UK, 1993; ISBN 0-7277-1696-4. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Technical Report EERC-83/19; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983; p. 132. [Google Scholar]
- Scott, B.D.; Park, P.; Priestley, M.J.N. Stress-Strain behavior of concrete by overlapping hoops at low and high strain rates. ACI Struct. J. 1982, 79, 13–27. [Google Scholar]
- SouthEast University. Concrete Structures: Volumne One, Principle of Concrete Structure Design; China Architecture & Building Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Park, R.; Priestley, M.J.N.; Gill, W.D. Ductility of square-confined concrete columns. J. Struct. Div. 1982, 108, 929–950. [Google Scholar]
- Hou, S.; Zhang, H.B.; Ou, J.P. SA-based concrete seismic stress monitoring: The influence of non-uniform stress fields. Eng. Struct. 2018. submitted. [Google Scholar]
- Hognestad, E.; Hanson, N.W.; McHenry, D. Concrete Stress Distribution in Ultimate Strength Design. ACI J. Proc. 1955, 52, 455–480. [Google Scholar]
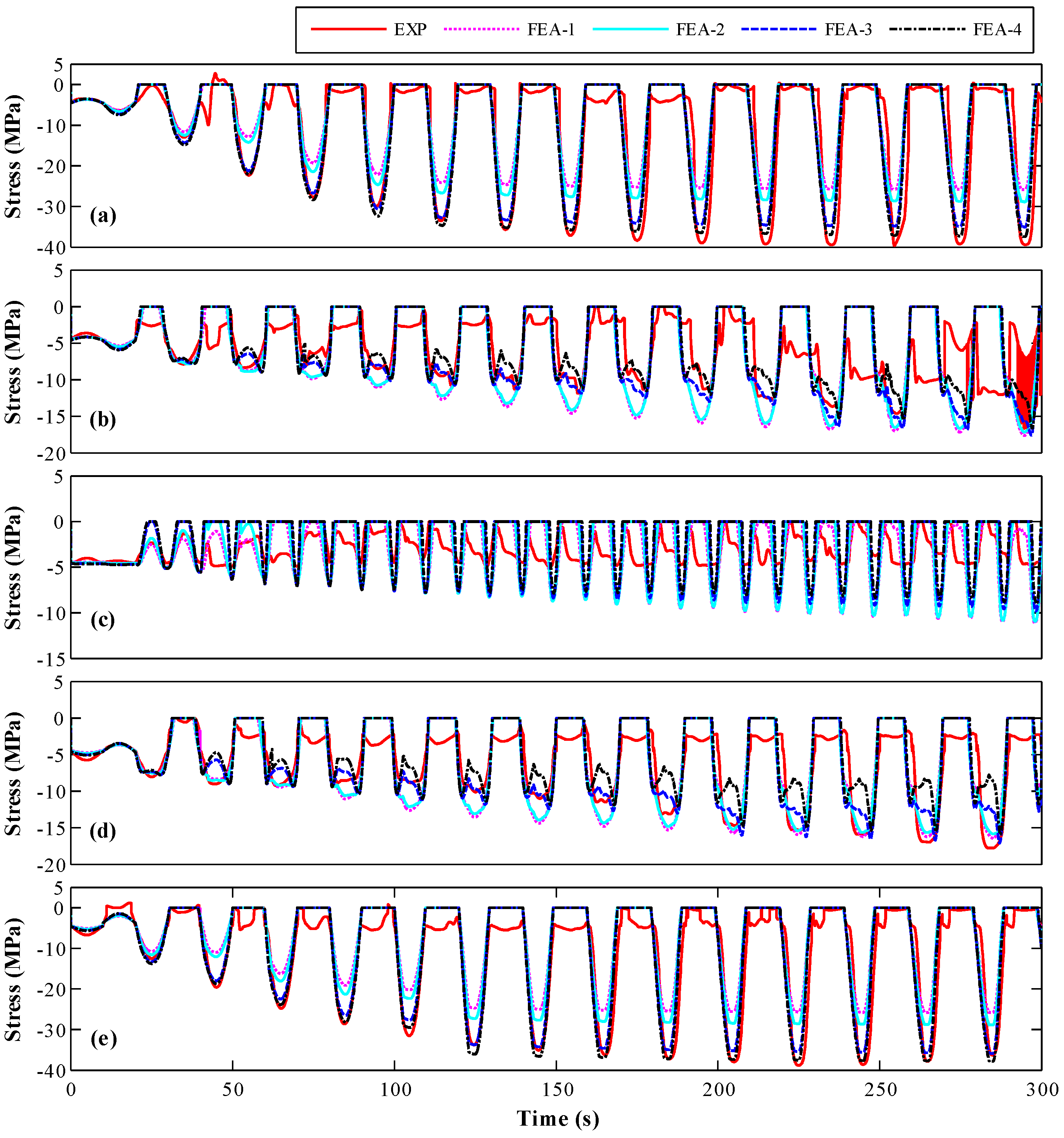
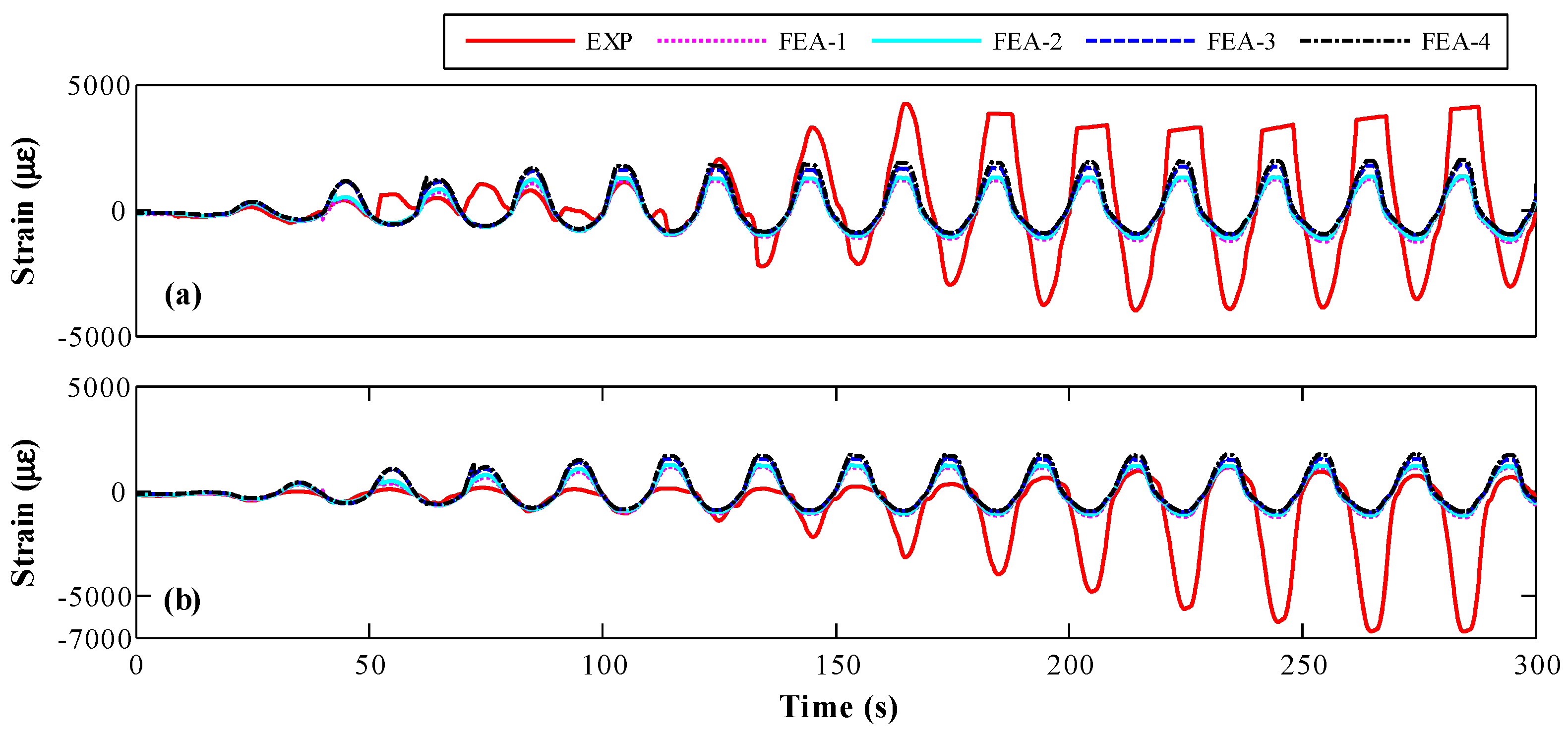
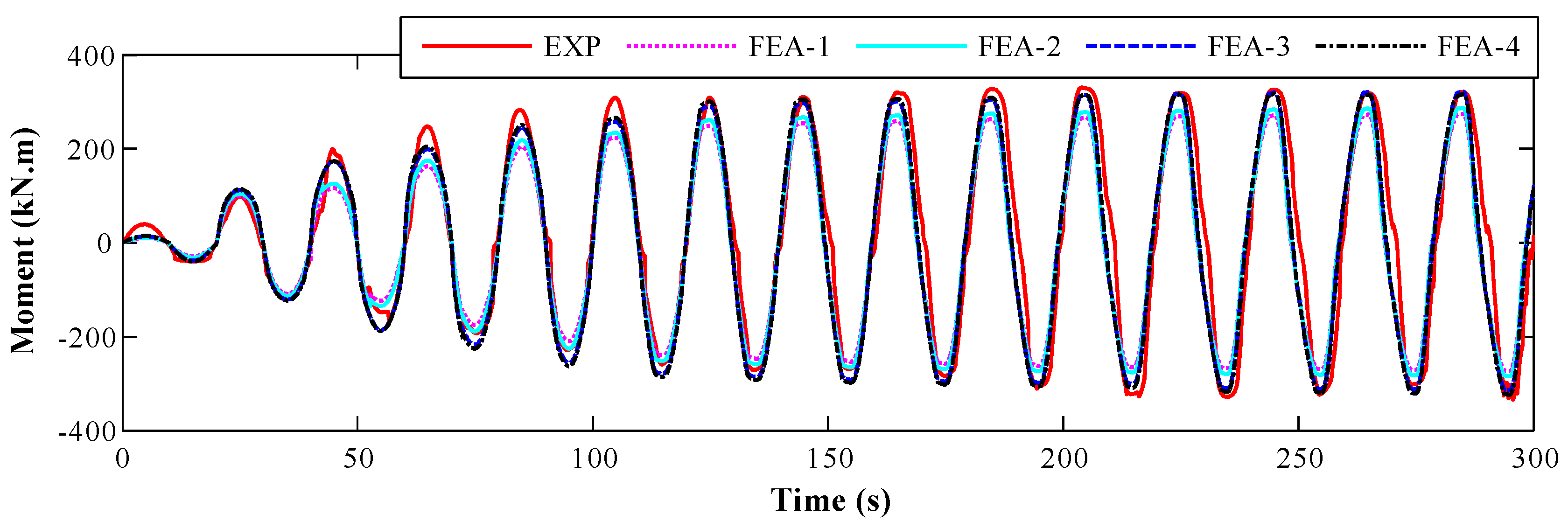
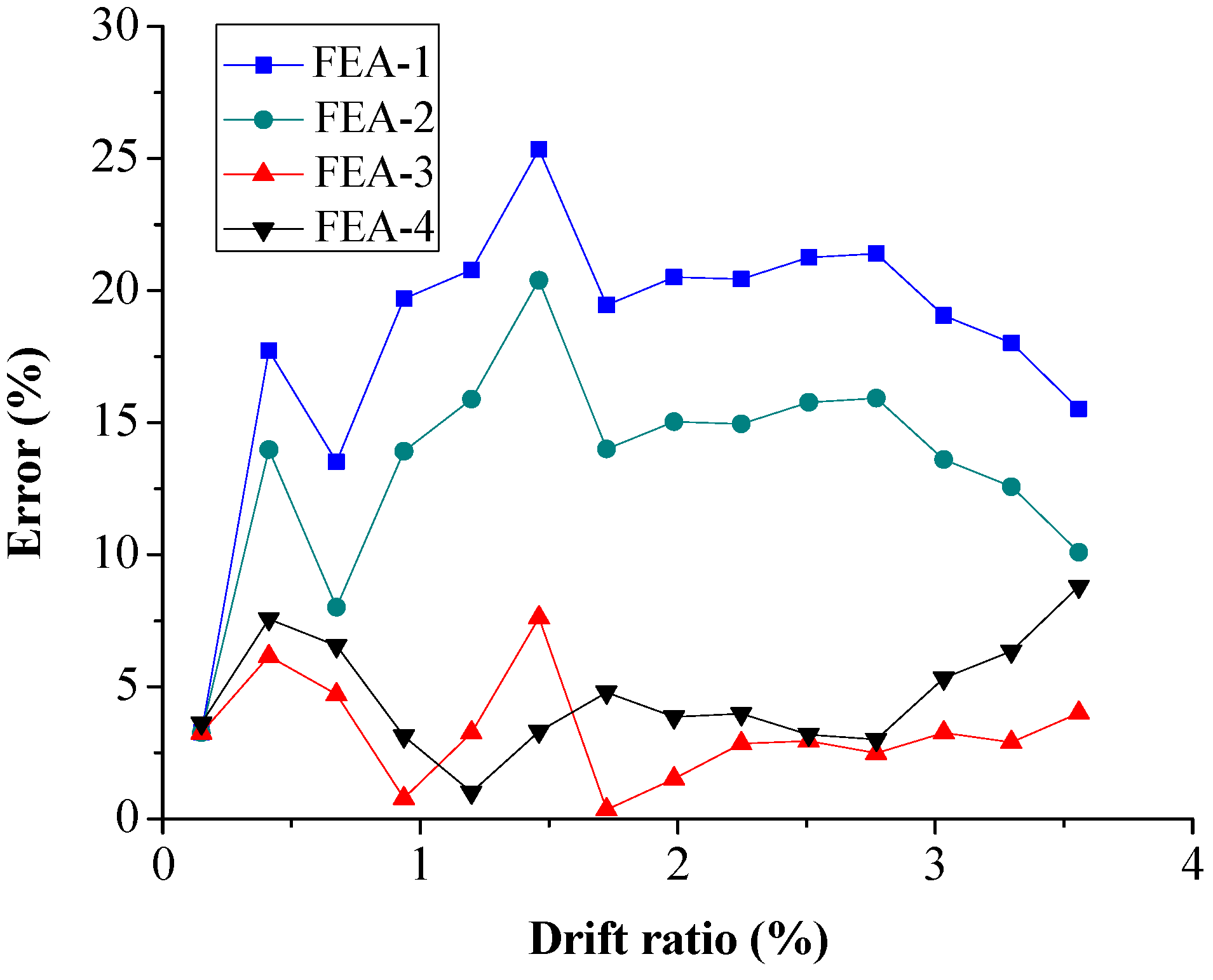
| Parameter | Lower Limit of Concrete Cube (FEA-1) | Average of Concrete Cube (FEA-2) | Monitored Peak Stress of SA (FEA-3) | Estimated Strength (FEA-4) |
|---|---|---|---|---|
| fcu | 23.0 | 26.5 | 36.5 | 40.0 |
| fcc | 26.0 | 29.7 | 39.4 | 42.9 |
| fuu | 4.6 | 5.3 | 7.3 | 8.0 |
| fuc | 20.8 | 23.7 | 31.5 | 34.3 |
| ε0u | 0.00153 | 0.00158 | 0.00174 | 0.00179 |
| ε0c | 0.00173 | 0.00177 | 0.00188 | 0.00192 |
| εuu | 0.0042 | 0.0038 | 0.0037 | 0.0035 |
| εuc | 0.02 | 0.02 | 0.02 | 0.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Hou, S.; Ou, J. Validation of Finite Element Model by Smart Aggregate-Based Stress Monitoring. Sensors 2018, 18, 4062. https://doi.org/10.3390/s18114062
Zhang H, Hou S, Ou J. Validation of Finite Element Model by Smart Aggregate-Based Stress Monitoring. Sensors. 2018; 18(11):4062. https://doi.org/10.3390/s18114062
Chicago/Turabian StyleZhang, Haibin, Shuang Hou, and Jinping Ou. 2018. "Validation of Finite Element Model by Smart Aggregate-Based Stress Monitoring" Sensors 18, no. 11: 4062. https://doi.org/10.3390/s18114062
APA StyleZhang, H., Hou, S., & Ou, J. (2018). Validation of Finite Element Model by Smart Aggregate-Based Stress Monitoring. Sensors, 18(11), 4062. https://doi.org/10.3390/s18114062





