Figure 1.
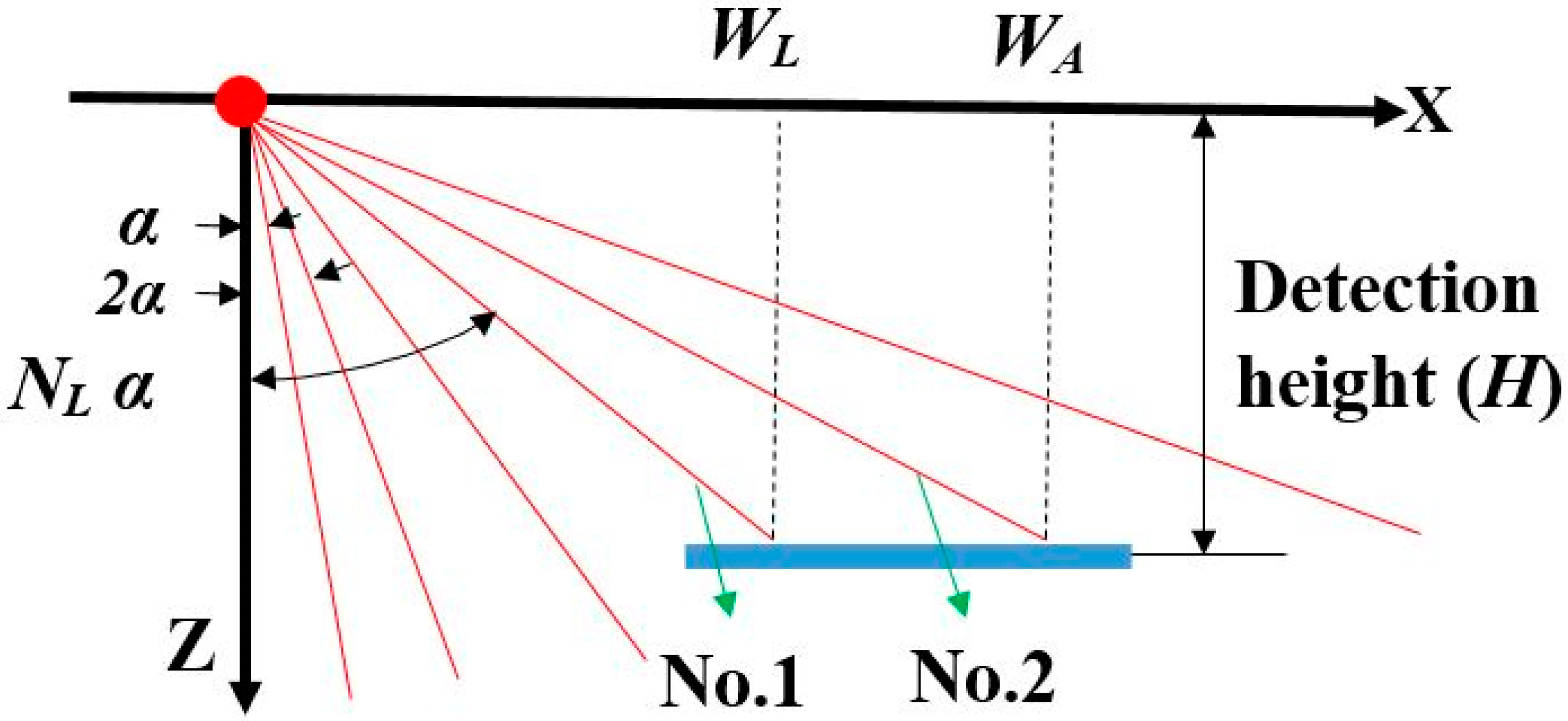
The 270° radial range laser sensor mounted on a constant-speed track to detect six rows of different objects (artificial plant 1, artificial plant 2, basketball, rectangular box, toy ball, and cylinder).
Figure 1.
The 270° radial range laser sensor mounted on a constant-speed track to detect six rows of different objects (artificial plant 1, artificial plant 2, basketball, rectangular box, toy ball, and cylinder).
Figure 2.
Geometry analysis of the laser beam points transmitted on the object surface on one side of the sensor.
Figure 2.
Geometry analysis of the laser beam points transmitted on the object surface on one side of the sensor.
Figure 3.
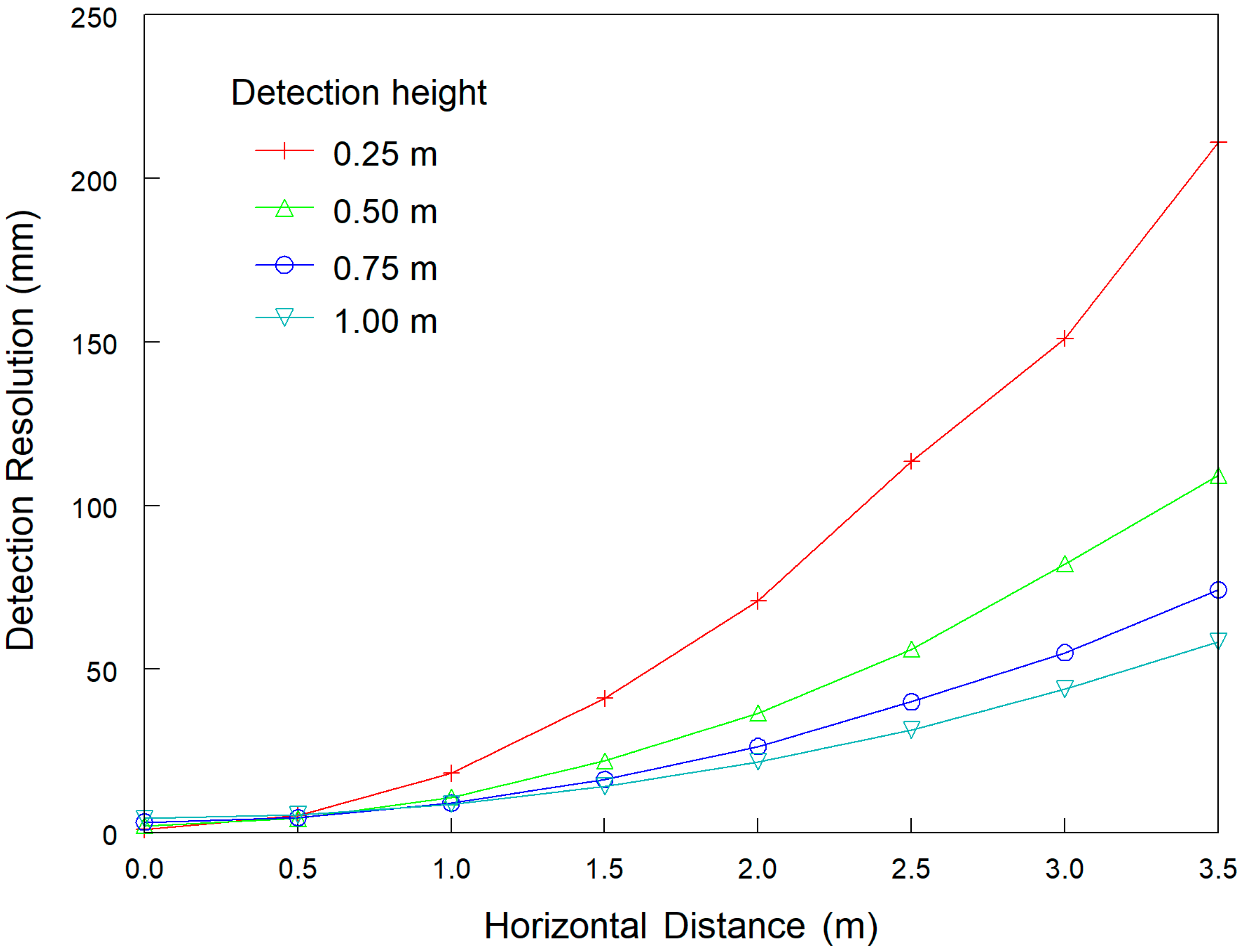
Calculated detection resolution of the laser sensor along the horizontal direction (DRH) with Equation (1) for different horizontal distances and detection heights.
Figure 3.
Calculated detection resolution of the laser sensor along the horizontal direction (DRH) with Equation (1) for different horizontal distances and detection heights.
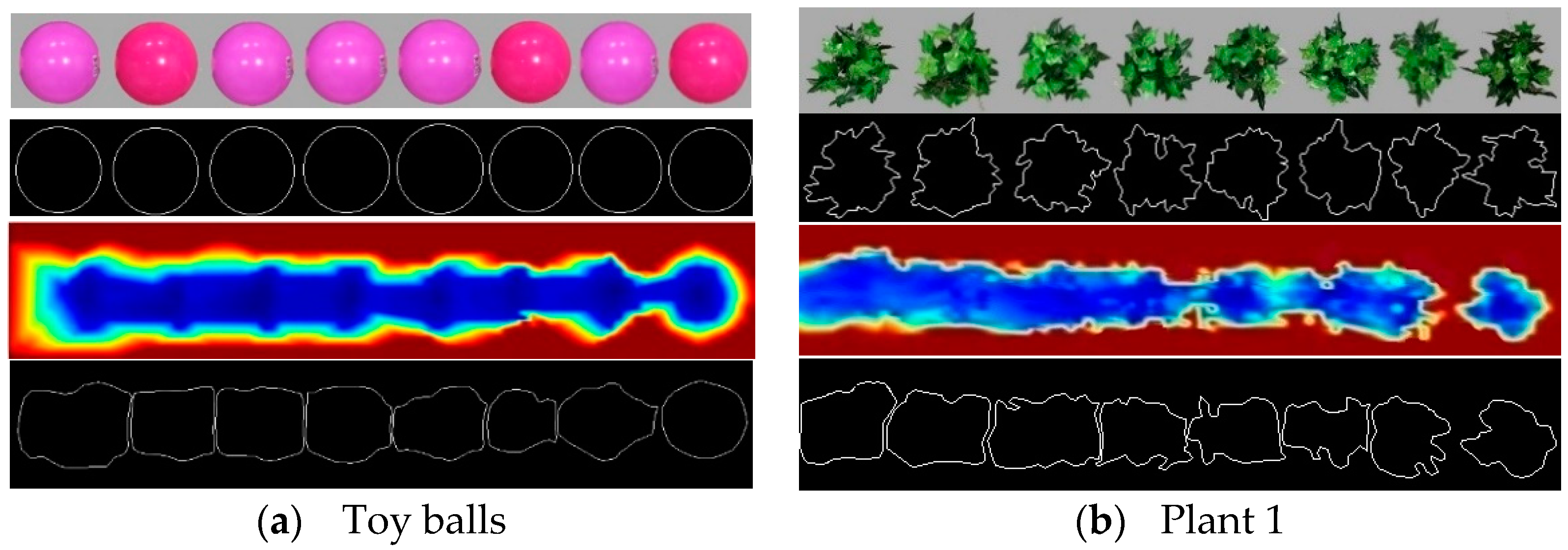
Figure 4.
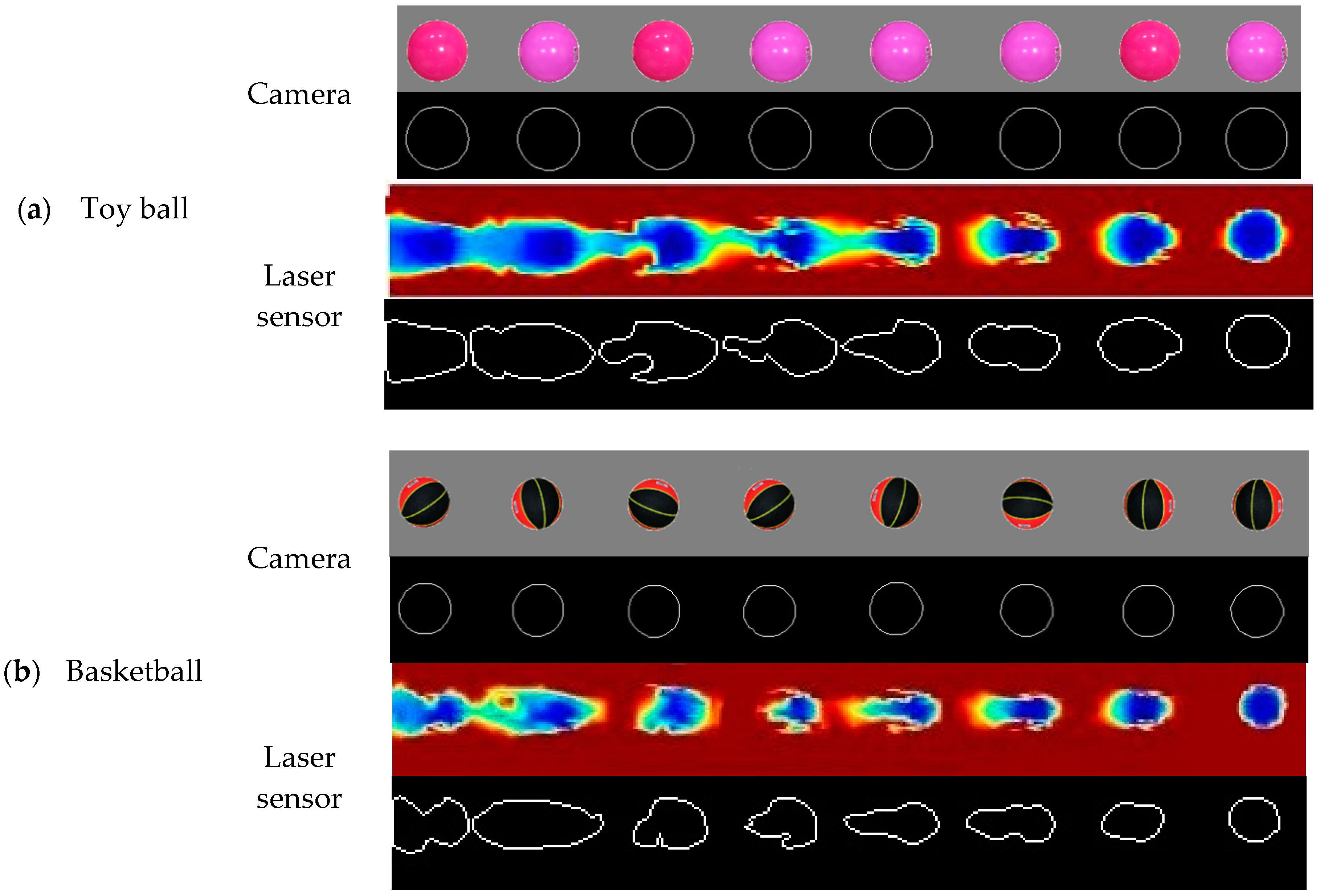
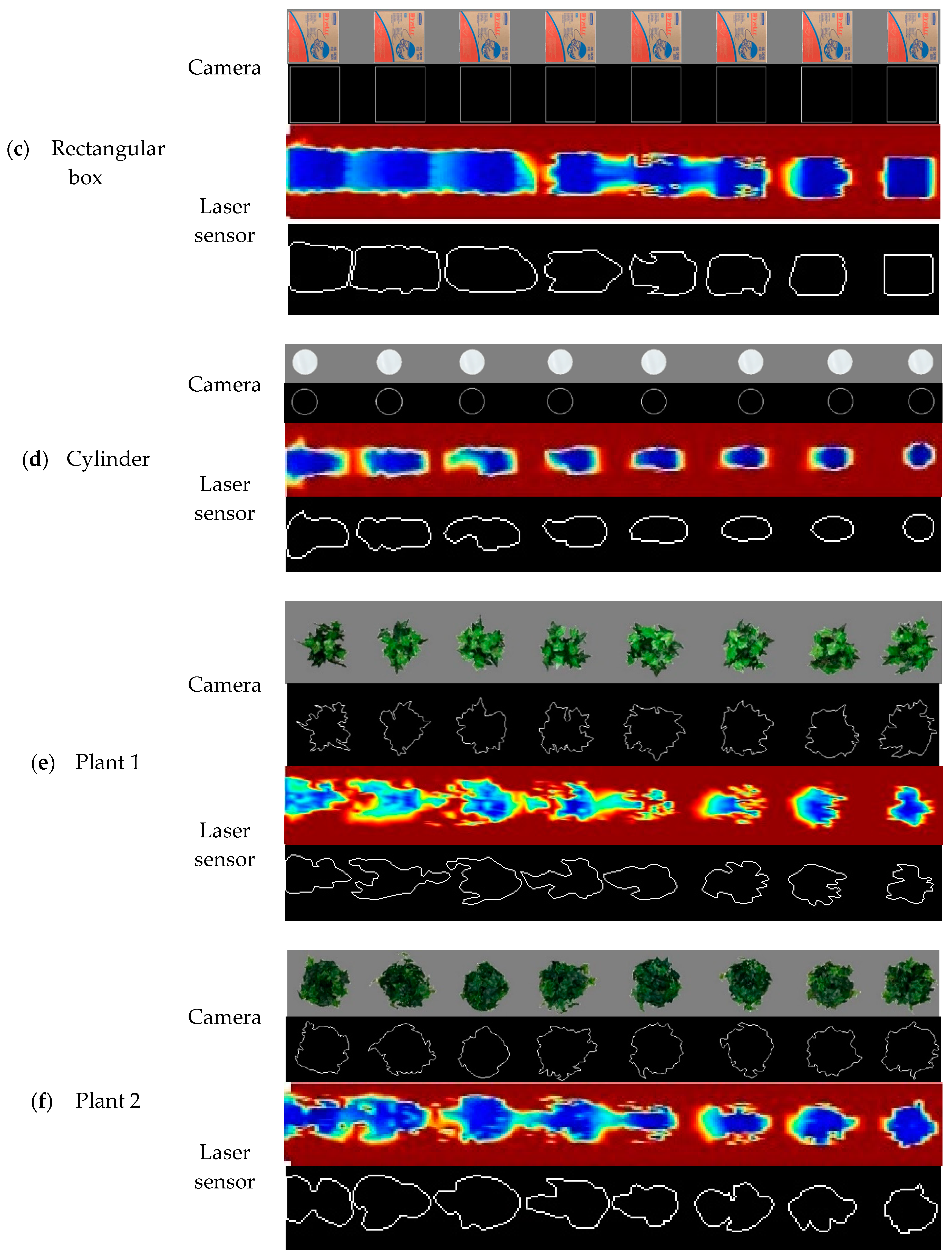
Processing edge similarity score (ESS) for paired images of eight 0.5 m evenly spaced objects obtained from the camera (upper) and laser sensor (lower): (a) toy ball, (b) basketball, (c) rectangular box, (d) cylinder, (e) artificial plant 1, and (f) artificial plant 2. The reconstructed images from the laser sensor were taken at 3.2 km h−1 travel speed and 0.5 m detection height. Different colors represent different vertical distances between the object surfaces and the laser sensor.
Figure 4.
Processing edge similarity score (ESS) for paired images of eight 0.5 m evenly spaced objects obtained from the camera (upper) and laser sensor (lower): (a) toy ball, (b) basketball, (c) rectangular box, (d) cylinder, (e) artificial plant 1, and (f) artificial plant 2. The reconstructed images from the laser sensor were taken at 3.2 km h−1 travel speed and 0.5 m detection height. Different colors represent different vertical distances between the object surfaces and the laser sensor.
Figure 5.
Processing ESS for paired images of eight 0.25 m evenly spaced objects obtained from the camera (upper) and laser sensor (lower): (a) toy ball, (b) artificial plant 1. The reconstructed images from the laser sensor were taken at 3.2 km h−1 travel speed and 0.5 m detection height. Different colors represent different vertical distances between the object surfaces and the laser sensor.
Figure 5.
Processing ESS for paired images of eight 0.25 m evenly spaced objects obtained from the camera (upper) and laser sensor (lower): (a) toy ball, (b) artificial plant 1. The reconstructed images from the laser sensor were taken at 3.2 km h−1 travel speed and 0.5 m detection height. Different colors represent different vertical distances between the object surfaces and the laser sensor.
Table 1.
Test variables in the test for validating the laser sensor detection accuracy for object edge profiles.
Table 1.
Test variables in the test for validating the laser sensor detection accuracy for object edge profiles.
| Test Part | Variable |
|---|
| 1 | Interval distance (m) | 0.5 |
| Speed (km h−1) | 1.6 | 2.4 | 3.2 | 4.0 | 4.8 |
| Detection height (m) | 0.25 | 0.50 | 0.75 | 1.00 |
| Replication | 3 |
| 2 | Interval distance (m) | 0.25 |
| Speed (km h−1) | 3.2 |
| Detection height (m) | 0.5 |
| Replication | 3 |
Table 2.
Mean edge similarity score (ESS) of toy balls at five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) across eight horizontal distances and four different detection heights.
Table 2.
Mean edge similarity score (ESS) of toy balls at five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) across eight horizontal distances and four different detection heights.
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.98 | 0.83 | 0.69 | 0.58 | 0.49 | 0.41 | 0.39 | 0.37 |
| 2.4 | 0.97 | 0.82 | 0.66 | 0.55 | 0.49 | 0.40 | 0.39 | 0.35 |
| 3.2 | 0.96 | 0.81 | 0.67 | 0.54 | 0.47 | 0.38 | 0.38 | 0.35 |
| 4.0 | 0.96 | 0.79 | 0.63 | 0.51 | 0.47 | 0.38 | 0.35 | 0.34 |
| 4.8 | 0.95 | 0.78 | 0.64 | 0.50 | 0.45 | 0.35 | 0.32 | 0.33 |
Table 3.
Mean ESS of toy balls at four detection heights (0.25, 0.5, 0.75 and 1.0 m) across eight horizontal distances and five laser sensor travel speeds.
Table 3.
Mean ESS of toy balls at four detection heights (0.25, 0.5, 0.75 and 1.0 m) across eight horizontal distances and five laser sensor travel speeds.
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.96 | 0.64 | 0.54 | 0.37 | 0.36 | 0.36 | 0.33 | 0.29 |
| 0.5 | 0.96 | 0.74 | 0.61 | 0.43 | 0.36 | 0.33 | 0.34 | 0.30 |
| 0.75 | 0.97 | 0.91 | 0.73 | 0.66 | 0.56 | 0.37 | 0.35 | 0.35 |
| 1.0 | 0.96 | 0.93 | 0.76 | 0.69 | 0.62 | 0.48 | 0.44 | 0.46 |
Table 4.
Mean ESS of four regularly-shaped objects (toy balls, basketballs, rectangular boxes and cylinders) and two sized artificial plants (plant 1 and plant 2) across all the combinations of five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1) and four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances.
Table 4.
Mean ESS of four regularly-shaped objects (toy balls, basketballs, rectangular boxes and cylinders) and two sized artificial plants (plant 1 and plant 2) across all the combinations of five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1) and four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances.
| Object | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| Toy ball | 0.96 | 0.80 | 0.66 | 0.54 | 0.47 | 0.38 | 0.37 | 0.35 |
| Basketball | 0.95 | 0.79 | 0.68 | 0.58 | 0.49 | 0.41 | 0.38 | 0.38 |
| Rectangular box | 0.97 | 0.90 | 0.84 | 0.73 | 0.64 | 0.54 | 0.49 | 0.48 |
| Cylinder | 0.96 | 0.85 | 0.69 | 0.61 | 0.51 | 0.37 | 0.33 | 0.31 |
| Plant 1 | 0.90 | 0.72 | 0.67 | 0.61 | 0.45 | 0.37 | 0.35 | 0.35 |
| Plant 2 | 0.94 | 0.81 | 0.78 | 0.64 | 0.48 | 0.44 | 0.41 | 0.38 |
Table 5.
Mean ESS of basketballs across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five travel speeds.
Table 5.
Mean ESS of basketballs across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five travel speeds.
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.96 | 0.81 | 0.72 | 0.63 | 0.52 | 0.43 | 0.40 | 0.40 |
| 2.4 | 0.95 | 0.80 | 0.69 | 0.60 | 0.52 | 0.42 | 0.38 | 0.37 |
| 3.2 | 0.96 | 0.79 | 0.68 | 0.58 | 0.48 | 0.40 | 0.37 | 0.37 |
| 4.0 | 0.94 | 0.79 | 0.65 | 0.54 | 0.50 | 0.40 | 0.35 | 0.35 |
| 4.8 | 0.95 | 0.77 | 0.66 | 0.53 | 0.45 | 0.39 | 0.34 | 0.36 |
Table 6.
Mean ESS of basketballs across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four different detection heights.
Table 6.
Mean ESS of basketballs across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four different detection heights.
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.95 | 0.61 | 0.53 | 0.41 | 0.38 | 0.30 | 0.34 | 0.36 |
| 0.5 | 0.95 | 0.71 | 0.64 | 0.50 | 0.43 | 0.35 | 0.35 | 0.35 |
| 0.75 | 0.96 | 0.91 | 0.72 | 0.64 | 0.50 | 0.38 | 0.36 | 0.39 |
| 1.0 | 0.95 | 0.94 | 0.84 | 0.75 | 0.66 | 0.61 | 0.45 | 0.42 |
Table 7.
Mean ESS of rectangular boxes across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five sensor travel speeds.
Table 7.
Mean ESS of rectangular boxes across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five sensor travel speeds.
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.98 | 0.92 | 0.86 | 0.79 | 0.68 | 0.60 | 0.50 | 0.51 |
| 2.4 | 0.97 | 0.91 | 0.85 | 0.73 | 0.64 | 0.55 | 0.50 | 0.48 |
| 3.2 | 0.97 | 0.90 | 0.84 | 0.73 | 0.64 | 0.53 | 0.49 | 0.48 |
| 4.0 | 0.97 | 0.90 | 0.84 | 0.71 | 0.62 | 0.51 | 0.48 | 0.47 |
| 4.8 | 0.96 | 0.90 | 0.81 | 0.70 | 0.61 | 0.50 | 0.45 | 0.46 |
Table 8.
Mean ESS of rectangular boxes across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
Table 8.
Mean ESS of rectangular boxes across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.98 | 0.88 | 0.82 | 0.71 | 0.60 | 0.54 | 0.42 | 0.41 |
| 0.5 | 0.98 | 0.91 | 0.82 | 0.72 | 0.64 | 0.49 | 0.44 | 0.43 |
| 0.75 | 0.97 | 0.91 | 0.84 | 0.73 | 0.65 | 0.56 | 0.52 | 0.53 |
| 1.0 | 0.96 | 0.92 | 0.87 | 0.75 | 0.66 | 0.57 | 0.55 | 0.54 |
Table 9.
Mean ESS of cylinders across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five travel speeds.
Table 9.
Mean ESS of cylinders across four different detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and five travel speeds.
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.97 | 0.86 | 0.74 | 0.66 | 0.55 | 0.39 | 0.35 | 0.33 |
| 2.4 | 0.95 | 0.85 | 0.72 | 0.63 | 0.54 | 0.39 | 0.33 | 0.32 |
| 3.2 | 0.96 | 0.86 | 0.68 | 0.60 | 0.51 | 0.37 | 0.33 | 0.31 |
| 4.0 | 0.94 | 0.85 | 0.66 | 0.59 | 0.49 | 0.36 | 0.33 | 0.29 |
| 4.8 | 0.95 | 0.85 | 0.65 | 0.58 | 0.46 | 0.35 | 0.31 | 0.30 |
Table 10.
Mean ESS of cylinders across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
Table 10.
Mean ESS of cylinders across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.96 | 0.83 | 0.58 | 0.56 | 0.43 | 0.30 | 0.26 | 0.24 |
| 0.5 | 0.95 | 0.83 | 0.63 | 0.56 | 0.47 | 0.30 | 0.23 | 0.22 |
| 0.75 | 0.96 | 0.86 | 0.73 | 0.61 | 0.55 | 0.43 | 0.38 | 0.37 |
| 1.0 | 0.95 | 0.90 | 0.81 | 0.73 | 0.58 | 0.47 | 0.44 | 0.41 |
Table 11.
Mean ESS of artificial plant 1 across four detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and the five travel speeds.
Table 11.
Mean ESS of artificial plant 1 across four detection heights (0.25, 0.5, 0.75 and 1.0 m) at eight horizontal distances and the five travel speeds.
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.92 | 0.74 | 0.70 | 0.64 | 0.50 | 0.42 | 0.39 | 0.37 |
| 2.4 | 0.91 | 0.73 | 0.69 | 0.63 | 0.47 | 0.42 | 0.37 | 0.37 |
| 3.2 | 0.90 | 0.73 | 0.67 | 0.61 | 0.46 | 0.36 | 0.35 | 0.35 |
| 4.0 | 0.89 | 0.71 | 0.66 | 0.60 | 0.41 | 0.32 | 0.33 | 0.34 |
| 4.8 | 0.88 | 0.71 | 0.64 | 0.57 | 0.40 | 0.32 | 0.32 | 0.31 |
Table 12.
Mean ESS of artificial plant 1 across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
Table 12.
Mean ESS of artificial plant 1 across five travel speeds (1.6, 2.4, 3.2, 4.0 and 4.8 km h−1) at eight horizontal distances and four detection heights.
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.91 | 0.69 | 0.66 | 0.60 | 0.38 | 0.26 | 0.27 | 0.29 |
| 0.5 | 0.89 | 0.74 | 0.65 | 0.60 | 0.40 | 0.27 | 0.27 | 0.27 |
| 0.75 | 0.91 | 0.73 | 0.66 | 0.61 | 0.45 | 0.46 | 0.42 | 0.40 |
| 1.0 | 0.89 | 0.73 | 0.71 | 0.64 | 0.56 | 0.47 | 0.45 | 0.44 |
Table 13.
Mean ESS of plant 2 across four detection heights (0.25, 0.5, 0.75, and 1.0 m) at eight horizontal distances (0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, and 3.5 m) and five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1).
Table 13.
Mean ESS of plant 2 across four detection heights (0.25, 0.5, 0.75, and 1.0 m) at eight horizontal distances (0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, and 3.5 m) and five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1).
| Speed (km h−1) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 1.6 | 0.94 | 0.83 | 0.80 | 0.68 | 0.54 | 0.49 | 0.45 | 0.42 |
| 2.4 | 0.94 | 0.82 | 0.79 | 0.67 | 0.52 | 0.45 | 0.43 | 0.41 |
| 3.2 | 0.94 | 0.81 | 0.80 | 0.63 | 0.47 | 0.45 | 0.40 | 0.37 |
| 4.0 | 0.94 | 0.80 | 0.76 | 0.63 | 0.44 | 0.43 | 0.39 | 0.36 |
| 4.8 | 0.93 | 0.82 | 0.74 | 0.61 | 0.41 | 0.40 | 0.37 | 0.36 |
Table 14.
Mean ESS of plant 2 at eight horizontal distances (0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, and 3.5 m) across five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1) at four different detection heights (0.25, 0.5, 0.75, and 1.0 m).
Table 14.
Mean ESS of plant 2 at eight horizontal distances (0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, and 3.5 m) across five travel speeds (1.6, 2.4, 3.2, 4.0, and 4.8 km h−1) at four different detection heights (0.25, 0.5, 0.75, and 1.0 m).
| Detection Height (m) | Horizontal Distance (m) |
|---|
| 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|
| 0.25 | 0.94 | 0.74 | 0.77 | 0.65 | 0.43 | 0.41 | 0.35 | 0.33 |
| 0.5 | 0.94 | 0.83 | 0.79 | 0.65 | 0.45 | 0.43 | 0.35 | 0.29 |
| 0.75 | 0.94 | 0.84 | 0.81 | 0.63 | 0.46 | 0.41 | 0.36 | 0.41 |
| 1.0 | 0.94 | 0.85 | 0.74 | 0.65 | 0.56 | 0.53 | 0.58 | 0.51 |