Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment
Abstract
1. Introduction
2. Materials and Methods
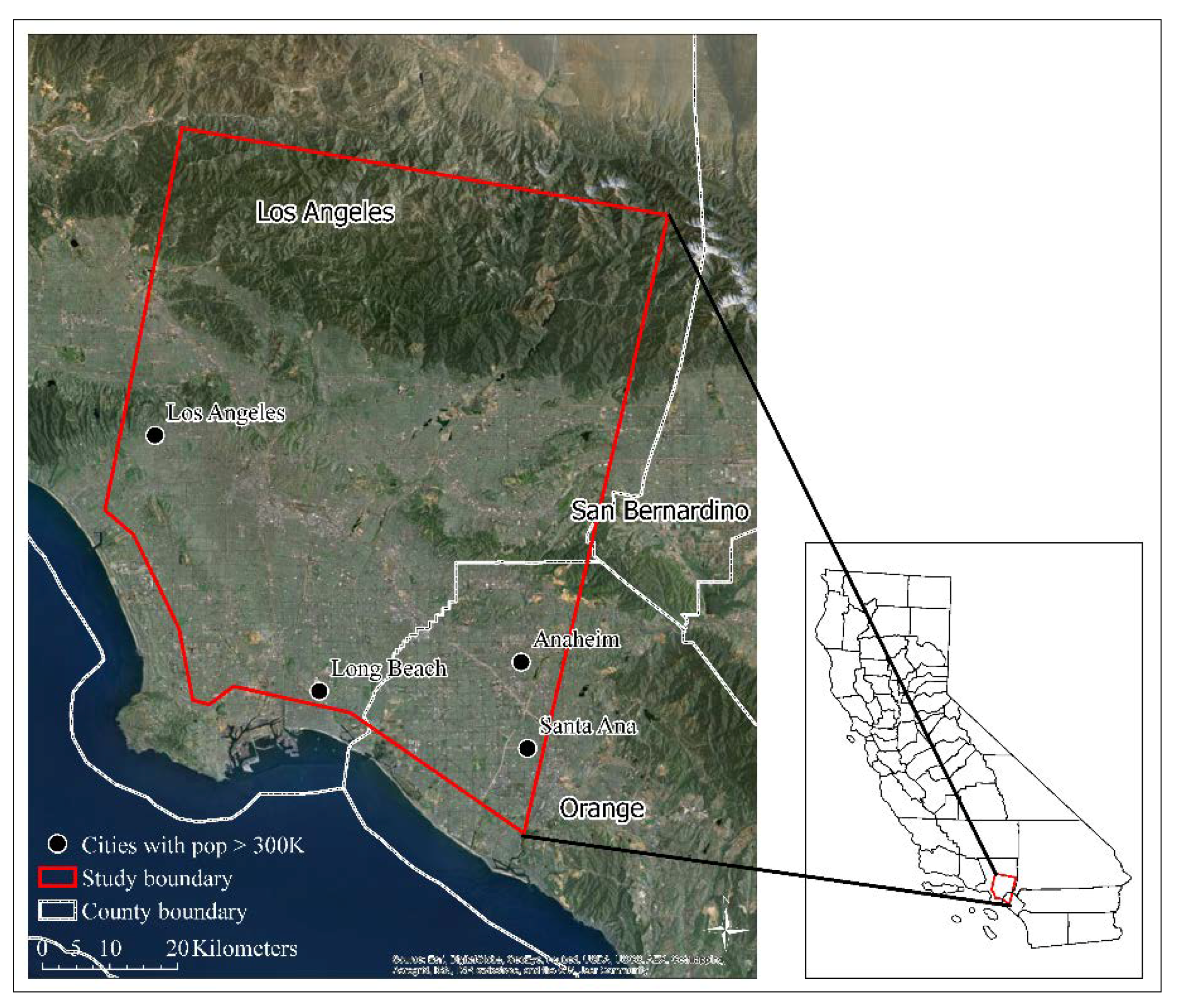
2.1. Study Area
2.2. Data Collection and Pre-Processing
2.3. LST Image Fusion
2.4. Downscaling Effect Analysis
3. Results
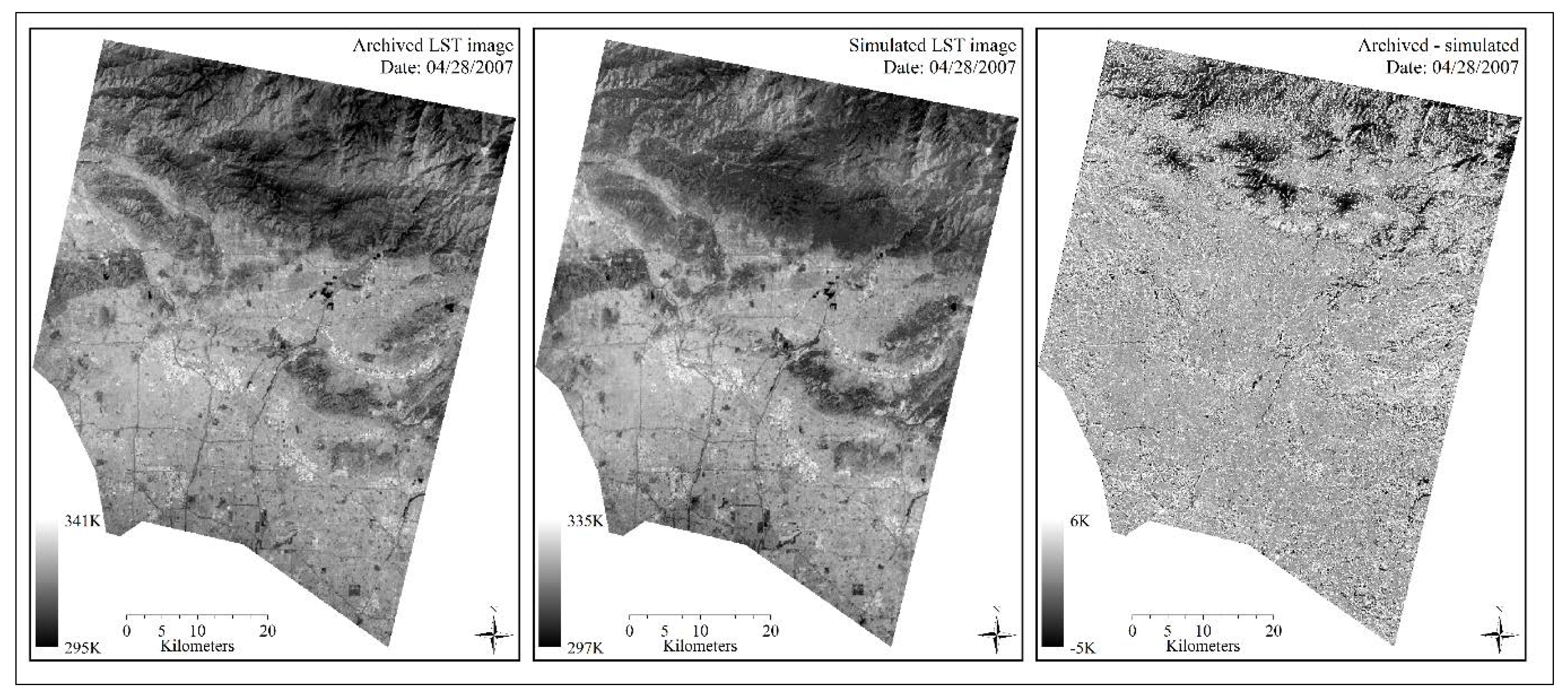
3.1. Simulated ASTER LST Image
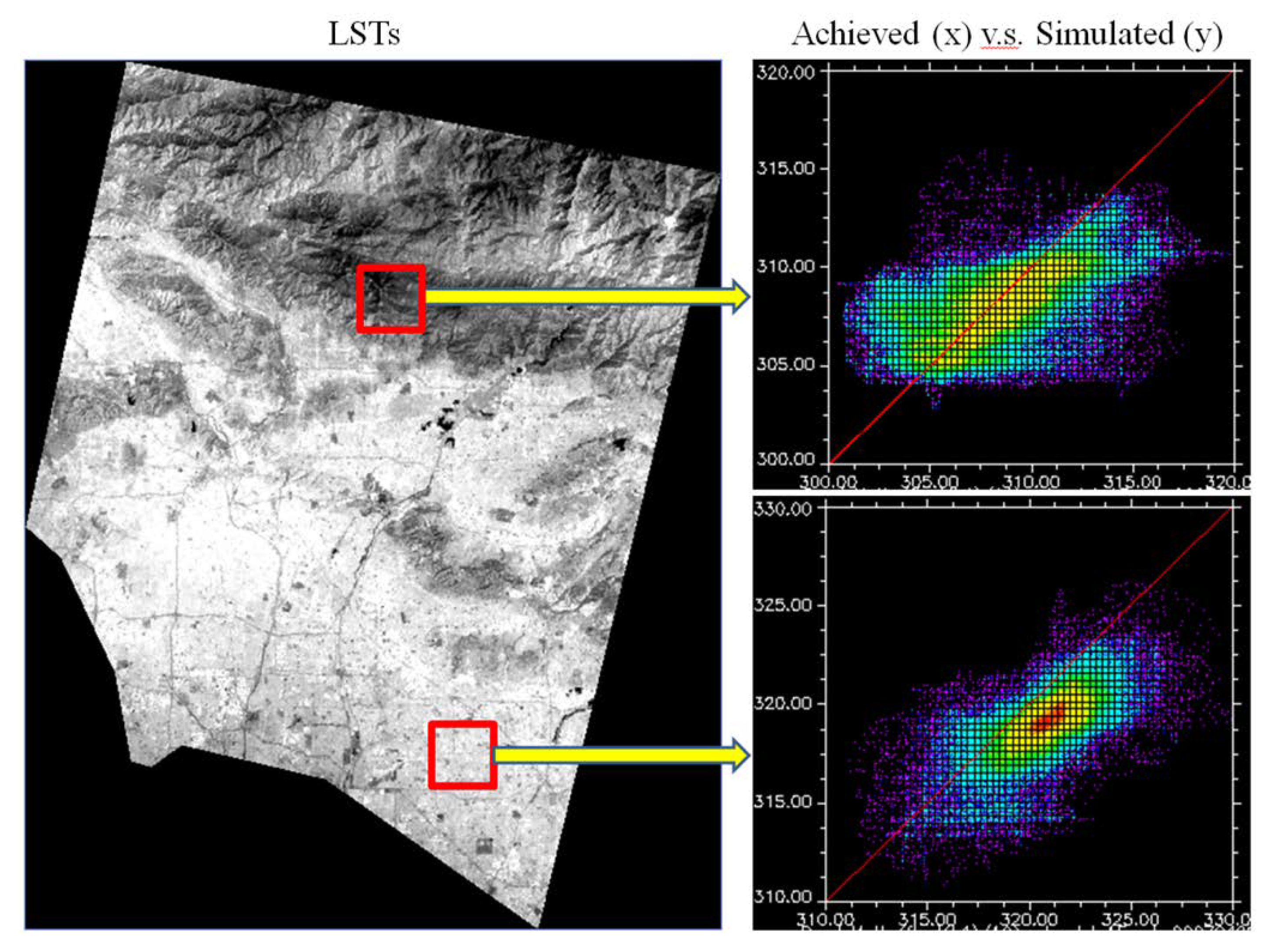
3.2. Image Fusion Validation
3.3. Downscaling Effect Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, Y. Estimation of storage heat flux in an urban area using ASTER data. Remote Sens. Environ. 2007, 110, 1–17. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Enhancing temporal resolution of satellite imagery for public health studies: A case study of West Nile Virus outbreak in Los Angeles in 2007. Remote Sens. Environ. 2012, 117, 57–71. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Bottyán, Z.; Unger, J. A multiple linear statistical model for estimating the mean maximum urban heat island. Theor. Appl. Climatol. 2003, 75, 233–243. [Google Scholar] [CrossRef]
- Hais, M.; Kučera, T. The influence of topography on the forest surface temperature retrieved from Landsat TM, ETM+ and ASTER thermal channels. ISPRS J. Photogramm. Remote Sens. 2009, 64, 585–591. [Google Scholar] [CrossRef]
- Neteler, M. Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Genderen, J.L.; Pohl, C. Image fusion: Issues, techniques and applications. In Proceedings of the EAReL Workshop Intelligent Image Fusion, Strasbourg, France, 11 September 1994; pp. 18–26. [Google Scholar]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Zheng, S.; Shi, W.; Liu, J.; Tian, J. Remote sensing image fusion using multiscale mapped LS-SVM. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1313–1322. [Google Scholar] [CrossRef]
- Chavez, P.S.; Bowell, J.A. Comparison of the spectral information content of Landsat thematic mapper and SPOT for three different sites in the Phoenix, Arizona region. Photogramm. Eng. Remote Sens. 1988, 54, 1699–1708. [Google Scholar]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images-II. Channel ratio and ‘chromaticity’ transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Li, Z.; Jing, Z.; Yang, X.; Sun, S. Color transfer based remote sensing image fusion using non-separable wavelet frame transform. Pattern Recognit. Lett. 2005, 26, 2006–2014. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Wilson, E.O. Theory of Island Biogeography (MPB-1); Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Huth, R. Statistical downscaling of daily temperature in central Europe. J. Clim. 2002, 15, 1731–1742. [Google Scholar] [CrossRef]
- Thornes, J.B. Markov chains and slope series: The scale problem. Geogr. Anal. 1973, 5, 322–328. [Google Scholar] [CrossRef]
- Goodchild, M.F. Scale in GIS: An overview. Geomorphology 2011, 130, 5–9. [Google Scholar] [CrossRef]
- Meentemeyer, V. Geographical perspectives of space, time, and scale. Landsc. Ecol. 1989, 3, 163–173. [Google Scholar] [CrossRef]
- Turner, M.G. Spatial and temporal analysis of landscape patterns. Landscape Ecology. 1990, 4, 21–30. [Google Scholar] [CrossRef]
- Petit, C.C.; Lambin, E.F. Integration of multi-source remote sensing data for land-cover change detection. Int. J. Geogr. Inf. Sci. 2001, 15, 785–803. [Google Scholar] [CrossRef]
- Chen, D.; Stow, D.A.; Gong, P. Examining the effect of spatial resolution and texture window size on classification accuracy: An urban environment case. Int. J. Remote Sens. 2004, 25, 2177–2192. [Google Scholar] [CrossRef]
- Wang, G.; Gertner, G.; Anderson, A.B. Upscaling methods based on variability-weighting and simulation for inferring spatial information across scales. Int. J. Remote Sens. 2004, 25, 4961–4979. [Google Scholar] [CrossRef]
- Schmid, H.P. Spatial Scales of Sensible Heat Flux Variability: Representativeness of Flux Measurements and Surface Layer Structure over Suburban Terrain. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 1988. [Google Scholar]
- Quattrochi, D.A.; Goel, N.S. Spatial and temporal scaling of thermal remote sensing data. Remote Sens. Rev. 1995, 12, 255–286. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Scaling effect on the relationship between landscape pattern and land surface temperature: A case study of Indianapolis, United States. Photogramm. Eng. Remote Sens. 2009, 75, 291–304. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Pardo-Iguzquiza, E.; Chica-Olmo, M. Downscaling cokriging for super-resolution mapping of continua in remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 573–580. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Ha, W.; Gowda, P.H.; Howell, T.A. A review of downscaling methods for remote sensing-based irrigation management: Part I. Irrig. Sci. 2013, 31, 831–850. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P. Modeling annual parameters of land surface temperature variations and evaluating the impact of cloud cover using time series of Landsat TIR data. Remote Sens. Environ. 2014, 140, 267–278. [Google Scholar] [CrossRef]
- Zakšek, K.; Oštir, K. Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ. 2012, 117, 114–124. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Jiang, Y.; Weng, Q. Estimation of hourly and daily evapotranspiration and soil moisture using downscaled LST over various urban surfaces. GISci. Remote Sens. 2017, 54, 95–117. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ. 2009, 113, 2592–2605. [Google Scholar] [CrossRef]
- Liu, D.; Pu, R. Downscaling thermal infrared radiance for subpixel land surface temperature retrieval. Sensors 2008, 8, 2695–2706. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Fu, P.; Weng, Q. Downscaling GOES land surface temperature for assessing heat wave health risks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1605–1609. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Evaluation of disaggregation methods for downscaling MODIS land surface temperature to Landsat spatial resolution in Barrax test site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1430–1438. [Google Scholar] [CrossRef]
- Rajasekar, U.; Weng, Q. Spatio-temporal modeling and analysis of urban heat islands by using Landsat TM and ETM+ Imagery. Int. J. Remote Sens. 2009, 30, 3531–3548. [Google Scholar] [CrossRef]
- Nowak, D.J.; Hoehn, R.E., III; Crane, D.E.; Weller, L.; Davila, A. Assessing Urban Forest Effects and Values-Los Angeles’ Urban Forest, USDA Forest Service, Northern Research Station, Resource Bulletin NRS-47. 2011. Available online: http://www.nrs.fs.fed.us/pubs/rb/rb_nrs47.pdf (accessed on 4 November 2018).
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wu, H.; Li, Z.L. Scale issues in remote sensing: A review on analysis, processing and modeling. Sensors 2009, 9, 1768–1793. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Dozier, J. Land-surface temperature measurement from space: Physical principles and inverse modeling. IEEE Trans. Geosci. Remote Sens. 1989, 27, 268–278. [Google Scholar]


| Satellite Data | Acquisition Date & Time (GWT) | Spatial Resolution (m) |
|---|---|---|
| Terra ASTER AST_08 | 3 April 2007, 18:46 | 90 |
| (Surface Kinetic Temperature) | 28 April 2007, 18:39 * | |
| 1 July 2007, 18:39 | ||
| Terra MODIS 11A1 LST/E | 3 April 2007, daily | 1000 |
| (Land Surface Temperature & Emissivity) | 28 April 2007, daily | |
| 1 July 2007, daily |
| Spatial Resolution (units: m) | Mean (Units: K) | Standard Deviation (SD) (Units: K) | ||||
|---|---|---|---|---|---|---|
| Cubic | Bilinear | Nearest Neighbor | Cubic | Bilinear | Nearest Neighbor | |
| 15 | 0.88 | 0.93 | 1.08 | 1.99 | 1.96 | 1.98 |
| 30 | 0.95 | 0.94 | 1.04 | 1.98 | 1.95 | 2.17 |
| 60 | 0.90 | 0.98 | −4.59 | 1.94 | 1.95 | 4.25 |
| 90 | 0.89 | 0.88 | −4.58 | 1.93 | 1.92 | 4.26 |
| 120 | −2.73 | 0.89 | −4.53 | 3.43 | 1.91 | 4.24 |
| 250 | 0.93 | 0.90 | −4.45 | 2.14 | 1.88 | 4.09 |
| 500 | 0.90 | 0.86 | −4.41 | 2.12 | 1.84 | 4.16 |
| 1000 | 0.92 | 0.90 | −4.33 | 2.12 | 1.85 | 4.20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Weng, Q. Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment. Sensors 2018, 18, 4058. https://doi.org/10.3390/s18114058
Liu H, Weng Q. Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment. Sensors. 2018; 18(11):4058. https://doi.org/10.3390/s18114058
Chicago/Turabian StyleLiu, Hua, and Qihao Weng. 2018. "Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment" Sensors 18, no. 11: 4058. https://doi.org/10.3390/s18114058
APA StyleLiu, H., & Weng, Q. (2018). Scaling Effect of Fused ASTER-MODIS Land Surface Temperature in an Urban Environment. Sensors, 18(11), 4058. https://doi.org/10.3390/s18114058






