Adding Active Slot Joint Larger Broadcast Radius for Fast Code Dissemination in WSNs
Abstract
:1. Introduction
- (1)
- How to quickly spread the code to each node in the network. Dissemination delay is the difference between the time when the sink starts the code dissemination and the time when the last node in the network receives the code. Reducing the dissemination delay is of great significance for the application of WSNs [6,7,8,12,14,17]. In general, the purpose of code dissemination is to update WSNs by adding new features, sensing new type of data, new data processing functions, and extending the field of their applications. Therefore, in the process of code dissemination, the data and data processing results of the node that first received the code are inconsistent with the nodes of the non-updated code. Obviously, this inconsistency will exist in any code updating process, however, the duration of such inconsistency is expected to be as short as possible, as this inconsistency may cause confusion and reduce the reliability of the application. For example: in large-scale crop monitoring, it is necessary to process the perceived data in near real-time. If updating the code takes a long time, it may cause data inconsistency, which will affect the correct decisions. In industrial monitoring applications where real-time requirements are very strict, the requirements are even more stringent, and the inconsistency of data is required to be as short as possible. Otherwise, it may cause significant production losses [23]. However, to quickly spread the new code to an entire network it is not an easy task. In WSNs, because the nodes are powered by battery energy, due to manufacturing costs and economic considerations, nodes should be as simple as possible and low in cost. Therefore, the capacity of the batteries is limited [26,27,28,29]. As nodes are generally deployed in places that are dangerous or difficult for humans to reach, it is generally difficult to replace the drained sensors. Therefore, how to save energy is one of the most important and hot topics of WSNs [30,31]. One of the most common methods used to save energy is the periodic sleep/awake rotation of the nodes [7,15,17] because when the node is in the sleep state, its energy consumption is less than of its energy consumption in the awake state [32,33,34,35]. Therefore, the node should be in the sleep state as much as possible to save energy [7,15,17]. Although duty cycle-based WSNs can save energy, it causes greater delays in code dissemination [7,15,17]. Because in duty cycle-based WSNs, the working period of the node is divided into equal slots, and the node is only active in one of the slots which is called active slot, and in other slots sleep. When the node is in the sleep state, the nodes cannot communicate with each other. When the sender sends the code to the receiver, the sender must wait for the receiver to awake before the code can be spread. The average expected delay in this case is approximately slots. The time for multi-hop code dissemination increases linearly as the number of hops increases. Thus, how to quickly spread code to the network is a challenge issue [7,15,17].
- (2)
- How to reduce the number of broadcasts. Since the energy in wireless sensor networks is the most valuable resource, reducing the number of broadcasts can reduce the energy consumption of the network, and reducing the number of broadcasts can also shorten the time required for code to spread. Therefore, reducing the number of broadcasts in the code dissemination process is another important research issue. This problem is summarized as the minimum-transmission broadcast (MTB) problem [7,12]. In non-duty cycle WSNs, the parent node only needs to broadcast once to get all the son nodes to receive the code. In the duty cycle-based WSNs, since the slots of the son nodes awake times may be different, the parent node may need to broadcast once for each active slot of its son nodes, so the number of broadcasts is greatly increased. This shows that the MTB problem is a challenging issue in duty cycle-based WSNs.
- (3)
- Improve network life. Lifetime has always been an important issue in WSN research. In general, reducing the energy consumption of node can extend the life of nodes. Therefore, the main way to improve the network lifetime is to reduce the energy consumption of nodes. The energy consumption of nodes is mainly due to data transmission, data reception, energy consumption during idle waiting tasks, therefore, reducing the number of broadcasts reduces the energy consumption of data operations (sending and receiving). The idle energy consumption refers to the energy consumption of the listening channel when the node is in the active state [36,37,38,39]. The key way to reduce the idle waiting energy consumption is to make the node sleep as much as possible when there is no data operation, so that the active time is as small as possible, but this will bring more delay. In other words, lifetime is closely related to the performance of delay and broadcast times, and comprehensive optimization is needed to achieve better results [40,41,42,43]. In addition, network lifetime and node lifetime in WSNs are not the same concept [44,45]. Due to the imbalance of energy consumption, in general, when data is collected by WSNs, the near-sink area node bears a large amount of data and consumes a large amount of energy, which may cause nodes in the near-sink area to die prematurely, resulting in network death [46,47,48]. According to studies [44,46], there may still be up to 90% energy remaining in the network, so the most important thing to improve the network lifetime is to improve the life of the nodes whose energy consumption is the largest. However, saving energy for the node with superfluous energy does not increase the network lifetime [47,48].
- (1)
- An Adding Active Slot joint Larger Broadcast Radius (AAS-LBR) scheme is proposed for reducing the number of broadcasts and fast code dissemination while retaining higher network lifetime for WSNs. The important innovation of the AAS-LBR scheme is that it can significantly improve the performance of code dissemination through increasing the active slots and increasing the broadcast radius. We find that WSNs consume more energy in the near-sink area during data collection, while the energy consumption in the far-sink area is low and there is energy remaining. Therefore, the AAS-LBR scheme makes full use of the remaining energy of the far-sink area node to add up to one active slot and increase the broadcast radius. Increasing the broadcast radius can expand the range of one broadcast, so that the number of nodes receiving the code in one broadcast becomes larger, thereby reducing the number of broadcasts needed. On the other hand, it makes the distance of one hop broadcast farther, so that it can spread to the whole network with fewer hops, reducing delays. Adding one active slot can double the time slot of the node receiving code, so that the probability of receiving the code is doubled, which can effectively reduce the number of broadcasts and reduce the delay. We demonstrate that at most only one active slot needs to be added to greatly improve the performance of code dissemination.
- (2)
- An effective code dissemination algorithm based on adding Active Slot joint Larger Broadcast Radius is proposed for duty cycle-based WSNs. The algorithm proposed in this paper significantly improves the performance of code dissemination. Compared with the previous algorithms, the code dissemination algorithm has the following two main improvements: (a) When the broadcast backbone is constructed, the active slot is added to the next hop node with pipeline style in the diffusion path, so that the code dissemination process can be continuously performed without any pause in the proposed scheme. Code can quickly spread to the entire broadcast backbone. (b) For the nodes on the non-broadcast backbone, an active slot is added coincident with its broadcast backbone’ active slot which can fully utilize the broadcast operation of the broadcast backbone to obtain the code, thereby reducing the time required for code dissemination and the number of broadcasts.
- (3)
- Through our extensive theoretical analysis and experiment, we demonstrate that the AAS-LBR scheme proposed in this paper has better performance. Compared to the schemes of previous strategies, our AAS-LBR scheme is superior in all important performance indicators. (a) Compared to previous strategies, the AAS-LBR scheme can reduce the number of broadcasts by 20.0%; (b) the code diffusion delay is reduced by 45.5% compared to previous strategies; (c) the proposed strategy can effectively improve energy utilization by 24.5%. While all major performance factors are improved, its network lifetime is higher than with previous strategies, which was difficult to achieve with the previous strategies.
2. Related Work
- (1)
- The energy consumption in wireless sensor network data collection has unbalanced characteristics. The most important function of a wireless sensor network is to monitor and perceive certain physical phenomena of interest, or events, so that the data of interest can be obtained in time [44,58]. Since sensor nodes can be deployed on a large scale, continuous and large-volumes of data can be obtained continuously for a long time. With the development of artificial intelligence technology, combined with big data network, Edge network, Cloud computing technology, the basic roles of WSNs have become more prominent [59,60,61]. An important feature of wireless sensor network data collection is the many-to-one data collection feature [48]. In WSNS, n sensor nodes and 1 sink are deployed. The sink is the center of the entire network, and all sensor nodes transmit the perceived data to the sink through multi-hop routing [48]. Therefore, in this data collection mode, the data sensed by the nodes in the network must be relayed to the sink through the node within the range of the near 1 hop. Thus, the energy consumption of the nodes in the near-sink hop range is much higher than that in the far-sink area. When the energy consumption of the nodes in the near-sink area is exhausted (called an energy hole), causing the network to die prematurely, no more sensing data cannot be routed to the sink, although there may still be a large number of surviving nodes in the network. According to the work in [14,15,43], when an energy hole occurs, up to 90% of the energy main still remain in the network.
- (2)
- Code dissemination in non-duty cycle-based WSNs. In non-duty cycle-based WSNs, nodes are always active, although its energy consumption is high, but this is beneficial for code dissemination, because as long as the sender broadcasts, the nodes in its broadcast range can receive the code, so its dissemination speed and complexity are much smaller than in duty cycle-based WSNs. However, at this time, it is necessary to optimize which nodes are selected for broadcasting [62]. If each node that receives the code broadcasts, it will form a broadcast storm, which will consume a lot of energy in the network. Therefore, it is often necessary to construct a Minimum Covering Node Set (MCNS) for the network [59,60]. The nodes in MCNS have the following characteristics: (a) Any two nodes in this set are connected; (b) and all nodes except the nodes in the set can be connected to the nodes in the set by one hop; (c) a minimum number of nodes. Since the MCNS has the above features, it is only necessary to send the code to the node in the MCNS to enable each node in the network to receive the code when the number of broadcasts is small. After the above discussion, the problem of code dissemination has turned into construction of the MCNS. For related research, see the Set-Cover-based Approximation (SCA) scheme in [63].
- (3)
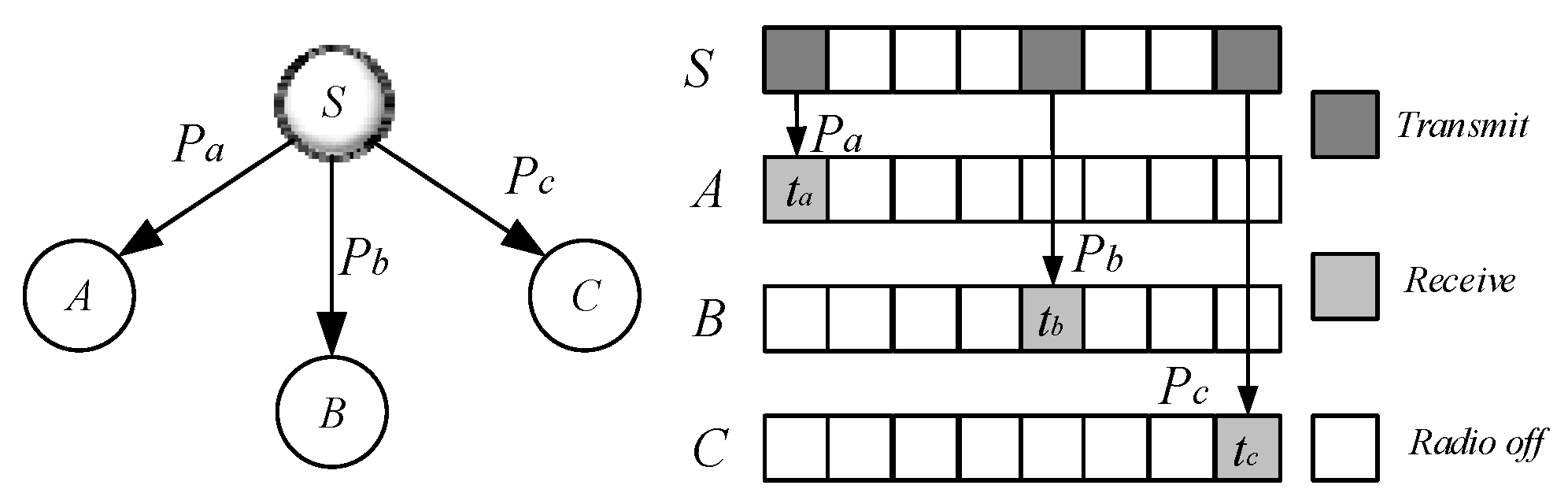
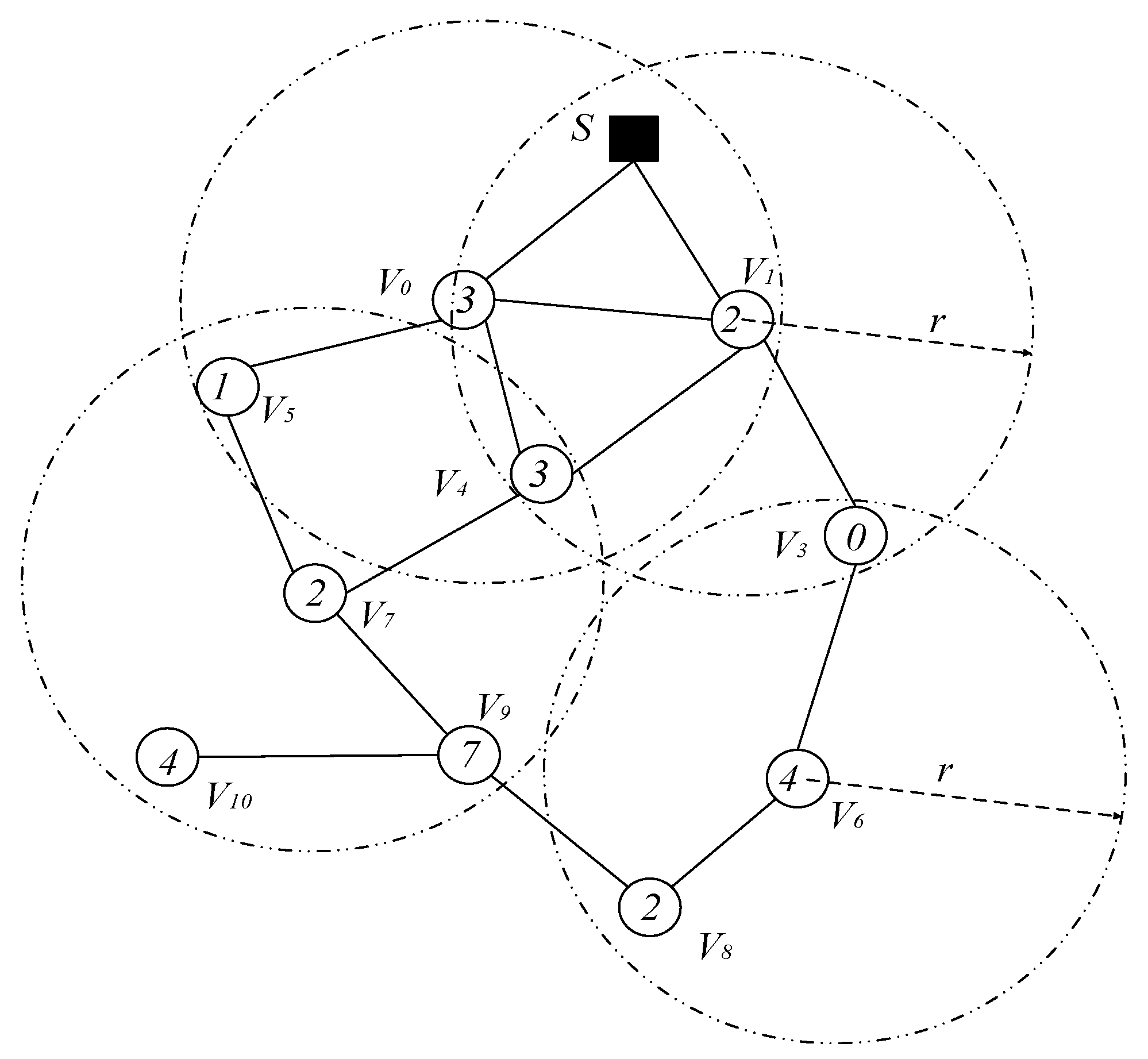
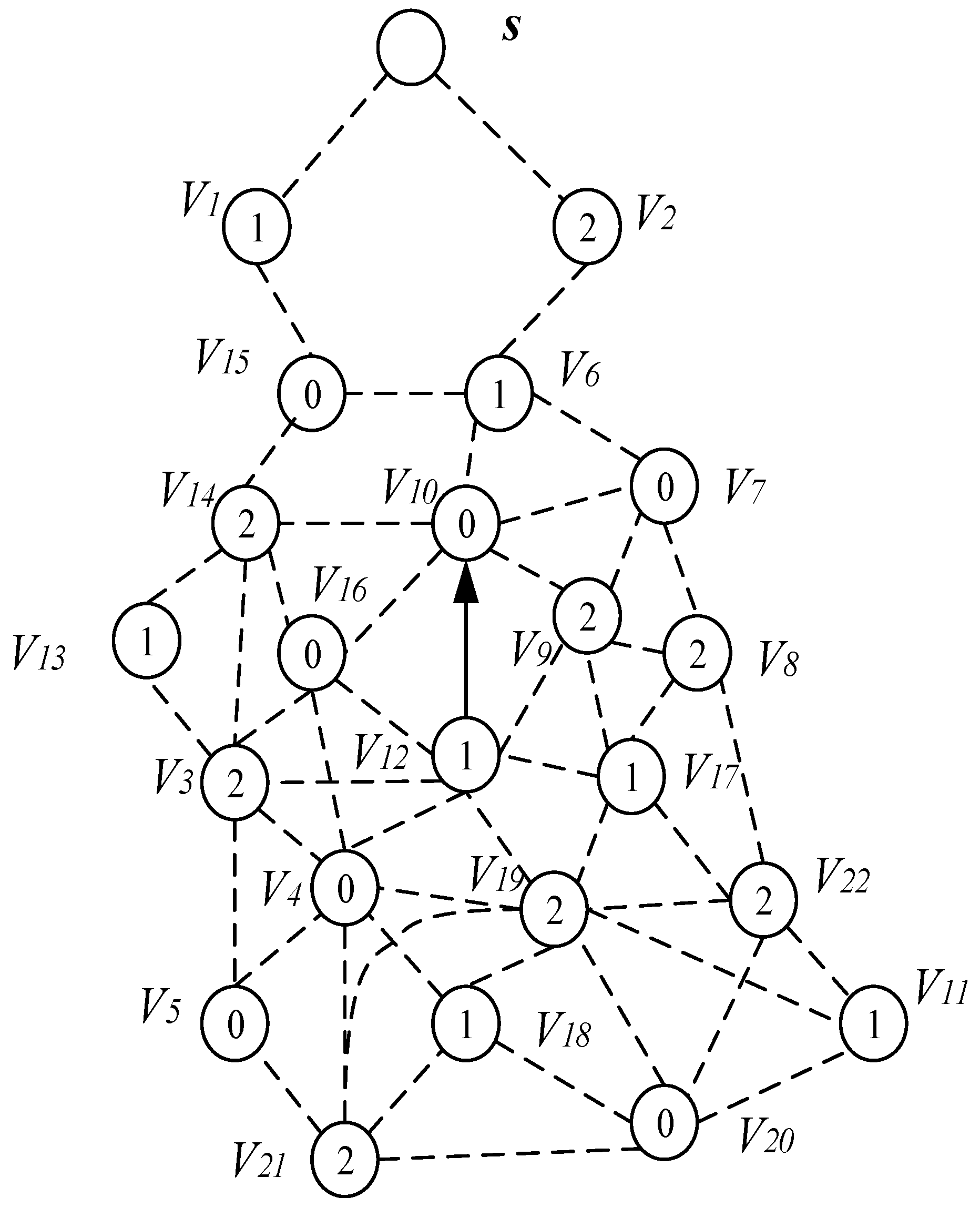
- Code dissemination in duty cycle-based WSNs. Code in duty cycle-based WSNs are very different from that in previous studies. In the duty cycle-based WSNs, the node is active in only one slot among slots of one cycle, and the other slots are in sleep state. When the sender sends the code in its active slot, not all nodes in its sending range active in this slot, so some nodes may be in sleep state and cannot receive the code. The sender needs to send multiple times in other slots to send the code to all nodes within its radius. As shown in Figure 1, the serial numbers of the active slots selected by node , , and are , , slot [53], node wants to pass the code to these three nodes, which need to be sent three times in slots , , respectively, instead of just broadcasting once like in a non-duty cycle-based WSN. Therefore, the method of code dissemination in such a network is very different from the previous ones. Researchers call such problems the minimum-transmission broadcast (MTB) problem in duty-cycled networks (MTB-DC problem) [53,63]. Obviously, the MCNS method similar to non-duty cycle-based WSNs can also be used to solve such problems. The main steps are as follows: (a) select a part of the node that can cover the entire network, which is called the Dominating Set (DS). (b) Constructing a routing path from the code source node to each node in the Dominating Set, called the broadcast backbone. The broadcast backbone may contain nodes in the non-Dominating Set. After the broadcast backbone is constructed, the code is routed through the nodes on the broadcast backbone. After the nodes on the broadcast backbone receive the codes, the nodes in the Dominating Set broadcast the code to their governed nodes. Since the nodes in the Dominating Set cover all the nodes in the network, this method enables each node in the network to obtain codes. However, the MTB-DC problem is very different from the MTB-non-DC problem. First, in the broadcast backbone route, since the node adopts the duty cycle mode, it must wait for the active slot of its next node to arrive when routing, thus increasing the delay. Secondly, in the non-duty cycle based WSNs, when all the nodes in the broadcast backbone obtain the codes, all the nodes in the network obtain the code. However, in the duty cycle based WSNs, when the nodes in broadcast back-bone obtains the code, some dominated nodes may have not got the code, so the dominator may need to be broadcast several times to complete code dissemination. The above study can be found in [63].
- (4)
- Code spread in loss and low duty cycle based WSNs. The previous discussion is based on the assumption that wireless communication is reliable. In other words, the sender only needs to send once, then the receiver can successfully receive the code. However, in actual WSNs, due to the attenuation of the wireless channel and the complexity of the transmission environment, the receiver receives the code successfully with a certain probability such as . Chen et al. [53] proposed a strategy for code dissemination in unreliable WSNs. As shown in Figure 1, node is ready to spread code to node , , and its transmission success rates are , , respectively. Therefore, node send code in , , slot, and node , , respectively receive data in these three active slots [53].
3. System Model
3.1. System Network Model
3.2. The Energy Consumption Model
3.3. Problem Statement
- (1)
- Minimize code dissemination delay. Obviously the first goal of this paper: Minimize code dissemination delay can be expressed by the following Equation (3):where indicates the time at which node obtains code, so max indicates the time at which the code node was last obtained. indicates the time at which the sink initiates code dissemination, and indicates the maximum delay of code dissemination. Therefore, the goal of optimization is to minimize the delay of the last code node in the network.
- (2)
- Minimum−transmission broadcast (MTB). The second optimization target of the strategy design is MTB, which makes the minimum number of broadcasts required from code sink to transmission to all nodes in the network. is the set of transmission slots of node , and represents the number of broadcasts of node . Then the minimum-transmission broadcast is as shown in Equation (4) below:
- (3)
- Maximize network life. The lifetime of the entire network can be defined as the time until the first node dies. Since the death of the first node may affect the connectivity of the network, the function of the entire network is impaired and the requirements for normal operations cannot be reached. Therefore, the network life cycle in this paper is the time when the first node dies. represents the initial energy of the node, and represents the average energy consumption of the node in a period . The maximum lifetime of the network is to maximize the lifetime of the node with the smallest lifetime in the network:
- (4)
- Maximize energy utilization. indicates the ratio of the energy consumed by the entire network to the initial energy of the entire network. indicates the energy consumption of node when the network dies. Then the energy utilization can be maximized as shown in Equation (6):
4. The Design of AAS-LBR Scheme
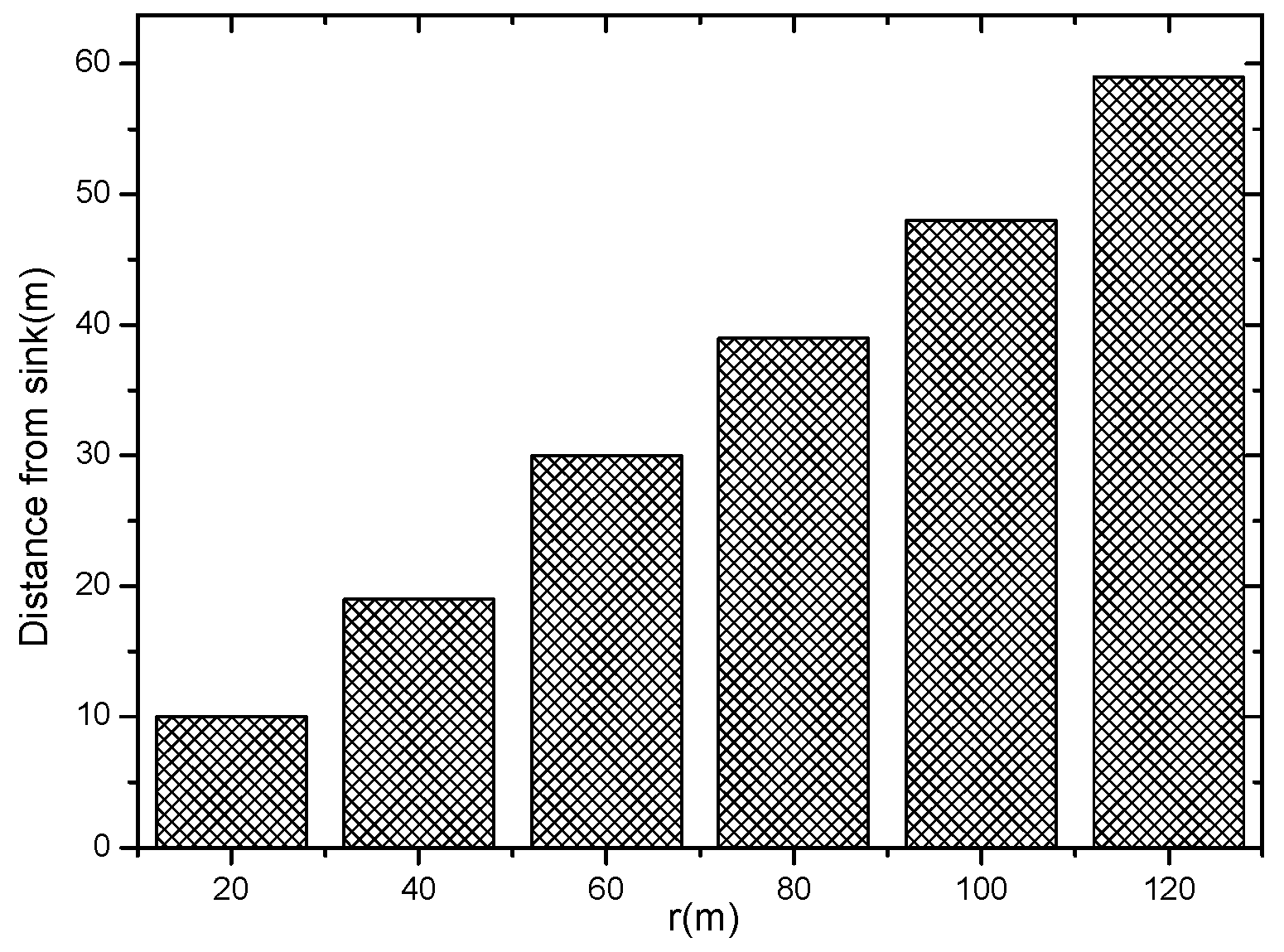
4.1. The Research Motivation
4.2. The AAS-LBR Scheme
- (1)
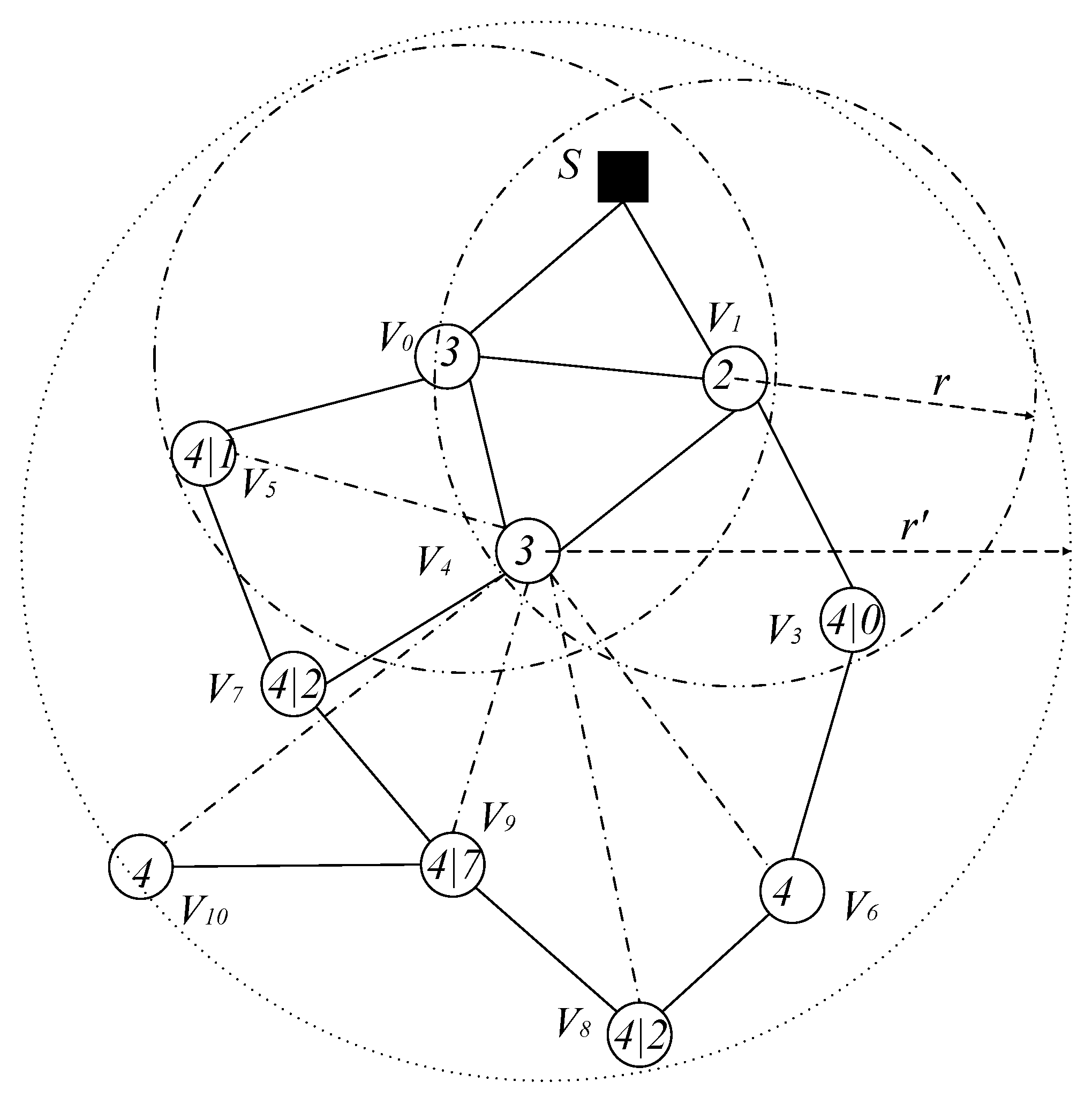
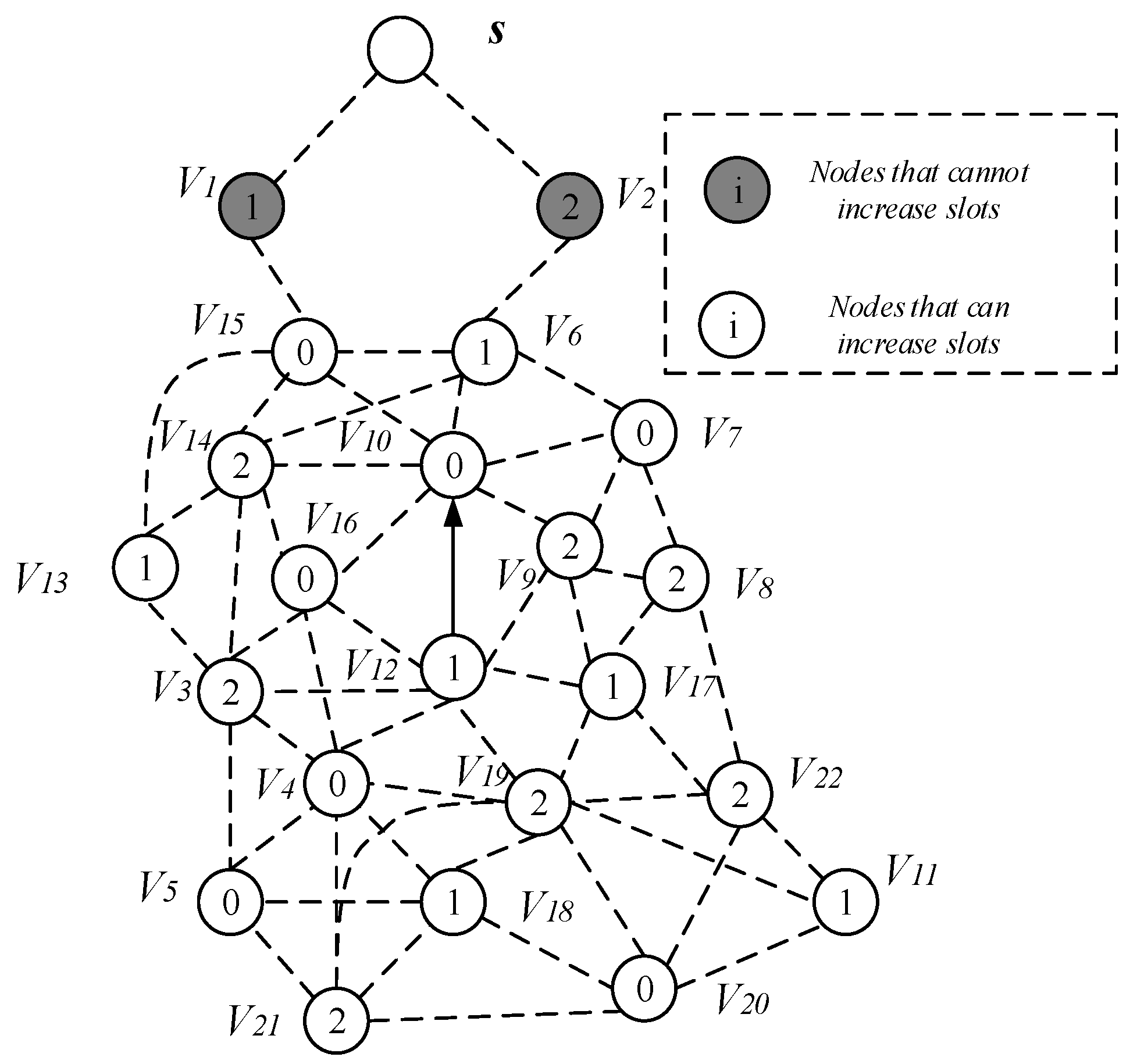
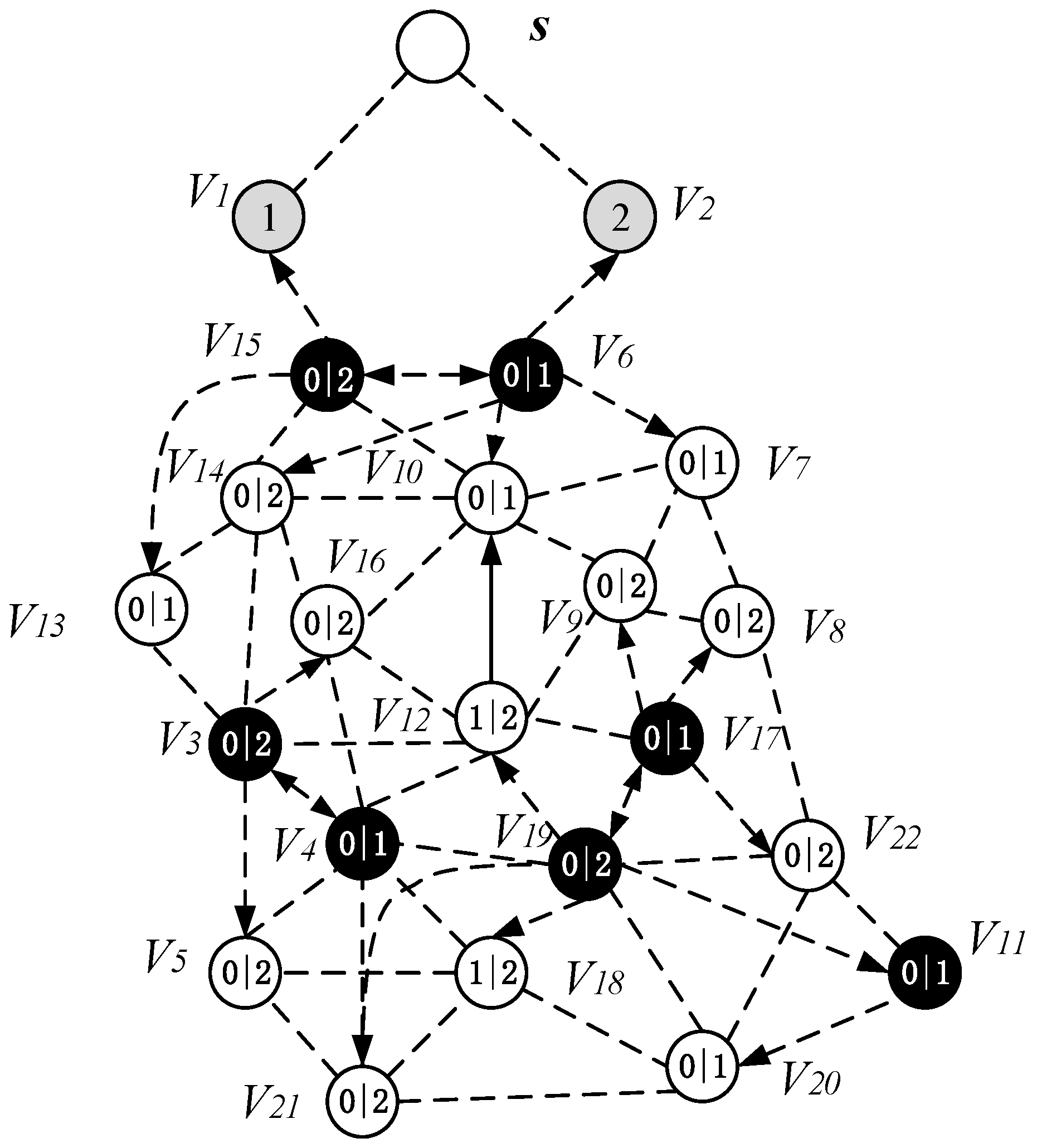
- Calculate the nodes that can increase the active slot according to the energy consumption of the nodes, then these nodes can add one active slot (although some nodes do not necessarily need to increase the active slot). If there is still remaining energy, then calculate the remaining energy that can increase the broadcast radius of the node.
- (2)
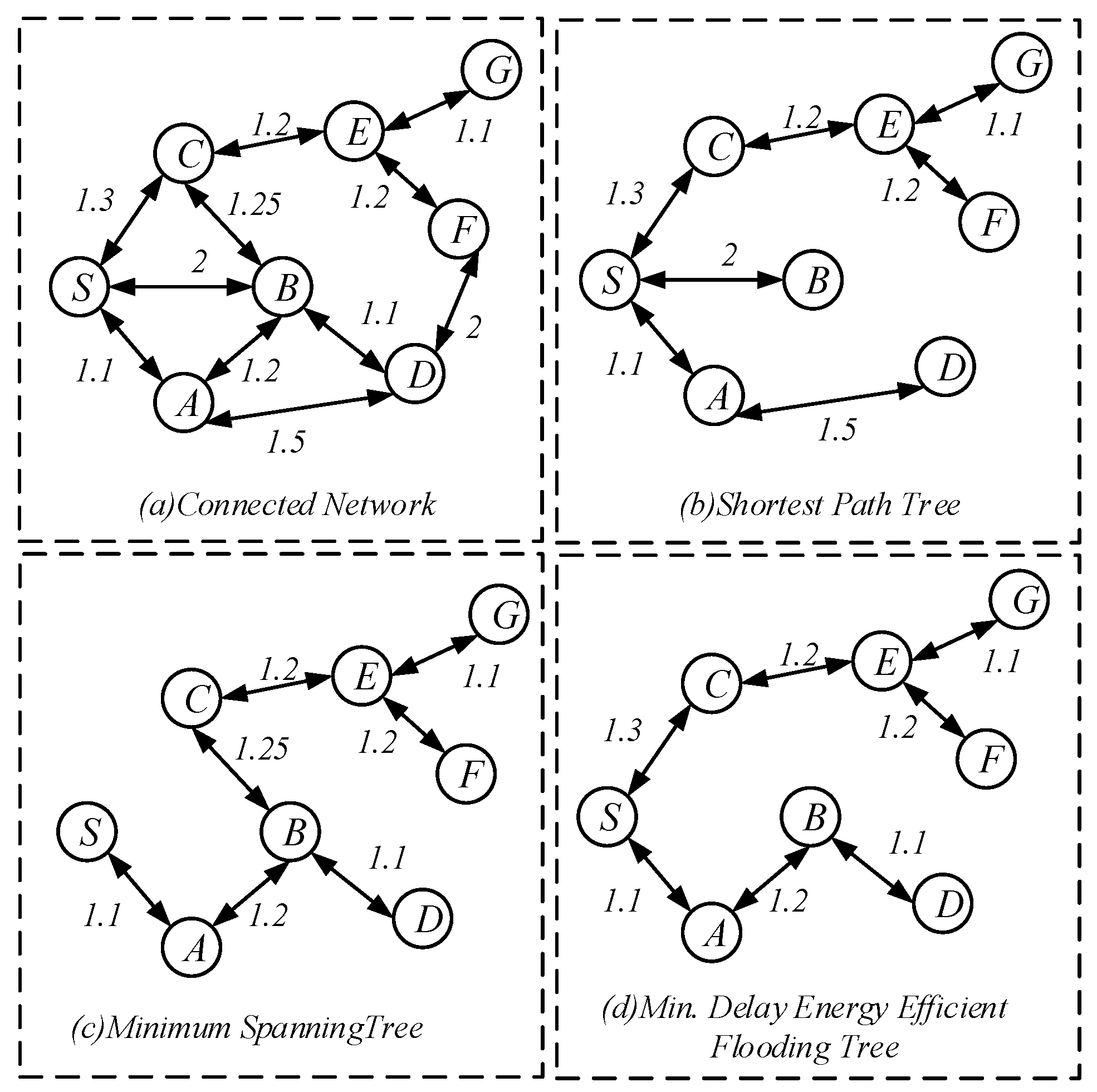
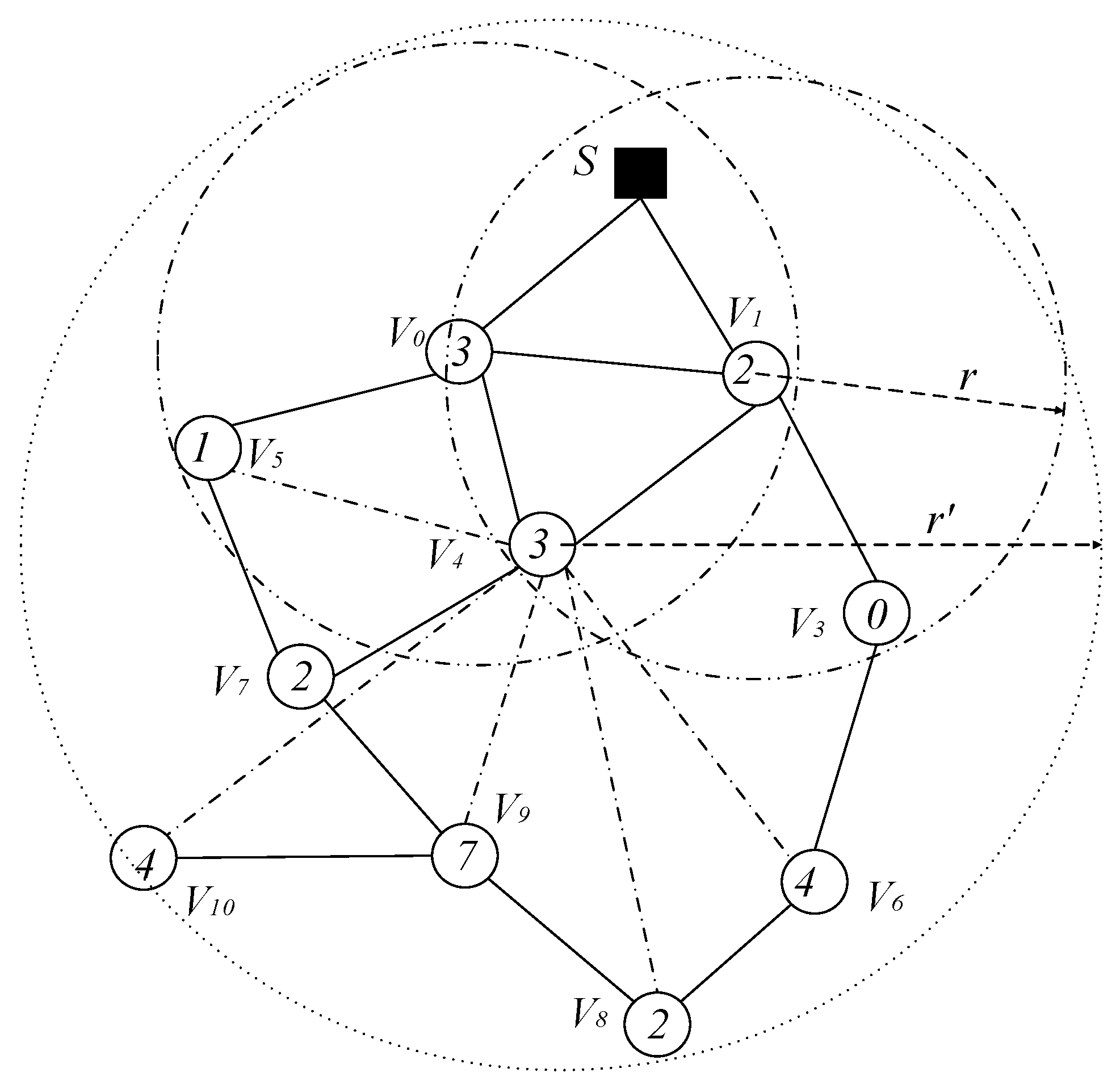
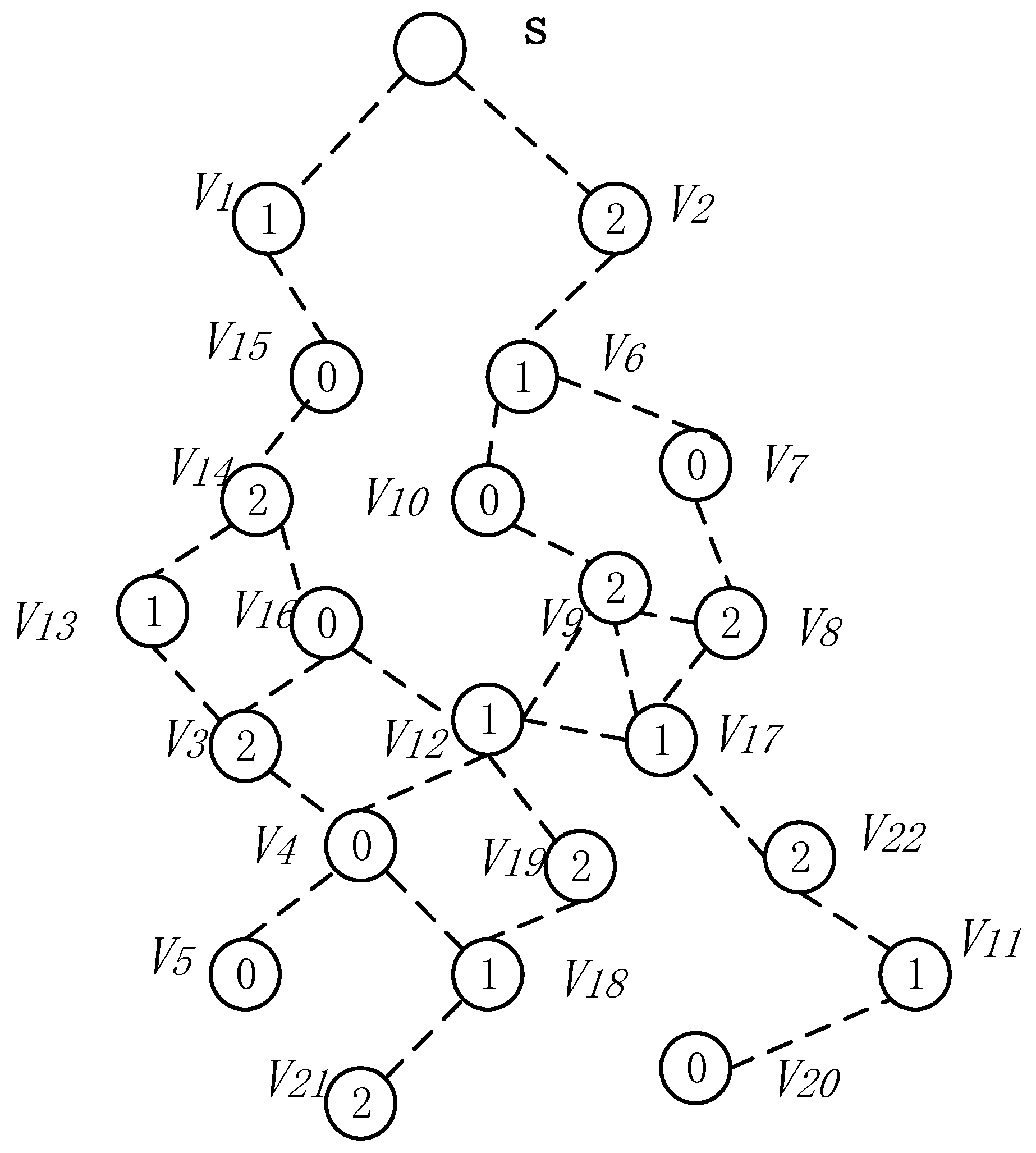
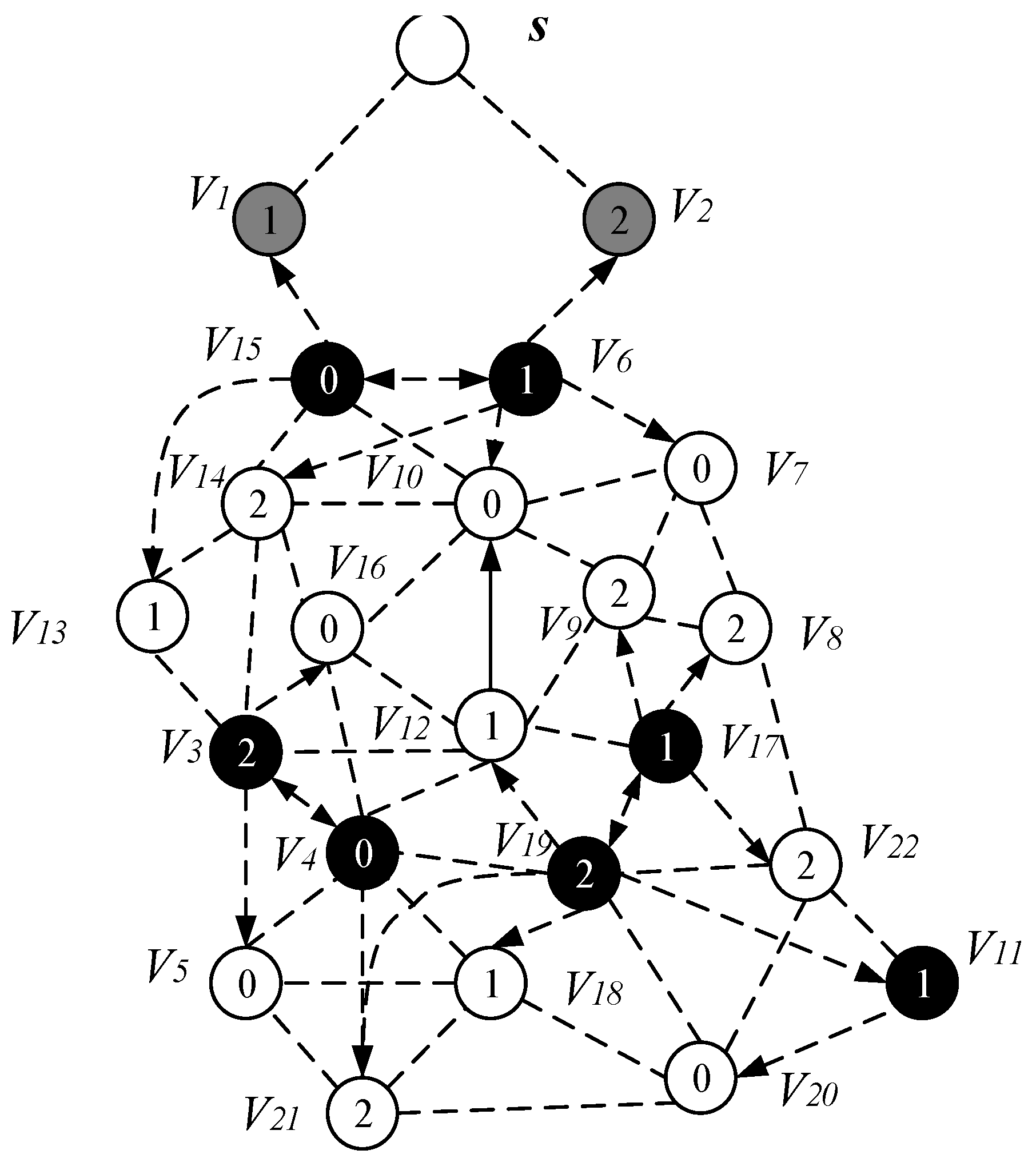
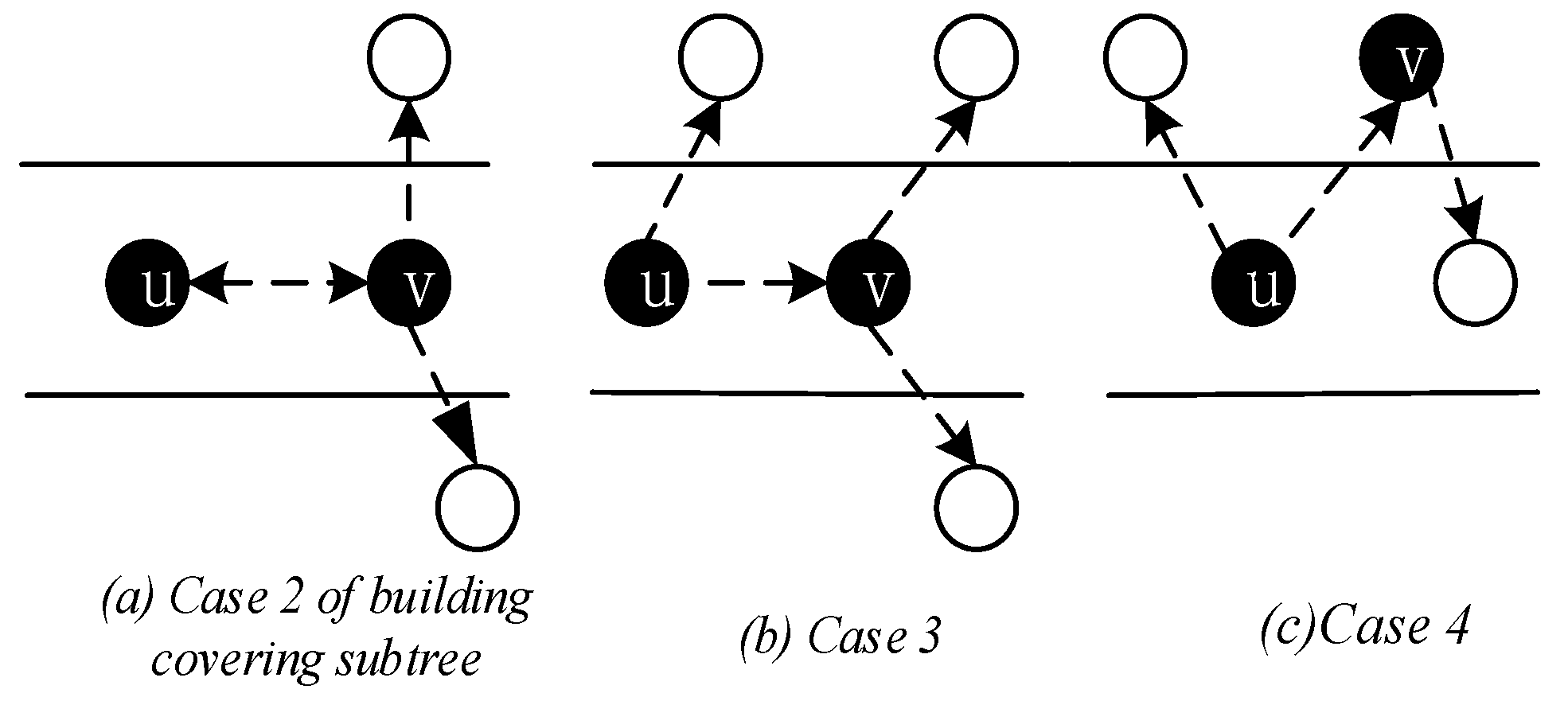
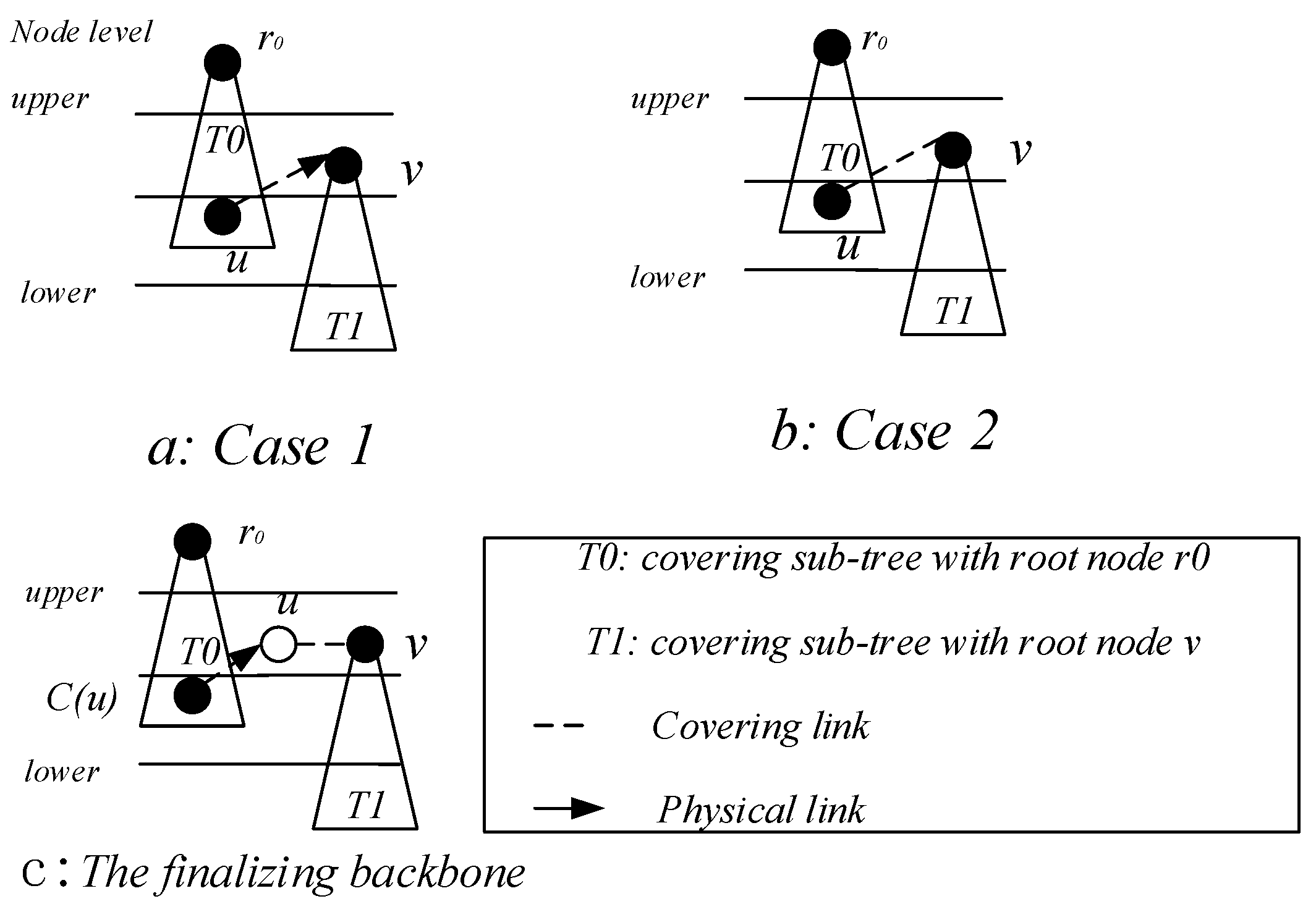
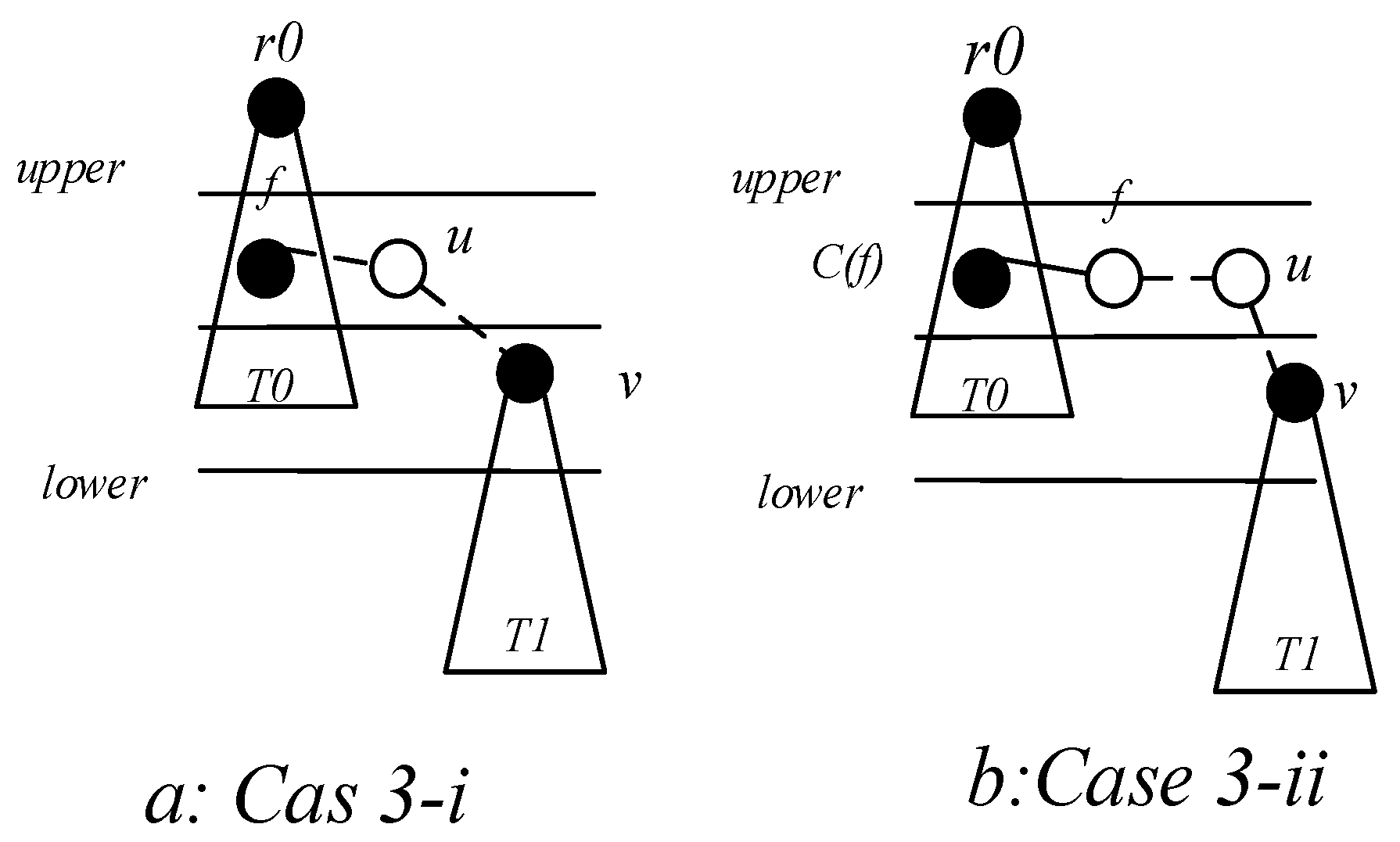
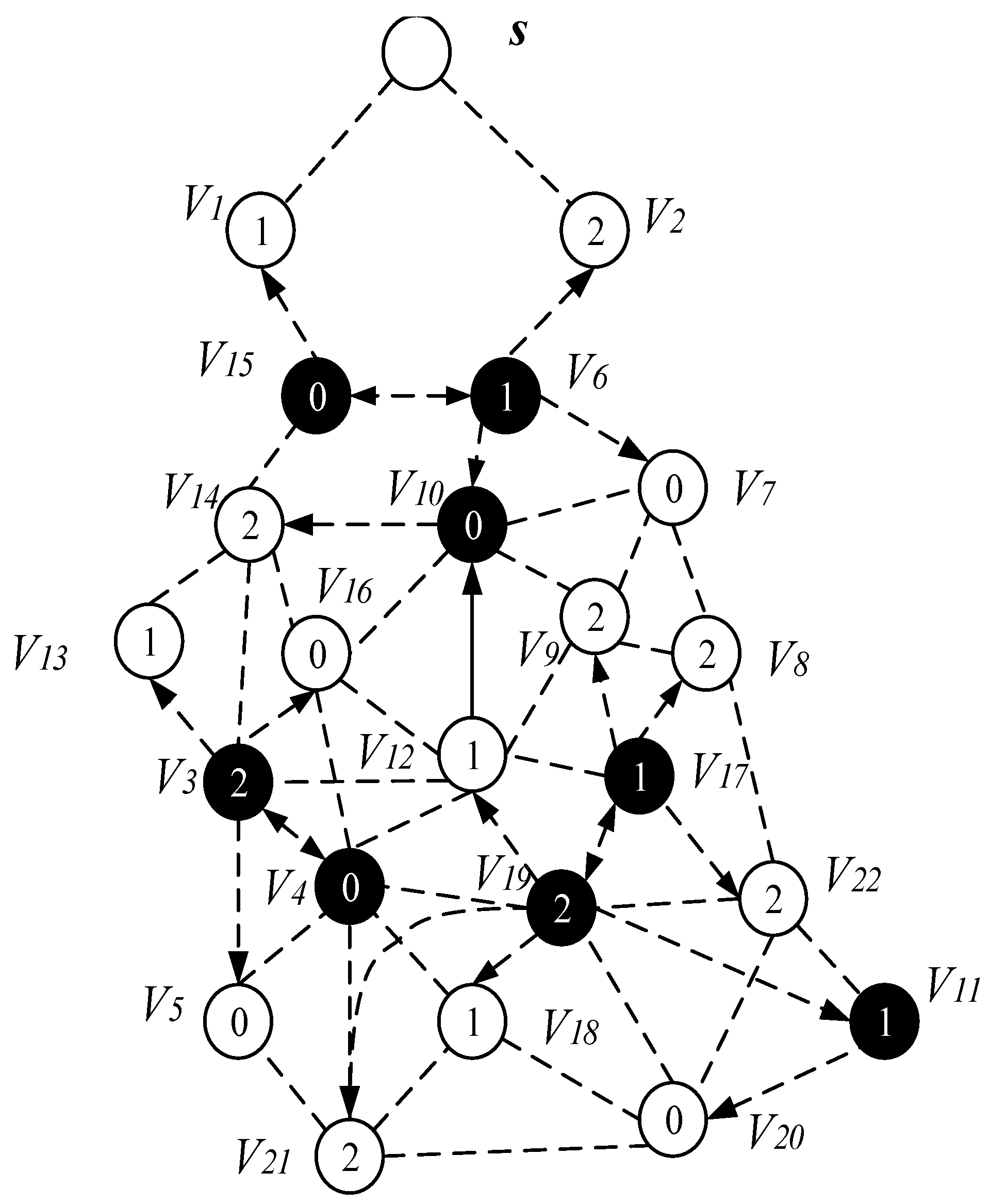
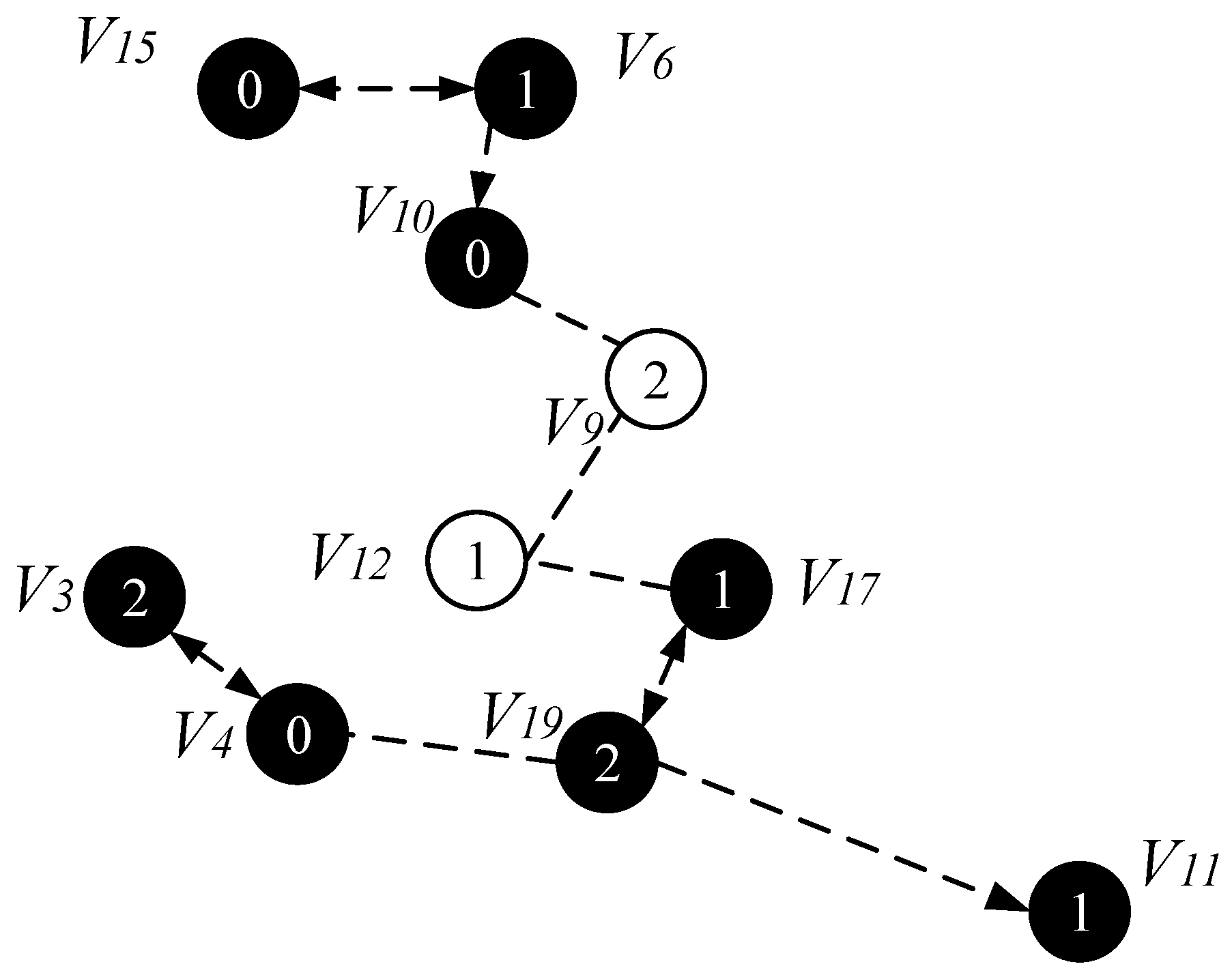
- Select a Minimum Covering Node set (MCNS) based on the network topology with the added broadcast radius but without increasing the active slots. MCNS can cover every node in the network, so it only needs to spread the code to each node of the MCNS, and then the node on the MCNS is responsible for code dissemination of its governed node, so that the code can be efficiently spread to the entire network. After selecting MCNS, it is necessary to route the code from the sink to each node in the MCNS, which is to construct the broadcast backbone. However, in the AAS-LBR scheme, constructing the broadcast backbone has greatly improved the previous strategy. In the AAS-LBR scheme, the node in the far-sink area can be incremented by one active, and the active slot can be added to any slot in the node. Therefore, when constructing the broadcast backbone, it is possible to construct a broadcast backbone with the smallest delay. That is to say, when constructing the broadcast backbone, each node can increase the added active slot to the next slot of the current node’s active slot when selecting the next hop node. In this way, after the current node receives the code, it can propagate forward in the next consecutive active slot, thus reducing the delay of constructing the broadcast backbone to a minimum.
- (3)
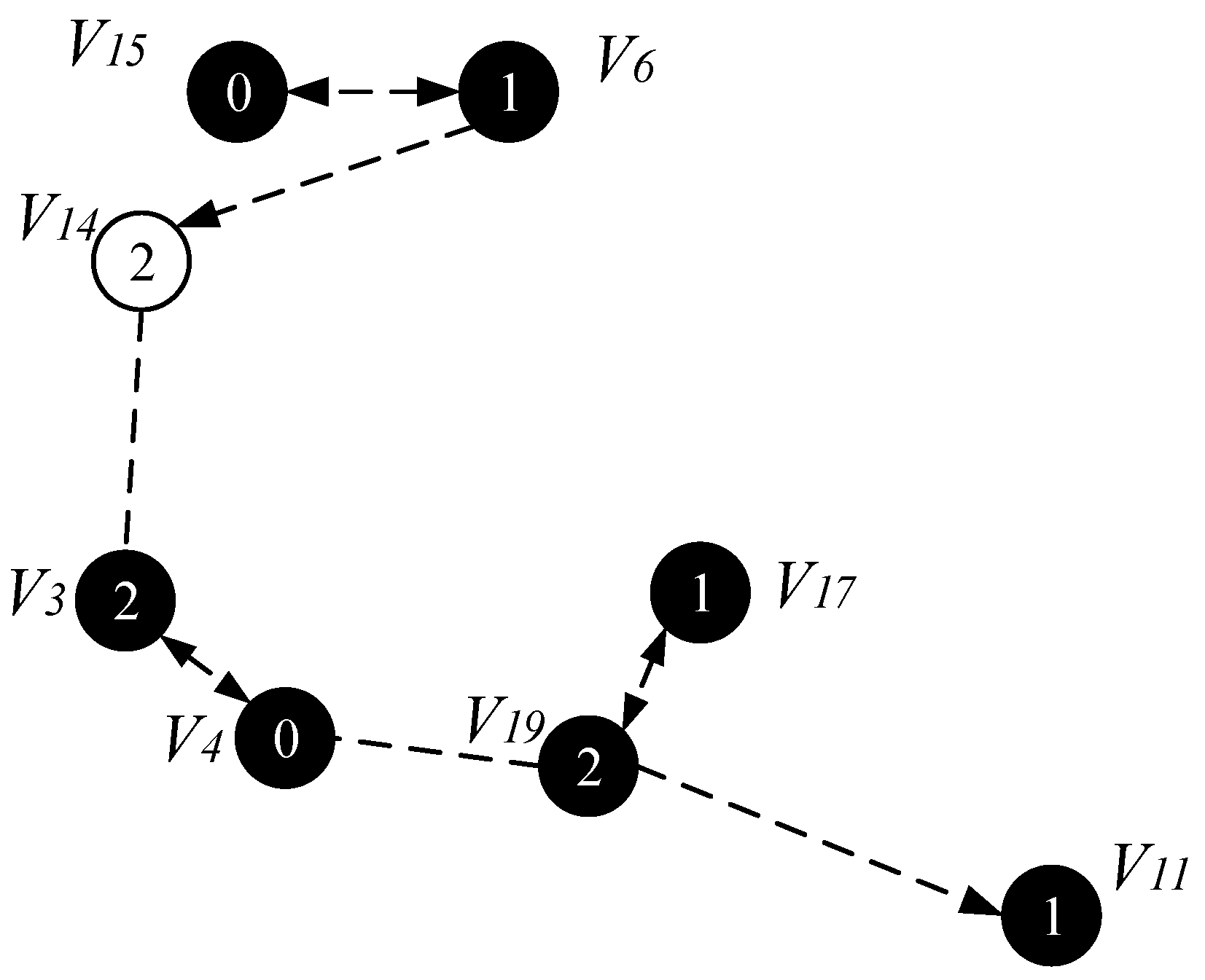
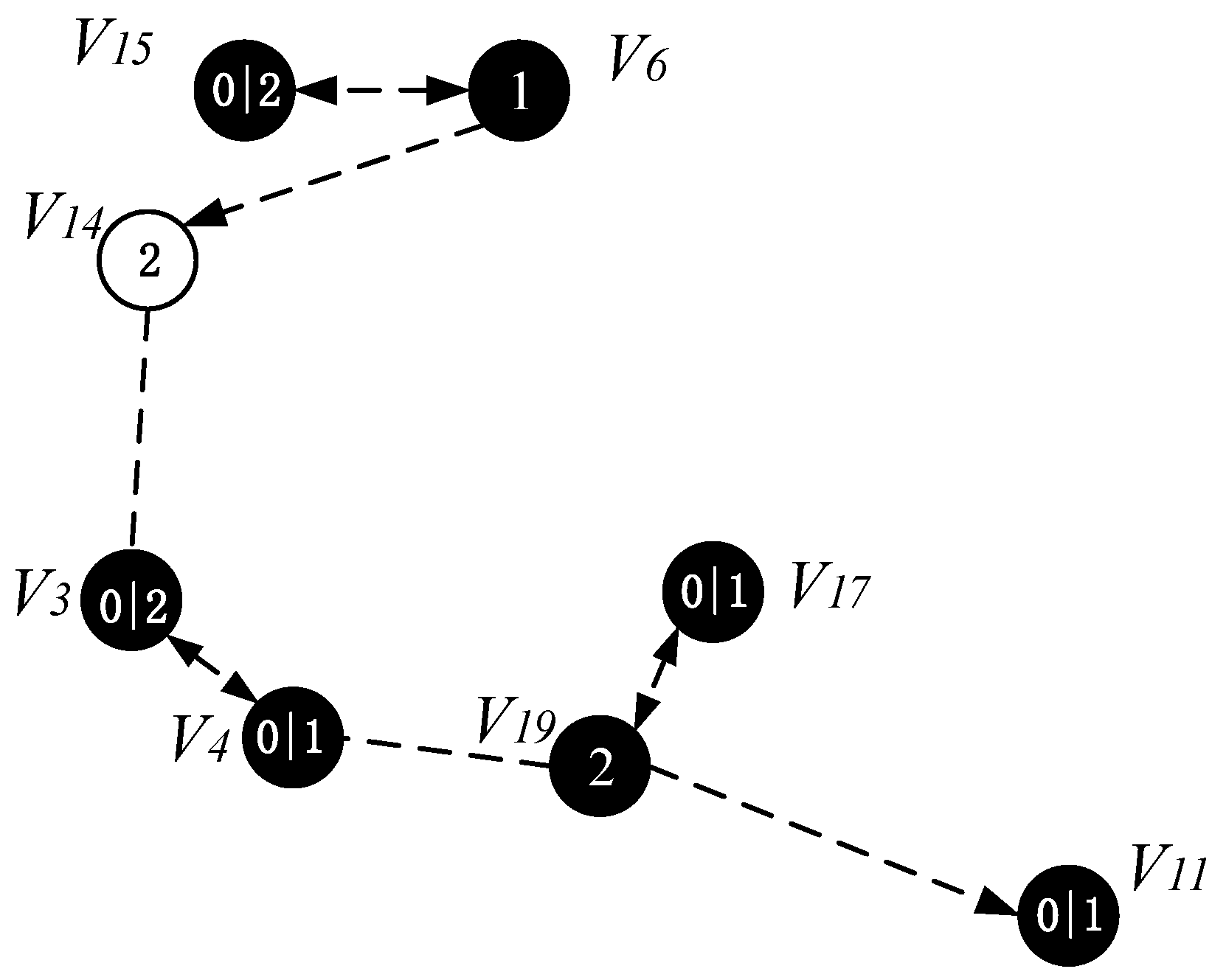
- Code dissemination stage. Since MCNS has covered the entire network, therefore, after the nodes on the broadcast backbone get the codes, the nodes in the MCNS only need to broadcast the code to the nodes covered by it. In the AAS -LBR scheme, different from the previous strategy, since the active of the node can be added, we will select the active slot of the node to be the same as one of the broadcast slots of the node in the MCNS. In this way, in MCNS, when the broadcast backbone is completed, the node that can increase the active slot has already obtained the code. Therefore, it is not necessary to perform code dissemination for the dominated node as in the previous strategy. This reduces the number of broadcasts and greatly reduces the delay.
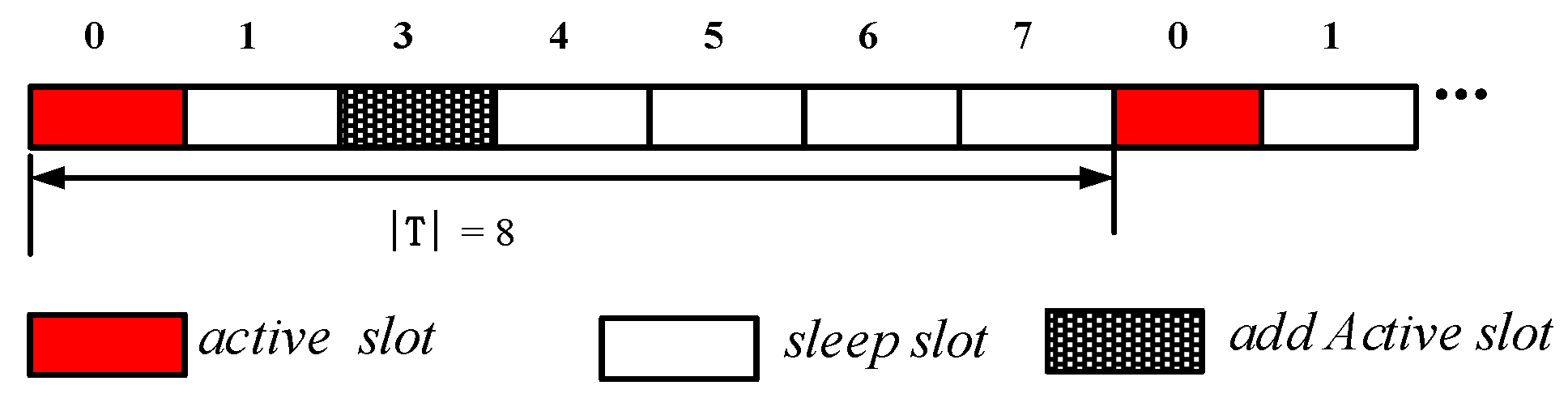
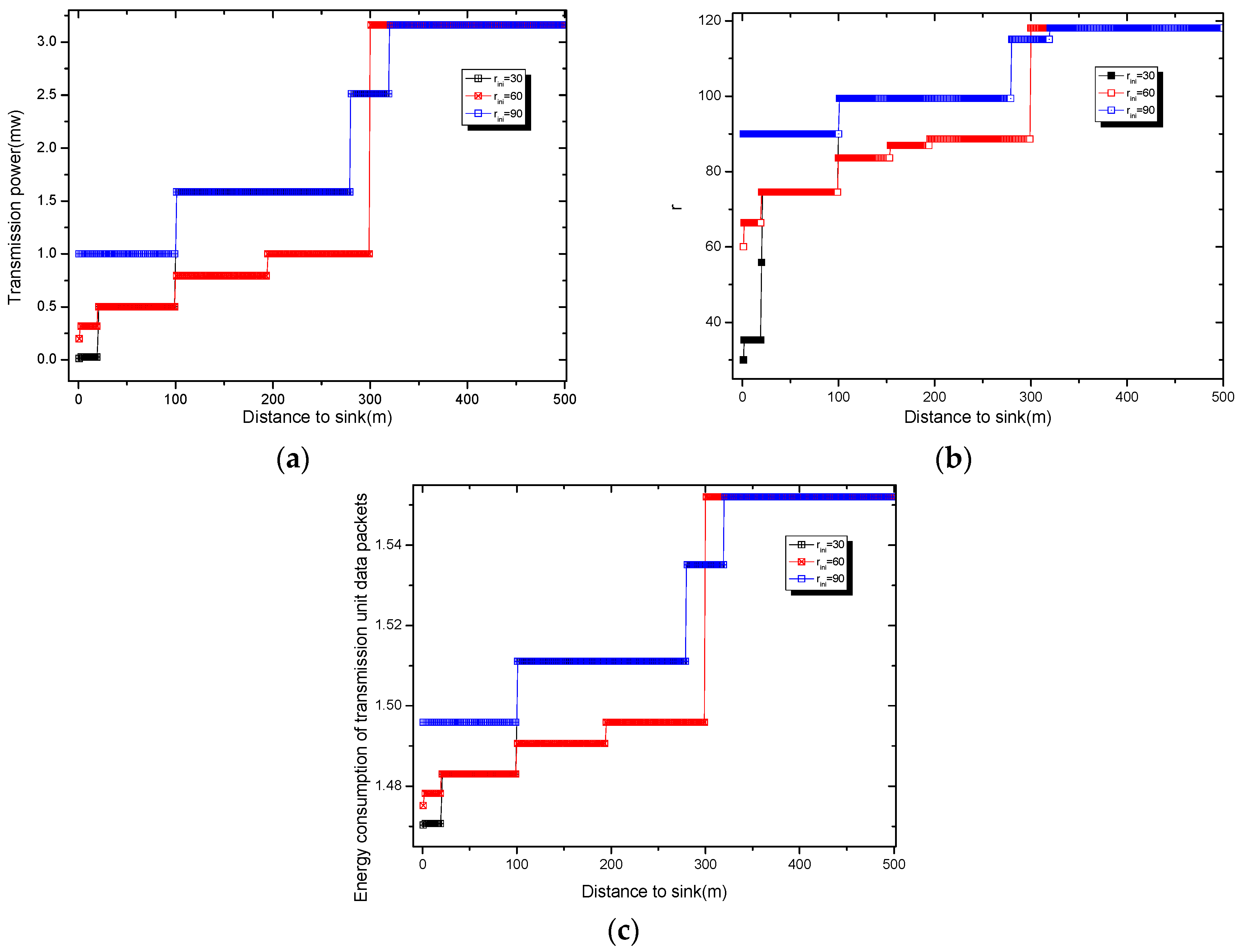
4.2.1. The Add Active Slot and Increased Broadcast Radius Calculation
| Algorithm 1. Calculate the Broadcast Radius at a Different Distance from the Sink |
| Input: The original broadcast radius , , the probability of generating data and energy parameters in Table 1 and Table 2 Output: The radius of the broadcast at distance |
| 1: Get the transmission power with ref. Table 2 2: ; 3: For each x from to 4: ; 5: Calculate and using Equation (9) with 6: Calculate using Equation (2) with ; 7: ; 8: While 9: ; 10: Get according to ref. Table 2 11: Calculating using Equation (2) with 12: If > 13: 14: ; 15: Else if == 16: The broadcast radius: 17: ; 18: Else if 19: = 20: End if 21: End while 22: Output: , 23: End For |
4.2.2. Construct Broadcast Backbone
4.2.3. Code Dissemination
| Algorithm 2. Adjust the Duty Cycle of the Node |
| Input: G = (V,E), A(v),v V, and P 1: While P Do 2: Find the node u that covering v 3: For the time slot of u 4: If the time slot of u, A(v) 5: Node v adds a time slot: A(v) = A(v) 6: Else 7: Node v adds a time slot: A(v) = A(v), 8: is the smallest time slot in u 9: End for 10: Remove node v from collection P: P = P\v 11: End while |
5. Theoretical Analysis
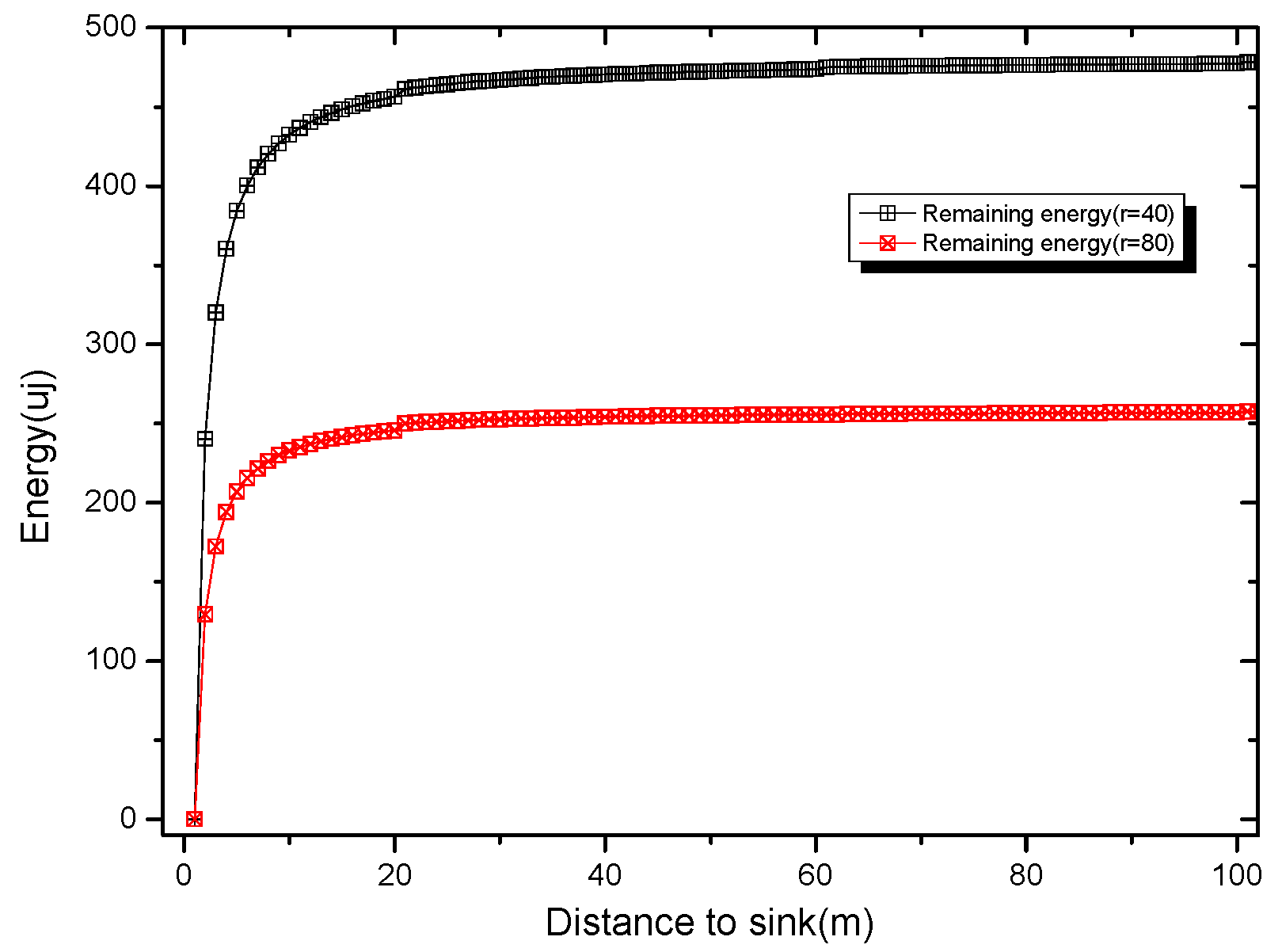
5.1. Analysis of Energy Consumption
5.2. Analysis of Energy Utilization Ratio and Network Lifetime
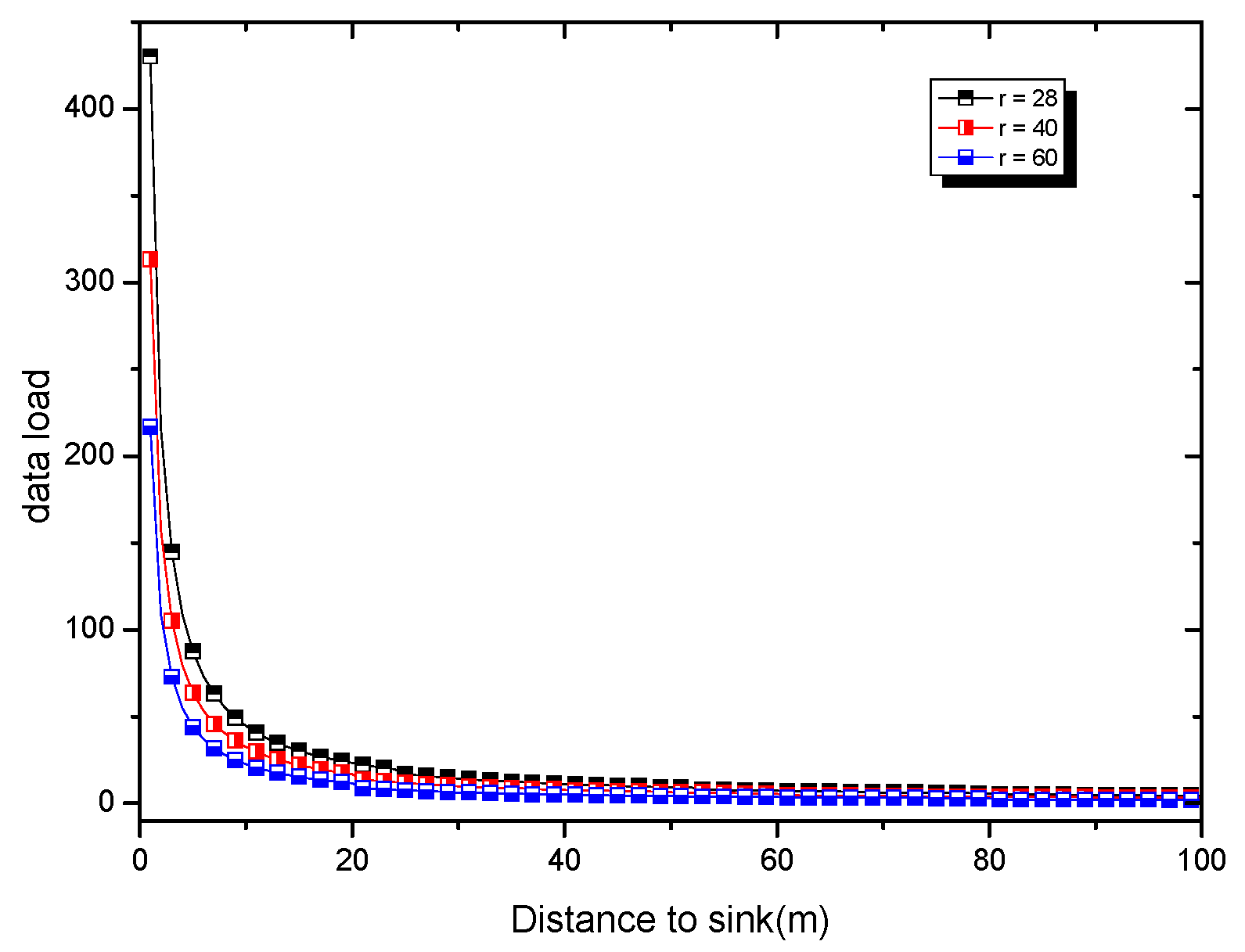
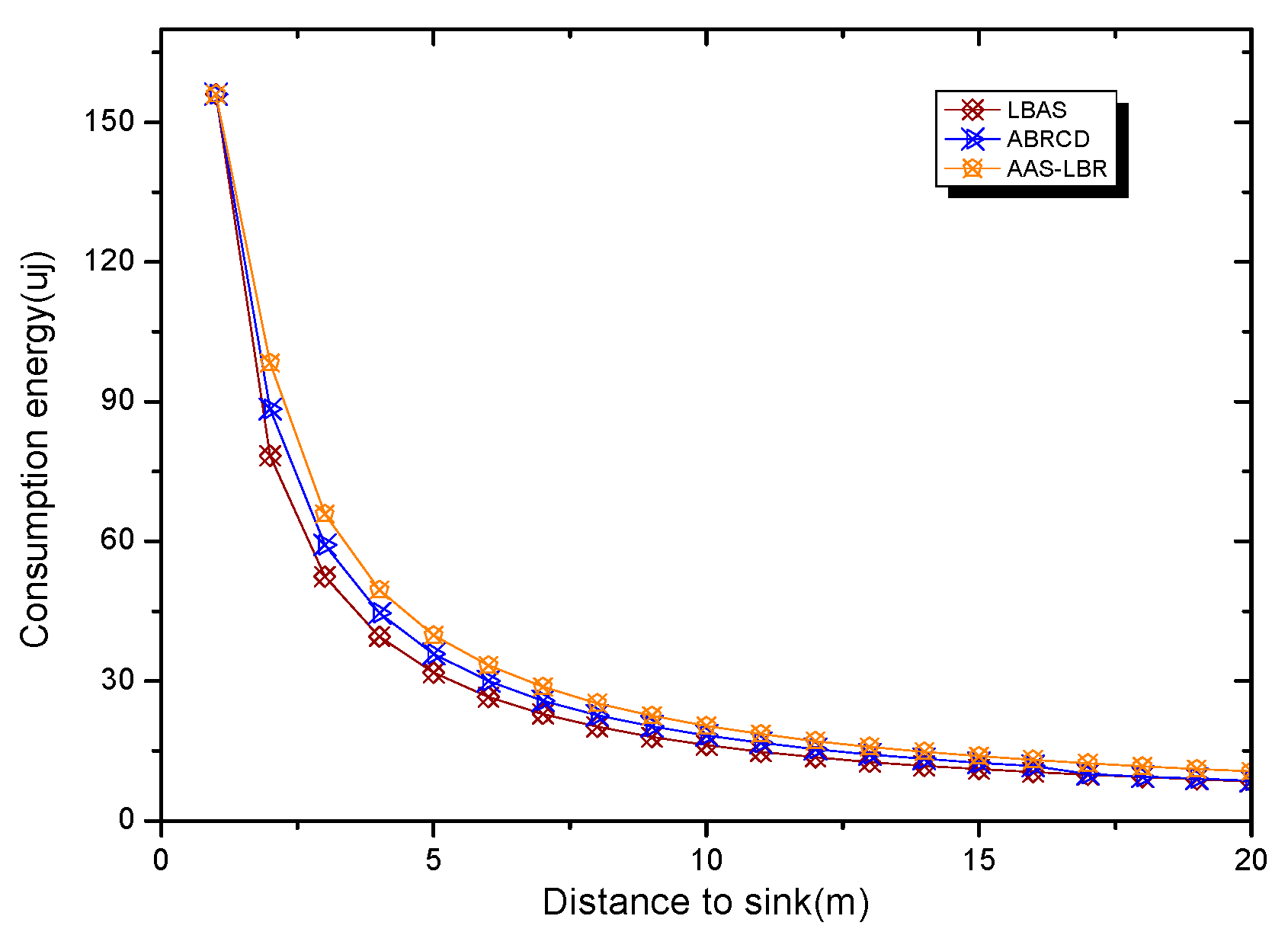
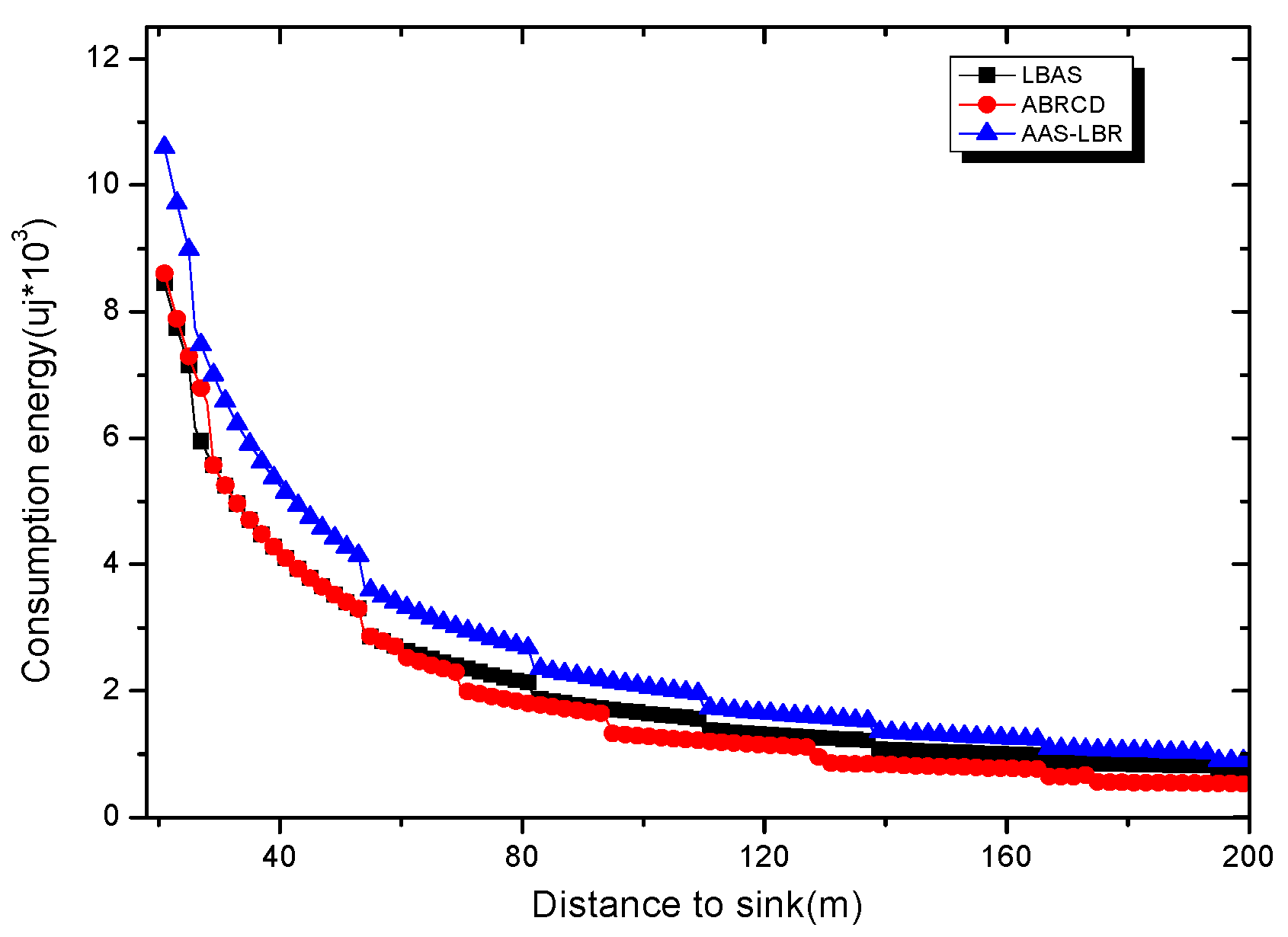
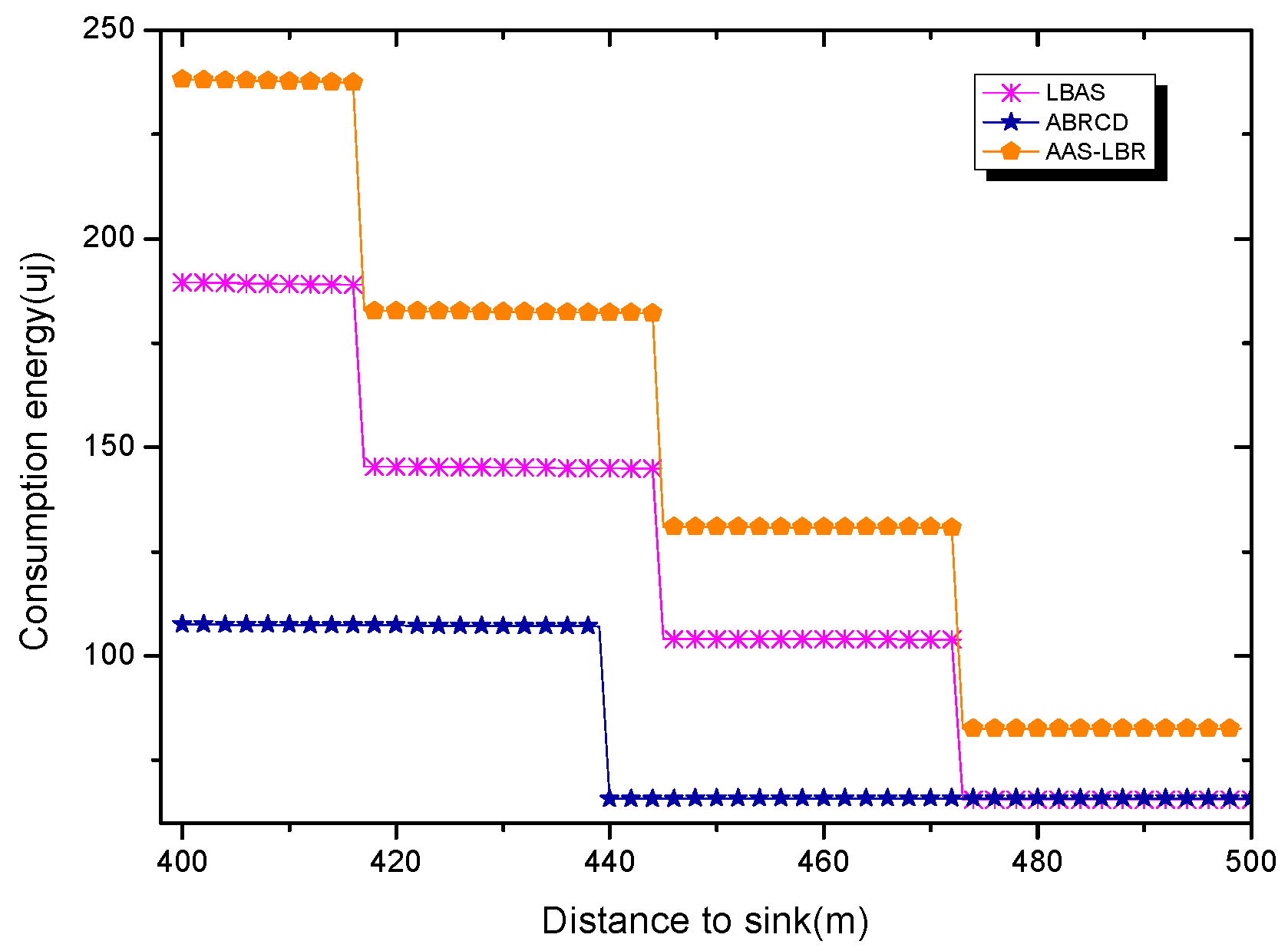
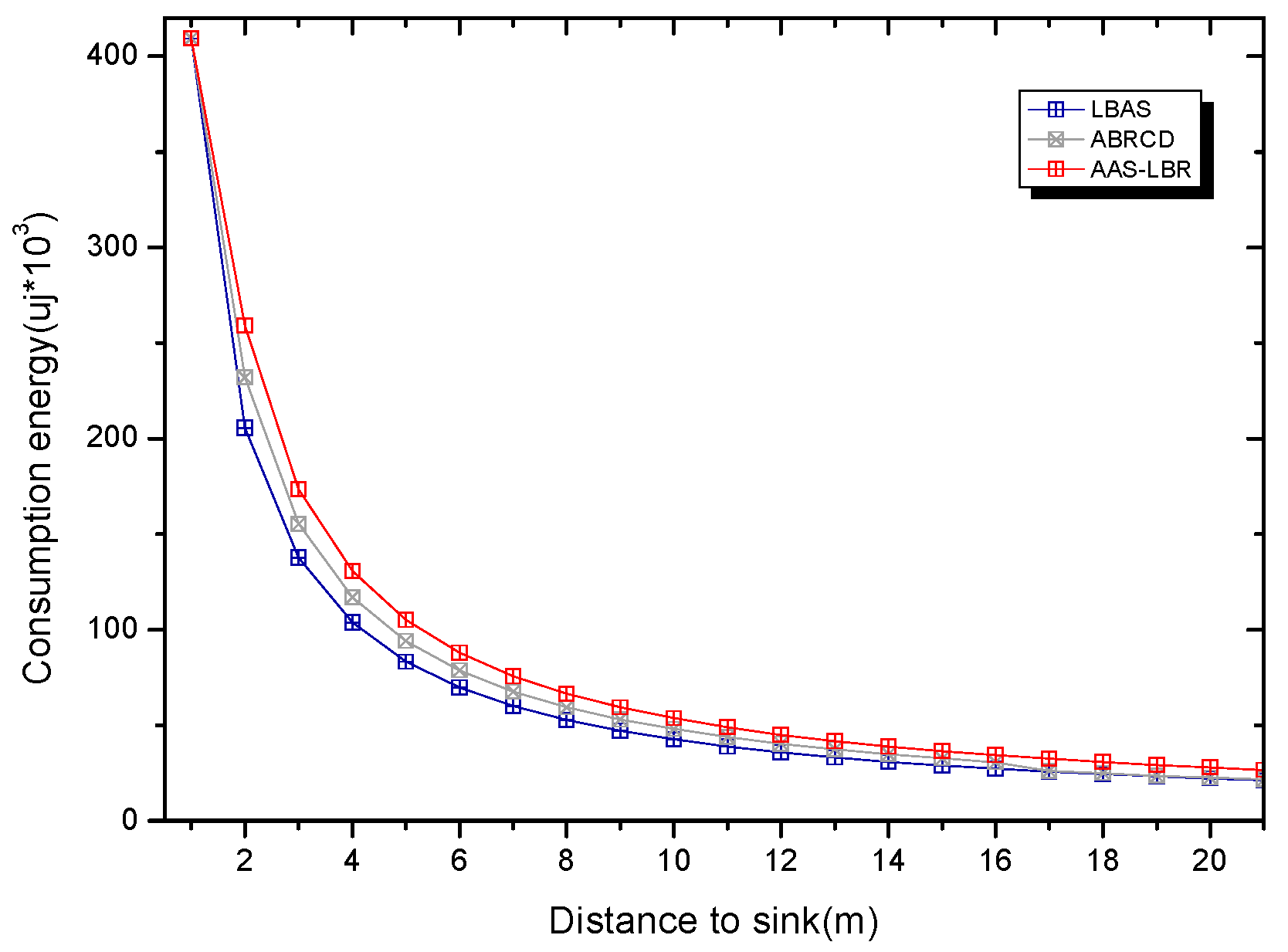
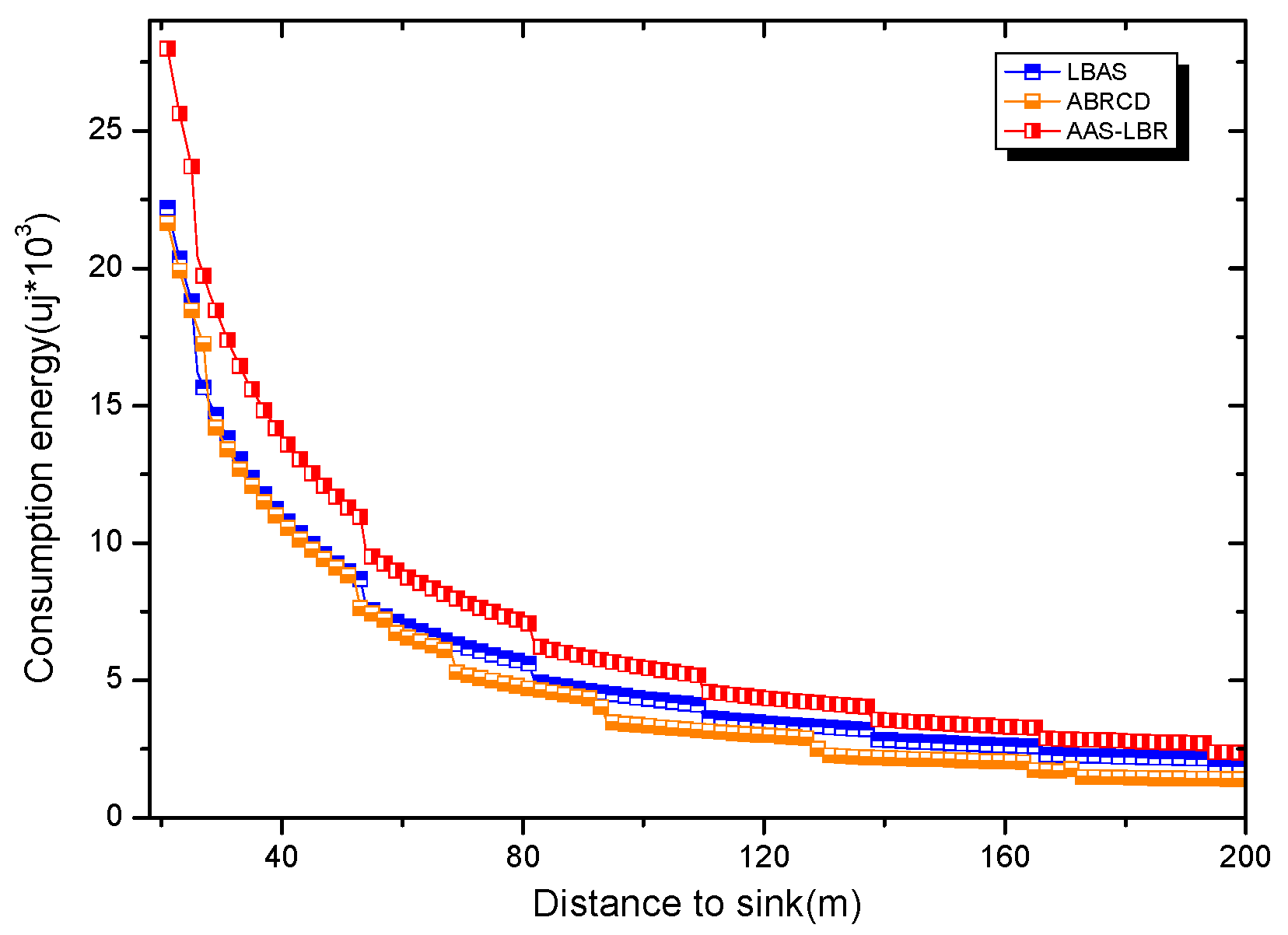
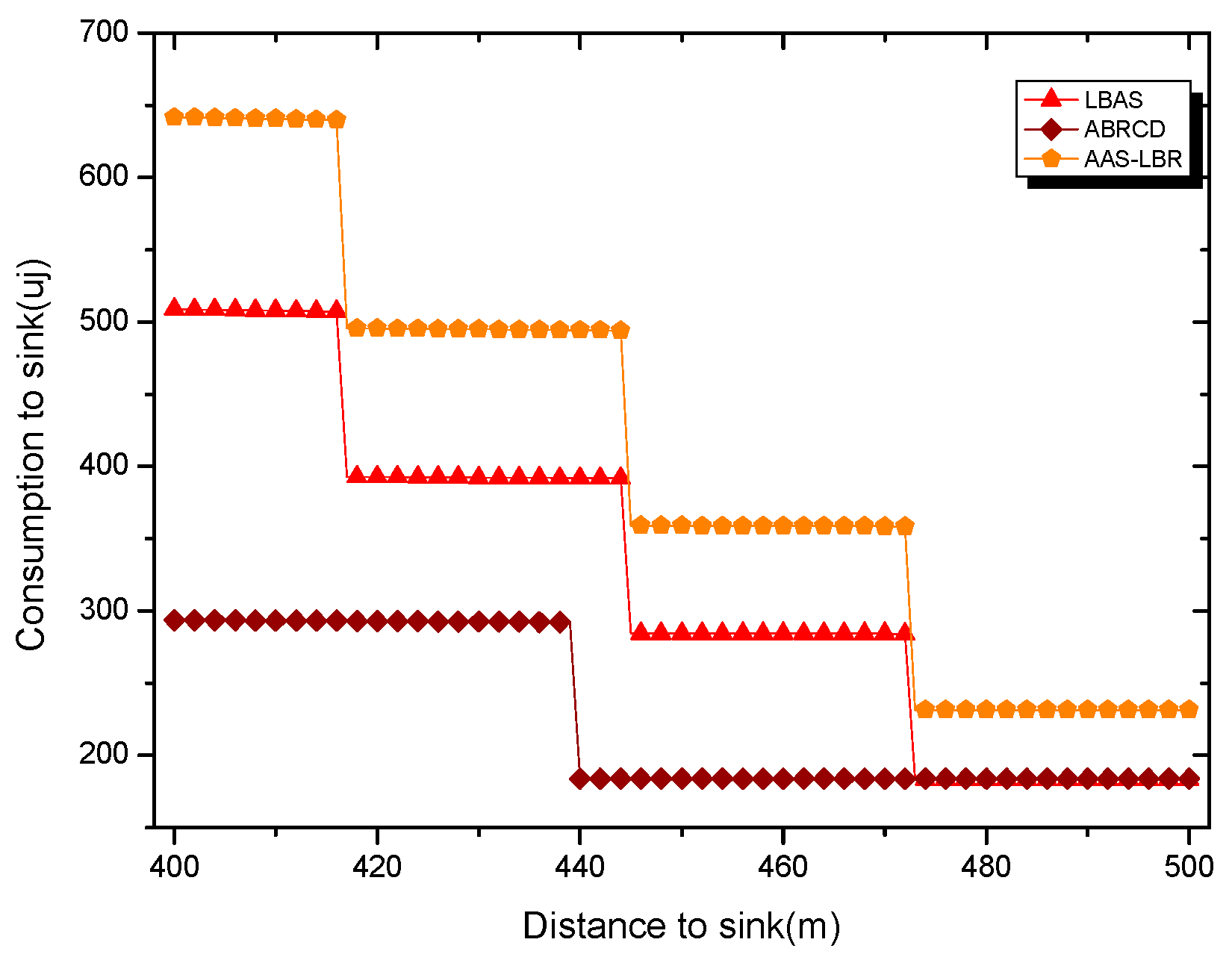
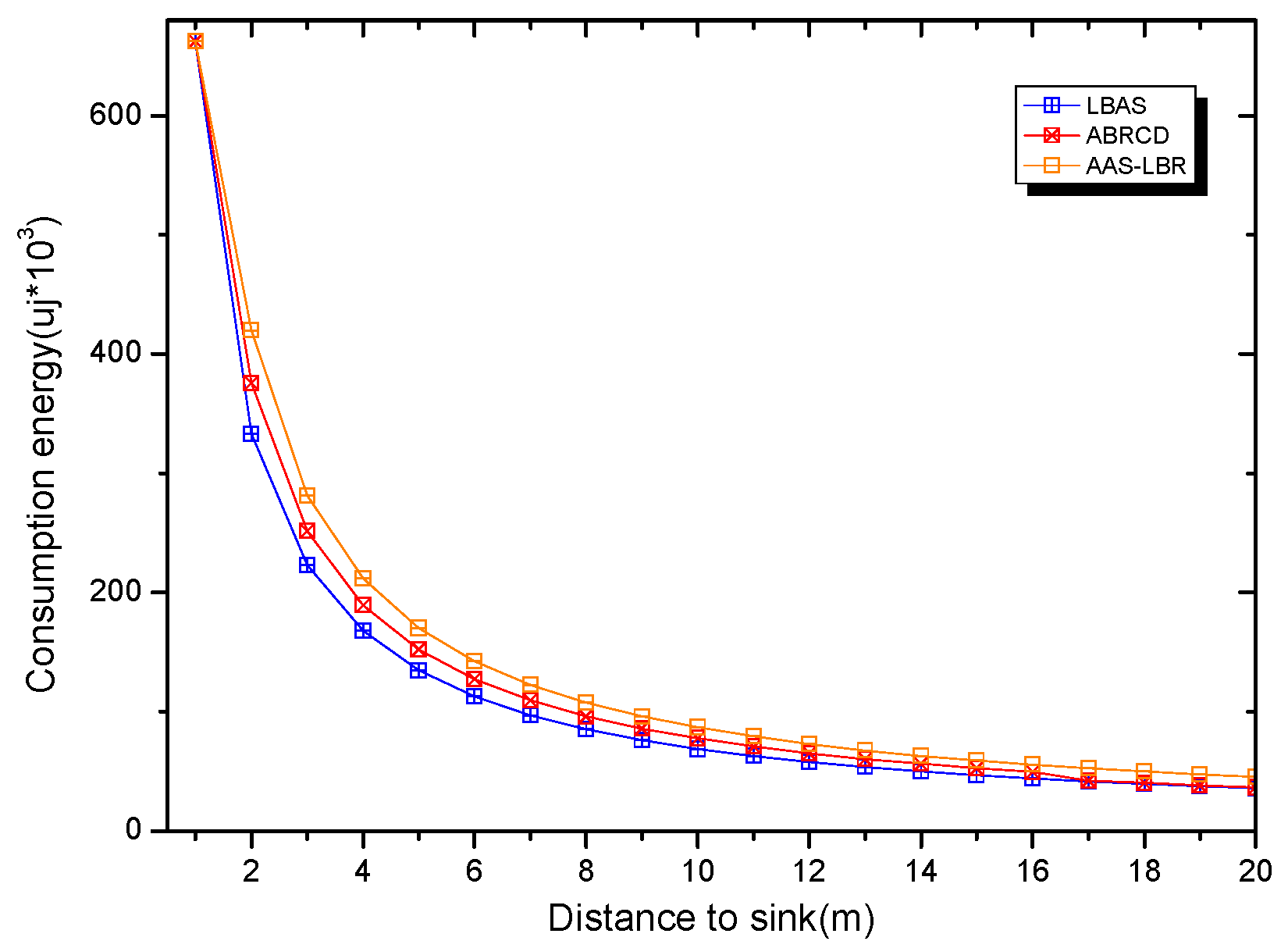
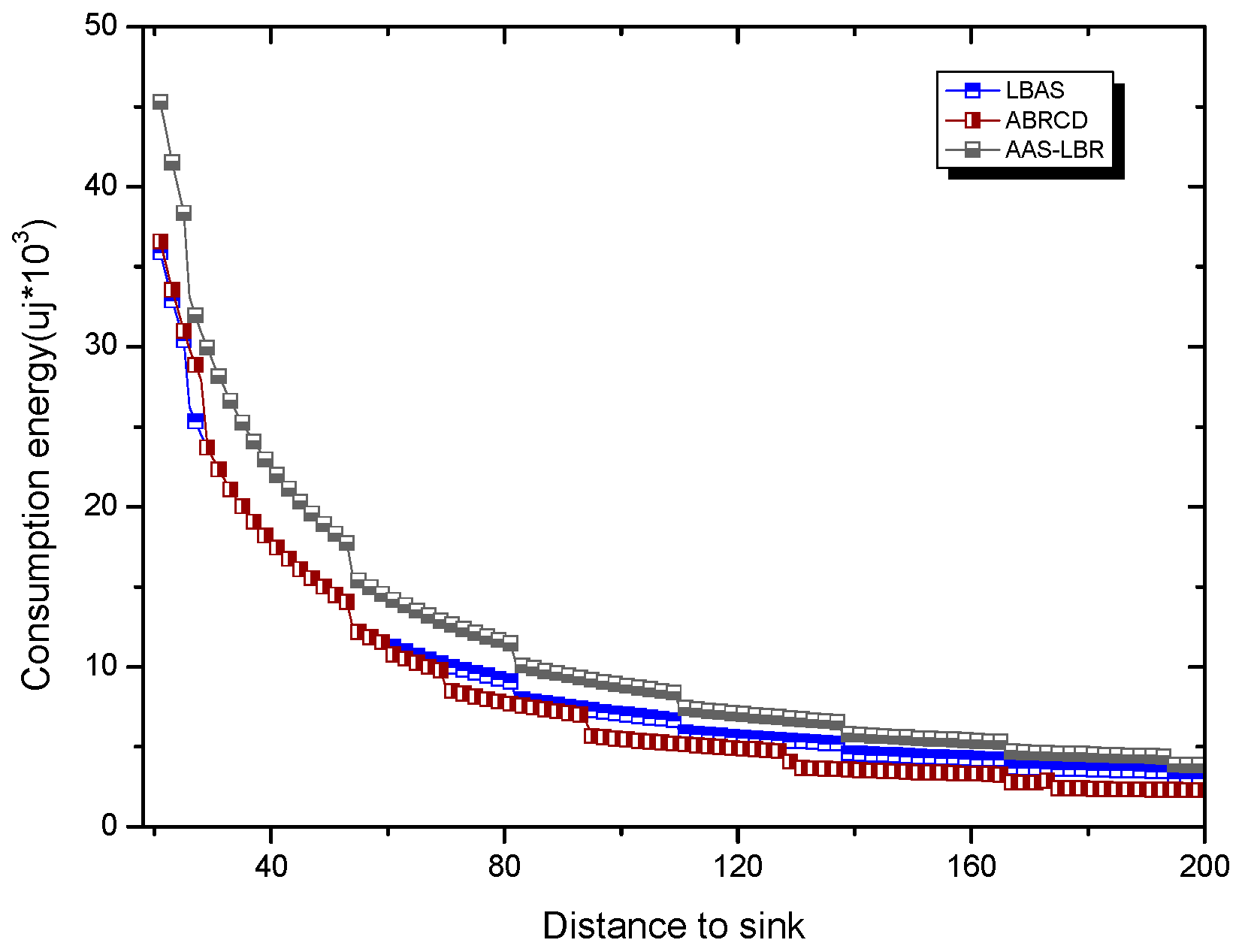
6. Experimental Results Analysis of ABRCD Scheme
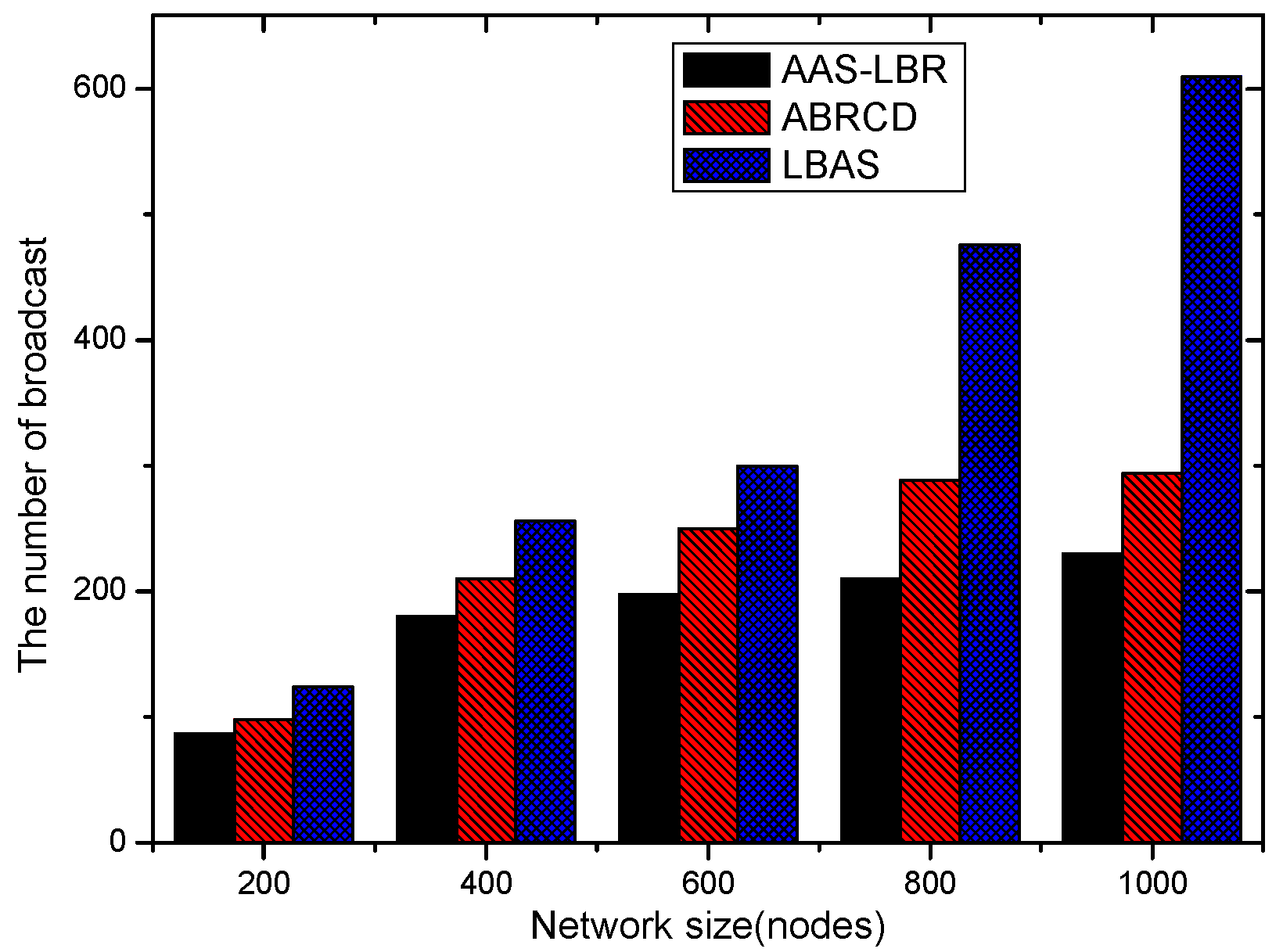
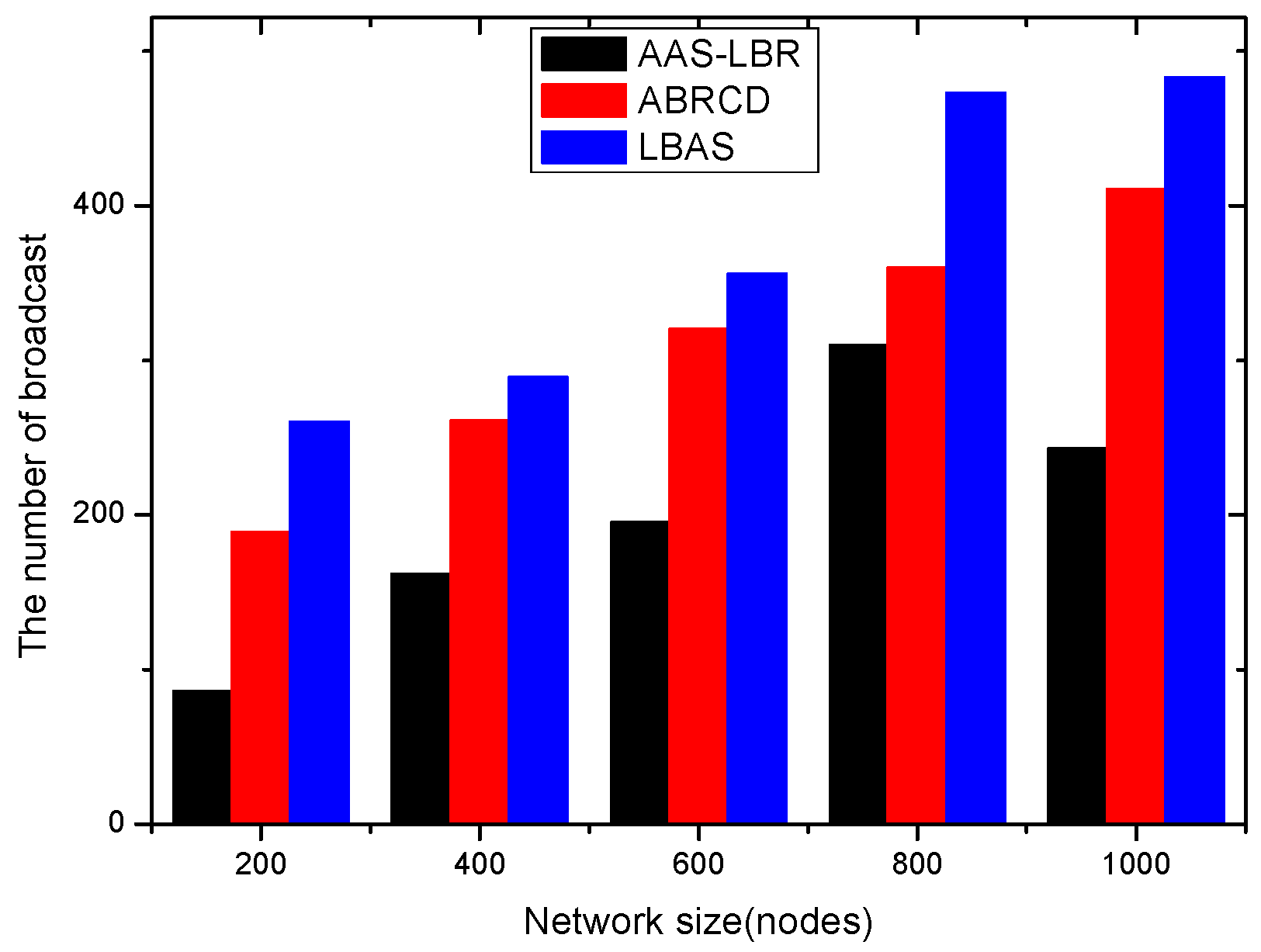
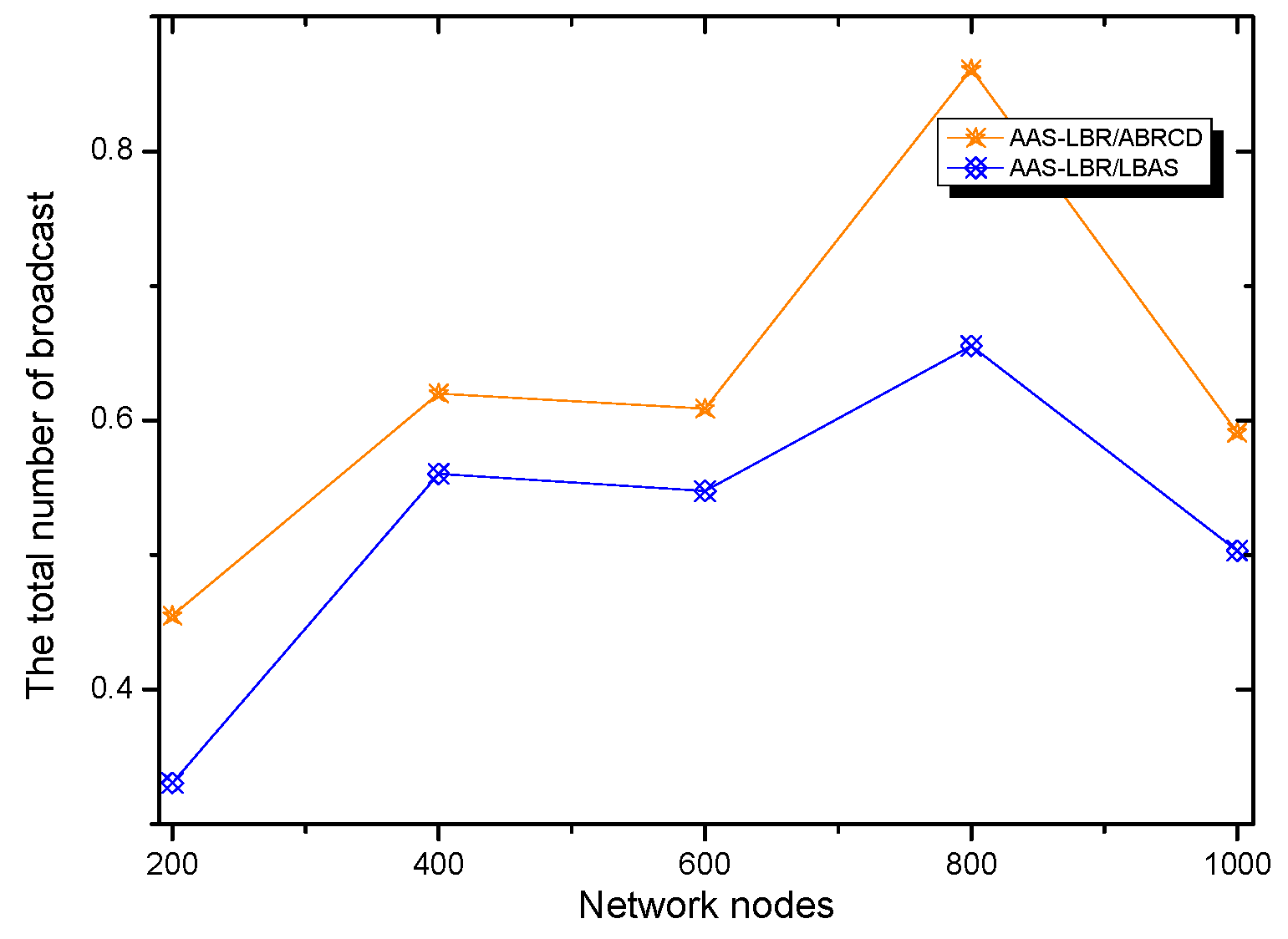
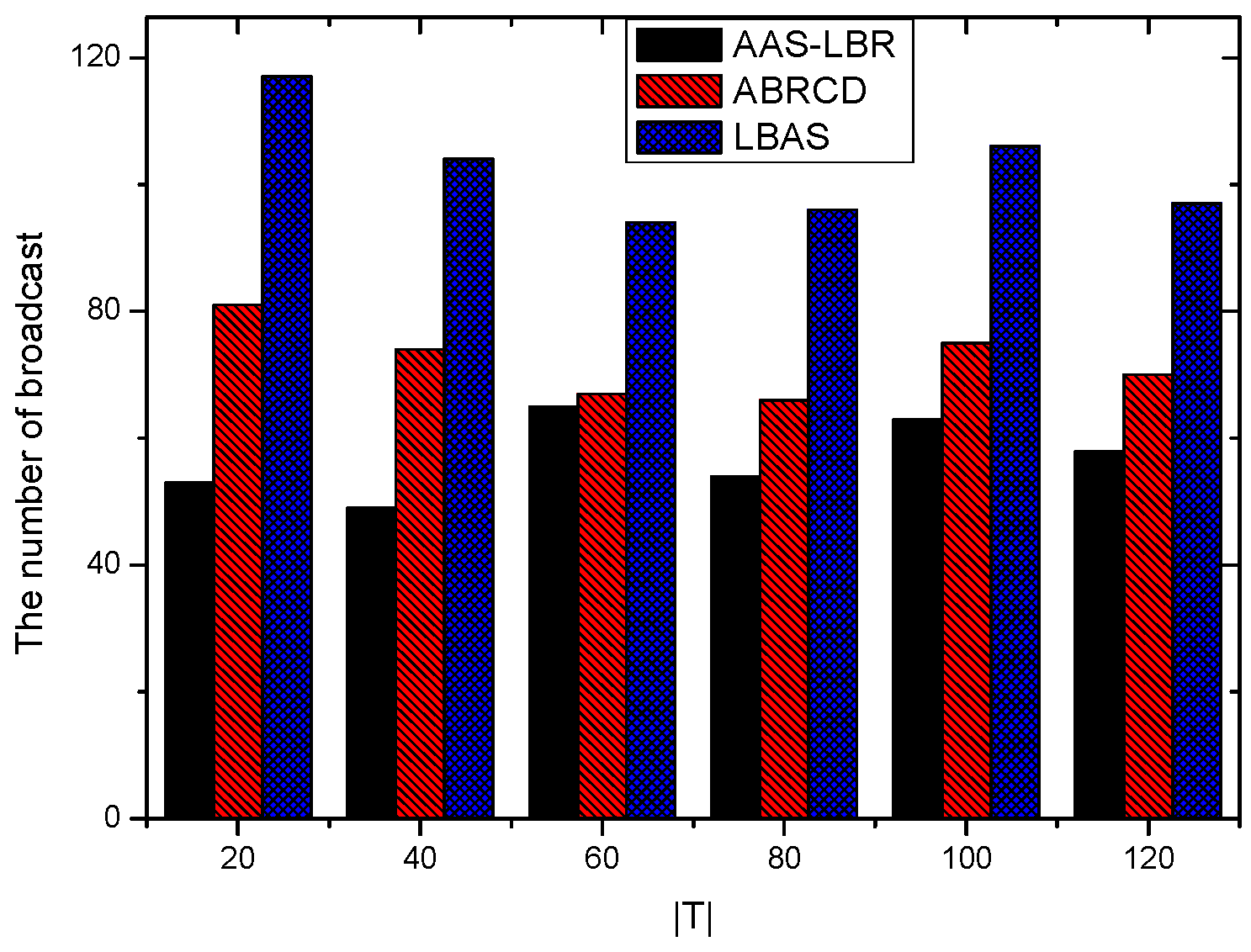
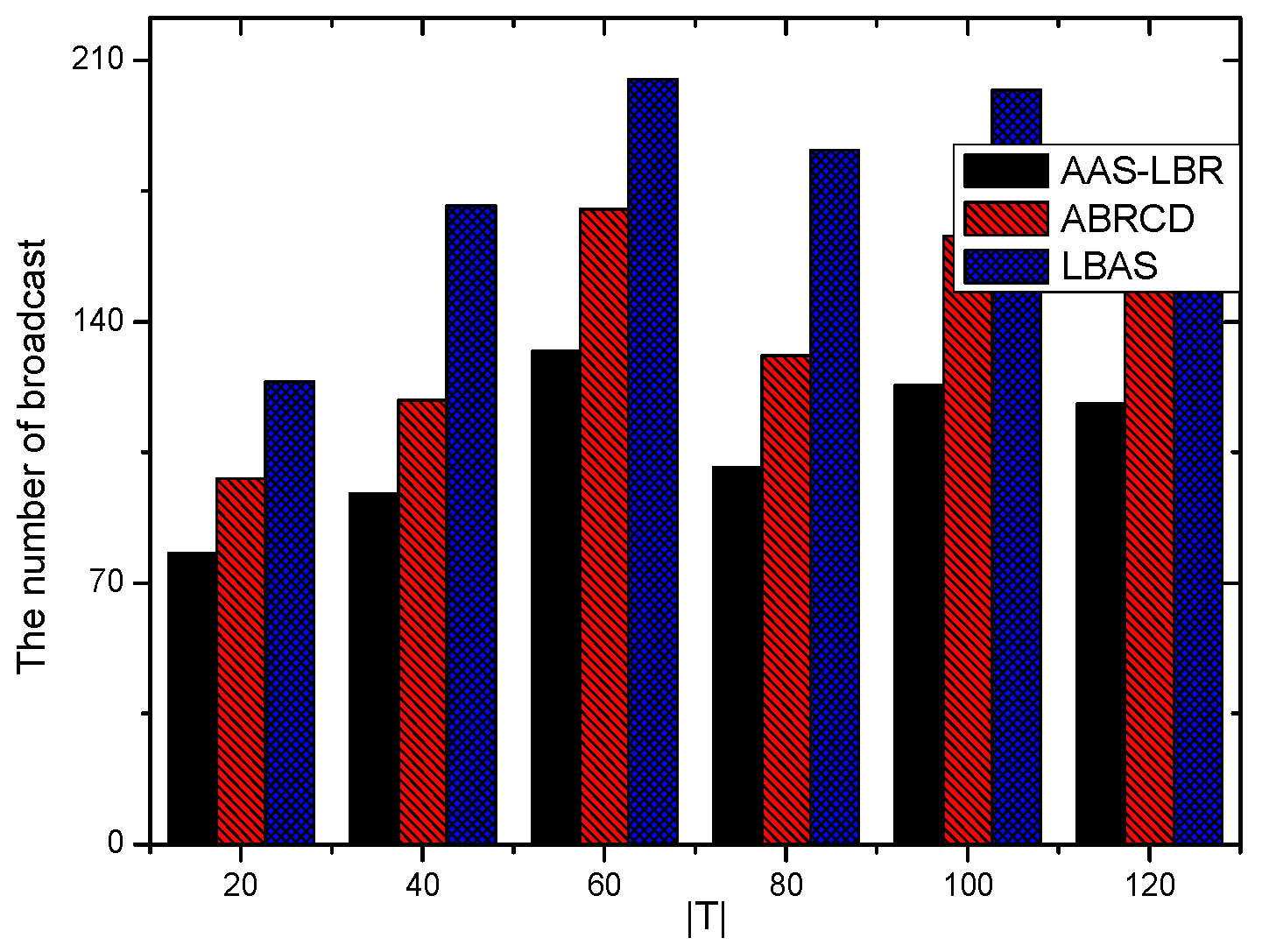
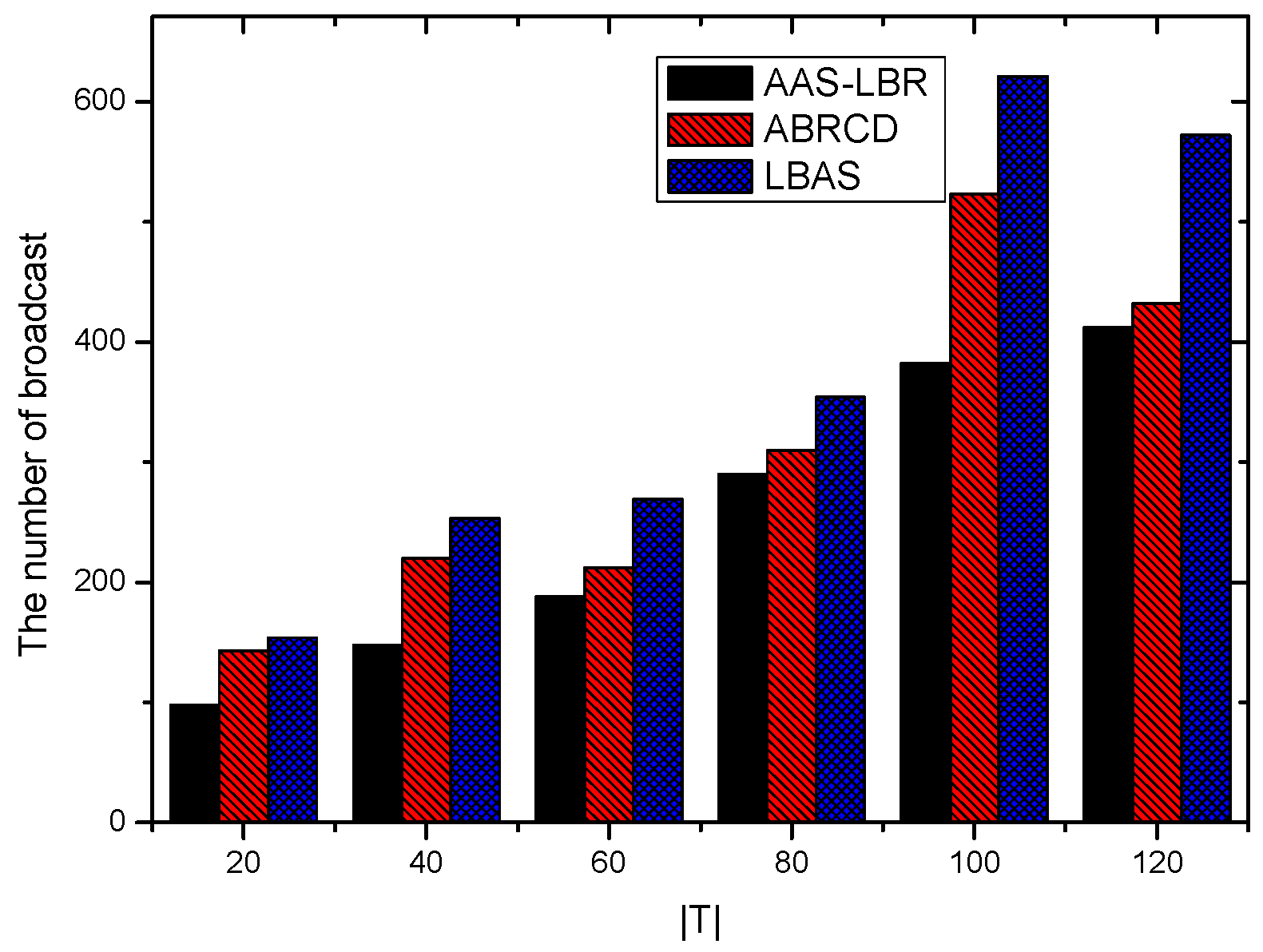
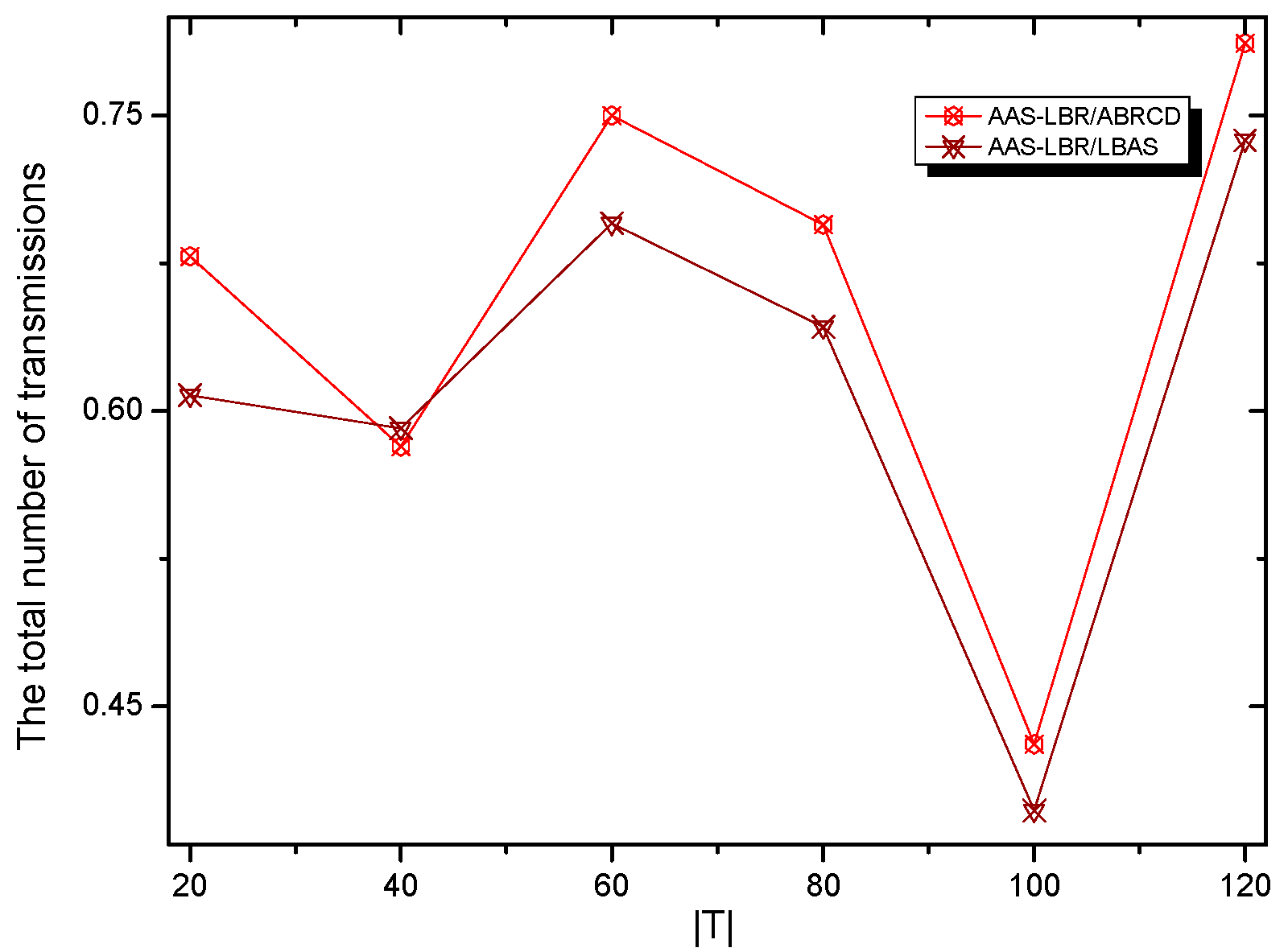
6.1. Transmissions Analysis
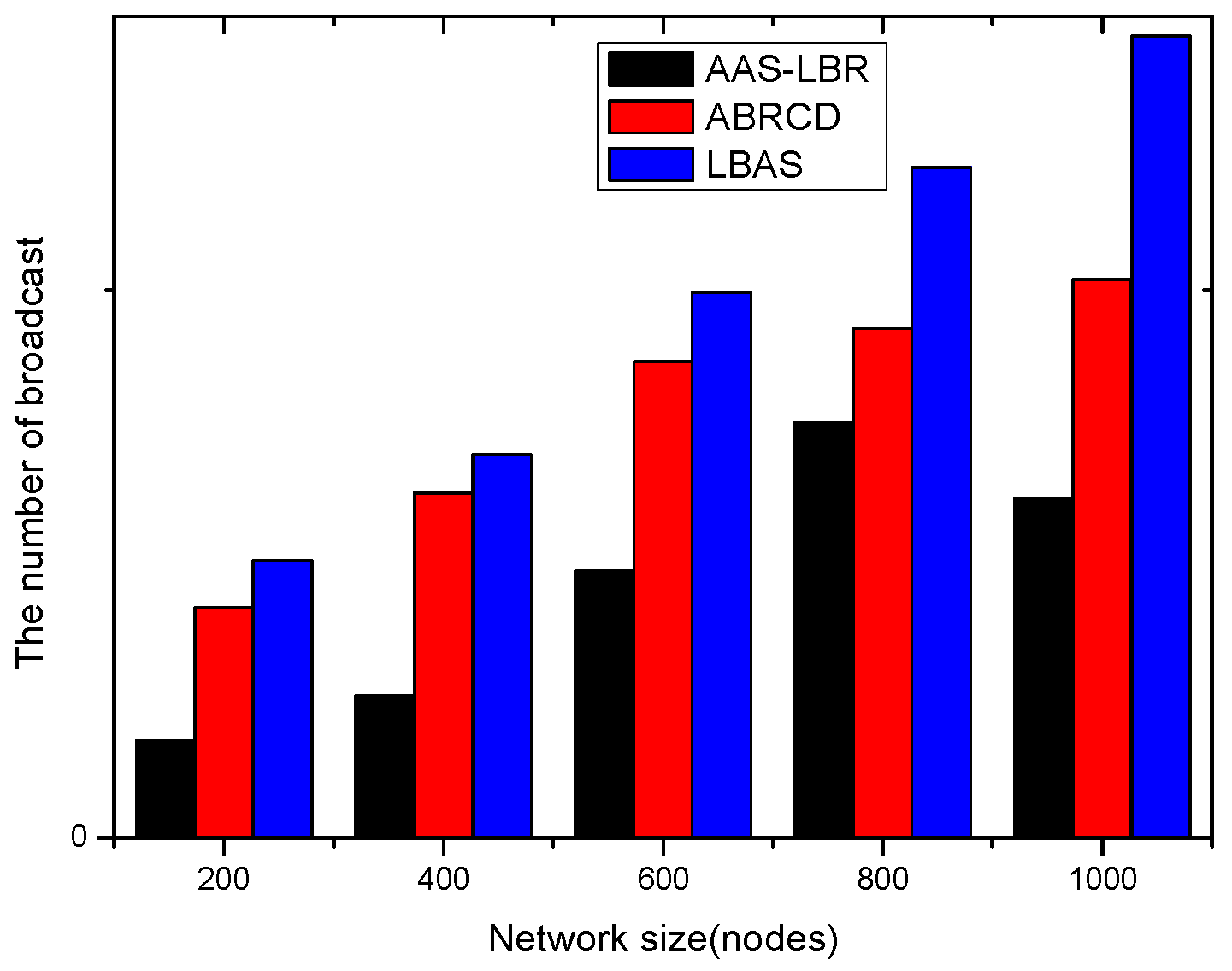
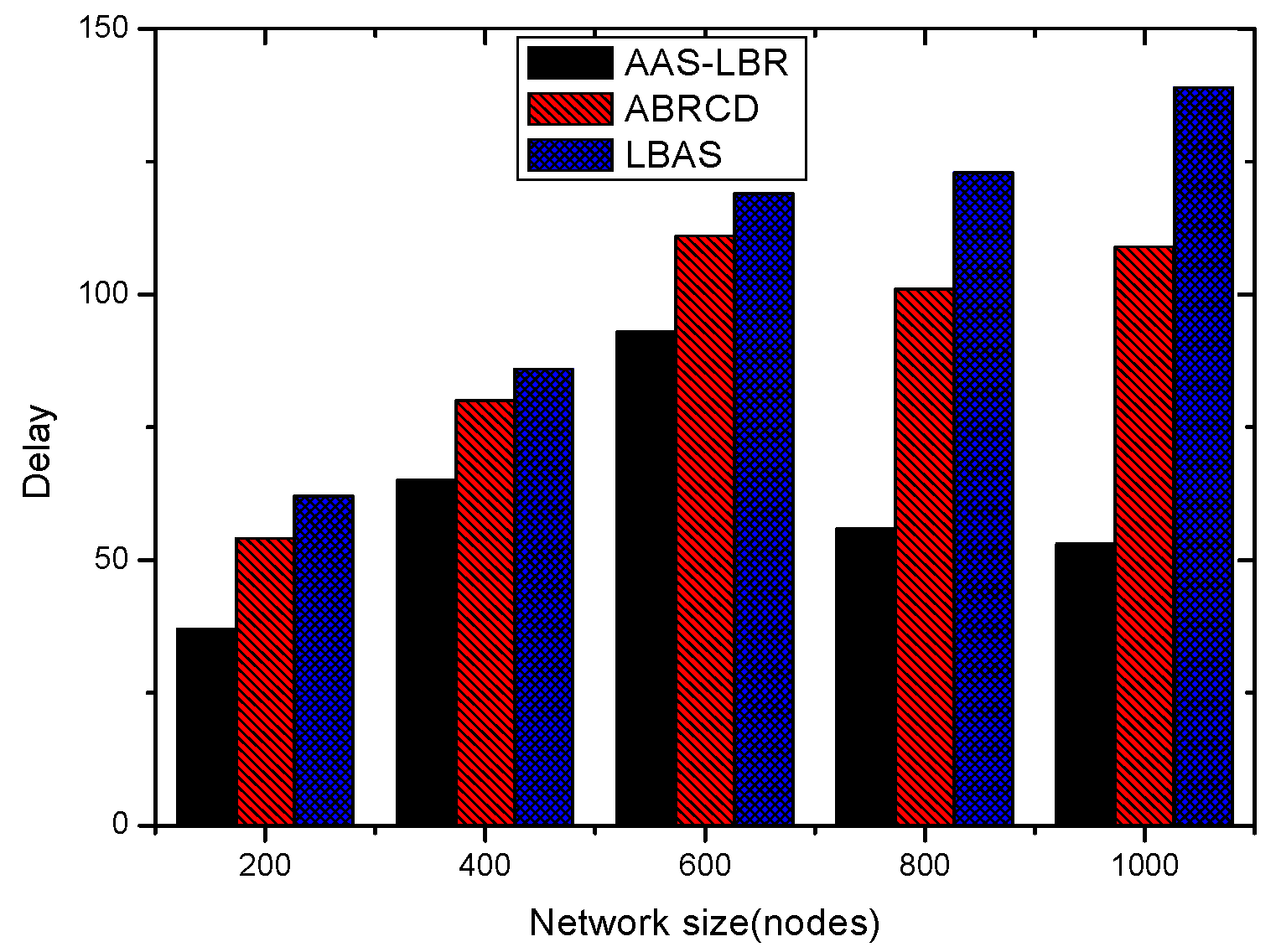
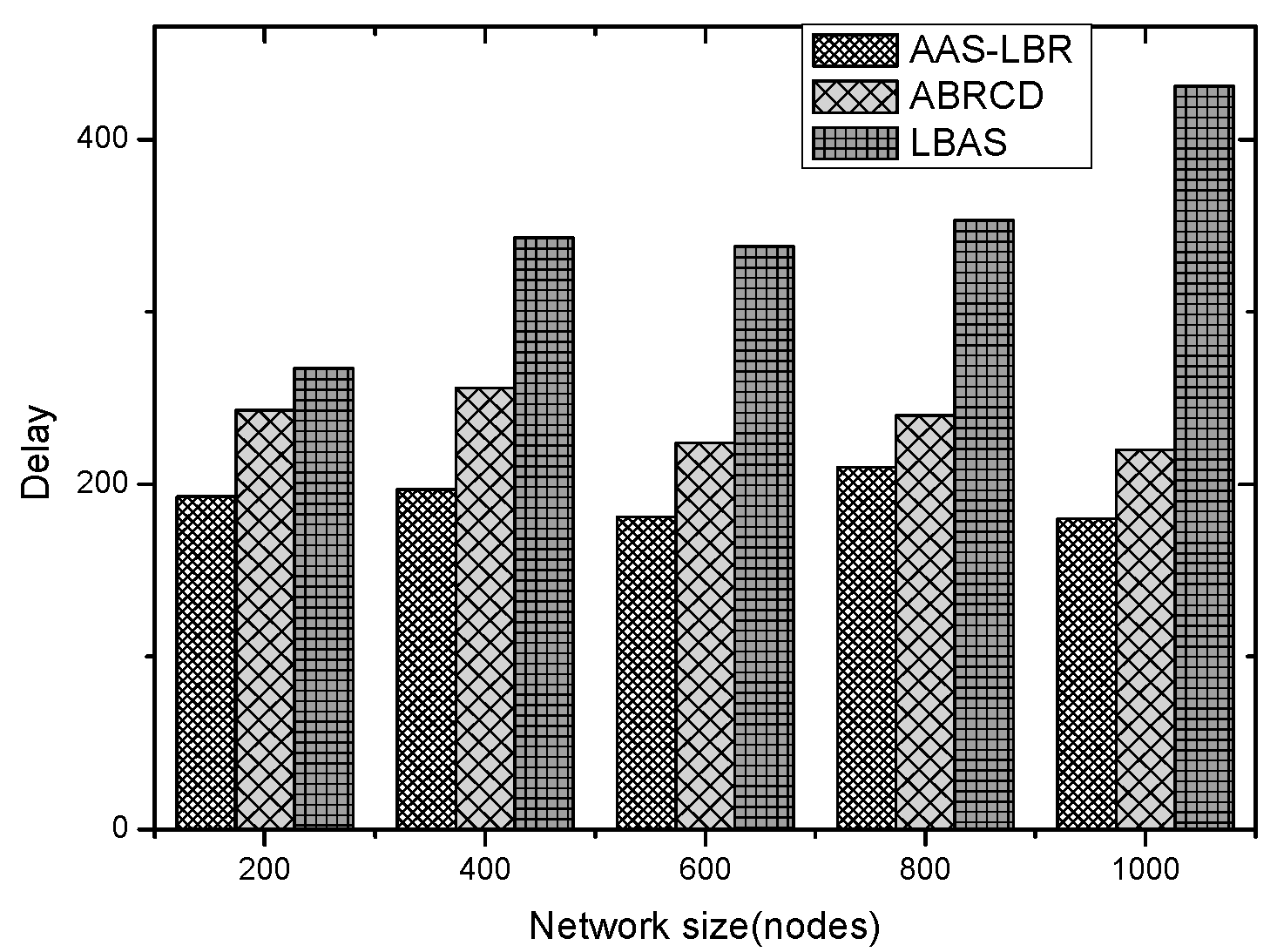
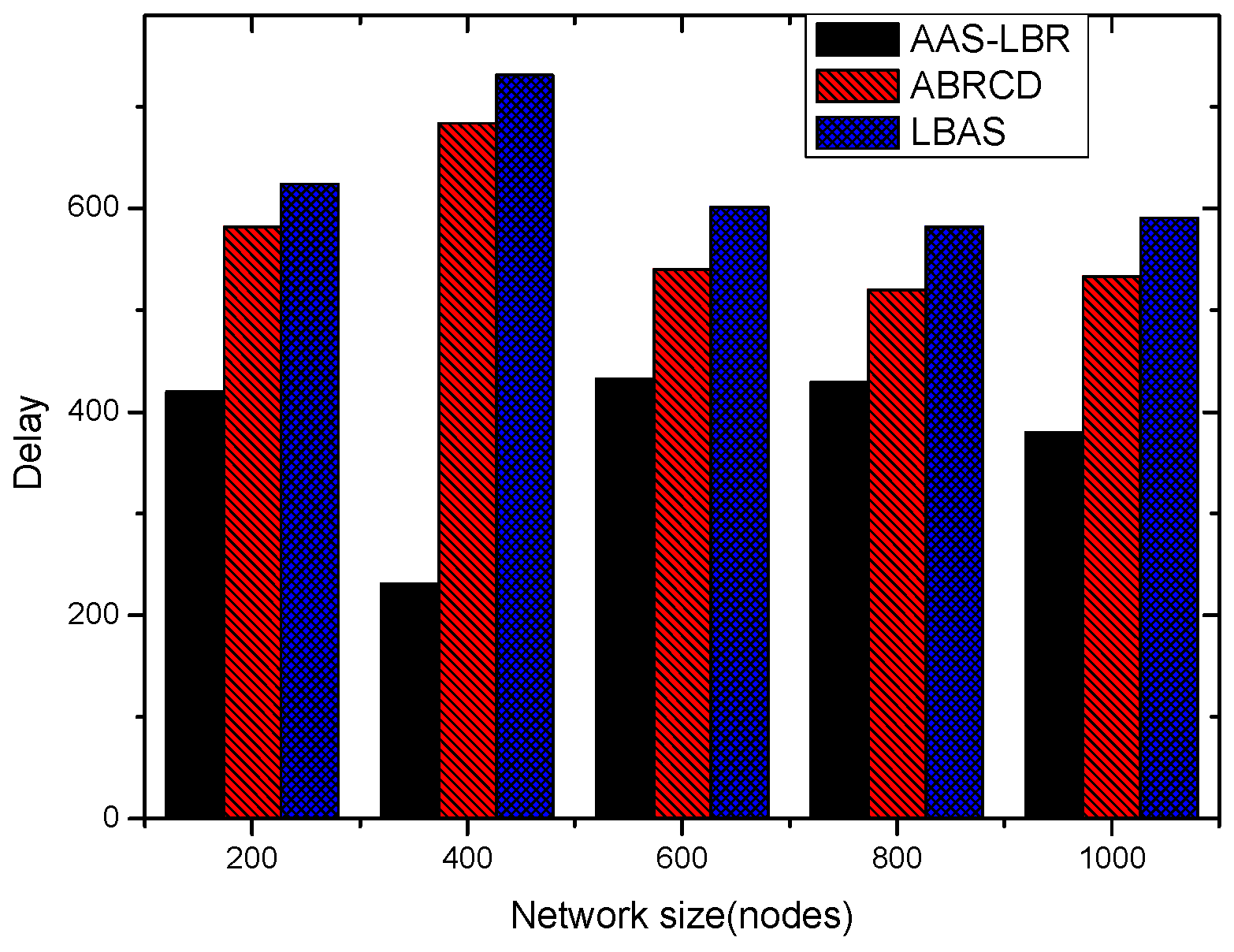
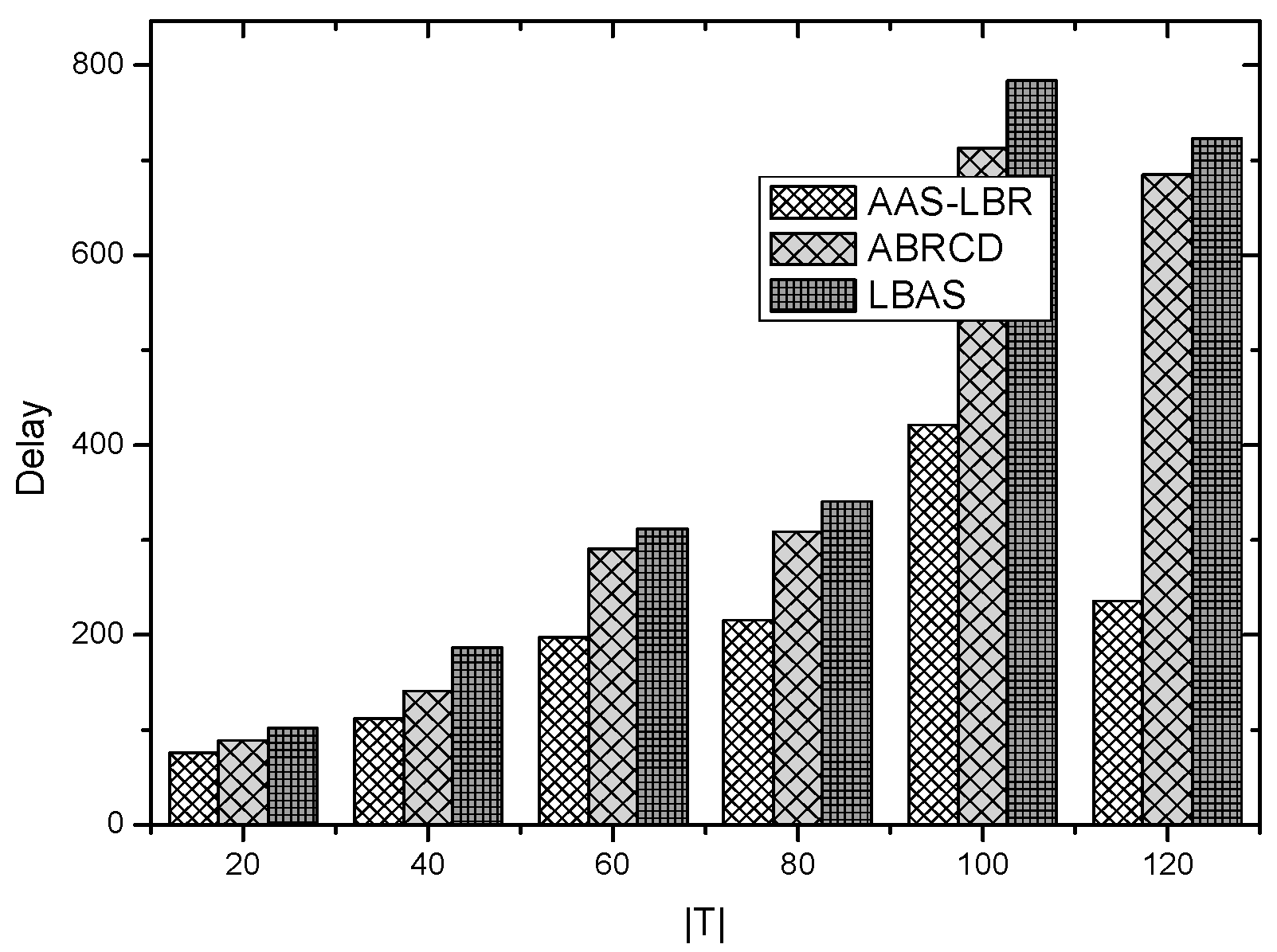
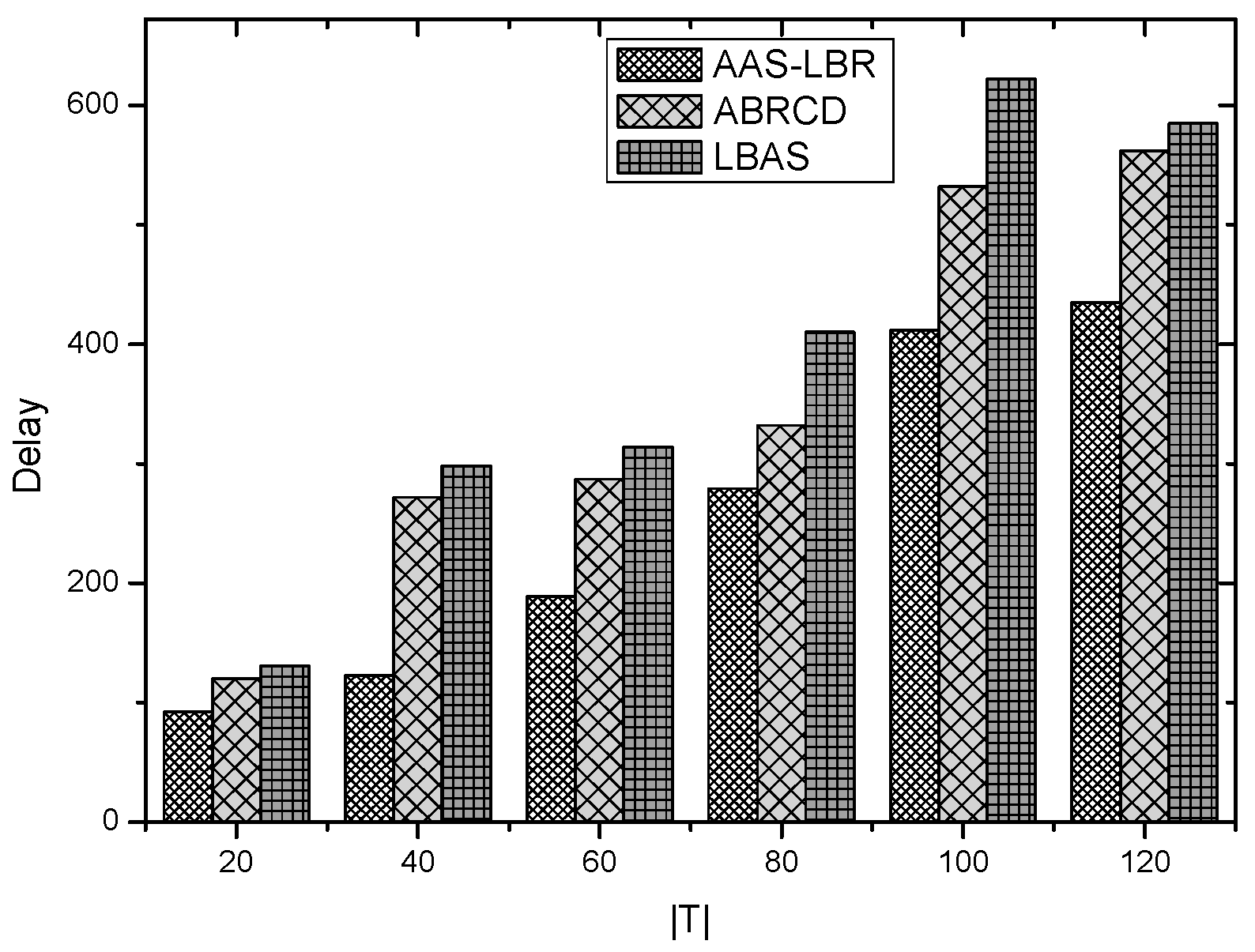
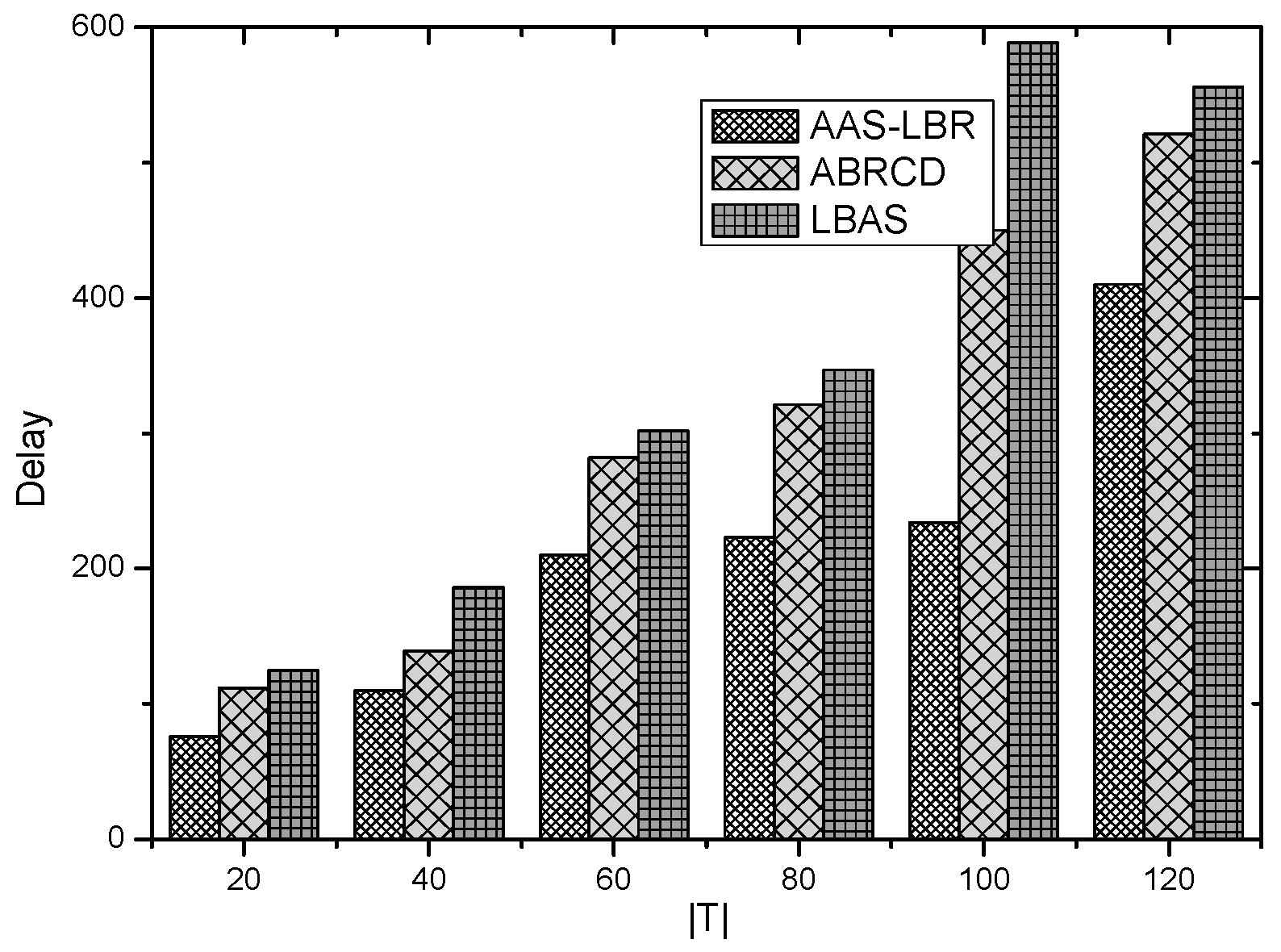
6.2. Delay Analysis
7. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fontanella, R.; Accardo, D.; Moriello, R.S.L.; Angrisani, L.; De Simone, D. MEMS Gyros Temperature Calibration through Artificial Neural Networks. Sens. Actuators A Phys. 2018, 279, 553–565. [Google Scholar] [CrossRef]
- Sarkar, S.; Chatterjee, S.; Misra, S. Assessment of the Suitability of Fog Computing in the Context of Internet of Things. IEEE Trans. Cloud Comput. 2018, 6, 46–59. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Liu, A.; Wang, S.; Liu, H. Minimizing Convergecast Time and Energy Consumption in Green Internet of Things. IEEE Trans. Emerg. Top. Comput. 2018. [Google Scholar] [CrossRef]
- Ding, Z.; Ota, K.; Liu, Y.; Zhang, N.; Zhao, M.; Song, H.; Liu, A.; Cai, Z. Orchestrating Data as Services based Computing and Communication Model for Information-Centric Internet of Things. IEEE Access 2018, 6, 38900–38920. [Google Scholar] [CrossRef]
- Huang, M.; Liu, A.; Xiong, N.; Wang, T.; Vasilakos, A.V. A Low-latency Communication Scheme for Mobile Wireless Sensor Control Systems. IEEE Trans. Syst. Man Cybern.-Syst. 2018. [Google Scholar] [CrossRef]
- Liu, X.; Li, G.; Zhang, S.; Liu, A. Big Program Code Dissemination Scheme for Emergency Software-Define Wireless Sensor Networks. Peer-to-Peer Netw. Appl. 2018, 11, 1038–1059. [Google Scholar] [CrossRef]
- Zhao, D.; Chin, K.W.; Raad, R. Approximation algorithms for broadcasting in duty cycled wireless sensor networks. Wirel. Netw. 2014, 20, 2219–2236. [Google Scholar] [CrossRef]
- Le Nguyen, P.; Ji, Y.; Liu, Z.; Vu, H.; Nguyen, K.V. Distributed hole-bypassing protocol in WSNs with constant stretch and load balancing. Comput. Netw. 2017, 129, 232–250. [Google Scholar] [CrossRef]
- Ju, X.; Liu, W.; Zhang, C.; Liu, A.; Wang, T.; Xiong, N.; Cai, Z. An Energy Conserving and Transmission Radius Adaptive Scheme to Optimize Performance of Energy Harvesting Sensor Networks. Sensors 2018, 18, 2885. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Wang, Z.; Ye, N.; Wang, R.; Li, X.Y. One More Tag Enables Fine-Grained RFID Localization and Tracking. IEEE/ACM Trans. Netw. 2018, 26, 161–174. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, S.; Ren, D.; Huang, C.; Zhang, H. Analysis of event-driven warning message propagation in vehicular ad hoc networks. Ad Hoc Netw. 2017, 55, 87–96. [Google Scholar] [CrossRef]
- Le Duc, T.; Le, D.T.; Zalyubovskiy, V.V.; Kim, D.S.; Choo, H. Level-based approach for minimum-transmission broadcast in duty-cycled wireless sensor networks. Pervasive Mob. Comput. 2016, 27, 116–132. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, F.; Sun, L.; Wang, R.; Yang, P. R-TTWD: Robust device-free through-the-wall detection of moving human with WiFi. IEEE J. Sel. Areas Commun. 2017, 35, 1090–1103. [Google Scholar] [CrossRef]
- Liu, X.; Liu, A.; Deng, Q.; Liu, H. Large-scale Programing Code Dissemination for Software Defined Wireless Networks. Comput. J. 2017, 60, 1417–1442. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Liu, C.; Cai, Z.; Xiong, N.; Liu, A.; Ma, M. An Effective Delay Reduction Approach through Portion of Nodes with Larger Duty Cycle for Industrial WSNs. Sensors 2018, 18, 1535. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, Y.; Liu, A.; Yang, L. Defending On-Off Attacks Using Light Probing Messages in Smart Sensors for Industrial Communication Systems. IEEE Trans. Ind. Informat. 2018, 14, 3801–3811. [Google Scholar] [CrossRef]
- Yu, S.; Liu, X.; Liu, A.; Xiong, N.; Cai, Z.; Wang, T. Adaption Broadcast Radius Based Code Dissemination Scheme for Low Energy Wireless Sensor Networks. Sensors 2018, 18, 1509. [Google Scholar] [CrossRef] [PubMed]
- Gui, J.S.; Hui, L.H.; Xiong, N.X. Enhancing Cellular Coverage Quality by Virtual Access Point and Wireless Power Transfer. Wirel. Commun. Mob. Comput. 2018, 2018, 9218239. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Xiong, N.; Zhang, N.; Liu, A.; Shen, H.; Huang, C. Construction of Large-Scale Low Cost Deliver Infrastructure using Vehicular Networks. IEEE Access 2018, 6, 21482–21497. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, H.; Li, X.; Leung, V. A Survey on Mobile Data Offloading Technologies. IEEE Access 2018, 6, 5101–5111. [Google Scholar] [CrossRef]
- Li, T.; Tian, S.; Liu, A.; Liu, H.; Pei, T. DDSV: Optimizing Delay and Delivery Ratio for Multimedia Big Data Collection in Mobile Sensing Vehicles. IEEE Internet Things J. 2018, 5, 3474–3486. [Google Scholar] [CrossRef]
- Gui, J.; Zhou, K. Cellular throughput optimization by game-based power adjustment and outband D2D communication. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 254. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, N.; Song, H.; Liu, A.; Zhao, M.; Zeng, Z. Adaptive Beaconing Based MAC Protocol for Sensor based Wearable System. IEEE Access 2018, 6, 9700–29714. [Google Scholar] [CrossRef]
- Yang, G.; He, S.; Shi, Z. Leveraging crowdsourcing for efficient malicious users detection in large-scale social networks. IEEE Internet Things J. 2017, 4, 330–339. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, W.; Liu, Y.; Xiong, N.; Liu, A.; Liu, X. An Effective Crowdsourcing Data Reporting Scheme to Compose Cloud-Based Services in Mobile Robotic Systems. IEEE Access 2018, 6, 54683–54700. [Google Scholar] [CrossRef]
- Zhou, H.; Ruan, M.; Zhu, C.; Leung, V.; Xu, S.; Huang, C. A Time-Ordered Aggregation Model-Based Centrality Metric for Mobile Social Networks. IEEE Access 2018, 6, 25588–25599. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, J.; Liu, A.; Bhuiyan, M.; Wang, G.; Jia, W. Fog-Based Computing and Storage Offloading for Data Synchronization in IoT. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Medagliani, P.; Leguay, J.; Ferrari, G.; Gay, V.; Lopez-Ramos, M. Energy-efficient mobile target detection in wireless sensor networks with random node deployment and partial coverage. Pervasive Mob. Comput. 2012, 8, 429–447. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G.; Bhuiyan, M.; Liu, A.; Jia, W.; Xie, M. A novel trust mechanism based on fog computing in Sensor-Cloud System. Futur. Gener. Comput. Syst. 2018. [Google Scholar] [CrossRef]
- Ye, X.; Li, J.; Xu, L. Distributed Separate Coding for Continuous Data Collection in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2014, 11, 17. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, R.; Zhu, L.; Liu, A.; Lin, Y.; Huang, F. Hierarchical Information Quadtree: Efficient Spatial Temporal Image Search for Multimedia Stream. Multimed. Tools Appl. 2018. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Luo, X.; Wang, W.; Wang, L.; Zhao, W. A novel human activity recognition scheme for smart health using multilayer extreme learning machine. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, A.; Guo, S.; Li, Z.; Choi, Y.J.; Sekiya, H. Context-aware collect data with energy efficient in Cyber–physical cloud systems. Futur. Gener. Comput. Syst. 2018. [Google Scholar] [CrossRef]
- Li, T.; Xiong, N.; Gao, J.; Song, H.; Liu, A.; Zeng, Z. Reliable Code Disseminations through Opportunistic Communication in Vehicular Wireless Networks. IEEE Access 2018, 6, 55509–55527. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, A. On the hybrid using of unicast-broadcast in wireless sensor networks. Comput. Electr. Eng. 2018, 71, 714–732. [Google Scholar] [CrossRef]
- Qi, W.; Liu, W.; Liu, X.; Liu, A.; Wang, T.; Xiong, N.; Cai, Z. Minimizing Delay and Transmission Times with Long Lifetime in Code Dissemination Scheme for High Loss Ratio and Low Duty Cycle WSNs. Sensors 2018, 18, 3516. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Zhang, G.; Liu, A.; Bhuiyan, M.Z.A.; Jin, Q. A Secure IoT Service Architecture with an Efficient Balance Dynamics Based on Cloud and Edge Computing. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, D.; Yang, T.; Liu, J.; Chang, X.; Ning, H. A kernel machine-based secure data sensing and fusion scheme in wireless sensor networks for the cyber-physical systems. Futur. Gener. Comput. Syst. 2016, 61, 85–96. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Wang, L. Offloading in Internet of Vehicles: A Fog-Enabled Real-Time Traffic Management System. IEEE Trans. Ind. Informat. 2018, 14, 4568–4578. [Google Scholar] [CrossRef]
- Fang, S.; Cai, Z.; Sun, W.; Liu, A.; Liu, F.; Liang, Z.; Wang, G. Feature Selection Method Based on Class Discriminative Degree for Intelligent Medical Diagnosis. Comput. Mater. Contin. 2018, 55, 419–433. [Google Scholar]
- Liu, X.; Liu, W.; Liu, Y.; Song, H.; Liu, A.; Liu, X. A Trust and Priority Based Code Updated Approach to Guarantee Security for Vehicles Network. IEEE Access 2018, 6, 55780–55796. [Google Scholar] [CrossRef]
- Huang, M.; Liu, A.; Zhao, M.; Wang, T. Multi Working Sets Alternate Covering Scheme for Continuous Partial Coverage in WSNs. Peer-to-Peer Netw. Appl. 2018. [Google Scholar] [CrossRef]
- Liu, A.; Zhao, S. High performance target tracking scheme with low prediction precision requirement in WSNs. Int. J. Ad Hoc Ubiquitous Comput. 2018, 29, 270–289. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Ning, Z.; Ngai, E.; Zhou, L.; Wei, J.; Cheng, J.; Hu, B. Energy-Latency Trade-Off for Energy-Aware Offloading in Mobile Edge Computing Networks. IEEE Internet Things J. 2018, 5, 2633–2645. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Zhou, M.; Hu, X.; Wang, L.; Hu, B.; Kwok, R.; Guo, Y. A Privacy-Preserving Message Forwarding Framework for Opportunistic Cloud of Things. IEEE Internet Things J. 2018. [Google Scholar] [CrossRef]
- Liu, X.; Dong, M.; Ota, K.; Yang, L.T.; Liu, A. Trace malicious source to guarantee cyber security for mass monitor critical infrastructure. J. Comput. Syst. Sci. 2018, 98, 1–26. [Google Scholar] [CrossRef]
- Huang, B.; Liu, A.; Zhang, C.; Xiong, N.; Zeng, Z.; Cai, Z. Caching Joint Shortcut Routing to Improve Quality of Experiments of Users for Information-Centric Networking. Sensors 2018, 18, 1750. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, Y.; Ma, M.; Liu, A.; Zhang, X.; Luo, G. MSDG: A Novel Green Data Gathering Scheme for Wireless Sensor Networks. Comput. Netw. 2018, 142, 223–239. [Google Scholar] [CrossRef]
- Teng, H.; Zhang, K.; Dong, M.; Ota, K.; Liu, A.; Zhao, M.; Wang, T. Adaptive Transmission Range Based Topology Control Scheme for Fast and Reliable Data Collection. Wirel. Commun. Mob. Comput. 2018, 2018, 4172049. [Google Scholar] [CrossRef]
- Li, X.; Liu, W.; Xie, M.; Liu, A.; Zhao, M.; Xiong, N.; Zhao, M.; Dai, W. Differentiated Data Aggregation Routing Scheme for Energy Conserving and Delay Sensitive Wireless Sensor Networks. Sensors 2018, 18, 2349. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; Shin, D.H. A Formal Approach to the Selection by Minimum Error and Pattern Method for Sensor Data Loss Reduction in Unstable Wireless Sensor Network Communications. Sensors 2017, 17, 1092. [Google Scholar]
- Liu, Y.; Liu, A.; Chen, Z. Analysis and Improvement of Send-and-Wait Automatic Repeat-reQuest protocols for Wireless Sensor Networks. Wirel. Pers. Commun. 2015, 81, 923–959. [Google Scholar] [CrossRef]
- Cheng, L.; Niu, J.; Luo, C.; Shu, L.; Kong, L.; Zhao, Z.; Gu, Y. Towards minimum-delay and energy-efficient flooding in low-duty-cycle wireless sensor networks. Comput. Netw. 2018, 134, 66–77. [Google Scholar] [CrossRef]
- Li, T.; Liu, Y.; Xiong, N.; Liu, A.; Cai, Z.; Song, H. Privacy-Preserving Protocol of Sink Node Location in Telemedicine Networks. IEEE Access 2018, 6, 42886–42903. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Z.; Han, K.; Zhang, J.; Gu, Y.; Qin, Z. Optimization of Particle CBMeMBer Filters for Hardware Implementation. IEEE Trans. Veh. Technol. 2018, 67, 9027–9031. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, Y.; Zhang, N.; Liu, A.; Xiong, N.; Cai, Z. Minimum-Cost Mobile Crowdsourcing with QoS Guarantee Using Matrix Completion Technique. Pervasive Mob. Comput. 2018, 49, 23–44. [Google Scholar] [CrossRef]
- Xiao, F.; Xie, X.; Li, Z.; Deng, Q.; Liu, A.; Sun, L. Wireless Network Optimization via Physical Layer Information for Smart Cities. IEEE Netw. 2018, 32, 88–93. [Google Scholar] [CrossRef]
- Luo, X.; Lv, Y.; Zhou, M.; Wang, W.; Zhao, W. A laguerre neural network-based ADP learning scheme with its application to tracking control in the Internet of Things. Pers. Ubiquitous Comput. 2016, 20, 361–372. [Google Scholar] [CrossRef]
- Clark, B.N.; Colbourn, C.J.; Johnson, D.S. Unit disk graphs. Discret. Math. 1990, 86, 165–177. [Google Scholar] [CrossRef]
- Guha, S.; Khuller, S. Approximation algorithms for connected dominating sets. Algorithmica 1998, 20, 374–387. [Google Scholar] [CrossRef]
- Lim, H.; Kim, C. Flooding in wireless ad hoc networks. Comput. Commun. 2001, 24, 353–363. [Google Scholar] [CrossRef]
- Khiati, M.; Djenouri, D. BOD-LEACH: Broadcasting over duty-cycled radio using LEACH clustering for delay/power efficient dissimilation in wireless sensor networks. Int. J. Commun. Syst. 2015, 28, 296–308. [Google Scholar] [CrossRef]
- Hong, J.; Cao, J.; Li, W.; Lu, S.; Chen, D. Minimum-transmission broadcast in uncoordinated duty-cycled wireless ad hoc networks. IEEE Trans. Veh. Technol. 2010, 59, 307–318. [Google Scholar] [CrossRef]
- Hou, W.; Ning, Z.; Hu, X.; Guo, L.; Deng, X.; Yang, Y.; Kwok, R.Y. On-Chip Hardware Accelerator for Automated Diagnosis through Human-Machine Interactions in Healthcare Delivery. IEEE Trans. Autom. Sci. Eng. 2018. [Google Scholar] [CrossRef]
- Guo, L.; Ning, Z.; Hou, W.; Hu, B.; Guo, P. Quick Answer for Big Data in Sharing Economy: Innovative Computer Architecture Design Facilitating Optimal Service-Demand Matching. IEEE Trans. Autom. Sci. Eng. 2018. [Google Scholar] [CrossRef]
| Symbol | Description | Value |
|---|---|---|
| Sleep power consumption | 2.4 × 10−7 W | |
| Preamble duration | 0.26 ms | |
| Packet duration | 0.93 ms | |
| Ack window duration | 0.26 ms | |
| Reception power consumption | 0.0588 W | |
| the probability of generating data | 0.1 |
| Rank (k) | Output Power (q(k)) | Range (r(k)) |
|---|---|---|
| 0 | −20 (0.0100 ) | 28.0 |
| 1 | −19 (0.0126 ) | 29.7 |
| 2 | −18 (0.0158 ) | 31.4 |
| 3 | −17 (0.0200 ) | 33.3 |
| 4 | −16 (0.0251 ) | 35.3 |
| 5 | −15 (0.0316 ) | 37.4 |
| 6 | −14 (0.0398 ) | 39.6 |
| 7 | −13 (0.0501 ) | 41.9 |
| 8 | −12 (0.0631 ) | 44.4 |
| 9 | −11 (0.0794 ) | 47 |
| 10 | −10 (0.1000 ) | 49.8 |
| 11 | −9 (0.1259 ) | 52.8 |
| 12 | −8 (0.1585 ) | 55.9 |
| 13 | −7 (0.1995 ) | 59.2 |
| 14 | −6 (0.2512 ) | 62.7 |
| 15 | −5 (0.3162 ) | 66.4 |
| 16 | −4 (0.3981 ) | 70.3 |
| 17 | −3 (0.5012 ) | 74.5 |
| 18 | −2 (0.6310 ) | 78.9 |
| 19 | −1 (0.7943 ) | 83.6 |
| 20 | 0 (1.0000 ) | 88.6 |
| 21 | 1 (1.2589 ) | 93.8 |
| 22 | 2 (1.5849 ) | 99.4 |
| 23 | 3 (1.9953 ) | 105.2 |
| 24 | 4 (2.5119 ) | 111.5 |
| 25 | 5 (3.1623 ) | 118.1 |
| Set of nodes capable of communicating with node v at time slot | |
| The root node of the subtree where node v is located | |
| Set of nodes with active time-slot | |
| Set of covering nodes for | |
| Set of nodes covering node v | |
| Set of nodes covered by node v |
| Cycle | Slot | Data Received at Node |
|---|---|---|
| 1 | 1 | |
| 2 | ||
| 2 | 0 | |
| 1 | , | |
| 2 | , | |
| 3 | 0 | , , , |
| 1 | , , , | |
| 2 | , , | |
| 4 | 0 | , , |
| 2 |
| Cycle | Slot | Data Received at Node |
|---|---|---|
| 1 | 1 | |
| 2 | ||
| 2 | 0 | , |
| 1 | ||
| 2 | ||
| 3 | 0 | , , |
| 1 | , | |
| 2 | , , | |
| 4 | 0 | , |
| 1 | , | |
| 2 | , , | |
| 5 | 0 | |
| 1 |
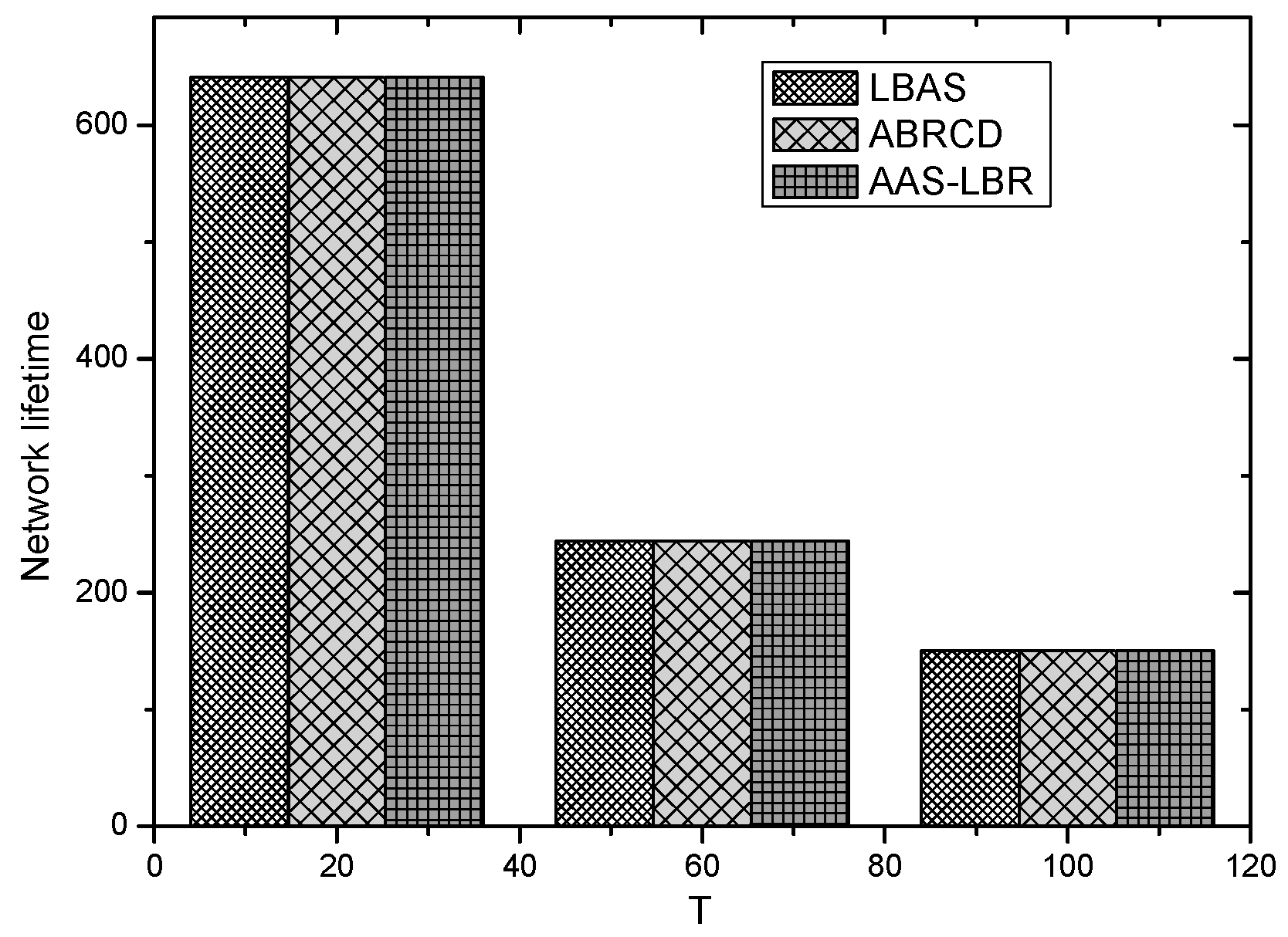
| The Scene or Parameter of Network | Scheme | The Number of Broadcast | The Reduce Ratio of Broadcast (%) | The Broadcast Delay | The Reduce Ratio of Delay (%) |
|---|---|---|---|---|---|
| = 30, number of nodes are 200 | AAS-LBR | 87 | 29.83 | 37 | 40.32 |
| ABRCD | 98 | 23.38 | 54 | 12.90 | |
| LBAS | 124 | 0 | 62 | 0 | |
| = 90, number of nodes are 200 | AAS-LBR | 86 | 66.92 | 193 | 27.71 |
| ABRCD | 189 | 27.30 | 243 | 8.98 | |
| LBAS | 260 | 0 | 267 | 0 | |
| = 150, number of nodes are 200 | AAS-LBR | 89 | 68.55 | 420 | 32.69 |
| ABRCD | 210 | 17.00 | 582 | 6.73 | |
| LBAS | 283 | 0 | 624 | 0 | |
| = 20, number of nodes are 200 | AAS-LBR | 53 | 54.70 | 76 | 25.49 |
| ABRCD | 81 | 30.80 | 89 | 12.74 | |
| LBAS | 117 | 0 | 102 | 0 | |
| = 20, number of nodes are 400 | AAS-LBR | 78 | 37.10 | 92 | 29.77 |
| ABRCD | 98 | 20.96 | 120 | 8.39 | |
| LBAS | 124 | 0 | 131 | 0 | |
| = 20, number of nodes are 600 | AAS-LBR | 98 | 36.36 | 76 | 48.99 |
| ABRCD | 143 | 6.54 | 136 | 8.72 | |
| LBAS | 154 | 0 | 149 | 0 |
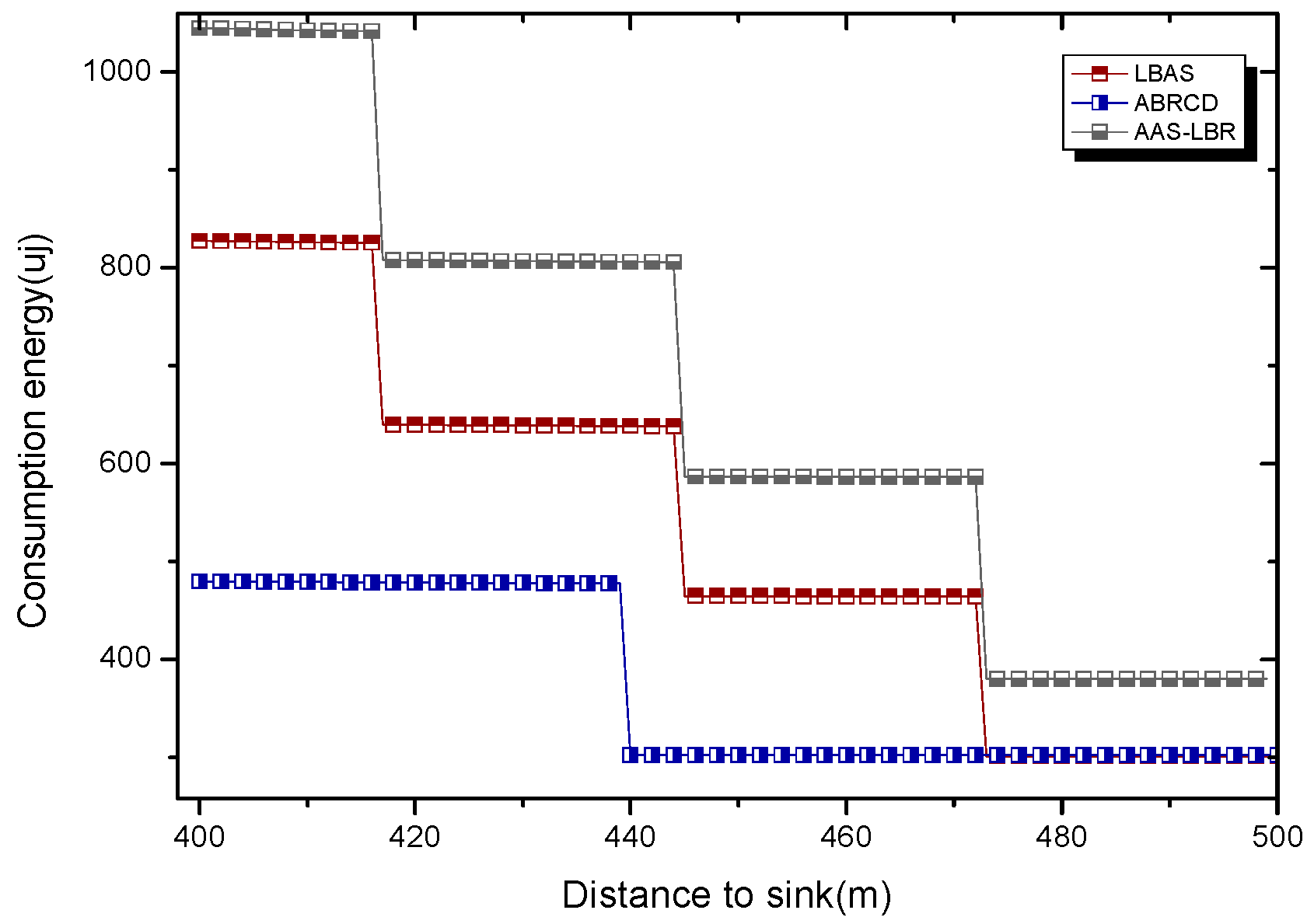
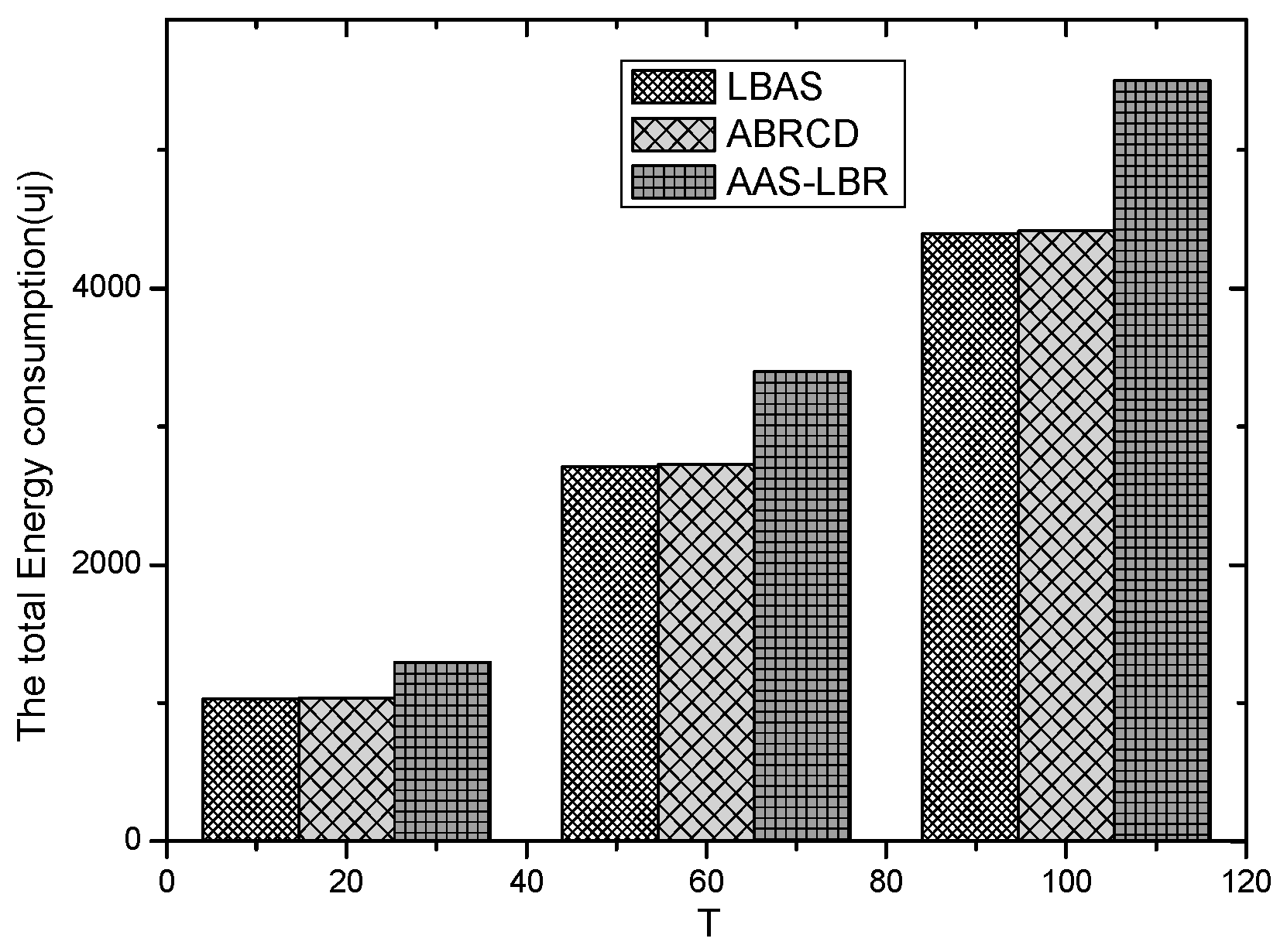
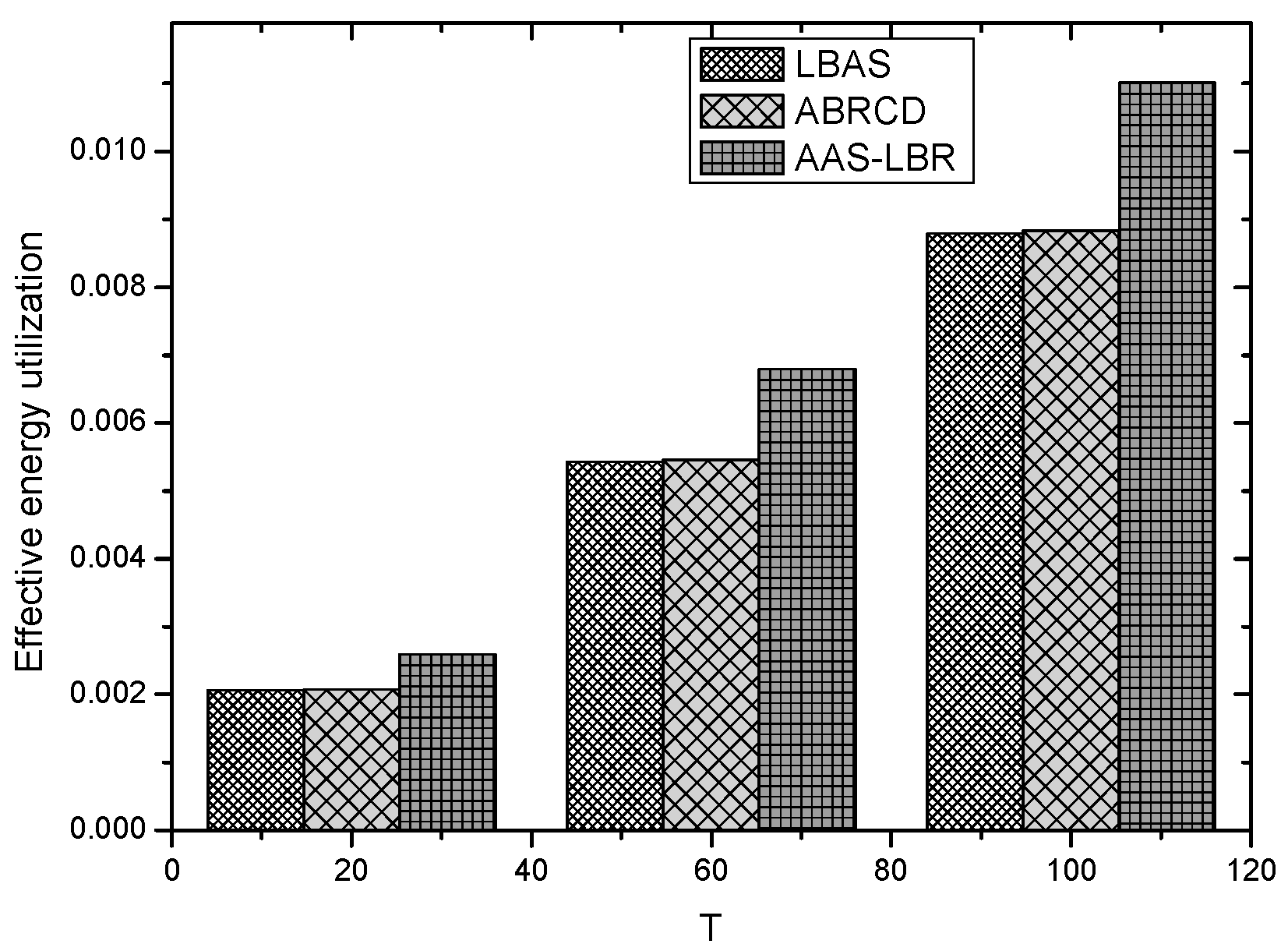
| The Scene or Parameter of Network | Scheme | The Maximum Energy Consumption (uj × ) | The Total Energy Consumption (uj × ) |
|---|---|---|---|
| , = 20, number of nodes are 200 | AAS-LBR | 155.97503 | 1295.02318 |
| ABRCD | 155.97503 | 1036.77183 | |
| LBAS | 155.97503 | 1036.80625 | |
| , = 60, number of nodes are 200 | AAS-LBR | 409.47297 | 3397.00115 |
| ABRCD | 409.47297 | 2727.33655 | |
| LBAS | 409.47297 | 2714.27026 | |
| , = 100, number of nodes are 200 | AAS-LBR | 662.6201 | 5504.79548 |
| ABRCD | 662.6201 | 4415.58208 | |
| LBAS | 662.6201 | 4394.42601 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Liu, W.; Zeng, Z.; Liu, A.; Huang, G.; Xiong, N.N.; Cai, Z. Adding Active Slot Joint Larger Broadcast Radius for Fast Code Dissemination in WSNs. Sensors 2018, 18, 4055. https://doi.org/10.3390/s18114055
Yang W, Liu W, Zeng Z, Liu A, Huang G, Xiong NN, Cai Z. Adding Active Slot Joint Larger Broadcast Radius for Fast Code Dissemination in WSNs. Sensors. 2018; 18(11):4055. https://doi.org/10.3390/s18114055
Chicago/Turabian StyleYang, Wei, Wei Liu, Zhiwen Zeng, Anfeng Liu, Guosheng Huang, Neal N. Xiong, and Zhiping Cai. 2018. "Adding Active Slot Joint Larger Broadcast Radius for Fast Code Dissemination in WSNs" Sensors 18, no. 11: 4055. https://doi.org/10.3390/s18114055
APA StyleYang, W., Liu, W., Zeng, Z., Liu, A., Huang, G., Xiong, N. N., & Cai, Z. (2018). Adding Active Slot Joint Larger Broadcast Radius for Fast Code Dissemination in WSNs. Sensors, 18(11), 4055. https://doi.org/10.3390/s18114055







