Reliable Positioning and mmWave Communication via Multi-Point Connectivity †
Abstract
:1. Introduction
- We derive the CRLB for localization in a mmWave based multi-point connectivity scenario, which is subsequently solved to obtain the lower bound on positioning accuracy across spatially distributed receivers.
- We reformulate closed-from expressions for the Fisher Information Matrix (FIM) and provide insight on the dependence of different parameters on the achievable positioning quality.
- We provide a robust receive beamforming strategy that can retain a stable connectivity to combat the uncertainties of mmWave channel.
- We validate the performance of the formulated theoretical bounds via extensive numerical results, i.e., quality of positioning and achievable user-rate with the joint reception.
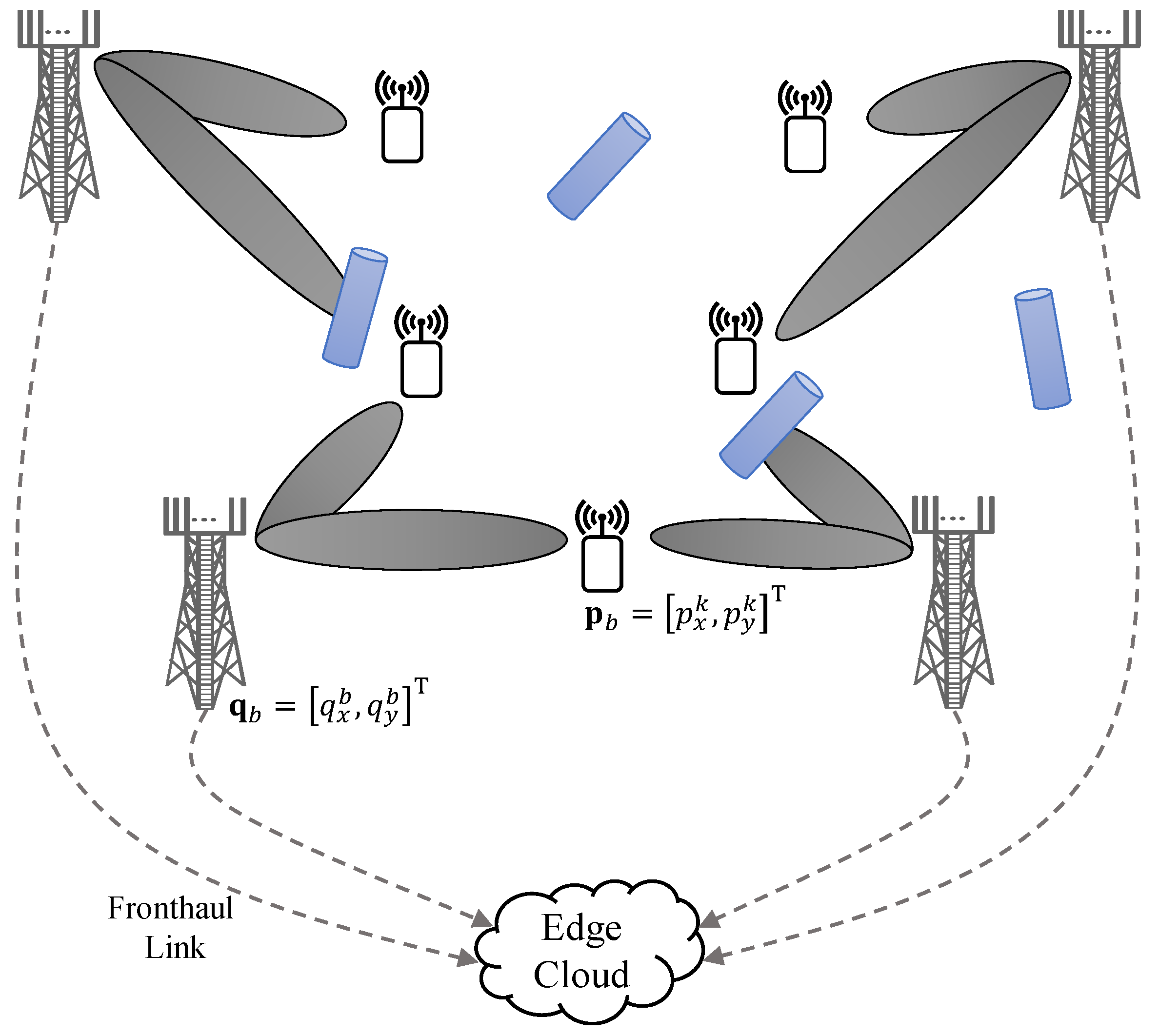
2. System Model
2.1. Channel Model
2.2. Signal Model
2.3. Performance Metrics
2.3.1. Positioning Accuracy
2.3.2. Effective Throughput
3. PEB Computation and Channel Estimate
3.1. FIM: Channel Parameters
3.2. CRB for Position
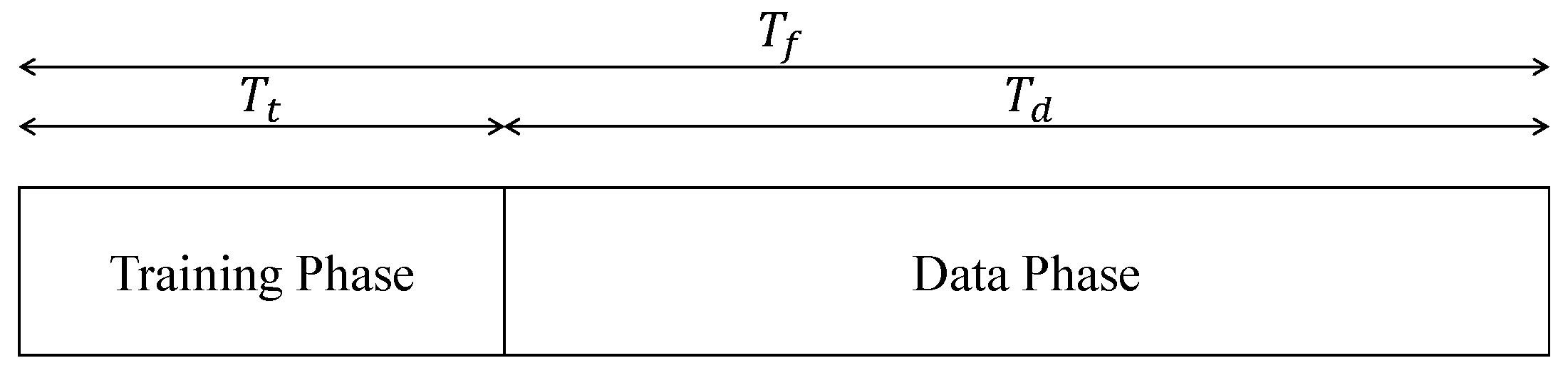
3.3. Channel Estimation
4. Simulation Results
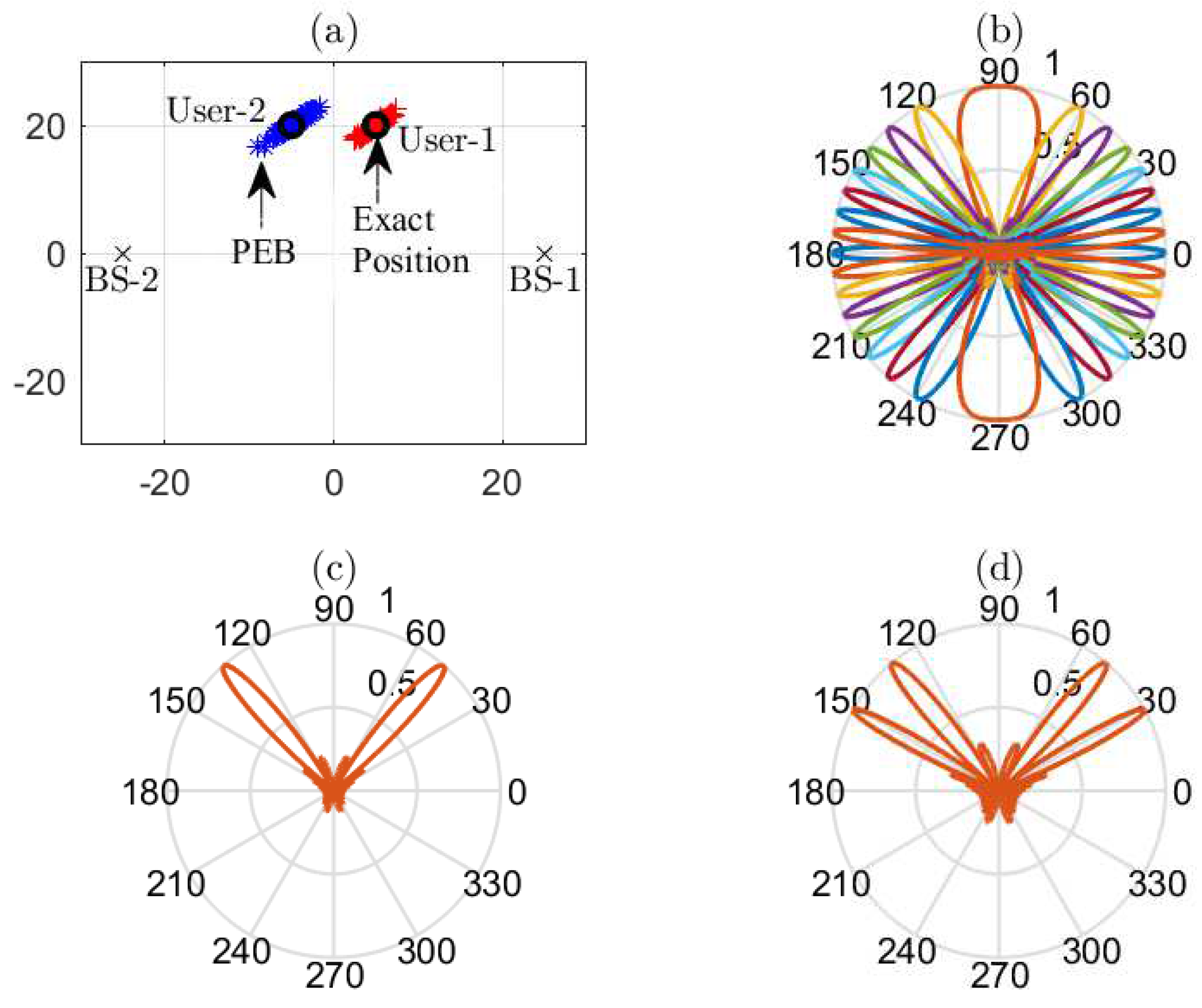
4.1. Simulation Setup
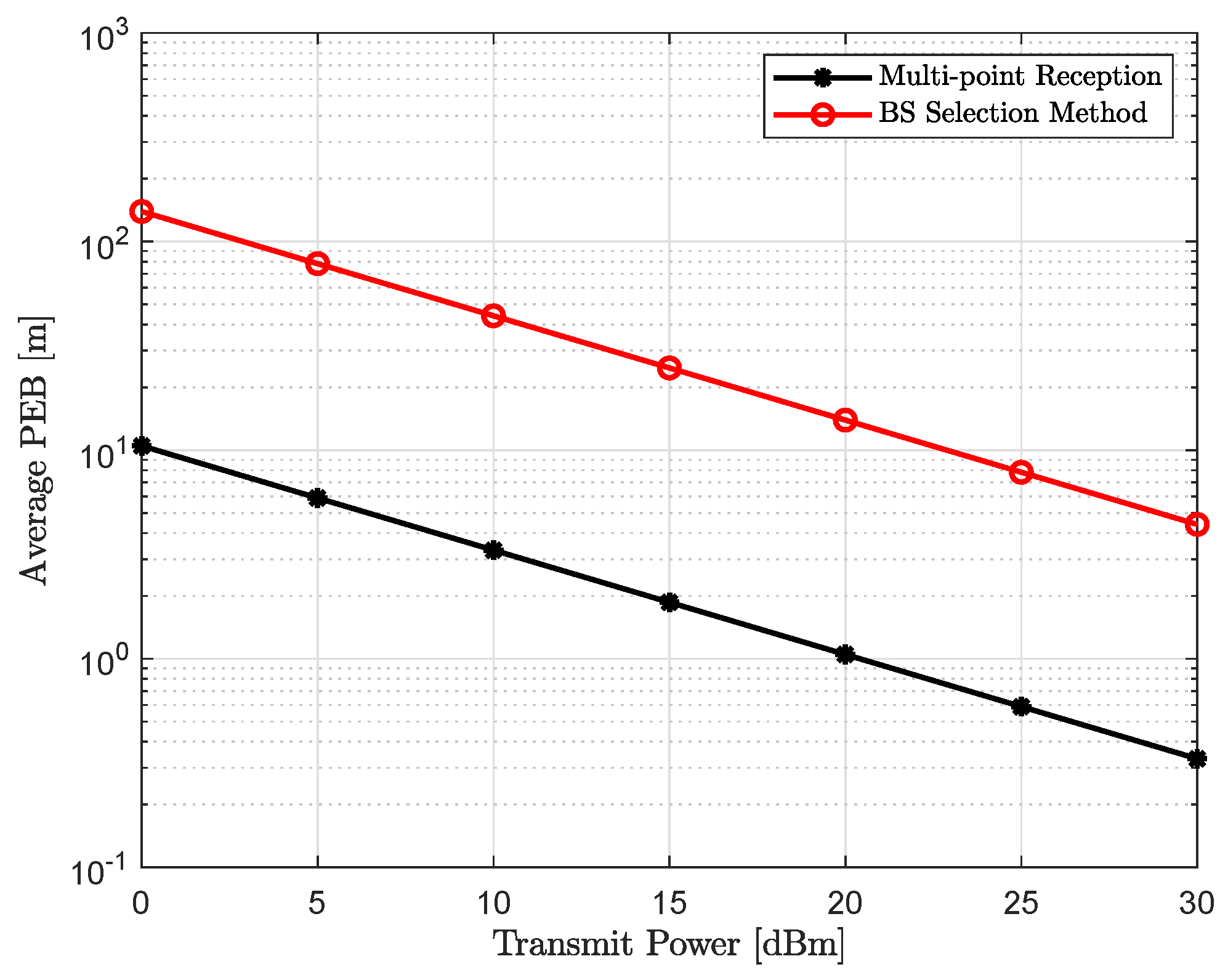
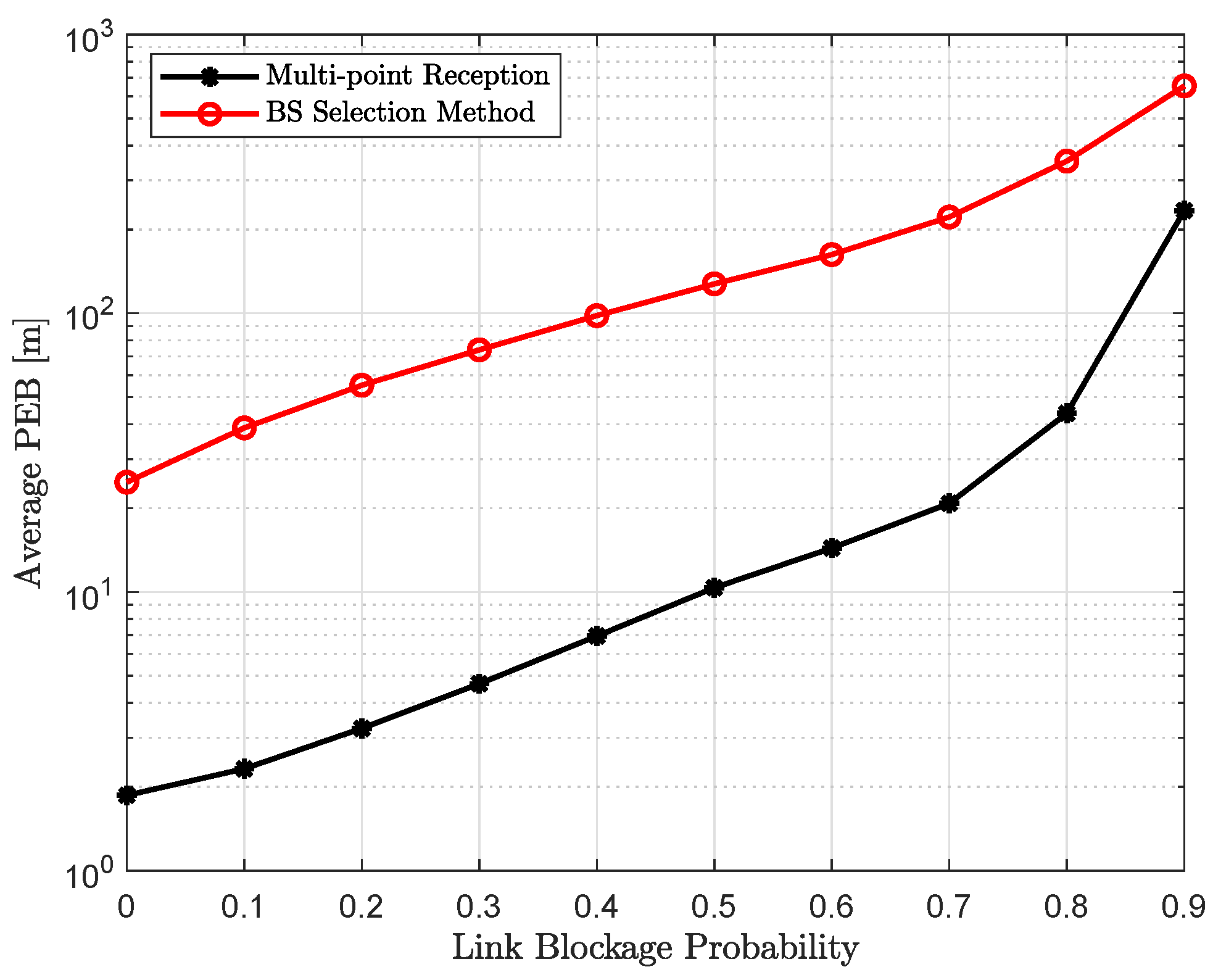
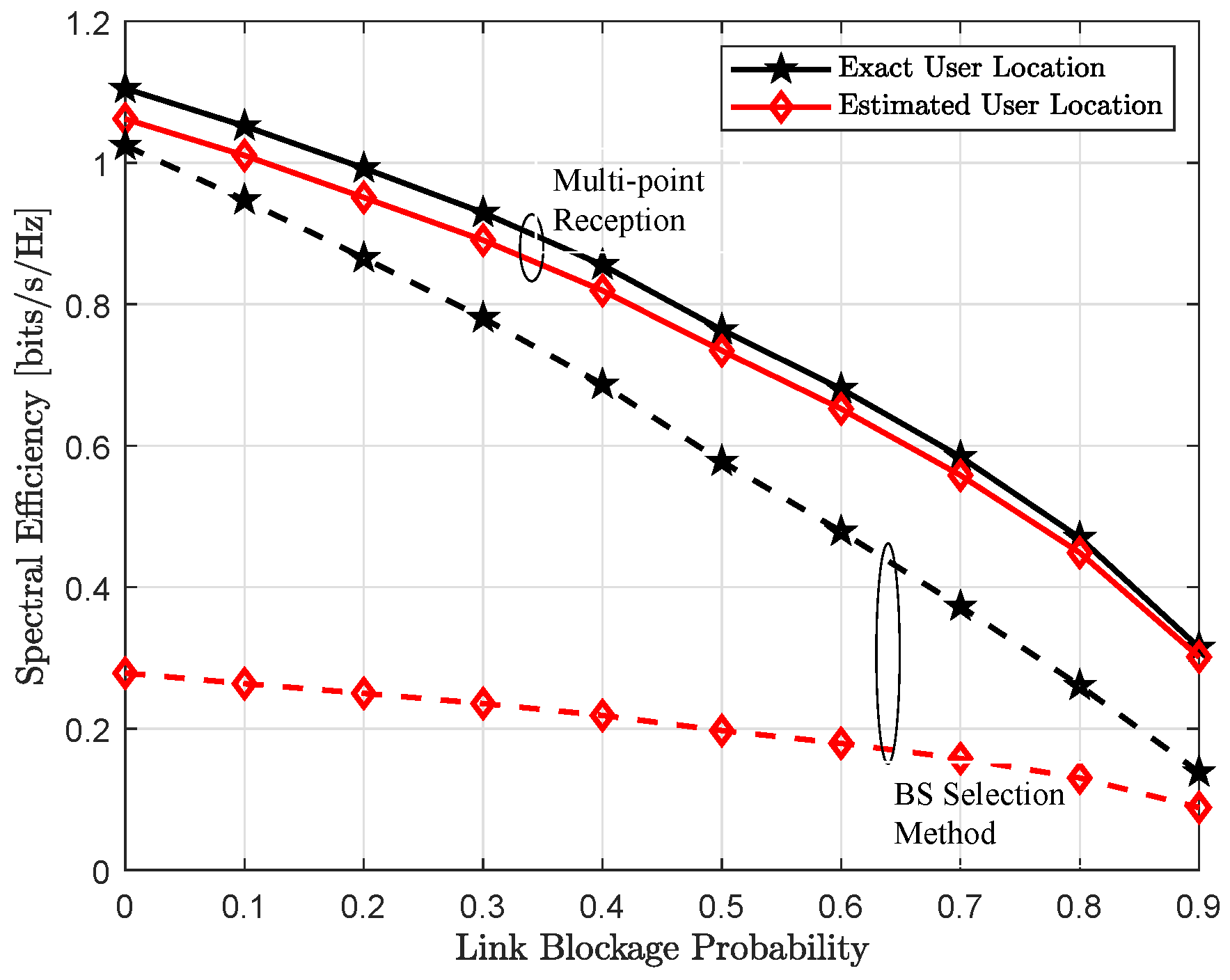
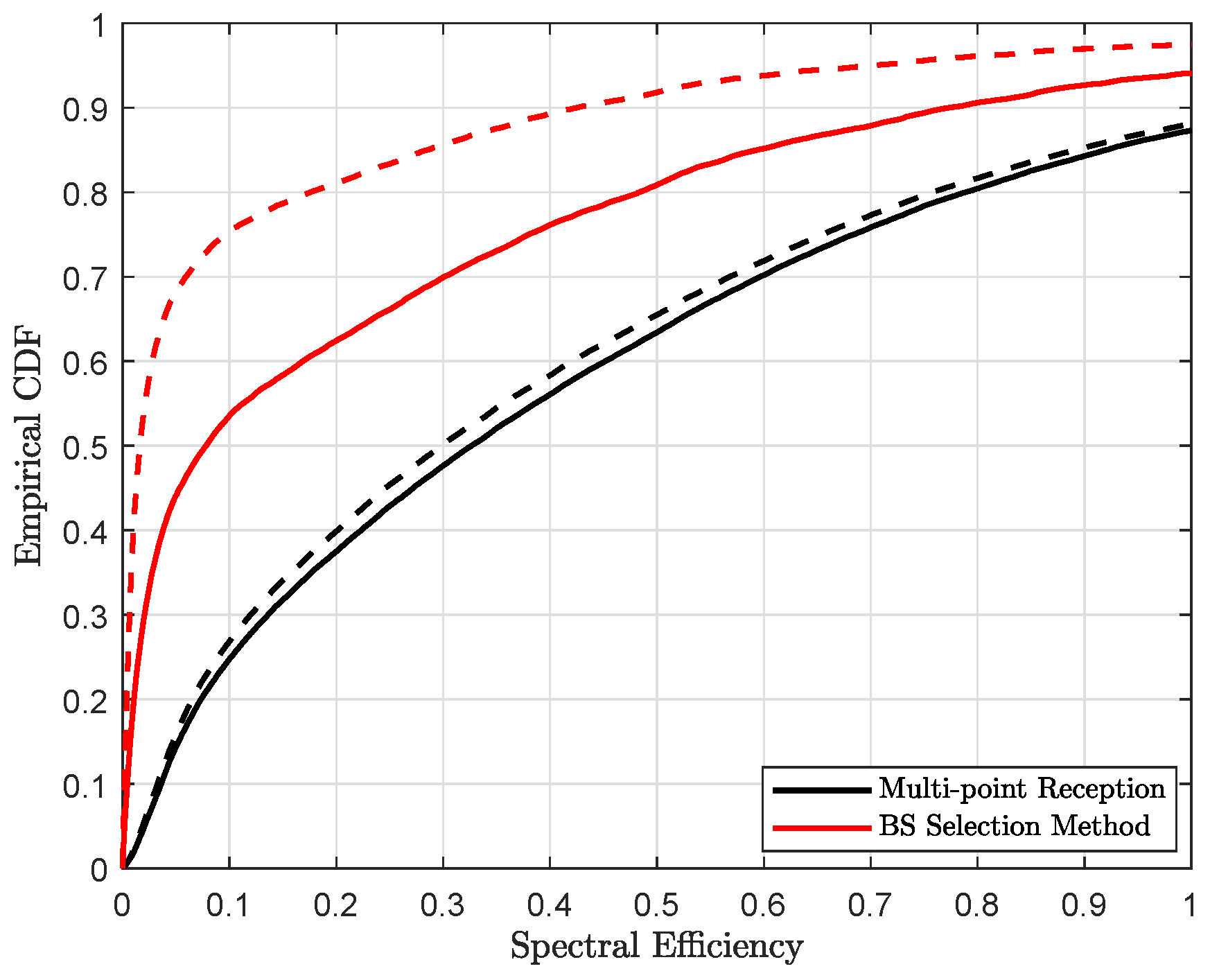
4.2. Position Accuracy
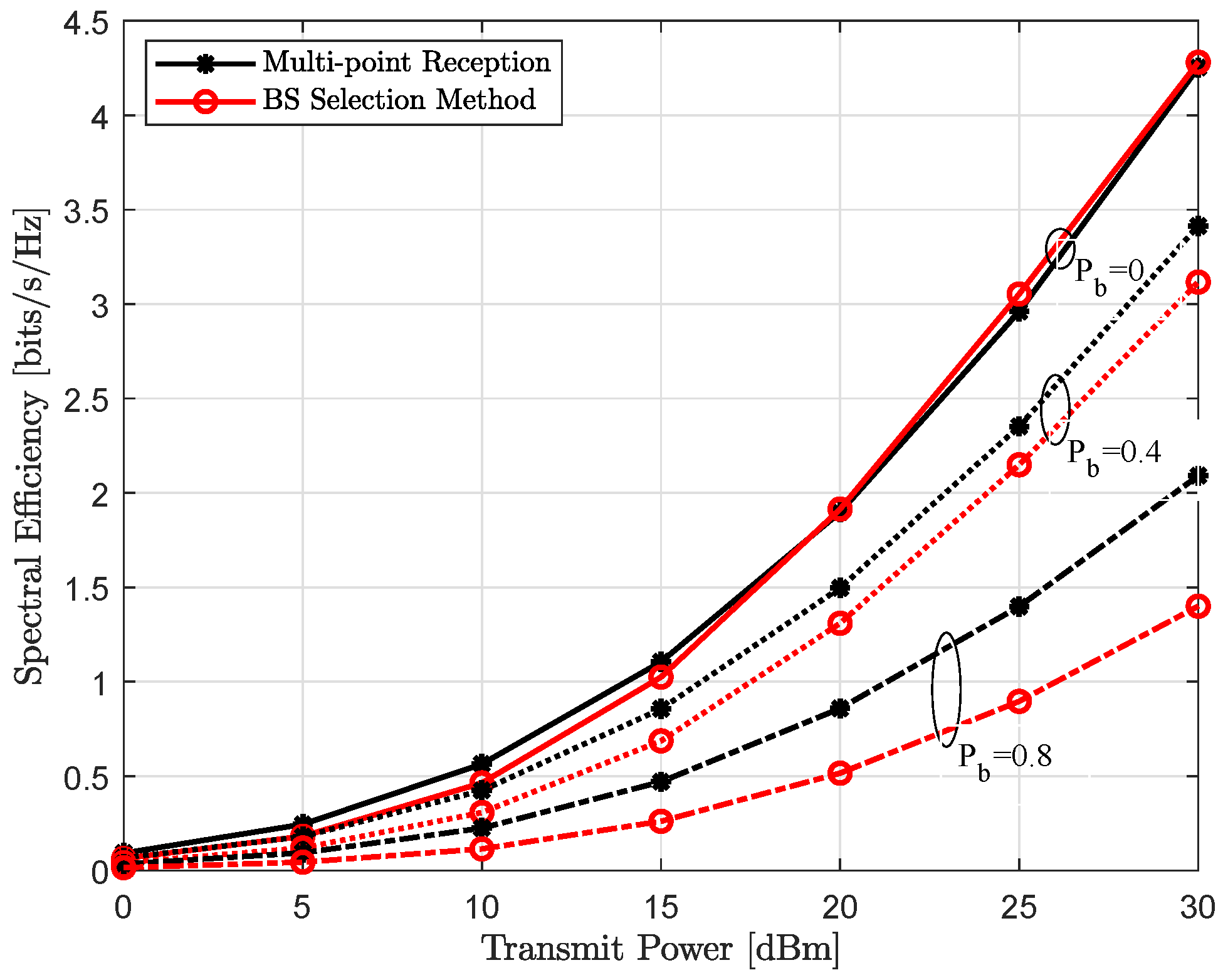
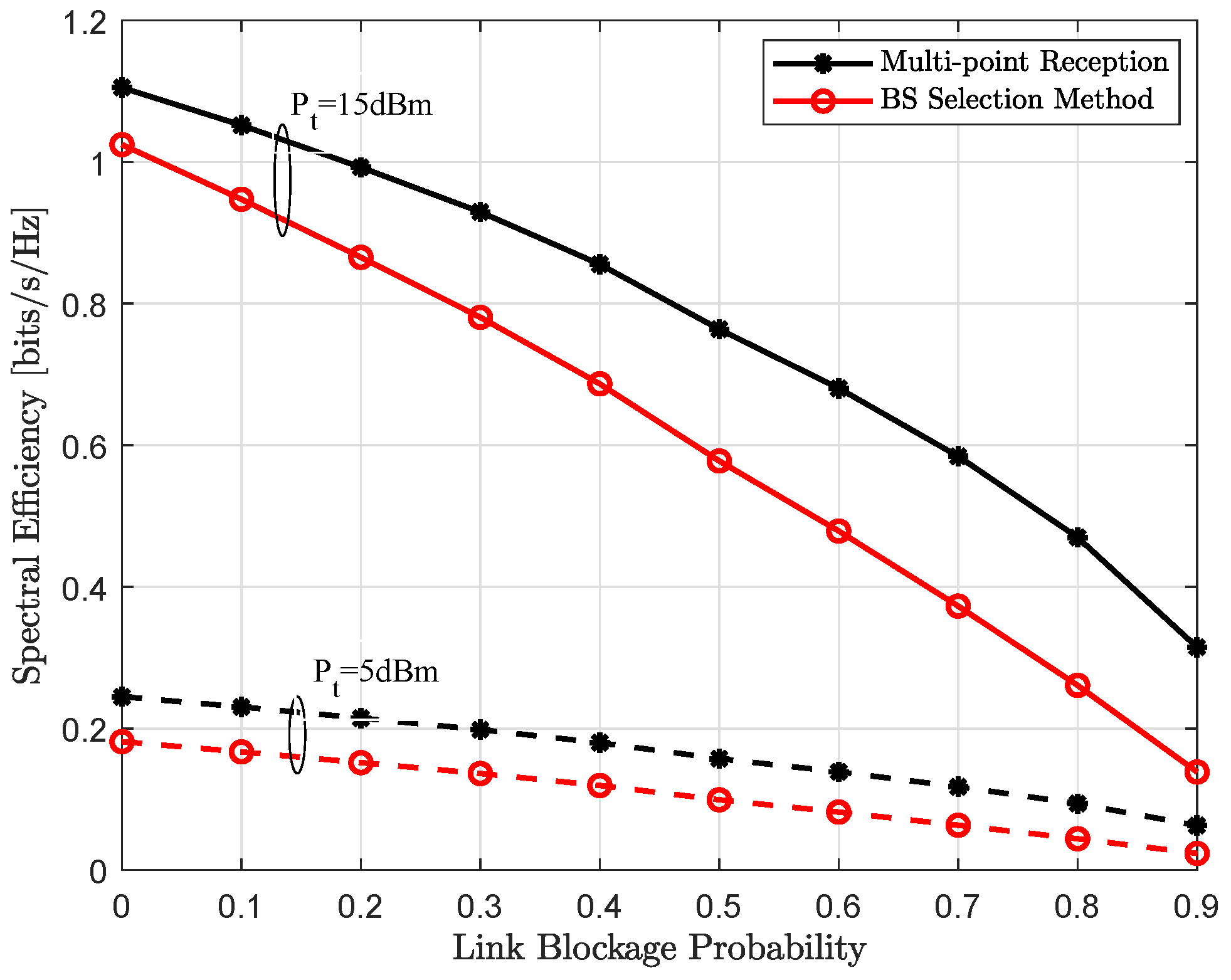
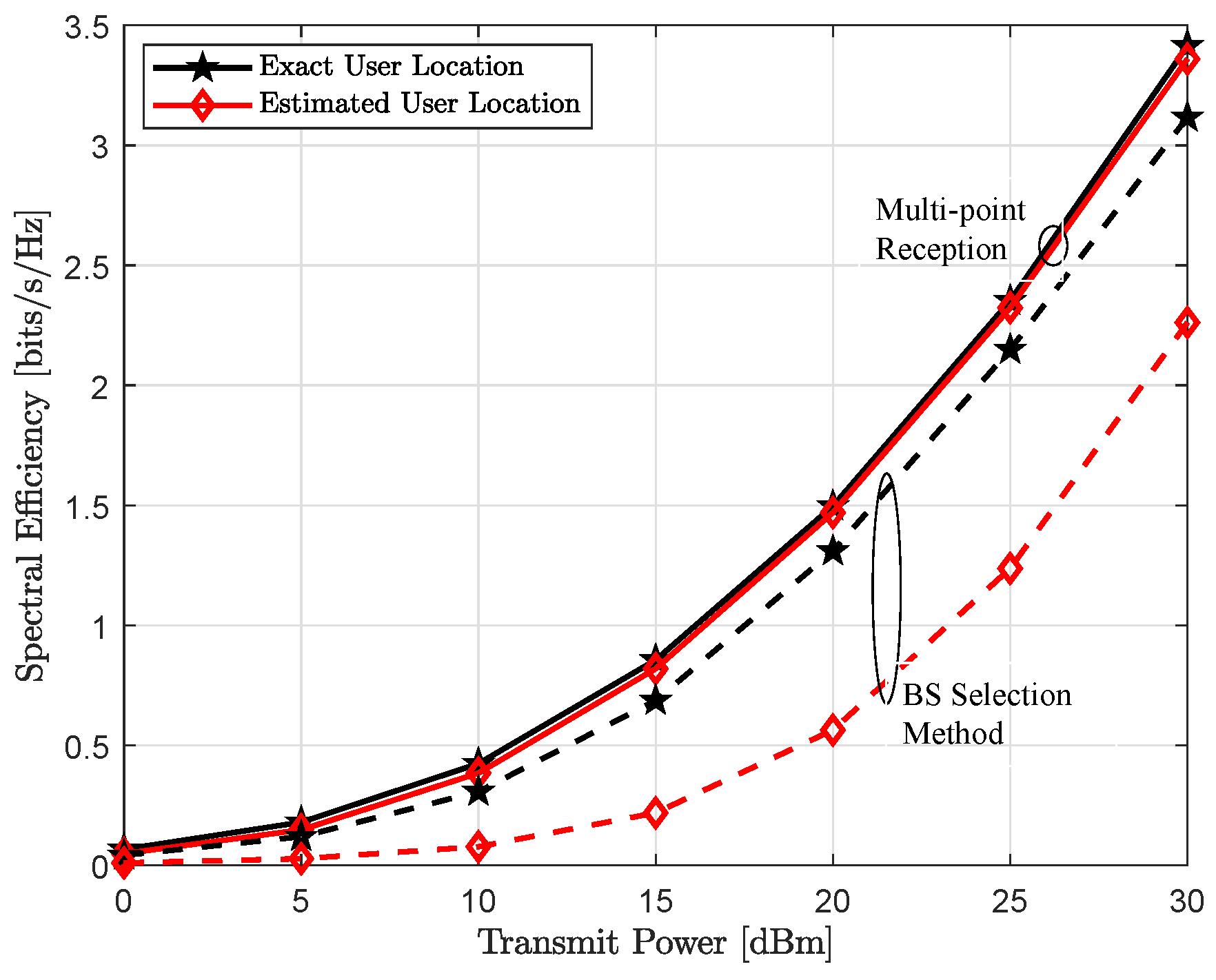
4.3. Achievable Throughput
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef] [Green Version]
- Lemic, F.; Martin, J.; Yarp, C.; Chan, D.; Handziski, V.; Brodersen, R.; Fettweis, G.; Wolisz, A.; Wawrzynek, J. Localization as a feature of mmWave communication. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 1033–1038. [Google Scholar] [CrossRef]
- 3GPP TSG RAN Meeting #80, RP-180897. New SID: Study on NR Positioning. 2018. Available online: https://portal.3gpp.org/ngppapp/CreateTdoc.aspx?mode=view&contributionId=909020 (accessed on 10 October 2018).
- El-Sayed, H.; Athanasiou, G.; Fischione, C. Evaluation of localization methods in millimeter-wave wireless systems. In Proceedings of the 2014 IEEE 19th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Athens, Greece, 1–3 December 2014; pp. 345–349. [Google Scholar] [CrossRef]
- Kurras, M.; Thiele, L.; Peng, X.; Ishii, N. Direction of Arrival Based Positioning in Three Dimensional Coordinates. In Proceedings of the WSA 2017 21th International ITG Workshop on Smart Antennas, Berlin, Germany, 15–17 March 2017; pp. 1–7. [Google Scholar]
- Deng, H.; Sayeed, A. Mm-wave MIMO channel modeling and user localization using sparse beamspace signatures. In Proceedings of the 2014 IEEE 15th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Toronto, ON, Canada, 22–25 June 2014; pp. 130–134. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Bielsa, G.; Palacios, J.; Loch, A.; Steinmetzer, D.; Casari, P.; Widmer, J. Indoor Localization Using Commercial Off-The-Shelf 60 GHz Access Points. In Proceedings of the 2018 IEEE Conference on Computer Communications (INFOCOM), Honolulu, HI, USA, 16–19 April 2018; pp. 1–5. [Google Scholar]
- Shahmansoori, A.; Garcia, G.E.; Destino, G.; Seco-Granados, G.; Wymeersch, H. 5G Position and Orientation Estimation through Millimeter Wave MIMO. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Shahmansoori, A.; Garcia, G.E.; Destino, G.; Seco-Granados, G.; Wymeersch, H. Position and Orientation Estimation Through Millimeter-Wave MIMO in 5G Systems. IEEE Trans. Wirel. Commun. 2018, 17, 1822–1835. [Google Scholar] [CrossRef] [Green Version]
- Destino, G.; Wymeersch, H. On the trade-off between positioning and data rate for mm-wave communication. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 797–802. [Google Scholar] [CrossRef]
- Kumar, D.; Saloranta, J.; Destino, G.; Tölli, A. On Trade-off Between 5G Positioning and mmWave Communication in a Multi-user Scenario. In Proceedings of the 2018 8th International Conference on Localization and GNSS (ICL-GNSS), Guimaraes, Portugal, 26–28 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Saloranta, J.; Destino, G.; Wymeersch, H. Comparison of different beamtraining strategies from a rate-positioning trade-off perspective. In Proceedings of the 2017 European Conference on Networks and Communications (EuCNC), Oulu, Finland, 12–15 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Saloranta, J.; Destino, G. Reconfiguration of 5G radio interface for positioning and communication. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 Auguat–2 September 2017; pp. 898–902. [Google Scholar] [CrossRef]
- Ghatak, G.; Koirala, R.; Domenico, A.D.; Denis, B.; Dardari, D.; Uguen, B. Positioning Data-Rate Trade-Off in mm-Wave Small Cells and Service Differentiation for 5G Networks. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- MacCartney, G.R.; Rappaport, T.S.; Rangan, S. Rapid Fading Due to Human Blockage in Pedestrian Crowds at 5G Millimeter-Wave Frequencies. In Proceedings of the GLOBECOM 2017–2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Bennis, M.; Debbah, M.; Poor, H.V. Ultra-reliable and low-latency wireless communication: Tail, risk and scale. arXiv, 2018; arXiv:1801.01270. [Google Scholar]
- Tölli, A.; Codreanu, M.; Juntti, M. Linear Cooperative Multiuser MIMO Transceiver Design with Per BS Power Constraints. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 4991–4996. [Google Scholar] [CrossRef]
- Tölli, A.; Codreanu, M.; Juntti, M. Cooperative MIMO-OFDM Cellular System with Soft Handover Between Distributed Base Station Antennas. IEEE Trans. Wirel. Commun. 2008, 7, 1428–1440. [Google Scholar] [CrossRef]
- Tölli, A.; Pennanen, H.; Komulainen, P. On the Value of Coherent and Coordinated Multi-Cell Transmission. In Proceedings of the 2009 IEEE International Conference on Communications Workshops, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Irmer, R. Coordinated multipoint: Concepts, performance, and field trial results. IEEE Commun. Mag. 2011, 49, 102–111. [Google Scholar] [CrossRef]
- MacCartney, G.R.; Rappaport, T.S.; Ghosh, A. Base Station Diversity Propagation Measurements at 73 GHz Millimeter-Wave for 5G Coordinated Multipoint (CoMP) Analysis. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Maamari, D.; Devroye, N.; Tuninetti, D. Coverage in mmWave Cellular Networks With Base Station Co-Operation. IEEE Trans. Wirel. Commun. 2016, 15, 2981–2994. [Google Scholar] [CrossRef]
- Skouroumounis, C.; Psomas, C.; Krikidis, I. Low-Complexity Base Station Cooperation for mmWave Heterogeneous Cellular Networks. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Skouroumounis, C.; Psomas, C.; Krikidis, I. Low complexity base station cooperation in cellular networks with blockages. In Proceedings of the 2016 IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, G.; Huang, K.; Lau, V.K.N.; Xia, B.; Li, X.; Zhang, S. Hybrid Beamforming via the Kronecker Decomposition for the Millimeter-Wave Massive MIMO Systems. IEEE J. Sel. Areas Commun. 2017, 35, 2097–2114. [Google Scholar] [CrossRef] [Green Version]
- Kay, S.M. Estimation theory. In Fundamentals of Statistical Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1993; Volume 1. [Google Scholar]
- Abu-Shaban, Z.; Zhou, X.; Abhayapala, T.; Seco-Granados, G.; Wymeersch, H. Error Bounds for Uplink and Downlink 3D Localization in 5G Millimeter Wave Systems. IEEE Trans. Wirel. Commun. 2018, 17, 4939–4954. [Google Scholar] [CrossRef]
- 3GPP TSG RAN Meeting #82, TS 38.300. NR and NG-RAN Overall Description. 2018. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3191 (accessed on 10 October 2018).

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, D.; Saloranta, J.; Kaleva, J.; Destino, G.; Tölli, A. Reliable Positioning and mmWave Communication via Multi-Point Connectivity. Sensors 2018, 18, 4001. https://doi.org/10.3390/s18114001
Kumar D, Saloranta J, Kaleva J, Destino G, Tölli A. Reliable Positioning and mmWave Communication via Multi-Point Connectivity. Sensors. 2018; 18(11):4001. https://doi.org/10.3390/s18114001
Chicago/Turabian StyleKumar, Dileep, Jani Saloranta, Jarkko Kaleva, Giuseppe Destino, and Antti Tölli. 2018. "Reliable Positioning and mmWave Communication via Multi-Point Connectivity" Sensors 18, no. 11: 4001. https://doi.org/10.3390/s18114001
APA StyleKumar, D., Saloranta, J., Kaleva, J., Destino, G., & Tölli, A. (2018). Reliable Positioning and mmWave Communication via Multi-Point Connectivity. Sensors, 18(11), 4001. https://doi.org/10.3390/s18114001




