1. Introduction
Cavity optomechanics exploring the radiation pressure force between the mechanical and optical modes have attracted considerable attention and progressed enormously over the past decades [
1,
2,
3,
4,
5]. A typical optomechanical system consists of a high-Q Fabry–Perot cavity with one movable mirror that is treated as a mechanical oscillator. This novel subject has created a new perspective to investigate light–matter interaction via radiation–pressure coupling between the mechanical degrees of freedom and the optical cavity mode [
3]. The development of cavity optomechanics has opened up avenues for providing a novel platform for many important applications, ranging from the ground-state cooling of mechanical motion [
6,
7,
8] and manipulation of light propagation [
9,
10,
11] to photon (phonon) blocking [
12,
13,
14]. In particular, with the development of nanophotonics, cavity optomechanical systems provide a unique platform to explore new availability for the precision measurement of weak force due to their important properties of small mass and high integrability [
15,
16,
17,
18,
19,
20].
In recent years, investigations of optomechanical nonlinearity [
21,
22,
23] have become a research hotspot, and many interesting phenomena have been revealed. As a fascinating nonlinear phenomenon, high-order sideband generation [
24,
25,
26] is not only of great significance in studying nonlinear characteristics of photon–phonon interaction, but also plays an indispensable role in excavating the potential applications of optomechanical systems. The process of high-order sideband generation is analogous to Stokes and anti-Stokes Raman scattering processes. By pumping the cavity field at frequency
, sidebands in the spectrum are created at
due to the radiation–pressure coupling of the photons with the mechanical motion. Here,
is the angular frequency of the mechanical oscillator and the integer
n represents the sideband order. Specifically, if the pump is red-detuned such that the upper sideband frequency is matched with the resonance frequency
, the anti-Stokes scattering is resonantly enhanced. Conversely, if the pump is blue-detuned such that the lower sideband frequency is matched with
, the Stokes scattering is resonantly enhanced. In addition, the rate of the Stokes and anti-Stokes scattering per phonon is proportional to the number of photons in the optical cavity. Note that the optomechanical nonlinearity originating from radiation–pressure coupling between the cavity mode and the mechanical mode can be substantively strengthened by atomic assistance [
27,
28]. The physical mechanism can be explained as follows: under specific parameter conditions, stimulated by the two-level atoms trapped in the optical cavity, the photon number in the cavity field will be greatly increased. Simultaneously, the distribution of photon number in the cavity field will be modified, and the radiation pressure coupling between the photon and the mechanical mode will be strengthened. Ultimately, the higher-order sidebands generation output from the cavity field will be greatly reinforced [
25].
Some previous studies [
29,
30] have shown that optomechanical nonlinearity is more sensitive to weak force, which have an attractive application prospect in precision measurement. In Ref. [
31] the high-order sideband generation shows a strong dependence on Coulomb interaction, and a proposal of detecting charge based on a Coulomb-interaction-dependent effect is proposed. However, this Coulomb-interaction-dependent effect is non-monotonic and can only been observed when the charge number is large enough, which severely limits the measurement accuracy of the charge sensor. In the present work, we report on a novel detection method that allows us to measure the charge number with an unprecedented sensitivity. Here, two dependent effects of the high-order sideband generation (i.e., Coulomb-interaction-dependent effect [
31] and atom-assisted-dependent effect [
25]) are combined. We reveal that the high-order sideband generation can not only be dramatically strengthened by atomic assistance, but also reveals a strong dependence on charge number. Furthermore, the sideband cutoff order and the charge number satisfy a monotonically increasing relationship, which is more sensitive than the atom-free case discussed previously. Calculations show that the sensitivity of the charge sensor in our scheme is improved by about 25 times. In particular, based on the current experimental conditions, we believe that the proposed scheme of a highly sensitive charge sensor will be highly accessible in experiments.
2. Charge Sensor Model
The charge sensor model is based on a hybrid atom–cavity optomechanical system, as schematically shown in
Figure 1, in which one mirror of the cavity is movable and is treated as a mechanical oscillator.
N identical two-level
atoms with the transition frequency
are located within the cavity field, and the Hamiltonian of these two-level atoms can be written as
=
, where
=
for
is the electronic projection operator and
is the population operator of the
i-th
atom. In the present work, we presume that most of two-level
atoms are originally prepared in the ground state. Therefore, the average number of the
atoms in the excited state is a small fraction of the total
atoms number
N. Under the weak excitation, the condition of the Holstein–Primakoff approximation [
32] is satisfied. Therefore, we can define
as an effective transition operator [
33].
represents the total coupling strength between the atomic en bloc and the cavity field, where
g is the single-atom vacuum Rabi frequency. The mechanical and cavity modes are coupled as
=
, where
G is the optomechanical coupling strength and
(
) indicates the annihilation (creation) operator of the cavity field. In analogy to nanoelectromechanical systems, the Coulomb interaction can also be introduced to an optomechanical system. A typical configuration is shown in
Figure 1, in which a tiny charged object is attached to the mechanical oscillator. In experiment [
34,
35], an ensemble of nitrogen-vacancy centers and electric charges can be embedded in a single crystal diamond nanobeam. In the same way, an ultra-miniature charged body can also be embedded in the movable mirror of the cavity in the lab. The Hamiltonian of the Coulomb interaction be written as
=
, with
the electrostatic force constant,
and
respectively the charge number of the mechanical oscillator and the charged body, and
r the distance between the mechanical oscillator and the charged object. For simplicity, we assume that the charge of the mechanical oscillator
is changeless and the variation of
can be written as
=
, with
e the elementary charge and
the charge number.
In this work, the system is driven by a strong control field with frequency
and a weak probe field with frequency
. Applying the rotating wave approximation, viz.,
, the evolutionary dynamics of this hybrid optomechanical system can be well depicted by the Heisenberg–Langevin equations as:
where
(
) is the momentum (position) operator of the mechanical oscillator with the effective mass
m and angular frequency
.
=
is the detuning of the cavity field and the two-level atoms with respect to the driving field, respectively.
are the amplitudes of the input field with
the power of the control field, and
the power of the probe field.
=
+
is the total decay rate of the cavity field containing an intrinsic loss rate
and an external loss rate
[
3]. The decay rates of the mechanical oscillator
and the two-level atom
are introduced classically. The thermal noise of the mechanical oscillator
satisfies the correlation function
[
37], with
the Boltzmann constant and
T the temperature of the mechanical oscillator. Additionally, the quantum noise of the cavity field
and the two-level atom
satisfy the correlation function
,
, respectively. Here, under the semiclassical approximation, the quantum noise can be dropped safely because their mean values are zero (i.e.,
,
, and
). Here, we need to point out that the photothermal forces [
38] in our scheme can be safely ignored because the delay time of the photothermal forces is much larger than the measurement time of the sideband spectrum in the laboratory [
9]. All the operators can be reduced to their expectation values, that is,
,
,
, and
, because we focus on the average response of the system [
1]. Using mean-field approximation, viz.,
, the Heisenberg–Langevin equations can be written as:
Equation (
2) is a group of partial differential equations that can be numerical solved by using the Runge–Kutta method. The output field
can be obtained by using the standard input–output notation
, where
are the effective driven fields. The output spectrum
in the frequency domain can be acquired by performing the fast Fourier transform of
, that is,
, where
is the spectrometer frequency of the output field [
24]. The physical picture of this transform is that the output field of the system in the time domain can be formally expressed by
, where
is the
n-th transmission coefficient of the output field. After the fast Fourier transform [
39], the frequency spectrum of the output field will generate a component at frequencies
in the frequency domain where
n is referred to as the sideband order.
Note that if
, our system is reduced to a traditional optomechanical system with Coulomb interaction, and a proposal for detecting charge based on a Coulomb-interaction-dependent effect has been proposed [
31]. Under weak driven fields (about a few mW), the variation of the sideband spectrum is about 11.83% per charge, and the relationship between the sideband order and the charge number is non-monotonic. In this context, we propose a novel scheme for the precision measurement of charge number based on atom-assisted high-order sideband generation in a hybrid optomechanical system, which allows us to measure the charge number with an unprecedented sensitivity. In our scheme, a monotonic relationship between the cutoff order of the sideband spectrum and the charge number is obtained, and the variation of the sideband spectrum is about 300% per charge. Calculations show that the sensitivity of the charge sensor is improved by about 25 times with respect to the atom-free case discussed previously.
3. Results and Discussion
In what follows, we discuss the relationship between the atom-assisted high-order sideband generation and the Coulomb interaction, and a feasible method for achieving highly sensitive charge sensor is proposed. First, it is necessary to evaluate the actual experimental possibilities of such a highly sensitive charge sensor. In the experiment, we chose a microscale optomechanical system with a size of about 50
m, mass of the mechanical oscillator
m = 10
, and half cavity linewidth
= 1
. An ensemble of identical
atoms were trapped in the cavity field. The amount of charge on the charged vibrator was
= 27.5 nC and the distance between the charged body and the charged vibrator was r = 67
m. The power of the control field
= 0.5
and the weak probe field with probe power
= 1.25
, and the transmission of the output field could be measured by the homodyne technique. All these conditions already have mature experimental foundations [
6,
34,
40], so the proposed scheme of a highly sensitive charge sensor will be highly accessible in the laboratory.
Figure 2 plots the high-order sideband generation output from the cavity field under different charge number
n. In the absence of two-level atoms, the optomechanical nonlinearity is quite weak so that the anti-Stokes scattering processes are severely suppressed. As shown in
Figure 2a, the sideband ended up at the order of 3 when the charge number
. In
Figure 2b, even though the charge number
n increased to 100, the cutoff order and the amplitude of the sideband spectrum were hardly enhanced. Obviously, it is very difficult to obtain a strong dependency between the high-order sideband generation and the Coulomb interaction when the charge number is not large enough. Upon further increase of the charge number
n to 150, as
Figure 2c shows, the cutoff order of the sideband spectrum was extended to about 10 and the amplitude of each sideband was also obviously enhanced. A similar result is shown in
Figure 2d, when we continued to increase the number of charges to
. From the above discussion, we can see that the Coulomb-interaction-dependent effect without atomic assistance is far from sufficient for the precision measurement of charge number, and is unsuitable for extremely weak charge measurement environments.
Previous studies have shown that resonantly enhanced feedback-backaction arising from optomechanical nonlinearity can be substantively reinforced by atomic assistance [
27,
28]. A strong dependence between the high-order sideband generation and the charge number
n is observed in
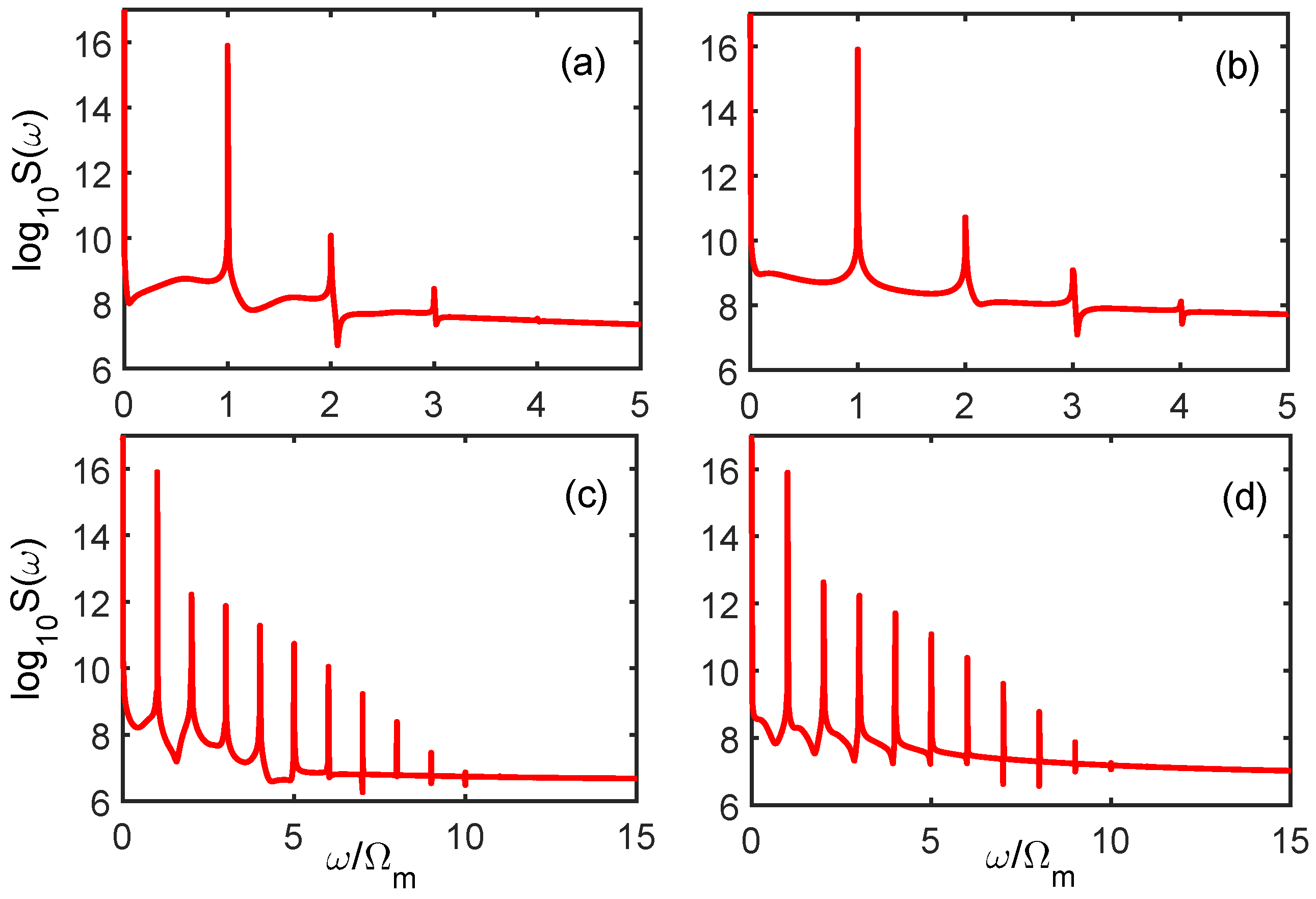
Figure 3. In contrast to
Figure 2a, both the cutoff order of the sideband spectrum and the amplitude of each sideband were markedly enhanced owing to the reinforcement of optomechanical nonlinearity between the cavity field and the mechanical oscillator. As shown in
Figure 3a, the higher-order sidebands ended up at the order of 6 and the intensity of each sideband was also strengthened. Intriguingly, high-order sideband generation in such atom–cavity optomechanical systems has a strong dependence on the charge number. As shown in
Figure 3b, when a single charge was added to the charged body (charge number
n = 2), we can clearly see that the order of the sidebands ended up at the order of 8, and the intensity of each sideband was also distinctly enhanced. More robust high-order sideband generations are shown in
Figure 3c,d, respectively, when the charge numbers
n = 3 and 4 are considered. Obviously, not only did the cutoff order extend to 14 and 15 corresponding to the charge numbers
n = 3 and 4, but the amplitude of the sideband spectra were increased significantly as well. In addition, the sideband spectra exhibiting a typical non-perturbative nature were quite different from
Figure 3a,b. That is, the intensity of the lower-order sidebands were smaller than the higher-order sidebands, which indicates that the strong optomechanical nonlinearity was greatly reinforced by atomic assistance. Comparing
Figure 2 and
Figure 3, the ultra-sensitive Coulomb-interaction-dependent effect of high-order sideband generation reminds us of the possibility of realizing a highly sensitive charge sensor using an atom-assisted optomechanical system.
Figure 4 plots the cutoff order of the high-order sideband varying with the charge number
n under the atom-existence case and the atom-free case, respectively. As the red columns show in
Figure 4, the cutoff order of the higher-order sidebands was almost unchanged when the number of charges was less than 100. Only when the charge number was sufficient (about 150), the cutoff order of the higher-order sidebands had obvious changes. In our scheme, as the blue columns show, a clear change in the cutoff order of the sideband spectrum was observed, even though a single charge was embedded in the charged object, which provides us with the possibility of proposing the precision measurement of single charges. Additionally, we note that the dependence of the cutoff order of the high-order sideband generation on the charge number had a monotonous relationship. As shown in
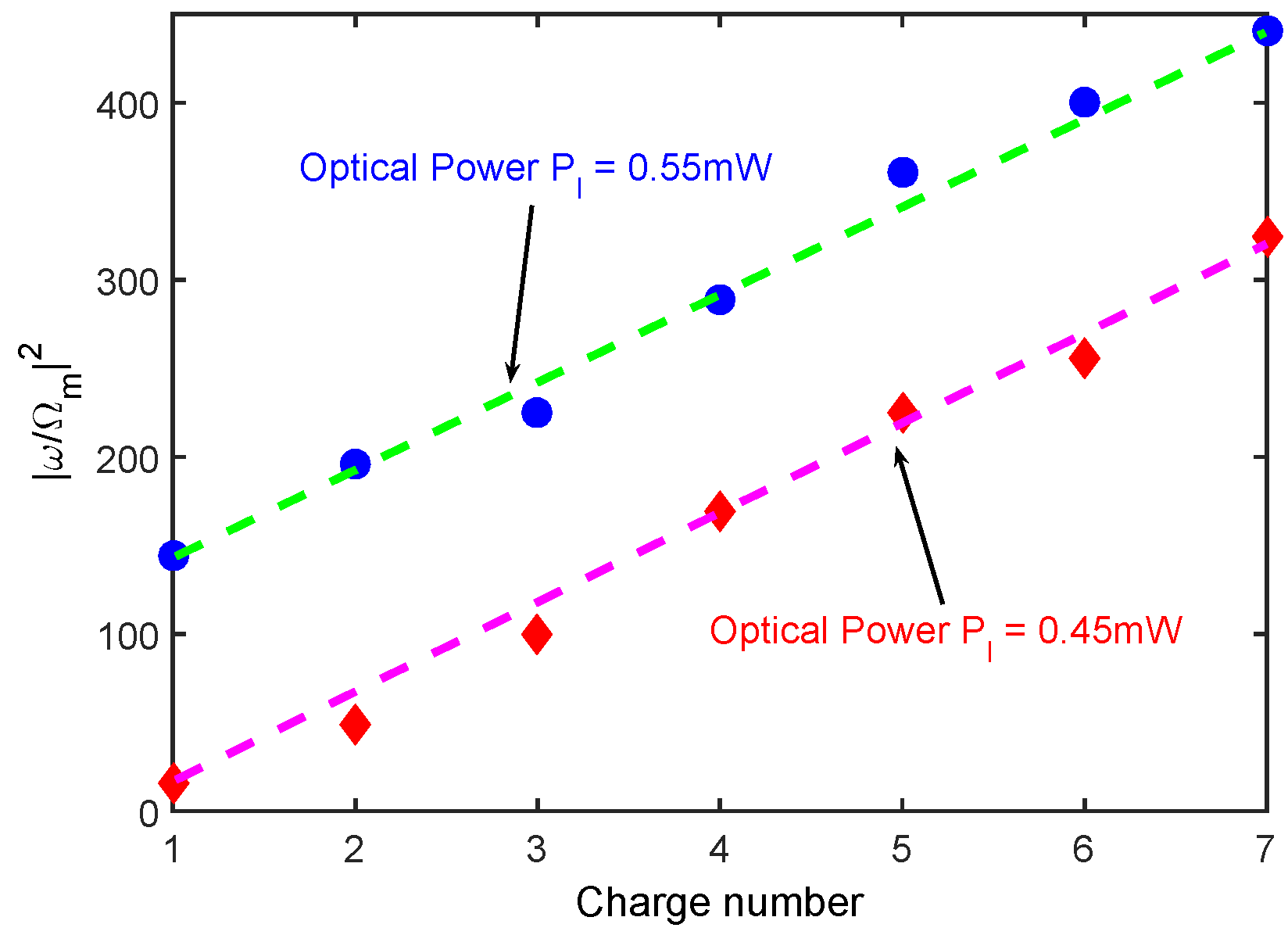
Figure 5, the monotonous relation between
and the charge number
n held for different optical powers. This monotonous relationship for the cutoff order of the sideband spectrum in the presence of electric interaction is more convenient and useful than the non-monotonous relationship discussed previously [
31].
In order to investigate the influences of other degrees of freedom of the system on the sideband sensitivity change, the cutoff order of the sideband spectrum as a function of the atom–cavity coupling
, the optomechanical coupling
G, and the atomic detuning
, respectively, are plotted in
Figure 6. We observed that in the case of weak atom–cavity coupling strength (i.e.,
), the order of the sidebands did not increase significantly. However, as the atom–cavity coupling strength increased, the order of sidebands increased sharply, and then tended to smooth. The physical mechanism is that the total coupling strength between the atomic en bloc and the cavity field is determined by the number of the two-level atoms (i.e.,
). In the case of a small number of atoms, the optomechanical nonlinearity cannot be significantly enhanced so that the generation of the high-order sideband is not obvious. As the number of atoms increases, the photon distribution of the cavity field changes, as well as the radiation pressure coupling between the photon and the mechanical mode will be strengthened. As expected, the sideband effect was conspicuously enhanced, as shown in
Figure 6a. Upon continuing to increase the number of atoms, however, the sideband effect was no longer strengthened because the system entered the over-coupling regime and the nonlinear strength tended to be saturated. Similar results are shown in
Figure 6b. As we increased the optomechanical coupling strength, the cutoff order of the sideband spectrum was observed to transit from a slow increase state to a region of rapid increase, finally entering the stationary regime. All these results agree very well with those of previous studies [
25]. The inset in
Figure 6b plots the cutoff order of the higher-order sidebands as a function of the atomic detuning
. We noted that the maximum sideband effect appeared if and only if the detuning of the atoms
was matched with the resonance frequency
.
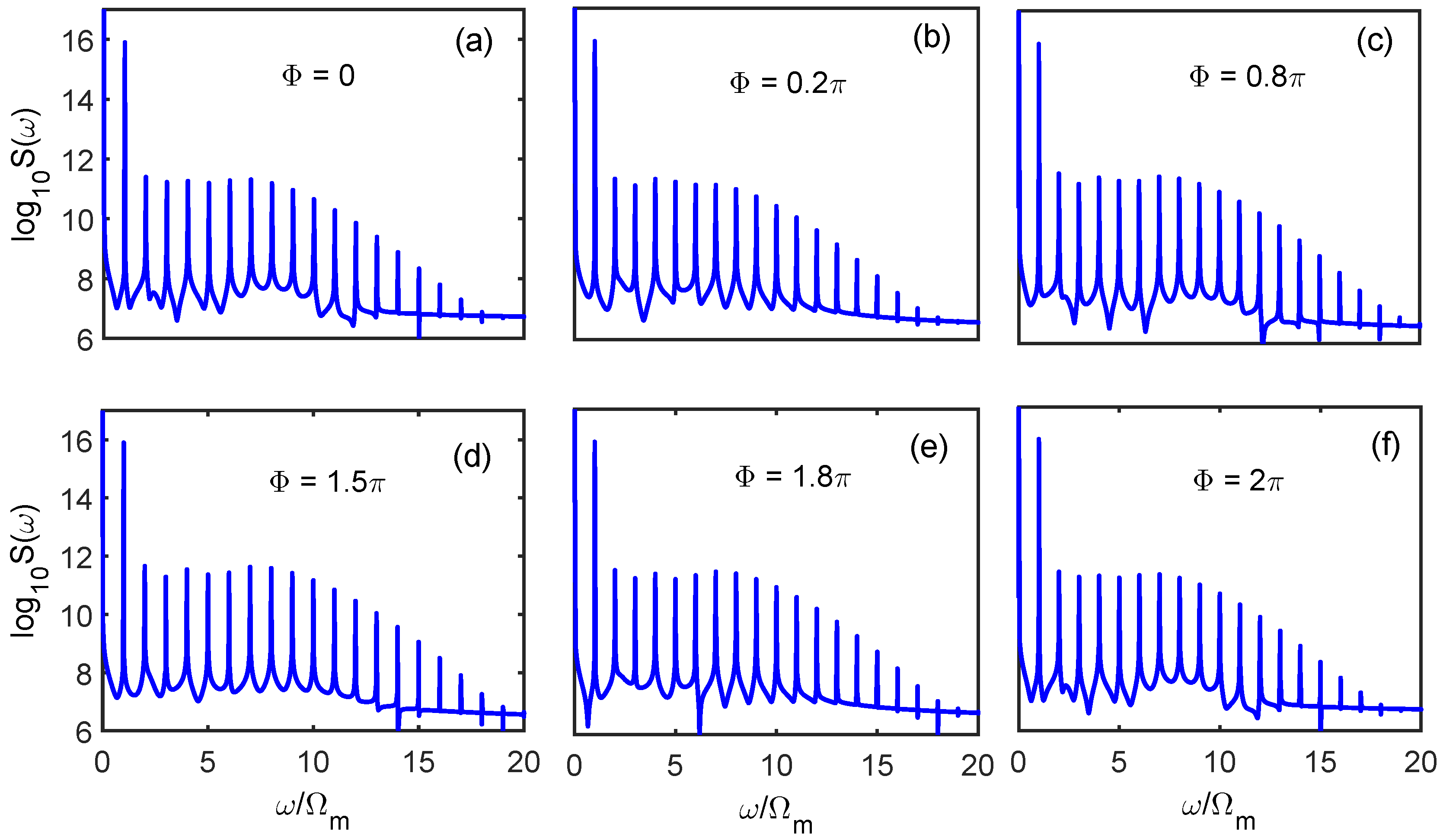
Finally, phase-dependent effects of the high-order sideband generation with electric interaction were investigated, which remains largely unexplored and may provide applications in phase-coherent measurement. We started with the Hamiltonian of the probe field
=
Here,
is the relative phase of the two input lasers, that is,
=
with
the initial phase of the probe field and
the initial phase of the driving field [
41].
Figure 7 shows the high-order sideband generation output from the cavity field under different phase
. Here, we chose the charge number
n = 5 for the purpose of obtaining a robust sideband spectrum. From
Figure 7 we can see that the relative phase of the two input lasers exhibited a certain influence on the sideband spectrum output from the cavity field. When we chose the relative phase
= 0.2
, the amplitude of each sideband was weaker than the circumstances without considering the phase effect. However, as shown in
Figure 7c, the intensity of each sideband amplitude was obviously enhanced. Physically, different phases will give rise to destructive interference or constructive interference processes, which corresponds to suppressing or enhancing the optomechanical nonlinearity of the system. The intensity of the sideband amplitude is ultimately reflected in the output spectrum. Phase is an important information carrier, and discussing phase-dependent effects may help to explore the coherence properties of photons. Therefore, our results may have potential applications in phase-coherent measurement and optical communications, as Refs. [
42,
43,
44,
45] recommend.