Simple Adaptive Single Differential Coherence Detection of BPSK Signals in IEEE 802.15.4 Wireless Sensor Networks
Abstract
:1. Introduction
2. System Model
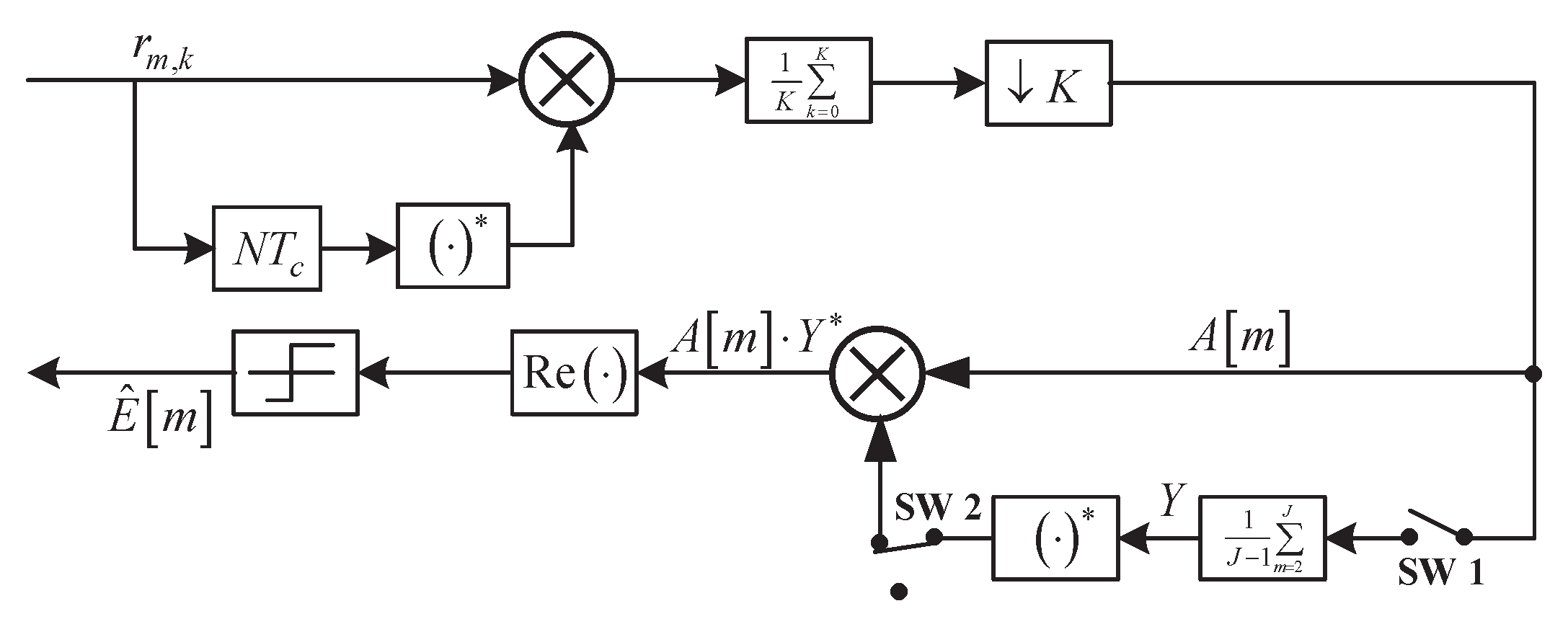
3. Generalized BSDCD Scheme
| Algorithm 1 Framework of GBSDCD Algorithm. |
| Input: : baseband sample for the mth bit ; : sample number for each bit of the actual data; : observation length of the preamble in bit intervals; : number of the autocorrelation sample mth bit of the preamble; J: bit number in preamble field; L: payload length of the PPDU. Output: : detection of the mth bit of the actual data.
|
4. The Available Optimal Quantization Function
5. Summary and Analysis of Some Simplified Estimation Schemes
5.1. Simplified Estimation—Estimation A
5.2. Simplified Estimation—Estimation B
5.3. Simplified Estimation—Estimation C
5.4. Remarks
- These estimators are obtained from approximations made to a structure motivated by DAML estimation of the CPOE.
- The estimator in Equation (10) is convenient and with acceptable complexity as compared with Equation (9). Since it works only for very small frequency-offset values and reasonably high SNRs, it is a CFO and SNR limited estimator. Correspondingly, a severe degradation to the system packet error performance in the detection process will be introduced, which is not suitable for our purposes.
- Equation (12) achieves an estimate with quite reasonable accuracy. It does so by four preconditions, i.e., smart geometric division to the observation space, accurate subspace locating criterion, equivalent avenue for the calculation of , and advisable approximation . One arctan operation is required for a DAML estimator given in Equation (9). However, this computationally intensive operation is completely avoided in Equation (12). Surprisingly, such a complexity reduction results in almost no frequency-offset invariance degradation in the detection process, as will be inferred in Section 7.
- The canonical approximation involved in Equation (12) is much more accurate than the atypical approximation involved in Equation (13). This implies that, as such inaccuracy frequently makes the measurement in Equation (13), either a large overestimation or a large underestimation of the CFOE, whereas no such inappropriate estimation is likely to occur in Equation (12). Actually, Equation (12) allows a real-time adjustment with additional one division and one addition operations, which, however, can achieve almost dB gains at PER of [10].
6. Proposed Divisor-Free CFOE Estimator
- Equation (19) are obtained from approximations made to a structure motivated by DAML estimation scheme in Equation (14) or Equation (18), and a simple adaptive offset terms is provided. This enables the receiver to intelligently adjust the estimated CPOE value according to the time-varying channel conditions with respect to each packet transmission.
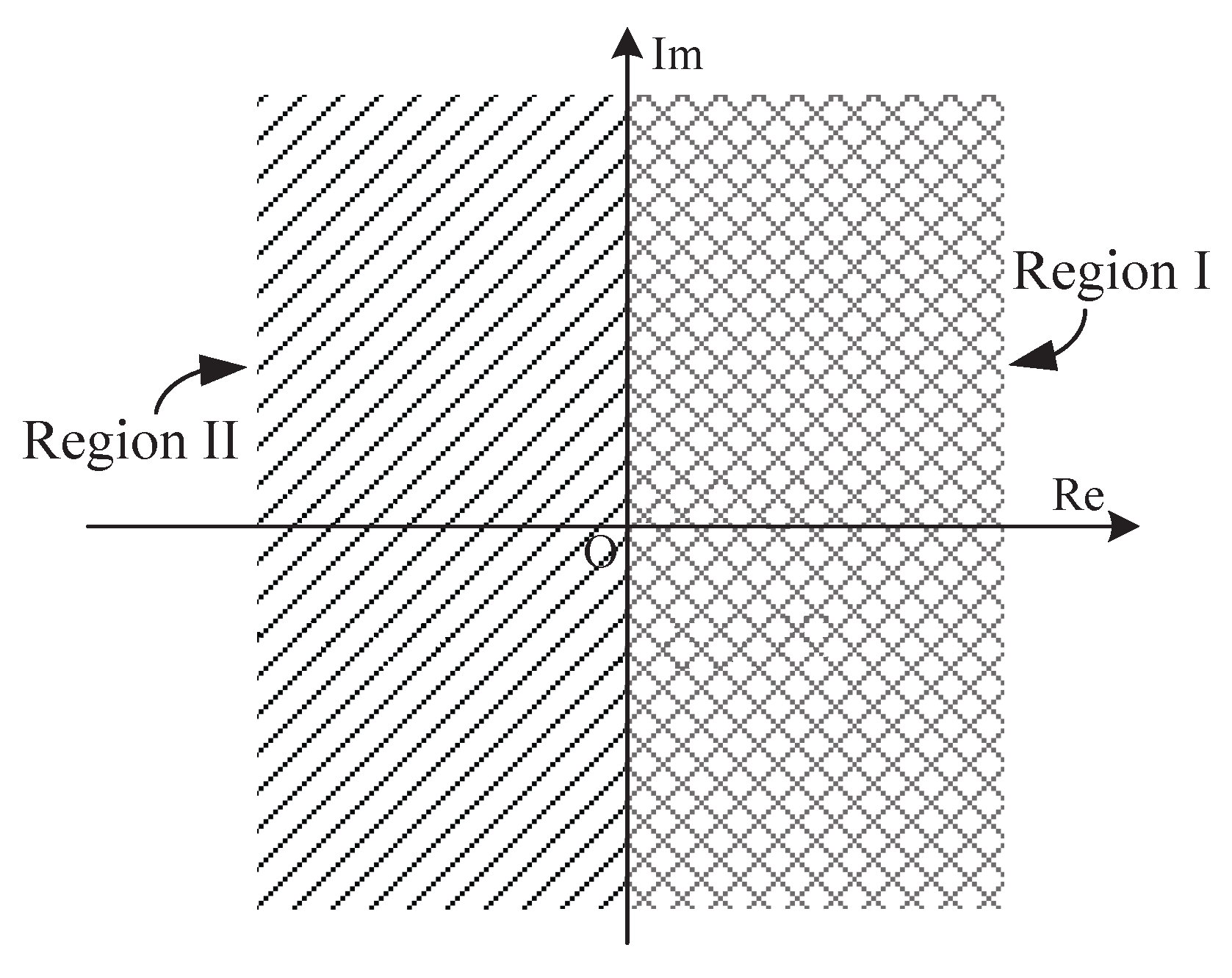
- The complex observation space is only divided into two subspaces as shown in Figure 3. They can be easily distinguished from one another just with the sign of the real part of Y. Thus, the absolute value operation of real and imaginary parts of Y in Equation (12) is not required in this case. An useful assumption, namely, the asymptotic or high chip SNR, is considered for simplification of Equation (15). Thus, the nonlinear division operation in Equation (12) is avoided.
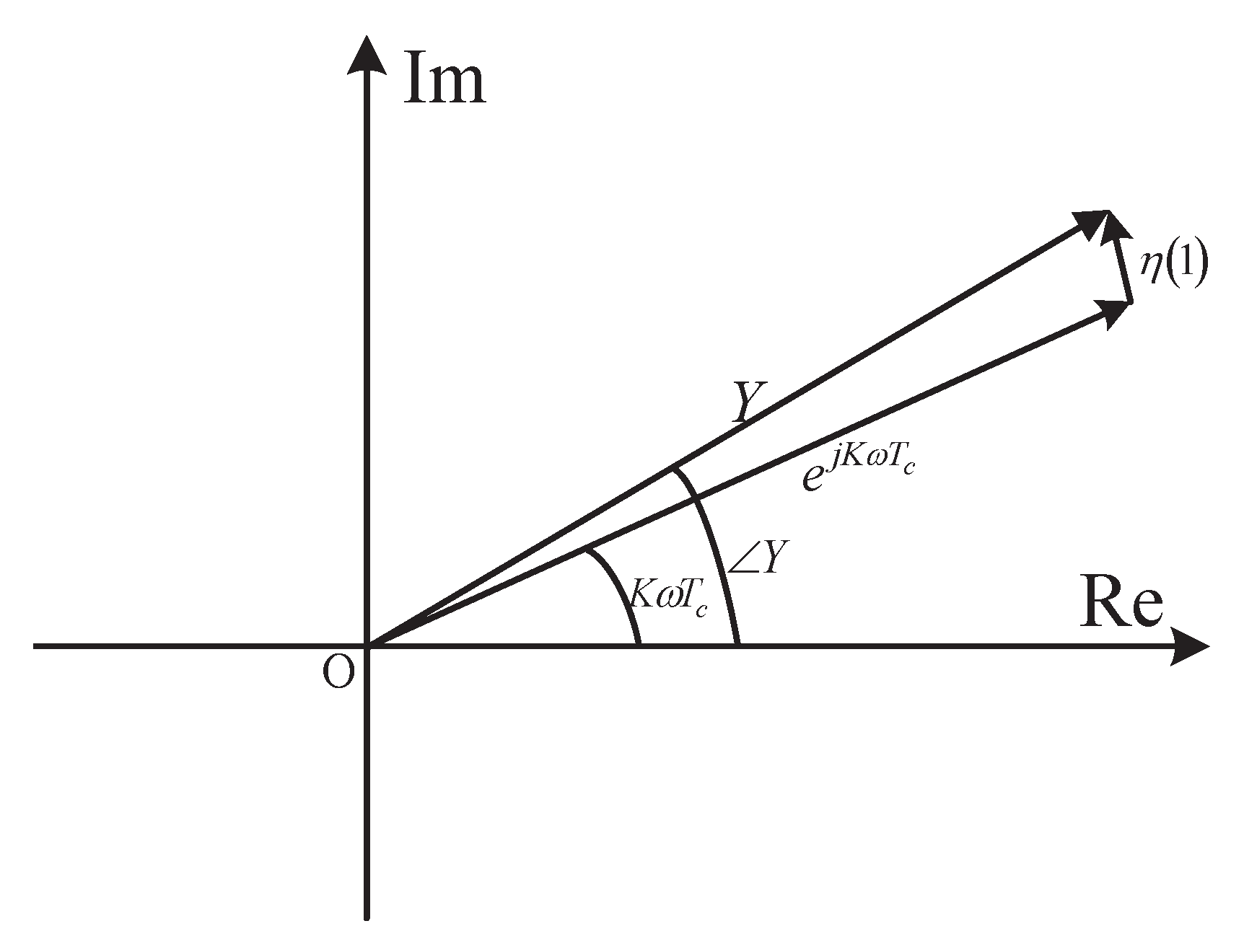
- No limitation on the CFOE range is required for the mathematical approximation in our estimator. That is to say, it appears to be a full-range estimator, and the corresponding receiver is a full-range detector, the same feature as the receiver with Equation (12). By the approximation valid at high chip SNR as illustrated in Figure 4, the result in Equation (19) may be shown to approximately hold for arbitrary SNRs, which is also the same as Equation (12). In a word, the CFO and chip SNR conditions do not need a priori knowledge for the mathematical approximation involved in Equation (19). As a result, an excellent detection performance is achieved at the receiver, which can completely meet the requirements of the IEEE 802.15.4 standard. This will be confirmed by the numerical results shown in the following section.
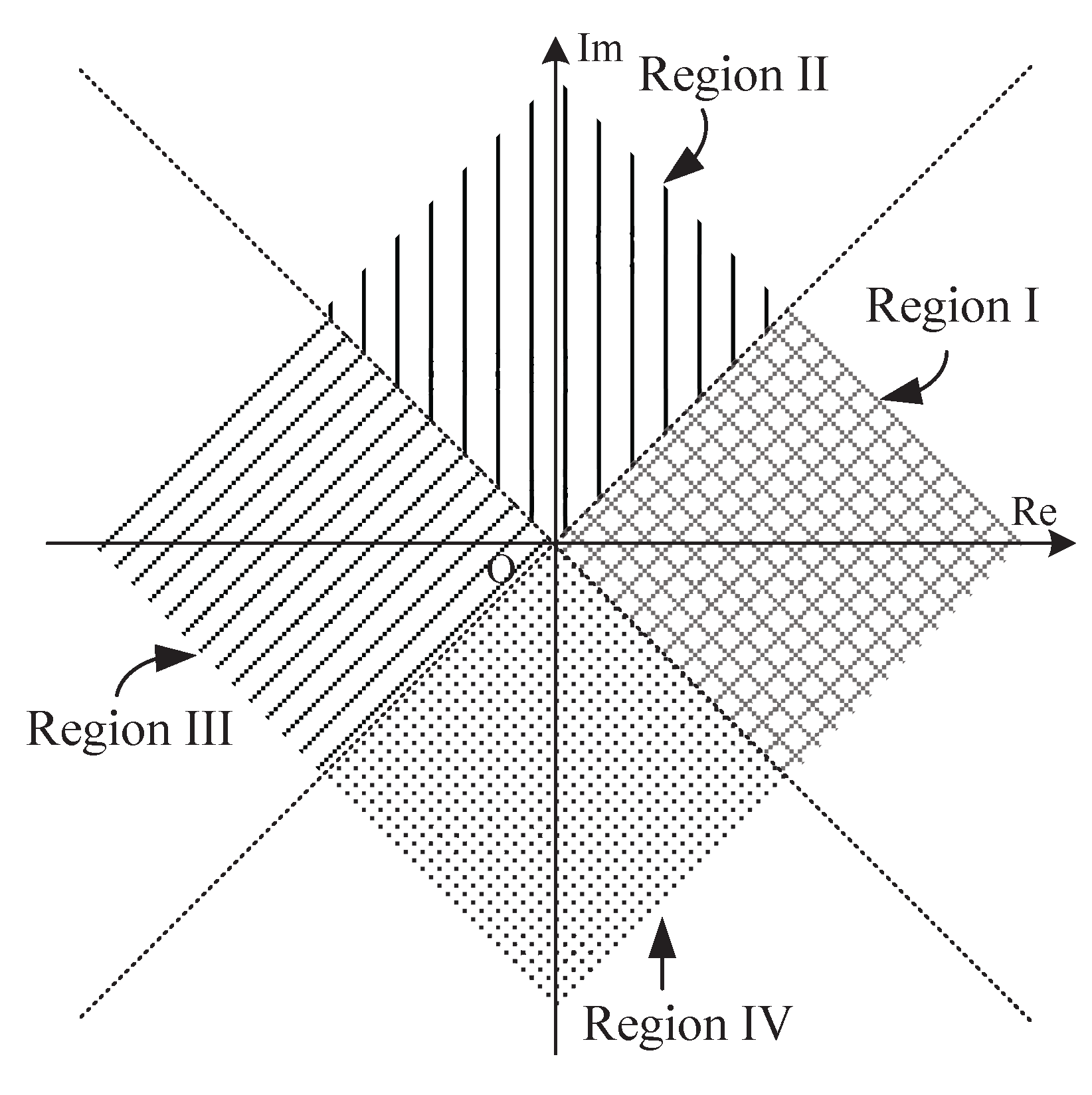
- Clearly, the estimation error is only introduced by the mathematical approximation if the noise is not considered. In this case, the absolute error for three simplified estimators is summarized and compared in Table 1 and Figure 5, respectively. As shown in Figure 5, the absolute error with Equation (12) is no more than for which the observation space is divided into four subspaces as indicated in Figure 2. It increases to for Equation (13). This is exactly half of the radians for the equi-angular sector in Figure 2. This value comes to be for our improved estimator in Equation (19) where the observation space is only divided into two subspaces. Furthermore, when the CFOE , our estimator is more efficient than Equation (12).
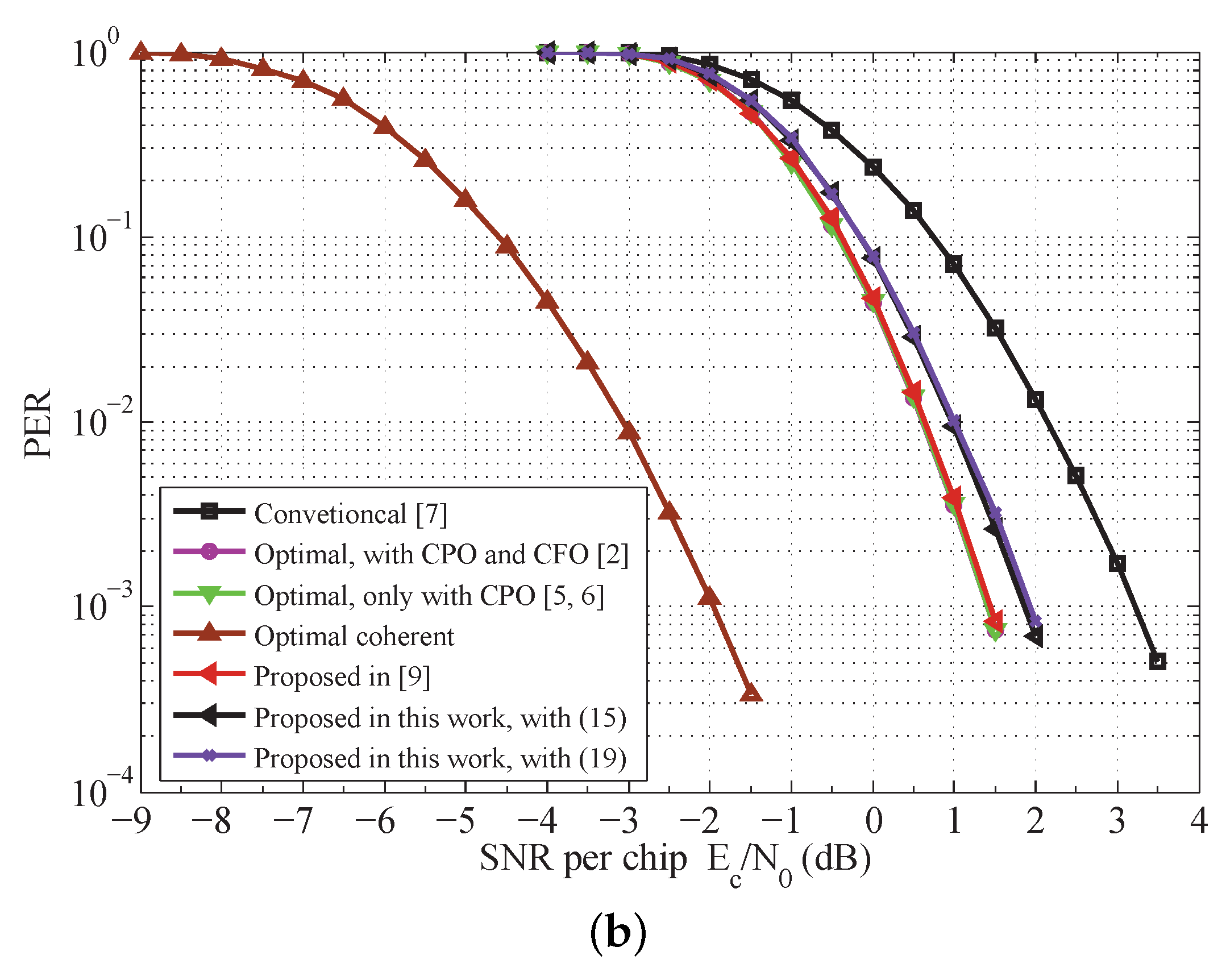
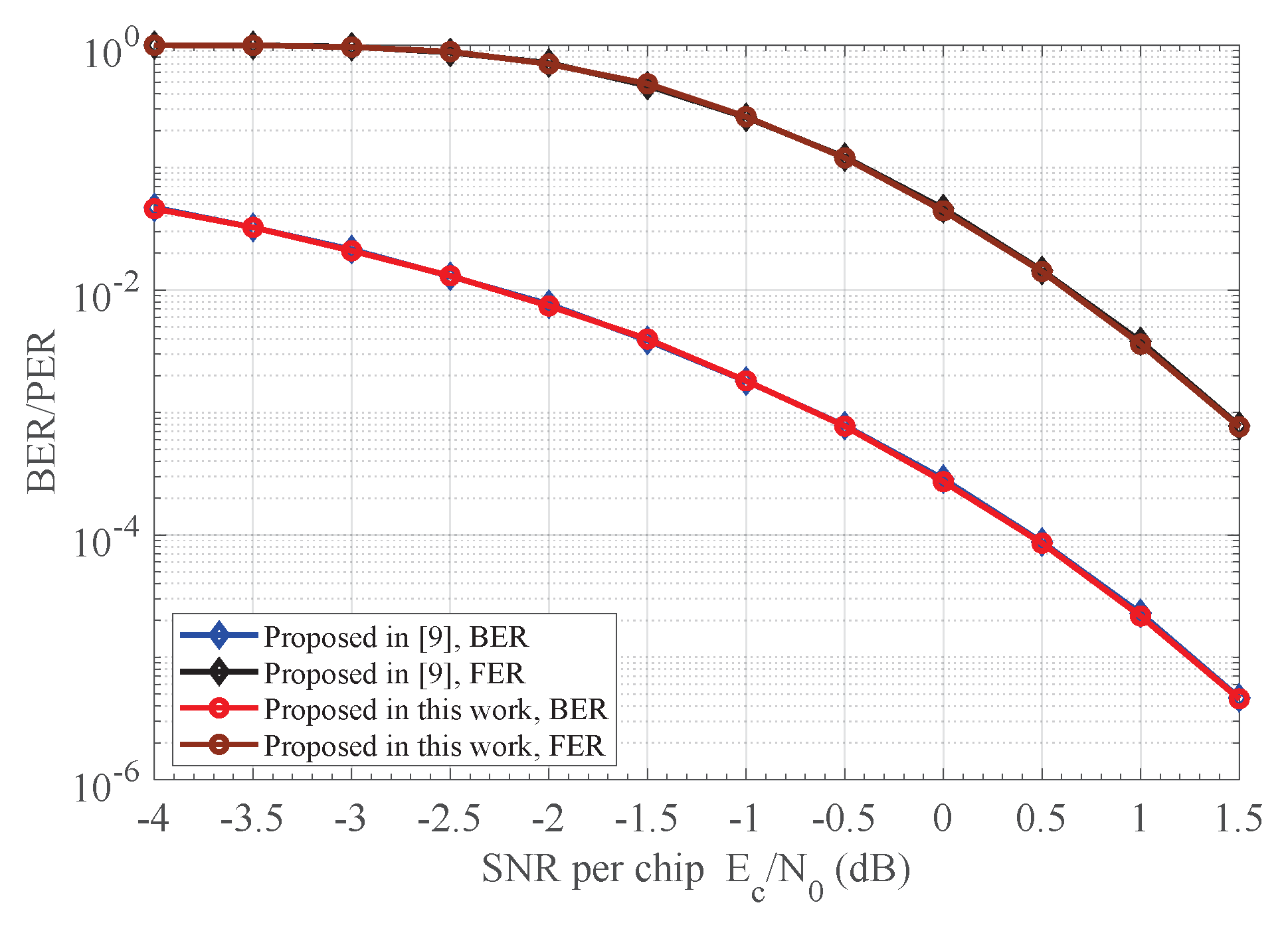
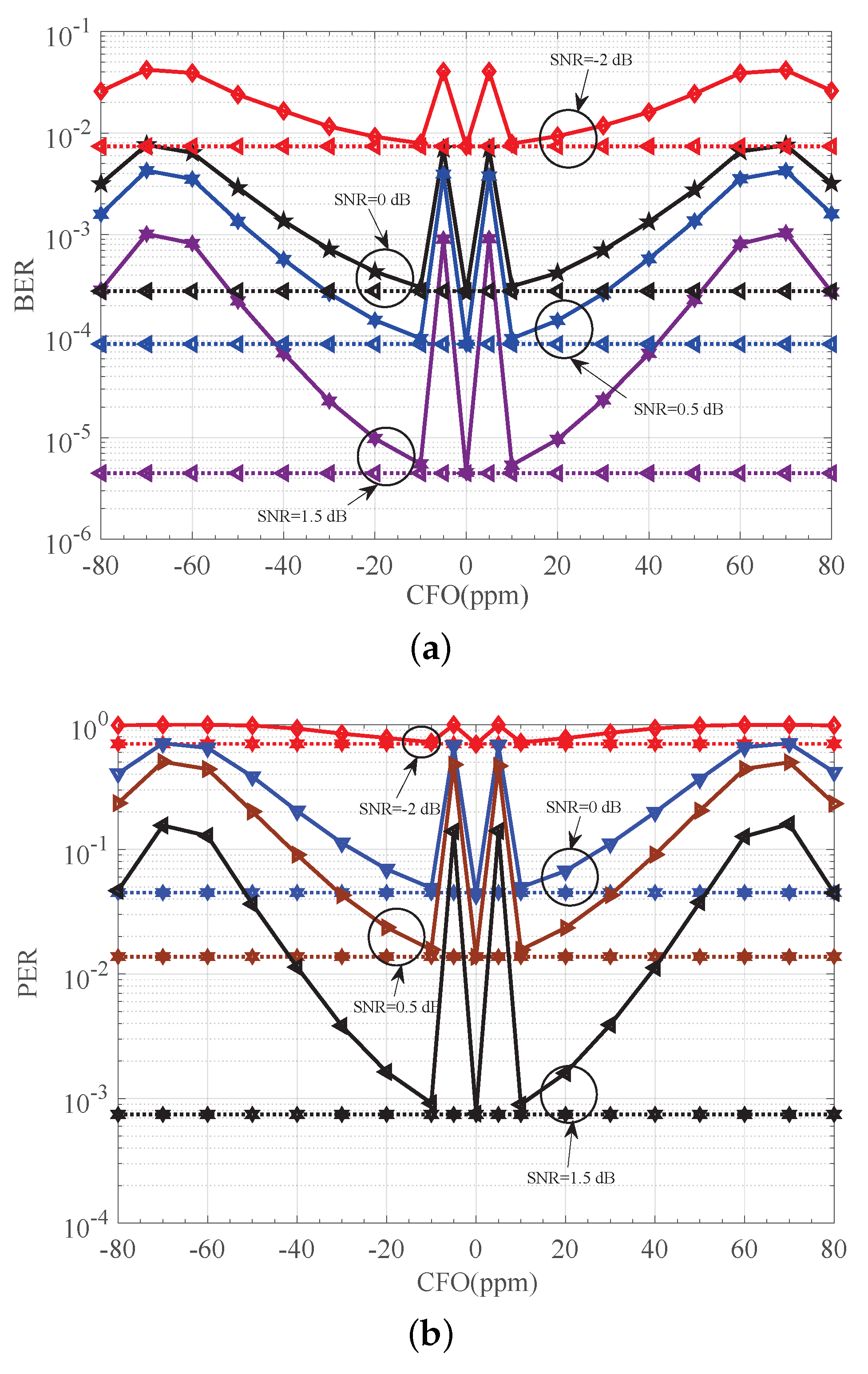
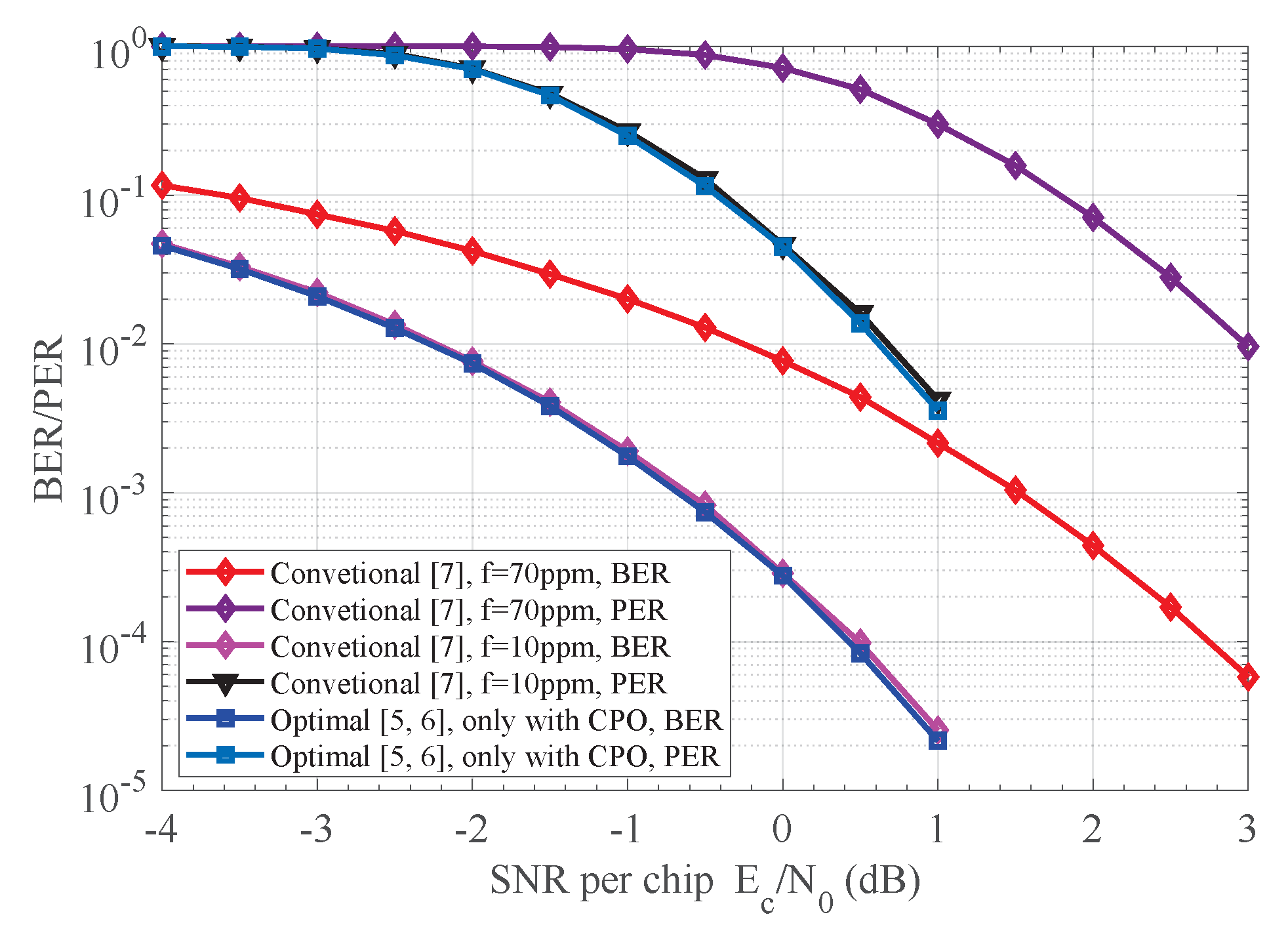
7. Numerical Results and Discussion
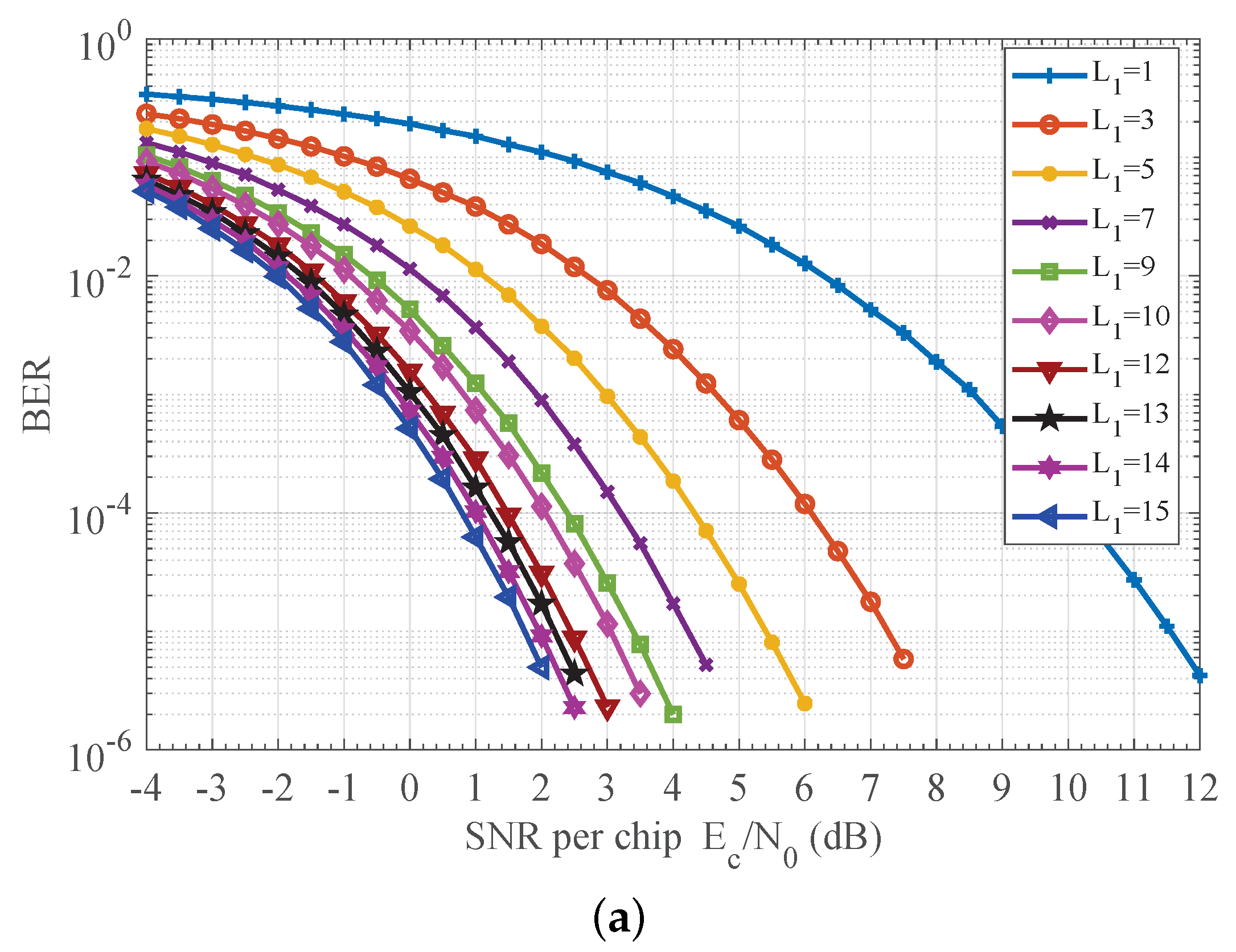
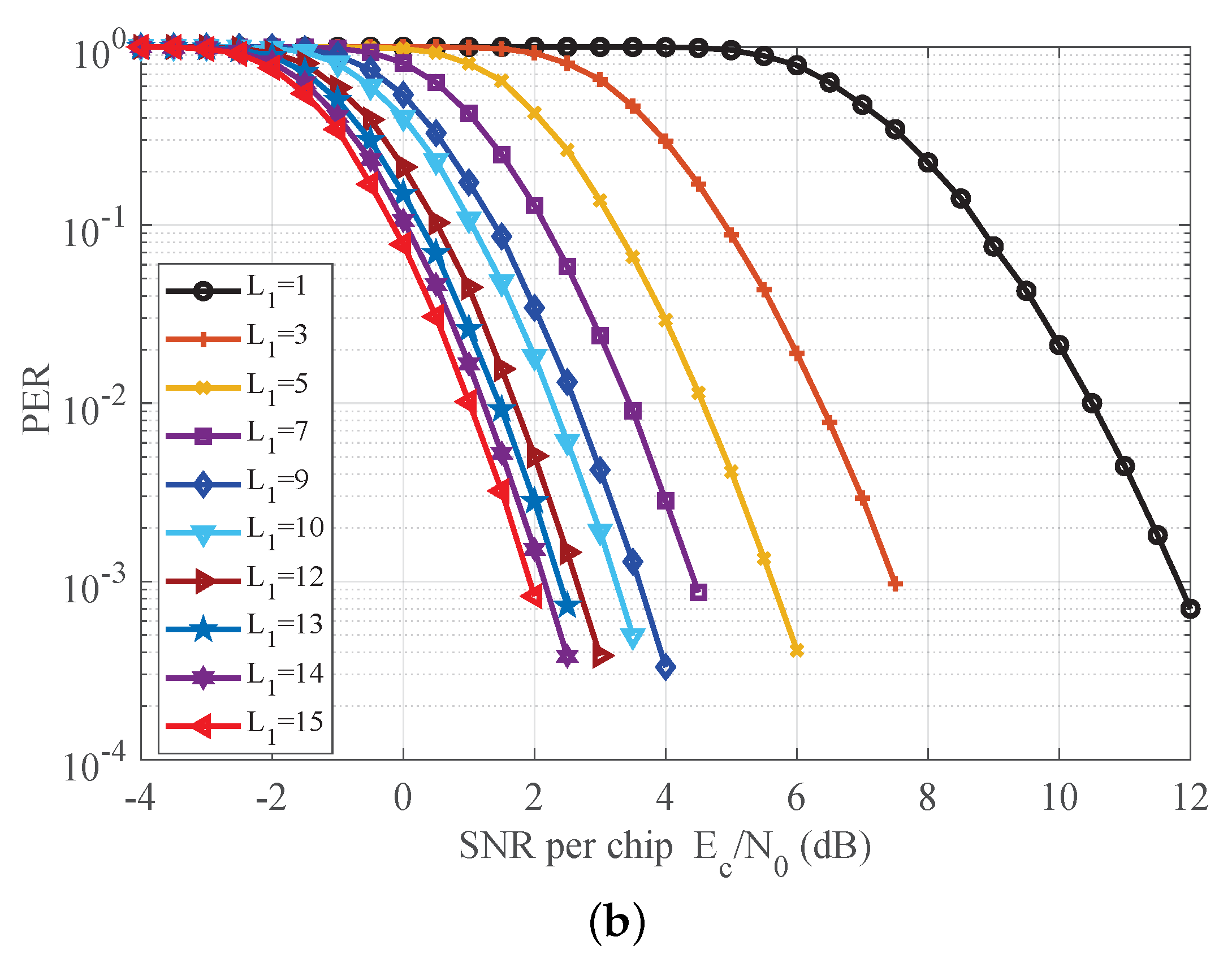
7.1. Effect of the Truncation Factors
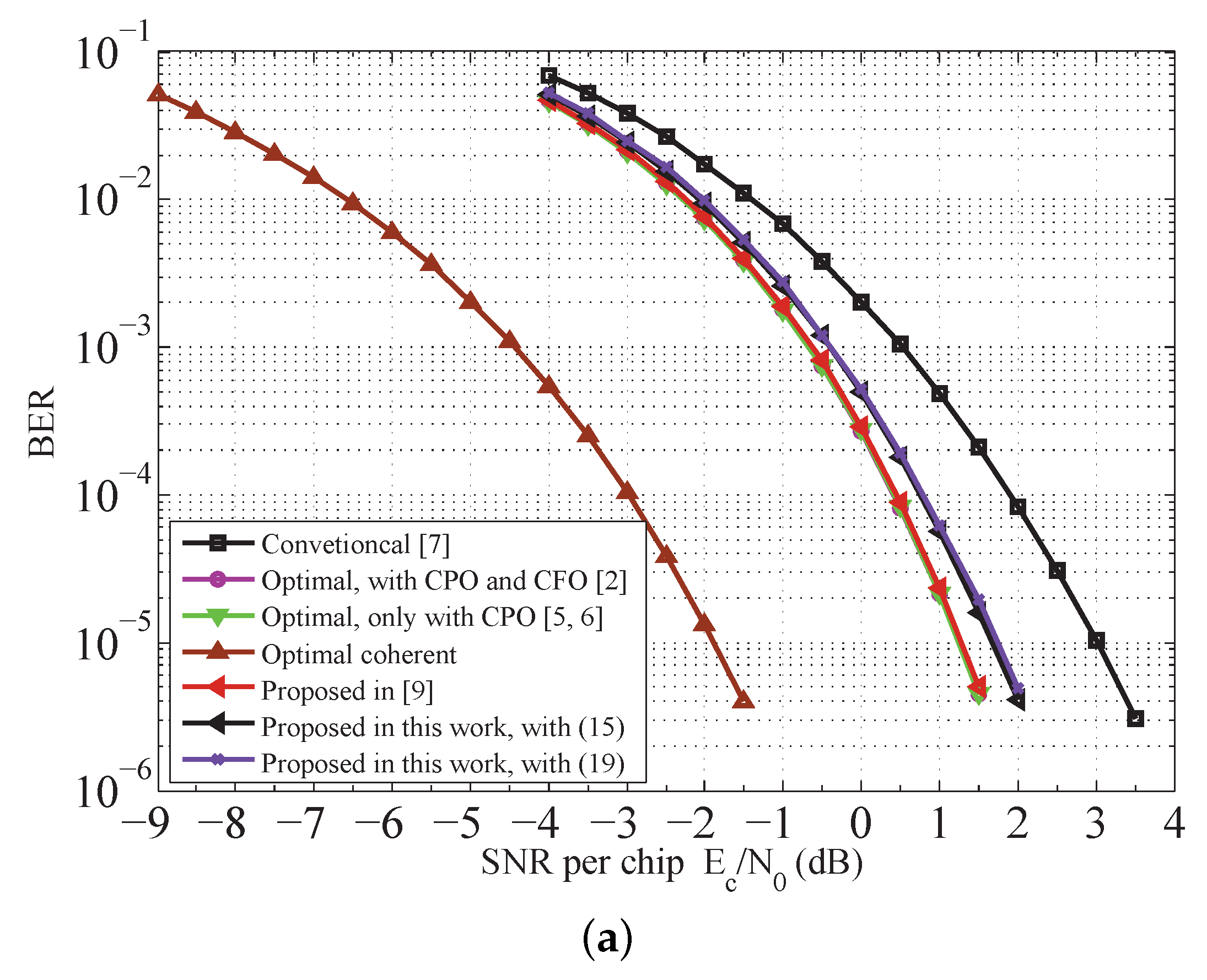
7.2. Detection Performance of the Receiver
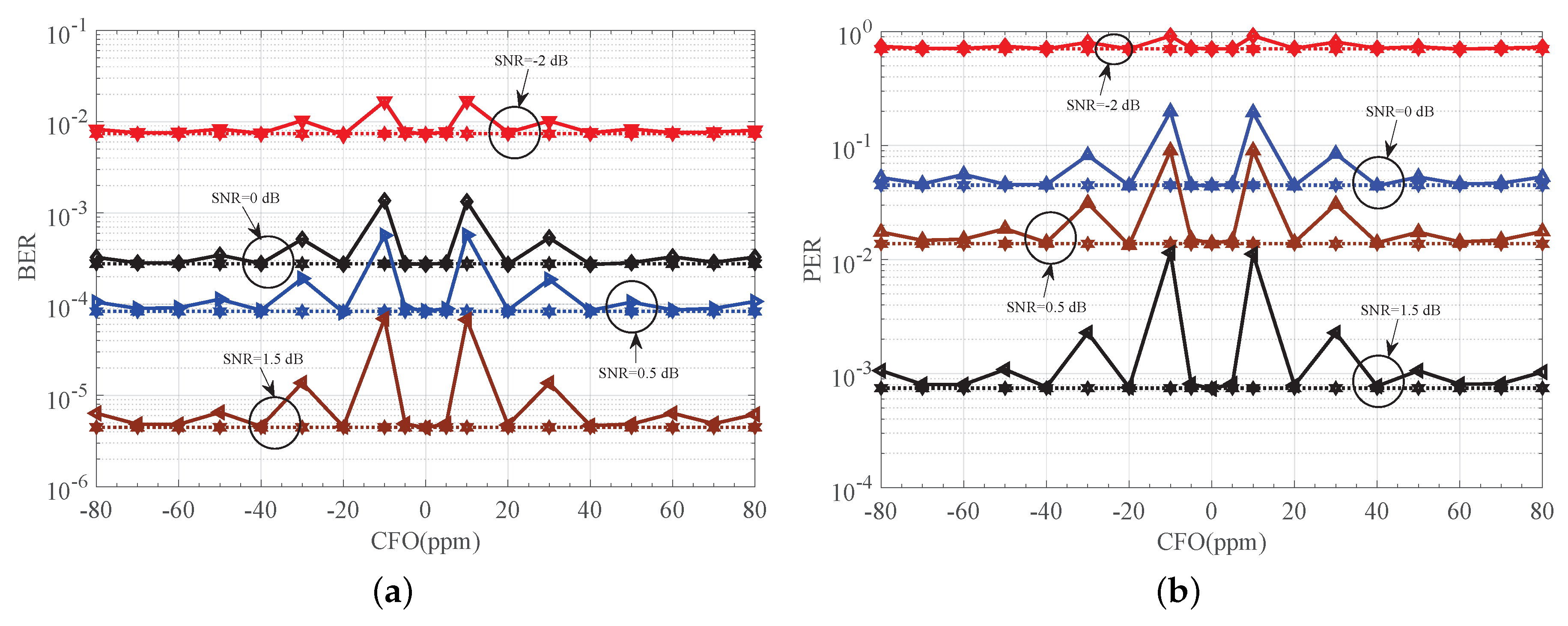
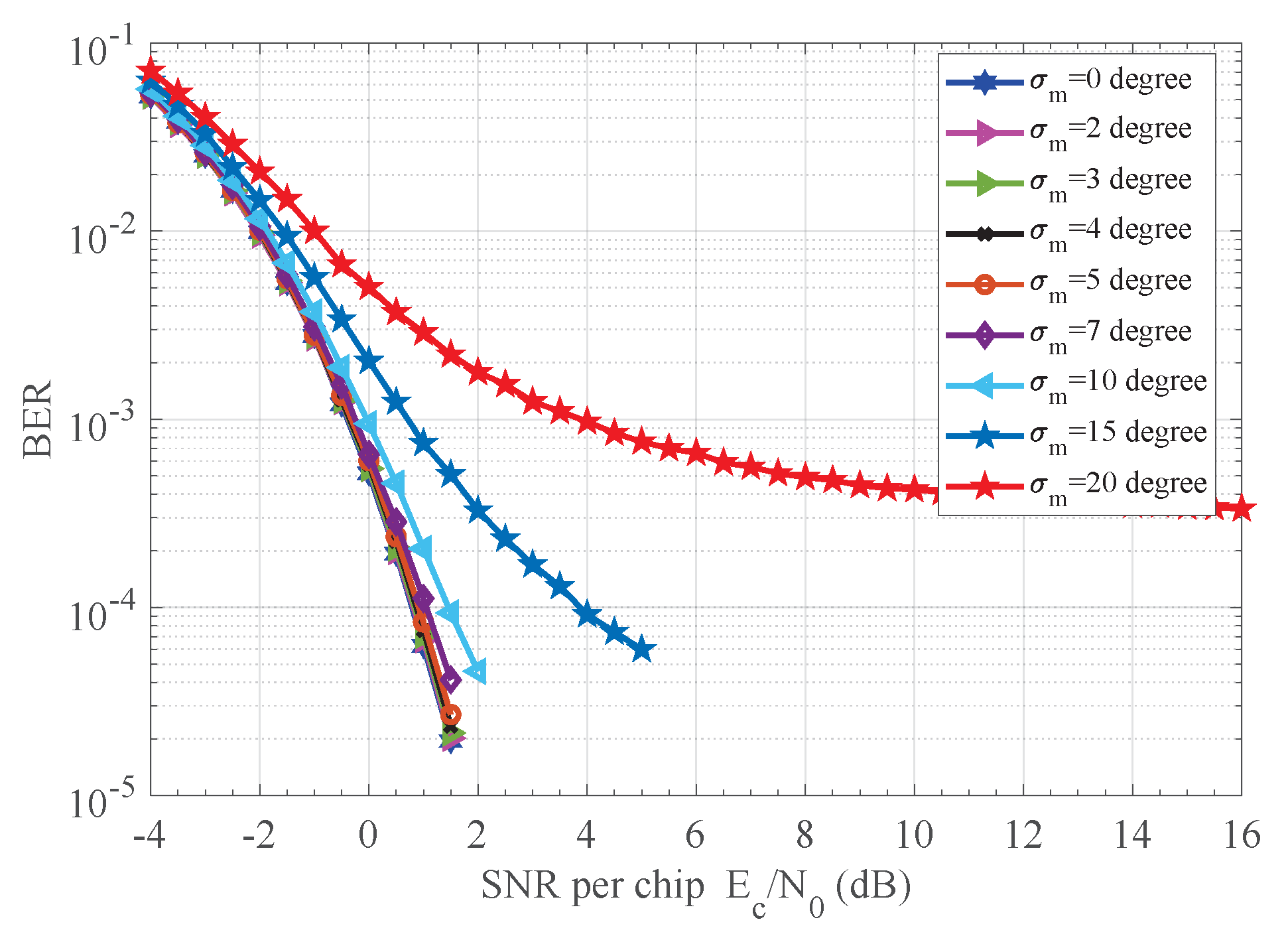
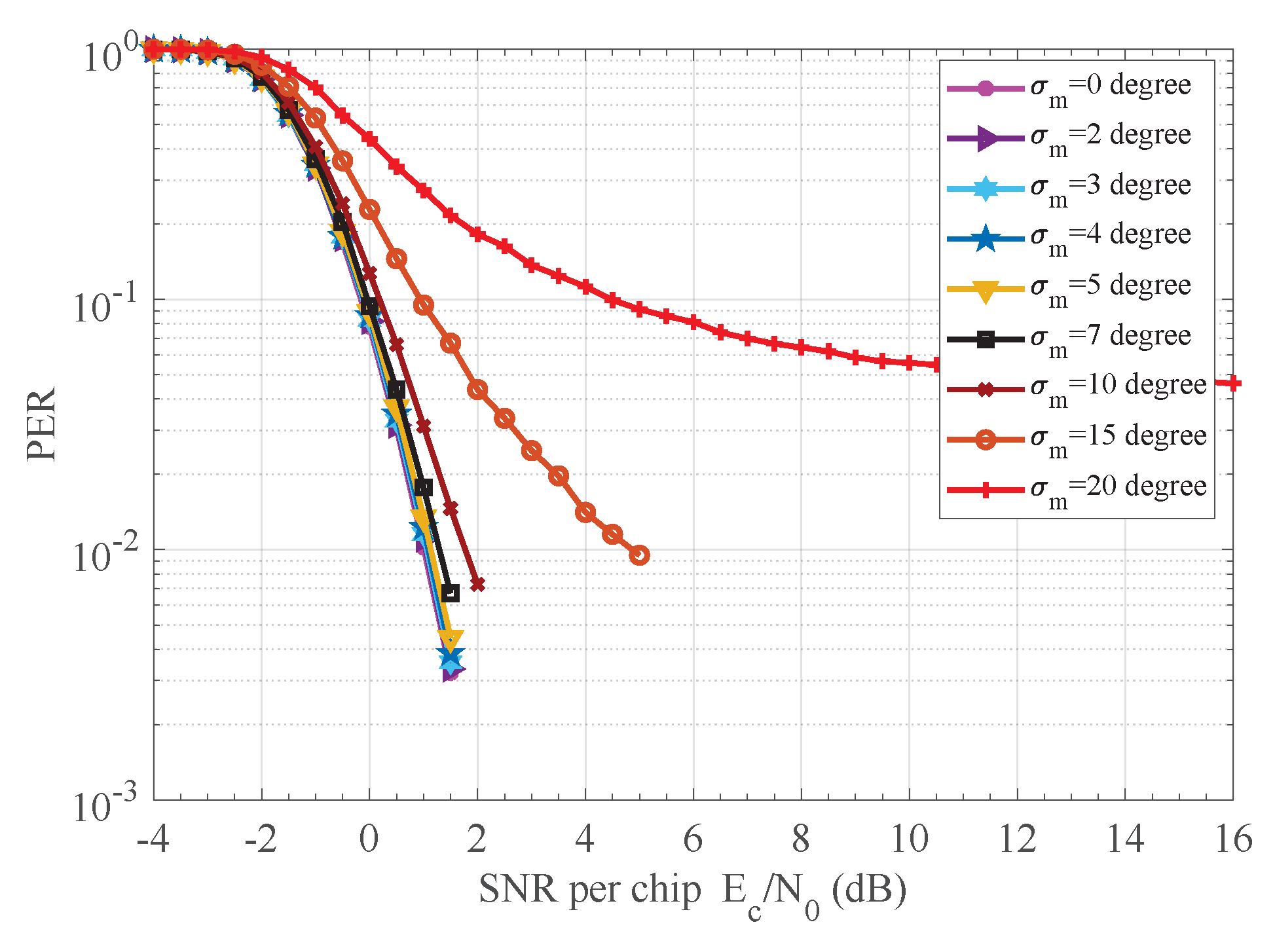
7.3. Robustness of the Receiver
7.4. Performance under Dynamic Channel
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IEEE 802.15.4-2011 Standard. IEEE Standard for Local and Metropolitan area Network-Part 15.4: Low Rate Wireless Personal Area Networks (LR-WPANs); IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar]
- Jeon, H.J.; Demeechai, T.; Lee, W.G.; Kim, D.H. IEEE 802.15.4 BPSK receiver architecture based on a new efficient detection scheme. IEEE Trans. Signal Process. 2010, 58, 4711–4719. [Google Scholar] [CrossRef]
- Tseng, H.W.; Pang, A.C.; Chen, J.H.; Kuo, C.F. An adaptive contention control strategy for IEEE 802.15.4-based wireless sensor networks. IEEE Trans. Veh. Technol. 2017, 58, 5164–5173. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhou, Y.D.; Gao, L.; Qian, Y.W.; Li, J.; Shu, F. A blind adaptive tuning algorithm for reliable and energy-efficient communication in IEEE 802.15.4 networks. IEEE Trans. Veh. Technol. 2017, 66, 8605–8609. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef]
- Divsalar, D.; Simon, M.K. Multiple-symbol differential detection of MPSK. IEEE Trans. Commun. 1990, 38, 300–308. [Google Scholar] [CrossRef]
- Makrakis, D.; Feher, K. Optimal noncoherent detection of PSK signals. Electron. Lett. 1990, 26, 398–400. [Google Scholar] [CrossRef]
- Lee, S.; Kwon, H.; Jung, Y.; Kim, J.S. Efficient non-coherent demodulation scheme for IEEE 802.15.4 LR-WPAN systems. Electron. Lett. 2007, 43, 879–880. [Google Scholar] [CrossRef]
- Howlader, M.; Chang, H. Performance of chip-level differential detection for DS-CDMA in multipath fading channels. In Proceedings of the IEEE International Conference on Military Communications, Boston, MA, USA, 13–16 October 2003; pp. 1065–1070. [Google Scholar]
- Zhang, G.Y.; Wang, D.; Song, L.; Wu, H.H.; Xie, P.; Ji, B.F.; Wen, H. Simple non-coherent detection scheme for IEEE 802.15.4 BPSK receivers. Electron. Lett. 2017, 53, 628–629. [Google Scholar] [CrossRef]
- Harry, L.V.T.; Kristine, L.B.; Zhi, T. Detection, Estimation, and Modulation Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kam, P.Y.; Ng, S.S.; Ng, T.S. Optimum symbol-by-symbol detection of uncoded digital data over the Gaussian channel with unknown carrier phase. IEEE Trans. Commun. 1994, 42, 2543–2552. [Google Scholar]
- Leib, H. Data-aided noncoherent demodulation of DPSK. IEEE Trans. Commun. 1995, 43, 722–725. [Google Scholar] [CrossRef]
- Liu, J.H.; Stoica, P.; Simon, M.K.; Li, J. Single differential modulation and detection for MPSK in the presence of unknown frequency offset. In Proceedings of the Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 1440–1444. [Google Scholar]
- Viterbi, A.J.; Viterbi, A.M. Nonlinear estimation of PSK-modulated carrier phase with applications to burst digital transmission. IEEE Trans. Inf. Theory 1983, 29, 543–551. [Google Scholar] [CrossRef]
- Soderquist, P.; Leeser, M. Area and performance trade-offs in floating-point divide and square root implementations. ACM Comput. Surv. 1997, 46, 518–564. [Google Scholar]
- Seimetz, M. High-Order Modulation for Optical Fiber Transmission; Springer: Berlin, Germany, 2009. [Google Scholar]
- Park, S.; Park, D.; Park, H.; Lee, K. Low-complexity frequency-offset insensitive detection for orthogonal modulation. Electron. Lett. 2005, 41, 1226–1227. [Google Scholar] [CrossRef]
- Park, D.; Park, C.S.; Lee, K. Simple Design of Detector in the Presence of Frequency Offset for IEEE 802.15.4 LR-WPANs. IEEE Trans. Circuits Syst. II Express Briefs 2010, 56, 330–334. [Google Scholar] [CrossRef]
- Buetefuer, J.L.; Cowley, W.G. Frequency offset insensitive multiple symbol detection of MPSK. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; pp. 2669–2672. [Google Scholar]
- Leib, H.; Pasupathy, S. The phase of a vector perturbed by Gaussian noise and differentially coherent receivers. IEEE Trans. Inf. Theory 1988, 34, 1491–1501. [Google Scholar] [CrossRef]
- Ferrari, G.; Colavolpe, G.; Raheli, R. Detection Algorithms for Wireless Communications with Applications to Wired and Storage Systems; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Proakis, J. Digital Communications; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Madhow, U. Fundamentals of Digital Communication; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Oh, J.Y.; Kwak, B.J.; Kim, J.Y. Carrier frequency recovery for in non-coherent demodulation for IEEE802.15.4 system. In Proceedings of the IEEE Vehicular Technology Conference, Montreal, QC, Canada, 25–28 September 2006; pp. 1–5. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Theory; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Adachi, F. Viterbi-decoding differential detection of DPSK. Electron. Lett. 1992, 28, 2196–2198. [Google Scholar] [CrossRef]
- Mackenthun, K.M. A fast algorithm for multiple-symbol differential detection of MPSK communications. IEEE Trans. Commun. 1994, 42, 1471–1474. [Google Scholar] [CrossRef]
- Li, B. A new reduced-complexity algorithm for multiple-symbol differential detection. IEEE Commun. Lett. 2003, 7, 269–271. [Google Scholar]
- Maunder, R.G.; Weddell, A.S.; Merrett, G.V.; Al-Hashimi, B.M.; Hanzo, L. Iterative decoding for redistributing energy consumption in wireless sensor networks. In Proceedings of the 17th International Conference on Computer Communications and Networks, St. Thomas, US Virgin Islands, USA, 3–7 August 2008; pp. 1–6. [Google Scholar]
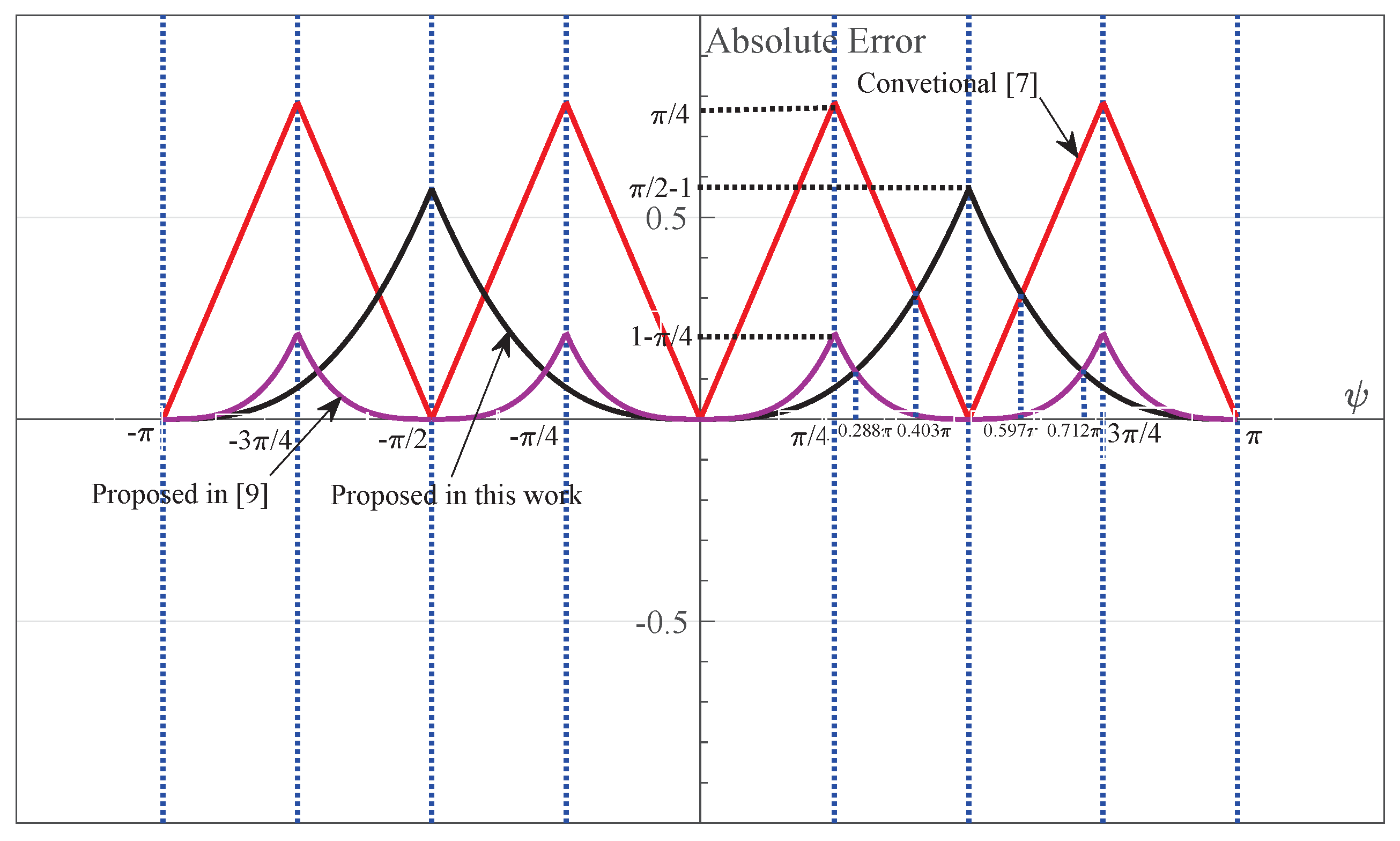
| Region | Absolute Error | ||
|---|---|---|---|
| Estimator in [8] | Estimator in [4] | Estimator in this work | |
| Parameter | Detailed Description |
|---|---|
| Channel condition | Complex AWGN |
| Power of the complex noise | 1/SNR |
| Detection Scheme | Bit-level noncoherent |
| Timing synchronisation | Perfect |
| Generator polynomial of PN code | |
| Payload length of PPDU (bits) | 160 |
| Carrier frequency (MHz) | 924 |
| CPO (rads) | Uniform distribution in (−, ) or Wiener process |
| CFO (ppm) | Performance Rank | Actual CFOE (Rads) | Estimated CFOE (Rads) | (Rads) |
|---|---|---|---|---|
| 5 | Eighth | 0.2310 | 0 | 0.2310 |
| 10 | First | 0.4620 | 0.0380 | |
| 20 | Second | 0.9240 | 0.0768 | |
| 30 | Third | −0.6275 | 0.1275 | |
| 40 | Fourth | −0.1520 | 0 | 0.1520 |
| 50 | Fifth | 0.3100 | 0.1900 | |
| 60 | Seventh | 0.7720 | 0.2280 | |
| 70 | Ninth | −0.7660 | 0.2340 | |
| 80 | Sixth | −0.3040 | 0.1960 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Wen, H.; Wang, L.; Xie, P.; Song, L.; Tang, J.; Liao, R. Simple Adaptive Single Differential Coherence Detection of BPSK Signals in IEEE 802.15.4 Wireless Sensor Networks. Sensors 2018, 18, 52. https://doi.org/10.3390/s18010052
Zhang G, Wen H, Wang L, Xie P, Song L, Tang J, Liao R. Simple Adaptive Single Differential Coherence Detection of BPSK Signals in IEEE 802.15.4 Wireless Sensor Networks. Sensors. 2018; 18(1):52. https://doi.org/10.3390/s18010052
Chicago/Turabian StyleZhang, Gaoyuan, Hong Wen, Longye Wang, Ping Xie, Liang Song, Jie Tang, and Runfa Liao. 2018. "Simple Adaptive Single Differential Coherence Detection of BPSK Signals in IEEE 802.15.4 Wireless Sensor Networks" Sensors 18, no. 1: 52. https://doi.org/10.3390/s18010052
APA StyleZhang, G., Wen, H., Wang, L., Xie, P., Song, L., Tang, J., & Liao, R. (2018). Simple Adaptive Single Differential Coherence Detection of BPSK Signals in IEEE 802.15.4 Wireless Sensor Networks. Sensors, 18(1), 52. https://doi.org/10.3390/s18010052






