Performance Analysis of Cluster Formation in Wireless Sensor Networks
Abstract
:1. Introduction
- (1)
- The cluster formation phase, where all the active nodes transmit a control packet directed to the sink node in order to be part of the cluster. Specifically, the active nodes in the supervised area transmit their control packet with probability in each time slot. If there is only one transmission, that is only one node transmits, the control packet is successfully received by the sink node, and the node that successfully transmitted this packet is considered to be already a member of a cluster. As such, this node no longer transmits in the cluster formation phase. The remaining nodes continue this process until all the active nodes successfully transmit their control packet. If there are two or more transmissions in the same time slot, all transmissions are considered to be corrupted, and the control packets involved in this collision have to be retransmitted in future time slots. Hence, when a collision occurs, none of the involved nodes are aggregated to a cluster.
- (2)
- The steady state phase, where all the nodes in the system transmit their data packets to a cluster head (CH), which in turn transmits an aggregated data packet to the sink node.
- Optimal transmission probability: For this strategy, the transmission probability that maximizes the successful transmission probability is used. The successful transmission probability is the probability that a node transmits a packet and it does not suffer a collision. This requires that all nodes in the surveilled area must be aware of the number of nodes that remain to transmit their control packet. In other words, all nodes in the system have to know the exact number of nodes that can potentially transmit in the next time slot. In a practical system, this is not feasible because there is no simple way to know the exact number of nodes inside the surveilled area since it is usually not fixed. Moreover, in many cases, the nodes are randomly deployed throughout the network. However, one way to implement this practically is to estimate the number of nodes inside the system by any means, if this is possible. Furthermore, observe that evaluating this optimal transmission strategy is of evident theoretical interest.
- Fixed transmission probability: In this scheme, a suitable value for the transmission probability is selected and remains unchanged during the cluster formation phase. As opposed to the optimal strategy, this scheme is very simple and easy to implement in a practical system. However, the selection of the value of the transmission probability is not straightforward, and it has a major impact on the performance of the system. This is because for high node densities, the transmission probability should be small in order to avoid a high number of collisions, and for low densities, the transmission probability should be high in order to avoid long idle-listening periods (that is, periods where there are no transmissions and where nodes have to continually listen to the channel). As such, once the transmission probability is appropriately selected for some particular conditions, the fixed transmission probability has a fair performance. The main problem with this strategy is that in WSNs, the system’s conditions are highly variable due to the death of nodes (nodes that consume all their battery’s power or are destroyed during the normal system operation) and to the addition of new nodes to the system. As such, when the number of nodes in the network changes, the performance of the system is degraded.
- Adaptive strategy: In this scheme, the transmission probability is adjusted according to the outcome of the previous slot. Specifically, the transmission probability is increased in the case of finding the channel idle; it is decremented in the case of collision; and it remains without change in the case of a successful transmission. In order to simplify the procedure and its tuning, the increment and decrement of the transmission probability is done according to a factor that has to be carefully selected. The performances achieved by this strategy are pretty close to those of the optimal one. It also has the advantage of constantly adapting to the conditions of the system. Hence, the death or addition of nodes has no important impact on the operation of the network. Finally, its practical implementation is easy since nodes only have to distinguish between a successful, collided or idle time slot, which is commonly used in previous work such as in [18]. It is important to notice that this scheme does not only adapt to different node densities, but it also adapts throughout the cluster formation procedure. Indeed, as the cluster begins to form, the initial number of nodes is relatively high, while at the end of the cluster formation phase, the number of nodes that can transmit is very low. Therefore, the transmission probability () at the beginning of the cluster formation phase should be relatively small, while at the end of the cluster formation, this value should be close to one. This behavior is close to that of the optimal strategy, but with the advantage that there is no need to know the number of remaining nodes trying to transmit their control packets.
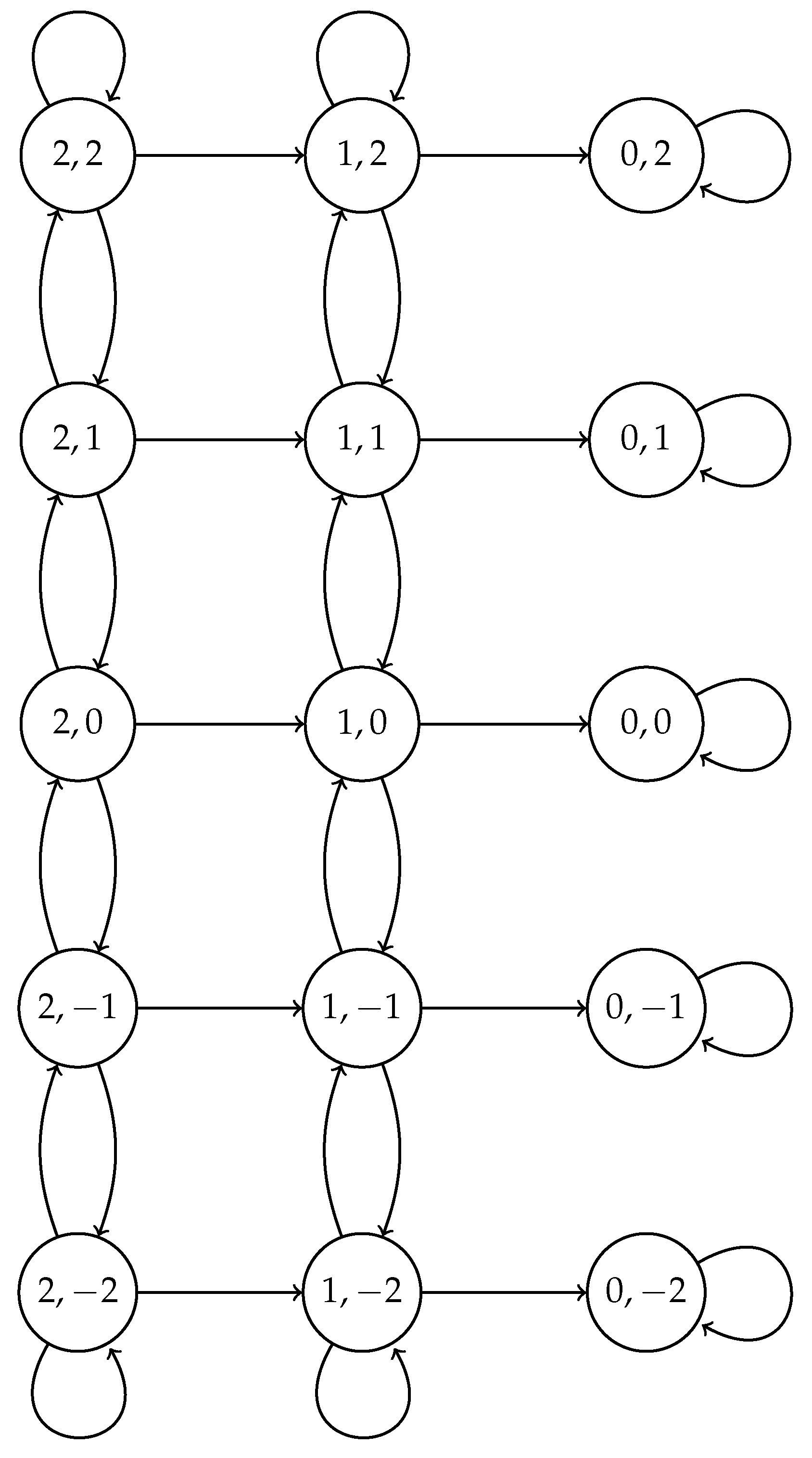
2. Model
2.1. Fixed Transmission Probability Scheme
2.2. Optimal Transmission Probability Scheme
2.3. Adaptive Transmission Probability Scheme
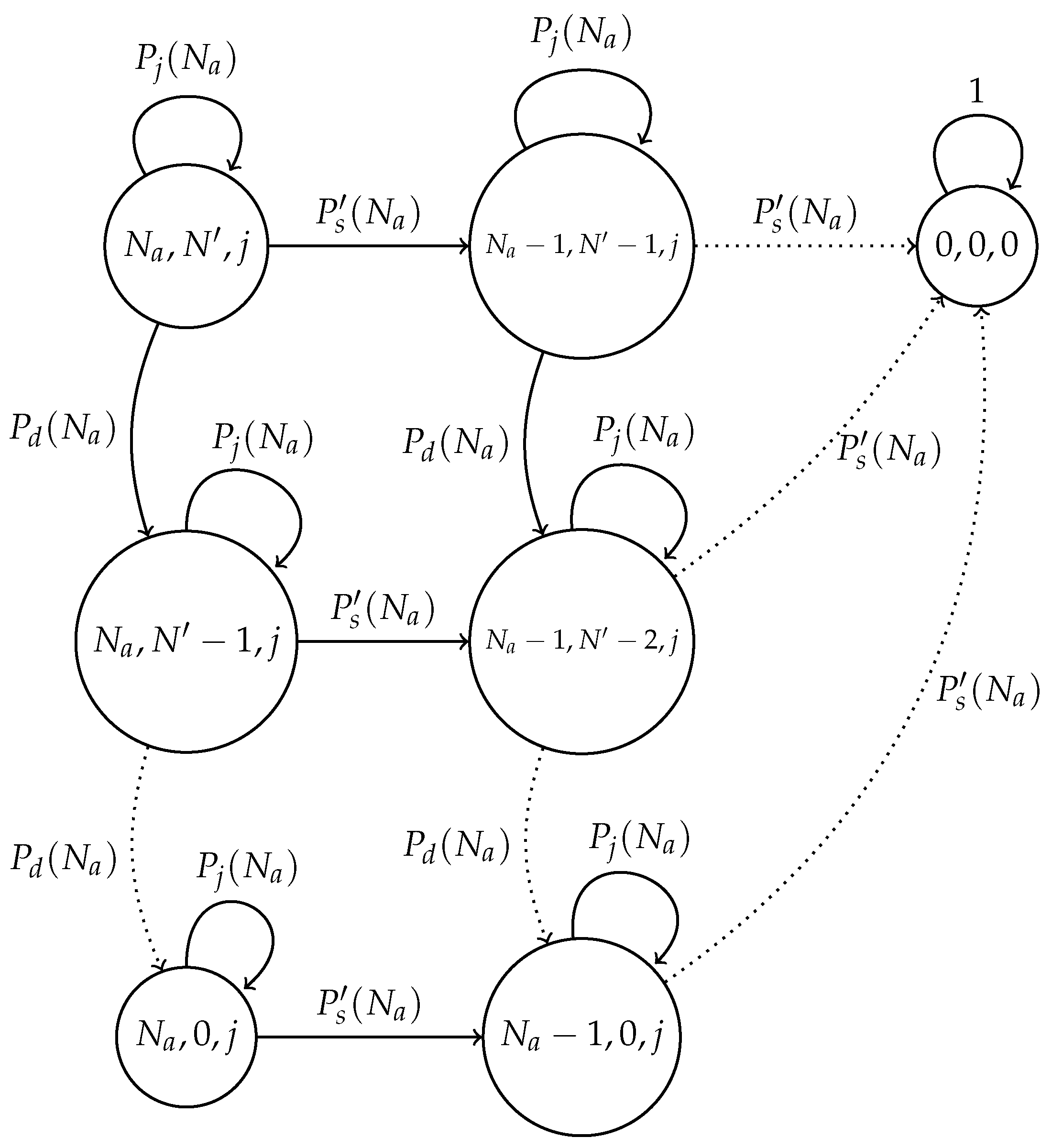
3. Model Considering a Noisy Channel
- False positive is an event in which no node transmits its data packet in the current slot, but the nodes detect that one successful transmission has occurred. This occurs with probability .
- False negative is an event in which only one node transmits, but it is not successfully decoded at the receiver. This event is assumed to occur with probability .
3.1. Fixed Transmission Probability Scheme with Channel Errors
- Only one node transmits and the channel is error-free, i.e., neither a false positive nor a false negative probability happens during the transmission.
- We assume that the channel is error-free when both false positive and false negative events occur in the same slot, because these events are mutually exclusive.
3.2. Optimal Transmission Probability Scheme with Channel Errors
- In the presence of false positives, active nodes estimate that there is one less node in the cluster formation procedure even if no node transmitted. Hence, the remaining nodes increase the value of . However, the actual number of nodes attempting to transmit remains unchanged; consequently, a non-optimal value of is now being used during the remaining procedure.
- When only one node transmits and a false positive occurs, a collision is detected, then that node has to retransmit in some future time slot. The impact in the system is similar to the previous case.
- On the other hand, false negative cases do not greatly affect the system’s performance. Indeed, in this case, the system fails to detect a successful transmission. Hence, the value of is not modified, and nodes continue to use an adequate value of the transmission probability.
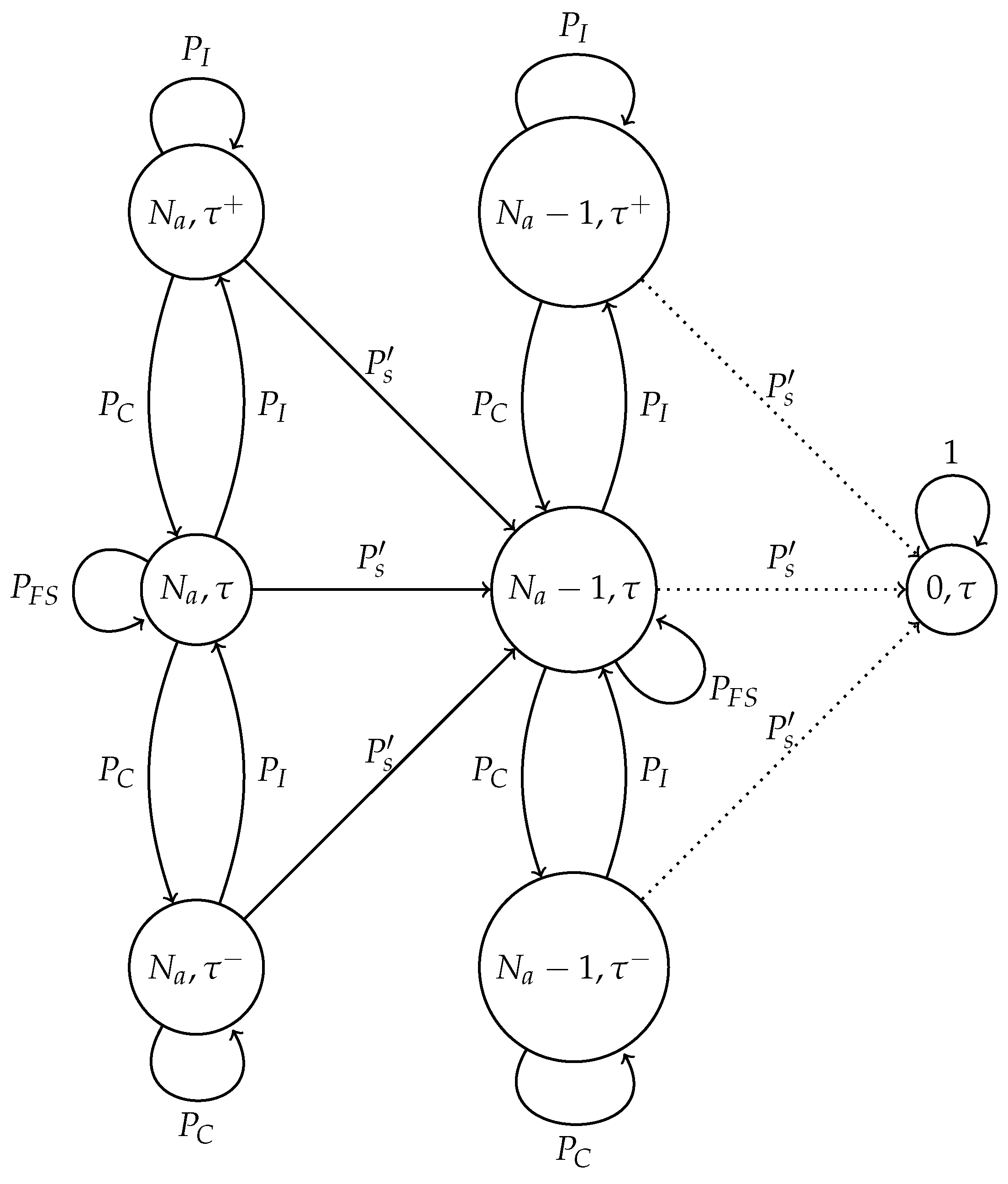
3.3. Adaptive Transmission Probability Scheme with Channel Errors
- No node transmits and the channel is error-free.
- No node transmits and a false negative occurs (consequently, no false positive occurs.)
- One node transmits and a false negative happens (consequently, no false positive occurs).
3.4. Threshold Selection
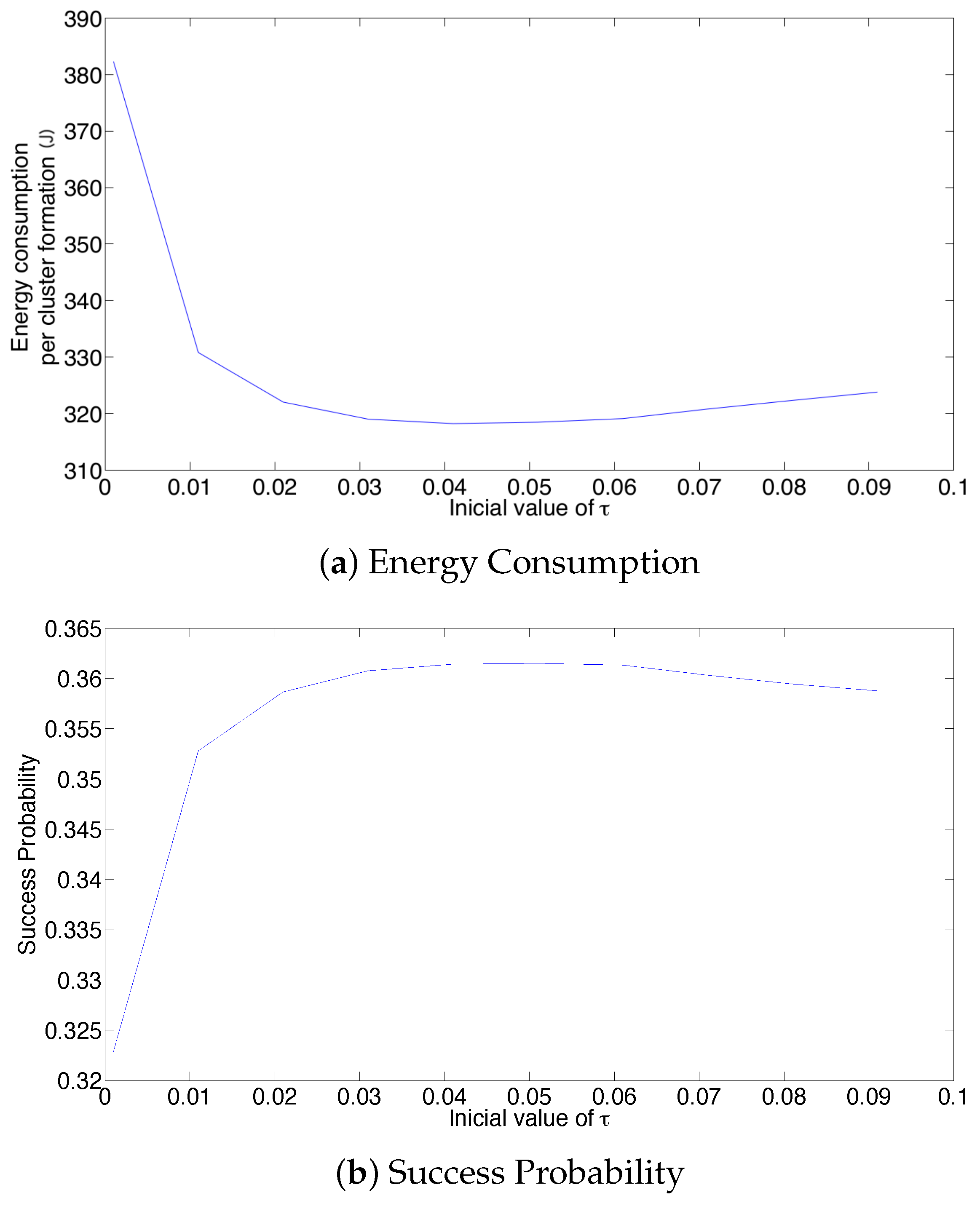
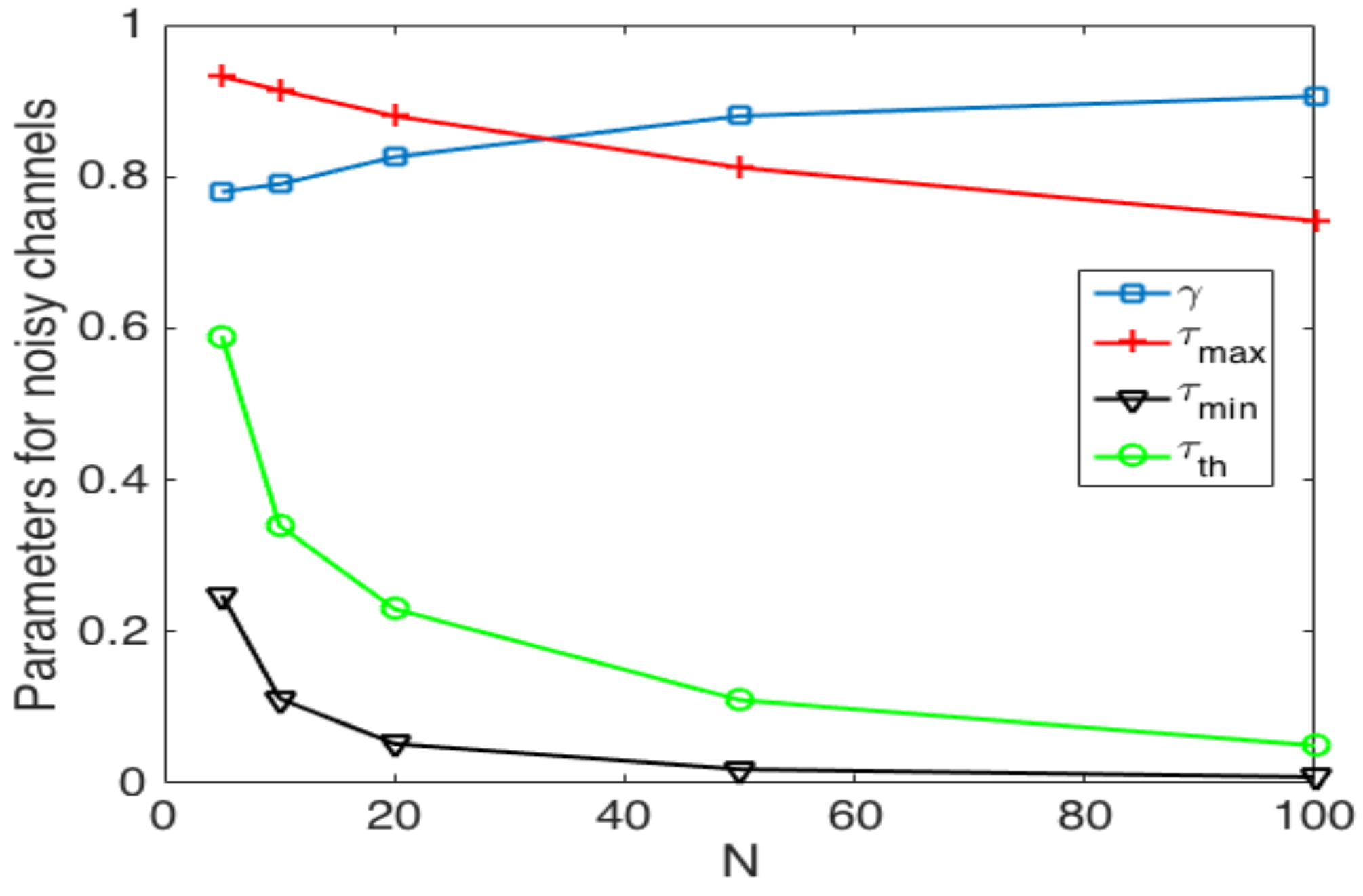
- In the optimal scheme, one particularly harmful event that can occur due to a noisy channel is when the estimated number of active nodes is low (i.e., the network estimates that most nodes have successfully transmitted their control packet), but in fact, there is a higher amount of nodes still active in the cluster formation phase. This situation can occur if the false positive probability is rather high. In this case, the estimated value of would be relatively high, causing a high number of collisions. Consider for instance the case when the estimated number of remaining nodes is one. Then, . In this case, if there are at least two nodes trying to transmit, a collision will occur. Hence, the clusters can never be formed, and all nodes would deplete their energy, rendering the network useless. A simple solution to avoid this situation is to establish a probability transmission threshold , in such a way that . However, the selection of the value of is not straightforward, as is shown in the Numerical Results section. Indeed, a very low value of or even a value of entails higher energy consumption and cluster formation delay due to higher idle listening or collision probabilities.
- In the adaptive transmission probability scheme, three harmful events occur in noisy channels. The first one is similar to the optimal scheme, when the estimated number of active nodes is low, but in fact, there is a higher amount of nodes attempting to transmit. In this case, the estimated value of would be relatively high, causing the issues described above. Again, the use of a threshold is advisable. On the other hand, this adaptive scheme is able to decrease the value of if the channel is found idle. The main problem is when a set of consecutive slots has been detected as idle slots, such that . In this case, nodes are not able to transmit in subsequent time slots. This case can happen if the false negative probability is rather high. To solve this issue, another threshold, , is proposed to limit the value of . Finally, in the adaptive scheme, the value of is updated with parameter based on the conditions of the channel. Hence, this last parameter has to be carefully selected in order to give a soft change in the value of and, thus, avoid collisions and idle listening periods.
4. Cluster Head Selection Schemes
4.1. Fuzzy C-Means
| Algorithm 1 Fuzzy C-means algorithm. |
|
4.2. K-Medoids
| Algorithm 2 K-medoids algorithm. |
|
4.3. K-Trans
5. Numerical Evaluation
5.1. Transmission Probability Strategies
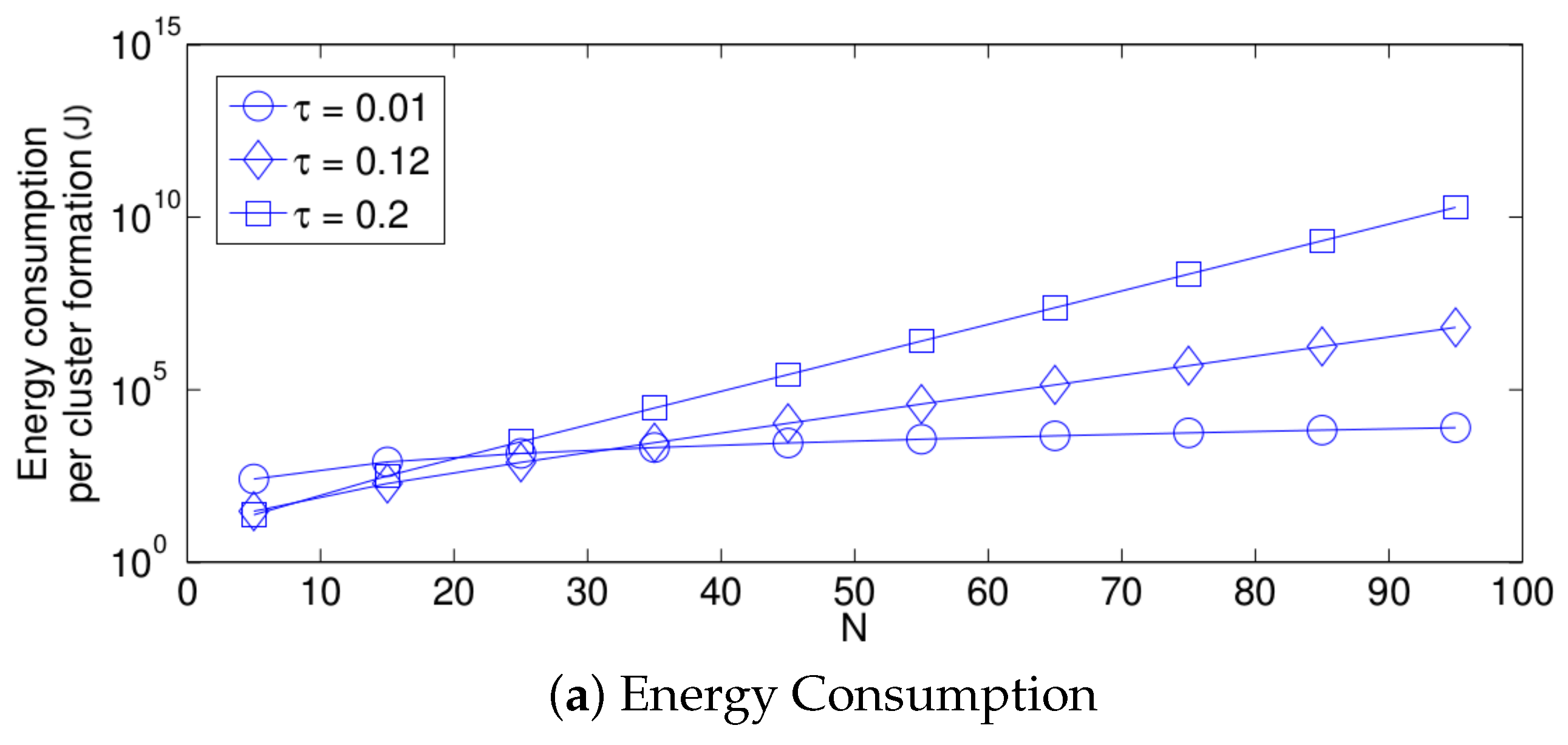
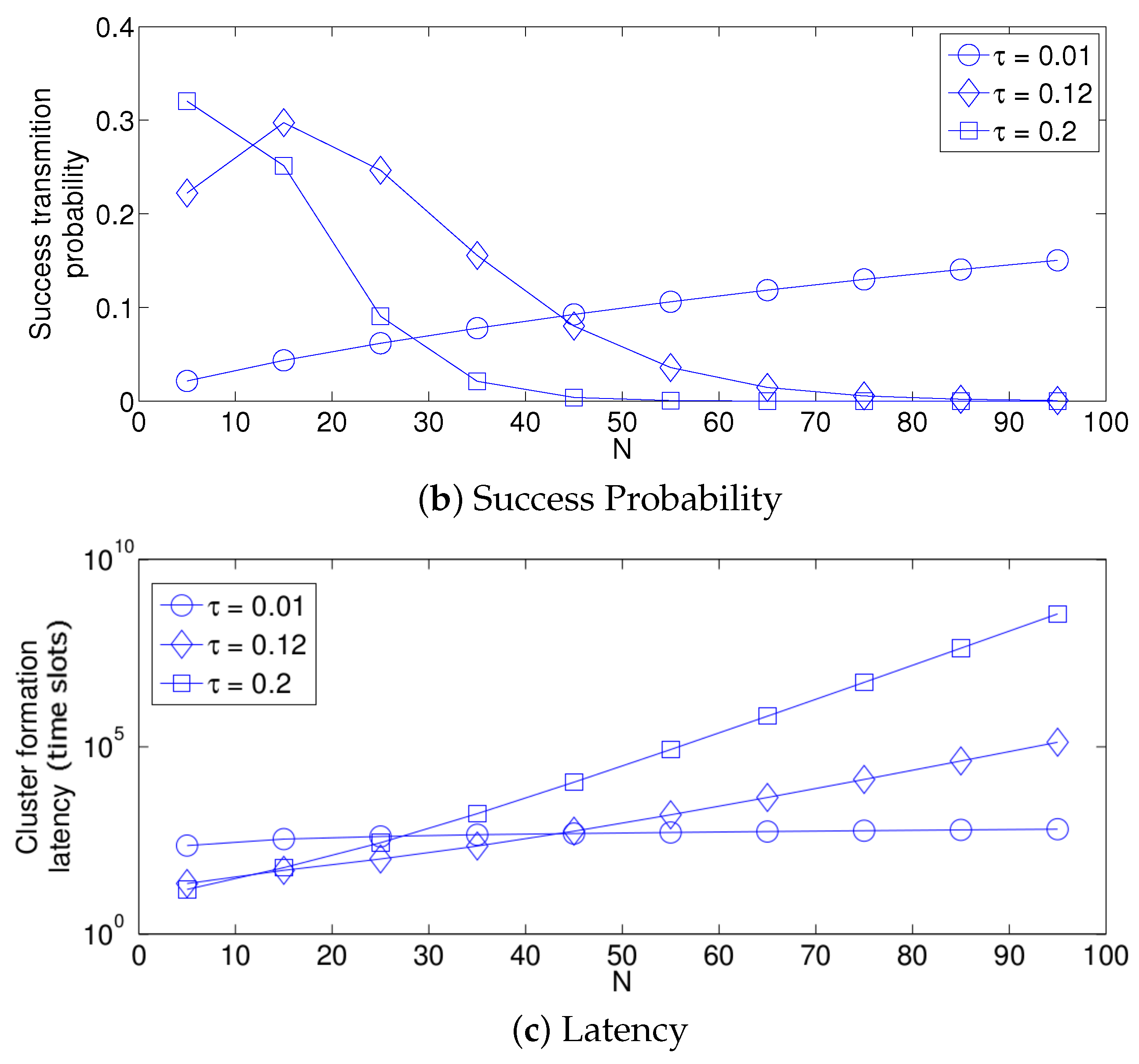
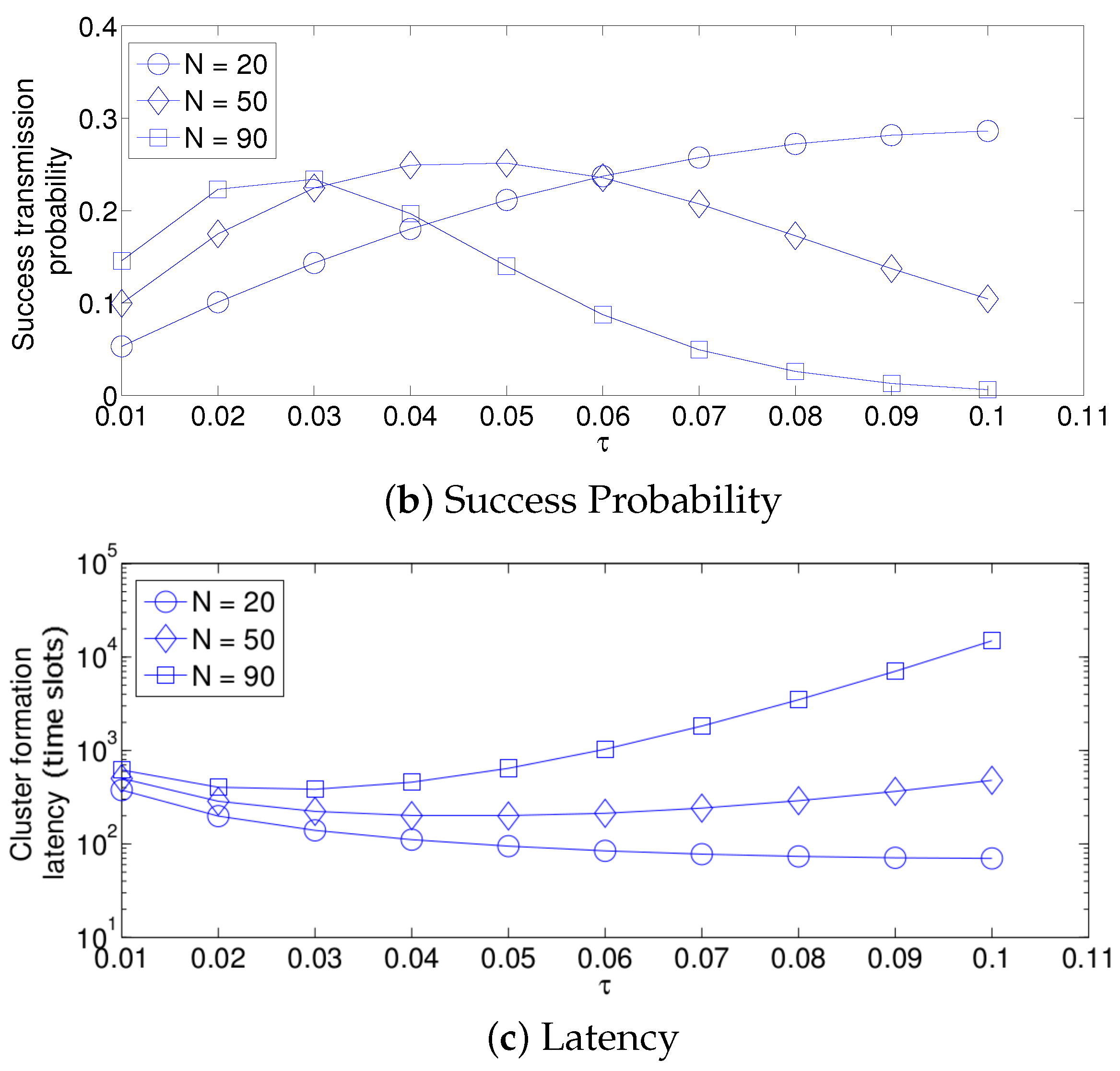
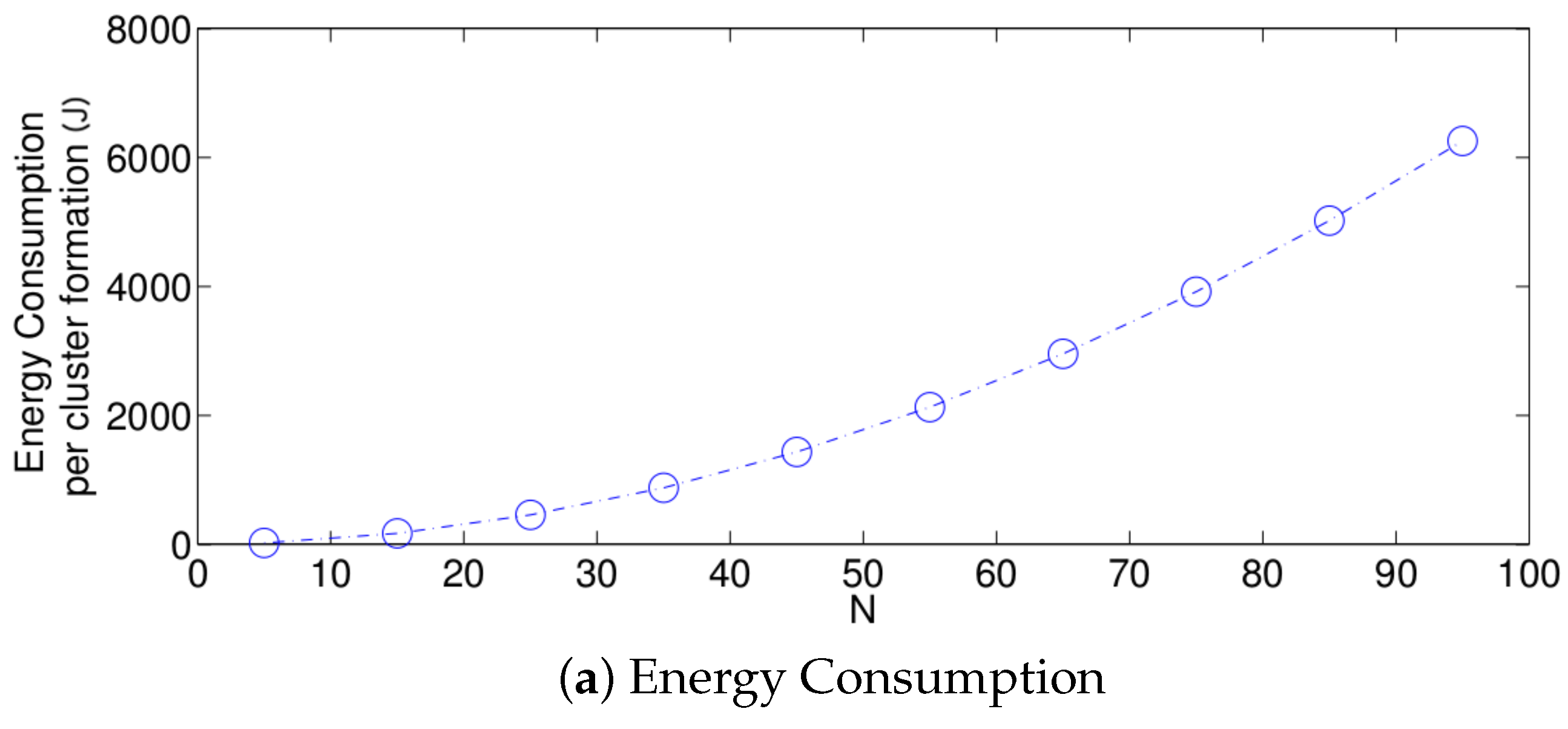
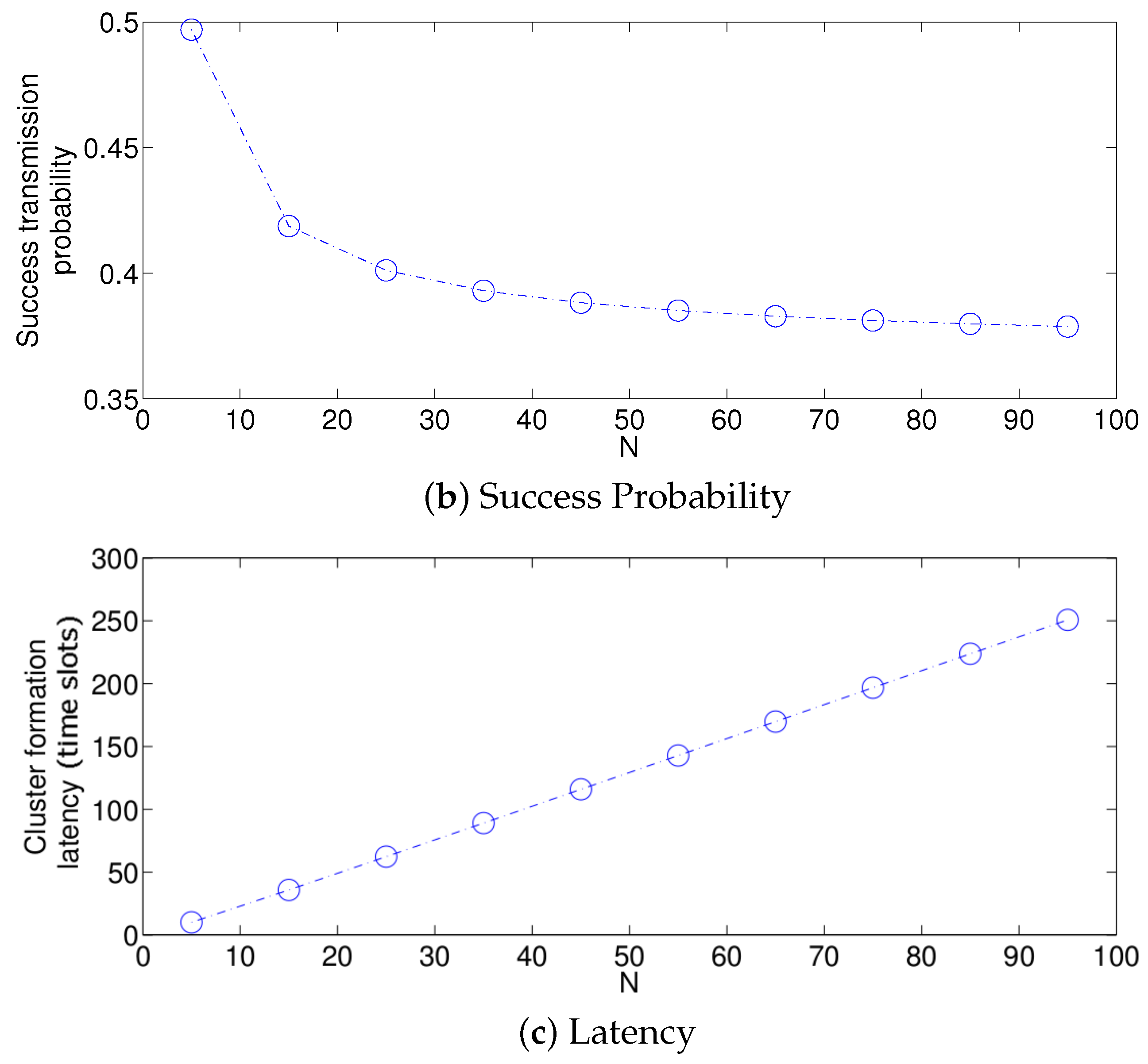
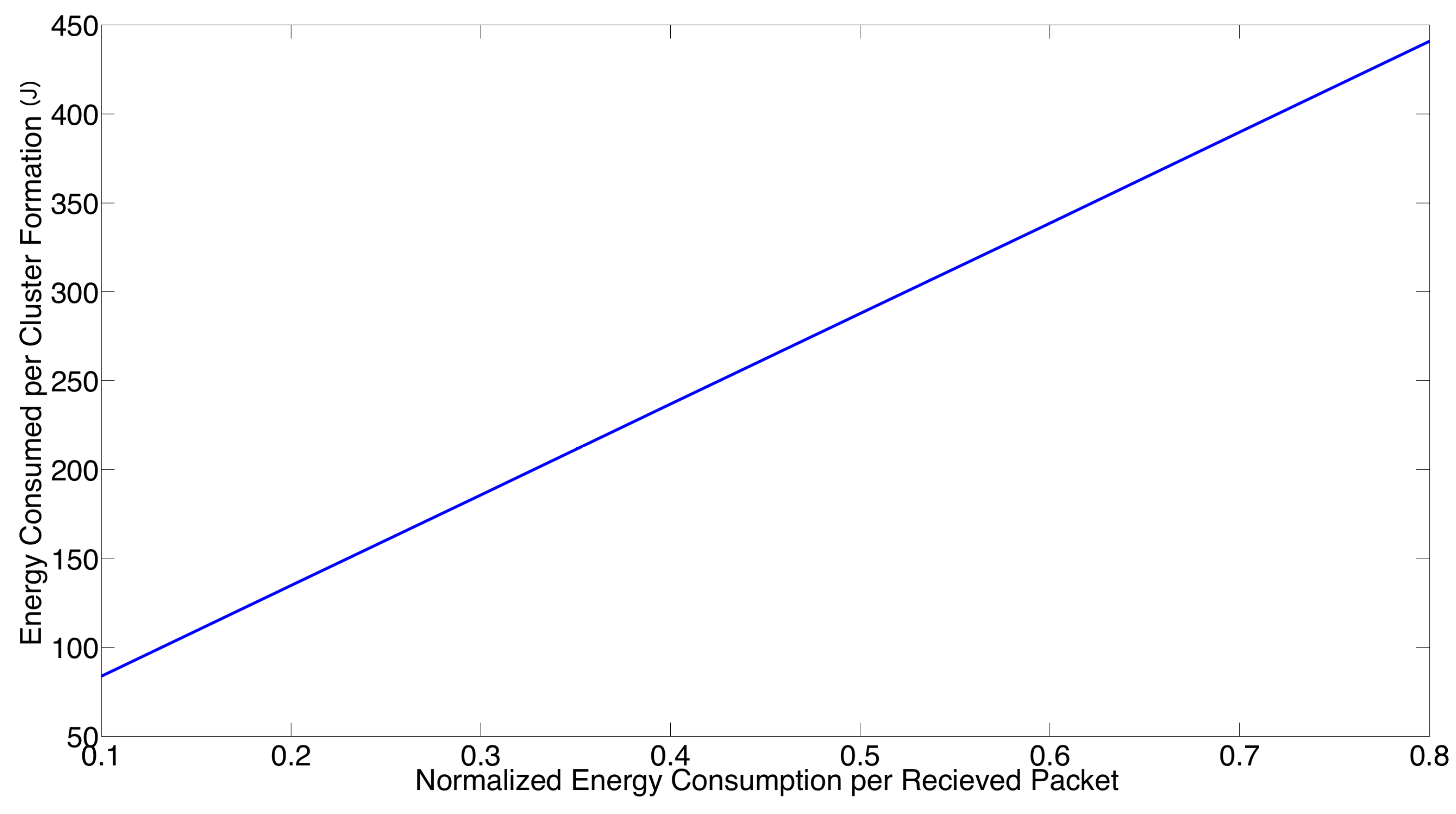
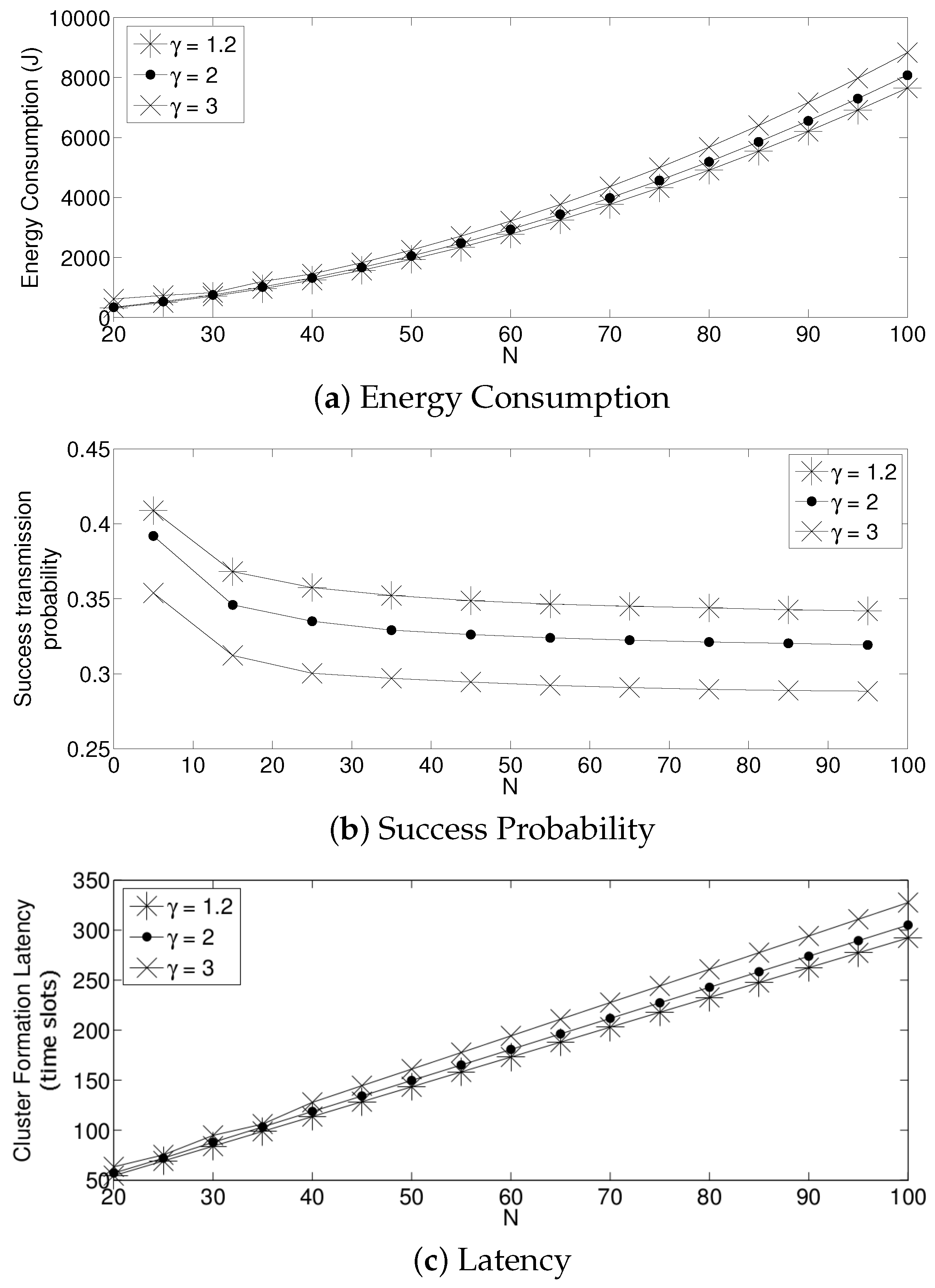
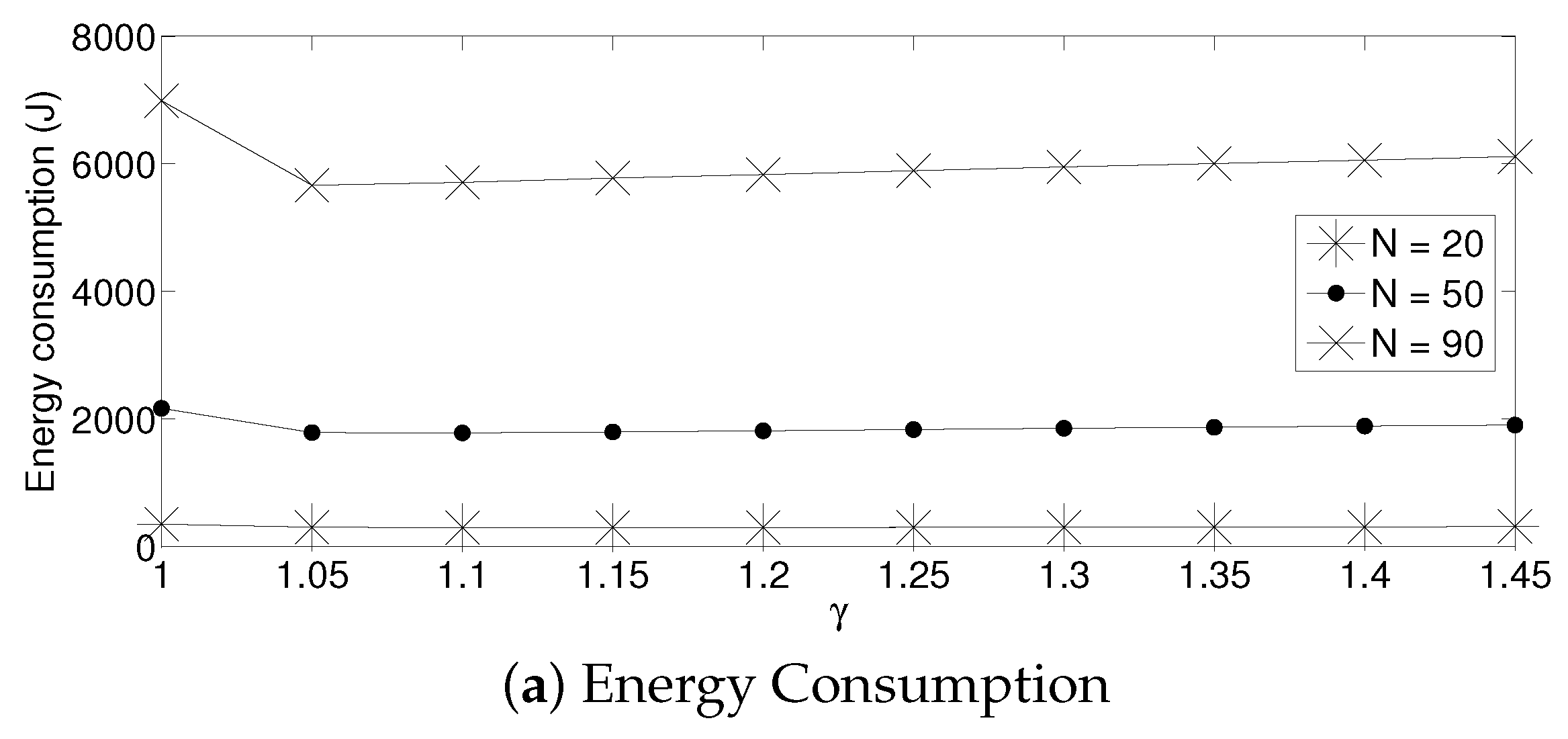
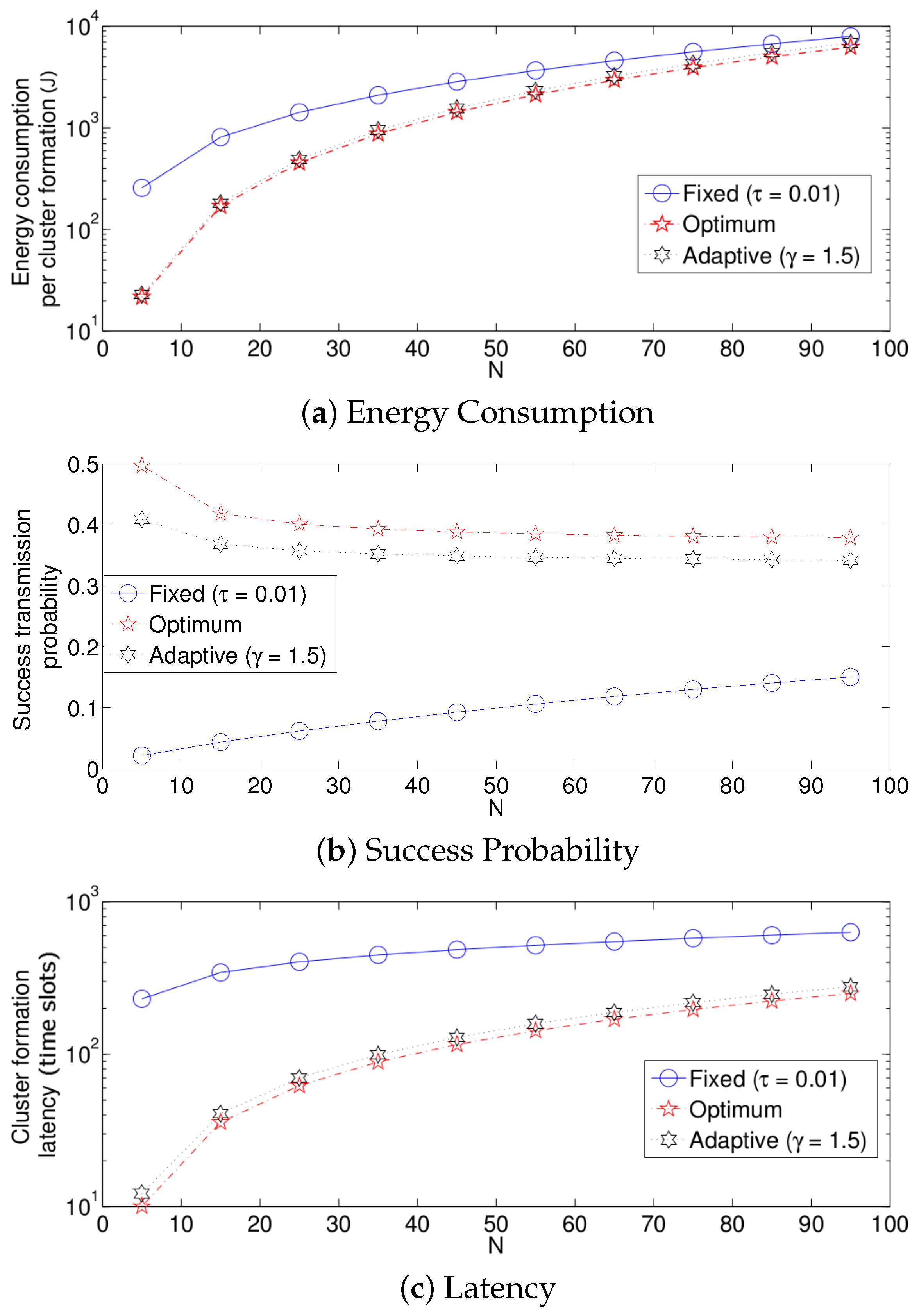
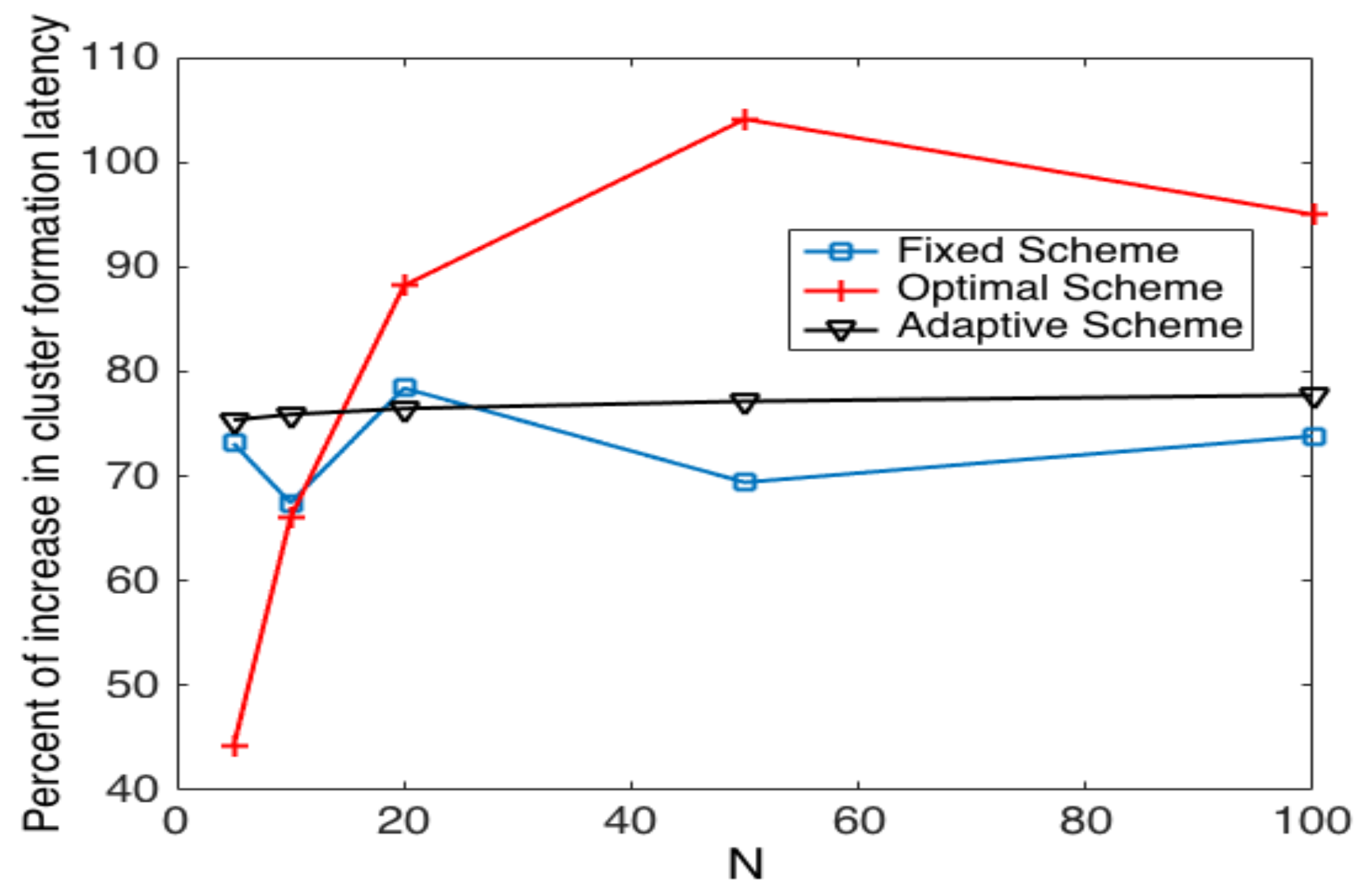
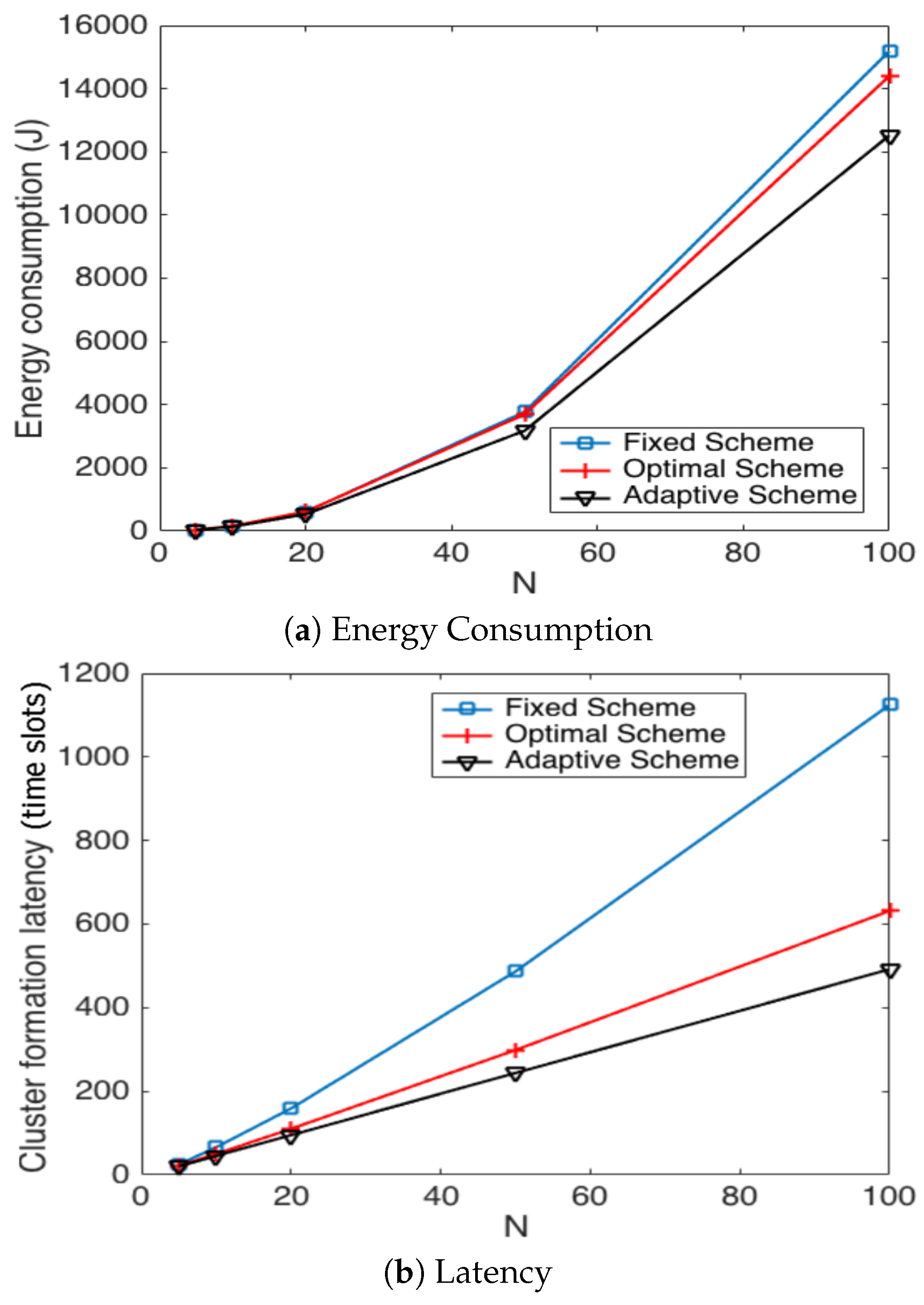
- The performance of the system is very sensitive to the value of as shown in Figure 6. For low network densities, the value of should be high in order to achieve a low energy consumption. For instance, by observing the case where the number of active nodes is relatively small (), a low value of () causes higher energy consumption. This is because the nodes spend a lot of time in reception mode consuming unnecessary energy. On the other hand, for high values of N, the transmission probability should be rather small. Observe the case where . A value of causes a high number of collisions, and consequently, the energy consumption is very high, while a value of achieves a low energy consumption. Then, it is clear that has to be carefully selected depending on the value of N. In the case of the values considered in this section, when , the performance of the system is better with . When , the value of achieves the lowest energy consumption and cluster formation latency, as well as the highest success probability. Conversely, when , the system has the best performance for .
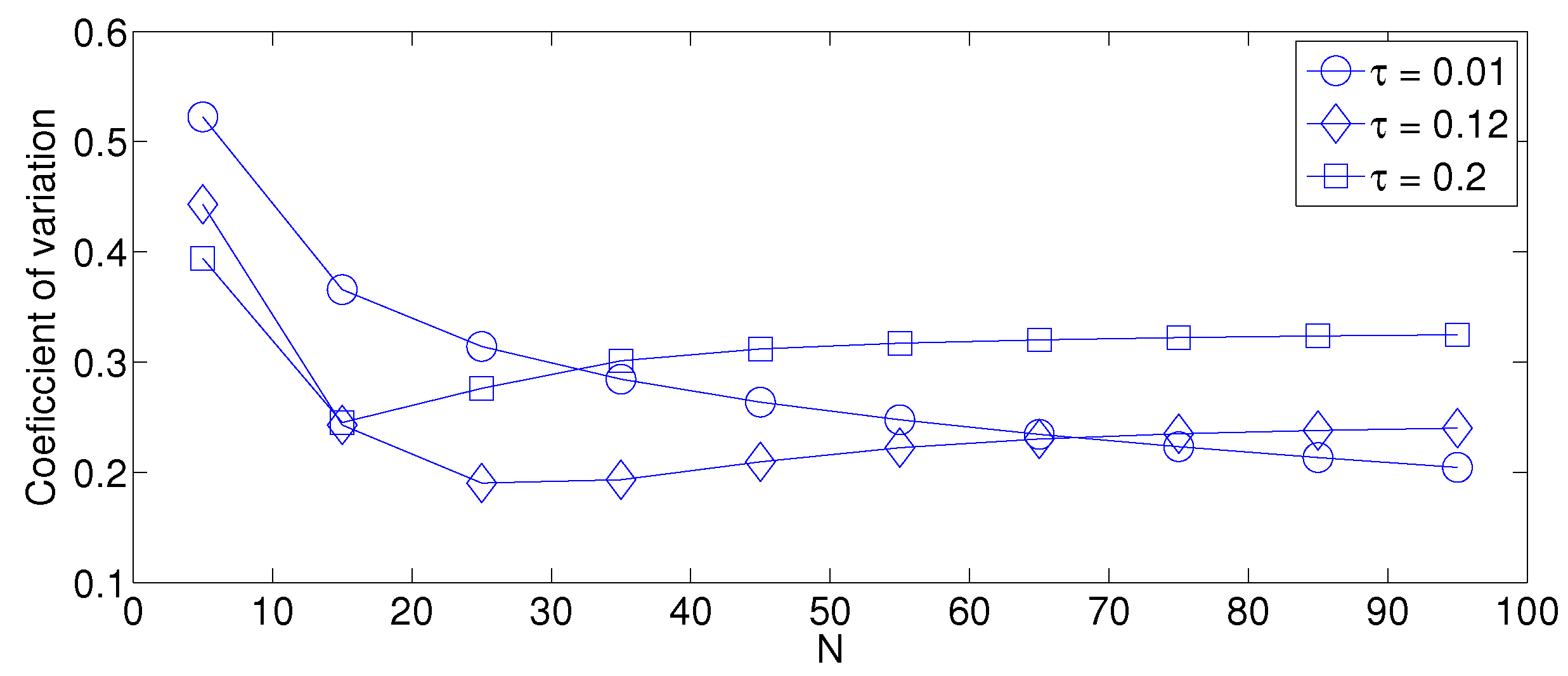
- As mentioned in Section 2, there is a low variation in the cluster formation delay that can be evaluated in terms of the coefficient of variation presented in Figure 7. Since the cluster delay can be calculated by the sum of geometrically-distributed random variables, we can observe that the coefficient of variation is lower than 0.6 for any value of and N.
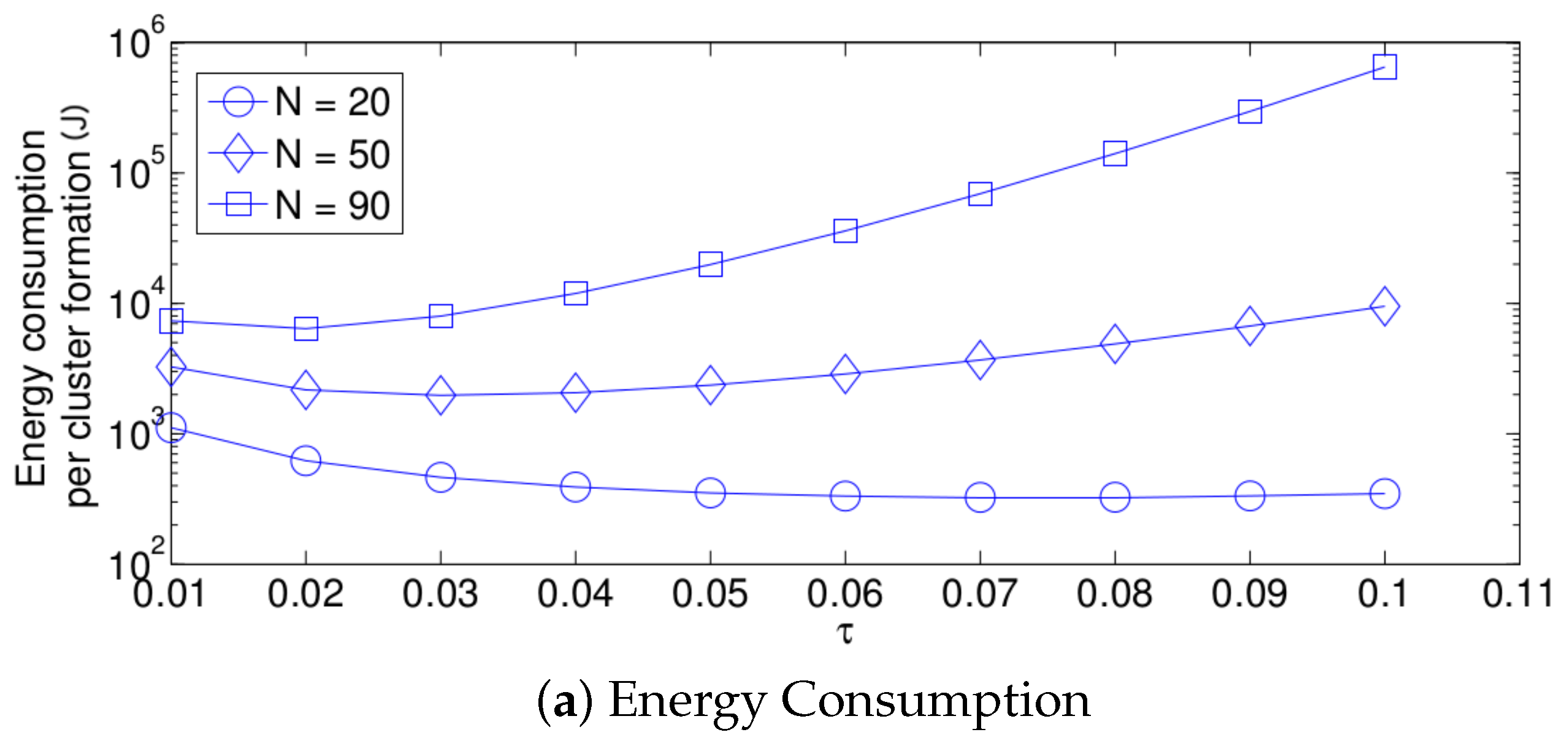
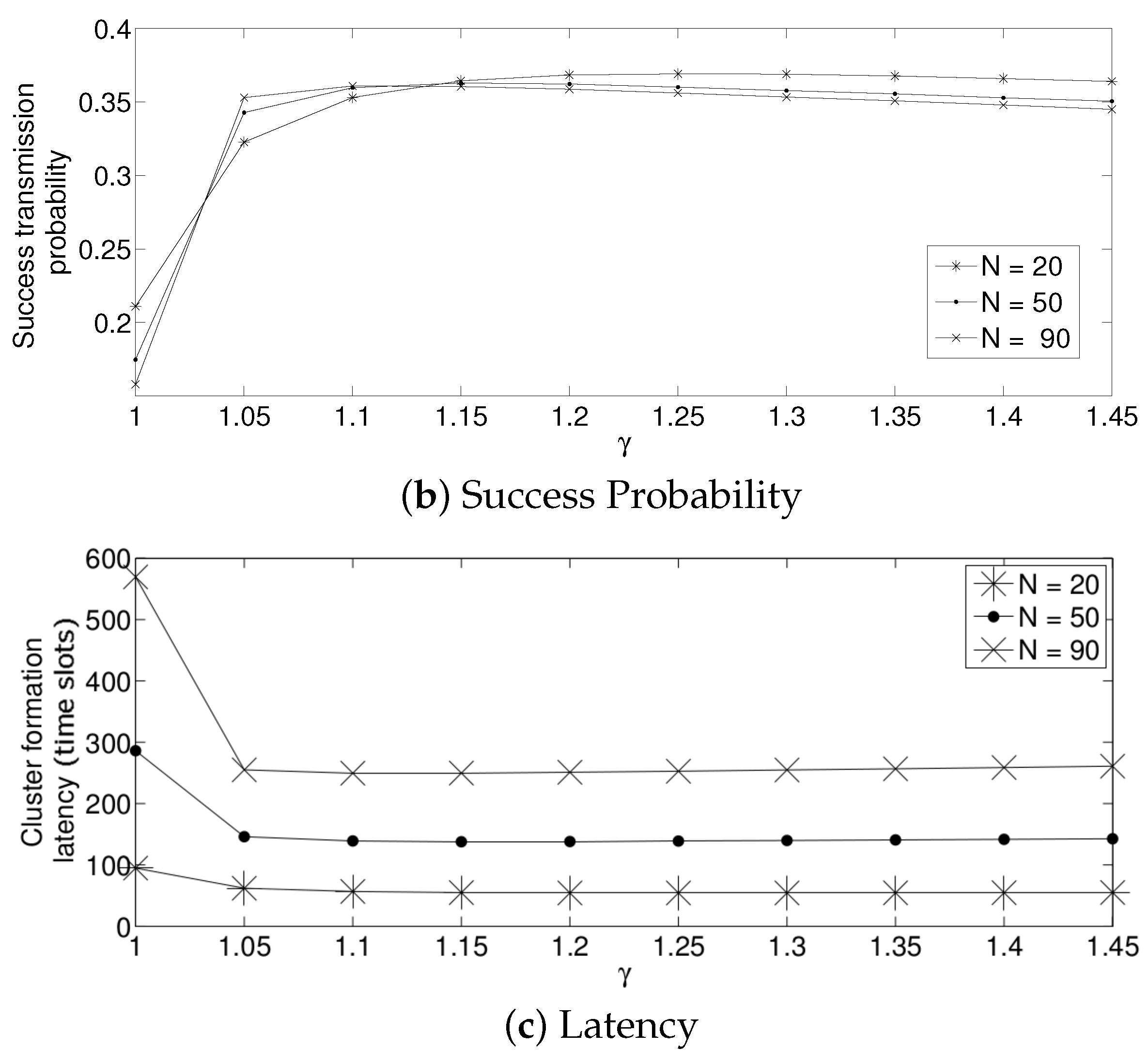
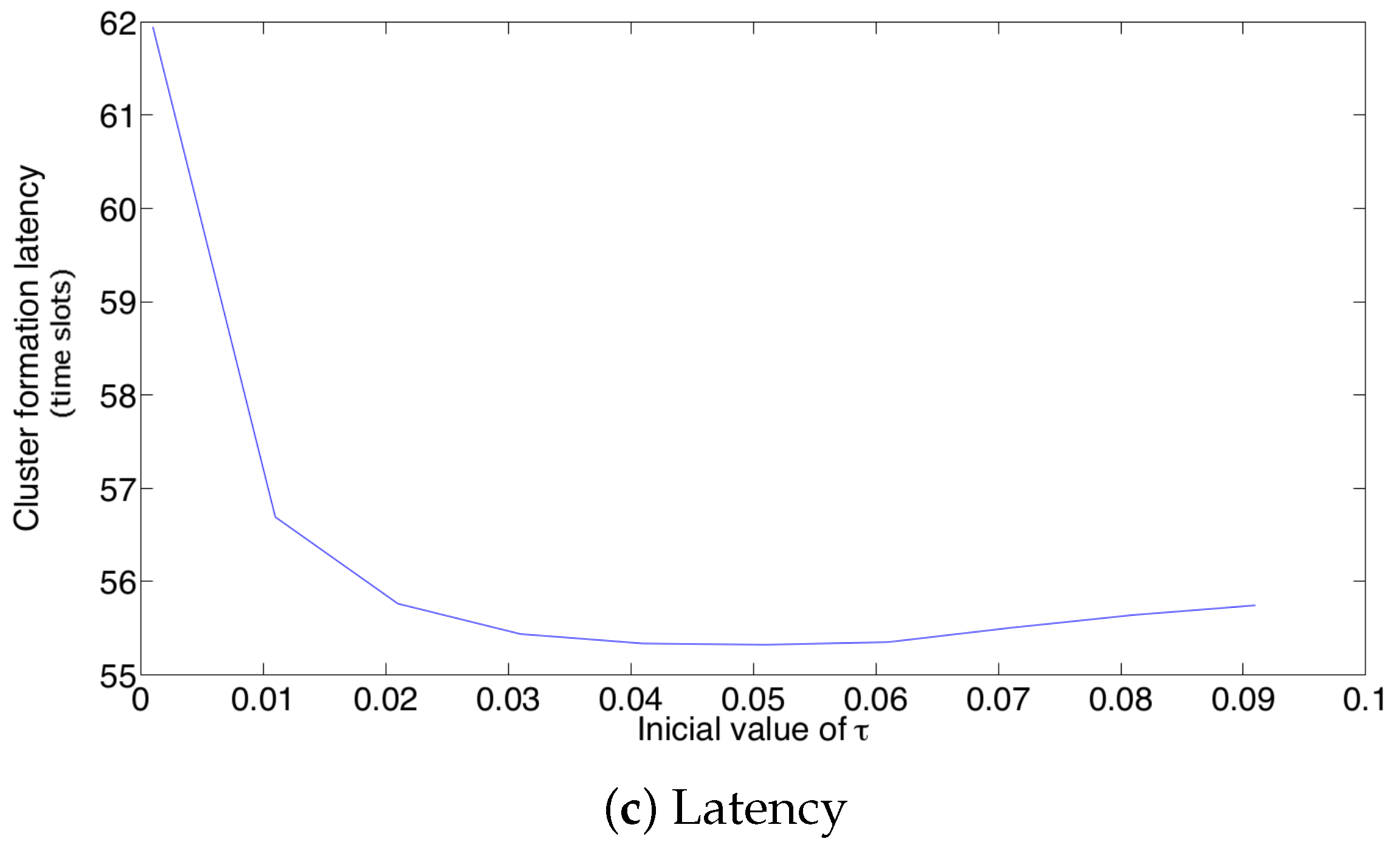
- For a practical implementation of the fixed strategy, in order to select an appropriate value of , Figure 8 presents the performance of the system for N fixed vs. . From these results, we can see that for , an appropriate value of the transmission probability is close to 0.02. This corresponds to a case of a very dense network. For a medium-high density network, , a suitable value of is 0.04. Additionally, for a medium-low density network, , a suitable value of is higher than 0.1.
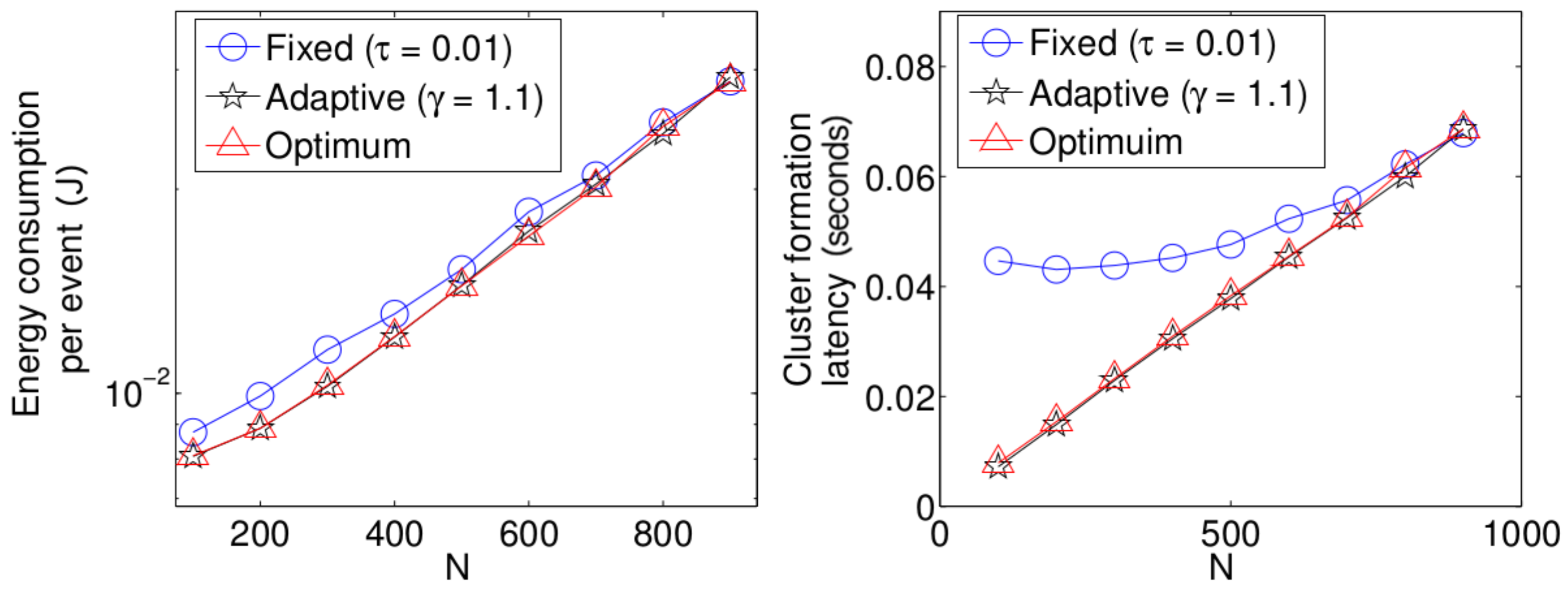
5.2. System Performance in Noisy Channels
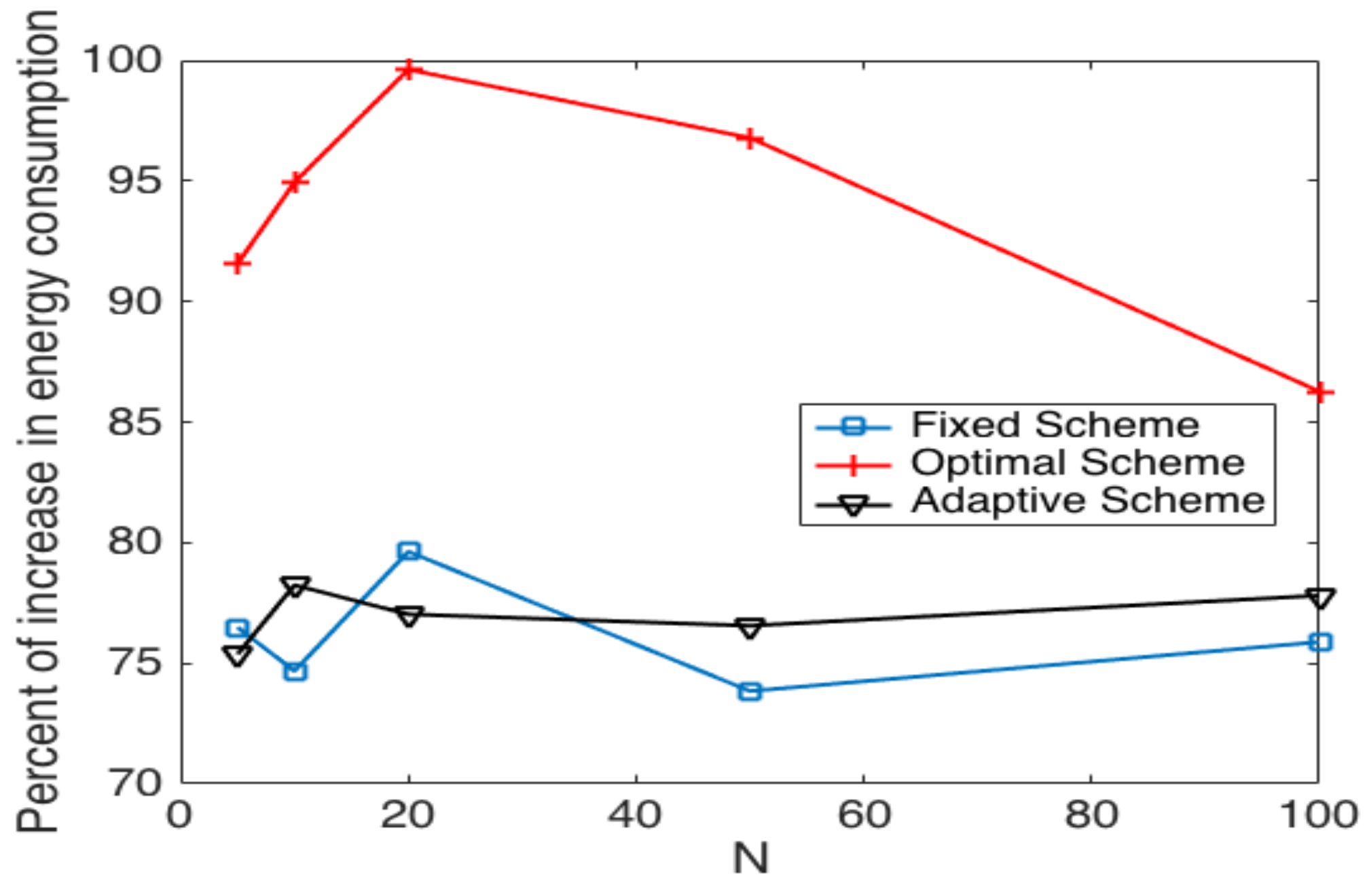
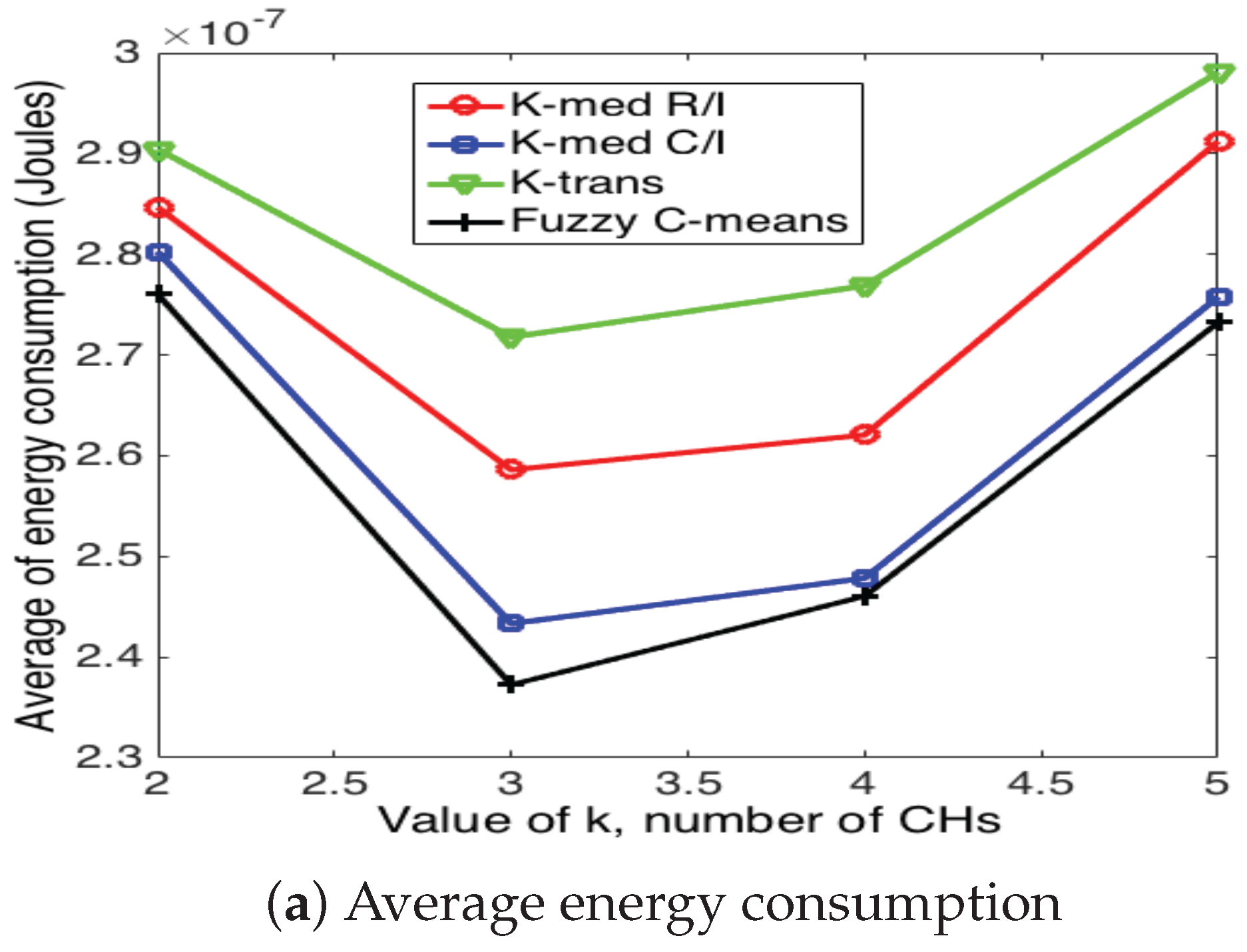
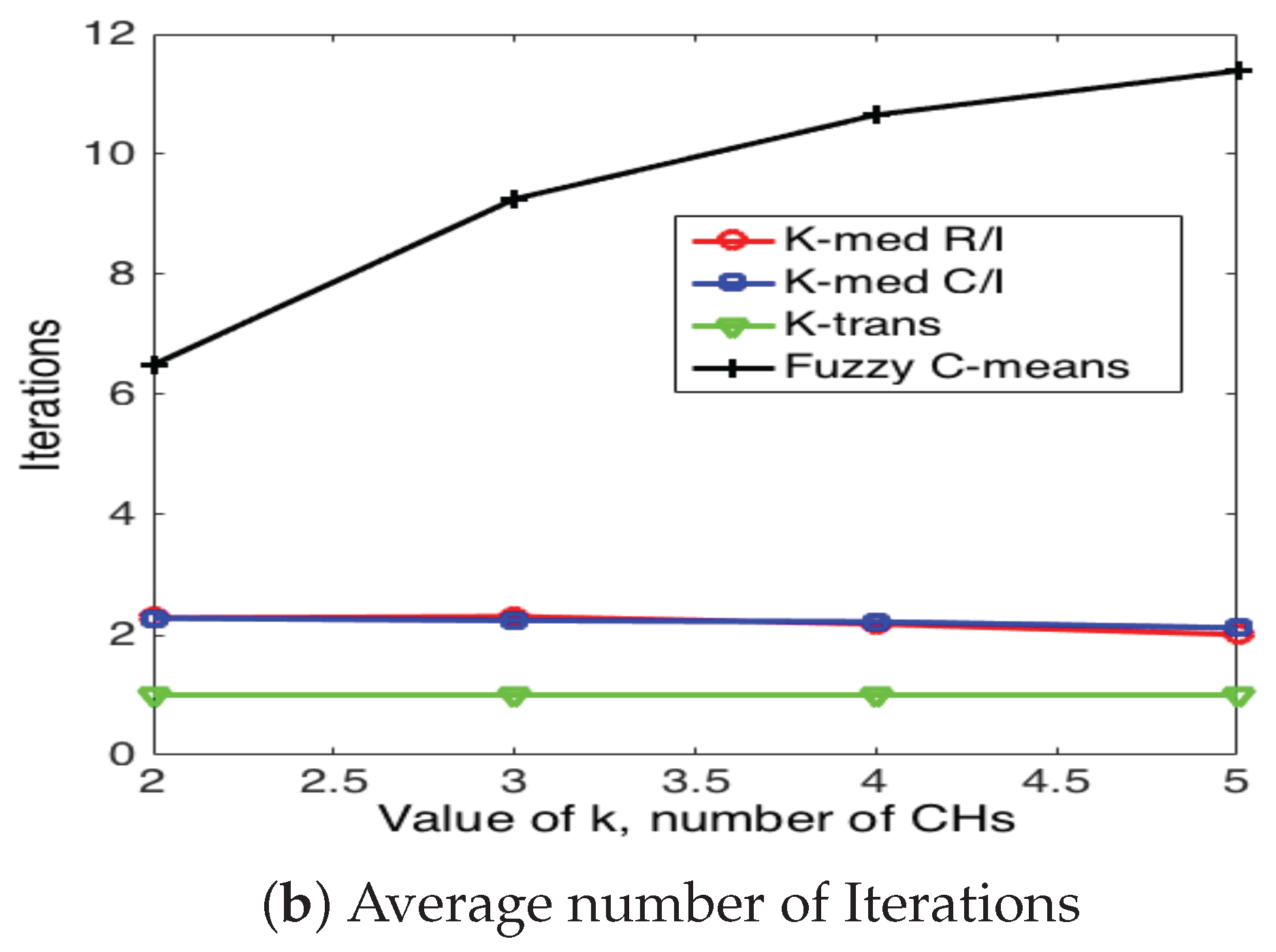
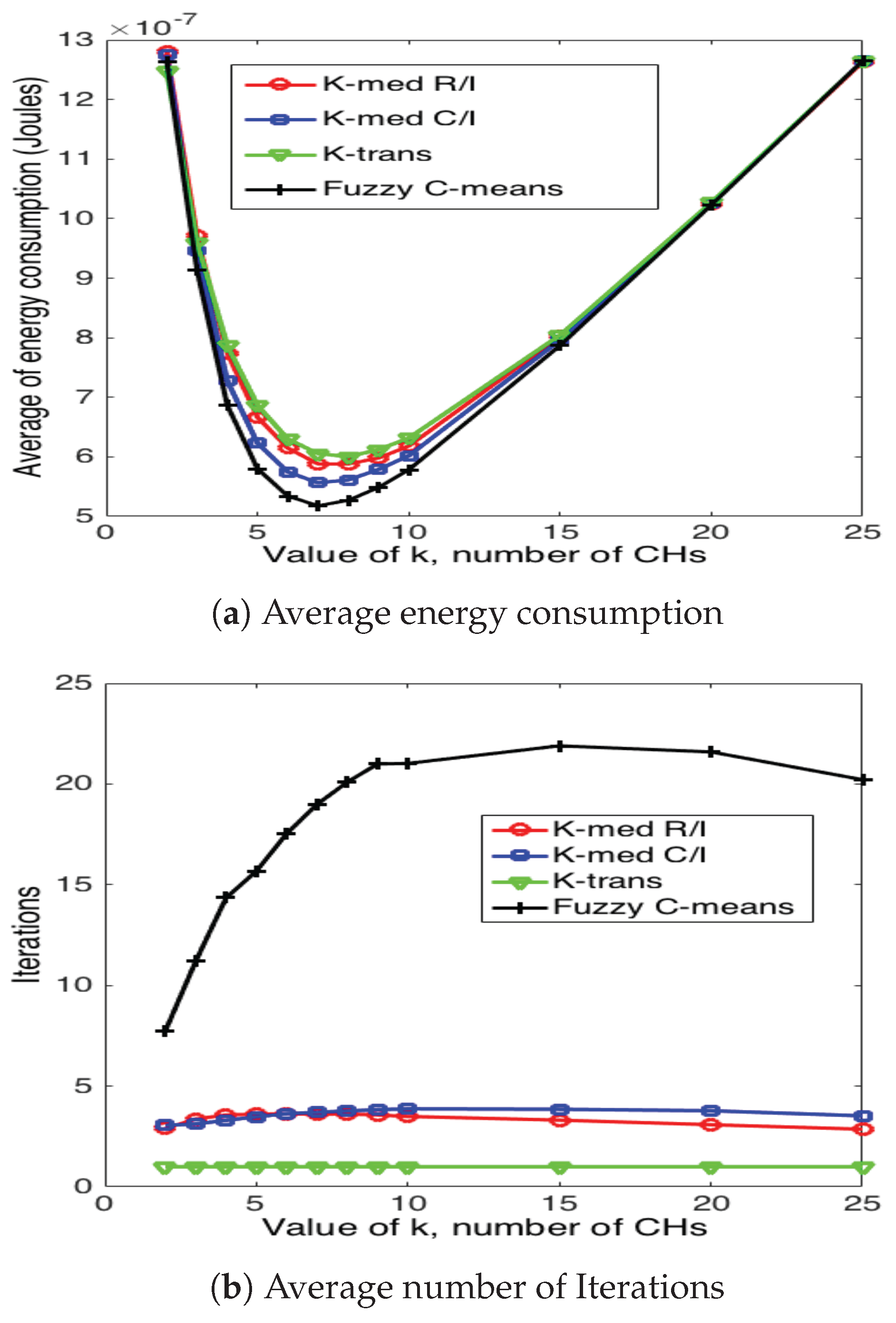
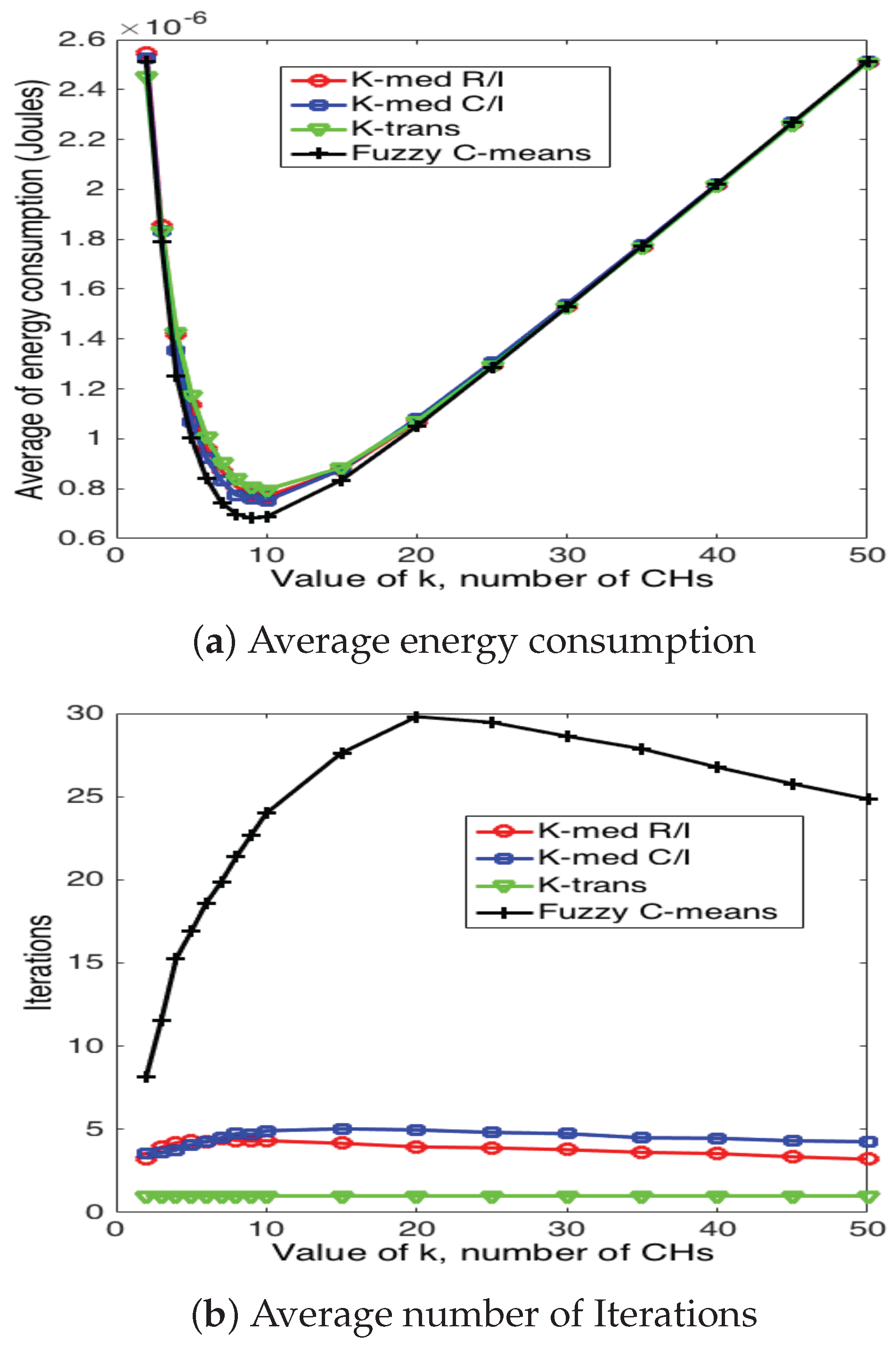
5.3. Cluster Head Selection Schemes
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akiyldiz, I.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A survey on sensor networks. IEEE Commun. Mag. 2002, 40, 102–114. [Google Scholar] [CrossRef]
- Fahmy, H.M.A. Wireless Sensor Networks, Concepts, Applications, Experimentation and Analysis; Springer: Singapore, 2016. [Google Scholar]
- Bouabdallah, N.; Rivero-Angeles, M.E.; Sericola, B. Continuos monitoring using event-driven reporting for cluster-based wireless sensor networks. IEEE Trans. Veh. Technol. 2009, 58, 3460–3479. [Google Scholar] [CrossRef]
- Afsar, M.M.; Tayarani-N, M.-H. Clustering in sensor networks: A literature survey. J. Netw. Comput. Appl. 2015, 46, 198–226. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Kredo, K.; Mohapatra, P. Medium access control in wireless sensor networks. Comput. Netw. 2007, 51, 961–994. [Google Scholar] [CrossRef]
- Verma, A.; Singh, M.P.; Singh, J.P.; Kumar, P. Survey of MAC Protocol for Wireless Sensor Networks. In Proceedings of the 2015 Second International Conference on Advances in Computing and Communication Engineering, Dehradun, India, 1–2 May 2015; pp. 92–97. [Google Scholar]
- Fanian, F.; Rafsanjani, M.K.; Bardsiri, V.K. A Survey of Advanced LEACH-Based Protocols. Int. J. Energy Inf. Commun. 2016, 7, 1–16. [Google Scholar] [CrossRef]
- Dabas, P.; Gupta, N. LEACH and its Improved Versions-A Survey. Int. J. Sci. Eng. Res. 2015, 6, 184–188. [Google Scholar]
- Younis, O.; Fahamy, S. Distributed Clustering in Ad-Hoc Sensor Networks: A hybrid, Energy-Efficient Approach. In Proceedings of the INFOCOM 2004 Twenty-Third AnnualJoint Conference of the IEEE Computer and Communications Societies, Hong Kong, China, 7–11 March 2004; Volume 1, pp. 629–640. [Google Scholar]
- Bandyopadhyay, S.; Coyle, E.J. An Energy Efficient Hierarchical Clustering Algorithm for Wireless Sensor Networks. In Proceedings of the INFOCOM Twenty-Second Annual Joint Conference of the IEEE Computer and Communications, San Francisco, CA, USA, 30–31 April 2003; Volume 3, pp. 1713–1723. [Google Scholar]
- Vuran, M.C.; Akyildiz, I.F. Spatial correlation-based Collaborative Medium Access Control in Wireless Sensor Networks. IEEE ACM Trans. Netw. 2006, 14, 316–329. [Google Scholar] [CrossRef]
- Chatzigiannakis, I.; Kinalis, A.; Nikoletseas, S. Wireless Sensor Networks Protocols for Efficient Collision Avoidance in Multi-Path Data Propagation. In Proceedings of the 1st ACM International Workshop on Performance Evaluation of Wireless Ad Hoc, Sensor, and Ubiquitous Networks, Venice, Italy, 7 October 2004; pp. 8–16. [Google Scholar]
- AlSkaif, T.; Guerrero Zapata, M.; Bellalta, B. Game theory for energy efficiency in wireless sensor networks: Latest trends. J. Netw. Comput. Appl. 2015, 54, 33–61. [Google Scholar] [CrossRef]
- Wu, X.; Zeng, X.; Fang, B.; Yang, L.; Zhang, W. An energy-balance and game-theory-based cluster formation method for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2017. [Google Scholar] [CrossRef]
- Movassagh, M.; Aghdasi, H.S. Game theory based node scheduling as a distributed solution for coverage control in wireless sensor networks. Eng. Appl. Artif. Intell. 2017, 65, 137–146. [Google Scholar] [CrossRef]
- Rivero-Angeles, M.E.; Orea-Flores, I.Y. Tools for the selection of the transmission probability in the cluster formation phase for Event-Driven Wireless Sensor Networks. Rev. Fac. Ing. Univ. Antioq. 2014, 73, 101–110. [Google Scholar]
- Sagduyu, Y.E.; Ephremides, A. The problem of medium access control in wireless sensor networks. IEEE Wirel. Commun. 2004, 11, 44–53. [Google Scholar] [CrossRef]
- Park, H.; Jun, C. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Çöplü, T.; Oktuğ, S.F. Predictive Channel Access Scheme for Wireless Sensor Networks Using Received Signal Strength Statistics. In Proceedings of the 2011 IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2011; pp. 590–594. [Google Scholar]
- Tang, S.; Mark, B.L. Modeling and analysis of opportunistic spectrum sharing with unreliable spectrum sensing. IEEE Trans. Wirel. Commun. 2009, 8, 1934–1943. [Google Scholar] [CrossRef]
- Suliman, I.; Lehtomski, J.; Brsysy, T.; Umebayashi, K. Analysis of Cognitive Radio Networks with Imperfect Sensing. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 1616–1620. [Google Scholar]
- Gelabert, X.; Salient, O.; Pzrez-Romero, J.; Agust, R. Spectrum sharing in cognitive radio networks with imperfect sensing: A discrete- time Markov model. Comput. Netw. 2010, 54, 2519–2536. [Google Scholar] [CrossRef]
- Wang, Z. Comparison of Four Kinds of Fuzzy C Means Clustering Methods. In Proceedings of the Third International Symposium on Information Processing (ISIP), Qingdao, China, 15–17 October 2010; pp. 563–566. [Google Scholar]
- Mei, J.; Chen, L. Fuzzy relational clustering around medoids: A unified view. Fuzzy Sets Syst. 2011, 183, 44–56. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Joshi, A.; Nasraoui, O.; Yi, L. Low-complexity fuzzy relational clustering algorithms for Web mining. IEEE Trans. Fuzzy Syst. 2001, 9, 595–607. [Google Scholar] [CrossRef]

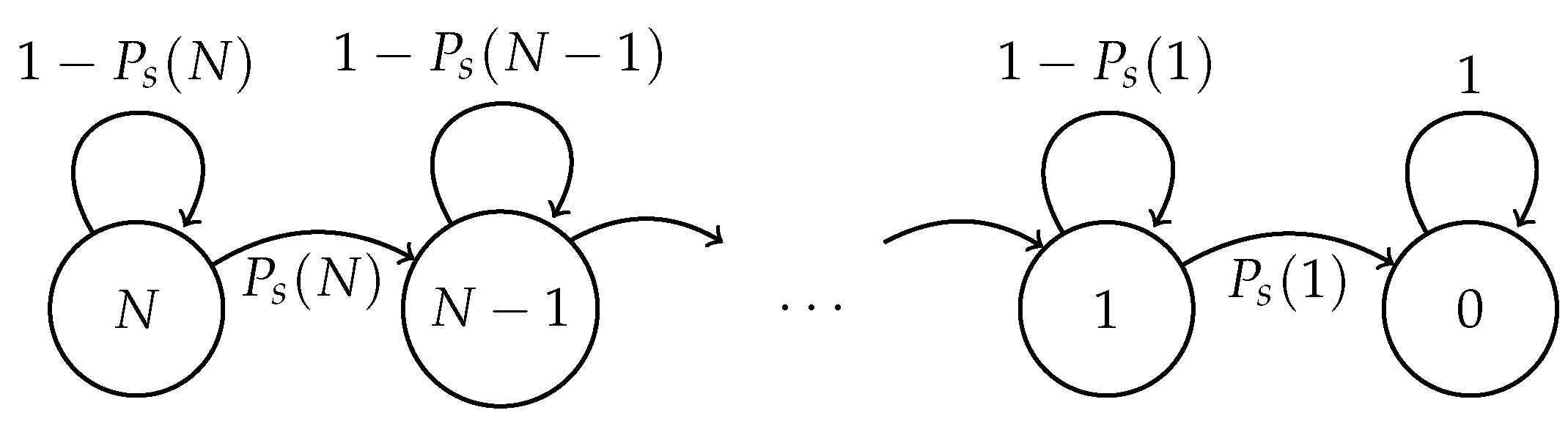
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montiel, E.R.; Rivero-Angeles, M.E.; Rubino, G.; Molina-Lozano, H.; Menchaca-Mendez, R.; Menchaca-Mendez, R. Performance Analysis of Cluster Formation in Wireless Sensor Networks. Sensors 2017, 17, 2902. https://doi.org/10.3390/s17122902
Montiel ER, Rivero-Angeles ME, Rubino G, Molina-Lozano H, Menchaca-Mendez R, Menchaca-Mendez R. Performance Analysis of Cluster Formation in Wireless Sensor Networks. Sensors. 2017; 17(12):2902. https://doi.org/10.3390/s17122902
Chicago/Turabian StyleMontiel, Edgar Romo, Mario E. Rivero-Angeles, Gerardo Rubino, Heron Molina-Lozano, Rolando Menchaca-Mendez, and Ricardo Menchaca-Mendez. 2017. "Performance Analysis of Cluster Formation in Wireless Sensor Networks" Sensors 17, no. 12: 2902. https://doi.org/10.3390/s17122902
APA StyleMontiel, E. R., Rivero-Angeles, M. E., Rubino, G., Molina-Lozano, H., Menchaca-Mendez, R., & Menchaca-Mendez, R. (2017). Performance Analysis of Cluster Formation in Wireless Sensor Networks. Sensors, 17(12), 2902. https://doi.org/10.3390/s17122902



