A New Quaternion-Based Kalman Filter for Real-Time Attitude Estimation Using the Two-Step Geometrically-Intuitive Correction Algorithm
Abstract
:1. Introduction
2. Methods
2.1. Orientation Representation and Determination
2.1.1. Quaternion-Based Orientation Representation
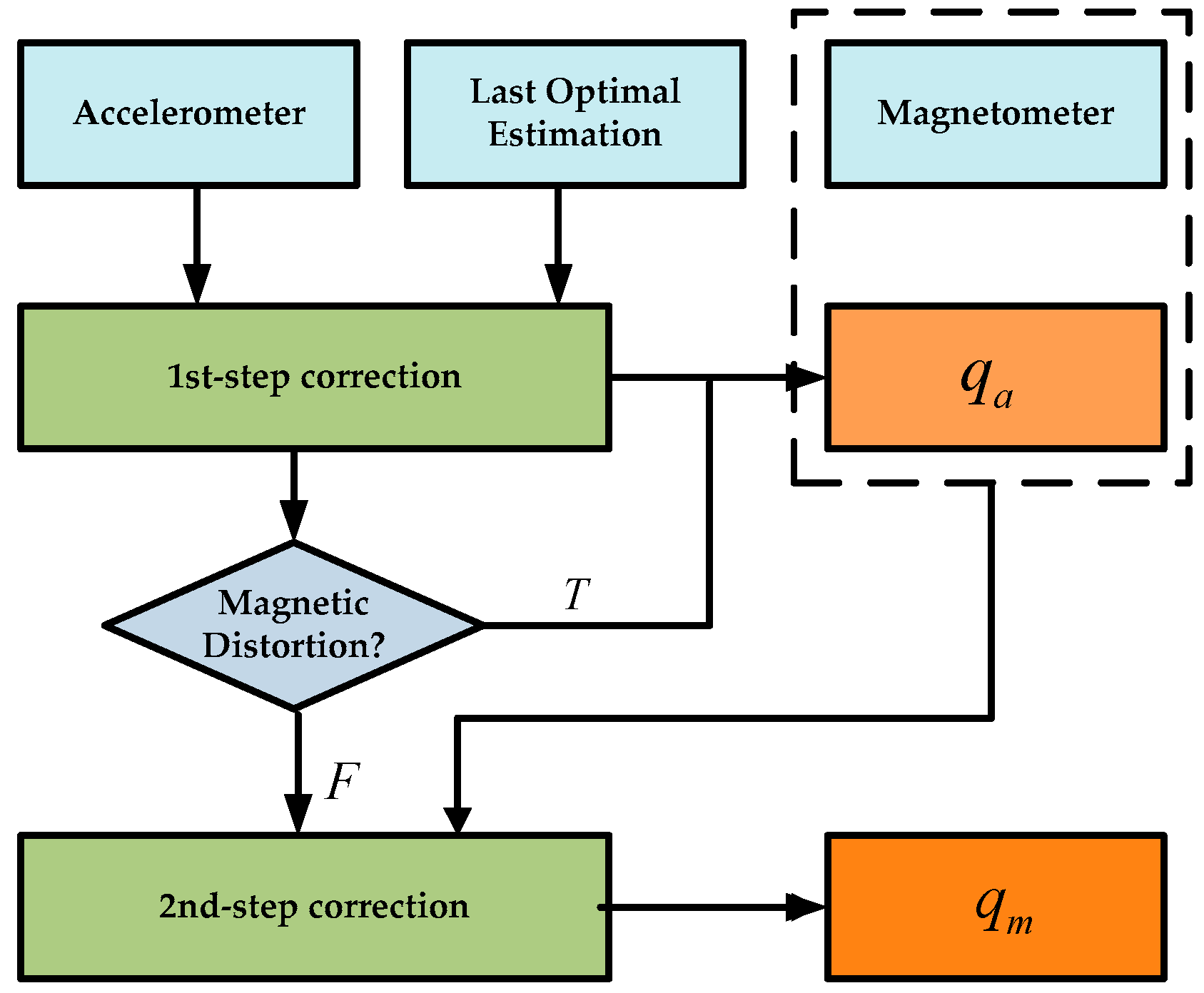
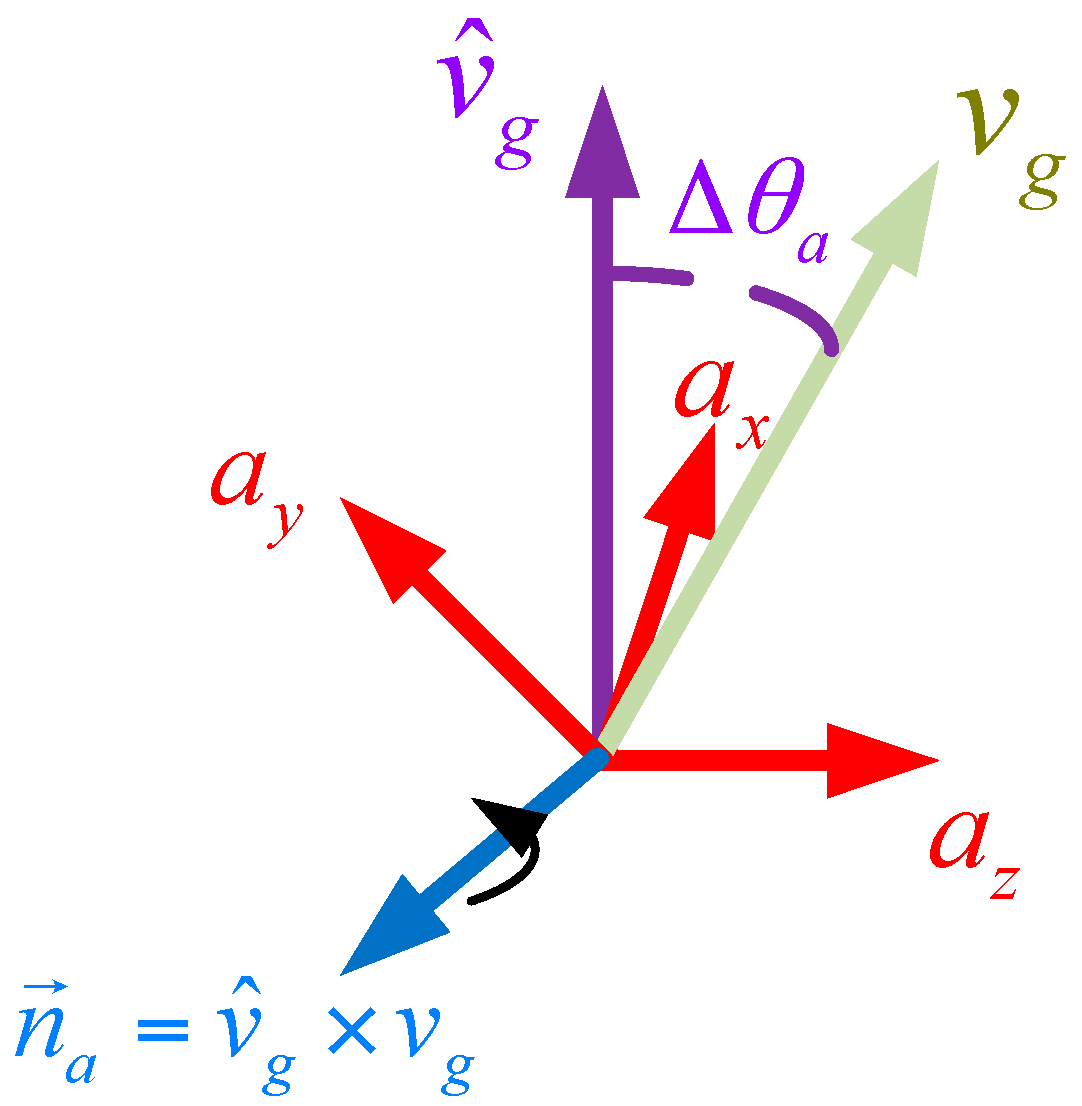
2.1.2. Accelerometer/Magnetometer-Based Attitude Determination
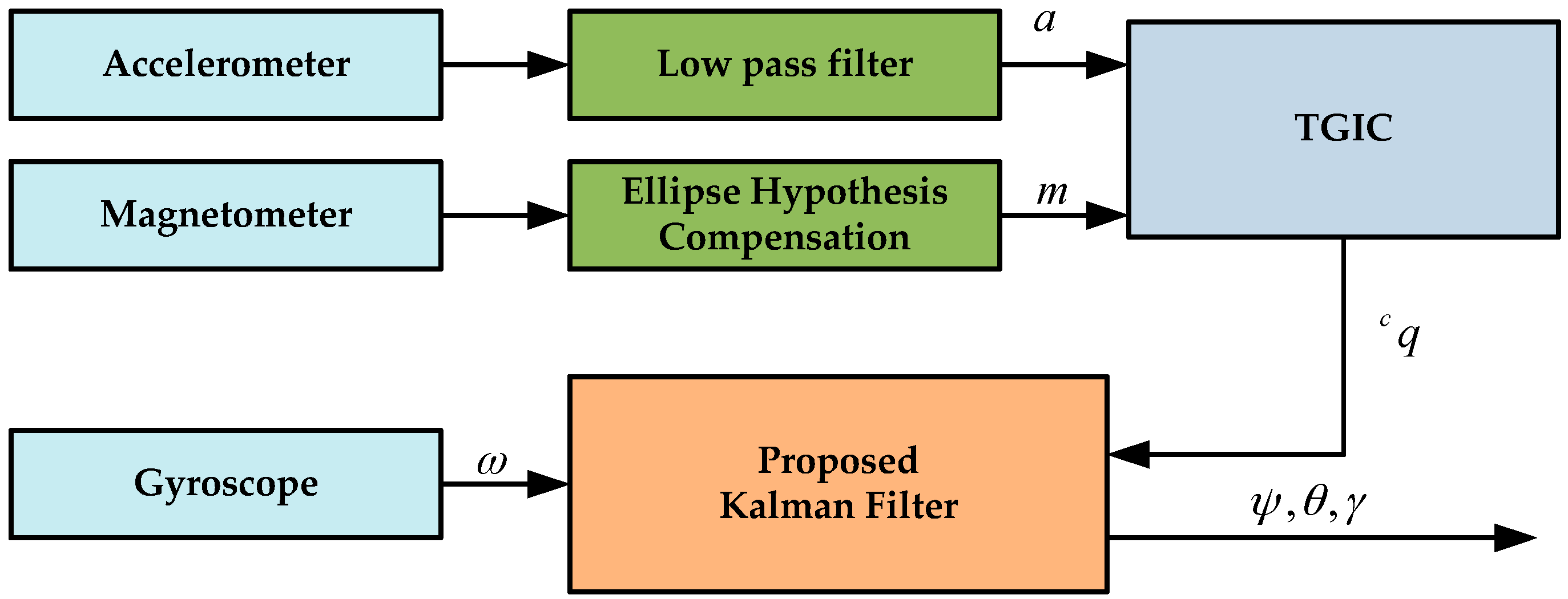
2.2. Data Fusion Based on a Kalman Filter
2.2.1. Process Model
2.2.2. Observation Model
2.2.3. Kalman Filter Fusion
2.3. Noise Characteristics
2.3.1. Process Noise Covariance Determination
2.3.2. Measurement Noise Covariance Determination
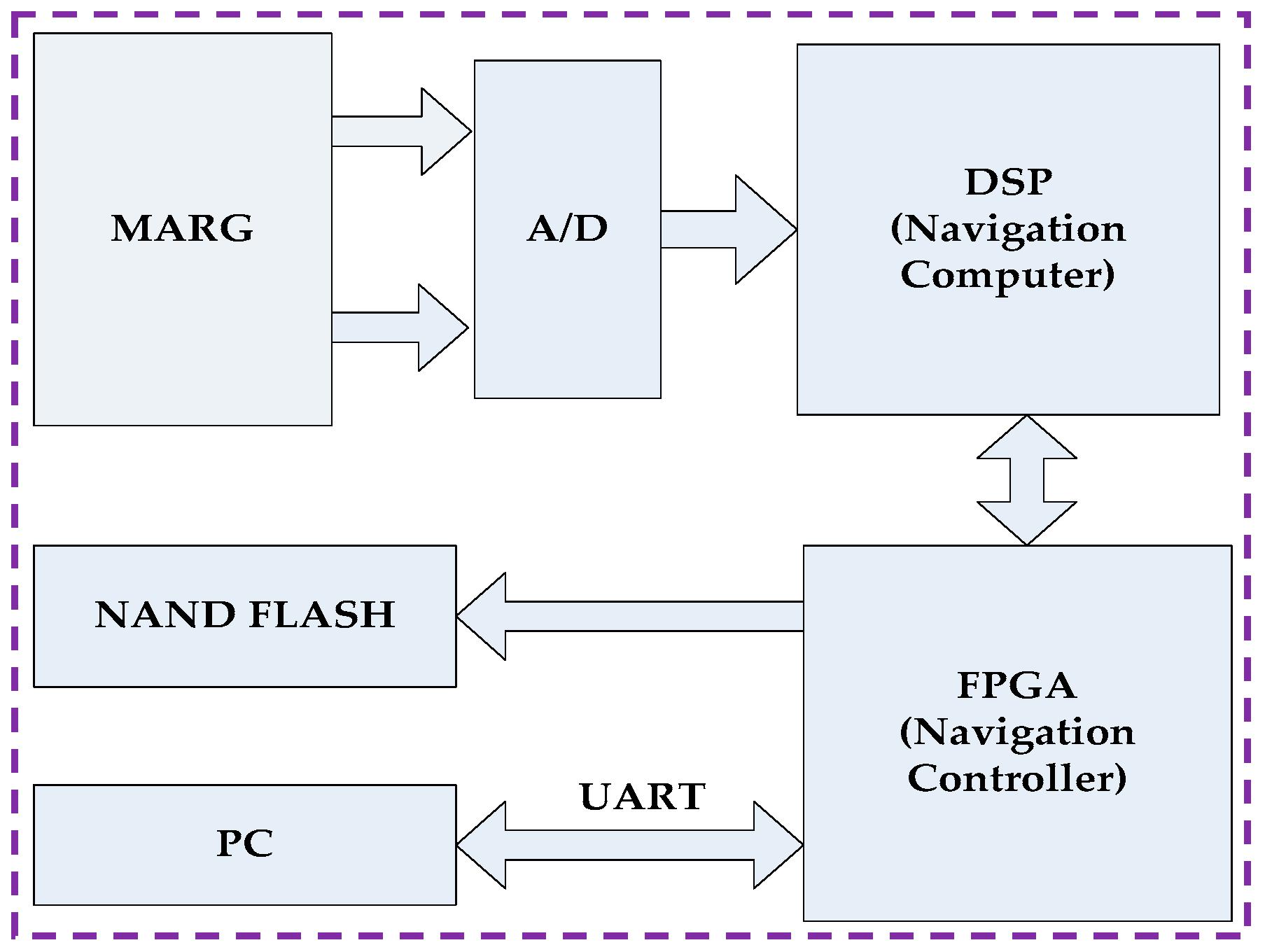
2.4. Hardware Design
2.5. Experimental Setup
3. Results and Discussion
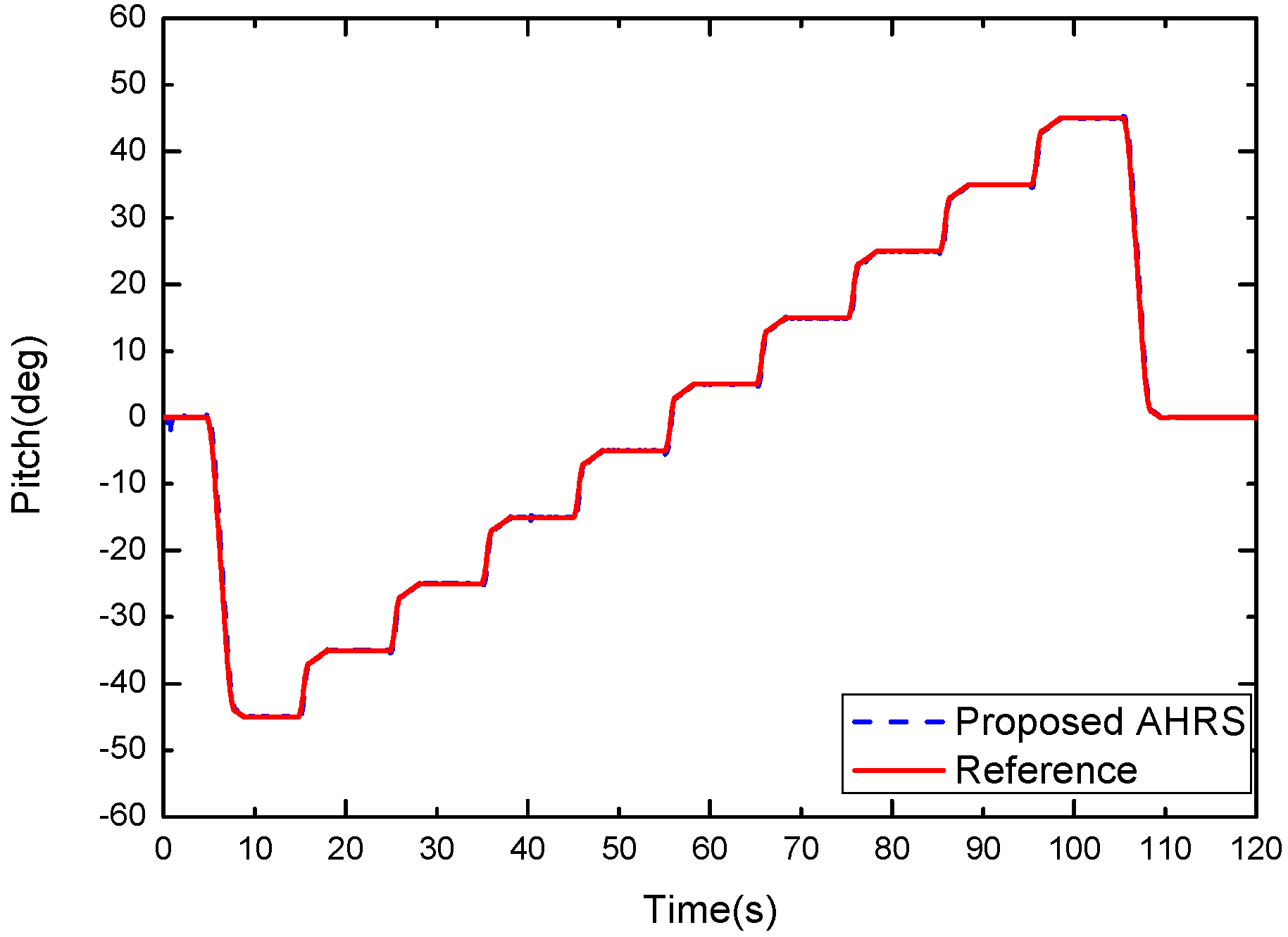
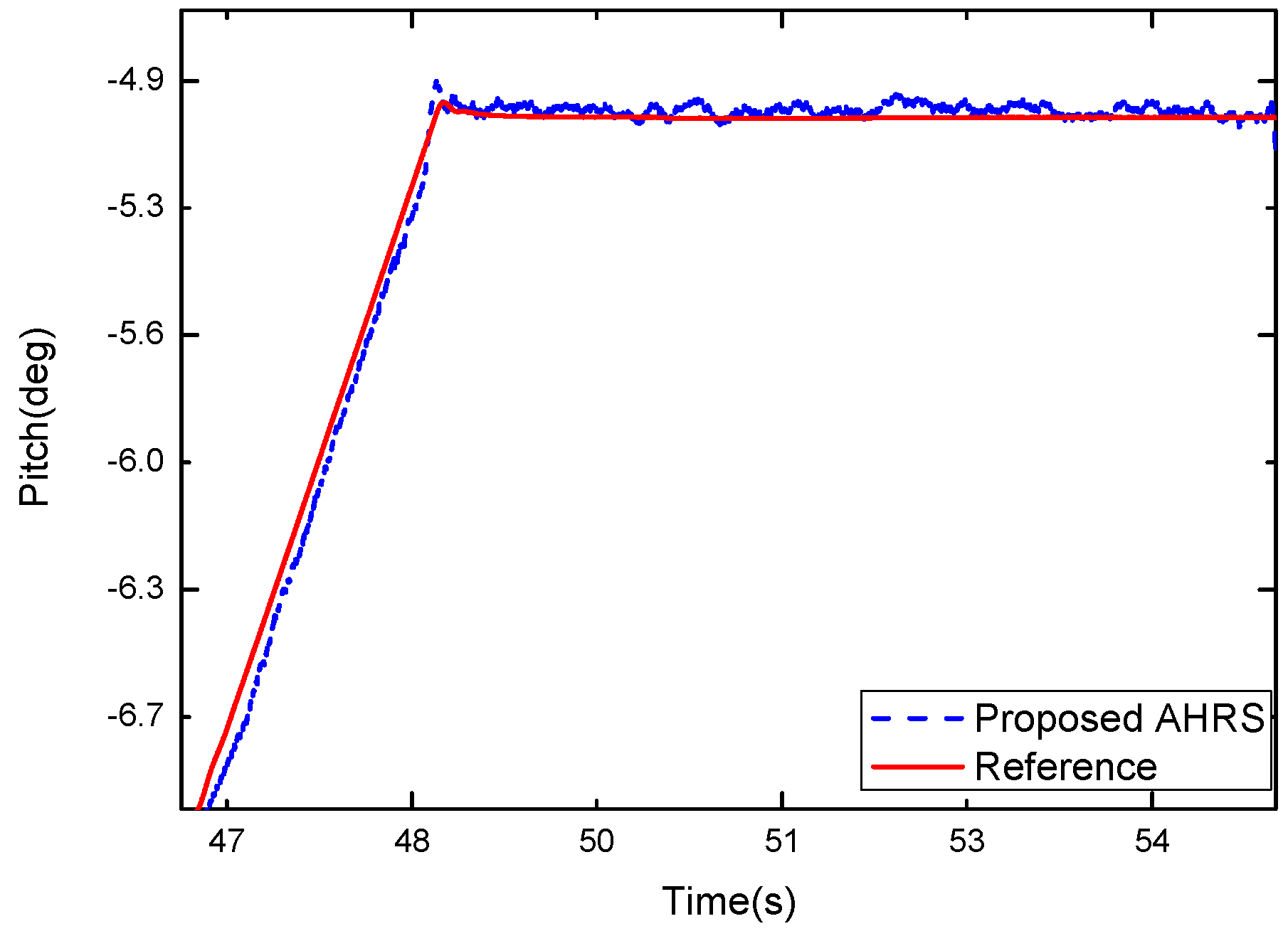
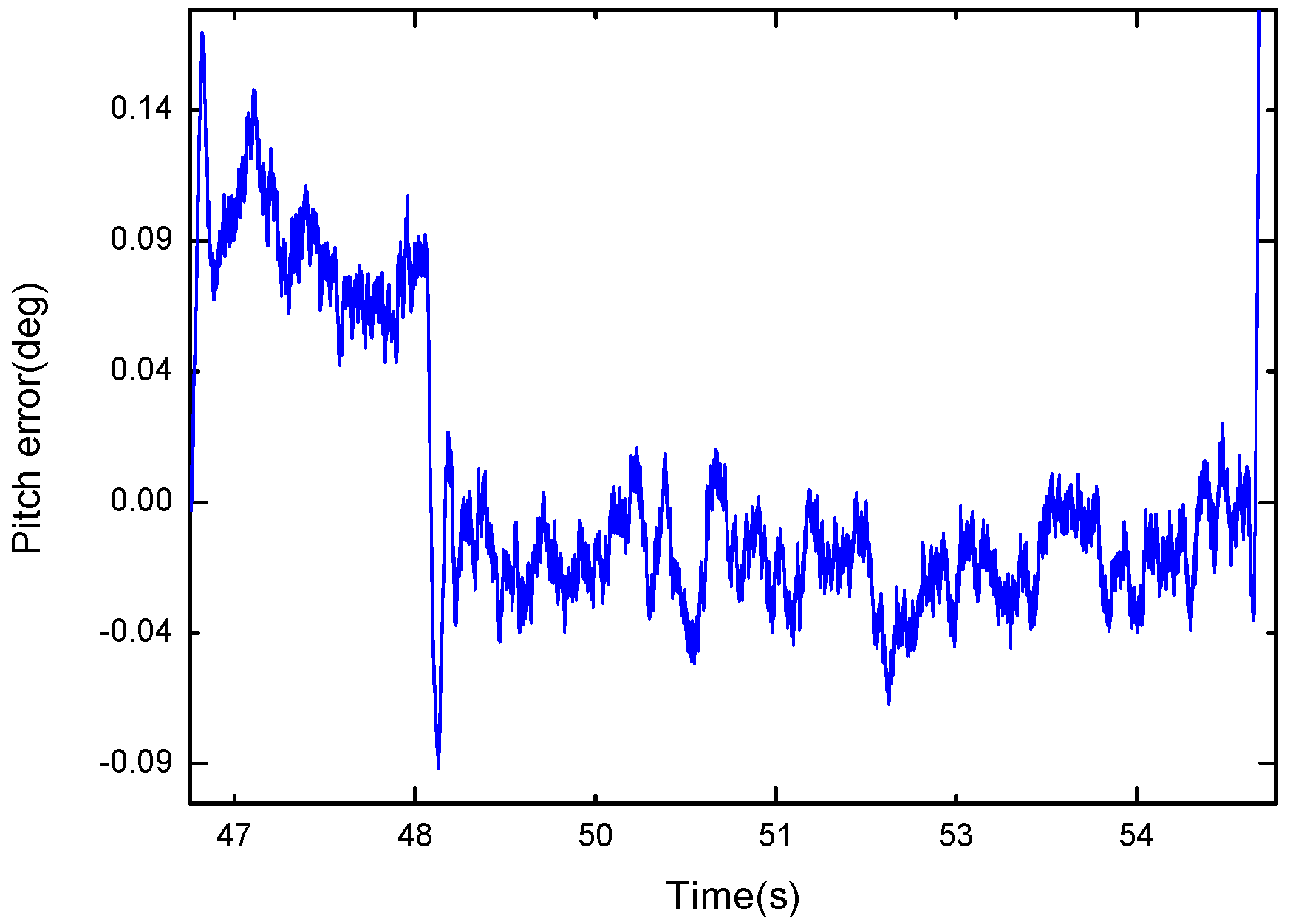
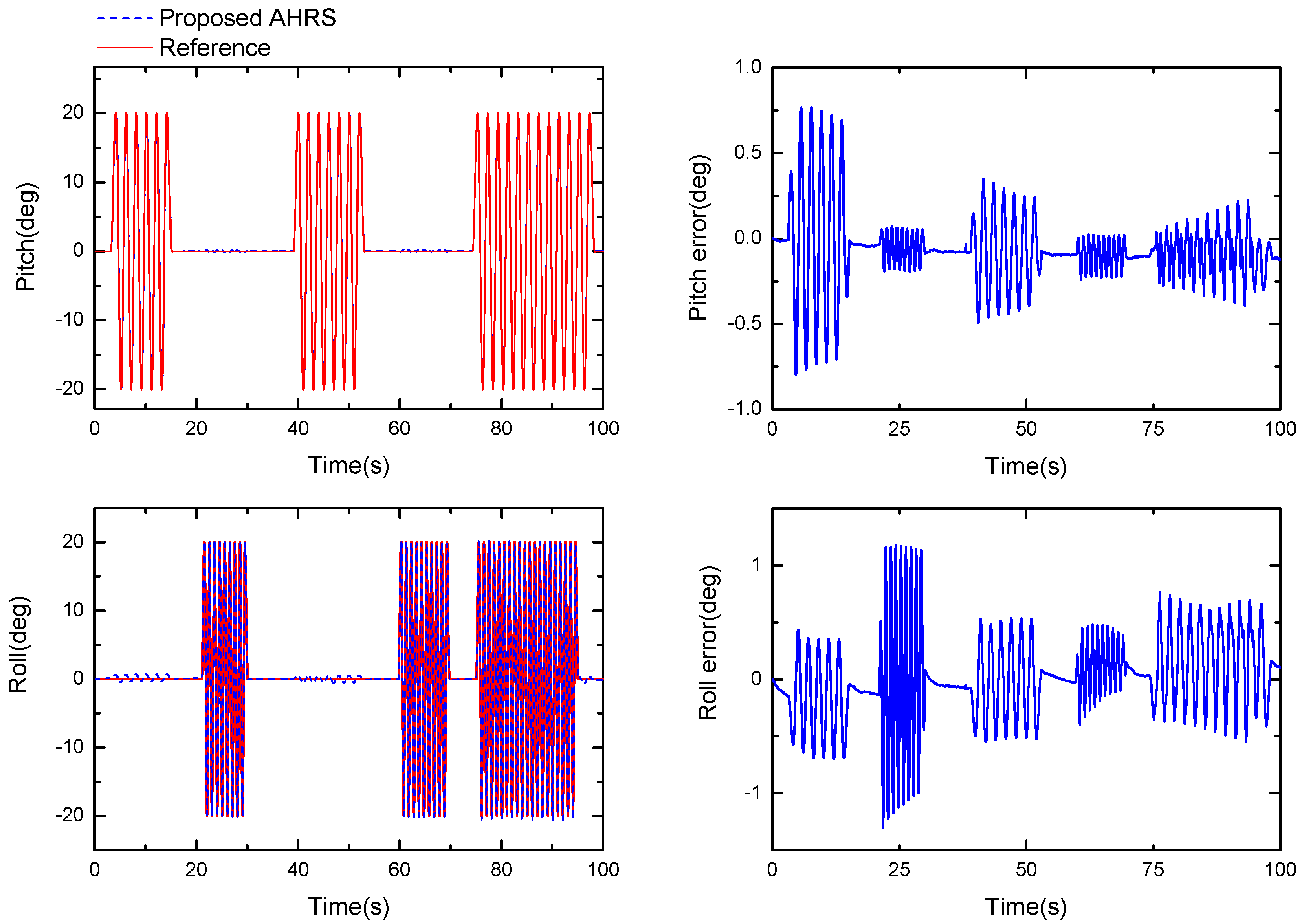
3.1. Tri-Axis Turntable Experiments for the Proposed AHRS
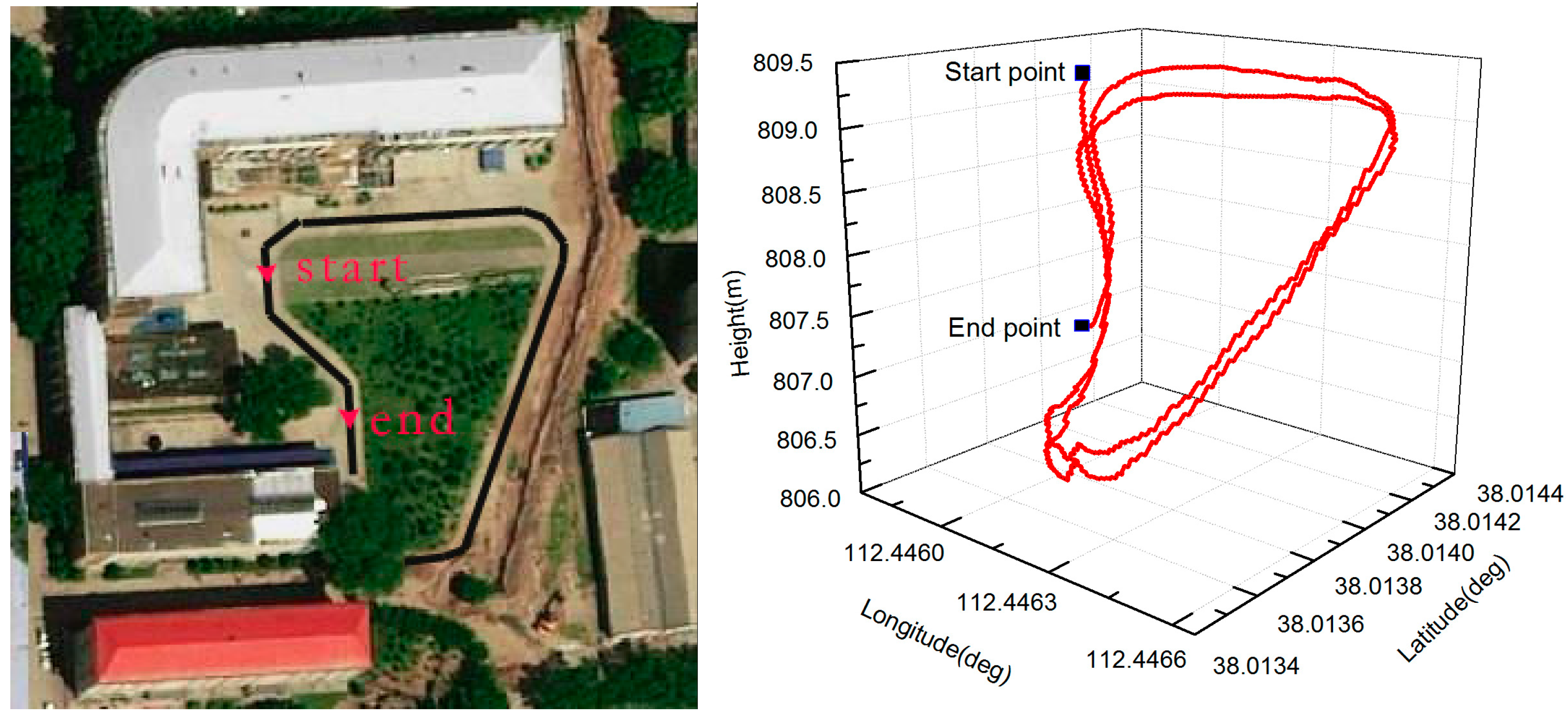
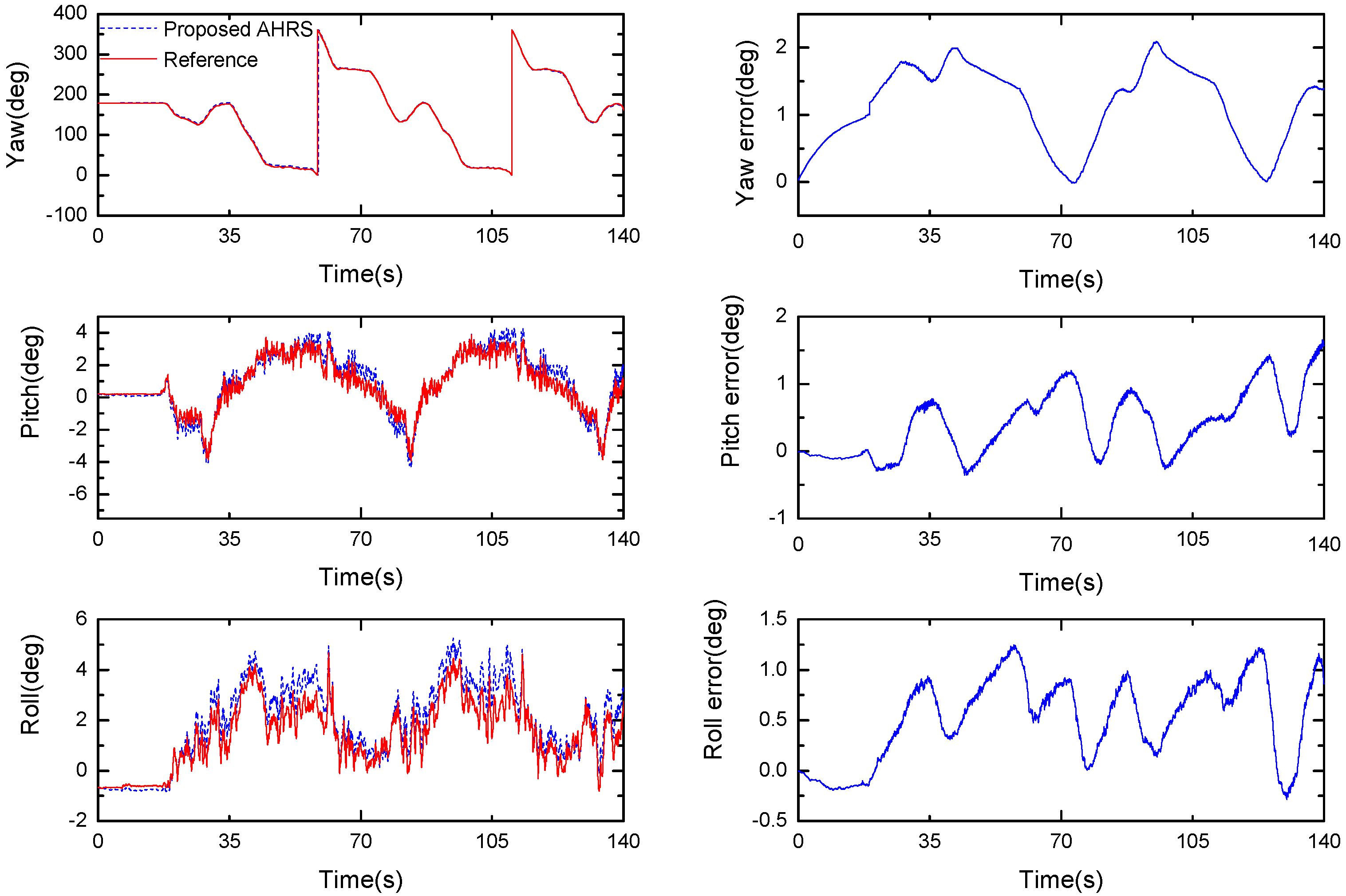
3.2. Experiments on the Driving Vehicle
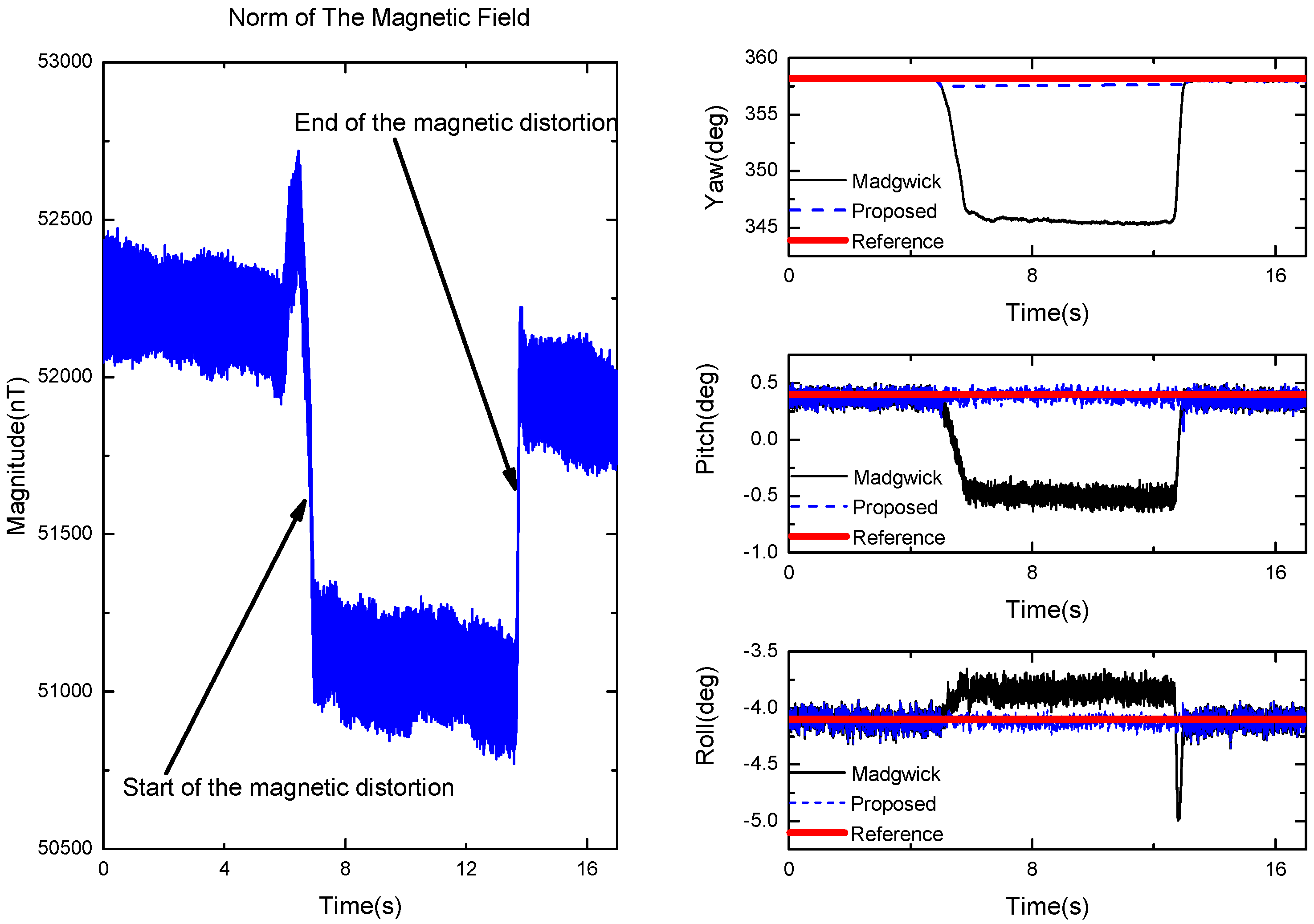
3.3. Experiments with Magnetic Distortion
3.4. Time Consumption Evaluation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Renaudin, V.; Combettes, C. Magnetic, acceleration fields and gyroscope quaternion (MAGYQ)-based attitude estimation with smartphone sensors for indoor pedestrian navigation. Sensors 2014, 14, 22864–22890. [Google Scholar] [CrossRef] [PubMed]
- Gośliński, J.; Nowicki, M.; Skrzypczyński, P. Performance comparison of EKF-based algorithms for orientation estimation on android platform. IEEE Sens. J. 2015, 15, 3781–3792. [Google Scholar] [CrossRef]
- Yoon, P.K.; Zihajehzadeh, S.; Kang, B.S.; Park, E.J. Robust biomechanical model-based 3-D indoor localization and tracking method using UWB and IMU. IEEE Sens. J. 2017, 17, 1084–1096. [Google Scholar] [CrossRef]
- Hung, T.N.; Suh, Y.S. Inertial sensor-based two feet motion tracking for gait analysis. Sensors 2013, 13, 5614–5629. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.W.; Kim, H.J.; Park, C.G. A human motion tracking algorithm using adaptive EKF based on markov chain. IEEE Sens. J. 2016, 16, 8953–8962. [Google Scholar] [CrossRef]
- Collinson, R.P. Introduction to Avionics Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Baerveldt, A.-J.; Klang, R. A low-cost and low-weight attitude estimation system for an autonomous helicopter. In Proceedings of the 1997 IEEE International Conference on Intelligent Engineering Systems, INES’97, Budapest, Hungary, 17 September 1997; pp. 391–395. [Google Scholar]
- Wang, Y.; Soltani, M.; Hussain, D.M.A. An attitude heading and reference system for marine satellite tracking antenna. IEEE Trans. Ind. Electron. 2017, 64, 3095–3104. [Google Scholar] [CrossRef]
- Sheng, H.L.; Zhang, T.H. Mems-based low-cost strap-down ahrs research. Measurement 2015, 59, 63–72. [Google Scholar] [CrossRef]
- Euston, M.; Coote, P.; Mahony, R.; Kim, J.; Hamel, T. A complementary filter for attitude estimation of a fixed-wing UAV. In Proceedings of the IROS 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 340–345. [Google Scholar]
- Fourati, H.; Manamanni, N.; Afilal, L.; Handrich, Y. Complementary observer for body segments motion capturing by inertial and magnetic sensors. IEEE/ASME Trans. Mechatron. 2014, 19, 149–157. [Google Scholar] [CrossRef]
- Madgwick, S.O.; Harrison, A.J.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics (ICORR), Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Calusdian, J.; Yun, X.; Bachmann, E. Adaptive-gain complementary filter of inertial and magnetic data for orientation estimation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1916–1922. [Google Scholar]
- Wu, J.; Zhou, Z.B.; Chen, J.J.; Fourati, H.; Li, R. Fast complementary filter for attitude estimation using low-cost MARG sensors. IEEE Sens. J. 2016, 16, 6997–7007. [Google Scholar] [CrossRef]
- Chang, L.B.; Zha, F.; Qin, F.J. Indirect kalman filtering based attitude estimation for low-cost attitude and heading reference systems. IEEE-ASME Trans. Mechatron. 2017, 22, 1850–1858. [Google Scholar] [CrossRef]
- Lee, J.K.; Choi, M.J. A sequential orientation kalman filter for AHRS limiting effects of magnetic disturbance to heading estimation. J. Electr. Eng. Technol. 2017, 12, 1675–1682. [Google Scholar]
- Sabatini, A.M. Quaternion-based extended kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman Filter for 3D Attitude Estimation; 2005-002; EE/CS Building: Minneapolis, MN, USA, March 2005. [Google Scholar]
- Zhang, Z.-Q.; Meng, X.-L.; Wu, J.-K. Quaternion-based kalman filter with vector selection for accurate orientation tracking. IEEE Trans. Instrum. Meas. 2012, 61, 2817–2824. [Google Scholar] [CrossRef]
- Yun, X.; Bachmann, E.R. Design, implementation, and experimental results of a quaternion-based kalman filter for human body motion tracking. IEEE Trans. Robot. 2006, 22, 1216–1227. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Sun, P. Quaternion-based kalman filter for AHRS using an adaptive-step gradient descent algorithm. Int. J. Adv. Robot. Syst. 2015, 12. [Google Scholar] [CrossRef]
- Marins, J.L.; Yun, X.; Bachmann, E.R.; McGhee, R.B.; Zyda, M.J. An extended kalman filter for quaternion-based orientation estimation using marg sensors. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; pp. 2003–2011. [Google Scholar]
- Liu, F.; Li, J.; Wang, H.; Liu, C. An improved quaternion Gauss–Newton algorithm for attitude determination using magnetometer and accelerometer. Chin. J. Aeronaut. 2014, 27, 986–993. [Google Scholar] [CrossRef]
- Yun, X.; Bachmann, E.R.; McGhee, R.B. A simplified quaternion-based algorithm for orientation estimation from earth gravity and magnetic field measurements. IEEE Trans. Instrum. Meas. 2008, 57, 638–650. [Google Scholar]
- Markley, F.L.; Mortari, D. Quaternion attitude estimation using vector observations. J. Astronaut. Sci. 2000, 48, 359–380. [Google Scholar]
- Wahba, G. A least squares estimate of satellite attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control Dyn. 2012, 4, 70–77. [Google Scholar] [CrossRef]
- Yun, X.; Aparicio, C.; Bachmann, E.R.; McGhee, R.B. Implementation and experimental results of a quaternion-based kalman filter for human body motion tracking. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 317–322. [Google Scholar]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Quan, W.; Li, J.; Gong, X.; Fang, J. INS/CNS/GNSS Integrated Navigation Technology; Springer: Berlin, Germany, 2015. [Google Scholar]
- Del Rosario, M.B.; Lovell, N.H.; Redmond, S.J. Quaternion-based complementary filter for attitude determination of a smartphone. IEEE Sens. J. 2016, 16, 6008–6017. [Google Scholar]
- Valenti, R.G.; Dryanovski, I.; Xiao, J.Z. A linear kalman filter for marg orientation estimation using the algebraic quaternion algorithm. IEEE Trans. Instrum. Meas. 2016, 65, 467–481. [Google Scholar]




| Bias | Standard Deviation | |
|---|---|---|
| Gyroscope | [−6.7e−3 −4.9e−3 −9.7e−3] (rad/s) | [0.001 0.001 0.001] (rad/s) |
| Accelerometer | [0.09 −0.01 0.7] (m/s2) | [0.039 0.036 0.039] (m/s2) |
| Magnetometer | [280 −439 −22] (mGauss) | [0.22 1.11 0.28] (mGauss) |
| Gyroscope | Accelerometer | |
|---|---|---|
| Range | ±800 °/s | ±40 g |
| Bias | <1°/h | <1 mg |
| Scale Factor | <500 ppm | <1000 ppm |
| Position(CEP) | Attitude (1σ Value) | |||
|---|---|---|---|---|
| Yaw | Pitch | Roll | ||
| Accuracy | 0.3–5 m | <0.01° | <0.01° | <0.01° |
| Case | Filters | Yaw/° | Pitch/° | Roll/° |
|---|---|---|---|---|
| Static | Madgwick | — | 0.0362 | 0.0375 |
| EKF | — | 0.0384 | 0.0331 | |
| Proposed KF | — | 0.0252 | 0.0341 | |
| Slow Movement | Madgwick | — | 0.3543 | 0.4350 |
| EKF | — | 0.2088 | 0.3345 | |
| Proposed KF | — | 0.2159 | 0.3614 | |
| Fast Movement | Madgwick | 2.0327 | 1.0268 | 1.1563 |
| EKF | 1.5365 | 0.7253 | 0.6525 | |
| Proposed KF | 1.2765 | 0.6276 | 0.6686 |
| Algorithm | Mean Time Consumption (ms) | Standard deviation (ms) |
|---|---|---|
| Proposed KF | 0.1832 | 0.0191 |
| Madgwick’s filter | 0.1255 | 0.0238 |
| EKF | 0.2028 | 0.0360 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, K.; Li, J.; Zhang, X.; Shen, C.; Bi, Y.; Zheng, T.; Liu, J. A New Quaternion-Based Kalman Filter for Real-Time Attitude Estimation Using the Two-Step Geometrically-Intuitive Correction Algorithm. Sensors 2017, 17, 2146. https://doi.org/10.3390/s17092146
Feng K, Li J, Zhang X, Shen C, Bi Y, Zheng T, Liu J. A New Quaternion-Based Kalman Filter for Real-Time Attitude Estimation Using the Two-Step Geometrically-Intuitive Correction Algorithm. Sensors. 2017; 17(9):2146. https://doi.org/10.3390/s17092146
Chicago/Turabian StyleFeng, Kaiqiang, Jie Li, Xiaoming Zhang, Chong Shen, Yu Bi, Tao Zheng, and Jun Liu. 2017. "A New Quaternion-Based Kalman Filter for Real-Time Attitude Estimation Using the Two-Step Geometrically-Intuitive Correction Algorithm" Sensors 17, no. 9: 2146. https://doi.org/10.3390/s17092146
APA StyleFeng, K., Li, J., Zhang, X., Shen, C., Bi, Y., Zheng, T., & Liu, J. (2017). A New Quaternion-Based Kalman Filter for Real-Time Attitude Estimation Using the Two-Step Geometrically-Intuitive Correction Algorithm. Sensors, 17(9), 2146. https://doi.org/10.3390/s17092146





