3.1. High-Resolution Remote Sensing Image Classification
The study area in this experiment is located in the Jiulong River basin, the second largest river in Fujian province. The landforms in the area are dominated by mountains, the types of land cover primarily consist of forest land and waters, and the settlements are primarily distributed along the mountains. In order to verify the effectiveness of the proposed algorithm, experiments were conducted on three types of images: the GaoFen-2 multispectral image, with 410 × 382 pixels and 4 m spatial resolution, QuickBird multispectral image, with 450 × 436 pixels and 2.44 m spatial resolution, and GeoEye-1 multispectral image, with 480 × 402 pixels and 1.65 m spatial resolution.
In this experiment, two kinds of methods were used to classify different types of images based on texture feature extraction. With the first method, the mean values of the texture values in multiple directions are employed as the image texture features. With the second method, texture feature extraction is based on the direction measure and gray level co-occurrence matrix fusion algorithm. First, we selected parameters for the GLCM in the two methods: (1) Kernel window: the kernel window of 3 × 3, 5 × 5, 7 × 7 and so on were selected and compared in order to obtain the appropriate kernel wind; (2) moving step: this experiment selected Δx = 1, Δy = 1 and Δx = 2, Δy = 2 as the moving step and made comparison. Compared with the different kernel window that obtained texture features, the smaller window can better reflect subtle changes of the image, while the larger window can better reflect the object contour and get a more vague effect. The distance between adjacent pixels is related to the image texture information, and the smaller distance between pixels can better represent the detail of the texture. Therefore, selecting the appropriate kernel window and moving step is necessary, which ensures that the image texture information can be fully extracted. By comparison, this experiment finally chose a 5 × 5 kernel window, Δx = 1, Δy = 1, which better reflect the coarse texture and fine texture, so we chose this size to get the calculations. Second, principal component analysis (PCA) was performed on the image in order to reduce computation and information redundancy. Through the linear transformation of the original variables, the minimal number of new variables is determined by using PCA, which can represent the data structure of the original variables to the maximum extent without losing information. The first principal component of each kind of image is used as the band which specializes in extracting the texture, and the other components are only some noise for the image information, which cannot play much effect for the image. Third, according to the characteristics of land cover in the study area, land covers were divided into six categories: forest land, arable land, water, residential land, roads, and bare land. Then, an image classification was performed based on the training samples in the study area.
A support vector machine (SVM) is a supervised machine learning algorithm that has gained popularity within visual pattern recognition and image classification [
27,
28]. In this experiment, the SVM classifier was used to classify the image with a combination of spectral features and texture features by using a Gaussian radial basis function (RBF). Using the same test samples, a confusion matrix was constructed for the classification results, and two types of precision evaluation indexes were established for the experimental results: the first index is to evaluate the overall accuracy (OA) of the classification by the OA and the Kappa coefficient; the second index is to measure the individual object accuracy of the classification by the conditional Kappa coefficient [
29,
30]. The accuracy of these two indicators was employed to compare the classification accuracy of a remote sensing image by different methods.
3.1.1. GaoFen-2 Data
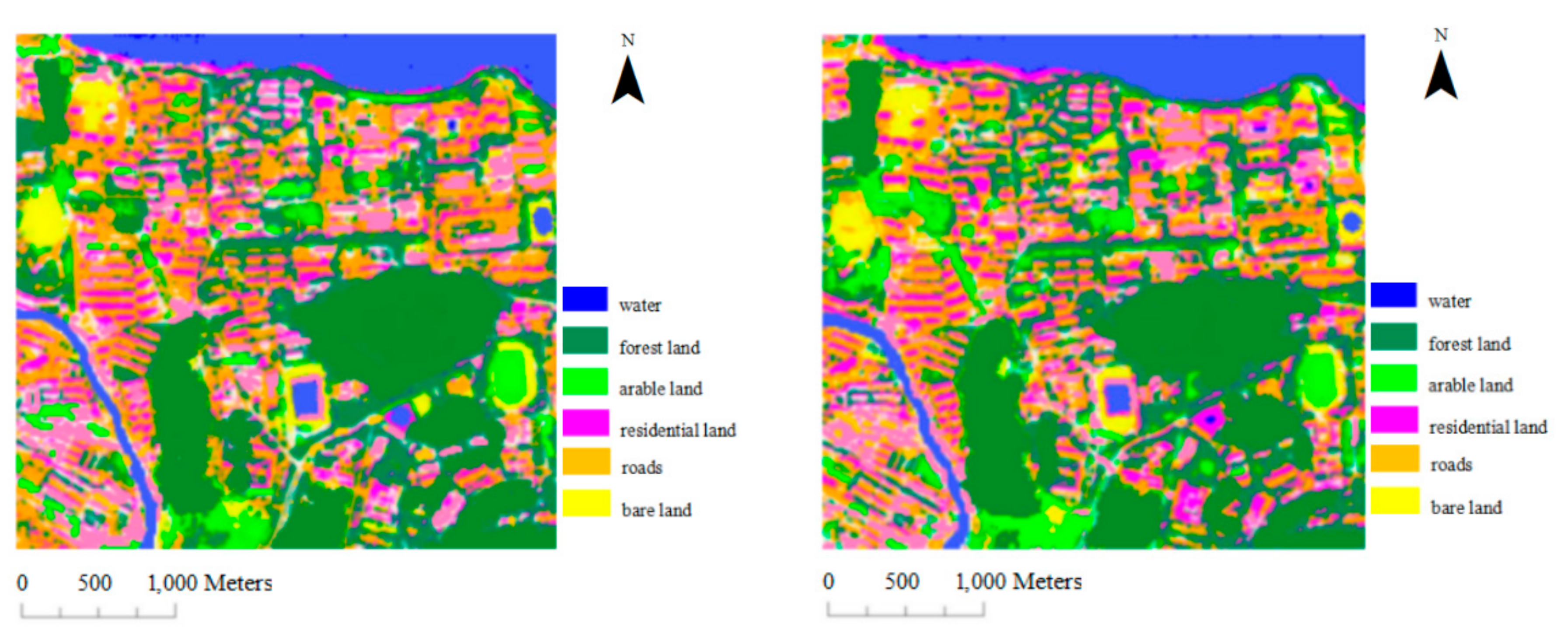
The multispectral image of GaoFen-2 satellites was used to classify the samples under the two methods. According to the characteristics of the image in the study area, the number of training samples (100 pixels per category) selected for each type of object was 6000, and the rest were as the test samples. The SVM classification results are shown in
Figure 2, where the first image is derived by method one, and the second image is generated by method two. The overall accuracy, Kappa coefficient and conditional Kappa coefficient are shown in
Table 2.
Based on the reported SVM classification accuracy of the GaoFen-2 image, the overall classification accuracy with method two has improved (92.42% vs. 86.92%), and the Kappa coefficient with method two was 0.04 greater than that with method one. The classification accuracy of arable land and water significantly increased, and the conditional Kappa coefficient increased by 0.1602 and 0.0854, respectively. Residential land and bare land increased by a lesser amount, at 0.0548 and 0.0425, respectively. No significant change was observed in the classification accuracy of forest land, which increased by only 0.0122. The classification accuracy of roads was reduced by 0.0325.
3.1.2. QuickBird Data
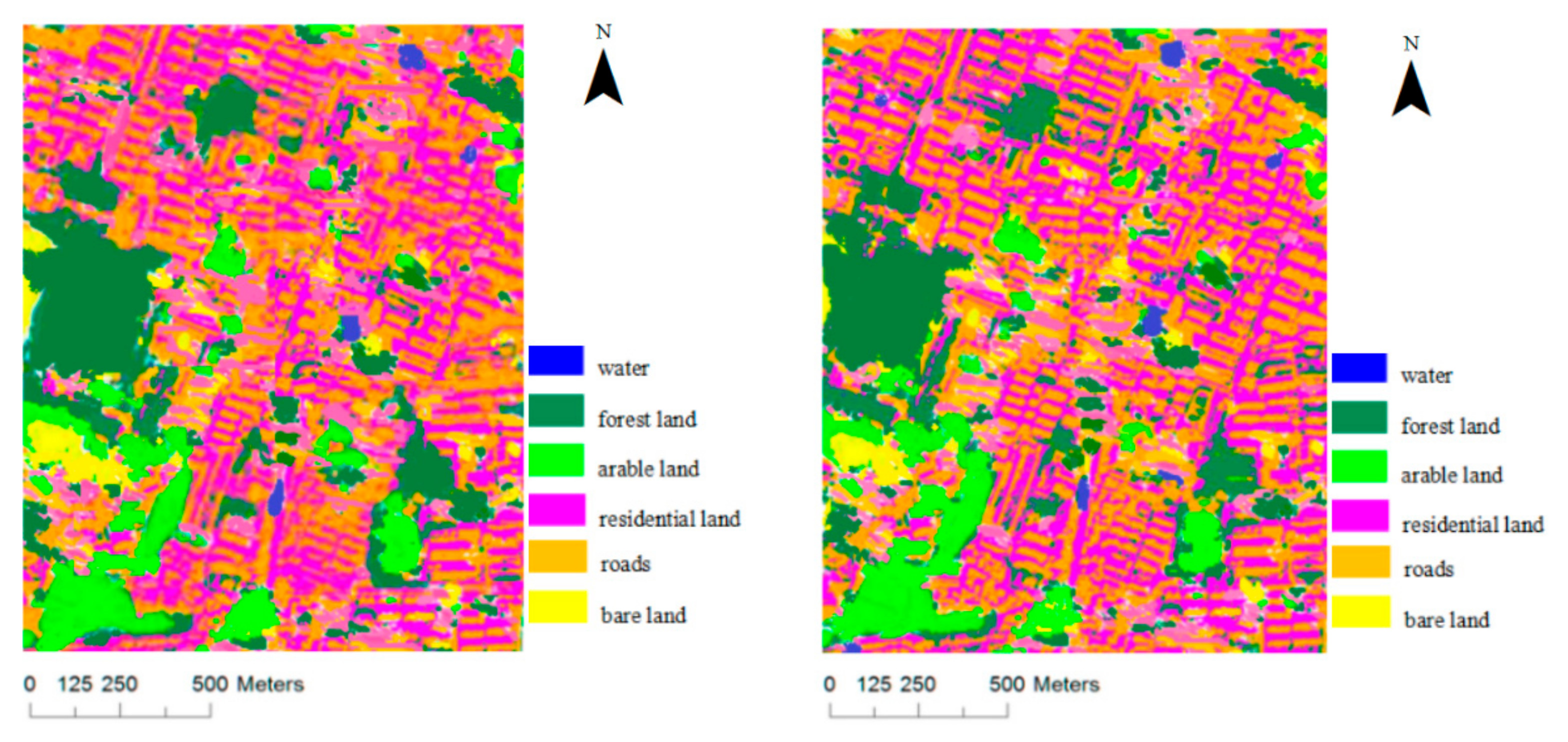
The QuickBird multispectral image, with four spectral bands (red, green, blue, and near-infrared) and a 2.44 m spatial resolution, was also used to validate the proposed direction measure and gray level co-occurrence matrix fusion algorithm. In the image, the training samples (100 pixels per category) were selected for each type of object, among which forest land samples were 10,967, arable land samples were 8746, water samples were 6023, residential land samples were 6120, road samples were 5480, bare land samples were 5746, and the rest were the test samples. The SVM classification results are shown in
Figure 3, where the first image is derived by method one, and the second image is generated by method two. The overall accuracy, Kappa coefficient and conditional Kappa coefficient are shown in
Table 3.
Based on the reported SVM classification accuracy of the QuickBird image, the overall classification accuracy with method two has largely improved (93.26% vs. 85.70%), which was improved by 7.56%, and the Kappa coefficient with method two was 0.07 greater than that with method one. The classification accuracy of arable land and water significantly increased, and the conditional Kappa coefficient increased by 0.1316 and 0.1367, respectively. Residential land and bare land increased by a lesser amount, at 0.0674 and 0.0525, respectively. No significant change was observed in the classification accuracy of forest land and roads, which increased by only 0.0078 and 0.0045, respectively.
3.1.3. GeoEye-1 Data
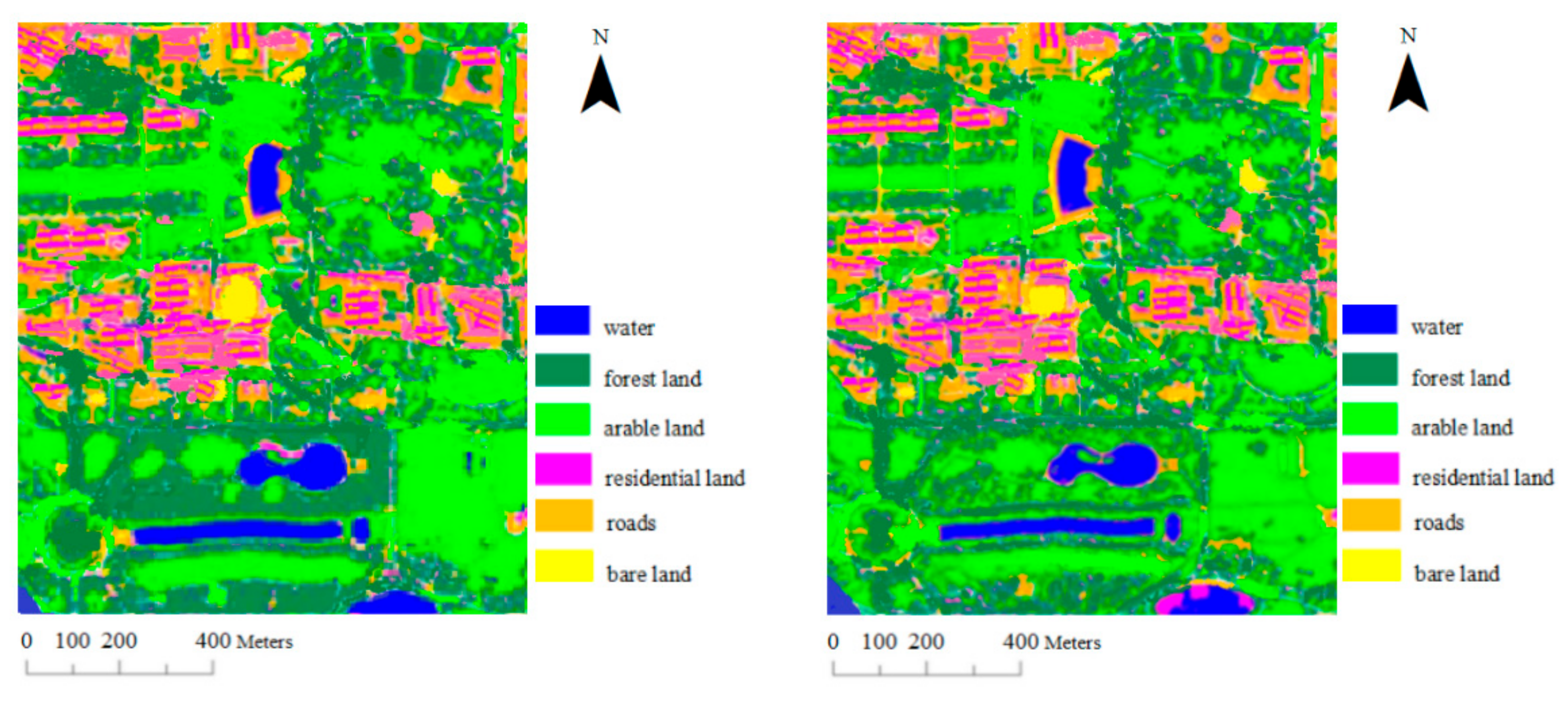
The proposed algorithm was further tested with the GeoEye-1 multispectral dataset from the study area. This image comprises 480 × 402 pixels, with four spectral bands (red, green, blue, and near-infrared) and a 1.65 m spatial resolution. Using the same method, we randomly chose training samples (100 pixels per category) for each type of object in the GeoEye-1 image; forest land samples were 8010, arable land samples were 9872, water samples were 5820, residential land samples were 7583, road samples were 6451, bare land samples were 5867, and the rest were as the test samples. The SVM classification results are shown in
Figure 4, where the first image is derived by method one, and the second image is generated by method two. The overall accuracy, Kappa coefficient and conditional Kappa coefficient are shown in
Table 4.
By analyzing the results in
Table 4, it can be concluded that method two has the best effect on the classification of GeoEye-1 image with higher resolution in the classification experiments of the three types of images, the overall classification accuracy reached 96.75%, and the increase of accuracy was also the most (8.24%). According to the comparison among the conditional Kappa coefficient of various types of objects, it was similar to the first two experiments that the classification accuracy of arable land and water dramatically increased, and the conditional Kappa coefficient improved by 0.1425 and 0.1232, respectively. Residential land increased less, at 0.0645. There were basically no changes in the conditional Kappa coefficient of roads, forest land and bare land, which improved by only 0.0034, 0.0082 and 0.0095, respectively.
By comparing the classification results of three types of high resolution remote sensing images, the following conclusions can be obtained through the above research:
Accuracies: By using the proposed direction measure and gray level co-occurrence matrix fusion algorithm, the overall classification accuracy of GaoFen-2 image (4 m spatial resolution), QuickBird image (2.44 m spatial resolution) and GeoEye-1 image (1.65 m spatial resolution) were 92.43%, 93.26% and 96.75%, respectively, which were improved by 5.51%, 7.56%, and 8.24%, respectively, by comparison of method one. Also, for the increase of Kappa coefficient, the GeoEye-1 image improved the most, followed by the QuickBird image and GaoFen-2 image. It is interesting to see that when the spatial resolution of the image increases, using the fusion algorithm to extract the texture values to participate in the classification, the overall accuracy of the image classification is higher, and it has better classification results than the mean values of the texture values. Therefore, it can be deduced that with the increase in spatial resolution of image and the refinement of classification method, the morphological distribution within the class will become more concentrated and concrete, and the differences between the classes are more significant. The introduction of direction measure increases the validity of texture feature values, thereby increasing the separability of objects.
Comparison: For the conditional Kappa coefficient of different objects, in the experiment of the GaoFen-2 image, the classification accuracy was improved obviously in arable land and water, slightly in residential land and bare land, basically no change in forest land, and the conditional Kappa coefficient of roads was reduced; in the same experiment carried out in the QuickBird image, it can be summarized that the classification accuracy of arable land and water significantly improved, residential land and bare land increased by a lesser amount, and no significant change was noticed in the classification accuracy of forest land and roads; the further test with the GeoEye-1 image showed it was similar to the first two experiments in that the classification accuracy of arable land and water dramatically increased; however, residential land of that increased less, and the conditional Kappa coefficient of roads, forest land and bare land changed slightly. Using the algorithm proposed in this paper, the classification accuracy of arable land and water has been greatly improved in the three types of image experiments. The arable land belongs to the land use type of human transformation, which is adjacent to each other in the spatial distribution, and the shape is regular; from the characteristics of the ground features, the surface of the water body is smooth and continuous, the fluctuation is small and the texture is fine. The surface roughness of the water area is significantly lower than that of other ground objects, and the change of gray scale in the water image is relatively continuous. Due to the characteristics of water body texture, the water area is extremely homogeneous in the image. Therefore, the texture values of these two types of objects can reflect the slight changing regularity of the direction, and the classification results have been significantly improved by using the fusion algorithm proposed in this paper. Through the analysis of the above experimental results, using the fusion algorithm proposed in this paper for classification is more accurate, especially for the image texture distribution with a certain regularity and directionality. For other objects, due to the difference in spatial resolution, image spectrum, characteristics of object structure and so on, the change of the conditional Kappa coefficient varies. However, the introduction of directionality has not much of a negative impact on the classification accuracy.
3.3. Image Classification with or without Distinct Directionality
According to the previous two experiments, the classification accuracy of arable land with a distinct texture direction was improved, and forest land without a distinct texture direction exhibited no change in the classification results of the SVM. Therefore, this experiment selected a typical sample of arable land and forest land images in the first principal component of GaoFen-2 image after pretreatment, each of which included 100 pieces. The KNN (k-nearest neighbor) classifier, a machine learning classification method, was employed for the classification of images with or without a distinct texture direction, and the accuracy of method one was compared with the accuracy of method two. The input of KNN is the feature vector of samples, and the output is the type of samples. KNN assumes that a training dataset is given, in which the sample class has been determined and classified, and the new samples are predicted by the majority of the k samples of the nearest neighbor training samples.
Methods one and two were used to extract the texture feature values of forest land and arable land, including energy (ASM), contrast (CON), correlation (COR), and entropy (ENT). The results of the two methods are shown in
Table 6 and
Table 7. Using MATLAB R2014a as the experimental platform, the KNN classifier was edited, and the images were divided into a training set and a test set, respectively. After the size of the selected image was normalized, the size of each sample was 150 × 150 pixels, and all samples were numbered. The first 50 sub-samples were employed as the training set, and the latter 50 sub-samples were employed as the test set. Therefore, the total number in the training set was 100, and the total number of test samples was 100. The training set was trained and the test set was classified by the KNN classifier. Using cross-validation to select the optimal k value and the KNN classifier based on Euclidean distance, the samples were input into the KNN classifier to verify the classification accuracy of the two methods (
Table 8).
Different methods were used to extract the texture features as the input data of the KNN classifier, and the experimental results were different. By comparing
Table 6 and
Table 7, the differences among the texture feature value in the different categories extracted by method two were more distinct than the texture feature value in the different categories extracted by method one. The weighting factor obtained from the direction measure further modified the texture features value in the multiple directions obtained by the GLCM. As shown in
Table 8, using method one and method two, which had minimal impact on the classification accuracy, the latter increased by 0.88% for the forest land without a distinct texture direction. For arable land with a distinct texture direction, the method proposed in this paper achieved a classification accuracy of 95.46% and an increase in accuracy by 4.21% compared to method one, which demonstrated the results of experiment 1 and experiment 2.