Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking
Abstract
:1. Introduction
2. Fifth-Degree Simplex-Spherical Cubature Kalman Filter
2.1. Review of the Fifth-Degree Spherical Simplex-Radial Cubature Rule
2.1.1. Spherical Simplex Rule
2.1.2. Radial Rule
2.1.3. Fifth-Degree Spherical Simplex-Radial Rule
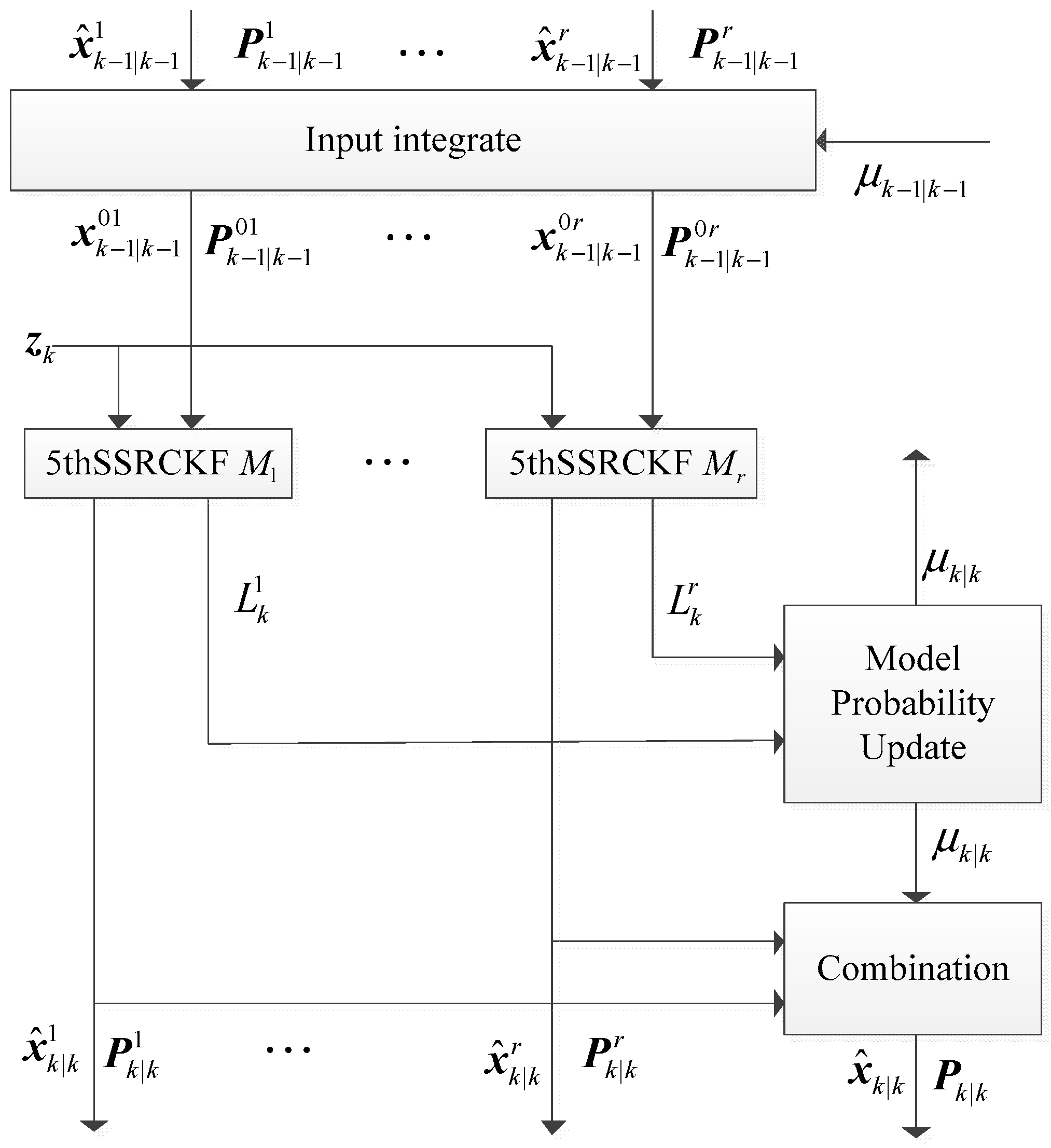
3. IMM5thSSRCKF Algorithm
Step 1. Model Interaction
Step 2. Model Conditional Filtering
A. Time Update
B. Measurement Update
Step 3. Updating the Mode Probability at Time
A. Computing the likelihood function at time k
B. Updating the mode probability at time k
Step 4. Output Integration
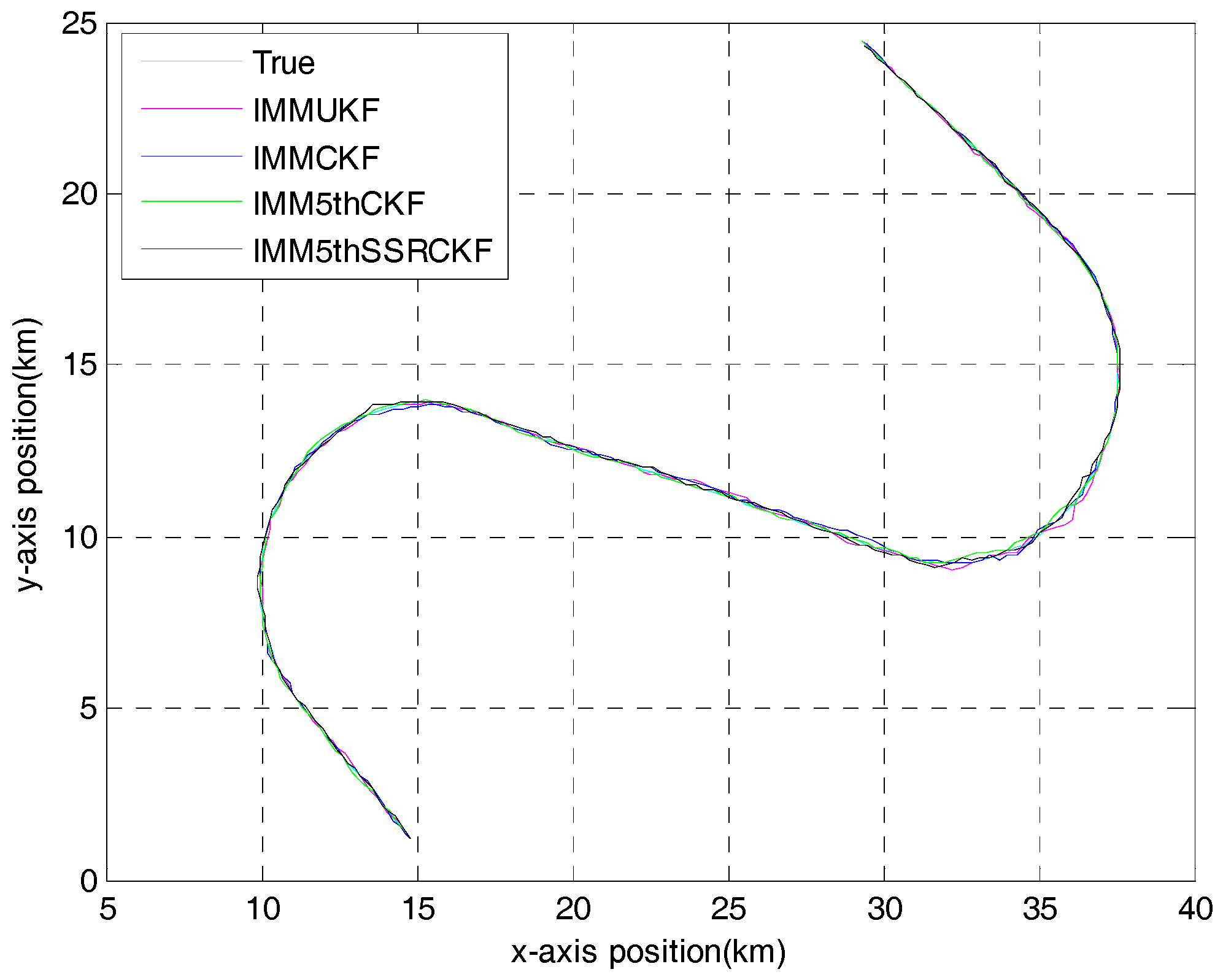
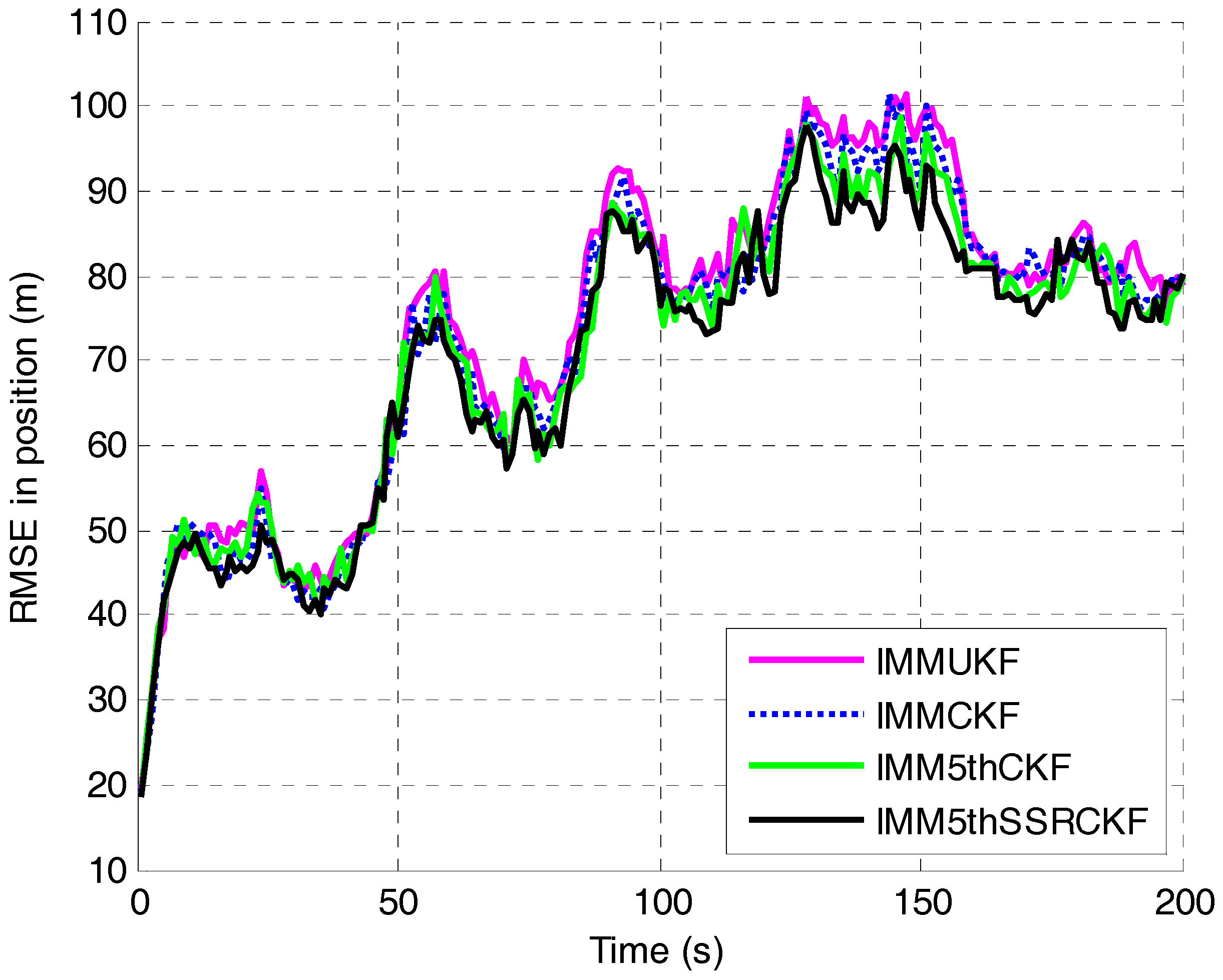
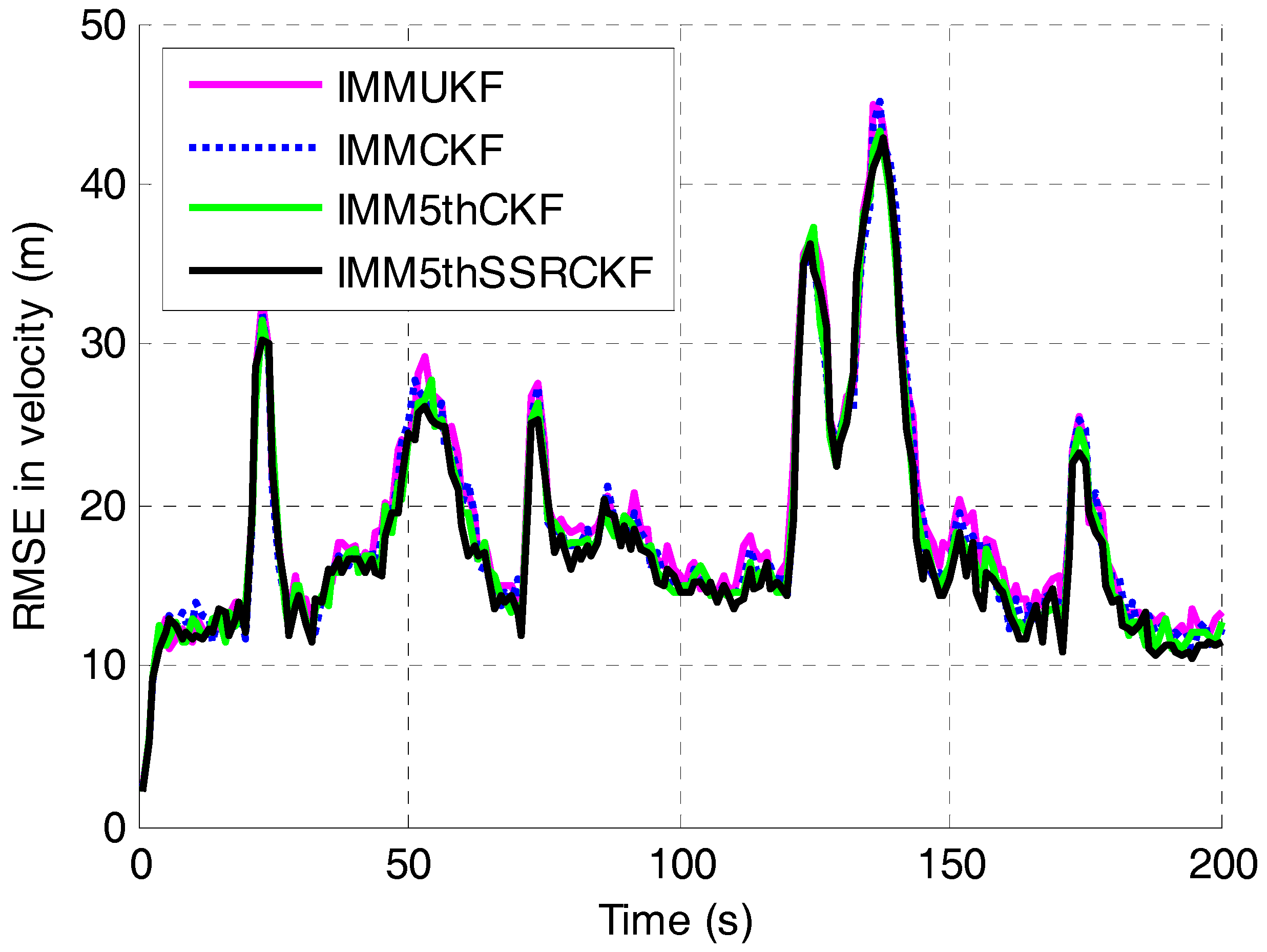
4. Simulation and Results
4.1. Tracking Model and Measurement Model
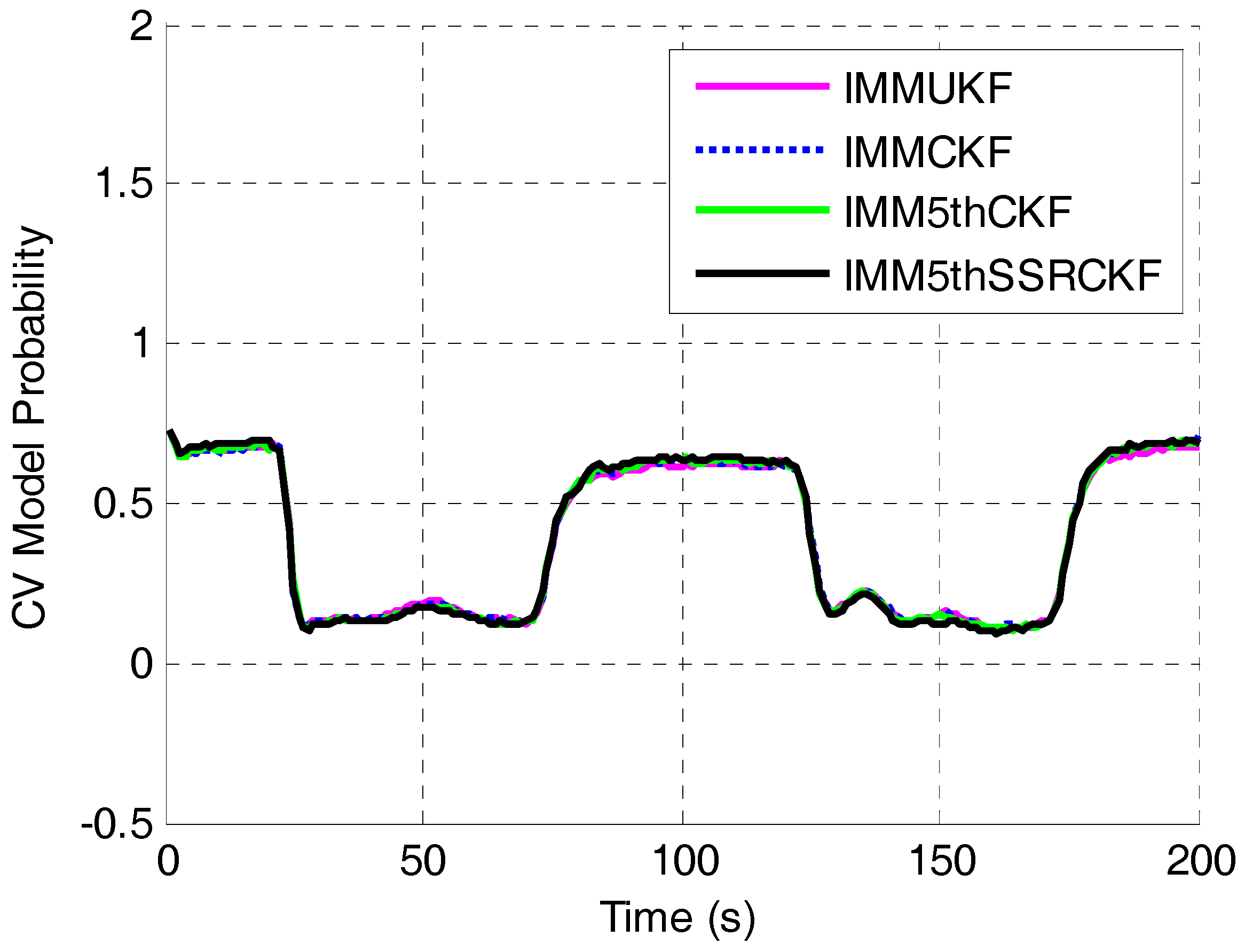
4.2. Simulation of the IMM5thSSRCKF
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Cho, T.; Lee, C.; Choi, S. Multi-Sensor fusion with interacting multiple model filter for improved aircraft position accuracy. Sensors 2013, 13, 4122–4137. [Google Scholar] [CrossRef] [PubMed]
- Ehrman, L.M.; Lanterman, A.D. Extended Kalman filter for estimating aircraft orientation from velocity measurements. IET Radar Sonar Navig. 2008, 2, 12–16. [Google Scholar] [CrossRef]
- Oh, H.; Shin, H.S.; Kim, S.; Tsourdos, A.; White, B.A. Airborne behaviour monitoring using Gaussian processes with map information. IET Radar Sonar Navig. 2013, 7, 393–400. [Google Scholar] [CrossRef]
- Toledo-Moreo, R.; Zamora-Izquierdo, M.A.; Ubeda-Miarro, B.; Gomez-Skarmeta, A.F. High-Integrity IMM-EKF-based road vehicle navigation with low-cost GPS/SBAS/INS. IEEE Trans. Intell. Transp. Syst. 2007, 8, 491–511. [Google Scholar] [CrossRef]
- Zhu, Z.W. Shipborne radar maneuvering target tracking based on the variable structure adaptive grid interacting multiple model. J. Zhejiang Univ. Sci. C 2013, 14, 733–742. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Ristic, B.; Gordon, N.; Mansell, T. Bearings-only tracking of manoeuvring targets using particle filters. Eurasip J. Appl. Signal Process. 2004, 2004, 2351–2365. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.H.; Duan, D.P. Improved robust Huber-based divided difference filtering. Proc. Inst. Mech. Eng. Part G 2014, 228, 2123–2129. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part V: Multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Kazimierski, W.; Stateczny, A. Optimization of multiple model neural tracking filter for marine targets. In Proceedings of the 13th International Radar Symposium (IRS), Warsaw, Poland, 23–25 May 2012; pp. 543–548. [Google Scholar]
- Blom, H.A.P.; Bar-Shalom, Y. The interacting multiple model algorithm for systems with Markovian switching coefficients. IEEE Trans. Autom. Control 1988, 33, 780–783. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Challa, S.; Blom, H.A.P. IMM estimator versus optimal estimator for hybrid systems. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 986–991. [Google Scholar] [CrossRef]
- Munir, A.; Atherton, D.P. Adaptive interacting multiple model algorithm for tracking a manoeuvring target. IEE Proc. Radar Sonar Navig. 1995, 142, 11–17. [Google Scholar] [CrossRef]
- Lee, B.J.; Park, J.B.; Lee, H.J.; Joo, Y.H. Fuzzy-logic-based IMM algorithm for tracking a manoeuvring target. IEE Proc. Radar Sonar Navig. 2005, 152, 16–22. [Google Scholar] [CrossRef]
- Mazor, E.; Averbuch, A.; Bar-Shalom, Y.; Dayan, J. Interacting multiple model methods in target tracking: A survey. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 103–123. [Google Scholar] [CrossRef]
- Qu, H.Q.; Pang, L.P.; Li, S.H. A novel interacting multiple model algorithm. Signal Process. 2009, 89, 2171–2177. [Google Scholar] [CrossRef]
- Gao, L.; Xing, J.P.; Ma, Z.L.; Sha, J.C.; Meng, X.Z. Improved IMM algorithm for nonlinear maneuvering target tracking. Procedia Eng. 2012, 29, 4117–4123. [Google Scholar] [CrossRef]
- Kim, B.; Yi, K.; Yoo, H.J.; Chong, H.J.; Ko, B. An IMM/EKF approach for enhanced multitarget state estimation for application to integrated risk management system. IEEE Trans. Veh. Technol. 2015, 64, 876–889. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Ito, K.; Xiong, K.Q. Gaussian filters for nonlinear filtering problems. IEEE Trans. Autom. Control 2000, 45, 910–927. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Elliott, R.J. Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature. Proc. IEEE 2007, 95, 953–977. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman smoothers. Automatica 2011, 47, 2245–2250. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
- Wang, S.Y.; Feng, J.C.; Tse, C.K. Spherical simplex-radial cubature Kalman filter. IEEE Signal Proc. Lett. 2014, 21, 43–46. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, W.; Yuan, G.N. An improved interacting multiple model filtering algorithm based on the cubature Kalman filter for maneuvering target tracking. Sensors 2016, 16, 805. [Google Scholar] [CrossRef] [PubMed]
- Jia, B.; Xin, M. Multiple sensor estimation using a new fifth-degree cubature information filter. Trans. Inst. Meas. Control 2015, 37, 15–24. [Google Scholar] [CrossRef]
| Filters | Position ARMSE/m | Velocity ARMSE/(m/s) |
|---|---|---|
| IMMUKF | 74.3 | 23.4 |
| IMMCKF | 72.4 | 22.5 |
| IMM5thCKF | 68.1 | 20.9 |
| IMM5thSSRCKF | 66.2 | 19.3 |
| Filters | Number of Points (n = 4) | Computational Time (s) |
|---|---|---|
| IMMUKF | 9 | 0.289 |
| IMMCKF | 8 | 0.279 |
| IMM5thCKF | 33 | 0.604 |
| IMM5thSSRCKF | 31 | 0.581 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wu, W. Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2017, 17, 1374. https://doi.org/10.3390/s17061374
Liu H, Wu W. Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors. 2017; 17(6):1374. https://doi.org/10.3390/s17061374
Chicago/Turabian StyleLiu, Hua, and Wen Wu. 2017. "Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking" Sensors 17, no. 6: 1374. https://doi.org/10.3390/s17061374
APA StyleLiu, H., & Wu, W. (2017). Interacting Multiple Model (IMM) Fifth-Degree Spherical Simplex-Radial Cubature Kalman Filter for Maneuvering Target Tracking. Sensors, 17(6), 1374. https://doi.org/10.3390/s17061374





