A Novel 2-D Coherent DOA Estimation Method Based on Dimension Reduction Sparse Reconstruction for Orthogonal Arrays
Abstract
:1. Introduction
2. Signal Model and 2-D DOA Estimation Based on Direct Sparse Representation
2.1. Signal Model
2.2. 2-D DOA Estimation Based on Direct Sparse Representation (DSR)
2.2.1. Single Snapshot Estimation
2.2.2. Multiple Snapshots Estimation
3. 2-D DOA Estimation by Dimension Reduction Sparse Reconstruction
3.1. Single Snapshot Estimation
3.2. Multiple Snapshots Estimation
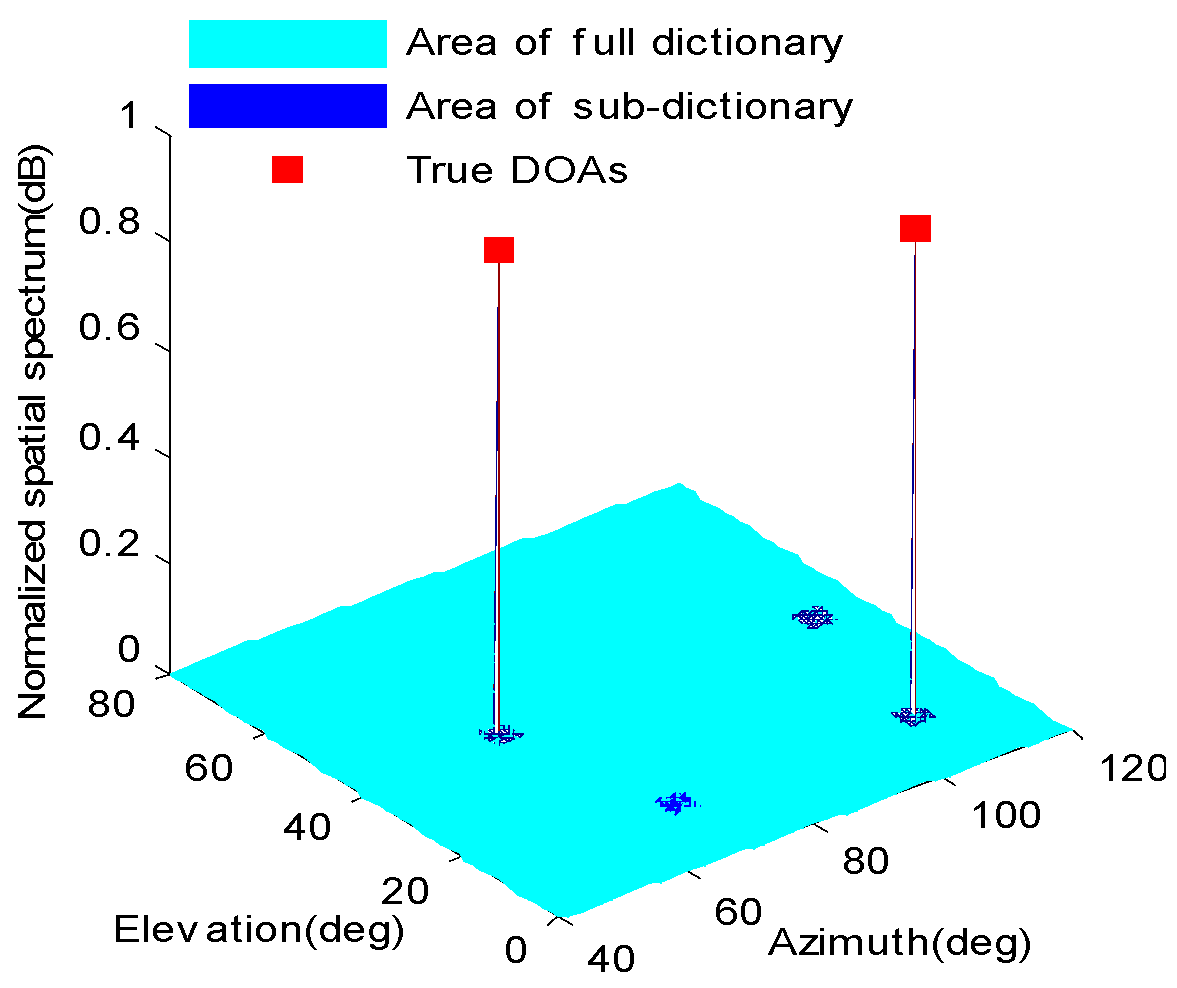
4. Angle Pair-Matching Scheme Based on Sub-Dictionary Spatial Spectrum Reconstruction
- Step 1:
- Construct the 1-D redundant dictionary of subarray and according to Equations (19) and (20).
- Step 2:
- Find the sparse solution and according to Equation (26), then estimate the elevation angles and synthesis azimuth angles of K sources according to Equations (27) and (28).
- Step 3:
- Calculate the corresponding azimuth angle according to Equation (29) and form all combination according to Equation (30).
- Step 4:
- Angle matching. Construct 2-D sub-dictionary according to Equations (31)–(34), then obtainits 2-D spatial spectrum according to Equations (36)–(38), and finally get the indexes of the sub-dictionary corresponding to the largest K spectrum peaks and their central angles are the estimated DOAs.
5. Performance Analysis
5.1. Cramer–Rao Lower Bound
5.2. Computational Complexity Analysis
6. Simulation and Analysis
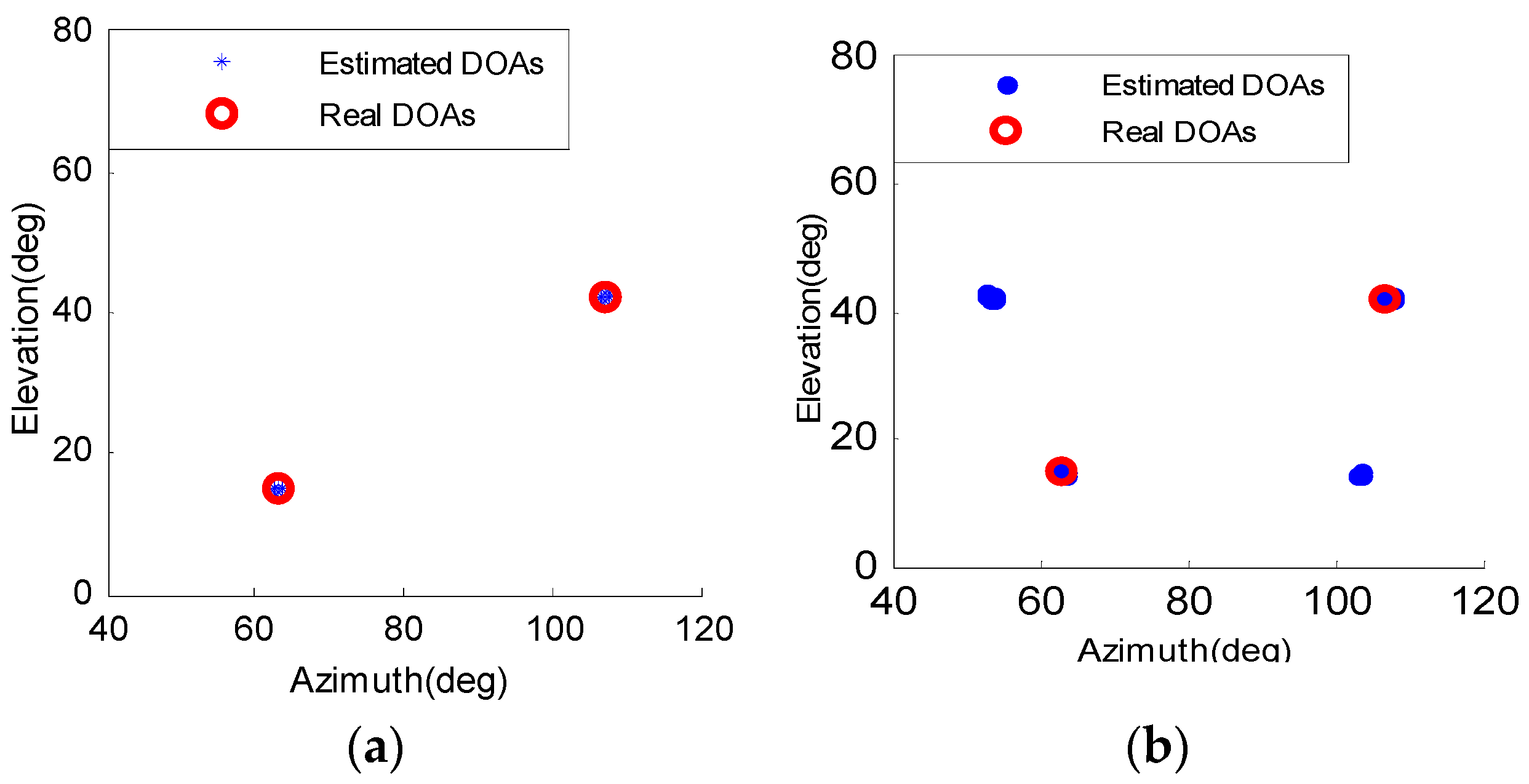
6.1. DOA Estimated under Identical Source Amplitudes
6.2. Performance Analysis under Different SNRs
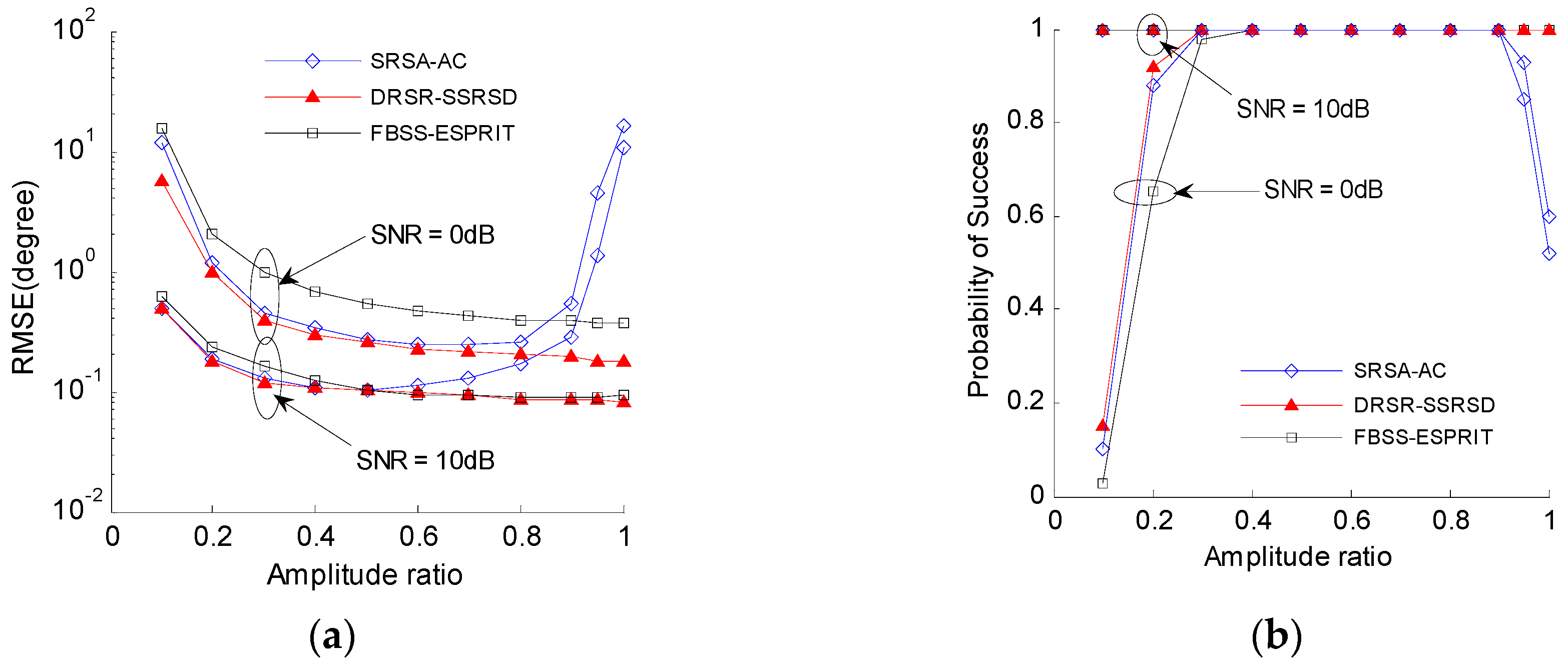
6.3. Performance Analysis under Different Amplitudes
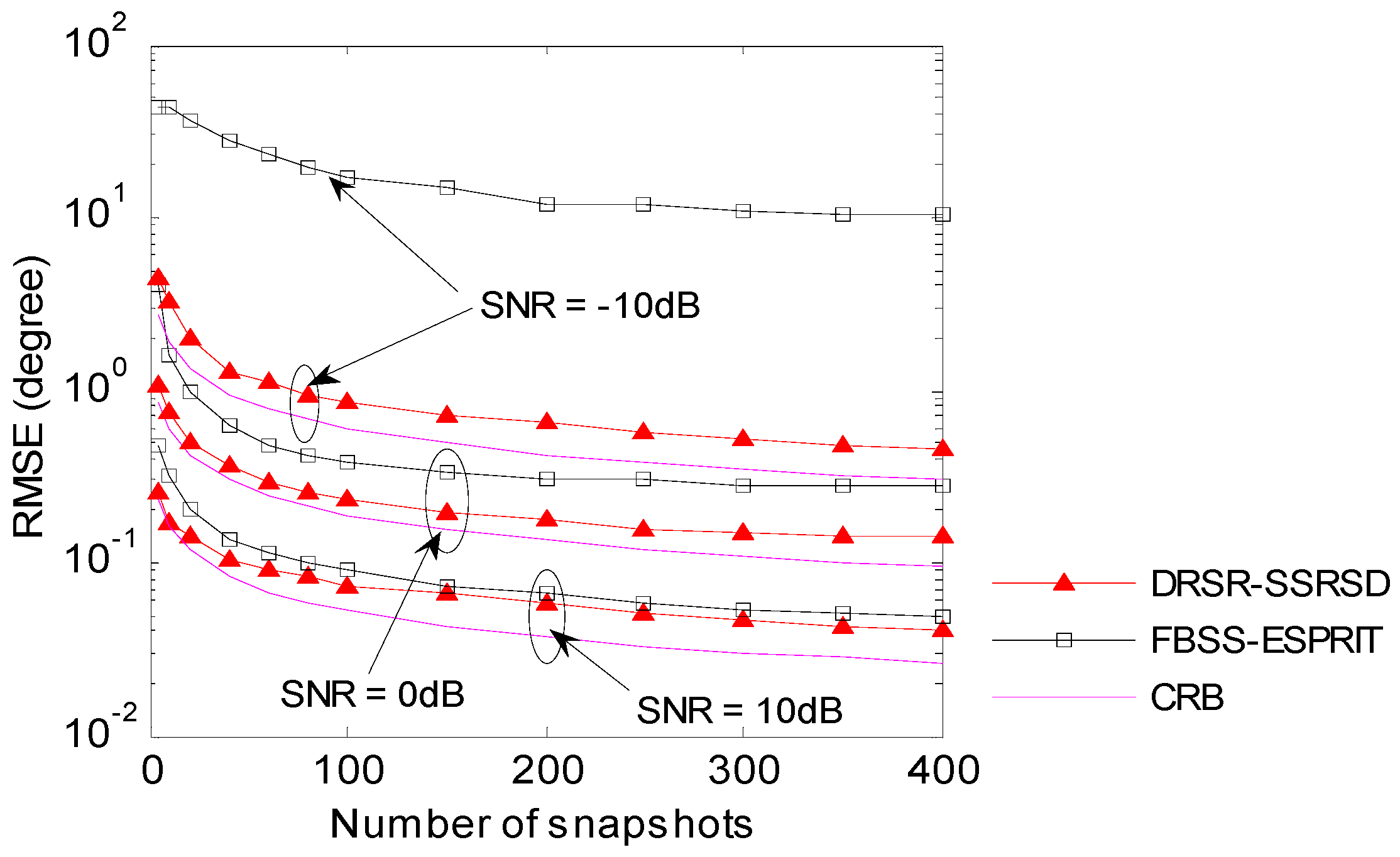
6.4. RMSE Analysis in Different Number of Snapshots
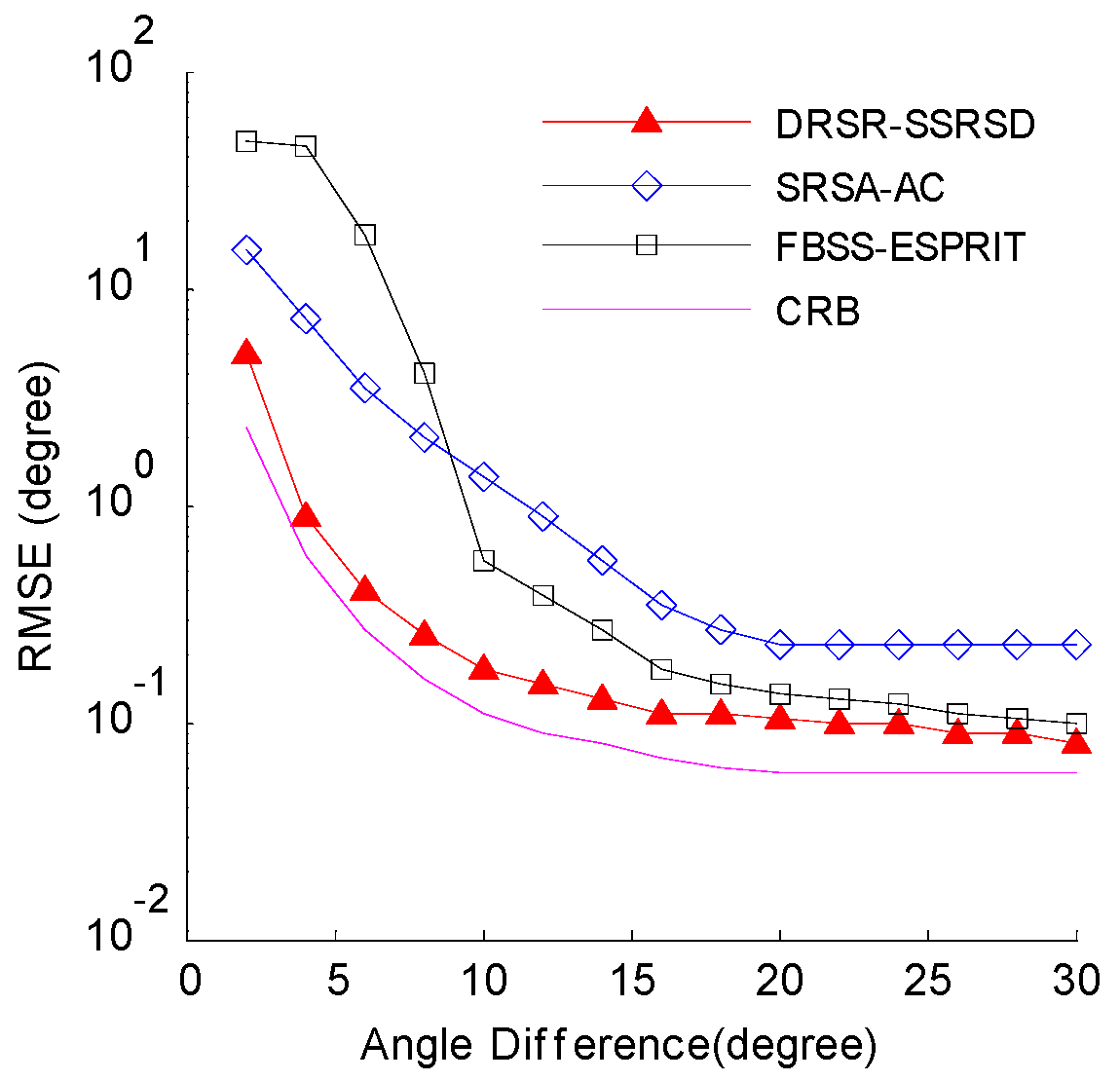
6.5. RMSE Analysis in Different Angle Intervals
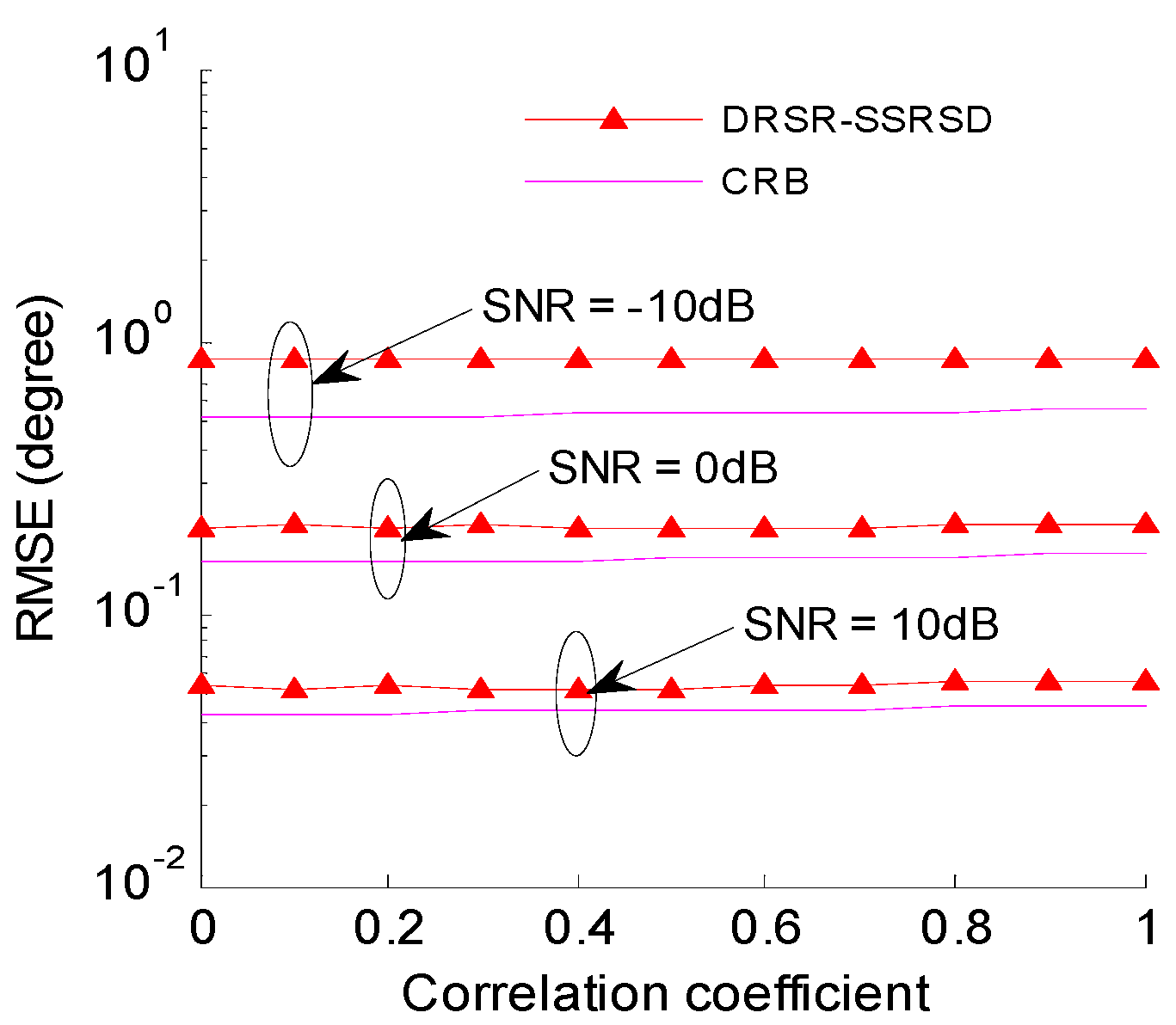
6.6. RMSE Analysis under Different Correlation Coefficients
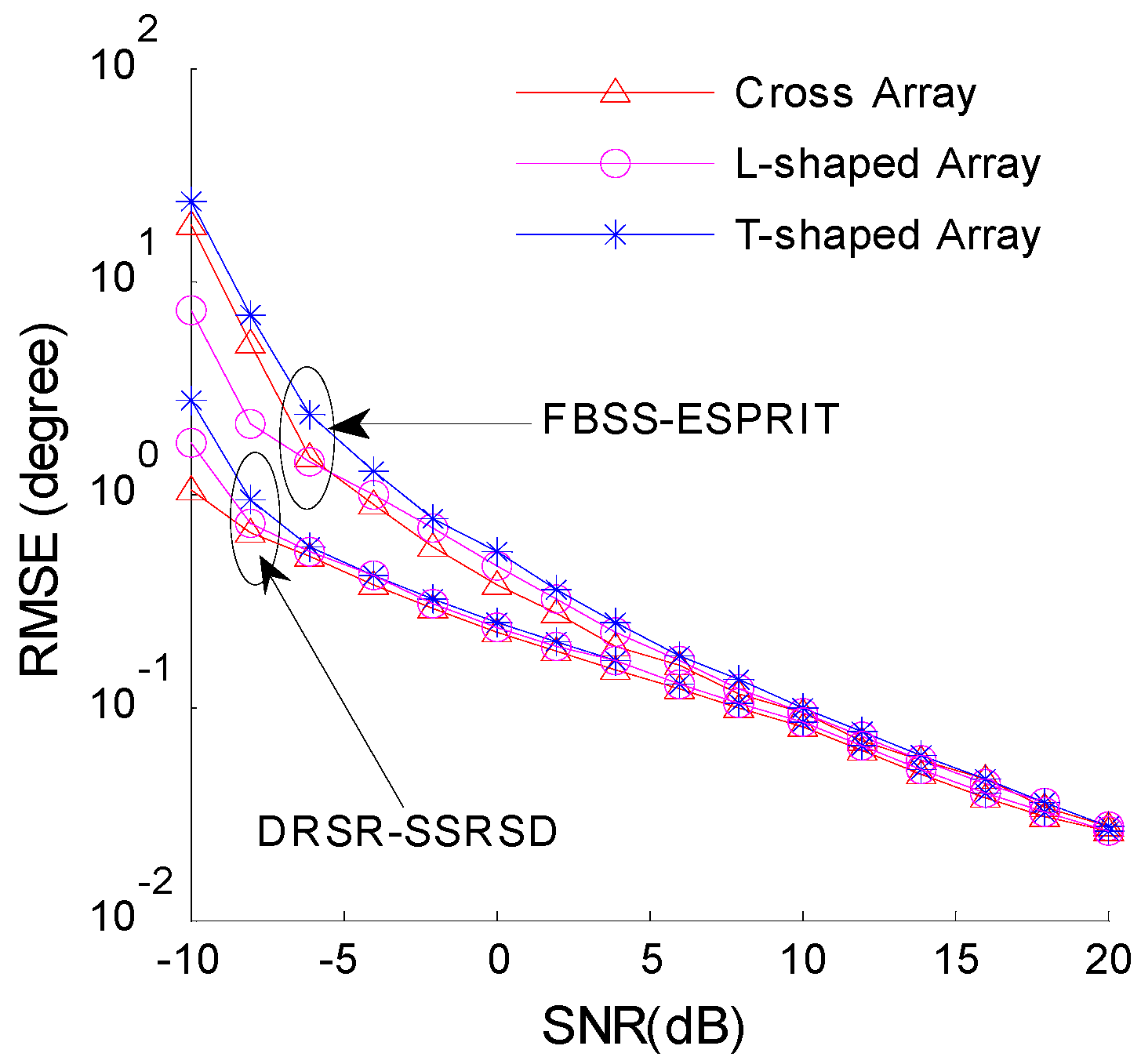
6.7. RMSE Analysis of Uniform T-Shaped, l-Shaped and Cross Arrays
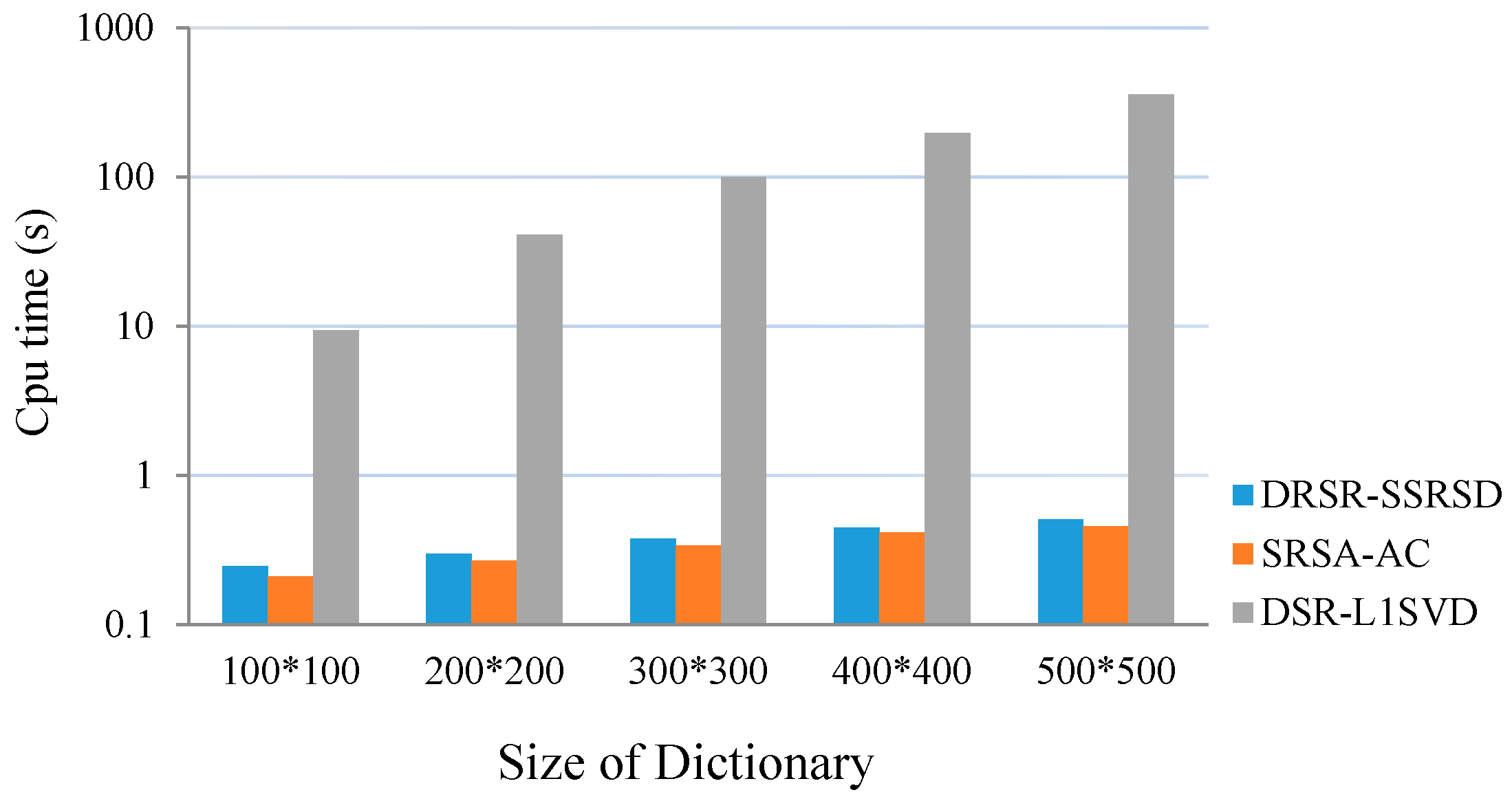
6.8. Computational Complexity Analysis
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Wang, G.M.; Xin, J.M.; Zheng, N.N.; Sano, A. Computationally Efficient Method for Joint Azimuth-Elevation Direction Estimation with l-Shaped Array. In Proceedings of the IEEE 14th Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Darmstadt, Germany, 16–19 June 2013; pp. 470–474.
- Nie, X.; Li, L.P. A computationally efficient subspace algorithm for 2-D DOA estimation with l-shaped array. IEEE Signal Process. Lett. 2014, 21, 971–974. [Google Scholar]
- Luo, X.Y.; Fei, X.C.; Wei, P.; Gan, L. Sparse Representation-Based Method for Two-Dimensional Direction-of-Arrival Estimation with l-Shaped Array. In Proceedings of the IEEE International Conference on Communication Problem-solving (ICCP2014), Beijing, China, 5–7 December 2014; pp. 277–280.
- Gu, J.F.; Zhu, W.P.; Swamy, M.N.S. Joint 2-D DOA estimation via sparse l-shaped Array. IEEE Trans. Signal Process. 2015, 63, 1171–1182. [Google Scholar] [CrossRef]
- Chan, A.Y.J.; Litva, J. MUSIC and Maximum Techniques on Two-Dimensional DOA Estimation with Uniform Circular Array. IEE Proc. Radar Sonar Nav. 1995, 142, 105–114. [Google Scholar] [CrossRef]
- Kedia, V.S.; Chandna, B. A new algorithm for 2-D DOA estimation. Signal Process. 1997, 60, 325–332. [Google Scholar] [CrossRef]
- Wang, G.M.; Xin, J.M.; Zheng, N.N.; Sano, A. Computationally efficient subspace-based method for two-dimensional direction estimation with l-shaped array. IEEE Trans. Signal Process. 2011, 59, 3197–3212. [Google Scholar] [CrossRef]
- Shan, T.J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Pillai, S.U.; Won, B.H.K. Forward/backward spatial smoothing techniques for coherent signals identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, Y.; Yang, J. A Novel 2-D DOA Estimation for Coherent Signals Based on l-Shaped Array. In Proceedings of the 2012 International Conference on Wireless Communication and Signal Processing (WCSP 2012), Huangshan, China, 25–27 October 2012; pp. 1–5.
- Wu, Y.; Chen, H.; Chen, Y.C. A Method of 2-D DOA Estimation of Coherent Signals Based on Uniform Circular Array via Spatial Smoothing. In Proceedings of the 6th International Conference on Radar (RADAR 2011), Chengdu, China, 24–27 October 2011; pp. 312–314.
- Palanisamy, P.; Kalyanasundaram, N.; Swetha, P.M. Two-dimensional DOA estimation of coherent signals using acoustic vector sensor array. Signal Process. 2012, 92, 19–28. [Google Scholar] [CrossRef]
- Tayem, N. Estimation 2D DOA of Coherent Signals Using a New Antenna Array Configuration. In Proceedings of the 2012 IEEE Military Communications Conference (MILCOM 2012), Orlando, FL, USA, 29 October–1 November 2012; pp. 1–5.
- Ren, S.; Ma, X.; Yan, S.; Hao, C. 2-D unitary ESPRIT-like direction-of-arrival (DOA) estimation for coherent signals with a uniform rectangular array. Sensors 2013, 13, 4272–4288. [Google Scholar] [CrossRef] [PubMed]
- Si, W.J.; Li, X.L.; Wu, N. 2-D DOA Estimation of Improved Toeplitz Algorithms to Coherent Sources. In Proceedings of the 2nd International Conference on Instrumentation, Measurement, Computer, Communication and Control (IMCCC 2012), Harbin, China, 8–10 December 2012; pp. 1251–1254.
- Chen, H.; Zhang, X. Two-dimensional DOA estimation of coherent sources for acoustic vector-sensor array using a single snapshot. Wirel. Pers. Commun. 2013, 72, 1–13. [Google Scholar] [CrossRef]
- Chen, H.; Hou, C.P.; Wang, Q.; Huang, L.; Yan, W. Cumulants-based Toeplitz matrices reconstruction method for 2-D coherent DOA estimation. IEEE Sens. J. 2014, 14, 2824–2832. [Google Scholar] [CrossRef]
- Tao, H.; Xin, J.M.; Wang, J.S.; Zheng, N.; Sano, A. Two-dimensional direction estimation for a mixture of noncoherent and coherent signals. IEEE Trans. Signal Process. 2015, 63, 318–333. [Google Scholar] [CrossRef]
- Miron, S.; Yang, S.; Brie, D.; Wong, K. A multilinear approach of direction finding using a sensor-array with multiple scales of spatial invariance. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2057–2070. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Wong, K.T. Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid. IEEE Trans. Signal Process. 2000, 48, 2205–2210. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Direction-finding with sparse rectangular dual-size spatial invariance array. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1320–1336. [Google Scholar] [CrossRef]
- Wong, K.T.; Li, L.; Zoltowski, M.D. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 129–132. [Google Scholar] [CrossRef]
- Wong, K.T.; Zoltowski, M.D. Root-MUSIC-based azimuth-elevation angle-of-arrival estimation with uniformly spaced but arbitrarily oriented velocity hydrophones. IEEE Trans. Signal Process. 1999, 47, 3250–3260. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source location with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Hyder, M.M.; Mahata, K. Direction-of-arrival estimation using a mixed l2,0 norm appoximation. IEEE Trans. Signal Process. 2010, 58, 4646–4655. [Google Scholar] [CrossRef]
- Li, P.F.; Zhang, M.; Zhong, Z.F. Two dimensional DOA estimation based on sparse representation of space angle. J. Electron. Inform. Technol. 2011, 33, 2402–2406. (In Chinese) [Google Scholar] [CrossRef]
- Northardt, E.T.; Bilik, I.; Abramovich, Y.I. Spatial compressive sensing for direction-of-arrival estimation with bias mitigation via expected likelihood. IEEE Trans. Signal Process. 2013, 61, 1183–106. [Google Scholar] [CrossRef]
- Massa, A.; Rocca, P.; Oliveri, G. Compressive sensing in electromagnetics—A review. IEEE Antennas Propag. Mag. 2015, 57, 224–238. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inform. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process. 2006, 86, 589–602. [Google Scholar] [CrossRef]



| Algorithms | Single-Snapshot Case | Multiple Snapshots Case |
|---|---|---|
| DSR-OMP | ||
| DSR-BP | ||
| DSR-L1SVD | ||
| DRSR-SSRSD |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Mao, X.; Wang, Y.; Zhang, N.; Li, B. A Novel 2-D Coherent DOA Estimation Method Based on Dimension Reduction Sparse Reconstruction for Orthogonal Arrays. Sensors 2016, 16, 1496. https://doi.org/10.3390/s16091496
Wang X, Mao X, Wang Y, Zhang N, Li B. A Novel 2-D Coherent DOA Estimation Method Based on Dimension Reduction Sparse Reconstruction for Orthogonal Arrays. Sensors. 2016; 16(9):1496. https://doi.org/10.3390/s16091496
Chicago/Turabian StyleWang, Xiuhong, Xingpeng Mao, Yiming Wang, Naitong Zhang, and Bo Li. 2016. "A Novel 2-D Coherent DOA Estimation Method Based on Dimension Reduction Sparse Reconstruction for Orthogonal Arrays" Sensors 16, no. 9: 1496. https://doi.org/10.3390/s16091496
APA StyleWang, X., Mao, X., Wang, Y., Zhang, N., & Li, B. (2016). A Novel 2-D Coherent DOA Estimation Method Based on Dimension Reduction Sparse Reconstruction for Orthogonal Arrays. Sensors, 16(9), 1496. https://doi.org/10.3390/s16091496






