On-Chip Magnetic Bead Manipulation and Detection Using a Magnetoresistive Sensor-Based Micro-Chip: Design Considerations and Experimental Characterization
Abstract
:1. Introduction
2. Theoretical Basis
3. Materials and Methods
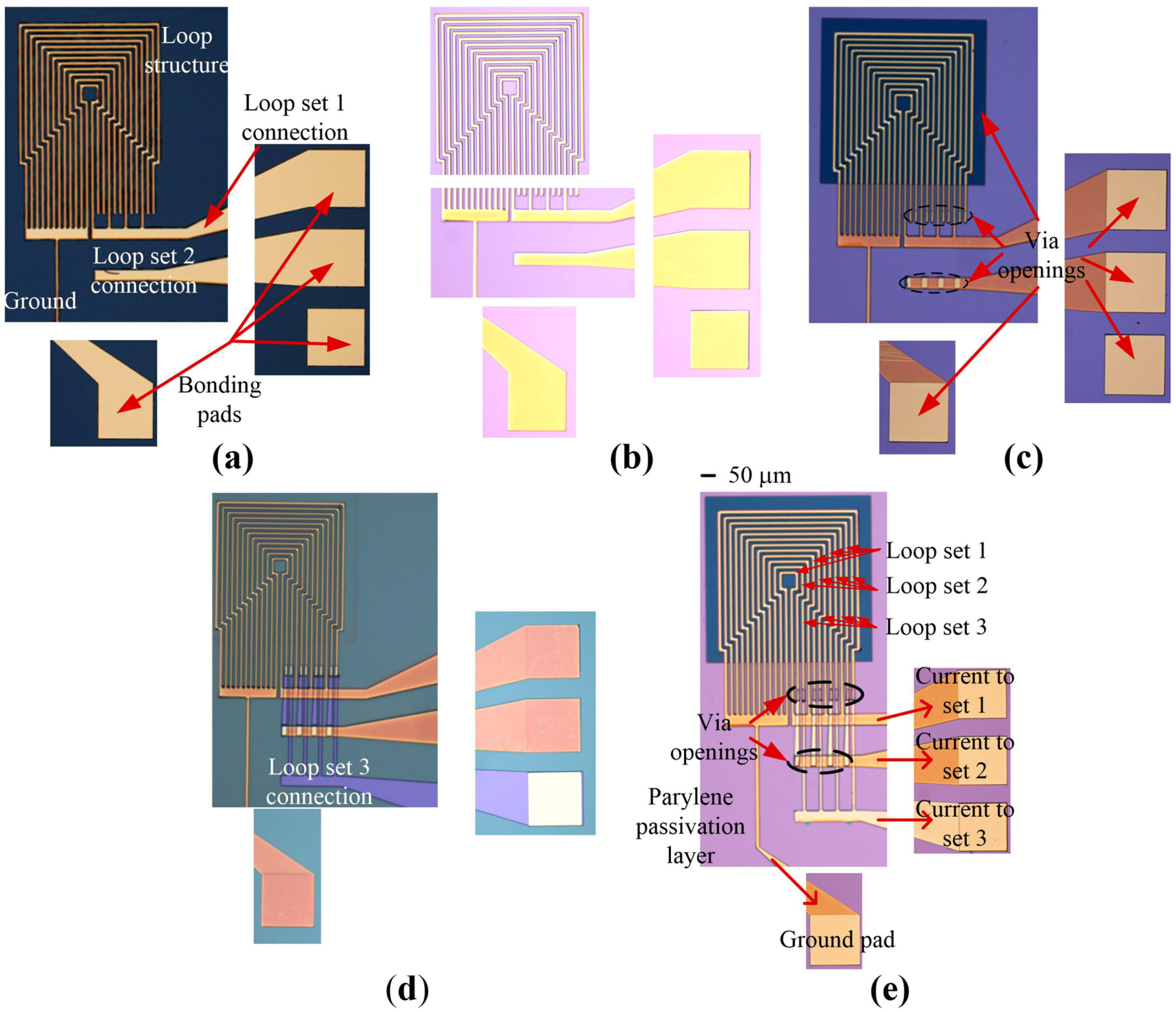
3.1. Fabrication of the Magnetic Actuator
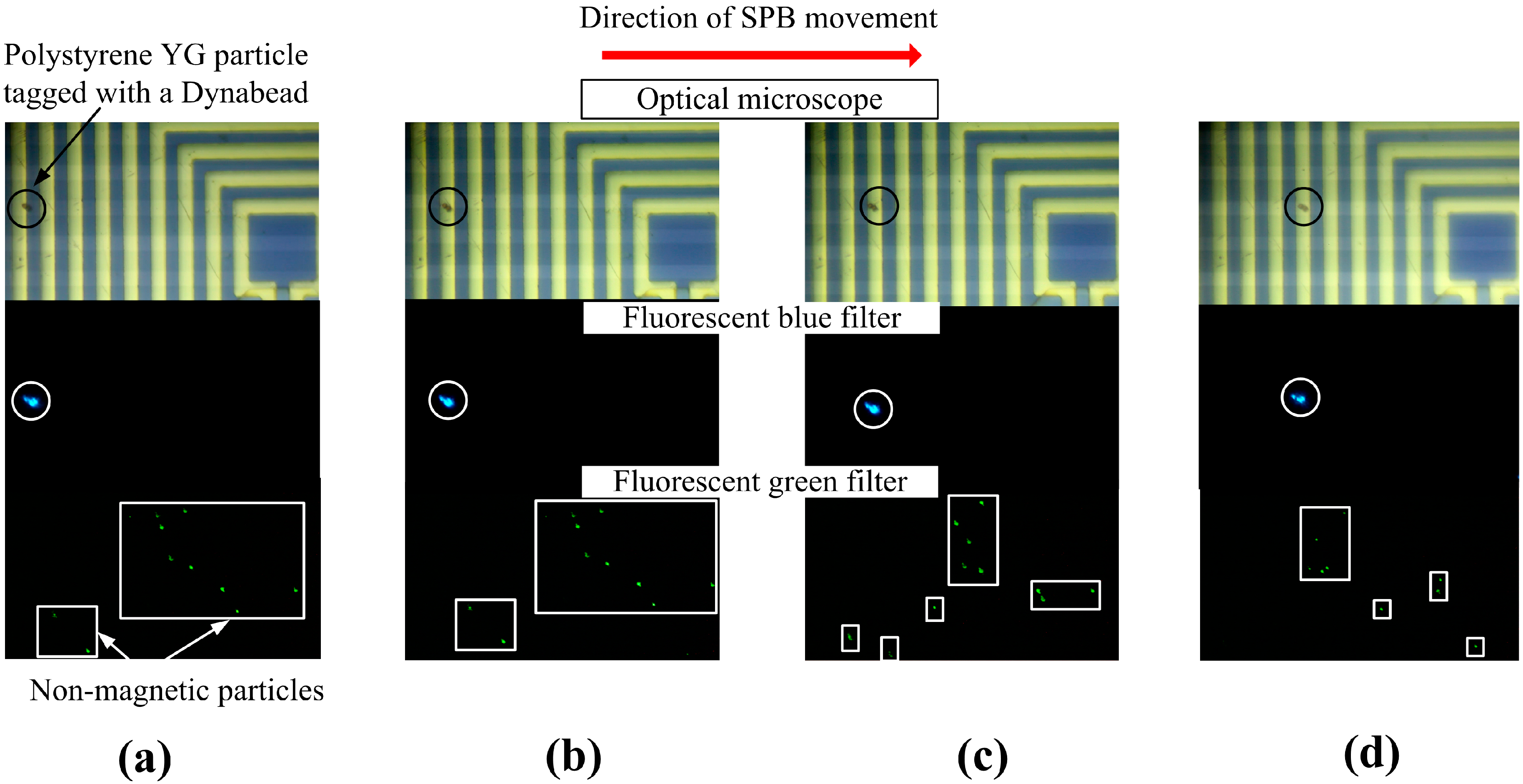
3.2. Sample Preparation and Experimental Setup for SPB Manipulation
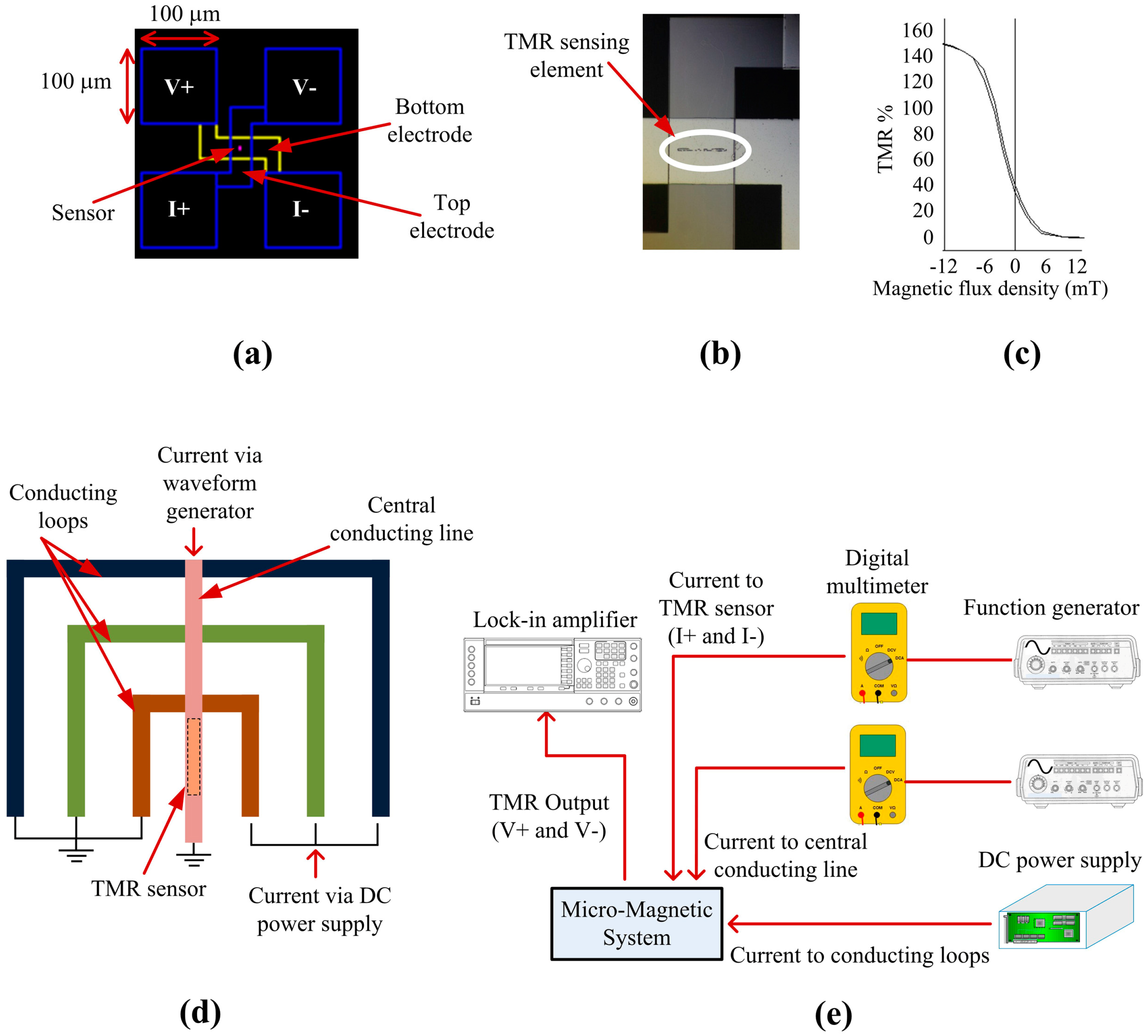
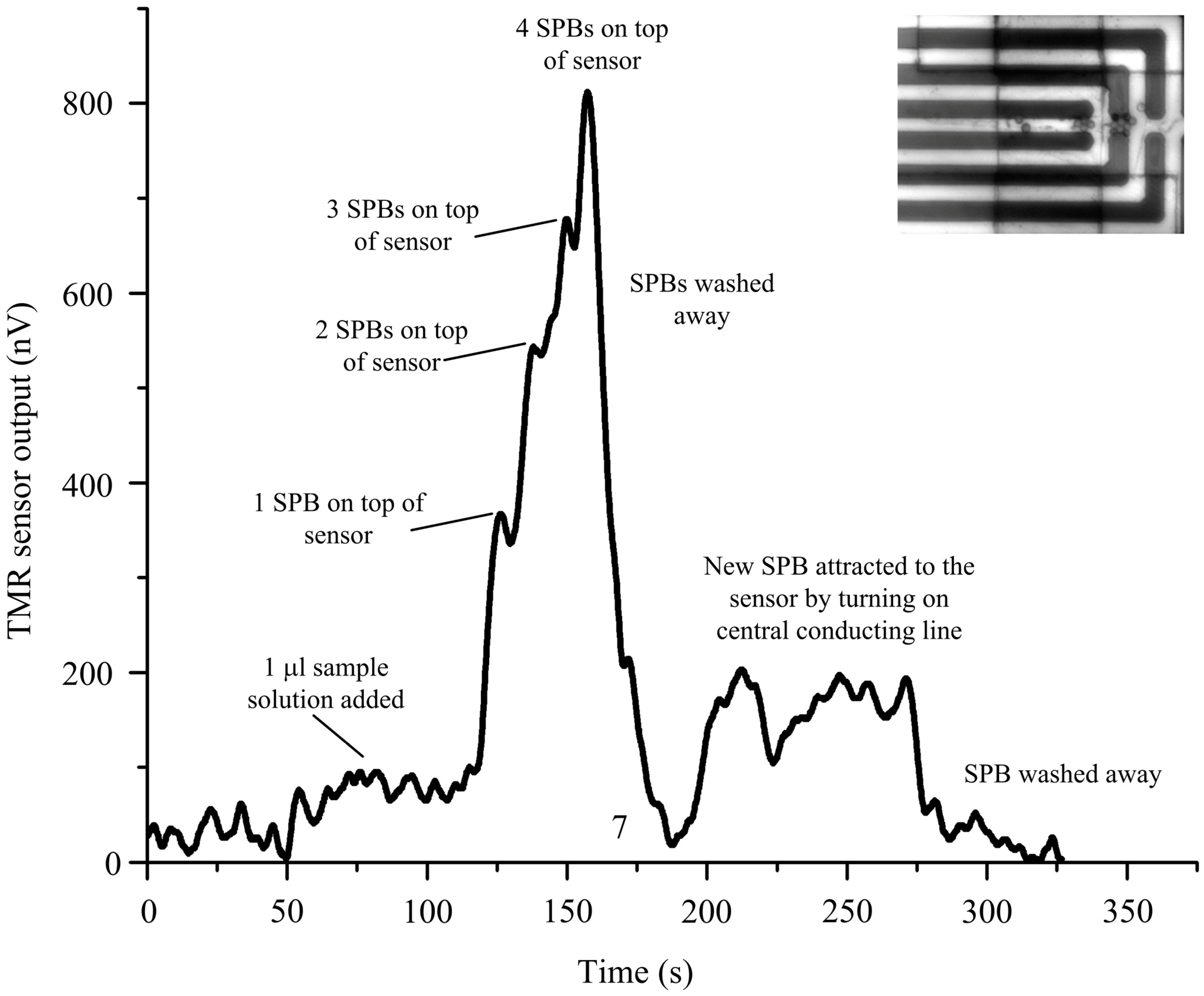
3.3. TMR Sensor Integration and Experimental Setup for Magnetic Bead Detection
4. Results
4.1. Numerical Results
4.2. Experimental Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
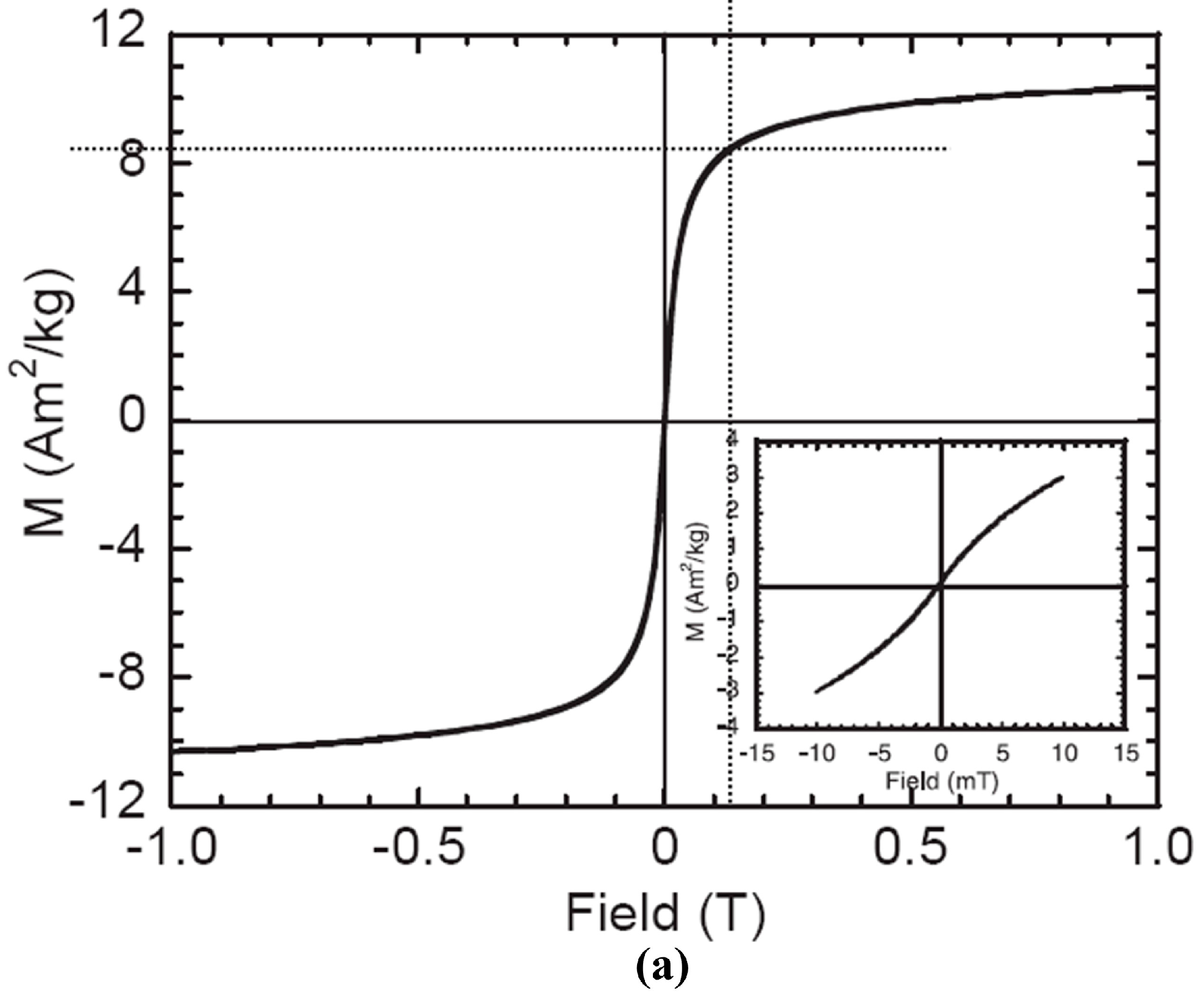
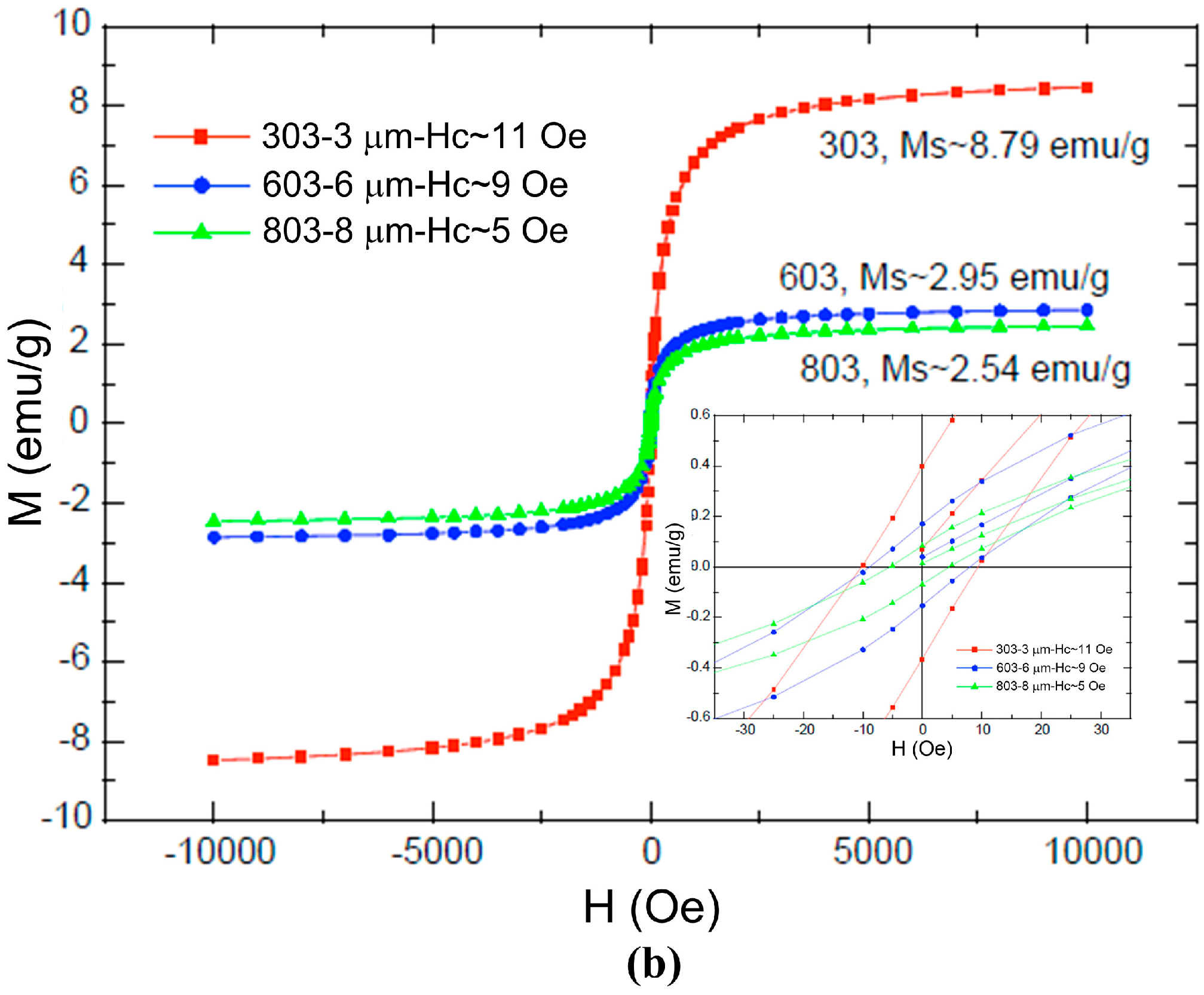
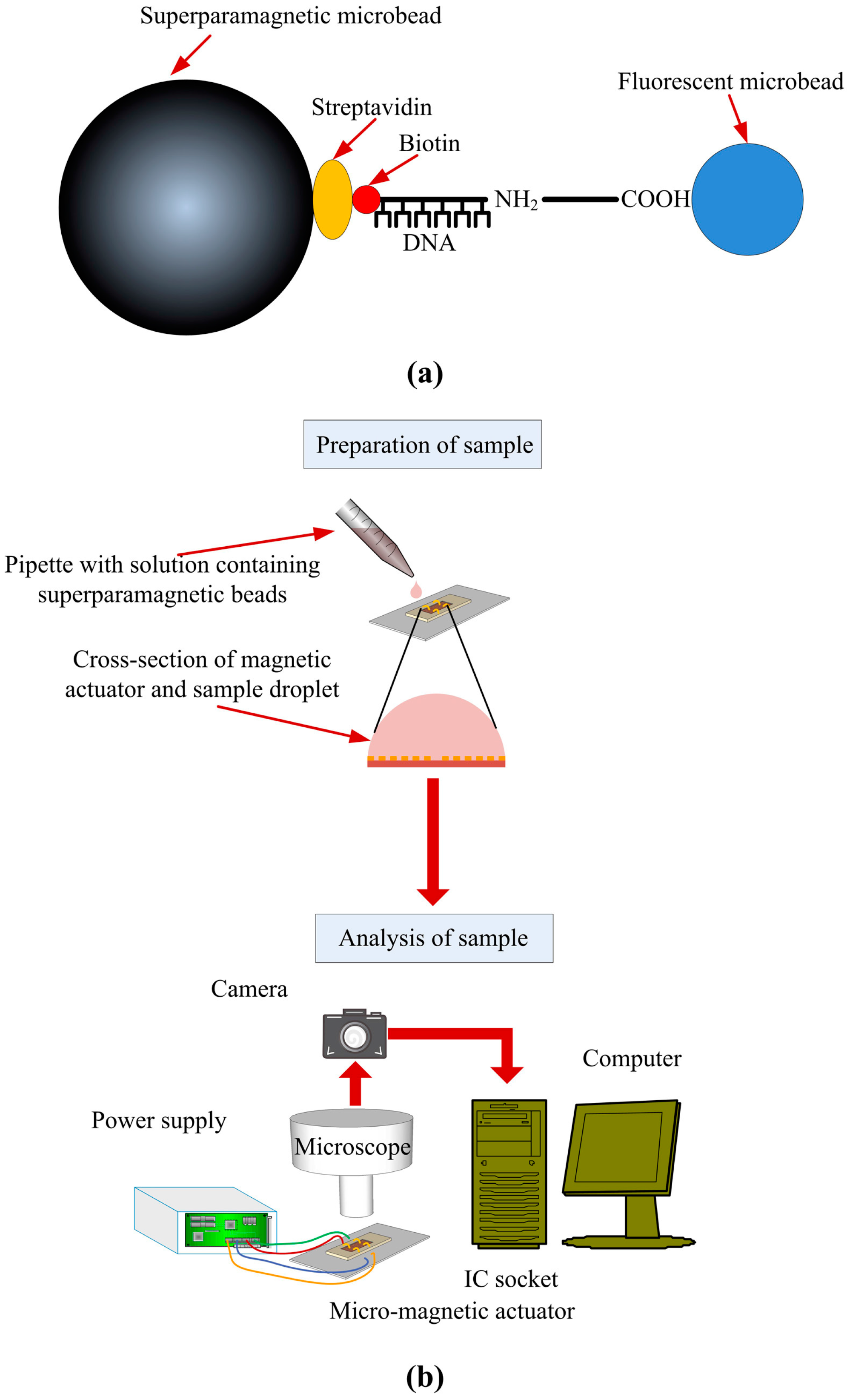
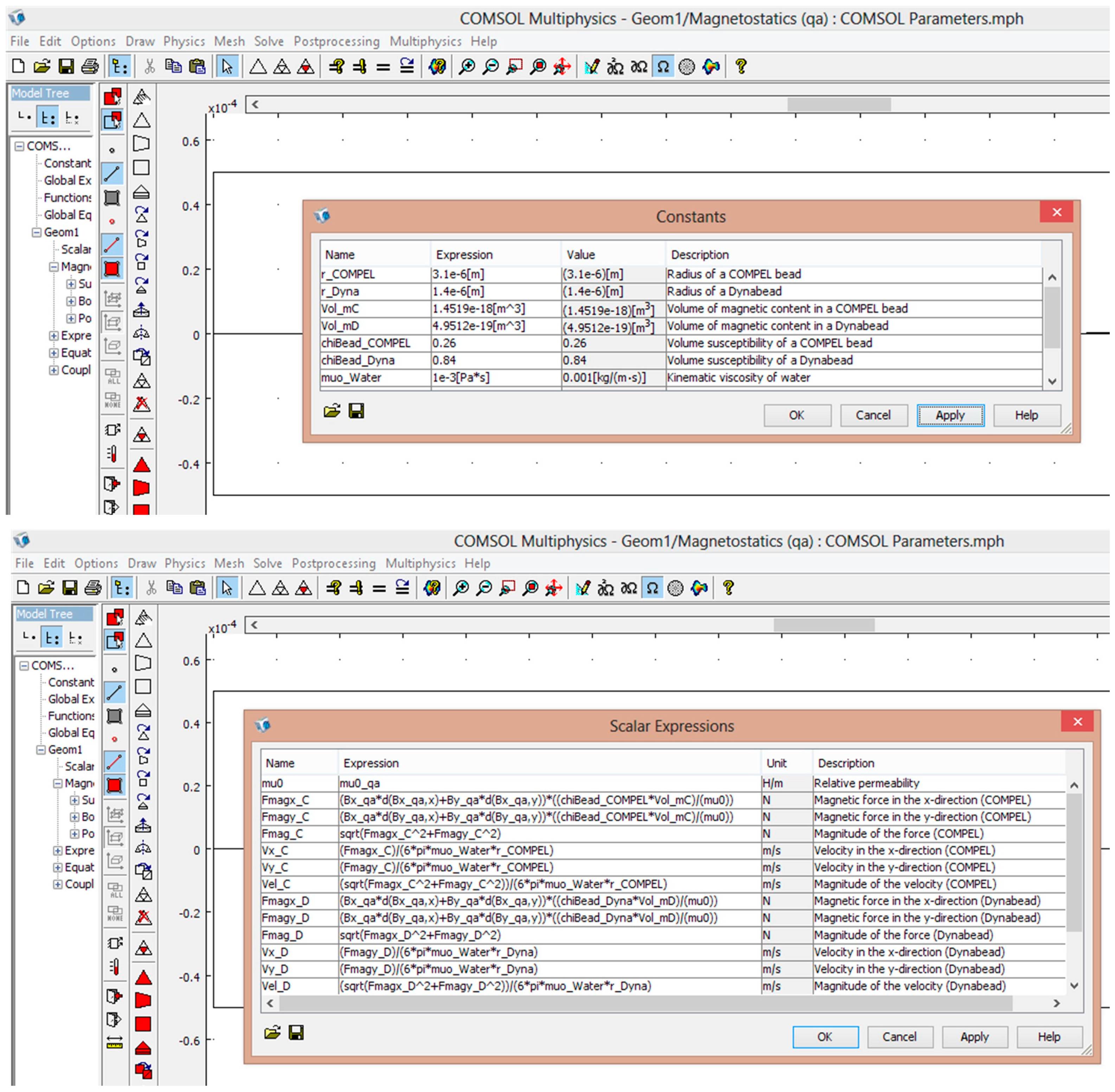

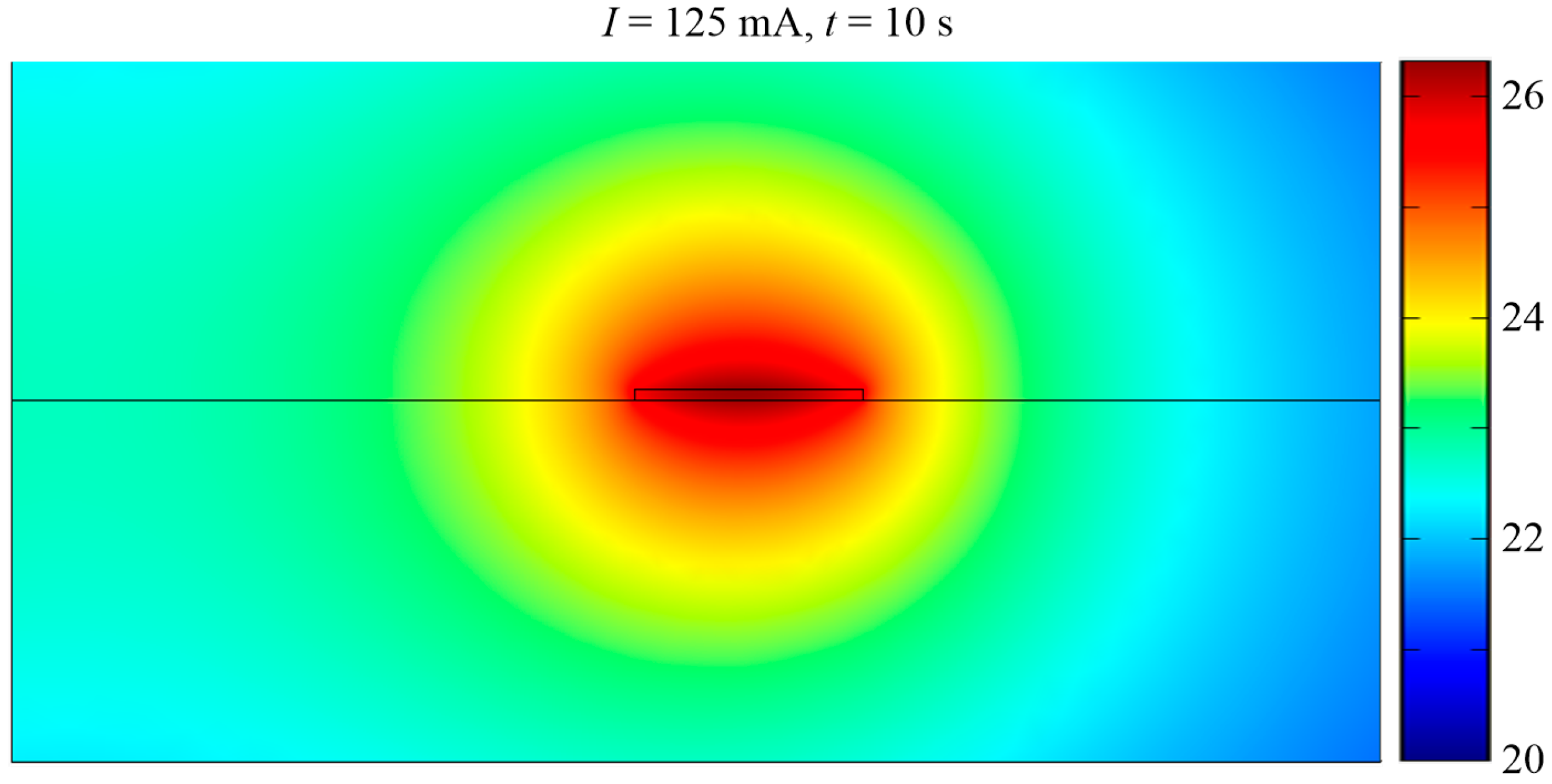
| Material | Thermal Conductivity (W/m·K) | Density | Material | Thermal conductivity (W/m·K) |
|---|---|---|---|---|
| Water | 130 | 2329 | 700 | - |
| Silicon | 0.58 | 1000 | 4183 | - |
| Gold | 317 | 19300 | 129 | Q × t |
References
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D: Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Ehresmann, A.; Koch, I.; Holzinger, D. Manipulation of Superparamagnetic Beads on Patterned Exchange-Bias Layer Systems for Biosensing Applications. Sensors 2015, 15, 28854–28888. [Google Scholar] [CrossRef] [PubMed]
- Gijs, M.A.M.; Lacharme, F.; Lehmann, U. Microfluidic applications of magnetic particles for biological analysis and catalysis. Chem. Rev. 2010, 110, 1518–1563. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Wang, H.; Li, S.; Wen, W. Applications of Micro/Nanoparticles in Microfluidic Sensors: A Review. Sensors 2014, 14, 6952–6964. [Google Scholar] [CrossRef] [PubMed]
- Yassine, O.; Gooneratne, C.P.; Smara, D.A.; Li, F.; Mohammed, H.; Merzaban, J.; Kosel, J. Isolation of cells for selective treatment and analysis using a magnetic microfluidic chip. Biomicrofluidics 2014, 8, 034114. [Google Scholar] [CrossRef] [PubMed]
- Sakaki, K.; Foulds, I.G.; Liu, W.; Dechev, N.; Burke, R.D.; Park, E.J. RoboSCell: An automated single cell arraying and analysis instrument. Biomed. Microdevices 2009, 11, 1317–1330. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Dechev, N.; Foulds, I.G.; Burke, R.; Parameswaran, A.; Park, E.J. A novel permalloy based magnetic single cell micro array. Lab Chip 2009, 9, 2381–2390. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Kosel, J. An efficient biosensor made of an electromagnetic trap and a magneto-resistive sensor. Biosens. Bioelectron. 2014, 59, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Sofla, A.; Cirkovic, B.; Hsieh, A.; Miklas, J.W.; Filipovic, N.; Radisic, M. Enrichment of live unlabelled cardiomyocytes from heterogeneous cell populations using manipulation of cell settling velocity by magnetic field. Biomicrofluidics 2013, 7, 014110. [Google Scholar] [CrossRef] [PubMed]
- Gooneratne, C.P.; Yassine, O.; Giouroudi, I.; Kosel, J. Selective Manipulation of Superparamagnetic Beads by a Magnetic Microchip. IEEE Trans. Magn. 2013, 49, 3418–3421. [Google Scholar] [CrossRef]
- Darabi, J.; Guo, C. On-chip magnetophoretic isolation of CD4 + T cells from blood. Biomicrofluidics 2013, 7, 054106. [Google Scholar] [CrossRef] [PubMed]
- Tarn, M.D.; Peyman, S.A.; Pamme, N. Simultaneous trapping of magnetic and diamagnetic particle plugs for separations and bioassays. RSC Adv. 2013, 3, 7209–7214. [Google Scholar] [CrossRef]
- Pamme, N. Magnetism and Microfluidics. Lab Chip 2006, 6, 24–38. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Stakenborg, T.; Peeters, S.; Lagae, L. Cell manipulation with magnetic particles toward microfluidic cytometry. J. Appl. Phys. 2009, 105, 102014. [Google Scholar] [CrossRef]
- Suwa, M.; Watarai, H. Magnetoanalysis of micro/nanoparticles: A review. Anal. Chim. Acta 2011, 690, 137–147. [Google Scholar] [CrossRef] [PubMed]
- Donolato, M.; Vavassori, P.; Gobbi, M.; Deryabina, M.; Hansen, M.F.; Metlushko, V.; Ilic, B.; Cantoni, M.; Petti, D.; Brivio, S.; et al. On-Chip Manipulation of Protein-Coated Magnetic Beads via Domain-Wall Conduits. Adv. Mater. 2010, 22, 2706–2710. [Google Scholar] [CrossRef] [PubMed]
- Anandakumar, S.; Rani, V.S.; Oh, S.; Sinha, B.L.; Takahashi, M.; Kim, C. Translocation of bio-functionalized magnetic beads using smart magnetophoresis. Biosens. Bioelectron. 2010, 26, 1755–1758. [Google Scholar] [CrossRef] [PubMed]
- Rapoport, E.; Montana, D.; Beach, G.S.D. Integrated capture, transport, and magneto-mechanical resonant sensing of superparamagnetic microbeads using magnetic domain walls. Lab Chip 2012, 12, 4433–4440. [Google Scholar] [CrossRef] [PubMed]
- Sushruth, M.; Ding, J.; Duczynski, J.; Woodward, R.C.; Begley, R.; Fanghor, H.; Fuller, R.O.; Adeyeye, A.O.; Kostylev, M.; Metaxas, P.J. Resonance-based Detection of Magnetic Nanoparticles and Microbeads Using Nanopatterned Ferromagnets. 2016; arXiv:1604.05835 [cond-mat.mes-hall]. [Google Scholar]
- Corte-León, H.; Krzysteczko, P.; Schumacher, H.W.; Manzin, A.; Cox, D.; Antonov, V.; Kazakova, O. Magnetic bead detection using domain wall-based nanosensor. J. Appl. Phys. 2015, 117, 17E313. [Google Scholar] [CrossRef]
- Quynh, L.K.; Tu, B.D.; Dang, D.X.; Viet, D.Q.; Hien, L.T.; Huong Giang, D.T.; Duc, N.H. Detection of magnetic nanoparticles using simple AMR sensors in Wheatstone bridge. J. Sci. Adv. Mat. Dev. 2016, 1, 98–102. [Google Scholar] [CrossRef]
- Monticelli, M.; Torti, A.; Cantoni, M.; Petti, D.; Albisetti, E.; Manzin, A.; Guerriero, E.; Sordan, R.; Gervasoni, G.; Carminati, M.; et al. On-Chip Magnetic Platform for Single-Particle Manipulation with Integrated Electrical Feedback. Small 2016, 17, 921–929. [Google Scholar] [CrossRef] [PubMed]
- Gooneratne, C.P.; Kurnicki, A.; Yamada, S.; Mukhopadhyay, S.C.; Kosel, J. Analysis of the Distribution of Magnetic Fluid inside Tumors by a Giant Magnetoresistance Probe. PLoS ONE 2013, 8, e81227. [Google Scholar] [CrossRef] [PubMed]
- Freitas, P.P.; Ferreira, H.A.; Graham, D.L.; Clarke, L.A.; Amaral, M.D.; Martins, V.; Fonseca, L.; Cabral, J.S. Magnetoelectronics; Johnson, M., Ed.; Academic: New York, NY, USA, 2004; pp. 331–386. [Google Scholar]
- Albon, C.; Weddemann, A.; Augel, A.; Rott, K.; Hütten, A. Tunneling magnetoresistance sensors for high resolutive particle detection. Appl. Phys. Lett. 2009, 95, 023101. [Google Scholar] [CrossRef]
- Cubells-Beltran, M.D.; Reig, C.; De Marcellis, A.; Figueras, E.; Yufera, A.; Zadov, B.; Paperno, E.; Cardoso, S.; Freitas, P.P. Monolithic integration of Giant Magnetoresistance (GMR) devices onto standard processed CMOS dies. Microelectron. J. 2014, 45, 702–707. [Google Scholar] [CrossRef]
- Wang, S.X.; Li, G. Advances in Giant Magnetoresistance Biosensors with Magnetic Nanoparticle Tags: Review and Outlook. IEEE. Trans. Magn. 2008, 44, 1687–1702. [Google Scholar] [CrossRef]
- Cubells-Beltrán, M.D.; Reig, C.; Madrenas, J.; De Marcellis, A.; Santos, J.; Cardoso, S.; Freitas, P.P. Integration of GMR Sensors with Different Technologies. Sensors 2016, 16, 939. [Google Scholar] [CrossRef] [PubMed]
- Gaster, R.S.; Xu, L.; Han, S.J.; Wilson, R.J.; Hall, D.A.; Osterfeld, S.J.; Yu, H.; Wang, S.X. Quantification of protein interactions and solution transport using high-density GMR sensor arrays. Nat. Nanotechnol. 2011, 6, 314–320. [Google Scholar] [CrossRef] [PubMed]
- Osterfeld, S.J.; Yu, H.; Gaster, R.S.; Caramuta, S.; Xu, L.; Han, S.J.; Hall, D.A.; Wilson, R.J.; Sun, S.; White, R.L.; et al. Multiplex protein assays based on real-time magnetic nanotag sensing. Proc. Natl. Acad. Sci. USA 2008, 105, 20637–20640. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.L.; Ferreira, H.A.; Feliciano, N.; Freitas, P.P.; Clarke, L.A.; Amaral, M.D. Magnetic field-assisted DNA hybridisation and simultaneous detection using micron-sized spin-valve sensors and magnetic nanoparticles. Sens. Actuators B 2005, 107, 936–944. [Google Scholar] [CrossRef]
- Ferreira, H.A.; Graham, D.L.; Feliciano, N.; Clarke, L.A.; Amaral, M.D.; Freitas, P.P. Detection of cystic fibrosis related DNA targets using AC field focusing of magnetic labels and spin-valve sensors. IEEE. Trans. Magn. 2005, 41, 4140–4142. [Google Scholar] [CrossRef]
- Rizzi, G.; Østerberg, F.W.; Dufva, M.; Hansen, M.F. Magnetoresistive sensor for real-time single nucleotidepolymorphism genotyping. Biosens. Bioelectron. 2014, 52, 445–451. [Google Scholar] [CrossRef] [PubMed]
- Koets, M.; van der Wijk, T.; van Eemeren, J.T.W.M.; van Amerongen, A.; Prins, M.W.J. Rapid DNA multi-analyte immunoassay on a magneto-resistance biosensor. Biosens. Bioelectron. 2009, 24, 1893–1898. [Google Scholar] [CrossRef] [PubMed]
- Mak, A.C.; Osterfeld, S.J.; Yu, H.; Wang, S.X.; Davis, R.W.; Jejelowo, O.A.; Pourmand, N. Sensitive giant magnetoresistive-based immunoassay for multiplex mycotoxin detection. Biosens. Bioelectron. 2009, 25, 1635–1639. [Google Scholar] [CrossRef] [PubMed]
- Kokkinis, G.; Cardoso, S.F.; Cardoso, F.A.; Giouroudi, I. Microfluidics for the Rapid Detection of Pathogens Using Giant Magnetoresistance Sensors. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.R.; Shen, E.; Wang, S.X. Modeling and experiments of magneto-nanosensors for diagnostics of radiation exposure and cancer. Biomed. Microdevices 2013, 15, 665–671. [Google Scholar] [CrossRef] [PubMed]
- Loureiro, J.; Andrade, P.Z.; Cardoso, S.; da Silva, C.L.; Cabral, J.M.; Freitas, P.P. Magnetoresistive chip cytometer. Lab Chip 2011, 11, 2255–2261. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.Q.; Li, L.; Li, G.J.; Leung, C.W.; Shi, J.; Wong, C.M.; Lo, K.C.; Chan, W.K.; Mak, C.S.K.; Chan, S.B.; et al. Liver cancer immunoassay with magnetic nanoparticles and MgO-based magnetic tunnel junction sensors. J. Appl. Phys. 2012, 111, 07E505. [Google Scholar] [CrossRef]
- Gaster, R.S.; Hall, D.A.; Wang, S.X. nanoLAB: An ultraportable, handheld diagnostic laboratory for global health. Lab Chip 2011, 11, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Chen, S.; Qiu, Y.; Zhang, S.; Shi, S.; Gao, Y. A fully automated in vitro diagnostic system based on magnetic tunnel junction arrays and superparamagnetic particles. J. Appl. Phys. 2012, 111, 07B315. [Google Scholar] [CrossRef]
- Schotter, J.; Shoshi, A.; Brueckl, H. Development of a magnetic lab-on-a-chip for point-of-care sepsis diagnosis. J. Magn. Magn. Mater. 2009, 321, 1671–1675. [Google Scholar] [CrossRef]
- Weddemann, A.; Albon, C.; Auge, A.; Wittbracht, F.; Hedwig, P.; Akemeier, D.; Rott, K.; Meißner, D.; Jutzi, P.; Hütten, A. How to design magneto-based total analysis systems for biomedical applications. Biosens. Bioelectron. 2010, 26, 1152–1163. [Google Scholar] [CrossRef] [PubMed]
- Lagae, L.; Wirix-Speetjens, R.; Das, J.; Graham, D.; Ferreira, H.; Freitas, P.P.F.; Borghs, G.; De Boeck, J. On-chip manipulation and magnetization assessment of magnetic bead ensembles by integrated spin-valve sensors. J. Appl. Phys. 2002, 91, 7445–7447. [Google Scholar] [CrossRef]
- Wirix-Speetjens, R.; Fyen, W.; De Boeck, J.; Borghs, G. Single magnetic particle detection: Experimental verification of simulated behavior. J. Appl. Phys. 2006, 99, 103903. [Google Scholar] [CrossRef]
- Wirix-Speetjens, R.; Reekmans, G.; De Palma, R.; Liu, C.; Laureyn, W.; Borghs, G. Magnetoresistive biosensors based on active guiding of magnetic particles towards the sensing zone. Sens. Actuators B. 2007, 128, 1–4. [Google Scholar] [CrossRef]
- Megens, M.; Prins, M. Magnetic biochips: A new option for sensitive diagnostics. J. Magn. Magn. Mater. 2005, 293, 702–708. [Google Scholar] [CrossRef]
- Van Ommering, K.; Lamers, C.C.H.; Nieuwenhuis, J.H.; van IJzendoorn, L.J.; Prins, M.W.J. Analysis of individual magnetic particle motion near a chip surface. J. Appl. Phys. 2009, 105, 104905. [Google Scholar] [CrossRef]
- Gooneratne, C.P.; Giouroudi, I.; Liang, C.; Kosel, J. A giant magnetoresistance ring-sensor based microsystem for magnetic bead manipulation and detection. J. Appl. Phys. 2011, 109, 07E517. [Google Scholar] [CrossRef]
- Gooneratne, C.P.; Liang, C.; Kosel, J. A planar conducting microstructure to guide and confine magnetic beads to a sensing zone. Microelectron. Eng. 2011, 88, 1757–1760. [Google Scholar] [CrossRef]
- Gooneratne, C.P.; Giouroudi, I.; Kosel, J. A planar conducting micro-loop structure for transportation of magnetic beads: An approach towards rapid sensing and quantification of biological entities. Sens. Lett. 2011, 10, 770–774. [Google Scholar] [CrossRef]
- Donolato, M.; Dalslet, B.T.; Hansen, M.K. Microstripes for transport and separation of magnetic particles. Biomicrofluidics 2012, 6, 024110. [Google Scholar] [CrossRef] [PubMed]
- Kokkinis, G.; Keplinger, F.; Giouroudi, I. On-chip microfluidic biosensor using superparamagnetic microparticles. Biomicrofluidics 2013, 7, 054117. [Google Scholar] [CrossRef] [PubMed]
- Gooneratne, C.P.; Liang, C.; Giouroudi, I.; Kosel, J. An integrated micro-chip for rapid detection of magnetic particles. J. Appl. Phys. 2012, 111, 07B327. [Google Scholar] [CrossRef]
- Li, F.; Kodzius, R.; Gooneratne, C.P.; Foulds, I.; Kosel, J. Magneto-mechanical trapping systems for biological target detection. Microchim. Acta 2014, 181, 1743–1748. [Google Scholar] [CrossRef]
- Fonnum, G.; Johansson, C.; Molteberg, A.; Mørup, S.; Aksnes, E. Characterisation of Dynabeads® by magnetization measurements and Mössbauer spectroscopy. J. Magn. Magn. Mater. 2005, 293, 41–47. [Google Scholar] [CrossRef]
- Bangs Laboratories, Inc.™. Available online: https://www.bangslabs.com (accessed on 18 March 2016).
- Ruffert, C. Magnetic Bead—Magic Bullet. Micromachines 2016, 7, 21. [Google Scholar] [CrossRef]
- Henriksen, A.D.; Ley, M.W.H.; Flyvbjerg, H.; Hansen, M.F. Configurational Statistics of Magnetic Bead Detection with Magnetoresistive Sensors. PLoS ONE 2015, 10, e0141115. [Google Scholar] [CrossRef] [PubMed]



| Bead Type | Radius (m) × 10−6 | Volume (m3) × 10−16 | Density (g/m3) × 106 | Mass (g) × 10−10 | Magnetic Content (%) | Mass of Magnetic Content (g) × 10−12 | Volume of Magnetic Content (m3) × 10−18 | Volume Susceptibility |
|---|---|---|---|---|---|---|---|---|
| COMPELTM | 3.1 | 1.2479 | 1.1 | 1.3727 | 5.5 | 7.5499 | 1.4519 | 0.26 |
| Dynabead® | 1.4 | 0.11494 | 1.6 | 0.1839 | 14 | 2.5746 | 0.49512 | 0.84 |
| Bead Type | Method | 5 μm | 10 μm | 15 μm | 20 μm |
|---|---|---|---|---|---|
| COMPEL™ | Dipole approximation | 0.9 s | 7.47 | 30.59 | 101.7 |
| Volume integration | 3.9 | 18.7 | 60.6 | 164.8 | |
| Dynabead® | Dipole approximation | 0.36 | 3.06 | 12.54 | 41.7 |
| Volume integration | 0.75 | 4.72 | 17.3 | 55.79 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gooneratne, C.P.; Kodzius, R.; Li, F.; Foulds, I.G.; Kosel, J. On-Chip Magnetic Bead Manipulation and Detection Using a Magnetoresistive Sensor-Based Micro-Chip: Design Considerations and Experimental Characterization. Sensors 2016, 16, 1369. https://doi.org/10.3390/s16091369
Gooneratne CP, Kodzius R, Li F, Foulds IG, Kosel J. On-Chip Magnetic Bead Manipulation and Detection Using a Magnetoresistive Sensor-Based Micro-Chip: Design Considerations and Experimental Characterization. Sensors. 2016; 16(9):1369. https://doi.org/10.3390/s16091369
Chicago/Turabian StyleGooneratne, Chinthaka P., Rimantas Kodzius, Fuquan Li, Ian G. Foulds, and Jürgen Kosel. 2016. "On-Chip Magnetic Bead Manipulation and Detection Using a Magnetoresistive Sensor-Based Micro-Chip: Design Considerations and Experimental Characterization" Sensors 16, no. 9: 1369. https://doi.org/10.3390/s16091369
APA StyleGooneratne, C. P., Kodzius, R., Li, F., Foulds, I. G., & Kosel, J. (2016). On-Chip Magnetic Bead Manipulation and Detection Using a Magnetoresistive Sensor-Based Micro-Chip: Design Considerations and Experimental Characterization. Sensors, 16(9), 1369. https://doi.org/10.3390/s16091369






